广州二模试卷高清打印版

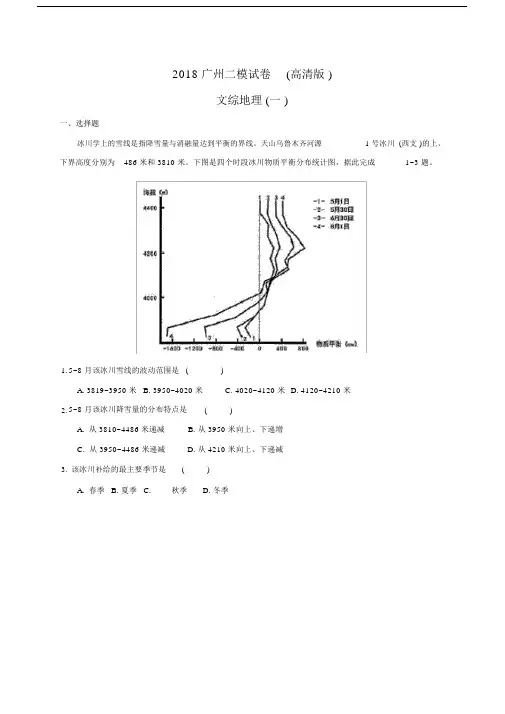
2018 广州二模试卷(高清版 )文综地理 (一 )一、选择题冰川学上的雪线是指降雪量与消融量达到平衡的界线。

天山乌鲁木齐河源 1 号冰川下界高度分别为486 米和 3810 米。

下图是四个时段冰川物质平衡分布统计图，据此完成(西支 )的上、1~3 题。

1. 5~8 月该冰川雪线的波动范围是 ( )A. 3819~3950 米B. 3950~4020 米C. 4020~4120 米D. 4120~4210 米2. 5~8 月该冰川降雪量的分布特点是( )A. 从 3810~4486 米递减B. 从 3950 米向上、下递增C. 从 3950~4486 米递减D. 从 4210 米向上、下递减3. 该冰川补给的最主要季节是( )A. 春季B. 夏季C. 秋季D. 冬季2017 年 12 月我国成功进行了开发干热岩资源实验。

干热岩是指埋藏于地下3~10 千米，没有水或蒸汽，致密不渗透，温度在 150℃以上的高温岩体。

它是一种新兴地热资源，可广泛用于发电、供暖等。

据此完成 4~6 题。

4. 干热岩主要属于 ( )A. 岩浆B. 喷出岩C. 沉积岩D. 侵入岩5. 我国干热岩最主要分布在()A.东南沿海B. 华北地区C. 西北内陆D.青藏高原6. 与传统地热资源相比，干热岩( )A.开发难度小，成本低B. 埋藏较浅，分布广C. 无季节变化，污染少D. 产业链短，效率低1946~1964 年美国出生婴儿高达7600 万人，这个群体被称为“婴儿潮一代”。

“婴儿潮一代”对美国的政治、经济、文化有着巨大的影响。

下图是1970 年和2000 年美国人口年龄金字塔统计图，据此完成 7~8 题。

7. 引起“婴儿潮一代”人口高增长率的最主要原因是 ( )A. 战后经济恢复和发展B. 鼓励生育的人口政策C. 实行宽松的移民政策D. 新时期科学技术革命8. 随着“婴儿潮一代”步入中年期，美国人口增长特点转变为()A. 快速增长B. 负增长C. 稳定增长D. 零增长铁盖乡地处黄河上游龙羊峡地区，由于气候变化、超载放牧等原因，土地沙漠化率高达 98.5%。

2025届广东省广州市教研室高三二诊模拟考试语文试卷注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。

用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。

将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

1、阅读下面的小说，完成下列小题。

老街担家刘建超老街的清晨，有两种人最忙碌：挑担卖菜的和担尿赶路的。

老街人嘴刁，吃菜讲究新鲜水灵。

卖菜的主直接从菜园里摘得新鲜蔬菜，在潺河边淘洗去泥沙，用稻草绳绑扎结实，新鲜的叶子菜摆放在箩筐里，挑起担子沿街叫卖，吆喝声有板有眼、有腔有调。

老街从明末清初磕绊至今，沿街住户还用的是旱厕。

有的家用大水缸嵌入地下，有的家砌个池子。

每天早上，有专门担尿的人来家里清理茅厕的粪便。

起粪时臭味弥漫，为了不影响住户内眷生活，担尿人都起五更赶大早。

老街把一些手艺活做得精湛的人称为家，被称为家的就是最高赞誉了。

老街人厚道，将做担尿营生的人称为担家。

老干就是个担家。

可别小看了担家的活计，这可是个体力活也是个技术活。

说体力，担尿用的木桶，有六十厘米高，柏木做成，没有把子力气，担一副空桶也累得你脸红脖子粗。

老街住户的茅厕都建在后院，从后院到前街也有五十多米距离。

如果是二进院或三进院，那就是百十米长的距离，担起尿桶要一鼓作气，举步生风，一路小跑，没有个硬扎的身板儿可不中。

说技术，担起木桶途中不能让桶里的污物溅出来，否则就弄脏了住家的院儿，即便用水冲洗，那气味大半天散不了，很是影响人家的情绪。

★启用前注意保密2024年广州市普通高中毕业班综合测试(二)语文本试卷共10页，23小题，满分150分。

考试用时150分钟。

注意事项：1.答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号、试室号、座位号填写在答题卡上，用2B铅笔将试卷类型(B)填涂在答题卡的相应位置上，并在答题卡相应位置上填涂考生号。

2.作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上、3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上：如需改动，先划掉原来的答案，然后再写上新答案：不准使用铅笔和涂改液。

不按以上要求作答无效。

4.考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、现代文阅读(35分)(一)现代文阅读1(本题共5小题，17分)阅读下面的文字，完成1～5题。

在人类历史上，大概没有哪个地城、哪个族群的人，比生活在华夏大地上的人们更喜欢筑城了。

“无邑不城”,只要是人扎堆的地方就得围起来。

学术界也一般把“无邑不城”作为中国古代都城的一个显著特色来加以强调：“城墙是构成都城的基本要素，没有‘城墙’的都城实际上是不存在的。

”但如果我们说，从二里头文化诞生到汉代，在这两千余年的绝大部分时间里，都城(都邑)是没有城墙的，甚至可以说是不设防的，你相信吗?“大都无城”,就是我们对汉代及其以前中国古代都城形态的概括。

要讲清这个问题，就要先了解城市这个概念。

城市是一种区别于乡村的聚落形态，出现于人类社会发展的高级阶段。

是国家与前国家社会的关健区分点。

古代城市往往是区城或社会组织的中心，作为国家权力中心的都城就是这类城市的重中之重。

可见城市的本质特征中并不包含城墙，有没有城墙是从空间布局、从有无防御设施角度来说的，并不是所有的城市都有城墙。

考古学所观察到的现象是，在中国城市发展的早期阶段，并非所有的城市都有防御设施(城墙),“大都无城”概念的提出，正是出于这样的观察。

广东广州市届高三第二次模拟考试语文试题Word版含答案试卷类型：A）年广州市普通高中毕业班综合测试（二）语文试题本试卷共10页，22小题，满分150分。

考试用时150分钟。

注意事项：1．答题前，考生先将自已所在县（市、区）、姓名、试室号、座位号和考生号填写清楚，将条形码粘贴在指定区域。

2．选择题每小题选出答案后，用2B铅笔把答题卷上对应题目的答案标号涂黑，如需改动请先用橡皮擦擦干净，再选涂其他答案标号。

主观题请用黑色墨水签字笔在答题卷上作答。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．考试结束，监考人员将试卷、答题卷一并收回。

5．保持答题卷清洁，不要折叠、不要弄破。

一、现代文阅读（36分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1～3题。

“天下”是中国传统文化对世界秩序的一种原初想象，“天下主义”是以“天下”理念为核心，由具有普遍性和开放性的世界秩序、价值规范与理想人格构成的思想体系。

在当今全球化语境之下，中国文化理念和文化战略的自觉自信体现的正是“天下主义”的精神内核。

文化自信首先是一种“以天下观天下”的世界观的自信。

《道德经》有云：“修之于天下，其德乃普。

故以身观身，以家观家，以乡观乡，以国观国，以天下观天下。

”“天下”是中国文化特有的思维尺度，是一个最宏大、最完备的分析单位，具有最广阔的容纳力。

面对差异性的多元文化格局，西方文化多以民族国家为基本单位，文化视域限于国家、民族内部，虽然也有关于世界的思考，比如斯多葛学派的“世界主义”等，但其思考方式是“以国家观世界”，与中国文化的立足点和尺度不同。

中国文化的“天下”蕴含了“天下无外”的理想，各个民族的历史文化在世界内部是平等共存的；中国文化依循“修身、齐家、治国、平天下”1 / 1。

2024年广东省广州二中中考语文二模试卷第一部分积累与运用（24分）一、（16分）1．（2分）下列词语中，每对加点字的读音都相同的一项是（）A．偏僻．/譬．如B．间．或/间．不容发C．屏．障/屏．气D．拙．劣/相形见绌．2．（2分）下列句子中，加点词语使用最恰当的一项是分（）A．电影《第二十条》的主创团队锋芒毕露．．．．，将镜头对准现实问题，唤起观众对法与情的思考。

B．面对教练的严厉批评，他诚惶诚恐．．．．地站在那里，生怕一句话说得不对就引来更大的责难。

C．“有作为者，定有不凡，要敢坚持做自己”，父亲的话，真是如雷贯耳．．．．，让我茅塞顿开。

D．运动会上，因为参赛同学受伤，小豪临时上场，借的运动服很不合身，真是捉襟见肘．．．．。

3．（2分）下列句子中，没有语病一项是（）A．“粤菜师傅”大赛不仅是一场传承粤菜文化的人文盛宴，还是一场追求卓越的厨艺比拼。

B．老人传承着克勤克俭的家风，铭记着言传，身教，以行动为榜样，影响和教育着家族后人。

C．“广州119”报警小程序无障碍救助通道上线，旨在打造一条高效、人性化的救助新通道。

D．忧国忧民的杜甫，因其深邃的诗篇铸就了诗史般的传奇，使之成为中国文人景仰的典范。

4．（8分）请结合语境，按照括号中的提示补全对话。

五一假期，小元回到家乡，看到爷爷和堂弟每天都在刷短视频，就收集了一些资料想找机会和他们聊一聊。

【小元收集的资料】短视频是指在各种新媒体平台上播放的、适合在移动状态和短时休闲状态下观看的、高频推送的视频内容，几秒到几分钟不等。

在人人都有摄像头的时代，短视频让每个人都可以成为突发事件的记录者和传播者。

人们本来用短视频“杀死碎片时间”，现在变成了人们“被碎片时间杀死”。

短视频占据了人们大量的时间乃至睡眠。

短视频时代，快速移动、快速切换的画面让孩子们来不及停下来思考，他们拥有大量的碎片化知识，却只是对网络信息的搬运，形成不了自己独特的认知。

【对话内容】爷爷：手都酸了，眼都干了，这短视频怎么这样让人欲罢不能呢？小元：爷爷，这是短视频的特点决定的。

绝密★启用前试卷类型：B 2024届广州市普通高中毕业班综合测试（二）物理本试卷共6页，15小题，满分100分。

考试用时75分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号、试室号和座位号填写在答题卡上。

用2B铅笔将试卷类型（B）填涂在答题卡相应位置上，并在答题卡相应位置上填涂考生号。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、单项选择题：本题共7小题，每小题4分，共28分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．如图，光电管接入电路，用紫外线照射光电管阴极时，发生了光电效应，回路中形成电流．下列说法正确的是A．电流方向为a→R→bB．电流方向为b→R→aC．光照时间越长，光电子的最大初动能越大D．入射光光强增大，光电子的最大初动能增大2．如图甲，由细线和装有墨水的容器组成单摆，容器底端墨水均匀流出．当单摆在竖直面内摆动时，长木板以速度v垂直于摆动平面匀速移动距离L，形成了如图乙的墨痕图案，重力加速度为g，则该单摆的摆长为A．B．C．D．22216v πgL222v πgLvπ4gLvπgL3．如图是O为圆心、AB为直径的透明圆盘截面，一束激光从空气中平行AB由C点射入圆盘，在B点反射后从D点平行AB射出．已知圆盘半径和AC距离相等，则该圆盘对激光的折射率为A．1.5B．2CD5．如图，一辆汽车以恒定速率通过圆弧拱桥，N为桥面最高处，则汽车A．在N处所受支持力大小大于其重力B．在N处所受支持力大小等于其重力C．从M到N过程所受支持力逐渐增大D．从M到N过程所受支持力逐渐减小6．如图，在墙内或地面埋有一根通有恒定电流的长直导线.为探测该导线的走向，现用一个与灵敏电流计（图中未画出）串联的感应线圈进行探测，结果如下表．忽略地磁场的影响，则该导线可能的走向是A．Oa方向B．Ob方向C．Oc方向D．Oe方向7．如图，汽车定速巡航（即速率不变）通过路面abcd ，t 1时刻经过b ，t 2时刻经过c ，t 3时刻经过d ．若汽车行驶过程所受空气阻力和摩擦阻力的大小不变，则该过程汽车的功率P 随时间t 变化的图像是二、多项选择题：本题共3小题，每小题6分，共18分。

【新结构】（广州二模）2024年广州市普通高中毕业班综合测试（二）数学试卷一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的选项中，只有一项是符合题目要求的.1.已知集合{}{}0,2,4,12A B x x ==∈-≥Z ，则()A B ⋂=Zð（）A.{}2 B.{}0,2 C.{}0,1,2 D.{}0,1,2,4【答案】B 【解析】【分析】求出B 中不等式的解集，找出解集中的整数解，确定出B Z ð即可得出答案．【详解】由12x -≥解得，1x ≤-或3x ≥，即{}13B x x x =∈≤-≥Z 或，{}{}130,1,2B x x =∈-<<=Z Z ð{}0,2,4A = ，(){}0,2A B ∴=Z ð.故选：B ．2.已知一批沙糖桔的果实横径（单位：mm ）服从正态分布()245,5N ，其中果实横径落在[]40,55的沙糖桔为优质品，则这批沙糖桔的优质品率约为（）（若()2,X N μσ~，则()0.6827P X μσμσ-≤≤+≈，()220.9545P X μσμσ-≤≤+≈）A.0.6827B.0.8186C.0.8413D.0.9545【答案】B 【解析】【分析】根据正态分布三段区间的概率值以及正态分布的性质求解即可．【详解】因为所种植沙糖桔的果实横径（单位：mm ）服从正态分布()245,5N ，其中45,5μσ==，所以果实横径在[]40,55的概率为()2P X μσμσ-≤≤+()()112222P X P X μσμσμσμσ=-≤≤++-≤≤+0.477250.341350.8186≈+=.故选：B ．3.某学校安排4位教师在星期一至星期五值班，每天只安排1位教师，每位教师至少值班1天，至多值班2天且这2天相连，则不同的安排方法共有（）A.24种 B.48种C.60种D.96种【答案】D 【解析】【分析】由2天相连的情况有4种，利用排列数即可求解.【详解】由题意，从星期一至星期五值，2天相连的情况有4种，则不同的安排方法共有444A 96=种.故选：D4.某次考试后，甲、乙、丙、丁四位同学讨论其中一道考题，各自陈述如下，甲说：我做错了；乙说：甲做对了；丙说：我做错了；丁说：我和乙中有人做对．已知四人中只有一位同学的解答是正确的，且只有一位同学的陈述是正确的，则解正确的同学是（）A.甲 B.乙C.丙D.丁【答案】C 【解析】【分析】分别假设甲、乙、丙、丁做对，结合题意分析推理，利用矛盾律得出结论．【详解】若甲做对了，则甲说错了，乙说对，丙也说对了，2人说对了，不满足条件；若乙做对了，则甲说对了，乙说错误，丙也说对了，2人说对了，不满足条件；若丙做对了，则甲说对了，乙说错了，丙也说错了，其中只有甲1人说对了，满足条件；若丁做对了，则丁、甲、丙都说对了，不满足条件；故做对的是丙，说对的是甲．故选：C.5.已知,,αβγ是三个不重合的平面，且,l m αγβγ== ，则下列命题正确的是（）A.若,αγβγ⊥⊥，则lm B.若l m ，则αβ∥C.若,αβγβ⊥⊥，则l m ⊥ D.若l m ⊥，则αβ⊥【答案】C 【解析】【分析】根据空间中线面位置关系的性质定理和判定定理可判断各选项的正误．【详解】若,αγβγ⊥⊥，则l m 或l 与m 相交，故A 错误；若lm ，则αβ∥或α与β相交，故B 错误；若,αβγβ⊥⊥，则l m ⊥，故C 正确；若l m ⊥，则α与β相交，不一定是垂直，故D 错误．故选：C ．6.若0x 是方程()()()()f g x g f x =的实数解，则称0x 是函数()y f x =与()y g x =的“复合稳定点”．若函数()(0xf x a a =>且1)a ≠与()22g x x =-有且仅有两个不同的“复合稳定点”，则a 的取值范围为（）A.0,2⎛⎫⎪ ⎪⎝⎭B.2,12⎛⎫⎪⎪⎝⎭C.(D.)+∞【答案】D 【解析】【分析】2222x x a a -=-即()222220xx a a a a -+=有两个不同实根，令x t a =，则222220t a t a -+=在()0,∞+上有两个不同实根，利用二次方程根的分布即可．【详解】()(0xf x a a => 且1)a ≠与()22g x x =-有且仅有两个不同的“复合稳定点”，2222x x a a -∴=-，即()222220x x a a a a -+=有两个不同实根，令x t a =，则222220t a t a -+=在()0,∞+上有两个不同实根，()22222Δ280220a a a a a ⎧=->⎪∴⇒>⇒>⎨>⎪⎩则a的取值范围为)∞+．故选：D ．7.已知函数π())(0,||2f x x ωϕωϕ=+><的部分图象如图所示，若将函数()f x 的图象向右平移(0)θθ>个单位后所得曲线关于y 轴对称，则θ的最小值为（）A.π8B.π4C.3π8D.π2【答案】A 【解析】【分析】根据给定的图象特征，结合五点法作图列式求出ω和ϕ，再根据图象的平移变换，以及图象的对称性即可得解.【详解】由π()14f =，得π2sin()42ωϕ+=，又点π(,1)4及附近点从左到右是上升的，则ππ2π,Z 44k k ωϕ+=+∈，由5π(08f =，点5π(,0)8及附近点从左到右是下降的，且上升、下降的两段图象相邻，得5ππ2π,Z 8k k ωϕ+=+∈，联立解得2ω=，π2π,Z 4k k ϕ=-+∈，而π||2ϕ<，于是π4ϕ=-，π()2sin(2)4f x x =-，若将函数()f x 的图像向右平移(0)θθ>个单位后，得到πsin(22)4y x θ=--，则ππ2π,Z 42k k θ--=-∈，而0θ>，因此3ππ,N 82k k θ=-+∈，所以当1k =时，θ取得最小值为π8.故选：A8.已知函数()f x 的定义域为R ，且()()()()11,02f x f x f x f ++-==，则()()2024f f +=（）A.1B.2C.3D.4【答案】A 【解析】【分析】根据题意分析可知()f x 为偶函数，结合偶函数可得()()210f x f x ++-=，进而可知6为()f x 的周期，赋值可知()21f =-，结合周期性运算求解.【详解】由题意可知：函数()f x 的定义域为R ，因为()()()11f x f x f x ++-=，则()()()11f x f x f x -++=-，可得()()=f x f x -，所以()f x 为偶函数，由()()()11f x f x f x ++-=可得()()()21f x f x f x ++-=+，即()()()21f x f x f x ++=+，整理得()()210f x f x ++-=，可得()()()()330f x f x f x f x ++-=++=，则()()630f x f x +++=，可得()()6f x f x +=，所以6为()f x 的周期，由()()()()11,02f x f x f x f ++-==，令0x =，可得()()()1201f f f +==，可得()11f =；令1x =，可得()()()2011f f f +==，可得()21f =-；所以()()()()202420121f f f f +=+=-+=．故选：A ．【点睛】方法点睛：函数的性质主要是函数的奇偶性、单调性和周期性以及函数图象的对称性，在解题中根据问题的条件通过变换函数的解析式或者已知的函数关系，推证函数的性质，根据函数的性质解决问题．二、多选题：本题共3小题，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得2分，有选错的得0分.9.已知函数()1ln 1x f x x x +=--，则（）A.()f x 的定义域为()0,∞+B.()f x 的图像在()()22f ,处的切线斜率为52C.()01f f x x ⎛⎫+⎪⎝⎭= D.()f x 有两个零点12,x x ，且121=x x 【答案】BCD 【解析】【分析】根据题意直接求出x 的范围即可判断A ；求出导函数，进而求得()2f '即可判断B ；求得1f x ⎛⎫ ⎪⎝⎭即可判断C ；易知()f x 的单调性，结合零点存在定理及C 即可判断D ．。

广东省广州市高考数学二模试卷（文科）一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={﹣1，0，1，2，3，4，5}，B={b|b=n2﹣1，n∈Z}，则A∩B=（）A．{﹣1，3}B．{0，3}C．{﹣1，0，3}D．{﹣1，0，3，5}2．若复数z满足（3﹣4i+z）i=2+i，则z=（）A．4+6i B．4+2i C．﹣4﹣2i D．﹣2+2i．3．已知命题p：∀x∈R，x2+ax+a2≥0（a∈R），命题q：，，则下列命题中为真命题的是（）A．p∧q B．p∨q C．（¬p）∨q D．（¬p）∧（¬q）4．执行如图所示的程序图，则输出的S值为（）A．4 B．3 C．﹣2 D．﹣35．函数f（x）=ln（|x|﹣1）+x的大致图象是（）A．B．C．D．6．在区间[﹣1，5]上随机地取一个实数a，则方程x2﹣2ax+4a﹣3=0有两个正根的概率为（）A．B．C．D．7．已知三条直线2x﹣3y+1=0，4x+3y+5=0，mx﹣y﹣1=0不能构成三角形，则实数m的取值集合为（）A．{﹣， } B．{，﹣ } C．{﹣，， } D．{﹣，﹣， } 8．已知两点A（﹣1，1），B（3，5），点C在曲线y=2x2上运动，则的最小值为（）A．2 B．C．﹣2 D．9．在棱长为2的正方体ABCD﹣A1B1C1D1中，M是棱A1D1的中点，过C1，B，M作正方体的截面，则这个截面的面积为（）A．B．C．D．10．数列{a n}满足a2=2，a n+（﹣1）n+1a n=1+（﹣1）n（n∈N*），S n为数列{a n}+2前n项和，S100=（）A．5100 B．2550 C．2500 D．245011．已知函数f（x）=2sin（ωx+）（ω＞0）的图象在区间[0，1]上恰有3个最高点，则ω的取值范围为（）A．[，）B．[，）C．[，）D．[4π，6π）12．如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的体积为（）A．B．C．D．16二、填空题已知双曲线（a＞0）的离心率为2，则a的值为．14．在各项都为正数的等比数列{a n}中，已知a1=2，，则数列{a n}的通项公式a n=．15．《孙子算经》是我国古代重要的数学著作，约成书于四、五世纪，传本的《孙子算经》共三卷，其中下卷：“物不知数”中有如下问题：“今有物，不知其数，三三数之，剩二；五五数之，剩三；七七数之，剩二，问：物几何？”其意思为：“现有一堆物品，不知它的数目，3个3个数，剩2个，5个5个数，剩3个，7个7个数，剩2个，问这堆物品共有多少个？”试计算这堆物品至少有个．16．已知函数，若f（3a﹣1）≥8f（a），则实数a的取值范围为．三、解答题（本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（12分）△ABC的内角A，B，C的对边分别为a，b，c，已知bcosC+bsinC=a．（Ⅰ）求角B的大小；（Ⅱ）若BC边上的高等于，求cosA的值．18．（12分）某中学为了解高中入学新生的身高情况，从高一年级学生中按分层抽样共抽取了50名学生的身高数据，分组统计后得到了这50名学生身高的频数分布表：身高（cm）分组[145，155）[155，165）[165，175）[175，185]男生频数15124女生频数71542（Ⅰ）在答题卡上作出这50名学生身高的频率分布直方图；（Ⅱ）估计这50名学生身高的方差（同一组中的数据用该组区间的中点值作代表）；（Ⅲ）现从身高在[175，185]这6名学生中随机抽取3名，求至少抽到1名女生的概率．19．（12分）如图，ABCD是边长为a的正方形，EB⊥平面ABCD，FD⊥平面ABCD，．（Ⅰ）求证：EF⊥AC；（Ⅱ）求三棱锥E﹣FAC的体积．20．（12分）已知定点F（0，1），定直线l：y=﹣1，动圆M过点F，且与直线l相切．（Ⅰ）求动圆M的圆心轨迹C的方程；（Ⅱ）过点F的直线与曲线C相交于A，B两点，分别过点A，B作曲线C的切线l1，l2，两条切线相交于点P，求△PAB外接圆面积的最小值．21．（12分）已知函数．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）若函数g（x）=f（x）+4x存在极小值点x0，且，求实数a的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程]22．（10分）在平面直角坐标系xOy中．已知直线l的普通方程为x﹣y﹣2=0，曲线C的参数方程为（θ为参数），设直线l与曲线C交于A，B 两点．（1）求线段AB的长（2）已知点P在曲线C上运动．当△PAB的面积最大时，求点P的坐标及△PAB 的最大面积．[选修4-5：不等式选讲]23．（I）已知a+b+c=1，证明（a+1）2+（b+1）2+（c+1）2≥；（Ⅱ）若对任总实数x，不等式|x﹣a|+|2x﹣1|≥2恒成立，求实数a的取值范围．广东省广州市高考数学二模试卷（文科）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={﹣1，0，1，2，3，4，5}，B={b|b=n2﹣1，n∈Z}，则A∩B=（）A．{﹣1，3}B．{0，3}C．{﹣1，0，3}D．{﹣1，0，3，5}【考点】1E：交集及其运算．【分析】化简集合B，根据交集的定义写出A∩B．【解答】解：集合A={﹣1，0，1，2，3，4，5}，B={b|b=n2﹣1，n∈Z}={﹣1，0，3，8，15，…，}，∴A∩B={﹣1，0，3}．故选：C．【点评】本题考查了交集的定义与应用问题，是基础题．2．若复数z满足（3﹣4i+z）i=2+i，则z=（）A．4+6i B．4+2i C．﹣4﹣2i D．﹣2+2i．【考点】A5：复数代数形式的乘除运算．【分析】利用复数的运算法则、共轭复数的定义即可得出．【解答】解：（3﹣4i+z）i=2+i，则3﹣4i+z===﹣2i+1．∴z=﹣2+2i．故选：D．【点评】本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．3．已知命题p：∀x∈R，x2+ax+a2≥0（a∈R），命题q：，，则下列命题中为真命题的是（）A．p∧q B．p∨q C．（¬p）∨q D．（¬p）∧（¬q）【考点】2E：复合命题的真假．【分析】利用不等式的解法化简命题p，q，再利用复合命题的判定方法即可得出．【解答】解：命题p：∵△=a2﹣4a2=﹣3a2≤0，因此∀x∈R，x2+ax+a2≥0（a∈R），是真命题．命题q：由2x2﹣1≤0，解得≤x，因此不存在x0∈N*，使得，是假命题．则下列命题中为真命题的是p∨q．故选：B．【点评】本题考查了不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．4．执行如图所示的程序图，则输出的S值为（）A．4 B．3 C．﹣2 D．﹣3【考点】EF：程序框图．【分析】由已知中的程序语句可知该框图的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【解答】解：s=0，i=2，s=2，i=3，s=﹣1．i=4，s=3，i=5，s=﹣2，i=6，s=4，i=7＞6，结束循环，输出s=4，故选：A．【点评】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，属于基础题．5．函数f（x）=ln（|x|﹣1）+x的大致图象是（）A．B．C．D．【考点】3O：函数的图象．【分析】化简f（x），利用导数判断f（x）的单调性即可得出正确答案．【解答】解：f（x）的定义域为{x|x＜﹣1或x＞1}．f（x）=，∴f′（x）=，∴当x＞1时，f′（x）＞0，当x＜﹣2时，f′（x）＞0，当﹣2＜x＜﹣1时，f′（x）＜0，∴f（x）在（﹣∞，﹣2）上单调递增，在（﹣2，﹣1）上单调递减，在（1，+∞）上单调递增．故选A．【点评】本题考查了函数图象的判断，函数单调性的判断，属于中档题．6．在区间[﹣1，5]上随机地取一个实数a，则方程x2﹣2ax+4a﹣3=0有两个正根的概率为（）A．B．C．D．【考点】CF：几何概型．【分析】根据根与系数之间的关系，求出a的取值范围，结合几何概型的概率公式进行计算即可．【解答】解：若方程x2﹣2ax+4a﹣3=0有两个正根，则满足，即，得＜a≤1或a≥3，∵﹣1≤a≤5则对应的概率P=+=+=，故选：C【点评】本题主要考查几何概型的概率的计算，根据根与系数之间的关系求出a 的取值范围是解决本题的关键．7．已知三条直线2x﹣3y+1=0，4x+3y+5=0，mx﹣y﹣1=0不能构成三角形，则实数m的取值集合为（）A．{﹣， } B．{，﹣ } C．{﹣，， } D．{﹣，﹣， }【考点】IG：直线的一般式方程．【分析】三条直线若两两相交围成一个三角形，则斜率必不相同；否则，只要有两条直线平行，或三点共线时不能构成三角形．【解答】解：∵三条直线不能围成一个三角形，∴（1）l1∥l3，此时m=；l2∥l3，此时m=﹣；（2）三点共线时也不能围成一个三角形2x﹣3y+1=0与4x+3y+5=0交点是（﹣1，﹣）代入mx﹣y﹣1=0，则m=．故选：C．【点评】本题考查两直线平行的条件，当斜率相等且截距不相等时两直线平行．属于基础题．8．已知两点A（﹣1，1），B（3，5），点C在曲线y=2x2上运动，则的最小值为（）A．2 B．C．﹣2 D．【考点】9R：平面向量数量积的运算．【分析】设C（x，2x2），得出关于x的函数，根据函数性质求出最小值．【解答】解：设C（x，2x2），则=（4，4），=（x+1，2x2﹣1），∴=4（x+1）+4（2x2﹣1）=8x2+4x=8（x+）2﹣．∴当x=﹣时取得最小值﹣．故选D．【点评】本题考查了平面向量的数量积运算，函数最值得计算，属于中档题．9．在棱长为2的正方体ABCD﹣A1B1C1D1中，M是棱A1D1的中点，过C1，B，M作正方体的截面，则这个截面的面积为（）A．B．C．D．【考点】LA ：平行投影及平行投影作图法．【分析】由于截面被平行平面所截，所以截面为梯形，取AA 1的中点N ，可知截面为等腰梯形，利用题中数据可求．【解答】解：取AA 1的中点N ，连接MN ，NB ，MC 1，BC 1， 由于截面被平行平面所截，所以截面为梯形，且MN=BC 1=，MC 1=BN ，=，∴梯形的高为，∴梯形的面积为（）×=，故选C ．【点评】本题的考点是棱柱的结构特征，主要考查几何体的截面问题，关键利用正方体图形特征，从而确定截面为梯形．10．数列{a n }满足a 2=2，a n +2+（﹣1）n +1a n =1+（﹣1）n （n ∈N *），S n 为数列{a n }前n 项和，S 100=（ ） A ．5100B ．2550C ．2500D ．2450【考点】8H ：数列递推式．【分析】数列{a n }满足a 2=2，a n +2+（﹣1）n +1a n =1+（﹣1）n （n ∈N *），n=2k （k ∈N *）时，a 2k +2﹣a 2k =2，因此数列{a 2k }为等差数列，首项为2，公差为2．n=2k ﹣1（k ∈N *）时，a 2k +1+a 2k ﹣1=0．通过分组求和，利用等差数列的求和公式即可得出．【解答】解：数列{a n }满足a 2=2，a n +2+（﹣1）n +1a n =1+（﹣1）n （n ∈N *），n=2k （k ∈N *）时，a 2k +2﹣a 2k =2，因此数列{a 2k }为等差数列，首项为2，公差为2．n=2k ﹣1（k ∈N *）时，a 2k +1+a 2k ﹣1=0．∴S 100=（a 1+a 3+…+a 97+a 99）+（a 2+a 4+…+a 100）=0+2×50+=2550．故选：B．【点评】本题考查了等差数列的通项公式与求和公式、数列递推关系、分类讨论方法、分组求和，考查了推理能力与计算能力，属于中档题．11．已知函数f（x）=2sin（ωx+）（ω＞0）的图象在区间[0，1]上恰有3个最高点，则ω的取值范围为（）A．[，）B．[，）C．[，）D．[4π，6π）【考点】H2：正弦函数的图象．【分析】根据区间[0，1]上，求出ωx+的范围，由于在区间[0，1]上恰有3个最高点，建立不等式关系，求解即可．【解答】解：函数f（x）=2sin（ωx+）（ω＞0），∵x∈[0，1]上，∴ωx+∈[，]，图象在区间[0，1]上恰有3个最高点，∴+，解得：．故选C．【点评】本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用，利用三角函数公式将函数进行化简是解决本题的关键．属于中档题．12．如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的体积为（）A．B．C．D．16【考点】L!：由三视图求面积、体积．【分析】根据三视图可知三棱锥倒立放置，从而得出棱锥的高，根据俯视图找出三棱锥的底面，得出底面积，从而可求出棱锥的体积．【解答】解：由主视图和侧视图可知三棱锥倒立放置，棱锥的底面水平放置，故三棱锥的高为h=4，∵主视图为直角三角形，∴棱锥的一个侧面与底面垂直，=4，结合俯视图可知三棱锥的底面为俯视图中的左上三角形，∴S底=∴V==．故选：B．【点评】本题考查了棱锥的三视图和体积计算，根据三视图的特征找出棱锥的底面是关键，属于中档题．二、填空题（2017•广州二模）已知双曲线（a＞0）的离心率为2，则a的值为．【考点】KB：双曲线的标准方程．【分析】求得双曲线的b2=2，由c=和e=，解关于a的方程，即可得到所求值．【解答】解：由双曲线（a＞0）得到b2=2，则c=，所以=2，解得a=．故答案是：．【点评】本题考查双曲线的方程和性质，注意运用离心率公式和基本量a，b，c 的关系，考查方程思想和运算能力，属于基础题．14．在各项都为正数的等比数列{a n}中，已知a1=2，，则数列{a n}的通项公式a n=．【考点】8H：数列递推式．【分析】设等比数列{a n}的公比为q＞0，由a1=2，，可得+=4，化简解出q，再利用等比数列的通项公式即可得出．【解答】解：设等比数列{a n}的公比为q＞0，∵a1=2，，∴+=4，化为：q4﹣4q2+4=0，解得q2=2，q＞0，解得q=．则数列{a n}的通项公式a n==．故答案为：．【点评】本题考查了等比数列的通项公式、数列递推关系，考查了推理能力与计算能力，属于中档题．15．《孙子算经》是我国古代重要的数学著作，约成书于四、五世纪，传本的《孙子算经》共三卷，其中下卷：“物不知数”中有如下问题：“今有物，不知其数，三三数之，剩二；五五数之，剩三；七七数之，剩二，问：物几何？”其意思为：“现有一堆物品，不知它的数目，3个3个数，剩2个，5个5个数，剩3个，7个7个数，剩2个，问这堆物品共有多少个？”试计算这堆物品至少有23个．【考点】F4：进行简单的合情推理．【分析】根据“三三数之剩二，五五数之剩三，七七数之剩二”找到三个数：第一个数能同时被3和5整除；第二个数能同时被3和7整除；第三个数能同时被5和7整除，将这三个数分别乘以被7、5、3除的余数再相加即可求出答案．【解答】解：我们首先需要先求出三个数：第一个数能同时被3和5整除，但除以7余1，即15；第二个数能同时被3和7整除，但除以5余1，即21；第三个数能同时被5和7整除，但除以3余1，即70；然后将这三个数分别乘以被7、5、3除的余数再相加，即：15×2+21×3+70×2=233．最后，再减去3、5、7最小公倍数的整数倍，可得：233﹣105×2=23，或者105k+23（k为正整数）．∴这堆物品至少有23，故答案为：23．【点评】本题考查的是带余数的除法，简单的合情推理的应用，根据题意下求出15、21、70这三个数是解答此题的关键，属于中档题．16．已知函数，若f（3a﹣1）≥8f（a），则实数a的取值范围为．【考点】5B：分段函数的应用．【分析】根据条件判断函数f（x）的奇偶性和单调性即可．【解答】解：∵，∴f（﹣x）=f（x），即函数f（x）是偶函数，在[0，+∞）上为增函数，则不等式f（3a﹣1）≥8f（a），等价为f（|3a﹣1|）≥f（2|a|），∴|3a﹣1|≥2|a|，解得a∈．故答案为．【点评】本题主要考查不等式的求解，根据条件判断函数的奇偶性和单调性是解决本题的关键．综合考查函数的性质．三、解答题（本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（12分）（2017•广州二模）△ABC的内角A，B，C的对边分别为a，b，c，已知bcosC+bsinC=a．（Ⅰ）求角B的大小；（Ⅱ）若BC边上的高等于，求cosA的值．【考点】HT：三角形中的几何计算．【分析】（Ⅰ）利用正弦定理求和三角形的三角的关系，以及两角和的正弦公式sinB=cosB，即可求出B，（Ⅱ）设BC边上的高线为AD，运勾股定理和余弦定理，即可求得cosB，再由正弦定理，即可求出【解答】解：（Ⅰ）因为bcosC+bsinC=a，由正弦定理得，sinBcosC+sinBsinC=sinA．因为A+B+C=π，所以sinBcosC+sinBsinC=sin（B+C）．即sinBcosC+sinBsinC=sinBcosC+cosBsinC．因为sinC≠0，所以sinB=cosB．因为cosB≠0，所以tanB=1．因为B∈（0，π），所以．（Ⅱ）设BC边上的高线为AD，则．因为，则，．所以=，．由余弦定理得=．所以cosA=．【点评】本题考查正弦定理和余弦定理的运用，考查两角和的正弦公式的运用，考查运算能力，属于中档题．18．（12分）（2017•广州二模）某中学为了解高中入学新生的身高情况，从高一年级学生中按分层抽样共抽取了50名学生的身高数据，分组统计后得到了这50名学生身高的频数分布表：身高（cm）分组[145，155）[155，165）[165，175）[175，185]男生频数15124女生频数71542（Ⅰ）在答题卡上作出这50名学生身高的频率分布直方图；（Ⅱ）估计这50名学生身高的方差（同一组中的数据用该组区间的中点值作代表）；（Ⅲ）现从身高在[175，185]这6名学生中随机抽取3名，求至少抽到1名女生的概率．【考点】CC：列举法计算基本事件数及事件发生的概率；B8：频率分布直方图．【分析】（Ⅰ）由频率分布表能作出这50名学生身高的频率分布直方图．（Ⅱ）由频率分布直方图能估计这50名学生的平均身高，并能估计这50名学生身高的方差．（Ⅲ）记身高在[175，185]的4名男生为a，b，c，d，2名女生为A，B．利用列举法能求出从这6名学生中随机抽取3名学生，至少抽到1名女生的概率．【解答】解：（Ⅰ）这50名学生身高的频率分布直方图如下图所示：（Ⅱ）由题意可估计这50名学生的平均身高为=164．所以估计这50名学生身高的方差为s2==80．所以估计这50名学生身高的方差为80．（Ⅲ）记身高在[175，185]的4名男生为a，b，c，d，2名女生为A，B．从这6名学生中随机抽取3名学生的情况有：{a，b，c}，{a，b，d}，{a，c，d}，{b，c，d}，{a，b，A}，{a，b，B}，{a，c，A}，{a，c，B}，{a，d，A}，{a，d，B}，{b，c，A}，{b，c，B}，{b，d，A}，{b，d，B}，{c，d，A}，{c，d，B}，{a，A，B}，{b，A，B}，{c，A，B}，{d，A，B}共20个基本事件．其中至少抽到1名女生的情况有：{a，b，A}，{a，b，B}，{a，c，A}，{a，c，B}，{a，d，A}，{a，d，B}，{b，c，A}，{b，c，B}，{b，d，A}，{b，d，B}，{c，d，A}，{c，d，B}，{a，A，B}，{b，A，B}，{c，A，B}，{d，A，B}共16个基本事件．所以至少抽到1名女生的概率为．【点评】本题考查频率分布直方图的应用，概率的求法，是基础题，解题时要认真审题，注意列举法的合理运用．19．（12分）（2017•广州二模）如图，ABCD是边长为a的正方形，EB⊥平面ABCD，FD⊥平面ABCD，．（Ⅰ）求证：EF⊥AC；（Ⅱ）求三棱锥E﹣FAC的体积．【考点】LF：棱柱、棱锥、棱台的体积．【分析】（Ⅰ）连接BD，推导出AC⊥BD，AC⊥FD，从而AC⊥平面BDF．推导出EB∥FD，从而B，D，F，E四点共面，由此能证明EF⊥AC．（Ⅱ）设AC∩BD=O，连接EO，FO，由V E﹣FAC =V A﹣FEO+V C﹣FEO，能求出三棱锥E﹣FAC的体积．【解答】证明：：（Ⅰ）连接BD，因为ABCD是正方形，所以AC⊥BD．因为FD⊥平面ABCD，AC⊂平面ABCD，所以AC⊥FD．因为BD∩FD=D，所以AC⊥平面BDF．因为EB⊥平面ABCD，FD⊥平面ABCD，所以EB∥FD．所以B，D，F，E四点共面．因为EF⊂平面BDFE，所以EF⊥AC．解：（Ⅱ）设AC∩BD=O，连接EO，FO．由（Ⅰ）知，AC⊥平面BDFE，所以AC⊥平面FEO．因为平面FEO将三棱锥E﹣FAC分为两个三棱锥A﹣FEO和C﹣FEO，所以V E﹣FAC =V A﹣FEO+V C﹣FEO．因为正方形ABCD的边长为a，，所以，．取BE的中点G，连接DG，则FE=DG=．所以等腰三角形FEO的面积为=．所以V E﹣FAC =V A﹣FEO+V C﹣FEO====．所以三棱锥E﹣FAC的体积为．【点评】本题考查线线垂直的证明，考查三棱锥的体积的求法，考查空间中线线、线面、面面间的关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．20．（12分）（2017•广州二模）已知定点F（0，1），定直线l：y=﹣1，动圆M过点F，且与直线l相切．（Ⅰ）求动圆M的圆心轨迹C的方程；（Ⅱ）过点F的直线与曲线C相交于A，B两点，分别过点A，B作曲线C的切线l1，l2，两条切线相交于点P，求△PAB外接圆面积的最小值．【考点】KN：直线与抛物线的位置关系；J3：轨迹方程．【分析】（Ⅰ）利用直接法，即可求动圆M的圆心轨迹C的方程；（Ⅱ）证明△PAB的外接圆的圆心为线段AB的中点，线段AB是直径．得到当k=0时线段AB最短，最短长度为4，此时圆的面积最小，最小面积为4π．【解答】解：（Ⅰ）设点M到直线l的距离为d，依题意|MF|=d．设M（x，y），则有=|y+1|．化简得x2=4y．所以点M的轨迹C的方程为x2=4y．（Ⅱ）设l AB：y=kx+1，代入x2=4y中，得x2﹣4kx﹣4=0．设A（x1，y1），B（x2，y2），则x1+x2=4k，x1•x2=﹣4．所以．因为C：x2=4y，即，所以．所以直线l1的斜率为，直线l2的斜率为．因为，所以PA⊥PB，即△PAB为直角三角形．所以△PAB的外接圆的圆心为线段AB的中点，线段AB是直径．因为|AB|=4（k2+1），所以当k=0时线段AB最短，最短长度为4，此时圆的面积最小，最小面积为4π．【点评】本题考查轨迹方程，考查直线与抛物线位置关系的运用，考查学生的计算能力，属于中档题．21．（12分）（2017•广州二模）已知函数．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）若函数g（x）=f（x）+4x存在极小值点x0，且，求实数a的取值范围．【考点】6D：利用导数研究函数的极值；6B：利用导数研究函数的单调性．【分析】（I）计算f′（x），讨论a判断f′（x）的符号得出f（x）的单调区间；（II）由导数和二次函数的性质得g′（x）=0在（0，+∞）上有两解列不等式组得出a的范围，根据得出a的范围，再取交集即可．【解答】解：（Ⅰ）因为函数，所以其定义域为（0，+∞）．所以=．当a≤0时，f'（x）＜0，函数f（x）在区间（0，+∞）上单调递减．当a＞0时，f'（x）=．当时，f'（x）＜0，函数f（x）在区间上单调递减．当时，f'（x）＞0，函数f（x）在区间上单调递增．综上可知，当a≤0时，函数f（x）的单调递减区间为（0，+∞）；当a＞0时，函数f（x）的单调递增区间为，单调递减区间为．（Ⅱ）因为g（x）=f（x）+4x=，所以=（x＞0）．因为函数g（x）存在极小值点，所以g'（x）在（0，+∞）上存在两个零点x1，x2，且0＜x1＜x2．即方程x2﹣4x﹣a=0的两个根为x1，x2，且0＜x1＜x2，所以，解得﹣4＜a＜0．则=．当0＜x＜x1或x＞x2时，g'（x）＜0，当x1＜x＜x2时，g'（x）＞0，所以函数g（x）的单调递减区间为（0，x1）与（x2，+∞），单调递增区间为（x1，x2）．所以x=x1为函数g（x）的极小值点x0．由，得．由于等价于．由，得，所以alnx0+a＞0．因为﹣4＜a＜0，所以有lnx0+1＜0，即．因为，所以．解得．所以实数a的取值范围为．【点评】本题考查了导数与函数单调性、极值的关系，函数最值得计算，属于中档题．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程]22．（10分）（2017•广州二模）在平面直角坐标系xOy中．已知直线l的普通方程为x﹣y﹣2=0，曲线C的参数方程为（θ为参数），设直线l 与曲线C交于A，B两点．（1）求线段AB的长（2）已知点P在曲线C上运动．当△PAB的面积最大时，求点P的坐标及△PAB 的最大面积．【考点】KL：直线与椭圆的位置关系；QL：椭圆的参数方程．【分析】（1）根据题意，将曲线C的参数方程变形为普通方程，将直线x﹣y ﹣2=0代入其中，可得x2﹣3x=0，解可得x的值，由弦长公式计算可得答案；（2）分析可得要使△PAB的面积最大，则必须使P到直线直线l的距离最大，设P的坐标为（2cosθ，2sinθ），其中θ∈[0，2π），由点到直线l的距离公式可得d=，由余弦函数的性质分析可得当θ+=π，即θ=时，d取得最大值，代入点的坐标（2cosθ，2sinθ）中可得P的坐标，进而计算可得△PAB的最大面积，即可得答案．【解答】解：（1）根据题意，曲线C的参数方程为，则其普通方程为： +=1，将直线x﹣y﹣2=0代入+=1可得：x2﹣3x=0，解可得x=0或3，故|AB|=|x1﹣x2|=3；（2）要求在椭圆+=1上求一点P，使△PAB的面积最大，则P到直线直线l的距离最大；设P的坐标为（2cosθ，2sinθ），其中θ∈[0，2π），则P到直线l的距离d==，又由θ∈[0，2π），则≤θ+＜，所以当θ+=π，即θ=时，d取得最大值，且d max=3，此时P（﹣3，1），△PAB的最大面积S=×|AB|×d=9．【点评】本题考查椭圆与直线的位置关系，涉及椭圆的参数方程，关键是正确将参数方程化为普通方程．[选修4-5：不等式选讲]23．（2017•广州二模）（I）已知a+b+c=1，证明（a+1）2+（b+1）2+（c+1）2≥；（Ⅱ）若对任总实数x，不等式|x﹣a|+|2x﹣1|≥2恒成立，求实数a的取值范围．【考点】R4：绝对值三角不等式；R6：不等式的证明．【分析】（I）利用柯西不等式，即可证明；（Ⅱ）分：①a=、②a＞、③a＜三种情况，分别化简不等式，根据函数y=|2x ﹣1|+|x﹣a|的最小值大于或等于2，求得a的范围．【解答】（I）证明：由柯西不等式可得（1+1+1）[（a+1）2+（b+1）2+（c+1）2]≥（a+1+b+1+c+1）2，∵a+b+c=1，∴（a+1）2+（b+1）2+（c+1）2≥；（Ⅱ）解：①当a=时，不等式即|x﹣|≥，显然不能任意实数x均成立．②当a＞时，|2x﹣1|+|x﹣a|=，此时，根据函数y=|2x﹣1|+|x﹣a|的单调性可得y的最小值为﹣3×+a+1．∵不等式|2x﹣1|+|x﹣a|≥2对任意实数x均成立，∴﹣3×+a+1≥2，解得a≥．③当a＜时，|2x﹣1|+|x﹣a|=，此时，根据函数y=|2x﹣1|+|x﹣a|的单调性可得y的最小值为﹣﹣a+1．∵不等式|2x﹣1|+|x﹣a|≥2对任意实数x均成立，∴﹣﹣a+1≥2，解得a≤﹣．综上可得，实数a的取值范围是（﹣∞，﹣]∪[，+∞）．【点评】本题主要考查绝对值不等式的解法，体现了转化以及分类讨论的数学思想，属于中档题．。

你若盛开，蝴蝶自来。

2023广东二模语文试卷及参考答案(高清版)2023广东二模语文试卷及参考答案(高清版)4月26日，2023年广东省二模，物理、历史、英语、日语学科考试如期进行!以下是关于2023广东二模语文试卷及参考答案的相关内容，供大家参考!2023广东二模语文试卷2023广东二模语文试卷参考答案2023高三二模时间二模考试一般支配在4月初。

不同学校有所差别，详细以官方发布为准。

许多考生认为二模变简洁了，其实不然。

我们要知道二轮复习的作用是通过专题复习，能将学问系统化，利于学问的巩固与提升;通过专题和综合测试训练，有利于提高基本力量和综合力量;能提高应试水平，如审题技巧、答题技巧、应试心理素养，积累临场发挥阅历等;能增加答题的规范性;能查缺补漏等。

胜利的二轮复习将使成果大幅度提高，所以许多考生会觉得二模考试相对于一模考试来讲简洁了一些就是由于二轮复习使自己的学习成果有了提高。

接下来的复习中，既要重视课本基础学问，弥补学问盲点，又要兼顾学问网络的构建，在训练过程中不断提升敏捷运用学问解决物理第1页/共3页千里之行，始于足下。

学问题的力量。

二模到高考能提高多少分二模到高考能提高多少分在于高三同学的学习方法与力量,从二模到高考,提高50分以上的同学有许多,最主要的是总结并且针对性的学习,要把自己在各个科目上的得分状况做一个具体的分析;是由于失误失分的,还是不会做导致错误而失分的,还是自己本身学问储备不足失分的,假如是失误失分的,或者学问不足引起的,那么接下来就是要多加练习,削减失误是关键,假如是错误引起的,那就要查漏补缺,多找典型仔细做。

二模考试后的复习还要把自己的弱课,自己的强势课目分出来,区分对待,弱势课目削减失误,争取得分。

强势课目努力提升,再上台阶,让它的优势更明显。

每次考试都要正常发挥,力争超常发挥。

高三复习方法1、早做准备，提前复习。

许多同学在第一轮复习时感觉，反正高考还有一年，就浑水摸鱼地混着，把高三复习完全没当回事;而且由于第一轮复习时老师讲的学问很基础，反正都能听懂，因此心里也不焦急，结果呢，等到听不懂的时候已经来不及了。

秘密★启用前试卷类型B 2023年广州市普通高中毕业班综合测试(二)语文本试卷共10页，23小题，满分150分。

考试用时150分钟。

注意事项：1.答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号、试室号、座位号填写在答题卡上。

用2B铅笔将试卷类型（B）填涂在答题卡的相应位置上，并在答题卡相应位置上填涂考生号。

2.作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4.考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题，17分)阅读下面的文字，完成1~5题。

植物为人类和其他动物提供食物和住所，还能调节气候，给地球带来生机和活力。

但由于人类活动对环境的影响，地球上的物种正在加速灭绝，植物也不例外。

据统计，从1753年至2018年，全球范围内已经有571种种子植物在野外灭绝。

一种植物的消失，对我们来说，并不仅仅是单一物种的消亡，也将会引发一系列连锁反应。

地球上的生物并不是孤立存在的，一种植物的灭亡可能会导致几十种伴生物种的消失，植物的大量灭绝将会动摇人类生存和发展的塔基。

在人类历史上，曾发生过多次由于遗传基础狭窄而引起的粮食安全事件。

拥有相同基因的植物，一旦遭受疾病侵袭，很容易“全军覆没”。

有专家认为，从野生植物的基因中或许能找到解决办法。

如籼稻是由野生稻驯化而来的，在漫长的驯化过程中，籼稻获得了人们所期望的性状，但也失去了部分野生稻特有的基因，其中包括抗病虫、抗逆、高蛋白含量等优良基因。

因此，对于育种专家而言，不适合食用的野生稻可以为改良栽培稻储备丰富的基因源，对解决粮食安全、维护人类生存发展具有重大意义。

2023学年第二学期语文科九年级第二次学业水平综合测试一、选择题8分1. 下列词语中，每对加点字的读音都相同的一项是（）A. 行头/行业拜谒/声嘶力竭B. 伫立/贮存劳累/伤痕累累C. 啜泣/辍学喷薄/日薄云天D. 证券/豢养禁锢/忍俊不禁【答案】C【解析】本题考查读音。

A.xíng/háng，yè/jié；B.zhù/zhù，lèi/lěi；C.都读chuò，都读bó；D.quàn/huàn，jìn/jīn；故选C。

2. 下列词语中，没有错别字的一项是（）A. 秘决雕梁画栋舵手险象叠生B. 惦记不屑置辩亵渎哗众取宠C. 意蕴栩栩如生幅射不径而走D暇想变换多姿渊博身临其境【答案】B【解析】考查字形。

A.秘决——秘诀，险象叠生——险象迭生；C.幅射——辐射，不径而走——不胫而走；D.暇想——遐想，变换多姿——变幻多姿；故选B。

3. 下列句子中，加线词语使用最恰当的一项是（）A. 为了尽快找到一本论文集或目标参考书，我经常会在学校图书馆里漫不经心地浏览。

B. 这幅油画作品在勾勒轮廓的同时施以平涂的色彩，着色相得益彰，有点类似中国画。

C. 这出原创音乐剧中，每一首歌的歌词都富有创新意识，多首歌已成为炙手可热的单品。

D. 中西方“庙会”尽管表现方式大相径庭，但其形式之美，及其个体冀望都是相通的。

【答案】D【解析】本题考查成语运用。

A．漫不经心：随随便便，不放在心上。

与前半句“为了尽快找到一本论文集或目标参考书”说法不符；B．相得益彰：指互相帮助，互相补充，更能显出各自的长处。

用来形容“着色”不合适；C．炙手可热：手一挨近就感觉热，形容气焰很盛，权势很大。

不能形容歌曲受到追捧，使用有误；D．大相径庭：形容彼此相差很远。

使用正确；故选D。

4. 下列句子中，没有语病的一项是（）A. 大量的历史文献和法律文件，强烈地证明钓鱼岛及其附属岛屿都是中国的固有领土。

试卷类型：A20xx 年广州市普通高中毕业班综合测试（二）数学（理科）20xx.4 本试卷共4页，21小题， 满分150分.考试用时120分钟.注意事项：1．答卷前，考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型（A ）填涂在答题卡相应位置上.2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上.3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.4．作答选做题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再作答.漏涂、错涂、多涂的，答案无效.5．考生必须保持答题卡的整洁.考试结束后，将试卷和答题卡一并交回. 参考公式：锥体的体积公式是13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1. 若复数z 满足 i 2z =，其中i 为虚数单位，则z 的虚部为A ．2-B ．2C ．2-iD ．2i 2．若函数()y f x =是函数3x y =的反函数，则12f ⎛⎫⎪⎝⎭的值为A ．2log 3-B ．3log 2-C ．19D 3．命题“对任意x ∈R ，都有32x x >”的否定是A ．存在0x ∈R ，使得3200x x >B ．不存在0x ∈R ，使得3200x x > C ．存在0x ∈R ，使得3200x x ≤ D ．对任意x ∈R ，都有32x x ≤4. 将函数()2cos 2(f x x x x =+∈R )的图象向左平移6π个单位长度后得到函数 ()y g x =，则函数()y g x =A ．是奇函数B ．是偶函数图1俯视图侧视图正视图 C ．既是奇函数又是偶函数 D ．既不是奇函数，也不是偶函数5．有两张卡片，一张的正反面分别写着数字0与1，另一张的正反面分别写着数字2与3， 将两张卡片排在一起组成两位数，则所组成的两位数为奇数的概率是 A ．16 B ．13 C ．12 D ．386．设12,F F 分别是椭圆()2222:10x y C a b a b+=>>的左、右焦点，点P 在椭圆C 上，线段1PF的中点在y 轴上，若1230PF F ︒∠=，则椭圆C 的离心率为 A ．16 B ．13CD7．一个几何体的三视图如图1，则该几何体的体积为A ．6π4+B ．12π4+C ．6π12+D ．12π12+ 8．将正偶数2,4,6,8,按表1的方式进行排列，记ij a 表示第i 行第j 列的数，若2014ij a =，则i j +的值为A ．257B ．256C ．254D ．253 表1 二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分． （一）必做题（9～13题）9．不等式2210x x --<的解集为 .10．已知312nx x ⎛⎫- ⎪⎝⎭的展开式的常数项是第7项，则正整数n 的值为 .11．已知四边形ABCD 是边长为a 的正方形，若2,2DE EC CF FB ==，则A E A F ⋅的值 为 .12．设,x y 满足约束条件 220,840,0,0.x y x y x y -+≥⎧⎪--≤⎨⎪≥≥⎩若目标函数()0,0z ax by a b =+>>的最大值D CB A a 图3重量/克0.0320.02452515O 为8，则ab 的最大值为 .13．已知[]x 表示不超过x 的最大整数，例如[][]1.52,1.51-=-=.设函数()[]f x x x ⎡⎤=⎣⎦， 当[)0,(x n n ∈∈N *)时，函数()f x 的值域为集合A ，则A 中的元素个数为 . （二）选做题（14～15题，考生从中选做一题）14．（坐标系与参数方程选做题）在平面直角坐标系xOy 中，直线,(x a t t y t =-⎧⎨=⎩为参数)与圆1cos ,(sin x y θθθ=+⎧⎨=⎩为参数)相切，切点在第一象限，则实数a 的值为 .15．（几何证明选讲选做题）在平行四边形ABCD 中，点E 在线段AB 上，且 12A E EB =，连接,DE AC ，AC 与DE 相交于点F ，若△AEF 的面积为1 cm 2，则 △AFD 的面积为 cm 2.三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16.（本小题满分12分）如图2，在△ABC 中，D 是边AC 的中点， 且1AB AD ==，3BD =. (1) 求cos A 的值； （2）求sin C 的值. 图2 17．（本小题满分12分）一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取50个作为样 本，称出它们的重量（单位：克），重量分组区间为(]5,15，(]15,25，(]25,35，(]35,45， 由此得到样本的重量频率分布直方图，如图3. （1）求a 的值；（2）根据样本数据，试估计盒子中小球重量的平均值；（注：设样本数据第i 组的频率为i p ，第i 组区间的中点值为i x ()1,2,3,,i n =，则样本数据的平均值为112233n n X x p x p x p x p =++++. （3）从盒子中随机抽取3个小球，其中重量在(]5,15内的小球个数为ξ，求ξ的分布列和数学期望.FE D CBA18．（本小题满分14分） 如图4，在五面体ABCDEF 中，四边形ABCD 是边长为2的正方形，EF ∥平面ABCD ， 1EF =，,90FB FC BFC ︒=∠=，AE =（1）求证：AB ⊥平面BCF ；（2）求直线AE 与平面BDE 所成角的正切值. 图4 19．（本小题满分14分）已知数列{}n a 的前n 项和为n S ，且10a =，对任意n ∈N *，都有()11n n na S n n +=++. （1）求数列{}n a 的通项公式；（2）若数列{}n b 满足22log log n n a n b +=，求数列{}n b 的前n 项和n T .20．（本小题满分14分）已知定点()0,1F 和直线:1l y =-，过点F 且与直线l 相切的动圆圆心为点M ，记点M 的轨迹为曲线E .(1) 求曲线E 的方程;(2) 若点A 的坐标为()2,1, 直线1:1(l y kx k =+∈R ，且0)k ≠与曲线E 相交于,B C 两 点，直线,AB AC 分别交直线l 于点,S T . 试判断以线段ST 为直径的圆是否恒过两个 定点? 若是，求这两个定点的坐标；若不是，说明理由. 21．（本小题满分14分）已知函数()ln (,f x a x bx a b =+∈R )在点()()1,1f 处的切线方程为220x y --=. （1）求,a b 的值； （2）当1x >时，()0kf x x+<恒成立，求实数k 的取值范围； （3）证明：当n ∈N *，且2n ≥时，22111322ln 23ln 3ln 22n n n n n n--+++>+.20xx 年广州市普通高中毕业班综合测试（二）数学（理科）试题参考答案及评分标准说明：1．参考答案与评分标准指出了每道题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与参考答案不同，可根据试题主要考查的知识点和能力对照评分标准给以相应的分数．2．对解答题中的计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的得分，但所给分数不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数，选择题和填空题不给中间分．分．二、填空题：本大题考查基本知识和基本运算，体现选择性．共7小题，每小题5分，满分30分．其中14~15题是选做题，考生只能选做一题．9．1,12⎛⎫- ⎪⎝⎭10．8 11．2a12．4 13．222n n -+141 15．3三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（本小题满分12分） （1）解：在△ABD 中，1AB AD ==，3BD =，∴222cos 2AB AD BD A AB AD+-=⋅⋅2221112113+-⎝⎭==⨯⨯. ……………4分（2）解：由（1）知，1cos 3A =，且0A <<π，∴sin A ==. ……………6分 ∵D 是边AC 的中点，∴22AC AD ==.在△ABC 中，222222121cos 22123AB AC BC BC A AB AC +-+-===⋅⋅⨯⨯，………8分解得3BC =……………10分 由正弦定理得，sin sin BC ABA C=， ……………11分∴1sin sin AB AC BC⋅===. ……………12分17．（本小题满分12分）(1) 解：由题意，得()0.020.0320.018101x +++⨯=， ……………1分 解得0.03x =. ……………2分 （2）解：50个样本小球重量的平均值为0.2100.32200.3300.184024.6X =⨯+⨯+⨯+⨯=（克）. ……………3分由样本估计总体，可估计盒子中小球重量的平均值约为24.6克. ……………4分（3）解：利用样本估计总体，该盒子中小球重量在(]5,15内的概率为0.2，则13,5B ξ⎛⎫⎪⎝⎭. ……………5分 ξ的取值为0,1,2,3， ……………6分()30346405125P C ξ⎛⎫=== ⎪⎝⎭，()2131448155125P C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭， ()2231412255125P C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭，()3331135125P C ξ⎛⎫=== ⎪⎝⎭. ……………10分 ∴ξ的分布列为：……………11分∴6448121301231251251251255E ξ=⨯+⨯+⨯+⨯=. ……………12分 （或者13355E ξ=⨯=）18．（本小题满分14分）（1）证明：取AB 的中点M ，连接EM ，则1AM MB ==，∵EF ∥平面ABCD ，EF ⊂平面ABFE ，平面ABCD 平面ABFE AB =，M OH FED C B ∴EF ∥AB ，即EF ∥MB . ……………1分 ∵EF =MB 1=∴四边形EMBF 是平行四边形. ……………2分 ∴EM ∥FB ，EM FB =.在Rt △BFC 中，2224FB FC BC +==，又FB FC =，得FB =∴EM = ……………3分 在△AME中，AE =1AM =，EM = ∴2223AM EM AE +==，∴AM EM ⊥. ……………4分 ∴AM FB ⊥，即AB FB ⊥. ∵四边形ABCD 是正方形，∴AB BC ⊥. ……………5分 ∵FB BC B =，FB ⊂平面BCF ，BC ⊂平面BCF ，∴AB ⊥平面BCF . ……………6分 （2）证法1：连接AC ，AC 与BD 相交于点O ，则点O 是AC 的中点， 取BC 的中点H ，连接,OH EO ，FH ， 则OH ∥AB ，112OH AB ==. 由（1）知EF ∥AB ，且12EF AB =，∴EF ∥OH ，且EF OH =.∴四边形EOHF 是平行四边形.∴EO ∥FH ，且1EO F H == .……………7分 由（1）知AB ⊥平面BCF ，又FH ⊂平面BCF ，∴FH AB ⊥. ……………8分∵FH BC ⊥，,ABBC B AB =⊂平面ABCD ，BC ⊂平面ABCD ，∴FH ⊥平面ABCD . ……………9分 ∴EO ⊥平面ABCD . ∵AO ⊂平面ABCD ，∴EO ⊥AO . ……………10分 ∵AO BD ⊥，,EOBD O EO =⊂平面EBD ，BD ⊂平面EBD ，∴AO ⊥平面EBD . ……………11分 ∴AEO ∠是直线AE 与平面BDE 所成的角. ……………12分 在Rt △AOE中，tan AOAEO EO∠== ……………13分 ∴直线AE 与平面BDE……………14分证法2：连接AC ，AC 与BD 相交于点O ，则点O 取BC 的中点H ，连接,OH EO ，FH ， 则OH ∥AB ，112OH AB ==.由（1）知EF ∥AB ，且12EF AB =， ∴EF ∥OH ，且EF OH =. ∴四边形EOHF 是平行四边形.∴EO ∥FH ，且1EO FH ==. ……………7分 由（1）知AB ⊥平面BCF ，又FH ⊂平面BCF ， ∴FH AB ⊥.∵FH BC ⊥，,ABBC B AB =⊂平面ABCD ，BC ⊂平面ABCD ，∴FH ⊥平面ABCD .∴EO ⊥平面ABCD . ……………8分 以H 为坐标原点，BC 所在直线为x 轴，OH 所在直线为y 轴，HF 所在直线为z 轴， 建立空间直角坐标系H xyz -，则()1,2,0A -，()1,0,0B ，()1,2,0D --，()0,1,1E -.∴()1,1,1AE =-，()2,2,0BD =--，()1,1,1BE =--. ……………9分 设平面BDE 的法向量为=n (),,x y z ，由n 0BD ⋅=，n 0BE ⋅=， 得220x y --=，0x y z --+=，得0,z x y ==-.令1x =，则平面BDE 的一个法向量为=n ()1,1,0-. ……………10分 设直线AE 与平面BDE 所成角为θ， 则sin θ=cos ,n AE⋅=n AE nAE=. ……………11分∴cos 3θ==，sin tan cos θθθ== ……………13分 ∴直线AE 与平面BDE……………14分19．（本小题满分14分）（1）解法1：当2n ≥时，()11n n na S n n +=++，()()111n n n a S n n --=+-，……1分 两式相减得()()()11111n n n n na n a S S n n n n +---=-++--， ……………3分即()112n n n na n a a n +--=+，得12n n a a +-=. ……………5分 当1n =时，21112a S ⨯=+⨯，即212a a -=. ……………6分 ∴数列{}n a 是以10a =为首项，公差为2的等差数列.∴()2122n a n n =-=-. ……………7分 解法2：由()11n n na S n n +=++，得()()11n n n n S S S n n +-=++， ……………1分 整理得，()()111n n nS n S n n +=+++， ……………2分 两边同除以()1n n +得，111n nS S n n+-=+. ……………3分 ∴数列n S n ⎧⎫⎨⎬⎩⎭是以101S =为首项，公差为1的等差数列. ∴011nS n n n=+-=-. ∴()1n S n n =-. ……………4分 当2n ≥时，()()()111222n n n a S S n n n n n -=-=----=-. ……………5分 又10a =适合上式， ……………6分 ∴数列{}n a 的通项公式为22n a n =-. ……………7分 （2）解法1：∵22log log n n a n b +=，∴221224n an n n b n n n --=⋅=⋅=⋅. ……………9分∴1231n n n T b b b b b -=+++++()0122142434144n n n n --=+⨯+⨯++-⋅+⋅，①()1231442434144n n n T n n -=+⨯+⨯++-⋅+⋅，② ……………11分 ①-②得0121344444n nn T n --=++++-⋅14414n nn -=-⋅-()13413n n -⋅-=. ……………13分 ∴()131419n n T n ⎡⎤=-⋅+⎣⎦. ……………14分 解法2：∵22log log n n a n b +=， ∴221224n an n n b n n n --=⋅=⋅=⋅. ……………9分∴1231n n n T b b b b b -=+++++()0122142434144n n n n --=+⨯+⨯++-⋅+⋅.由()12311n nx x x x x x x x+-++++=≠-， ……………11分两边对x 取导数得，012123n x x x nx-++++=()()12111n n nx n x x +-++-. ………12分令4x =，得()()0122114243414431419n n n n n n --⎡⎤+⨯+⨯++-⋅+⋅=-⋅+⎣⎦. ……………13分 ∴ ()131419nn T n ⎡⎤=-⋅+⎣⎦. ……………14分 20．（本小题满分14分）（1）解法1：由题意, 点M 到点F 的距离等于它到直线l 的距离,故点M 的轨迹是以点F 为焦点, l 为准线的抛物线. ……………1分 ∴曲线E 的方程为24x y =. ……………2分 解法2：设点M 的坐标为(),x y ,依题意,得1MF y =+,1y =+, ……………1分化简得24x y =.∴曲线E 的方程为24x y =. ……………2分(2) 解法1: 设点,B C 的坐标分别为()()1122,,,x y x y ，依题意得，2211224,4x y x y ==.由21,4,y kx x y =+⎧⎨=⎩消去y 得2440xkx --=，解得1,22x k ==±.∴12124,4x x k x x +==-. ……………3分直线AB 的斜率2111111124224ABx y x k x x --+===--， 故直线AB 的方程为()12124x y x +-=-. ……………4分 令1y =-，得1822x x =-+，∴点S 的坐标为182,12x ⎛⎫-- ⎪+⎝⎭. ……………5分 同理可得点T 的坐标为282,12x ⎛⎫-- ⎪+⎝⎭. ……………6分 ∴()()()121212888222222x x ST x x x x -⎛⎫=---= ⎪++++⎝⎭ ()()()121212121288248x x x x x xx x x x k k---===+++. ……………7分∴2ST=()()()2221212122221614k x x x x x x k k k +-+-==. ……………8分设线段ST 的中点坐标为()0,1x -，则()()()12012124418822222222x x x x x x x ++⎛⎫=-+-=- ⎪++++⎝⎭ ()()()1212444444222248k k x x x x k k++=-=-=-+++. ……………9分∴以线段ST 为直径的圆的方程为()2222114x y ST k ⎛⎫+++= ⎪⎝⎭()2241k k +=. ……………10分展开得()()22222414414k x x y k k k++++=-=. ……………11分令0x =，得()214y +=，解得1y =或3y =-. ……………12分 ∴以线段ST 为直径的圆恒过两个定点()()0,1,0,3-. ……………14分 解法2：由（1）得抛物线E 的方程为24x y =.设直线AB 的方程为()112y k x -=-，点B 的坐标为()11,x y ，由()112,1,y k x y ⎧-=-⎨=-⎩解得122,1.x k y ⎧=-⎪⎨⎪=-⎩∴点S 的坐标为122,1k ⎛⎫-- ⎪⎝⎭. …………3分 由()1212,4,y k x x y ⎧-=-⎨=⎩消去y ，得2114840x k x k -+-=，即()()12420x x k --+=，解得2x =或142x k =-. ……………4分 ∴1142x k =-，22111114414y x k k ==-+. ∴点B 的坐标为()211142,441k k k --+. ……………5分同理，设直线AC 的方程为()212y k x -=-， 则点T 的坐标为222,1k ⎛⎫-- ⎪⎝⎭，点C 的坐标为()222242,441k k k --+. …………6分 ∵点,B C 在直线1:1l y kx =+上，∴()()()()()()22222211212121214414414242k k k k k k k k k k k k k -+--+---==----121k k =+-.∴121k k k +=+. ……………7分又()211144142k k k k -+=-1+，得()21111214442412k k kk k k k k k -=-=+--，化简得122kk k =. ……………8分 设点(),P x y 是以线段ST 为直径的圆上任意一点，则0SP TP ⋅=， ……………9分 得()()122222110x x y y k k ⎛⎫⎛⎫-+-++++= ⎪⎪⎝⎭⎝⎭， ……………10分 整理得，()224410x x y k+-++=. ……………11分 令0x =，得()214y +=，解得1y =或3y =-. ……………12分 ∴以线段ST 为直径的圆恒过两个定点()()0,1,0,3-. ……………14分 21．（本小题满分14分）（1）解：∵()ln f x a x bx =+， ∴()af x b x'=+. ∵直线220x y --=的斜率为12，且过点11,2⎛⎫- ⎪⎝⎭， ……………1分 ∴()()11,211,2f f ⎧=-⎪⎪⎨⎪'=⎪⎩即1,21,2b a b ⎧=-⎪⎪⎨⎪+=⎪⎩解得11,2a b ==-. ……………3分（2）解法1：由（1）得()ln 2x f x x =-. 当1x >时，()0k f x x +<恒成立，即ln 02x k x x -+<，等价于2ln 2x k x x <-. ……………4分令()2ln 2x g x x x =-，则()()ln 11ln g x x x x x '=-+=--. ……………5分 令()1ln h x x x =--，则()111x h x x x-'=-=. 当1x >时，()0h x '>，函数()h x 在()1,+∞上单调递增，故()()10h x h >=. ……………6分 从而，当1x >时，()0g x '>，即函数()g x 在()1,+∞上单调递增， 故()()112g x g >=. ……………7分 因此，当1x >时，2ln 2x k x x <-恒成立，则12k ≤. ……………8分 ∴所求k 的取值范围是1,2⎛⎤-∞ ⎥⎝⎦. ……………9分解法2：由（1）得()ln 2x f x x =-. 当1x >时，()0k f x x +<恒成立，即ln 02x kx x-+<恒成立. ……………4分 令()ln 2x k g x x x =-+，则()222112222k x x kg x x x x -+'=--=-.方程2220x x k -+=（﹡）的判别式48k ∆=-.（ⅰ）当0∆<，即12k >时，则1x >时，2220x x k -+>，得()0g x '<， 故函数()g x 在()1,+∞上单调递减.由于()()110,2ln 21022kg k g =-+>=-+>， 则当()1,2x ∈时，()0g x >，即ln 02x kx x-+>，与题设矛盾. …………5分（ⅱ）当0∆=，即12k =时，则1x >时，()()2222121022x x x g x x x --+'=-=-<.故函数()g x 在()1,+∞上单调递减，则()()10g x g <=，符合题意. ………6分 (ⅲ) 当0∆>，即12k <时，方程（﹡）的两根为1211,11x x =<=>， 则()21,x x ∈时，()0g x '>，()2,x x ∈+∞时，()0g x '<. 故函数()g x 在()21,x 上单调递增，在()2,x +∞上单调递减， 从而，函数()g x 在()1,+∞上的最大值为()2222ln 2x kg x x x =-+. ………7分 而()2222ln 2x k g x x x =-+2221ln 22x x x <-+， 由（ⅱ）知，当1x >时，1ln 022x x x-+<， 得2221ln 022x x x -+<，从而()20g x <. 故当1x >时，()()20g x g x ≤<，符合题意. ……………8分 综上所述，k 的取值范围是1,2⎛⎤-∞ ⎥⎝⎦. ……………9分（3）证明：由（2）得，当1x >时，1ln 022x x x -+<，可化为21ln 2x x x -<， …10分又ln 0x x >， 从而，21211ln 111x x x x x >=---+. ……………11分 把2,3,4,,x n =分别代入上面不等式，并相加得，11111111111112ln 23ln 3ln 32435211n n n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++>-+-+-+-+- ⎪ ⎪ ⎪ ⎪ ⎪--+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭……………12分 111121n n =+--+ ……………13分 223222n n n n--=+. ……………14分。

2024年广州市普通高中毕业班综合测试（二）思想政治满分100分。

考试用时75分钟注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号、试室号和座位号填写在答题卡上。

用2B铅笔将试卷类型（B）填涂在答题卡相应位置上，并在答题卡相应位置上填涂考生号。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、选择题：本大题共16小题，每小题3分，共48分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.广东英德岩山寨遗址是岭南地区迄今发现规模最大的新石器时代至夏商时期中心聚落遗址。

考古发现该遗址的高等级墓葬随葬品丰富且普遍随葬玉器，而低等级墓葬仅见零星陶器或石器。

由此可推断，当时该地区（）①处于原始社会早期②社会在加速分化和逐渐复杂化③实行君主专制且等级森严④具有显著的贫富差距和等级差异A.①③B.①④C.②③D.②④【答案】D【解析】【详解】①：广东英德岩山寨遗址是岭南地区迄今发现规模最大的新石器时代至夏商时期中心聚落遗址。

高等级墓葬随葬品丰富且普遍随葬玉器，而低等级墓葬仅见零星陶器或石器。

由此可推断，当时该地区生产资料相应的由氏族公有转归家庭私有，处于原始社会晚期，而不是早期，①错误。

②：考古发现该遗址的高等级墓葬随葬品丰富且普遍随葬玉器，而低等级墓葬仅见零星陶器或石器。

由此可推断，当时该地区社会在加速分化和逐渐复杂化，氏族成员的地位越来越不平等，②正确。

③：广东英德岩山寨遗址是岭南地区迄今发现规模最大的新石器时代至夏商时期中心聚落遗址，属于原始社会，封建社会实行君主专制且等级森严，③不符合题意。

2023年广州市普通高中毕业班综合测试(二)数学本试卷共5页，22小题，满分150分。

考试用时120分钟。

注意事项：1．答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。

用2B 铅笔在答题卡的相应位置填涂考生号。

2．作答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1若a 为实数，且7+ai3+i=2-i ，则a =()A.2B.1C.-1D.-22已知集合A =x ∣x =3n -2,n ∈N * ，B ={6,7,10,11}，则集合A ∩B 的元素个数为()A.1B.2C.3D.43已知两个非零向量a ，b 满足a =3b ，a +b ⊥b ，则cos ⟨a ，b ⟩=()A.12B.-12C.13D.-134已知a =323，b =234，c =413，则()A.c <a <bB.b <c <aC.b <a <cD.c <b <a5木升在古代多用来盛装稂食作物，是农家必备的用具，如图为一升制木升．某同学制作了一个高为40 cm 的正四棱台木升模型，已知该正四棱台的所有顶点都在一个半径为50 cm 的球O 的球面上，且一个底面的中心与球O 的球心重合，则该正四棱台的侧面与底面所成二面角的正弦值为()A.223 B.23C.255D.256已知椭圆C ：x 2a 2+y 2b2=1a >b >0 ，过点-a ,0 且方向向量为n =1,-1 的光线，经直线y =-b 反射后过C 的右焦点，则C 的离心率为()A.35B.23C.34D.457已知函数f x =sin 2x +φ ，若f x ≤f π3恒成立，且f π >f π4 ，则f x 的单调递增区间为()A.k π+π6,k π+2π3 k ∈ZB.k π-π6,k π+π3k ∈Z C.k π-π3,k π+π6k ∈Z D.k π-2π3,k π-π6k ∈Z 8已知偶函数f x 与其导函数f x 的定义域均为R ，且f x +e -x +x 也是偶函数，若f 2a -1 <f a +1 ，则实数a 的取值范围是()A.-∞,2B.0,2C.2,+∞D.-∞,0 ∪2,+∞二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9有3台车床加工同一型号的零件，第1台加工的次品率为8%，第2台加工的次品率为3%，第3台加工的次品率为2%，加工出来的零件混放在一起．已知第1，2，3台车床．加工的零件数分别占总数的10%，40%，50%，从混放的零件中任取一个零件，则下列结论正确的是()A.该零件是第1台车床加工出来的次品的概率为0.08B.该零件是次品的概率为0.03C.如果该零件是第3台轪床加工出来的，那么它不是次品的概率为0.98D.如果该零件是次品，那么它不是第3台车床加工出来的概率为1310已知函数f x =1-4xx 2+4的定义域是a ,b a ,b ∈Z ，值域为0,1 ，则满足条件的整数对a ,b 可以是()A.-2,0B.-1,1C.0,2D.-1,211已知双曲线Γ:x 2-y 2=a 2a >0 的左，右焦点分别为F 1，F 2，过F 2的直线l 与双曲线Γ的右支交于点B ，C ，与双曲线Γ的渐近线交于点A ，D (A ，B 在第一象限，C ，D 在第四象限)，O 为坐标原点，则下列结论正确的是()A.若BC ⊥x 轴，则△BCF 1的周长为6aB.若直线OB 交双曲线Γ的左支于点E ，则BC ⎳EF 1C.△AOD 面积的最小值为4a 2D.AB +BF 1 的取值范围为3a ,+∞12已知正四面体A -BCD 的棱长为2，点M ，N 分别为△ABC 和△ABD 的重心，P 为线段CN 上一点，则下列结论正确的是()A.若AP +BP 取得最小值，则CP =PNB.若CP =3PN ，则DP ⊥平面ABCC.若DP ⊥平面ABC ，则三棱雉P -ABC 外接球的表面积为27π2D.直线MN 到平面ACD 的距离为269三、填空题：本题共4小题，每小题5分，共20分．13某班有48名学生，一次考试的数学成绩X (单位：分)服从正态分布N 80,σ2 ，且成绩在80,90 上的学生人数为16，则成缋在90分以上的学生人数为。

2024年中考第二次模拟考试（广州卷）物理（考试时间：60分钟试卷满分：100分）注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅰ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共10小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一项最符合题目要求。

1．下列说法正确的是（）A．太阳能和电能都是可再生能源B．超导体可用来制作加热器内的电热丝C．太阳内部氢原子发生裂变释放出核能D．风能、水能、化石能源都是一次能源2．如图1，监测器接收到声源发出的M、N两声音，得到的数据如图2、3，则（）A．N的音调比M高B．M的响度比N大C．声源发出声音M时振动幅度比N大3．下列对生活现象的解释正确的是（）A．舞台上常见的“白雾”是干冰升华形成的二氧化碳气体B．烧开水时，壶嘴附近冒出的“白气”是壶嘴喷出的热气液化形成的C．冬天，晨练的人呼出的“白气”是空气中的水蒸气遇冷液化形成的小水珠D．冬天，窗户玻璃上的“冰花”是水蒸气在玻璃外壁凝华形成的4．如图，用甲、乙两个滑轮质量不同的滑轮组将相同质量的两个物体匀速提升相同高度，甲、乙滑轮组绳子自由端的拉力分别为F1和F2，移动的距离分别为s1和s2，若甲滑轮组的机械效率比乙高。

则（）A．F1做功比F2多B．F1一定比F2大C．s1一定比s2小D．甲滑轮做的有用功一定比乙多5．2021年4月，中国女足通过奋勇拼搏，晋级奥运会。

如图是足球落地后又弹起的示意图分析可知，足球（）A．在B点时受力平衡B．在A、D两点动能可能相等C．在C点时，若所受力全部消失，其运动状态将不断改变D．在运动过程中，只存在动能和势能的相互转化6．某智能家政机器人有三种识别启动方式:人脸识别(S1)、指纹识别(S2)、密码识别(S3),只要其中一种方式识别成功,则相应开关闭合,机器人启动(机器人用表示),下列电路设计符合要求的是A．B．C．D．7．电磁铁外部磁感线分布如图1，将磁化后的缝衣针放在电磁铁附近，静止时如图2，a表示垂直于纸面的一根导线，它是闭合电路的一部分，则（）A．针尖是S极B．a所处磁场方向向左C．a水平向右运动时，会产生感应电流D．a向上运动时，不会产生感应电流8．如图所示的电路是家庭电路的一部分，电工师傅按下面的顺序进行检测:Ⅰ闭合S1，灯L1亮；Ⅰ再闭合S2，灯L1亮，灯L2不亮；Ⅰ用试电笔测a、b、c、d四个接线点，试电笔只在c 点不发光。

广东广州市届高三第二次模拟考试数学（文）试题Word版含答案）年广州市普通高中毕业班综合测试（二）文科数学）.4本试卷共6页，23小题，满分150分。

考试用时120分钟。

注意事项：1．答卷前，考生务必将自己的姓名和考生号、试室号、座位号填写在答题卡上，用2B 铅笔在答题卡的相应位置填涂考生号，并将试卷类型(B)填涂在答题卡相应位置上。

2．作答选择题时，选出每小题答案后，用2B铅笔在答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合A={x∈N|0<x<6} , B={2, 4, 6, 8} ,则 A∩B=A.{0,1,3,5}B.{0,2,4,6}C. {1,3,5}D.{2,4,6}2．已知复数z=m(3+i)-(2+i)在复平面内对应的点在第三象限，则实数m的取值范围是A ． B. C ． D.3．某公司生产A，B，C三种不同型号的轿车，产量之比依次为2：3：4，为检验该公司的产品质量，用分层抽样的方法抽取一个容量为n的样本，若样本中A种型号的轿车比B种型号的轿车少8辆，则n=A. 96B. 72C. 48D. 364．执行如图所示的程序框图，则输出z的值是1 / 1。

广东省广州市高考数学二模试卷（文科）一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={﹣1，0，1，2，3，4，5}，B={b|b=n2﹣1，n∈Z}，则A∩B=（）A．{﹣1，3}B．{0，3}C．{﹣1，0，3}D．{﹣1，0，3，5}2．若复数z满足（3﹣4i+z）i=2+i，则z=（）A．4+6i B．4+2i C．﹣4﹣2i D．﹣2+2i．3．已知命题p：∀x∈R，x2+ax+a2≥0（a∈R），命题q：，，则下列命题中为真命题的是（）A．p∧q B．p∨q C．（¬p）∨q D．（¬p）∧（¬q）4．执行如图所示的程序图，则输出的S值为（）A．4 B．3 C．﹣2 D．﹣35．函数f（x）=ln（|x|﹣1）+x的大致图象是（）A．B．C．D．6．在区间[﹣1，5]上随机地取一个实数a，则方程x2﹣2ax+4a﹣3=0有两个正根的概率为（）A．B．C．D．7．已知三条直线2x﹣3y+1=0，4x+3y+5=0，mx﹣y﹣1=0不能构成三角形，则实数m的取值集合为（）A．{﹣， } B．{，﹣ } C．{﹣，， } D．{﹣，﹣， }8．已知两点A（﹣1，1），B（3，5），点C在曲线y=2x2上运动，则的最小值为（）A．2 B．C．﹣2 D．9．在棱长为2的正方体ABCD﹣A1B1C1D1中，M是棱A1D1的中点，过C1，B，M作正方体的截面，则这个截面的面积为（）A．B．C．D．10．数列{a n}满足a2=2，a n+（﹣1）n+1a n=1+（﹣1）n（n∈N*），S n为数列{a n}+2前n项和，S100=（）A．5100 B．2550 C．2500 D．245011．已知函数f（x）=2sin（ωx+）（ω＞0）的图象在区间[0，1]上恰有3个最高点，则ω的取值范围为（）A．[，）B．[，）C．[，）D．[4π，6π）12．如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的体积为（）A．B．C．D．16二、填空题已知双曲线（a＞0）的离心率为2，则a的值为．14．在各项都为正数的等比数列{a n}中，已知a1=2，，则数列{a n}的通项公式a n=．15．《孙子算经》是我国古代重要的数学著作，约成书于四、五世纪，传本的《孙子算经》共三卷，其中下卷：“物不知数”中有如下问题：“今有物，不知其数，三三数之，剩二；五五数之，剩三；七七数之，剩二，问：物几何？”其意思为：“现有一堆物品，不知它的数目，3个3个数，剩2个，5个5个数，剩3个，7个7个数，剩2个，问这堆物品共有多少个？”试计算这堆物品至少有个．16．已知函数，若f（3a﹣1）≥8f（a），则实数a的取值范围为．三、解答题（本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（12分）△ABC的内角A，B，C的对边分别为a，b，c，已知bcosC+bsinC=a．（Ⅰ）求角B的大小；（Ⅱ）若BC边上的高等于，求cosA的值．18．（12分）某中学为了解高中入学新生的身高情况，从高一年级学生中按分层抽样共抽取了50名学生的身高数据，分组统计后得到了这50名学生身高的频数分布表：（Ⅰ）在答题卡上作出这50名学生身高的频率分布直方图；（Ⅱ）估计这50名学生身高的方差（同一组中的数据用该组区间的中点值作代表）；（Ⅲ）现从身高在[175，185]这6名学生中随机抽取3名，求至少抽到1名女生的概率．19．（12分）如图，ABCD 是边长为a 的正方形，EB ⊥平面ABCD ，FD ⊥平面ABCD ，．（Ⅰ）求证：EF ⊥AC ；（Ⅱ）求三棱锥E ﹣FAC 的体积．20．（12分）已知定点F （0，1），定直线l ：y=﹣1，动圆M 过点F ，且与直线l 相切．（Ⅰ）求动圆M 的圆心轨迹C 的方程；（Ⅱ）过点F 的直线与曲线C 相交于A ，B 两点，分别过点A ，B 作曲线C 的切线l 1，l 2，两条切线相交于点P ，求△PAB 外接圆面积的最小值． 21．（12分）已知函数．（Ⅰ）求函数f （x ）的单调区间；（Ⅱ）若函数g （x ）=f （x ）+4x 存在极小值点x 0，且，求实数a 的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程]22．（10分）在平面直角坐标系xOy中．已知直线l的普通方程为x﹣y﹣2=0，曲线C的参数方程为（θ为参数），设直线l与曲线C交于A，B 两点．（1）求线段AB的长（2）已知点P在曲线C上运动．当△PAB的面积最大时，求点P的坐标及△PAB 的最大面积．[选修4-5：不等式选讲]23．（I）已知a+b+c=1，证明（a+1）2+（b+1）2+（c+1）2≥；（Ⅱ）若对任总实数x，不等式|x﹣a|+|2x﹣1|≥2恒成立，求实数a的取值范围．广东省广州市高考数学二模试卷（文科）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={﹣1，0，1，2，3，4，5}，B={b|b=n2﹣1，n∈Z}，则A∩B=（）A．{﹣1，3}B．{0，3}C．{﹣1，0，3}D．{﹣1，0，3，5}【考点】1E：交集及其运算．【分析】化简集合B，根据交集的定义写出A∩B．【解答】解：集合A={﹣1，0，1，2，3，4，5}，B={b|b=n2﹣1，n∈Z}={﹣1，0，3，8，15，…，}，∴A∩B={﹣1，0，3}．故选：C．【点评】本题考查了交集的定义与应用问题，是基础题．2．若复数z满足（3﹣4i+z）i=2+i，则z=（）A．4+6i B．4+2i C．﹣4﹣2i D．﹣2+2i．【考点】A5：复数代数形式的乘除运算．【分析】利用复数的运算法则、共轭复数的定义即可得出．【解答】解：（3﹣4i+z）i=2+i，则3﹣4i+z===﹣2i+1．∴z=﹣2+2i．故选：D．【点评】本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．3．已知命题p：∀x∈R，x2+ax+a2≥0（a∈R），命题q：，，则下列命题中为真命题的是（）A．p∧q B．p∨q C．（¬p）∨q D．（¬p）∧（¬q）【考点】2E：复合命题的真假．【分析】利用不等式的解法化简命题p，q，再利用复合命题的判定方法即可得出．【解答】解：命题p：∵△=a2﹣4a2=﹣3a2≤0，因此∀x∈R，x2+ax+a2≥0（a∈R），是真命题．命题q：由2x2﹣1≤0，解得≤x，因此不存在x0∈N*，使得，是假命题．则下列命题中为真命题的是p∨q．故选：B．【点评】本题考查了不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．4．执行如图所示的程序图，则输出的S值为（）A．4 B．3 C．﹣2 D．﹣3【考点】EF：程序框图．【分析】由已知中的程序语句可知该框图的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【解答】解：s=0，i=2，s=2，i=3，s=﹣1．i=4，s=3，i=5，s=﹣2，i=6，s=4，i=7＞6，结束循环，输出s=4，故选：A．【点评】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，属于基础题．5．函数f（x）=ln（|x|﹣1）+x的大致图象是（）A．B．C．D．【考点】3O：函数的图象．【分析】化简f（x），利用导数判断f（x）的单调性即可得出正确答案．【解答】解：f（x）的定义域为{x|x＜﹣1或x＞1}．f（x）=，∴f′（x）=，∴当x＞1时，f′（x）＞0，当x＜﹣2时，f′（x）＞0，当﹣2＜x＜﹣1时，f′（x）＜0，∴f（x）在（﹣∞，﹣2）上单调递增，在（﹣2，﹣1）上单调递减，在（1，+∞）上单调递增．故选A．【点评】本题考查了函数图象的判断，函数单调性的判断，属于中档题．6．在区间[﹣1，5]上随机地取一个实数a，则方程x2﹣2ax+4a﹣3=0有两个正根的概率为（）A．B．C．D．【考点】CF：几何概型．【分析】根据根与系数之间的关系，求出a的取值范围，结合几何概型的概率公式进行计算即可．【解答】解：若方程x2﹣2ax+4a﹣3=0有两个正根，则满足，即，得＜a≤1或a≥3，∵﹣1≤a≤5则对应的概率P=+=+=，故选：C【点评】本题主要考查几何概型的概率的计算，根据根与系数之间的关系求出a 的取值范围是解决本题的关键．7．已知三条直线2x﹣3y+1=0，4x+3y+5=0，mx﹣y﹣1=0不能构成三角形，则实数m的取值集合为（）A．{﹣， } B．{，﹣ } C．{﹣，， } D．{﹣，﹣， }【考点】IG：直线的一般式方程．【分析】三条直线若两两相交围成一个三角形，则斜率必不相同；否则，只要有两条直线平行，或三点共线时不能构成三角形．【解答】解：∵三条直线不能围成一个三角形，∴（1）l1∥l3，此时m=；l2∥l3，此时m=﹣；（2）三点共线时也不能围成一个三角形2x﹣3y+1=0与4x+3y+5=0交点是（﹣1，﹣）代入mx﹣y﹣1=0，则m=．故选：C．【点评】本题考查两直线平行的条件，当斜率相等且截距不相等时两直线平行．属于基础题．8．已知两点A（﹣1，1），B（3，5），点C在曲线y=2x2上运动，则的最小值为（）A．2 B．C．﹣2 D．【考点】9R：平面向量数量积的运算．【分析】设C（x，2x2），得出关于x的函数，根据函数性质求出最小值．【解答】解：设C（x，2x2），则=（4，4），=（x+1，2x2﹣1），∴=4（x+1）+4（2x2﹣1）=8x2+4x=8（x+）2﹣．∴当x=﹣时取得最小值﹣．故选D．【点评】本题考查了平面向量的数量积运算，函数最值得计算，属于中档题．9．在棱长为2的正方体ABCD﹣A1B1C1D1中，M是棱A1D1的中点，过C1，B，M作正方体的截面，则这个截面的面积为（）A．B．C．D．【考点】LA ：平行投影及平行投影作图法．【分析】由于截面被平行平面所截，所以截面为梯形，取AA 1的中点N ，可知截面为等腰梯形，利用题中数据可求．【解答】解：取AA 1的中点N ，连接MN ，NB ，MC 1，BC 1，由于截面被平行平面所截，所以截面为梯形，且MN=BC 1=，MC 1=BN ，=，∴梯形的高为，∴梯形的面积为（）×=，故选C ．【点评】本题的考点是棱柱的结构特征，主要考查几何体的截面问题，关键利用正方体图形特征，从而确定截面为梯形．10．数列{a n }满足a 2=2，a n +2+（﹣1）n +1a n =1+（﹣1）n （n ∈N *），S n 为数列{a n }前n 项和，S 100=（ ） A ．5100B ．2550C ．2500D ．2450【考点】8H ：数列递推式．【分析】数列{a n }满足a 2=2，a n +2+（﹣1）n +1a n =1+（﹣1）n （n ∈N *），n=2k （k ∈N *）时，a 2k +2﹣a 2k =2，因此数列{a 2k }为等差数列，首项为2，公差为2．n=2k ﹣1（k ∈N *）时，a 2k +1+a 2k ﹣1=0．通过分组求和，利用等差数列的求和公式即可得出．【解答】解：数列{a n }满足a 2=2，a n +2+（﹣1）n +1a n =1+（﹣1）n （n ∈N *），n=2k （k ∈N *）时，a 2k +2﹣a 2k =2，因此数列{a 2k }为等差数列，首项为2，公差为2．n=2k ﹣1（k ∈N *）时，a 2k +1+a 2k ﹣1=0．∴S 100=（a 1+a 3+…+a 97+a 99）+（a 2+a 4+…+a 100）=0+2×50+=2550．故选：B．【点评】本题考查了等差数列的通项公式与求和公式、数列递推关系、分类讨论方法、分组求和，考查了推理能力与计算能力，属于中档题．11．已知函数f（x）=2sin（ωx+）（ω＞0）的图象在区间[0，1]上恰有3个最高点，则ω的取值范围为（）A．[，）B．[，）C．[，）D．[4π，6π）【考点】H2：正弦函数的图象．【分析】根据区间[0，1]上，求出ωx+的范围，由于在区间[0，1]上恰有3个最高点，建立不等式关系，求解即可．【解答】解：函数f（x）=2sin（ωx+）（ω＞0），∵x∈[0，1]上，∴ωx+∈[，]，图象在区间[0，1]上恰有3个最高点，∴+，解得：．故选C．【点评】本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用，利用三角函数公式将函数进行化简是解决本题的关键．属于中档题．12．如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的体积为（）A．B．C．D．16【考点】L!：由三视图求面积、体积．【分析】根据三视图可知三棱锥倒立放置，从而得出棱锥的高，根据俯视图找出三棱锥的底面，得出底面积，从而可求出棱锥的体积．【解答】解：由主视图和侧视图可知三棱锥倒立放置，棱锥的底面水平放置，故三棱锥的高为h=4，∵主视图为直角三角形，∴棱锥的一个侧面与底面垂直，=4，结合俯视图可知三棱锥的底面为俯视图中的左上三角形，∴S底=∴V==．故选：B．【点评】本题考查了棱锥的三视图和体积计算，根据三视图的特征找出棱锥的底面是关键，属于中档题．二、填空题（2017•广州二模）已知双曲线（a＞0）的离心率为2，则a的值为．【考点】KB：双曲线的标准方程．【分析】求得双曲线的b2=2，由c=和e=，解关于a的方程，即可得到所求值．【解答】解：由双曲线（a＞0）得到b2=2，则c=，所以=2，解得a=．故答案是：．【点评】本题考查双曲线的方程和性质，注意运用离心率公式和基本量a，b，c 的关系，考查方程思想和运算能力，属于基础题．14．在各项都为正数的等比数列{a n}中，已知a1=2，，则数列{a n}的通项公式a n=．【考点】8H：数列递推式．【分析】设等比数列{a n}的公比为q＞0，由a1=2，，可得+=4，化简解出q，再利用等比数列的通项公式即可得出．【解答】解：设等比数列{a n}的公比为q＞0，∵a1=2，，∴+=4，化为：q4﹣4q2+4=0，解得q2=2，q＞0，解得q=．则数列{a n}的通项公式a n==．故答案为：．【点评】本题考查了等比数列的通项公式、数列递推关系，考查了推理能力与计算能力，属于中档题．15．《孙子算经》是我国古代重要的数学著作，约成书于四、五世纪，传本的《孙子算经》共三卷，其中下卷：“物不知数”中有如下问题：“今有物，不知其数，三三数之，剩二；五五数之，剩三；七七数之，剩二，问：物几何？”其意思为：“现有一堆物品，不知它的数目，3个3个数，剩2个，5个5个数，剩3个，7个7个数，剩2个，问这堆物品共有多少个？”试计算这堆物品至少有23个．【考点】F4：进行简单的合情推理．【分析】根据“三三数之剩二，五五数之剩三，七七数之剩二”找到三个数：第一个数能同时被3和5整除；第二个数能同时被3和7整除；第三个数能同时被5和7整除，将这三个数分别乘以被7、5、3除的余数再相加即可求出答案．【解答】解：我们首先需要先求出三个数：第一个数能同时被3和5整除，但除以7余1，即15；第二个数能同时被3和7整除，但除以5余1，即21；第三个数能同时被5和7整除，但除以3余1，即70；然后将这三个数分别乘以被7、5、3除的余数再相加，即：15×2+21×3+70×2=233．最后，再减去3、5、7最小公倍数的整数倍，可得：233﹣105×2=23，或者105k+23（k为正整数）．∴这堆物品至少有23，故答案为：23．【点评】本题考查的是带余数的除法，简单的合情推理的应用，根据题意下求出15、21、70这三个数是解答此题的关键，属于中档题．16．已知函数，若f（3a﹣1）≥8f（a），则实数a的取值范围为．【考点】5B：分段函数的应用．【分析】根据条件判断函数f（x）的奇偶性和单调性即可．【解答】解：∵，∴f（﹣x）=f（x），即函数f（x）是偶函数，在[0，+∞）上为增函数，则不等式f（3a﹣1）≥8f（a），等价为f（|3a﹣1|）≥f（2|a|），∴|3a﹣1|≥2|a|，解得a∈．故答案为．【点评】本题主要考查不等式的求解，根据条件判断函数的奇偶性和单调性是解决本题的关键．综合考查函数的性质．三、解答题（本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（12分）（2017•广州二模）△ABC的内角A，B，C的对边分别为a，b，c，已知bcosC+bsinC=a．（Ⅰ）求角B的大小；（Ⅱ）若BC边上的高等于，求cosA的值．【考点】HT：三角形中的几何计算．【分析】（Ⅰ）利用正弦定理求和三角形的三角的关系，以及两角和的正弦公式sinB=cosB，即可求出B，（Ⅱ）设BC边上的高线为AD，运勾股定理和余弦定理，即可求得cosB，再由正弦定理，即可求出【解答】解：（Ⅰ）因为bcosC+bsinC=a，由正弦定理得，sinBcosC+sinBsinC=sinA．因为A+B+C=π，所以sinBcosC+sinBsinC=sin（B+C）．即sinBcosC+sinBsinC=sinBcosC+cosBsinC．因为sinC≠0，所以sinB=cosB．因为cosB≠0，所以tanB=1．因为B∈（0，π），所以．（Ⅱ）设BC边上的高线为AD，则．因为，则，．所以=，．由余弦定理得=．所以cosA=．【点评】本题考查正弦定理和余弦定理的运用，考查两角和的正弦公式的运用，考查运算能力，属于中档题．18．（12分）（2017•广州二模）某中学为了解高中入学新生的身高情况，从高一年级学生中按分层抽样共抽取了50名学生的身高数据，分组统计后得到了这50名学生身高的频数分布表：（Ⅰ）在答题卡上作出这50名学生身高的频率分布直方图；（Ⅱ）估计这50名学生身高的方差（同一组中的数据用该组区间的中点值作代表）；（Ⅲ）现从身高在[175，185]这6名学生中随机抽取3名，求至少抽到1名女生的概率．【考点】CC：列举法计算基本事件数及事件发生的概率；B8：频率分布直方图．【分析】（Ⅰ）由频率分布表能作出这50名学生身高的频率分布直方图．（Ⅱ）由频率分布直方图能估计这50名学生的平均身高，并能估计这50名学生身高的方差．（Ⅲ）记身高在[175，185]的4名男生为a，b，c，d，2名女生为A，B．利用列举法能求出从这6名学生中随机抽取3名学生，至少抽到1名女生的概率．【解答】解：（Ⅰ）这50名学生身高的频率分布直方图如下图所示：（Ⅱ）由题意可估计这50名学生的平均身高为=164．所以估计这50名学生身高的方差为s2==80．所以估计这50名学生身高的方差为80．（Ⅲ）记身高在[175，185]的4名男生为a，b，c，d，2名女生为A，B．从这6名学生中随机抽取3名学生的情况有：{a，b，c}，{a，b，d}，{a，c，d}，{b，c，d}，{a，b，A}，{a，b，B}，{a，c，A}，{a，c，B}，{a，d，A}，{a，d，B}，{b，c，A}，{b，c，B}，{b，d，A}，{b，d，B}，{c，d，A}，{c，d，B}，{a，A，B}，{b，A，B}，{c，A，B}，{d，A，B}共20个基本事件．其中至少抽到1名女生的情况有：{a，b，A}，{a，b，B}，{a，c，A}，{a，c，B}，{a，d，A}，{a，d，B}，{b，c，A}，{b，c，B}，{b，d，A}，{b，d，B}，{c，d，A}，{c，d，B}，{a，A，B}，{b，A，B}，{c，A，B}，{d，A，B}共16个基本事件．所以至少抽到1名女生的概率为．【点评】本题考查频率分布直方图的应用，概率的求法，是基础题，解题时要认真审题，注意列举法的合理运用．19．（12分）（2017•广州二模）如图，ABCD是边长为a的正方形，EB⊥平面ABCD，FD⊥平面ABCD，．（Ⅰ）求证：EF⊥AC；（Ⅱ）求三棱锥E﹣FAC的体积．【考点】LF：棱柱、棱锥、棱台的体积．【分析】（Ⅰ）连接BD，推导出AC⊥BD，AC⊥FD，从而AC⊥平面BDF．推导出EB∥FD，从而B，D，F，E四点共面，由此能证明EF⊥AC．（Ⅱ）设AC∩BD=O，连接EO，FO，由V E﹣FAC =V A﹣FEO+V C﹣FEO，能求出三棱锥E﹣FAC的体积．【解答】证明：：（Ⅰ）连接BD，因为ABCD是正方形，所以AC⊥BD．因为FD⊥平面ABCD，AC⊂平面ABCD，所以AC⊥FD．因为BD∩FD=D，所以AC⊥平面BDF．因为EB⊥平面ABCD，FD⊥平面ABCD，所以EB∥FD．所以B，D，F，E四点共面．因为EF⊂平面BDFE，所以EF⊥AC．解：（Ⅱ）设AC∩BD=O，连接EO，FO．由（Ⅰ）知，AC⊥平面BDFE，所以AC⊥平面FEO．因为平面FEO将三棱锥E﹣FAC分为两个三棱锥A﹣FEO和C﹣FEO，所以V E﹣FAC =V A﹣FEO+V C﹣FEO．因为正方形ABCD的边长为a，，所以，．取BE的中点G，连接DG，则FE=DG=．所以等腰三角形FEO的面积为=．所以V E﹣FAC =V A﹣FEO+V C﹣FEO====．所以三棱锥E﹣FAC的体积为．【点评】本题考查线线垂直的证明，考查三棱锥的体积的求法，考查空间中线线、线面、面面间的关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．20．（12分）（2017•广州二模）已知定点F（0，1），定直线l：y=﹣1，动圆M过点F，且与直线l相切．（Ⅰ）求动圆M的圆心轨迹C的方程；（Ⅱ）过点F的直线与曲线C相交于A，B两点，分别过点A，B作曲线C的切线l1，l2，两条切线相交于点P，求△PAB外接圆面积的最小值．【考点】KN：直线与抛物线的位置关系；J3：轨迹方程．【分析】（Ⅰ）利用直接法，即可求动圆M的圆心轨迹C的方程；（Ⅱ）证明△PAB的外接圆的圆心为线段AB的中点，线段AB是直径．得到当k=0时线段AB最短，最短长度为4，此时圆的面积最小，最小面积为4π．【解答】解：（Ⅰ）设点M到直线l的距离为d，依题意|MF|=d．设M（x，y），则有=|y+1|．化简得x2=4y．所以点M的轨迹C的方程为x2=4y．（Ⅱ）设l AB：y=kx+1，代入x2=4y中，得x2﹣4kx﹣4=0．设A（x1，y1），B（x2，y2），则x1+x2=4k，x1•x2=﹣4．所以．因为C：x2=4y，即，所以．所以直线l1的斜率为，直线l2的斜率为．因为，所以PA⊥PB，即△PAB为直角三角形．所以△PAB的外接圆的圆心为线段AB的中点，线段AB是直径．因为|AB|=4（k2+1），所以当k=0时线段AB最短，最短长度为4，此时圆的面积最小，最小面积为4π．【点评】本题考查轨迹方程，考查直线与抛物线位置关系的运用，考查学生的计算能力，属于中档题．21．（12分）（2017•广州二模）已知函数．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）若函数g（x）=f（x）+4x存在极小值点x0，且，求实数a的取值范围．【考点】6D：利用导数研究函数的极值；6B：利用导数研究函数的单调性．【分析】（I）计算f′（x），讨论a判断f′（x）的符号得出f（x）的单调区间；（II）由导数和二次函数的性质得g′（x）=0在（0，+∞）上有两解列不等式组得出a的范围，根据得出a的范围，再取交集即可．【解答】解：（Ⅰ）因为函数，所以其定义域为（0，+∞）．所以=．当a≤0时，f'（x）＜0，函数f（x）在区间（0，+∞）上单调递减．当a＞0时，f'（x）=．当时，f'（x）＜0，函数f（x）在区间上单调递减．当时，f'（x）＞0，函数f（x）在区间上单调递增．综上可知，当a≤0时，函数f（x）的单调递减区间为（0，+∞）；当a＞0时，函数f（x）的单调递增区间为，单调递减区间为．（Ⅱ）因为g（x）=f（x）+4x=，所以=（x＞0）．因为函数g（x）存在极小值点，所以g'（x）在（0，+∞）上存在两个零点x1，x2，且0＜x1＜x2．即方程x2﹣4x﹣a=0的两个根为x1，x2，且0＜x1＜x2，所以，解得﹣4＜a＜0．则=．当0＜x＜x1或x＞x2时，g'（x）＜0，当x1＜x＜x2时，g'（x）＞0，所以函数g（x）的单调递减区间为（0，x1）与（x2，+∞），单调递增区间为（x1，x2）．所以x=x1为函数g（x）的极小值点x0．由，得．由于等价于．由，得，所以alnx0+a＞0．因为﹣4＜a＜0，所以有lnx0+1＜0，即．因为，所以．解得．所以实数a的取值范围为．【点评】本题考查了导数与函数单调性、极值的关系，函数最值得计算，属于中档题．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程]22．（10分）（2017•广州二模）在平面直角坐标系xOy中．已知直线l的普通方程为x﹣y﹣2=0，曲线C的参数方程为（θ为参数），设直线l 与曲线C交于A，B两点．（1）求线段AB的长（2）已知点P在曲线C上运动．当△PAB的面积最大时，求点P的坐标及△PAB 的最大面积．【考点】KL：直线与椭圆的位置关系；QL：椭圆的参数方程．【分析】（1）根据题意，将曲线C的参数方程变形为普通方程，将直线x﹣y ﹣2=0代入其中，可得x2﹣3x=0，解可得x的值，由弦长公式计算可得答案；（2）分析可得要使△PAB的面积最大，则必须使P到直线直线l的距离最大，设P的坐标为（2cosθ，2sinθ），其中θ∈[0，2π），由点到直线l的距离公式可得d=，由余弦函数的性质分析可得当θ+=π，即θ=时，d取得最大值，代入点的坐标（2cosθ，2sinθ）中可得P的坐标，进而计算可得△PAB的最大面积，即可得答案．【解答】解：（1）根据题意，曲线C的参数方程为，则其普通方程为： +=1，将直线x﹣y﹣2=0代入+=1可得：x2﹣3x=0，解可得x=0或3，故|AB|=|x1﹣x2|=3；（2）要求在椭圆+=1上求一点P，使△PAB的面积最大，则P到直线直线l的距离最大；设P的坐标为（2cosθ，2sinθ），其中θ∈[0，2π），则P到直线l的距离d==，又由θ∈[0，2π），则≤θ+＜，所以当θ+=π，即θ=时，d取得最大值，且d max=3，此时P（﹣3，1），△PAB的最大面积S=×|AB|×d=9．【点评】本题考查椭圆与直线的位置关系，涉及椭圆的参数方程，关键是正确将参数方程化为普通方程．[选修4-5：不等式选讲]23．（2017•广州二模）（I）已知a+b+c=1，证明（a+1）2+（b+1）2+（c+1）2≥；（Ⅱ）若对任总实数x，不等式|x﹣a|+|2x﹣1|≥2恒成立，求实数a的取值范围．【考点】R4：绝对值三角不等式；R6：不等式的证明．【分析】（I）利用柯西不等式，即可证明；（Ⅱ）分：①a=、②a＞、③a＜三种情况，分别化简不等式，根据函数y=|2x ﹣1|+|x﹣a|的最小值大于或等于2，求得a的范围．【解答】（I）证明：由柯西不等式可得（1+1+1）[（a+1）2+（b+1）2+（c+1）2]≥（a+1+b+1+c+1）2，∵a+b+c=1，∴（a+1）2+（b+1）2+（c+1）2≥；（Ⅱ）解：①当a=时，不等式即|x﹣|≥，显然不能任意实数x均成立．②当a＞时，|2x﹣1|+|x﹣a|=，此时，根据函数y=|2x﹣1|+|x﹣a|的单调性可得y的最小值为﹣3×+a+1．∵不等式|2x﹣1|+|x﹣a|≥2对任意实数x均成立，∴﹣3×+a+1≥2，解得a≥．③当a＜时，|2x﹣1|+|x﹣a|=，此时，根据函数y=|2x﹣1|+|x﹣a|的单调性可得y的最小值为﹣﹣a+1．∵不等式|2x﹣1|+|x﹣a|≥2对任意实数x均成立，∴﹣﹣a+1≥2，解得a≤﹣．综上可得，实数a的取值范围是（﹣∞，﹣]∪[，+∞）．【点评】本题主要考查绝对值不等式的解法，体现了转化以及分类讨论的数学思想，属于中档题．。