八年级(上)数学期中试题(珍藏版八)2018.11.

2018八年级数学上期中试卷（有答案和解释）
最短路线问题．
专题作图题．
分析作出点B关于cD的对称点B′，连接AB′交cD于点，连接B，根据对称性可知，在点处建水厂，铺设水管最短，所需费用最低．
解答解如图所示，点就是建水厂的位置，
∵Ac=1，BD=3，cD=3，
∴AE=Ac+cE=Ac+DB′=Ac+BD=1+3=4，
B′E=cD=3，
AB′= = =5，
铺设水管长度为A+B=A+B′=AB′=5，
∵铺设水管的工程费用为每千米20 000元，
∴铺设水管的总费用为5×20 000=100 000元．
故答案为100 000元．
点评本题考查了应用与设计作图，主要利用轴对称的性质，找出点B关于cD的对称点是确定建水厂位置的关键．
22．如图，在△ABc中，点E在AB上，点D在Bc上，BD=BE，∠BAD=∠BcE，AD与cE相交于点F，试判断△AFc的形状，并说明理由．
考点等腰三角形的判定；全等三角形的判定与性质．
专题探究型．
分析要判断△AFc的形状，可通过判断角的关系得出结论，那么就要看∠FAc和∠FcA的关系．因为∠BAD=∠BcE，因此我们只比较∠BAc和∠BcA的关系即可．根据题中的条BD=BE，∠BAD=∠BcE，△BDA。

2018学年第一学期八年级期中考试数学试卷时间：90分钟 满分：100分 2018.11 题号一 二 三 四 得分 得分一、填空题（每题2分，共30分）1.如果12-a 有意义，那么a 的取值范围是 ．2.计算：2)2(-=． 3.计算：62⋅= ．4.若最简二次根式a +4与1-2a 是同类二次根式，则=a． 5.不等式x x 22-<的解集是______________．6.方程()()525-=-x x x 的根是 ．7.若方程()01312=+--x x n 是关于x 的一元二次方程，则n ．8.已知关于x 的方程()0122=+--x x k 有两个不相等的实数根，则k 的取值范围是． 9.函数x x y -52-=的定义域是 ．10.已知函数xx x f 1)(-=，若2)(=x f ，则________=x ． 11.已知y 与x 成正比例，当8=x 时，12-=y ，则y 与x 的函数的解析式为 ．12. 在实数范围内分解因式：=--342x x ．13.某厂工业废气年排放量为450万立方米，为了改善上海市的大气环境质量，决定分二期投入治理，使废气的年排放量减少到288万立方米，如果每期治理中废气减少的百分率相同，每期减少的百分率是 ．14. 如果()()k k x k y 222-+-=是正比例函数，则k=．15. 已知a ，b 是实数，且()()11122=++++b b a a ，问a ，b 之间有怎样的关系： ．二、选择题（每题3分，共15分）16. 下列根式中，能与3合并的二次根式为………………………… （ ）A.24B.23 C.12 D. 18 17. 下列关于x 的一元二次方程中，有两个不相等的实数根的方程是…… （ ）A. 042=+xB. 01442=+-x xC. 032=++x xD. 01-22=+x x18. 下列各式中，一定成立的是………………………… （ ）A. ()b a b a +=+2B. ()11222+=+a aC. 1112-⋅+=-a a aD. ab bb a 1= 19. 下列说法正确的个数是………………………… （ ）①2+x 是x 的函数；②等腰三角形的面积一定，它的底边和底边上的高成正比例；③在函数x y 2-=中，y 随x 的增大而增大；④已知0<ab ，则直线x ba y -=经过第二、四象限. A. 1个 B.2个 C.3个 D. 4个20. 等腰ABC ∆的一边长为4，另外两边的长是关于x 的方程0012=+-m x x 的两个实数根，则等腰三角形底边的值是………………………… （ ）A.4B.25C.4或6D. 24或25三、简答题（每题5分，共20分）21. 计算：233-3135.012+-+ 22. 计算:()0312323>÷⎪⎭⎫ ⎝⎛-⋅a a b b a ab b23. 用配方法解方程02532=--x x 24. 解方程：()()33-2)23(2+=-x x x四、解答题（第25、26题每题6分，第27、28题每题7分，第29题9分，共35分） 25. 先化简，再求值：已知2231+=x ,求()2441-122--++-x x x x x 的值26. 已知y 与1-x 成正比例，且当3=x 时，4=y .(1)求y 与x 之间的函数解析式；(2)当1-=x 时，求y 的值；(3)当53-<<y 时，求x 的取值范围.27. 已知直线kx y =过点()12，-， A 是直线kx y =图像上的点，若过A 向x 轴作垂线，垂足为B ，且90=∆AB S ，求点A 的坐标.28. 某商店购进一种商品，进价30元。

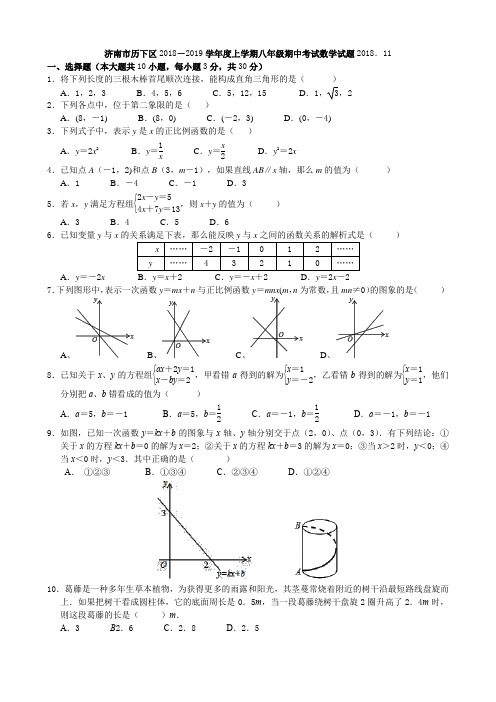
济南市历下区2018－2019学年度上学期八年级期中考试数学试题2018．11一、选择题（本大题共10小题，每小题3分，共30分）1．将下列长度的三根木棒首尾顺次连接，能构成直角三角形的是（ ） A ．1，2，3 B ．4，5，6 C ．5，12，15 D ．1，3，2 2．下列各点中，位于第二象限的是（ ）A ．(8，－1)B ．(8，0)C ．(－2，3)D ．(0，－4) 3．下列式子中，表示y 是x 的正比例函数的是（ ）A ．y ＝2x 2B ．y ＝1xC ．y ＝x 2D ．y 2＝2x4．已知点A （－1，2)和点B （3，m －1），如果直线AB ∥x 轴，那么m 的值为（ ）A ．1B ．－4C ．－1D ．35．若x ，y 满足方程组⎩⎨⎧2x －y ＝54x ＋7y ＝13，则x ＋y 的值为（ ）A ．3B ．4C ．5D ．66．已知变量y 与x 的关系满足下表，那么能反映y 与x 之间的函数关系的解析式是（ ）A ．y ＝－2xB ．y ＝x ＋2C ．y ＝－x ＋2D ．y ＝2x －2 7．下列图形中，表示一次函数y ＝mx ＋n 与正比例函数y ＝mnx (m ，n 为常数，且mn ≠0）的图象的是（ ）A 、B 、C 、D 、8．已知关于x 、y 的方程组⎩⎨⎧ax ＋2y ＝1x －by ＝2，甲看错a 得到的解为⎩⎨⎧x ＝1y ＝－2，乙看错b 得到的解为⎩⎨⎧x ＝1y ＝1，他们分别把a 、b 错看成的值为（ ）A ．a ＝5，b ＝－1B ．a ＝5，b ＝12C ．a ＝－1，b ＝12 D ．a ＝－1，b ＝－19．如图，已知一次函数y ＝kx ＋b 的图象与x 轴、y 轴分别交于点（2，0）、点（0，3）．有下列结论：①关于x 的方程kx ＋b ＝0的解为x ＝2；②关于x 的方程kx ＋b ＝3的解为x ＝0；③当x ＞2时，y ＜0；④当x ＜0时，y ＜3．其中正确的是（ ）A ． ①②③B ．①③④C ．②③④D ．①②④10．葛藤是一种多年生草本植物，为获得更多的雨露和阳光，其茎蔓常烧着附近的树干沿最短路线盘旋而上．如果把树干看成圆柱体，它的底面周长是0．5m ，当一段葛藤绕树干盘旋2圈升高了2．4m 时，则这段葛藤的长是（ ）m ．A ．3B 2．6C ．2．8D ．2．511．如图，△ABC 中，∠ACB ＝90°，AC ＝4，BC ＝2，点D 在AB 上，将△ACD 沿CD 折叠，点A 落在点A 1，A 1C 与AB 相交于点E ，若A 1D ∥BC ，则A 1E 的长为（ ） A ．22 B ．83 C ．523 D ．4－32212．端午节前乡，在大明湖举行第七届会民健身运动会龙舟比赛中，甲、乙两队在500米的赛道上，所划行的路程y （m ）与时间x （m i n ）之间的函数关系如图所示，下列说法：①乙队比甲队提前0．25m i n 到达终点；②0．5m i n 后，乙队比甲队每分钟快40m ；③当乙队划行110m 时，此时落后甲队15m ；④自1．5m i n 开始，甲队若要与乙队同时到达终点，甲队的速度需要提高到260m /m i n ． 其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个 二、填空题（本大题共6个小题，每小题4分，共24分） 13．点A （－3，4）到y 轴的距离为________；14．若一直角三角形两边长6，8，则第三边长为________； 15．直线y ＝kx 向上平移4个单位后，经过（－1，2），则________； 16．已知点P 1（－2，y 1）、P 2（－1，y 2）是函数y ＝－5x ＋9图象上的两个点，则y 1_______ y 2；（填“＞”，“＜“或＝”）17．如图，一次函数y ＝kx ＋b 与y ＝x ＋2的图象相交于点P （m ，4），则方程组⎩⎨⎧y ＝kx ＋by ＝x ＋2的解是________；18．如图，直线y ＝3x ，点A 1坐标为（1，0)，过点A 1作x 轴的垂线交直线于点B 1，以原点O 为圆心，OB 1长为半径画弧交x 轴于点A 2；再过点A 2作x 轴的垂线交直线于点B 2 ， 以原点O 为圆心，OB 2长为半径画弧交x 轴于点A 3 ， …，按此做法进行下去，点A n 的坐标为___________． 三、解答题（本大题共7小题，共78分）19．解方程组（本小题等题6分，共12分）(1)⎩⎨⎧y ＝2x －43x ＋y ＝1 (2)⎩⎪⎨⎪⎧3x －2(y －1)＝11x 4＋y 3＝320．（本小题6分）如图，在平面直角坐标系中， （1）描出A （2，1），B （－1，3）两点；（2）描出点A 关于y 轴的对称点C ，点B 关于x 轴的对称点D ；（3）依次连接点A 、B 、C 、D 得到四边形ABCD ，则四边形ABCD 的面积为_______．21．（本小题8分）如图是一块四边形绿地，其中AB ＝4m ，BC ＝13m ，CD ＝12m ，DA ＝3m ，∠A ＝90°，求这块绿地的面积。

2018年八年级上册期中考试数学试卷(含答案和解释)
轴对称变换．
【分析】利用关于x轴对称点的性质以及关于轴对称点性质分别得出对应点坐标进而得出答案．
【解答】解△ABc关于x轴对称的△A1B1c1的各顶点坐标分别为A1（﹣3，﹣2），B1（﹣4，3），c1（﹣1，1），
如图所示△A2B2c2，即为所求．
【点评】此题主要考查了关于坐标轴对称点的性质，正确把握横纵坐标关系是解题关键．
21．求出下列图形中的x值．
【考点】多边形内角与外角．
【分析】根据五边形的内角和等于540°，列方程即可得到结果．【解答】解∵五边形的内角和为（5﹣2）×180°=540，
∴90°x°+（x﹣10）°+x°+（x+20）°=540°，
解得x=110°．
【点评】本题考查了五边形的内角和，熟记五边形的内角和是解题的关键．
22．如图，△ABc，∠c=90°，∠ABc=60°，BD平分∠ABc，若AD=8，求cD的长．
【考点】含30度角的直角三角形；等腰三角形的判定与性质．【分析】根据题意得出∠A=30°，根据角平分线的性质得出∠A=∠ABD，根据30°角所对的直角边等于斜边的一半，得cD= DB，即可得出cD=4．
【解答】解∵∠c=90°，∠ABc=60°，
∴∠A=30°，
∵BD平分∠ABc，
∴∠ABD=∠cBD=30°，
∴∠A=∠ABD，。

2018年八年级上学期期中考试试卷数 学(满分120分 考试时间120分钟)一、选择题(本大题共12个小题,每小题3分,共36分)1、36的算术平方根是（ ）.A.6B.6±C.6D.6±2、若△ABC ≌△DEF,∠A=60°,∠B=50°,那么∠F 的度数是( ).A.120°B.80°C.70°D.60°33，-π，227( ). A ． 2个 B ． 3个 C ． 4个 D ． 5个4、如图，已知∠BAD=∠CAD ，则下列不能．．判定△ABD ≌△ACD 的条件是（ ）． A ． AB=AC B ． ∠B=∠C C ． BD=CD D ． ∠ADB=∠ADC5、如图所示，小明课本上的三角形被墨水污染了，他根据所学知识在另一张纸上画出了完全一样的一个三角形，他根据的定理是（ ）.A ． SSSB ． ASAC ． AASD ． SAS6、下列根式中属最简二次根式的是（ ）.AB73b =-，则（ ）.A ．b>3B ．b<3C ．b ≤3D ．b ≥38、如图，在△ABC 中，AB=AC ，∠A=36°，BD ，CE 是角平分线，则图中的等腰三角形共有（ ）.A ． 8个B ． 7个C ． 6个D ． 5个9、若8y ）.A ． 2B ． 2±C ． 4D ． 4±10、右图是一个正方体的展开图，已知这个正方体各对面的式子之积是相等的，那么x 为（ ）.A ．3B ．23C ．26D ．26 11、已知△ABC 的三个内角为∠A ，∠B ，∠C 且α=∠A+∠B ，β=∠C+∠A ，γ=∠C+∠B ，则α，β，γ中，锐角的个数最多为（ ）.A ． 1B ． 2C ． 3D ． 012、下列命题：①有两个角和第三个角的平分线对应相等的两个三角形全等；②有两条边和第三条边上的中线对应相等的两个三角形全等；③有两条边和第三条边上的高对应相等的两个三角形全等．其中是真命题的是（ ）.A ． ①②B ． ②③C ． ①③D ． ①②③二、填空题(本大题共6个小题,每小题3分,共18分)13、比较大小:26_____73.14、如果a ，b 分别是2018的两个平方根，那么a b ab +-＝_____．15、如图，△ABC 中，AB=AC ，AD ⊥BC 于D 点，DE ⊥AB 于点E ，BF ⊥AC 于点F ，DE=3cm ，则BF= cm ．16、a ，小数部分为b ，则)a b 的值为 ．17时，越给人一种美感．如果一本数学书的宽为14cm,为尽可能达到好的视觉效果，应把数学书的长设计为_____cm ．18、设如图钢架中，焊上等长的13根钢条来加固钢架，若AP 1=P 1P 2=P 2P 3=…=P 13P 14=P 14A ，则∠A 的度数是_________．三、解答题（本大题共2小题，每小题6分，共12分）19、计算：（1） （2）()()()3332221442--⎪⎭⎫ ⎝⎛-⋅-+-⋅20、尺规作图已知：线段a ，∠α．求作：Rt △ABC ，使斜边AB=a ，∠B=∠α．（不写作法，保留作图痕迹）四、解答题（本大题共2小题，每小题8分，共16分）21、如图，在数轴上的三点A 、B 、C 分别表示实数a 、b 、c ，a c +22、如图，点E 在△ABC 外部，点D 在BC 边上，DE 交AC 于点F ，若∠C=∠E ，DE=BC ，AC=AE ，求证：AD 平分∠BDE ．五、解答题（本大题共2小题，每小题9分，共18分）23、已知a 、b (27a b ++)2＝0，求a ba b-⋅2的值．24、如图，已知△ABC 为等边三角形，点D 、E 分别在BC 、AC 边上，且AE=CD ，AD 与BE 相交于点F .(1)求证：△ABE ≌△CAD ；⑵求∠BFD 的度数．六、解答题（本大题共2小题，每小题10分，共20分）25、小明在解决问题：已知a =2281a a -+的值，他是这样分析与解的：∵2a =-∴2a -=∴()223a -=，即2443a a -+= ∴241a a -=-∴()()111214218222-=+-⨯=+-=+-a a a a请你根据小明的分析过程，解决如下问题：（1（2）若a =2481a a -+的值（3）若1a ，求3227212a a a +--的值．26、（1）问题发现：如图，已知：AB=AC ，∠BAC=90°，直线m 经过点A ，过点B 作BD ⊥m 于D ， CE ⊥m 于E ．我们把这种常见图形定义为“K ”字图.很容易得到线段DE 、BD 、CE 之间的数量关系是 (直接写结论，无需证明）.（2）拓展探究：如图2，若AB=AC ，∠BAC=∠BDA=∠AEC ，则线段DE 、BD 、CE 之间的数量关系还成立吗？如果成立，请证明之.（3）解决问题：如图3，若AB=AC ，∠BAC=∠BDA=∠AEC=120°，点F 为∠BAC 平分线上的一点，且△ABF 和△ACF 均为等边三角形，BD=2，CE=4，求△DEF 的周长.。

2018年八年级数学上册期中试题（带答案）
2018年八年级数学上册期中试题（带答案）
说明本试题满分120分，考试时间100分钟。

一、选择题（每小题3分，共36分）
1．若等腰三角形的底角为54°，则顶角为
A．108° B．72° c．54°D．36°
2．下列各式由左边到右边的变形，属于因式分解的是
A．
B．
c．
D．
3．若分式的值为0，则的值是
A．－l B．－l或2 c．2 D．－2
4．下列说法正确的是
A．轴对称图形的对称轴只有一条B．角的对称轴是角的平分线
c．成轴对称的两条线段必在对称轴同侧D．等边三角形是轴对称图形
5．下列式子中总能成立的是
A． B．
c． D．
6．如果把分式中的都扩大3倍，那么分式的值
A．扩大3倍 B．不变 c．缩小3倍D．缩小6倍
7．若点A（，－l），与点B（4，）关于轴对称，则
A． B．
c． D．
8．下列分解因式正确的是
A． B．。

2018学年第一学期八年级期中考试数学试卷一、仔细选一选（本大题有10小题，每小题3分，共30分。

） 1．三根木条的长度如图，能组成三角形的是（ ▲ ）2．在下列各组图形中，是全等的图形是（ ▲ ）A. B. C. D. 3．把不等式x ＞2表示在数轴上，正确的是（ ▲ ）4. 下列命题属于真命题的是（ ▲） A. 由a b >，得22a b -<-B. 由a b >，得22a b -<-C. 由a b>，得a b >D. 由a b >，得22a b >5．用直尺和圆规作线段的垂直平分线,下列作法正确的是2cm2cm 5cmA.2cm 2cm 4cmB.2cm 3cm 5cmC. 2cm 3cm 4cmD.A .B .C .D .B ．D ．C ．6．若等腰三角形中有一个角等于50°，则这个等腰三角形的顶角为（ ▲ ）A ．50°B ．80°C ．50°或80°D ．50°或65°7．如图，△ABC 内有一点D ，且DA =DB =DC ，若∠DAB =20°， ∠DAC =30°，则∠BDC 的大小是（ ▲ ） A. 100° B. 80° C. 70°D. 50°8．如图，a 、b 、c 分别表示△ABC 的三边长，则下面与△ABC 一定．．全等的三角形是（ ▲ ）A B C DA. 0B. 1C. 2D. 39．已知直角三角形的两条边长分别是6cm 和8cm ，则它的第三边长为（ ▲ ）A ．5.5cmB ．cmC ．10cmD ．10cm 或10．设a 、b 、c 均为正整数，且c b a ≥≥，满足15=++c b a ，则以a 、b 、c 为边长的三角形有（ ▲ ）A ．5个B ．7个C ．10个D ．12个 二、认真填一填（本题有6小题，每小题3分，共18分） 11．“x 减去y 小于4-”用不等式可表示为 ▲ . 12. 在Rt △ABC 中，∠A ＝25°，则锐角∠B ＝ ▲ 度． 13．不等式2x ＞5x -6的正整数解是 ▲ .14. 如图,△ABC 中,AB ＋AC =6cm ,BC 的垂直平分线l 与AC 相交于点D ,则△ABD 的周长为 ▲ cm ．15．如图，点P 在AOB ∠的平分线上，若使AOP BOP △≌△，则需添加的一个条件是 ▲ （只写一个即可，不 添加辅助线）．AD 50° b a a 72° 50° a 50° b 58° ba AbC a c 72° B50°AB POABCDl（第14题图）21EDCBA16．如图,Rt △ABC ≌Rt △DEB ,点A ，B ，D 在同一直线上,AC=1,DE=3,则△BCE 的面积为 ▲ ．三、解答题（本大题有8小题，共52分） 17.（本题4分）解不等式5x ＞3(x －2)＋2.18.（本题4分）已知等腰△ABC 的腰长AB =AC =5，底边长BC =6，试求这个三角形的面积.19.（本题6分）如图，AD ∥BC ，∠A=90°,E 是AB 上一点，且AD=BE ， ∠1=∠2. R t △ADE 与Rt △BEC 全等吗？请说明理由；20．（本题6分）如图,在6×6方格纸中（每个小正方形的边长均为1个单位长度）,有直线MN 和线段AB ,其中点A ,B ,M ,N 均在小正方形的顶点上． （1）在方格纸中画出线段AB 关于直线MN 的轴对称图形CD ,点A 的对称点为点D ,点B 的对称点 为点C ,连接AD ,BC ； （2）求出四边形ABCD 的周长.B DC E（第16题图）（第20题图）AB M N21.（本题6分）将一副三角板按如图方式叠放在一起,（1）求∠AOD＋∠BOC的度数；（2）当AB的中点E恰好落在CD的中垂线上时,求∠AOC的度数．22.（本题8分）如图，在△ABC和△DCB中，AB = DC，AC = DB，AC与DB交于点M．（1）求证：△ABC≌△DCB；（2）过点C作CN∥BD，过点B作BN∥AC，CN与BN交于点N，若∠AMB=70°，求∠N的度数．23．（本题8分）如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点，求证：（1）ACE BCD△≌△；（2）222AD DB DE+=．24.（本题10分）△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向△ABC作等腰Rt△ABE和等腰Rt△ACF，过点E、F作射线GA的垂线，垂足分别为P、Q。

2018-2019（含答案）八年级（上）期中数学试卷 (11).................................................................................................................................................................2018.10.22一、选择题：下列每小题给出的四个选项中，只有一个是正确的，每小题3分，本大题共30分．1.下面四个图形中，线段是的高的图是（）A. B.C. D.2.已知，则三个角度数分别是（）A.、、B.、C.、、D.、、3.根据下列已知条件，能唯一画出的是（）A.，，B.，，C.，，D.，4.如图所示，在中，已知点、、分别为边、、的中点，且的面积是，则阴影部分面积等于（）A. B. C. D.5.三角形中，有一个外角是，则这个三角形的形状是（）A.锐角三角形B.直角三角形C.钝角三角形D.无法确定形状6.正多边形的一个内角等于，则该多边形是正（）边形．A. B. C. D.7.中，，中线，则边的取值范围是（）A. B.C. D.8.直角三角形的两个锐角平分线的夹角是（）A. B.C.或D.由两个锐角的大小决定9.如图，点是内一点，，，，则等于（）A. B. C. D.无法确定10.已知，，为三角形的三边，化简的值为（）A. B. C. D.二、填空题：本大题共8个小题，每小题3分，共24分．11.等腰三角形的周长为，一边长为，则底边长为________．12.已知，，，，则边上的高是________．13.如果三角形的一个外角等于和它相邻的内角的倍，等于与它不相邻的一个内角的倍，则此三角形各内角的度数是________．14.已知在中，，，则________．15.如图所示，________．16.在中，，，平分交于，于．若，则的长等于________．17.如图，在中，，三角形的外角和的平分线交于点，则________．18.如图，，，，，则的度数为________．三、解答题：本大题共7个小题，满分46分．19.已知在中，，．求三角形的各内角的度数．20.如图，，，，，若设，探究与的关系．21.如图所示，在中，是高，、是角平分线，它们相交于点，，，求、的度数．22.如图，过平分线上一点作交于点，是线段的中点，请过点画直线分别交射线、于点、，探究线段、、之间的数量关系，并证明你的结论．23.如图，在四边形中，是边的中点．若平分，，猜想线段、、的长度满足的数量关系为并证明．24.如图，已知：在中，，，直线经过点，直线，直线，垂足分别为点、．证明：．如图，将中的条件改为：在中，，、、三点都在直线上，并且有．请问结论是否还成立？如果成立，请你给出证明；若不成立，请说明理由．如图，、是直线上的两动点（、、三点互不重合），点为平分线上的一点，且和均为等边三角形，连接、，若，试判断的形状．25.如图，在等边的顶点、处各有一只蜗牛，它们同时出发，分别以相同的速度由向和由向爬行，经过分钟后，它们分别爬行到、处，设与的交点为点．求证：；蜗牛在爬行过程中，与所成的的大小有无变化？请证明你的结论．答案1. 【答案】A【解析】根据三角形高的画法知，过点作边上的高，垂足为，其中线段是的高，再结合图形进行判断．【解答】解：由题可得，线段是的高的图是选项．故选．2. 【答案】D【解析】设，则，，再根据三角形内角和定理求出的值即可．【解答】解：∵ ，∴设，则，，∵ ，∴ ，解得，∴ ，．故选．3. 【答案】C【解析】要满足唯一画出，就要求选项给出的条件符合三角形全等的判定方法，不符合判定方法的画出的图形不一样，也就是三角形不唯一，而各选项中只有选项符合，是满足题目要求的，于是答案可得．【解答】解：、因为，所以这三边不能构成三角形；、因为不是已知两边的夹角，无法确定其他角的度数与边的长度；、已知两角可得到第三个角的度数，已知一边，则可以根据来画一个三角形；、只有一个角和一个边无法根据此作出一个三角形．故选．4. 【答案】B【解析】如图，因为点是的中点，所以的底是的底的一半，高等于的高；同理，、、分别是、的中点，与同底，的高是高的一半；利用三角形的等积变换可解答．【解答】解：如图，点是的中点，∴ 的底是，的底是，即，高相等；∴，同理得，，∴，且，∴ ，即阴影部分的面积为．故选．5. 【答案】C【解析】根据外角求出三角形的内角，从而判断出三角形的形状．【解答】解：∵相邻的内角为，∴三角形为钝角三角形，故选．6. 【答案】C【解析】根据正多边形的每个内角相等，可得正多边形的内角和，再根据多边形的内角和公式，可得答案．【解答】解：设正多边形是边形，由题意得．解得，故选；．7. 【答案】D【解析】延长至，使，连接，使得，则将和已知线段转化到一个三角形中，进而利用三角形的三边关系确定的范围即可．【解答】解：延长至，使，连接．在和中，，，，∴ ．∴ ．在中，根据三角形的三边关系，得，即．则．故选．8. 【答案】B【解析】如图，，、分别平分和，利用角平分线的定义得到，，则，再根据三角形内角和得到，则，所以，然后利用两直线的夹角为锐角可判定直角三角形的两个锐角平分线的夹角是．【解答】解：如图，，、分别平分和，∵ 、分别平分和，∴，，∴，∵ ，∴ ，∴ ，∴ ，∴直角三角形的两个锐角平分线的夹角是或．故选．9. 【答案】C【解析】先根据三角形内角和定理求出的度数，再根据即可得出结论．【解答】解：∵ ，，，∴ ，∵ ，∴ ．故选．10. 【答案】D【解析】根据三角形的三边关系即可得到，，根据绝对值的性质即可去掉绝对值符号，从而化简．【解答】解：根据题意得：，．则，，则原式．故选．11. 【答案】或【解析】分是底边与腰长两种情况讨论求解．【解答】解：① 是底边时，腰长，此时三角形的三边分别为、、，能组成三角形，② 是腰长时，底边，此时三角形的三边分别为、、，能组成三角形，综上所述，底边长为或．故答案为：或．12. 【答案】【解析】根据三角形的面积公式和已知条件求出中边上的高，然后根据全等三角形的性质即可求出中边上的高．【解答】解：∵高，且，∴ 的高为，∵ ，∴ 边上的高是．故填．13. 【答案】，，【解析】先根据已知三角形的一个外角等于与它相邻的内角的倍，互为邻补角的两个角和为，从而求出这个外角与它相邻的内角的度数．根据这个外角还等于与它不相邻的一个内角的倍，可以得到这两个与它不相邻的内角的度数，进而得到这个三角形各角的度数．【解答】解：∵三角形的一个外角等于与它相邻的内角的倍，∴可设这一内角为，则与它相邻的外角为，∴ ，解得，∴ ，又∵这个外角还等于与它不相邻的一个内角的倍，∴与它不相邻的一个内角为：，∴第三个内角为，∴这个三角形各角的度数分别是，，．故答案为：，，．14. 【答案】【解析】先根据三角形内角和定理得出的度数，再由即可得出结论．【解答】解：∵在中，，∴ ①，∵ ②，∴①-②得，，解得．故答案为：．15. 【答案】【解析】根据三角形的性质，可得答案．【解答】解：连接，，故答案为：．16. 【答案】【解析】先利用等腰直角三角形的性质得，再判断为等腰直角三角形得到，接着证明得到，，则，然后证明即可．【解答】解：∵ ，，∴ ，∵ ，∴ 为等腰直角三角形，∴ ，∵ 平分，∴ ，在和中，∴ ，∴ ，，∴ ，∴ ．故答案为．17. 【答案】【解析】根据三角形内角和定理、角平分线的定义以及三角形外角定理求得；最后在中利用三角形内角和定理可以求得的度数．【解答】解：∵三角形的外角和的平分线交于点，∴，；又∵ （已知），（三角形内角和定理），∴（外角定理），∴．故答案为：．18. 【答案】【解析】首先利用三角形内角和计算出，再计算出的度数，然后再根据全等三角形的性质可得答案．【解答】解：∵ ，，∴ ，∵ ，∴ ，∵ ，∴ ，∴ ，即，故答案为：．19. 【答案】解：∵ ，，∴ ，在中，，解得，∴ ，．所以，三角形的各内角的度数分别为，，．【解析】根据已知条件用表示出，然后根据三角形的内角和等于列式计算求出，然后求解即可．【解答】解：∵ ，，∴ ，在中，，解得，∴ ，．所以，三角形的各内角的度数分别为，，．20. 【答案】解：∵ ，，∴，∵ ，，∴ ，∴，∴．∴．【解析】由于，根据三角形的内角和为即可求出、的度数，利用余角的性质和平角的定义即可求出与的关系．【解答】解：∵ ，，∴，∵ ，，∴ ，∴，∴．∴．21. 【答案】解：∵∴∵∴ ；∵ ，∴ ，∵ 是的角平分线∴∴ ．【解析】因为是高，所以，又因为，所以度数可求；因为，，所以，，是的角平分线，则，故的度数可求．【解答】解：∵∴∵∴ ；∵ ，∴ ，∵ 是的角平分线∴∴ ．22. 【答案】解：线段、、之间的数量关系是：．证明：∵ 是的平分线，∴ ，又∵ ，∴ ，∴ ，∴ ，∵ 是线段的中点，∴ ，∵ ，∴，∴ ，又∵ ，∴ ．【解析】首先根据是的平分线，，判断出，所以；然后根据是线段的中点，，推得，即可判断出，据此解答即可．【解答】解：线段、、之间的数量关系是：．证明：∵ 是的平分线，∴ ，又∵ ，∴ ，∴ ，∴ ，∵ 是线段的中点，∴ ，∵ ，∴，∴ ，又∵ ，∴ ．23. 【答案】解：；理由：在上取一点，使．∵ 平分，∴ ．在和中，，∴ ，∴ ，．∵ 是边的中点．∴ ，∴ ．∵ ，∴ ，∴ ．在和中，，∴ ，∴ ．∵ ，∴ ．【解析】在上取一点，使，即可得出，就可以得出，，就可以得出．就可以得出结论．【解答】解：；理由：在上取一点，使．∵ 平分，∴ ．在和中，，∴ ，∴ ，．∵ 是边的中点．∴ ，∴ ．∵ ，∴ ，∴ ．在和中，，∴ ，∴ ．∵ ，∴ ．24. 【答案】证明： ∵ 直线，直线，∴ ，∵ ，∴ ，∵ ，∴ ，在和中，，∴ ，∴ ，，∴ ；; ∵ ，∴ ，∴ ，在和中，，∴ ，∴ ，，∴ ；; ∵ 和均为等边三角形，∴ ，∴ ，∴ ，∴ ，在和中，，∴ ，∴ ，，∵ ，，∴ ，在与中，，∴ ，∴ ，，∵ ，∴ ，即，∴ 是等边三角形．【解析】根据直线，直线得，而，根据等角的余角相等得，然后根据“ ”可判断，则，，于是；; 利用，则，得出，进而得出即可得出答案；; 由和均为等边三角形，得到，利用，则，得出，进而得出，根据全等三角形的性质得到，，得到，根据全等三角形的性质得到，，根据得到结论．【解答】证明： ∵ 直线，直线，∴ ，∵ ，∴ ，∵ ，∴ ，在和中，，∴ ，∴ ，，∴ ；; ∵ ，∴ ，∴ ，在和中，，∴ ，∴ ，，∴ ；; ∵ 和均为等边三角形，∴ ，∴ ，∴ ，∴ ，在和中，，∴ ，∴ ，，∵ ，，∴ ，在与中，，∴ ，∴ ，，∵ ，∴ ，即，∴ 是等边三角形．25. 【答案】证明：∵ ，两只蜗牛速度相同，且同时出发，∴ ；，在与中，，∴ ； ; 解：和所成的的大小不变．理由如下：∵ ，∴ ．【解析】根据即可判断出；; 根据，可知．【解答】证明：∵ ，两只蜗牛速度相同，且同时出发，∴ ；，在与中，，∴ ； ; 解：和所成的的大小不变．理由如下：∵ ，∴ ．。

2018年八年级数学上期中试卷（附答案和解释）
最短路线问题．
【分析】分别作点P关于A、B的对称点c、D，连接cD，分别交A、B于点、N，连接c、D、P、PN、N，由对称的性质得出P=D，P=c，∠cA=∠PA；PN=DN，P=D，∠DB=∠PB，得出∠AB= ∠cD，证出△cD 是等边三角形，得出∠cD=60°，即可得出结果．
【解答】解分别作点P关于A、B的对称点c、D，连接cD，
分别交A、B于点、N，连接c、D、P、PN、N，如图所示
∵点P关于A的对称点为D，关于B的对称点为c，
∴P=D，P=D，∠DA=∠PA；
∵点P关于B的对称点为c，
∴PN=cN，P=c，∠cB=∠PB，
∴c=P=D，∠AB= ∠cD，
∵△PN周长的最小值是5c，
∴P+PN+N=5，
∴D+cN+N=5，
即cD=5=P，
∴c=D=cD，
即△cD是等边三角形，
∴∠cD=60°，
∴∠AB=30°；
故选B．
12．为了求1+2+22+23+…+22018+22018的值，可令S=1+2+22+23+…+22018+22018，则2S=2+22+23+24+…+22018+22018+22018，因此2S﹣S=22018﹣1，所以1+2+22+23+…+22018=22018﹣1．仿照以上推理计算出1+5+52+53+…52018的值是（）。

2018年八年级上册数学期中试卷(含答案和解释)
最短路线问题；作图—应用与设计作图．
【分析】（1）首先作出A点的对称点A′，然后连接BA′，找到交点P点；
（2）首先连接AB，由题意知AB=3，A A′=4，然后由勾股定理求得A′B的长，即PA+PB的最小值．
【解答】解（1）作图，如右图，
作出A点的对称点A′，
连接BA′，找到交点P点；
（2）连接AB，由题意知AB=3，A A′=4，
在Rt△A A′B中，根据勾股定理得A′B2=42+32，
∴A′B=5，
即PA+PB=A′B=5，
答PA+PB的最小值是5．
【点评】此题考查了最短路径问题以及勾股定理．注意准确找到点P是解此题的关键．
四、耐心做一做本大题共2小题，每小题7分，共14分．解答应写出字说明、推理过程或演算步骤．
21．如图在△ABc中，AB=Ac，求证∠B=∠c．
【考点】全等三角形的判定与性质；等腰三角形的性质．
【专题】证明题．
【分析】作中线AD，根据三角形全等的判定定理证明△ABD≌△AcD，根据全等三角形的性质定理证明结论．
【解答】证明作中线AD，
在△A BD和△AcD中，
，
∴△ABD≌△AcD，。