K表达式书写专项训练

确定一次函数表达式的方法 习题精选（一）l ．正比例函数y=kx 的图像过点(一l ，3)，则解析式为 _____。

2．一次函数y=kx ＋b 的图像过点(1，5)和(0，2)，则函数的解析式为 ______。

3．若一次函数y=kx －(2k ＋1)图像与y 轴交于点A(0，3)，则k= _______。

4．已知y 与x －2成正比例，且x=4时y=2，则y 与x 的函数关系式为 ______。

5．已知一次函数的图像经过点P(1，2)，写出满足条件的一个一次函数的解析式： ______。

6．已知函数y=mx －(m 2－m －4)，y 随x 的增大而增大，它的图像过点(2，0)，则m 的值为()A ．－1B ．4C ．1或－4D ．－1或47．根据图像确定直线的解析式为()A ．223y x =+B ．223y x =- C ．223y x =-- D ．223y x =-+ 8．已知两个一次函数y=x ＋3k 和y=2x －6的图像交点在y 轴上，则k 的值为()A ．3B ．1C ．2D ．－29．如右图，变量y 与x 之间的函数关系式为()A ．223y x =-+(－3<x<0) B ．223y x =--(－3<x<0) C ．223y x =-+(－3≤x<0)D ．223y x =--(－3≤x<0) 10．一次函数y=kx ＋b ，y 随x 的增大而减小，kb>0，则它的图像大致是()11．按要求分别写出相应的函数解析式：(1)y 与x 成正比例，其图像过点)P(2)函数y=kx －(2k ＋1)的图像过原点。

(3)一次函数y=kx ＋b ，当x ＝5时，y ＝－2；当x ＝2时，y ＝1。

(4)y 与x －1成正比例，且当x=－5时，y=312．根据图像，求出相应的函数关系式。

13．已知正比例函数的图像过(2，－3a)，(a ，－6)两点，且y 随x 的增大而减小，求其解析式，并求当y ＝－3时x 的值。

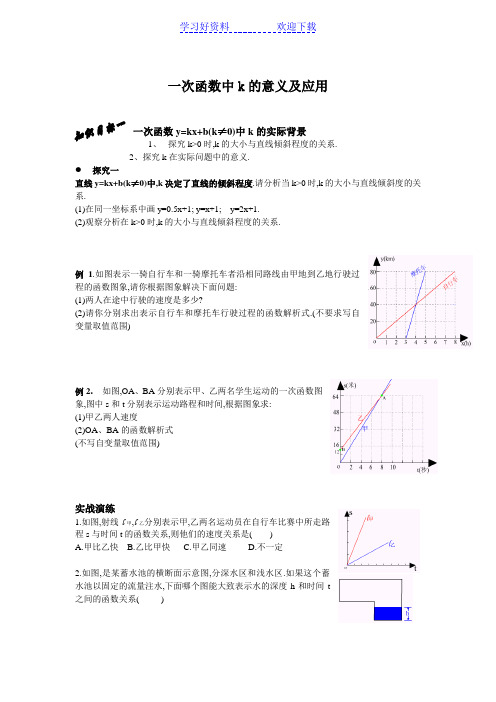
一次函数中k的意义及应用一次函数y=kx+b(k≠0)中k的实际背景1、探究k>0时,k的大小与直线倾斜程度的关系.2、探究k在实际问题中的意义.探究一直线y=kx+b(k≠0)中,k决定了直线的倾斜程度.请分析当k>0时,k的大小与直线倾斜度的关系.(1)在同一坐标系中画y=0.5x+1; y=x+1; y=2x+1.(2)观察分析在k>0时,k的大小与直线倾斜程度的关系.例1.如图表示一骑自行车和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象,请你根据图象解决下面问题:(1)两人在途中行驶的速度是多少?(2)请你分别求出表示自行车和摩托车行驶过程的函数解析式.(不要求写自变量取值范围)例2.如图,OA、BA分别表示甲、乙两名学生运动的一次函数图象,图中s和t分别表示运动路程和时间,根据图象求:(1)甲乙两人速度(2)OA、BA的函数解析式(不写自变量取值范围)实战演练1.如图,射线l甲,l乙分别表示甲,乙两名运动员在自行车比赛中所走路程s与时间t的函数关系,则他们的速度关系是( )A.甲比乙快B.乙比甲快C.甲乙同速D.不一定2.如图,是某蓄水池的横断面示意图,分深水区和浅水区.如果这个蓄水池以固定的流量注水,下面哪个图能大致表示水的深度h和时间t之间的函数关系( )3.有一个附有进水管、出水管的水池,每单位时间内进出水量都分别固定,设从某时刻开始,4h 内只进水不出水,在随后时间内不进水只出水,得到时间x (h)与水量y (m3)之间的关系图:回答下列问题:(1)进水管4h内共进水多少?每小时进水多少?(2)当0≤x≤4,求y与x的关系式.(3)当x=9时,水池中的水量是多少?(4)若4h后,只放水不进水,那么多少小时可将水池中的水放完?探究二:小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完.销售金额y(元)与卖瓜数x(千克)之间的关系如图所示.求y与x的函数关系式综合演练1.如图是龟兔赛跑的路程和时间变化图. 结合图象,你能读到哪些信息?请列举出来2.阅读函数图象,并根据你所获得的信息回答问题.折线OAB表示某个具体问题的函数图象,请你编写一道符合该图象意义的应用题;3、有一游泳池注满水，现按一定速度将水排尽，然后进行清洗，再按相同速度注满清水，使用一段时间后，又按相同的速度将水排尽，则游泳池的存水量为h(米)随时间t(小时)变化A th hB thCtDth一次函数应用题1、 车间有20名工人，每人每天加式甲种零件5个或乙种零件4个，在这20名工人中，派x 人加工甲种零件，其余的加工乙种零件，已知每加工一个甲种零件可获利16元，每加工一个乙种零件可获利24元。

确定一次函数表达式专项练习1 设一次函数y = kx+b(k ^0) > 当x = 2时,y =-3 9当x = —\时,y = 4 o(1)求这个一次函数的解析式；(2)求这条直线与两坐标轴围成的三角形的面积。

2已知一次函数y = kx^b的图像与另一个一次函数y = 3兀+ 2的图像相交于y轴上的点人且JV轴卜•方的一点B(3‘)在一次函数y = kx + b的图像上，刀满足关系式求这个一次函数的解析式。

n3求直线2兀+y + l = 0关于x轴成轴对称的图形的解析式。

4已知一次函数的图象交正比例函数图象于M点，交x轴于点N(-6, 0),又知点M位于第二象限，其横坐标为-4,若AMON面积为15,求正比例函数和一次函数的解析式.5 求下列一次函数的解析式：(1)图像过点(1, -1)且与直线2兀+〉=5平行;(2)图像和直线y = -3兀+ 2在y轴上相交于同一点，且过(2, —3)点.6选择题(1)下面图像中，不可能是关于％的一次函数y = mx-(m-3)的图像的是()(2)已知：b + c = d + c = d+b = k(a + b + c H 0),那么y = kx + k的图像一定不经过()a b c「A.第一象限B.第二象限C.第三象限D.第四象限(3)已知直线y = b + b伙工0)与x轴的交点在x轴的正半轴,下列结论：®k>0,b>0；®k>0,b<0；③Ev0,b>0；④kvO,bvO,其中正确结论的个数是()A. 1 B. 2 C. 3 D. 4(4)止比例函数的图像如图所示，则这个函数的解析式是()A. y = x B・ y二一兀C・ y = -2兀D・ y =—丄兀y o7 已知一次函数y = (6 + 3加)兀+川一4,求;(1)加为何值时，y随x增大I佃减小；(2)斤为何值时，函数图像与y轴的交点在x轴下方；(3)m , n分别取何值时，函数图像经过原点；(4)若m = -, n = 5,求这个一次函数的图像与两个坐标轴交点的坐标；3(5)若图像经过一、二、三象限，求加，〃的取值范围.8 (1)已知一次函数图像经过点(0, 2)和(2, 1) •求此一次函数解析式.(2)已知一次函数图像平行于正比例函数y = 的图像，且经过点(4, 3).求此一次函数的解析式.9已知一次函数图像如图所示，那么这个一次函数的解析式是()A.)=-2x-2 B・y = -2无+ 21. 如果正比例函数的图象经过点(2,4),那么这个函数的表达式为_______________ .2. 已知y与兀成正比例，且x = 3时，y = -6,贝ll y与x的函数关系式是____________ •3. 若直线)=也+ 1,经过点(3,2),贝1«= ____________ .4. 已知—次函数y二厶一2,当兀二2吋，y =-6 f贝9当兀二一3吋，y = _____ .5. 若一次函数)=也-(2/; + 1)的图象与y轴交于点4(0,2),贝必= __________ .6. 已知点A (3,0), 3(0,—3), C(l,加)在同一条直线上，贝=.7•直线y=x—l的图像经过彖限是( )A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象限10. 己知一次函数的图象经过点(2,1)和(-1,-3)・(1)求此一次函数的解析式. (2)求此一次函数与兀轴、y轴的交点坐标.11. 已知一次函数y = d + b(kH0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,求此一次函数的解析式.1 •一次函数y=2x-1的图彖经过点(°, 3),则c匸_________ .2•—次函数y=-2x+3中，y的值随x值增大______ .(填“增大”或滅小”)3. 若一次函数尸也一3£+6的图象过原点，则⑴________ ，一次函数的解析式为_______4. 若y—1与兀成正比例，且当x=—2时，)=4,那么y与x之间的函数关系式为_________ •5. ___________________________________________________________________________ 如右图:直线是一次函数y=kx+b的图彖，若1/131=石，则函数的表达式为 _______________________6 —次函数y = 的图象如右图所示，当y<0时，工的取值范围是( )A. x>0B. x <0C. x >2D. x <28. 一次函数^ = 3x-4的图象不经过()A第一象限B第二象限C第三象限D第四象限参考答案例1分析(1)己知一次函数图像上两个点的坐标，代入解析式中可以求乩方值。

《课时集训》 已知234x y z == ，且xyz ≠0，求233x y zx z-+- 的值。

答案：4已知一次函数y=kx-k ，其中a b b c c ak c a b+++===（a ，b ，c 为实数），求这个一次函数。

答案：y=2x-2 y= －x+13．（2006•临沂）如果x ：y=2：3，则下列各式不成立的是（ ） A ． B ． C ． D ．4．（2000•荆门）若，则的值是（ ） A ．B ．﹣C ．D ．，5．已知2x=3y ，则下列比例式成立的是（ ） A ． = B ． = C ．= D ．=6．如果mn=ab ，则下列比列式中错误的是（ ） A ． B ． C ．D ．7．已知x ：y=4：5，则（x+y ）：（x ﹣y ）的值为（ ） A ． 1：9 B ． ﹣9 C ． 9 D ． ﹣1：98．若x=，且x+2y ﹣z=4，则x+y+z 等于（ ）A ． 6B ． 10C ． 12D ． 149．若x：y：z=1：2：3，则的值是（）A．0.5 B．﹣2 C．2D．﹣0.510．若k===，则k的值是（）C．﹣1 D．A．B．或﹣111．数2和8的比例中项为（）A．4B．±4 C．6D．±612．如果a：b=12：8，且b是a和c的比例中项，那么b：c等于（）A．4：3 B．3：2 C．2：3 D．3：413．（2002•广西）已知线段a=4，b=16，线段c是a、b的比例中项，那么c等于（）A．10 B．8C．﹣8 D．±826．已知x、y、z都是不为零的有理数，且满足，求x：y：z的值．27．已知4x﹣3y﹣6z=0，x+2y﹣7z=0，xyz≠0，求的值．14．（2012•仙桃天门潜江江汉）如图，△ABC为等边三角形，点E在BA的延长线上，点D在BC边上，且ED=EC．若△ABC的边长为4，AE=2，则BD的长为（）A．2B．3C．D．+115．（2005•黄冈）如图，在平行四边形ABCD中，EF∥AB，DE：EA=2：3，EF=4，则CD 的长为（）A．B．8C．10 D．1616．已知，则分式的值为8或﹣1．21．（2009•太原）如图是一种贝壳的俯视图，点C分线段AB近似于黄金分割．已知AB=10cm，则AC的长约为 6.2或3.8cm（结果精确到0.1cm）．22．如图，C是AB的黄金分割点，BG=AB，以CA为边的正方形的面积为S1，以BC、BG 为边的矩形的面积为S2，则S1=S2（填“＞”“＜”“=”）．如图，边长为a的三个方形拼成一个矩形AEDF，求∠1+∠2的度数。

k稳表达式K稳=[Ag(CN)2]-/([Ag+][CN-]2)。

在18℃时，-的稳定常数为1021.1。

不同的络合物各具一定的稳定常数。

同类型的络合物稳定常数愈大，络合物愈稳定。

从络合物稳定常数的大小可以判断络合反应的完成程度。

测定稳定常数的方法：1、电位法以研究溶液中离子与电极的相互作用为基础，来测定金属离子或配体的活度。

电位法所测的数据精确，适用于单核、混合和多核配合物的研究，应用范围最广泛。

用电位法测定稳定常数时，要求电极反应必须是可逆的。

2、极谱法也是以研究溶液中离子与电极的相互作用为基础的方法。

根据加入配体后金属离子的半波电位的改变来计算稳定常数，在金属离子可逆还原条件下，能得到单核和混合配合物的稳定常数。

该法数据准确可靠，灵敏度高，特别适用于浓度和稳定性较低的配合物。

对某些不可逆还原的金属离子，可采用竞争法或利用扩散电流随配体浓度改变的关系来计算(见极谱法和伏安法)。

3、分光光度法当配合物的吸收光谱与金属离子有所不同，且溶液在某一波长的光密度与组成的关系符合比尔定律时，稳定常数可通过计算求得。

其优点是迅速可靠，适用于低浓度(10-4～10-5)的配合物，溶剂选择的范围比电位法广，但处理数据的未知数比电位法多，对较复杂体系的计算有一定困难(见紫外-可见分光光度法)。

4、萃取法和离子交换法均以金属配合物的异相分配为基础，通过测定分配比来测定稳定常数。

这两种方法的精确度不如电位法，但不低于分光光度法，特别是当金属离子浓度很低时，可采用放射性手段来测定，这是其独特的优点。

萃取法（见溶剂萃取）适用于研究螯合物，不适用于稳定性较低的配合物。

离子交换法适用于微量的或含放射性金属离子的配合物的研究，但手续较麻烦，数据不够精确。

【必刷题】2024七年级数学上册代数表达式简化专项专题训练（含答案）试题部分一、选择题：1. 下列代数表达式中，哪个是简化后的结果？（）A. a + a + a = 3aB. 2a a = a^2C. 3b + 4b = 7bD. 4x 2x + x = 3x2. 简化代数表达式 5m 3m + 2m 的结果是（）A. 4mB. 6mC. 10mD. 7m3. 下列哪个选项是代数表达式 6n 4n + 2n n 的简化结果？（）A. 3nB. 5nC. 7nD. 9n4. 若 a = 3，则代数表达式 2a + 4a a 的值为（）A. 5B. 6C. 9D. 105. 简化代数表达式 8x 5x + 2x 3x 的结果是（）A. 2xB. 4xC. 6xD. 8x6. 下列代数表达式中，哪个是同类项？（）A. 3m 和 4nB. 5a^2 和 6aC. 7x^2 和 8x^2D. 9p 和 10q7. 简化代数表达式 4y^2 2y^2 + y^2 的结果是（）A. 3y^2B. 5y^2C. 6y^2D. 7y^28. 若 b = 2，则代数表达式 3b^2 2b^2 + b^2 的值为（）A. 2B. 4C. 6D. 89. 下列哪个选项是代数表达式 5c 3c + 2c c 的简化结果？（）A. 3cB. 4cC. 6cD. 7c10. 简化代数表达式 9d 6d + 3d 2d 的结果是（）A. 4dB. 6dC. 8dD. 10d二、判断题：1. 代数表达式 2x + 3x x 可以简化为 4x。

（）2. 代数表达式 5a 3a + 2a 和 6a 4a 是同类项。

（）3. 简化代数表达式 7b 4b + 2b 的结果是 5b。

（）4. 代数表达式 8c 5c + 3c 2c 可以简化为 4c。

（）5. 代数表达式 6d^2 3d^2 + 2d^2 d^2 的简化结果是 4d^2。

（）三、计算题：1. 简化代数表达式：3x + 4x 2x + x2. 简化代数表达式：5a 3a + 2a a3. 简化代数表达式：7b + 2b 4b4. 简化代数表达式：6c 3c + c 2c5. 简化代数表达式：8d^2 4d^2 + 2d^26. 简化代数表达式：9m^2 5m^2 + m^2 3m^27. 简化代数表达式：4n^2 + 3n^2 2n^28. 简化代数表达式：7p 4p + p 2p9. 简化代数表达式：6q + 3q 2q q10. 简化代数表达式：5r^2 2r^2 + r^211. 简化代数表达式：8s 5s + 2s s12. 简化代数表达式：9t^2 + 4t^2 3t^213. 简化代数表达式：6u 3u + 2u u14. 简化代数表达式：7v + 2v 4v15. 简化代数表达式：5w^2 + 3w^2 w^216. 简化代数表达式：4x^2 2x^2 + x^217. 简化代数表达式：6y + 3y y18. 简化代数表达式：8z 4z + 2z z19. 简化代数表达式：9a^2 5a^2 + a^2 3a^220. 简化代数表达式：7b^2 + 2b^2 4b^2四、应用题：1. 若一个数的2倍加上它的3倍等于20，求这个数。

平衡常数K（Kp）的计算和应用化学平衡常数K（Kp）的计算和应用教学设计广州市第三中学魏勤高考情况分析：在近几年全国卷中，直接计算平衡常数K的题目有8道。

它们在《题型训练》中的位置分别是：原理题1（2013全国甲卷28题）P178原理题3（2014全国甲卷26题）P182原理题4（2014全国乙卷28题）P183原理题5（2015全国甲卷27题）P185（只写表达式）原理题6（2015全国乙卷28题）P187（只写计算式）原理题8（2016全国乙卷27题）P191原理题11（2017全国乙卷28题）P196原理题12（2017全国丙卷28题）P198专题目标习惯依赖计算器的学生，对于化学试卷中的计算有一种恐惧，经常是直接放弃，特别是二卷中的计算。

平衡常数和压强平衡常数还涉及转化率等有关平衡的相关计算，既是化工生产中必须关注的，也是高考的必考考点和热点。

不管是速率、起始（或平衡）浓度（或物质的量）、转化率，还是平衡常数的计算，都涉及到三段式，这是学生最容易想到的方法。

通过本训练，希望学生能够熟练应用三段式，掌握平衡常数和压强平衡常数的计算方法，从而克服对计算的恐惧心理。

引出问题1——直接利用数据或列三段式计算K或K p例1．题型训练P182（2014全国甲卷26题）——直接代数型在容积为1.00L的容器中，通入一定量的N2O4，发生反应N2O4(g)2NO2(g)，随温度升高，混合气体的颜色变深。

回答下列问题：（1）……反应的平衡常数K1为。

（2）100℃时达到平衡后，改变反应温度为T，c(N2O4)以0.0020 mol?L-1?s-1的平均速率降低，经10s又达到平衡。

……②列式计算温度T是反应的平衡常数K2：。

答案:0.36mol/L 1.28mol/L【变式训练1】上题(1)中, 若起始压强为1.0 MPa，则平衡压强p总= ；分压p(NO2)= ，p(N2O4)= ，压强平衡常数K p= 。

专题01 反比例函数K 的三种考法类型一、求K 值例1．如图，菱形ABCD 的顶点分别在反比例函数y ＝1k x 和y ＝2k x的图象上，若∠BCD ＝60°，则12k k 的值是（ ）A ．－13B ．－23CD【答案】A【详解】解：连接AC 、BD ，∵四边形ABCD 是菱形，例2.如图，放置含30°的直角三角板，使点B 在y 轴上，点C 在双曲线y =k x上，且AB ⊥y 轴，BC 的延长线交x 轴于点D ，若S △ACD =3．则k =（ ）A ．3B ．C ．6D ．9【变式训练1】如图，函数()0k y x x=>的图象过矩形OBCD 一边的中点，且图象过矩形OAPE 的顶点P ，若阴影部分面积为6，则k 的值为______．∴k =6．综上，k 的值为6．故答案为：6．【变式训练2】如图，点A ，B 分别在函数11(0)k y k x=>与22(0)k y k x =<的图象上，线段AB 的中点M 在y 轴上．若AOB 的面积为2，则12k k -的值是______．【变式训练3】如图，在ABC 中，AB AC =，点A 在反比例函数()0,0k y k x x=>>的图像上，点B ，C 在x 轴上，5OB OC =，延长AC 交y 轴于点D ，连接BD ，若COD △的面积等于12，则k 的值为______．【变式训练4】如图，在平面直角坐标系中，矩形OABC 的两边OC ，OA 分别在x 轴，y 轴的正半轴上，双曲线k y x=（x ＞0）分别与边AB ，BC 相交于点E ，F ，且点E ，F 分别为AB ，BC 的中点，连接EF ．若△BEF 的面积为5，则k 的值是_____．【变式训练5】如图，在平面直角坐标系xOy 中，点A ，B 是反比例函数k y x=（0k >，k 为常数）的图像上两点（点A 在第一象限，点B 在第三象限），线段AB 交x 轴于点C ，若AOC △，BOC 的面积分别为：3AOC S = 和2BOC S = ，则k =______________．【答案】12【变式训练6】如图，直角坐标系中，矩形ABCD 的对角线AC 的中点与原点O 重合，点E 为x 轴上一点，连接AE ，F 为AE 的中点，反比例函数(0,0)k y k x x=>>的图像经过A ，F 两点，若AD 平分CAE Ð，ADE 的面积为6，则k 的值为_____________．类型二、求面积例1．在平面直角坐标系xOy 中，矩形OBCD 的顶点B 在x 轴正半轴上，顶点D 在y 轴正半轴上如图，若反比例函数y =k x (x >0)的图象与CD 交于点M ，与BC 交于点N ，CM =2DM ，连接OM ，ON ，MN ，则CMN OMNS S =△△（ ）A ．14B．13C ．12D ．1∵点M 、N 是反比例函数y =∴OME OBN S S D D =，∴OMN EBNM S S D =梯形，例2．如图，一次函数y x b =-+与反比例函数4(0)y x x=>的图像相交于A 、B 两点，与x 轴，y 轴分别相交于C 、D 两点，连接OA 、OB ．过点A 作AE x ^轴于点E ，交OB 于点F ．设点A 的横坐标为m ．若4OAF EFBC S S +=△四边形，则m 的值为( )A ．1B C ．2D ．4【详解】x 轴于G 点，4m )，B (n ，4n )，例3．如图，四边形OABC 为平行四边形，A 在x 轴上，且∠AOC ＝60°，反比例函数=ky x（k ＞0）在第一象限内过点C ，且与AB 交于点E ．若E 为AB 的中点，且S △OCE ＝OC 的长为（ ）A ．8B ．4CD 【答案】D【详解】过点C 作CD ⊥x 轴于点D ，过点E 作EF ⊥x 轴于点F ，如图，【变式训练1】如图，过原点的直线与反比例函数4y x=的图象交于A 、B 两点，点A 在第一象限，点C 在x 轴正半轴上，连接AC 交反比例函数图象于点D ，AE 为∠BAC 的平分线，过点B 作AE 的垂线，垂足为E ，连接DE ，OE ，若2AD DC =，则△ADE 的面积为（ ）A ．83B ．163C ．8D ．323【变式训练2】如图平面直角坐标系中，菱形OBCD 的边OB 在x 轴上，反比例函数(0)k y x x=>的图象经过菱形对角线的交点A ，且与边BC 交于点F ，点C 的坐标为(8,4)，则OBF 的面积为（ ）A ．103B ．83C ．113D ．114【变式训练3】如图，矩形ABCD 的顶点A 、B 分别在反比例函数()120y x x=>与()60y x x -=<的图象上，点C 、D 在x 轴上，AB ，BD 分别交y 轴于点E 、F ，则阴影部分的面积为（ ）A ．3B ．5C ．6D ．9【变式训练4】如图，在平面直角坐标系中，O 为坐标原点，OABC Y 的顶点A 在反比例函数2(0)y x x=>的图像上，顶点B在反比例函数8(0)y xx=>的图像上，顶点C在x轴的正半轴上，则OABCY的面积是______________．【变式训练5】如图，点M在函数5yx=（x＞0）的图像上，过点M分别作x轴和y轴的平行线交函数2yx=（x＞0）的图像于点B、C，连接OB、OC，则△OBC的面积为_________．【答案】2.1【详解】延长MB、MC，分别交y轴、x轴于点E、D，【变式训练6】如图，分别位于反比例函数1yx=，kyx=在第一象限图象上的两点A、B，与原点O在同一直线上，且13OAOB=．过点A作x轴的平行线交kyx=的图象于点C，连接BC，则ABC的面积为________．【答案】8【详解】作AE，BF分别垂直于x轴，垂足为E，F，∴AE∥BF，∴△AOE∽△BOF，∴OEOF＝EAFB＝OAOB＝13.由点A在函数y＝1x的图象上，设A的坐标是1mmæöç÷èø，，【变式训练7】如图，在反比例函数()100y x x=>的图象上，有点1234,,,,P P P P L ，它们的横坐标依次为2，4，6，8，…分别过这些点作x 轴与y 轴的垂线，图中所构成的阴影部分的面积从左到右依次记为123,,,S S S L ，则123S S S ++=_______，123n S S S S ++++=L _______（用含n 的代数式表示，n 为正整数）．类型三、求点的坐标例1．如图，平行四边形OABC 的项点A 在x 轴的正半轴上，点()2,1D 在对角线OB 上，反比例函数()0,0ky k x x=>>的图象经过C 、D 两点．已知平行四边形OABC 的面积是6，则点B 的坐标为（ ）A ．84,3æöç÷B ．()4,2C ．()5,2.5D ．2412,55æöç÷例2．如图，一次函数y x b =-+与反比例函数4(0)y x x=>的图像相交于A 、B 两点，与x 轴，y 轴分别相交于C 、D 两点，连接OA 、OB ．过点A 作AE x ^轴于点E ，交OB 于点F ．设点A 的横坐标为m ．若4OAF EFBC S S +=△四边形，则m 的值为( )A ．1BC ．2D ．4【答案】B【详解】x轴于G点，设A(m，4m)，B(n，知，直线AB与x轴夹角为45º，=45º，∴∠CBG=45º，∴GB=CB=4 n轴，∴OE=m，例3．如图，点A，D分别在函数6yx=-和10yx=的图象上，点B，C在x轴上，若四边形ABCD为正方形，点D在第一象限，则D的坐标是__________．根据反比例函数k的几何意义可知:10ABOP DCOP S S ì=ïí=ïî矩形矩形∴61016ABCD ABOP DCOP S S S =+=+=正方形矩形矩形．∵2S CD =，【变式训练1】如图，平面直角坐标系中，矩形OABC 的边OC ，OA 分别在x 轴和y 轴上，反比例函数0)y x=>的图象与AB，BC分别交于点E，点F，若矩形对角线的交点D在反比例函数图象上，且ED^ OB，则点E的坐标是_______．∵反比例函数82(0) y xx=>∴1822AOES=´△42=，设D(m，n)【变式训练2】如图，点A 在函数12(0)y x x =>的图像上，点B ，C 在函数18(0)y x x =>的图像上，若AC ∥y 轴，AB ∥x 轴，且AB ＝34AC ，则BC ＝________．设A （m ，n ），∵点A 在函数()120y x x =>的图像上，点∴S 四边形CDOF =S 四边形BEOG =18，mn ∴S 四边形AEDC =S 四边形ABGF ，∴AC •∵AB =34AC ，∴m =34n ，∴34n •n =12∴(3,6)C ，∴6CF =，∴64AC =-∴22223(2)()2BC AB AC =+=+【变式训练3】如图，在平面直角坐标系中，C，A分别为x轴、y轴正半轴上的点，以OA，OC为边，在第一象限内作矩形OABC，且S矩形OABC＝，将矩形OABC翻折，使点B与原点O重合，折痕为MN，点C的对应点C'落在第四象限，过M点的反比例函数y＝kx（k≠0）的图象恰好过MN的中点，则k的值为_____，点C'的坐标为_____．2【变式训练4】如图，已知直线y＝kx＋b与函数y＝mx（x＞0）的图象交于第一象限内点A，与x轴负半轴交于点B，过点A作AC⊥x轴于点C，点D为AB中点，线段CD交y轴于点E，连接BE．若△BEC的面积为272，则m的值为___．【变式训练5】如图，直线34y x=-与双曲线12yx=-相交于A，B两点．平行四边形OCDE的顶点C在双曲线上，点E在x轴上且DE过点A，连接BC ．若BOC的面积为5，则D点坐标为_______．。

化学平衡常数应用及练习题一．平衡常数表达式的书写CaCO3(s)CaO(s)+CO2(g) K=[CO2]CO2(g)+H2(g)CO(g)+H2O(g) K=[CO][H2O]/([CO2][H2]Cr2O72-+H2O2CrO42-+2H+ K=[CrO4][H]/[Cr2O7]二．平衡常数的换算H2(g)＋I2(g)2HI(g) K12HI(g)H2(g)＋I2(g) K212H2(g)＋12I2(g)HI(g) K3上面反应中K1与K2的关系是K1＝，K1与K3的关系是K1＝:练习：已知: ①NO2+CO CO2+NO 该反应的平衡常数为K1②N2(g)+O2(g) 2NO(g) K2 ③2NO(g) + O2(g) 2NO2(g) △H=-112.3kJ/mol K3试写出NO与CO反应生成无污染物气体的方程式2NO(g)+ 2CO(g) N2(g)+2CO2(g)以及此方程式的平衡常数K=2312•K KK(用K1、K2、K3表示)三．判断反应进行的程度K值越大，证明反应向正方向进行的程度，生成物所占的比例越高。

一般来说，当K ，就认为反应可以进行完全。

当K ，就认为反应很难发生。

当K介于,该反应是一个可逆反应。

四．判断平衡移动1．高温下，炼铁高炉中存在下列平衡：FeO（s）+CO（g）Fe（s）+CO2（g）△H＞0。

已知1100℃时该反应的平衡常数K=0.263．在该温度测得高炉中c（CO2）=0.025mol·L﹣1，c （CO）=0.1mol·L﹣1，此时该反应的化学反应速率是v（正）________ v（逆）（填“＞”、“＜”、“=”）。

2．在密闭容器中进行的如下反应：2SO2(g)＋O2(g)2SO3(g)。

SO2的起始浓度是0.4 mol·L －1，O2的起始浓度是1 mol·L－1，当SO2的转化率为80%时，反应达到平衡状态。