材料力学计算试题库完整
- 格式:doc
- 大小:4.99 MB
- 文档页数:58

可编辑修改精选全文完整版一.是非题:(正确的在括号中打“√”、错误的打“×”) (60小题) 1.材料力学研究的主要问题是微小弹性变形问题,因此在研究构件的平衡与运动时,可不计构件的变形。
( √ )2.构件的强度、刚度、稳定性与其所用材料的力学性质有关,而材料的力学性质又是通过试验测定的。
( √ ) 3.在载荷作用下,构件截面上某点处分布内力的集度,称为该点的应力。
(√ ) 4.在载荷作用下,构件所发生的形状和尺寸改变,均称为变形。
( √ ) 5.截面上某点处的总应力p 可分解为垂直于该截面的正应力σ和与该截面相切的剪应力τ,它们的单位相同。
( √ )6.线应变ε和剪应变γ都是度量构件内一点处变形程度的两个基本量,它们都是无量纲的量。
( √ )7.材料力学性质是指材料在外力作用下在强度方面表现出来的性能。
( ) 8.在强度计算中,塑性材料的极限应力是指比例极限p σ,而脆性材料的极限应力是指强度极限b σ。
( )9.低碳钢在常温静载下拉伸,若应力不超过屈服极限s σ,则正应力σ与线应变ε成正比,称这一关系为拉伸(或压缩)的虎克定律。
( )10.当应力不超过比例极限时,直杆的轴向变形与其轴力、杆的原长成正比,而与横截面面积成反比。
( √ )11.铸铁试件压缩时破坏断面与轴线大致成450,这是由压应力引起的缘故。
( )12.低碳钢拉伸时,当进入屈服阶段时,试件表面上出现与轴线成45o 的滑移线,这是由最大剪应力max τ引起的,但拉断时截面仍为横截面,这是由最大拉应力max σ引起的。
( √ )13.杆件在拉伸或压缩时,任意截面上的剪应力均为零。
( ) 14.EA 称为材料的截面抗拉(或抗压)刚度。
( √ ) 15.解决超静定问题的关键是建立补充方程,而要建立的补充方程就必须研究构件的变形几何关系,称这种关系为变形协调关系。
( √ ) 16.因截面的骤然改变而使最小横截面上的应力有局部陡增的现象,称为应力集中。

一、一结构如题一图所示。
钢杆1、2、3的横截面面积为A=200mm 2,弹性模量E=200GPa,长度l =1m 。
制造时3杆短了△=0。
8mm.试求杆3和刚性梁AB 连接后各杆的内力。
(15分)aalABC123∆二、题二图所示手柄,已知键的长度30 mm l =,键许用切应力[]80 MPa τ=,许用挤压应力bs[]200 MPa σ=,试求许可载荷][F 。
(15分)三、题三图所示圆轴,受eM 作用。
已知轴的许用切应力[]τ、切变模量G ,试求轴直径d 。
(15分)四、作题四图所示梁的剪力图和弯矩图。
(15分)五、小锥度变截面悬臂梁如题五图所示,直径2bad d =,试求最大正应力的位置及大小。
(10分)六、如题六图所示,变截面悬臂梁受均布载荷q 作用,已知q 、梁长l 及弹性模量E .试用积分法求截面A 的得分评分人F键40633400Aal bM eBd a a aqqaqa 2dbBda AF挠度w A 和截面C 的转角θC .(15分)七、如图所示工字形截面梁AB ,截面的惯性矩672.5610zI -=⨯m 4,求固定端截面翼缘和腹板交界处点a 的主应力和主方向。
(15分)一、(15分)(1)静力分析(如图(a))1N F2N F3N F图(a)∑=+=231,0N N N yF F F F(a)∑==31,0N N CF F M(b)(2)几何分析(如图(b))1l∆2l∆3l∆∆图(b)wql /3x lhb 0b (x )b (x )BAC 50kN AB0.75m303030140150zya∆=∆+∆+∆3212l l l(3)物理条件EA l F l N 11=∆,EA l F l N 22=∆,EAl F l N 33=∆ (4)补充方程∆=++EAlF EA l F EA l F N N N 3212 (c) (5)联立(a)、(b)、(c)式解得:kN FkN FF N N N 67.10,33.5231===二、(15分)以手柄和半个键为隔离体,S0, 204000OM F F ∑=⨯-⨯=取半个键为隔离体,bsS20F F F ==由剪切:S []s FA ττ=≤,720 N F = 由挤压:bs bs bs bs[][], 900N FF Aσσ=≤≤取[]720N F =.三、(15分)eABM M M +=0ABϕ=, A B M a M b ⋅=⋅得 e B a M M a b =+, e A b MM a b=+当a b >时 e316π ()[]M ad a b τ≥+;当b a >时 e316π ()[]M bd a b τ≥+。

材料力学考试和答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪个量是标量?A. 应力B. 应变C. 位移D. 力答案:C2. 材料力学中,下列哪个量是矢量?A. 应力B. 应变C. 位移D. 温度答案:A3. 材料力学中,下列哪个量是二阶张量?A. 应力B. 应变C. 位移D. 力答案:A4. 在材料力学中,下列哪个量是描述材料弹性特性的?A. 应力B. 应变C. 弹性模量D. 屈服强度答案:C5. 材料力学中,下列哪个量是描述材料塑性特性的?A. 应力B. 应变C. 弹性模量D. 屈服强度答案:D6. 在材料力学中,下列哪个量是描述材料断裂特性的?A. 应力B. 应变C. 弹性模量D. 断裂韧性答案:D7. 材料力学中,下列哪个量是描述材料硬度特性的?A. 应力B. 应变C. 弹性模量D. 布氏硬度答案:D8. 在材料力学中,下列哪个量是描述材料疲劳特性的?A. 应力B. 应变C. 弹性模量D. 疲劳寿命答案:D9. 材料力学中,下列哪个量是描述材料蠕变特性的?A. 应力B. 应变C. 弹性模量D. 蠕变速率答案:D10. 在材料力学中,下列哪个量是描述材料热膨胀特性的?A. 应力B. 应变C. 弹性模量D. 热膨胀系数答案:D二、填空题(每题2分,共20分)1. 材料力学中,应力的单位是________。
答案:帕斯卡(Pa)2. 材料力学中,应变的单位是________。
答案:无单位(无量纲)3. 材料力学中,弹性模量的单位是________。
答案:帕斯卡(Pa)4. 材料力学中,屈服强度的单位是________。
答案:帕斯卡(Pa)5. 材料力学中,断裂韧性的单位是________。
答案:帕斯卡·平方米根号米(Pa·m^(1/2))6. 材料力学中,布氏硬度的单位是________。
答案:布氏硬度值(HB)7. 材料力学中,疲劳寿命的单位是________。
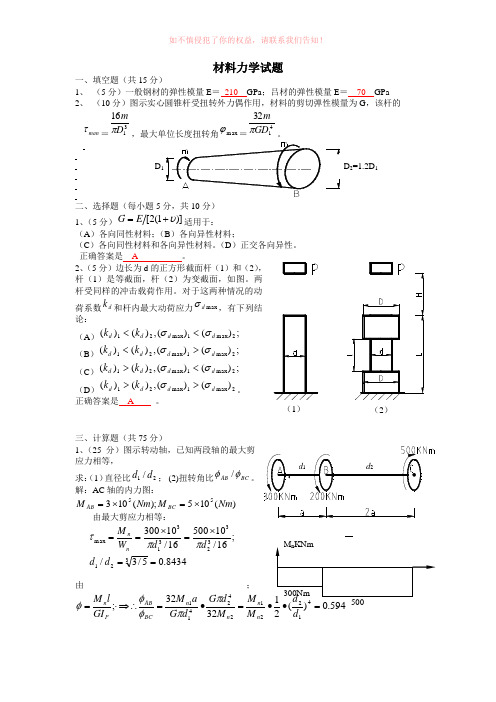
材料力学试题一、填空题(共15分)1、 (5分)一般钢材的弹性模量E = 210 GPa ;吕材的弹性模量E = 70 GPa2、 (10分)图示实心圆锥杆受扭转外力偶作用,材料的剪切弹性模量为G ,该杆的man τ1、(5(A )各向同性材料;(B )各向异性材料; (C 正确答案是 A 。
2、(5分)边长为d 杆(1)是等截面,杆(2荷系数d k 和杆内最大动荷应力d σ论:(A )()(,)()(1max 21d d d k k σ<<(B )()(,)()(1max 21d d d k k σ><(C )()(,)()(1max 21d d d k k σ<>(D )1max 21()(,)()(d d d k k σ>>正确答案是 A 。
三、计算题(共75分) 1、(25应力相等,求:(1)直径比21/d d ; (2)扭转角比AB φ解:AC 轴的内力图:(105);(10355M Nm M BC AB ⨯=⨯= 由最大剪应力相等:8434.05/3/16/1050016/10300321323313max==⨯=⨯==d d d d W M n n ππτ 由;594.0)(23232;41221242411=••=•=⇒∴⋅=d M M M d G d G a M GI l M n n n n BC AB P n ππφφφ(2)2、(3、(15分)有一厚度为6mm 的钢板在板面的两个垂直方向受拉,拉应力分别为150Mpa 和55Mpa ,材料的E=2.1×105Mpa ,υ =0.25。
求钢板厚度的减小值。
解:钢板厚度的减小值应为横向应变所产生,该板受力后的应力状态为二向应力状态,由广义胡克定律知,其Z 向应变为:0244.010)55150(101.225.0)(69-=⨯+⨯-=+-=y x z E σσνε则 mm t Z Z 146.0-=⨯=∆ε(本资料素材和资料部分来自网络,仅供参考。

材料力学试题及答案一、选择题(每题5分,共25分)1. 下列哪个选项是材料力学的基本假设之一?A. 材料是各向同性的B. 材料是各向异性的C. 材料是均匀的D. 材料是线弹性的答案:A2. 在材料力学中,下列哪个公式表示杆件的正应力?A. σ = F/AB. τ = F/AC. σ = F/LD. τ = F/L答案:A3. 当材料受到轴向拉伸时,下列哪个选项是正确的?A. 拉伸变形越大,材料的强度越高B. 拉伸变形越小,材料的强度越高C. 拉伸变形与材料的强度无关D. 拉伸变形与材料的强度成正比答案:B4. 下列哪种材料在拉伸过程中容易发生断裂?A. 钢材B. 铸铁C. 铝合金D. 塑料答案:B5. 下列哪个选项表示材料的泊松比?A. μ = E/GB. μ = G/EC. μ = σ/εD. μ = ε/σ答案:C二、填空题(每题10分,共30分)6. 材料力学研究的是材料在______作用下的力学性能。
答案:外力7. 材料的强度分为______强度和______强度。
答案:屈服强度、断裂强度8. 材料在受到轴向拉伸时,横截面上的正应力公式为______。
答案:σ = F/A三、计算题(每题25分,共50分)9. 一根直径为10mm的圆钢杆,受到轴向拉伸力F=20kN 的作用,求杆件横截面上的正应力。
解:已知:d = 10mm,F = 20kNA = π(d/2)^2 = π(10/2)^2 = 78.5mm^2σ = F/A = 20kN / 78.5mm^2 = 255.8N/mm^2答案:杆件横截面上的正应力为255.8N/mm^2。
10. 一根长度为1m的杆件,受到轴向拉伸力F=10kN的作用,已知材料的弹性模量E=200GPa,泊松比μ=0.3,求杆件的伸长量。
解:已知:L = 1m,F = 10kN,E = 200GPa,μ = 0.3ε = F/(EA) = 10kN / (200GPa × π(10mm)^2) =0.025δ = εL = 0.025 × 1000mm = 25mm答案:杆件的伸长量为25mm。

材料力学的试题及答案### 材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪个量不是基本力学量?A. 应力B. 应变C. 位移D. 力答案:C2. 根据胡克定律,弹性模量E与杨氏模量G的关系是?A. E = 2GB. E = 3GC. E = G/2D. E = 2G/3答案:D3. 材料力学中的应力集中现象通常发生在:A. 材料的均匀区域B. 材料的接合处C. 材料的表面D. 材料的内部答案:B4. 以下哪个不是材料力学的基本原理?A. 材料的连续性原理B. 材料的均匀性原理C. 材料的各向同性原理D. 材料的各向异性原理答案:D5. 在材料力学中,下列哪项不是材料的力学性能指标?A. 屈服强度B. 抗拉强度C. 硬度D. 密度答案:D二、简答题(每题10分,共20分)1. 简述材料力学中应力和应变的关系,并说明它们的区别。
答案:应力是单位面积上的内力,表示材料内部抵抗变形的能力。
应变是材料在受力后发生的形变程度,是无量纲的比值。
它们的区别在于应力是力的度量,而应变是形变的度量。
在弹性范围内,应力与应变成正比,遵循胡克定律。
2. 解释什么是材料的屈服点,并说明其在工程应用中的重要性。
答案:屈服点是材料从弹性变形转变为塑性变形的临界点,即材料开始产生永久变形的应力值。
在工程应用中,屈服点是设计和制造结构时的重要参数,它决定了材料在多大应力下会失去弹性,对于确保结构的安全性和可靠性至关重要。
三、计算题(每题30分,共40分)1. 一根直径为d的圆杆,受到轴向拉力P,求圆杆的轴向应力。
答案:轴向应力 \( \sigma \) 可以通过以下公式计算:\[ \sigma = \frac{P}{A} \]其中,\( A \) 是圆杆的横截面积,\( A = \frac{\pi d^2}{4} \)。
2. 已知一个材料的弹性模量E和泊松比ν,求该材料在单轴拉伸时的应力-应变关系。
答案:在单轴拉伸情况下,应力-应变关系遵循胡克定律:\[ \sigma = E \epsilon \]其中,\( \epsilon \) 是应变,\( \nu \) 是泊松比,但在此关系中不直接使用。
材料力学试卷及答案一、选择题(每题2分,共20分)1. 下列哪个选项不属于材料力学的范畴?A. 材料的力学性能B. 材料的微观结构C. 材料在外力作用下的变形与破坏D. 材料的制备工艺答案:D2. 在拉伸试验中,下列哪个参数表示材料的强度?A. 屈服强度B. 断裂强度C. 弹性模量D. 伸长率答案:A3. 在弹性范围内,下列哪个关系式成立?A. σ = EεB. σ = EδC. σ = EτD. σ = Eγ答案:A4. 下列哪个因素对材料的疲劳性能影响最大?A. 材料的化学成分B. 材料的微观结构C. 材料的表面质量D. 材料的力学性能答案:C5. 在纯弯曲状态下,下列哪个选项描述了梁的变形情况?A. 梁的上部受拉,下部受压B. 梁的上部受压,下部受拉C. 梁的上下部均受拉D. 梁的上下部均受压答案:A6. 下列哪个选项描述了材料的塑性?A. 断裂前的最大变形B. 断裂前的最大伸长率C. 断裂前的最大压缩率D. 断裂前的最大扭转角答案:A7. 下列哪个选项表示材料的韧度?A. 材料在断裂前所吸收的能量B. 材料在屈服前所吸收的能量C. 材料在弹性范围内所吸收的能量D. 材料在塑性范围内所吸收的能量答案:A8. 下列哪个选项表示材料的硬度?A. 材料抵抗塑性变形的能力B. 材料抵抗弹性变形的能力C. 材料抵抗断裂的能力D. 材料抵抗磨损的能力答案:A9. 下列哪个选项表示材料的疲劳寿命?A. 材料在疲劳试验中断裂前所经历的循环次数B. 材料在疲劳试验中所承受的最大应力C. 材料在疲劳试验中所承受的最小应力D. 材料在疲劳试验中的应力幅值答案:A10. 下列哪个选项表示材料的断裂韧性?A. 材料在断裂前所吸收的能量B. 材料在屈服前所吸收的能量C. 材料在弹性范围内所吸收的能量D. 材料在塑性范围内所吸收的能量答案:A二、填空题(每题2分,共20分)1. 材料力学研究的三个基本问题是________、________和________。
材料力学计算题(总5页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除计算题一等截面杆在轴向拉力P 作用下,测得杆件A 点处的横向线应变0.00003ε'=-,已知杆的横截面积2300A mm =,材料的弹性模量5210E MPa =⨯、泊松比0.28μ=,试求(1)轴向拉力的数值;(2)图1所示A 点在图2截面处的正应力和剪应力。
30解:(1)E Eεσεμ'==-= N P F A E A EA εσεμ'====-=×103N (2)在A 点取单元体,并画A 点的应力状态图 21.43MPa x σσ==0y xy στ==cos 2sin 222cos602216.07MPax yx yxy x xασσσσσατασσ+-=+-=+=sin 2cos 22sin 6029.28MPax yxy xασστατασ-=+==计算题杆件上同时作用有如图所示的轴向力和横向力,大小均为10kN P =,杆件的截面为方形截面,截面边长为a =100mm ,杆件长度为l =1m 。
试求出杆件的最大、最小正应力的大小。
解答:画出其轴力图和弯矩图。
杆件的轴向应力为2/PP A a σ==轴(拉应力) 杆件的最大弯矩为max M Pl =maxmax M y Iσ=弯曲max 412a I = max 2a y =±带入可得max 436212M a Pla a σ=±=±弯曲max则最大、最小正应力为:max max 2423min6212M P a P Pl a a a a σσσ=±=±=±弯曲max 轴计算题承受均布荷载作用的矩形截面木梁如图所示,已知l=4m ,b=140mm ,h=210mm ,q=2kN/m ,弯曲时木材的容许正应力[]10MPa σ=,(1)校核该梁的强度;(2)计算该梁能承受的极限荷载。
材料力学试题含答案一、选择题(每题5分,共25分)1. 下列哪个选项是材料力学的基本假设之一?A. 材料是各向同性的B. 材料是各向异性的C. 材料是线弹性的D. 材料是塑性的答案:A2. 在拉伸试验中,下列哪个物理量表示材料的强度?A. 屈服强度B. 抗拉强度C. 延伸率D. 断面收缩率答案:B3. 下列哪种材料具有较小的泊松比?A. 钢材B. 铝材C. 橡胶D. 玻璃答案:A4. 下列哪个选项是材料力学中常用的力学模型?A. 杆件B. 梁件C. 壳件D. 所有选项均正确答案:D5. 下列哪个选项表示材料的疲劳极限?A. 材料的最大应力B. 材料的平均应力C. 材料的应力幅D. 材料的疲劳寿命答案:C二、填空题(每题5分,共25分)1. 材料力学研究的主要对象是__________,其基本假设包括__________、__________和__________。
答案:杆件;材料是连续的;材料是均匀的;材料是各向同性的2. 在拉伸试验中,材料的屈服强度是指__________,抗拉强度是指__________。
答案:材料开始发生塑性变形时的应力;材料断裂前的最大应力3. 材料的泊松比是指__________,其值越大,材料的横向变形越__________。
答案:材料在拉伸或压缩时,横向应变与纵向应变的比值;大4. 材料的疲劳极限是指在__________条件下,材料在__________次应力循环内不发生__________的最大应力。
答案:给定;预定;疲劳破坏5. 材料力学中,梁的弯曲正应力公式为__________,其中M为__________,I为__________,y为__________。
答案:σ = My/I;弯矩;惯性矩;截面形心到中性轴的距离三、计算题(每题25分,共75分)1. 一根直径为d的圆形杆,受到轴向拉伸力F的作用,已知材料的弹性模量为E,泊松比为μ。
求杆的伸长量ΔL。
材料力学试题及答案一、选择题(每题10分,共40分)1. 材料力学研究的主要内容是()A. 材料的力学性能B. 材料在外力作用下的变形和破坏规律C. 材料的制备工艺D. 材料的微观结构答案:B2. 下列哪种材料属于塑性材料()A. 钢B. 铝C. 玻璃D. 碳纤维答案:A3. 在材料力学中,下列哪个公式表示胡克定律()A. σ = EεB. σ = F/AC. τ = F/AD. σ = F·l/A答案:A4. 下列哪个现象属于弹性变形()A. 钢筋的拉伸B. 铅笔的弯曲C. 橡皮的压缩D. 玻璃的破碎答案:C二、填空题(每题10分,共40分)1. 材料力学中的基本假设之一是材料是各向______的。
答案:同性2. 在弹性范围内,材料的应力与应变之间的关系称为______。
答案:胡克定律3. 材料在受到拉伸或压缩时,单位面积上的内力称为______。
答案:应力4. 材料在受到剪切力作用时,单位面积上的内力称为______。
答案:剪应力三、计算题(每题20分,共60分)1. 一根直径为10mm的圆形截面低碳钢杆,受到轴向拉力F=10kN的作用。
已知材料的弹性模量E=200GPa,泊松比ν=0.3。
求杆的伸长量。
解:首先,计算杆的横截面积:A = πd^2/4 = π(10×10^-3)^2/4 = 7.85×10^-5 m^2根据胡克定律,杆的伸长量可以表示为:δ = Fl/AE代入已知数据,得到:δ = 10×10^3 × 7.85×10^-5 / (200×10^9 × 7.85×10^-5) = 5×10^-5 m = 0.5mm答案:杆的伸长量为0.5mm。
2. 一根矩形截面木梁,宽b=100mm,高h=200mm,受到弯矩M=10kN·m的作用。
已知木材的弹性模量E=10GPa。
第一章绪论【例1-1】钻床如图1-6a所示,在载荷P作用下,试确定截面m-m上的内力。
【解】(1)沿m-m 截面假想地将钻床分成两部分。
取m-m 截面以上部分进行研究(图1-6b),并以截面的形心O为原点。
选取坐标系如图所示。
(2)为保持上部的平衡,m-m 截面上必然有通过点O的内力N和绕点O的力偶矩M。
(3)由平衡条件∴【例1-2】图1-9a所示为一矩形截面薄板受均布力p作用,已知边长=400mm,受力后沿x方向均匀伸长Δ=0.05mm。
试求板中a点沿x方向的正应变。
【解】由于矩形截面薄板沿x方向均匀受力,可认为板内各点沿x方向具有正应力与正应变,且处处相同,所以平均应变即a 点沿x 方向的正应变。
x 方向【例1-3】 图1-9b 所示为一嵌于四连杆机构内的薄方板,b=250mm 。
若在p 力作用下CD 杆下移Δb=0.025,试求薄板中a 点的剪应变。
【解】由于薄方板变形受四连杆机构的制约,可认为板中各点均产生剪应变,且处处相同。
第二章 拉伸、压缩与剪切【例题2.1】 一等直杆所受外力如图2. 1 (a)所示,试求各段截面上的轴力,并作杆的轴力图。
解:在AB 段范围内任一横截面处将杆截开,取左段为脱离体(如图2. 1 (b)所示),假定轴力N1F 为拉力(以后轴力都按拉力假设),由平衡方程0xF=∑,N1300F -=得 N130kN F =结果为正值,故N1F 为拉力。
同理,可求得BC 段内任一横截面上的轴力(如图2. 1 (c)所示)为N2304070(kN)F =+=在求CD 段内的轴力时,将杆截开后取右段为脱离体(如图2. 1 (d)所示),因为右段杆上包含的外力较少。
由平衡方程0xF=∑,N330200F --+=得 N3302010(kN)F =-+=-结果为负值,说明N3F 为压力。
同理,可得DE 段内任一横截面上的轴力N4F 为N420kN F =F N4(f)(a)C BA 20kN30kNF30kN(b)(c)20kN20kN (e)(d)(a)N1F N2F N3F N4(f)(a)EDCBA 20kN20kNF 30kN 40kN(b)(c)30kN20kN20kN(e)(d)(b) F N2F N3F N4(f)(a)30kNED C20kN20kN80kN 40kN F(b)(c)30kN 20kN20kN (e)(d)30kN(c)N2F N4(f)(a)30kNEB A70kN30kN20kN80kN40kN 30kNF 30kN 40kN (b)(c)20kN(e)(d)30kN(d)F N2F N3F (f)(a)E D C BA 70kN30kN80kN 40kN30kNF 30kN 40kN (b)(c)(e)(d)30kN(f)(a)30kNEA20kN 80kN 40kN 30kN F30kN(b)(c)20kN(e)(d)30kN(f)图2. 1 例题2.1图【例题2.2】 一正方形截面的阶梯形砖柱,其受力情况、各段长度及横截面尺寸如图2.8(a)所示。
已知40kN P =。
试求荷载引起的最大工作应力。
解:首先作柱的轴力图,如图 2.8(b)所示。
由于此柱为变截面杆,应分别求出每段柱的横截面上的正应力,从而确定全柱的最大工作应力。
Ι、ΙΙ两段柱横截面上的正应力,分别由已求得的轴力和已知的横截面尺寸算得3N1114010N 0.69(MPa)(240mm)(240mm)σ-⨯===-⨯F A (压应力)3N22212010N 0.88(MPa)(370mm)(370mm)F A σ-⨯===-⨯(压应力)由上述结果可见,砖柱的最大工作应力在柱的下段,其值为0.88MPa ,是压应力。
【例题2.3】 一钻杆简图如图2.9(a)所示,上端固定,下端自由,长为l ,截面面积为A ,材料容重为γ。
试分析该杆由自重引起的横截面上的应力沿杆长的分布规律。
解:应用截面法,在距下端距离为x 处将杆截开,取下段为脱离体(如图2.8(b)所示),设下段杆的重量为()G x ,则有()G x xA γ= (a)设横截面上的轴力为N ()F x ,则由平衡条件0=∑xF,N ()()0-=F x G x (b)将(a)式值代入(b)式,得N ()F x A x γ=⋅⋅ (c)即N ()F x 为x 的线性函数。
当0x =时,N (0)0F =当x l =时,N N,max ()F l F A l γ==⋅⋅(a) (b) (a) (b) (c)图2.8 例题2.2图 图2.9 例题2.3图式中N,max F 为轴力的最大值,即在上端截面轴力最大,轴力图如图2.9(c)所示。
那么横截面上的应力为N ()()F x x x Aσγ==⋅ (d) 即应力沿杆长是x 的线性函数。
当0x =时,(0)0σ=当x l =时,max ()l l σσγ==⋅式中max σ为应力的最大值,它发生在上端截面,其分布类似于轴力图。
【例题2.4】 气动吊钩的汽缸如图2.10(a)所示,内径180mm D =,壁厚8mm δ=,气压2MPa p =,活塞杆直径10mm d =,试求汽缸横截面B —B 及纵向截面C —C 上的 应力。
解:汽缸内的压缩气体将使汽缸体沿纵横方向胀开,在汽缸的纵、横截面上产生拉应力。
(1) 求横截面B —B 上的应力。
取B —B 截面右侧部分为研究对象(如图 2.10(c)所示),由平衡条件0x F =∑,22N ()04D d p F π--=当D d >>时,得B —B 截面上的轴力为2N 4F D p π≈B —B 截面的面积为2()()A D D D δδδδδ=π⋅+⋅=π⋅+≈π那么横截面B —B 上的应力为2N 1802411.25(MPa)448x D p F Dp A D σδδπ⨯=≈===π⨯x σ称为薄壁圆筒的轴向应力。
图2.10 例题2.4图(2) 求纵截面C —C 上的应力。
取长为l 的半圆筒为研究对象(如图2.10(d)所示),由平衡条件0y F =∑,N10d sin 202D p l F θθπ⎛⎫⋅⋅⋅-= ⎪⎝⎭⎰ 得C —C 截面上的内力为N12F plD =C —C 截面的面积为12A l δ=当20D δ≥时,可认为应力沿壁厚近似均匀分布,那么纵向截面C —C 上的应力为N112180222.5(MPa)2228σδδ⨯=====⨯y F plD pD A ly σ称为薄壁圆筒的周向应力。
计算结果表明:周向应力是轴向应力的两倍。
【例题 2.7】 螺纹内径15mm d =的螺栓,紧固时所承受的预紧力为22kN F =。
若已知螺栓的许用应力[]150σ=MPa ,试校核螺栓的强度是否足够。
解:(1) 确定螺栓所受轴力。
应用截面法,很容易求得螺栓所受的轴力即为预紧力,有N 22kN F F ==(2) 计算螺栓横截面上的正应力。
根据拉伸与压缩杆件横截面上正应力计算公式(2-1),螺栓在预紧力作用下,横截面上的正应力为3N 2242210124.63.14154σ⨯⨯====π⨯F F d A (MPa)(3) 应用强度条件进行校核。
已知许用应力为[]150(MPa)σ= 螺栓横截面上的实际应力为124.6σ=MPa <[]150σ=(MPa)所以,螺栓的强度是足够的。
【例题2.8】 一钢筋混凝土组合屋架,如图2.25(a)所示,受均布荷载q 作用,屋架的上弦杆AC 和BC 由钢筋混凝土制成,下弦杆AB 为Q235钢制成的圆截面钢拉杆。
已知:10kN/m q =,8.8m l =, 1.6m h =,钢的许用应力[]170σ=MPa ,试设计钢拉杆AB 的 直径。
解:(1) 求支反力A F 和B F ,因屋架及荷载左右对称,所以11108.844(kN)22A B F F ql ===⨯⨯=图2.25 例题2.8图(2) 用截面法求拉杆内力N AB F ,取左半个屋架为脱离体,受力如图2.25(b)所示。
由0CM=∑,N 4.4 1.6024A AB l lF q F ⨯-⨯⨯-⨯=得22N 144 4.4108.8184.4/1.660.5(kN)8 1.6ABA F F ql ⨯-⨯⨯⎛⎫=⨯-== ⎪⎝⎭(3) 设计Q235钢拉杆的直径。
由强度条件N N 24[]σ=πAB ABF F A d ≤ 得21.29(mm)==d【例题2.9】 防水闸门用一排支杆支撑着,如图2.26(a)所示,AB 为其中一根支撑杆。
各杆为100mm d =的圆木,其许用应力[]10σ=MPa 。
试求支杆间的最大距离。
解:这是一个实际问题,在设计计算过程中首先需要进行适当地简化,画出简化后的计算简图,然后根据强度条件进行计算。
(1) 计算简图。
防水闸门在水压作用下可以稍有转动,下端可近似地视为铰链约束。
AB 杆上端支撑在闸门上,下端支撑在地面上,两端均允许有转动,故亦可简化为铰链约束。
于是AB 杆的计算简图如图2.26(b)所示。
图2.26 例题2.9图(2) 计算AB 杆的内力。
水压力通过防水闸门传递到AB 杆上,如图2.26(a)中阴影部分所示,每根支撑杆所承受的总水压力为2P 12F h b γ=其中γ为水的容重,其值为103kN/m ;h 为水深,其值为3m ;b 为两支撑杆中心线之间的距离。
于是有323P 11010345102F b b =⨯⨯⨯⨯=⨯根据如图2.26(c)所示的受力图,由平衡条件0CM=∑,P N 10AB F F CD -⨯+⨯=其中3sin 3 2.4(m)CD α=⨯==得33P N 451018.75102.4 2.4AB F b F b ⨯===⨯(3) 根据AB 杆的强度条件确定间距b 的值。
由强度条件3N 2418.7510[]σσπ⨯⨯==⨯AB F b A d ≤得26233[]1010 3.140.1 4.19(m)418.7510418.7510σ⨯π⨯⨯⨯⨯==⨯⨯⨯⨯d b ≤【例题2.10】 三角架ABC 由AC 和BC 两根杆组成,如图2.34(a)所示。
杆AC 由两根No.14a 的槽钢组成,许用应力[]160σ=MPa ;杆BC 为一根No.22a 的工字钢,许用应力为[]100σ=MPa 。
求荷载F 的许可值[]F 。
(a) (b)图2.34 例题2.10图解:(1) 求两杆内力与力F 的关系。
取节点C 为研究对象,其受力如图2.34(b)所示。
节点C 的平衡方程为0x F =∑,N N cos cos 066BC AC F F ππ⨯-⨯= 0yF=∑,N N sinsin 066BC AC F F F ππ⨯+⨯-= 解得N N BC AC F F F == (a)(2) 计算各杆的许可轴力。