下载文档原格式
我对有限元方法的认识1有限元法概念有限元方法（The Finite Element Method, FEM）是计算机问世以后迅速发展起来的一种分析方法。
每一种自然现象的背后都有相应的物理规律，对物理规律的描述可以借助相关的定理或定律表现为各种形式的方程（代数、微分、或积分）。
这些方程通常称为控制方程（Governing equation）。
针对实际的工程问题推导这些方程并不十分困难，然而，要获得问题的解析的数学解却很困难。
人们多采用数值方法给出近似的满足工程精度要求的解答。
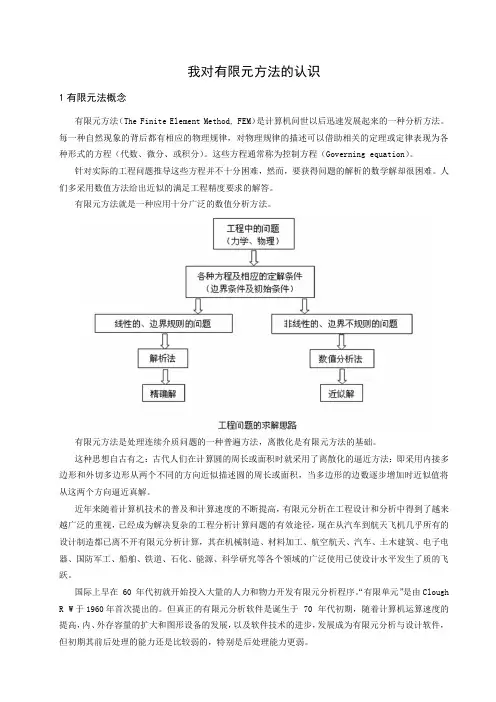
有限元方法就是一种应用十分广泛的数值分析方法。
有限元方法是处理连续介质问题的一种普遍方法，离散化是有限元方法的基础。
这种思想自古有之：古代人们在计算圆的周长或面积时就采用了离散化的逼近方法：即采用内接多边形和外切多边形从两个不同的方向近似描述圆的周长或面积，当多边形的边数逐步增加时近似值将从这两个方向逼近真解。
近年来随着计算机技术的普及和计算速度的不断提高，有限元分析在工程设计和分析中得到了越来越广泛的重视，已经成为解决复杂的工程分析计算问题的有效途径，现在从汽车到航天飞机几乎所有的设计制造都已离不开有限元分析计算，其在机械制造、材料加工、航空航天、汽车、土木建筑、电子电器、国防军工、船舶、铁道、石化、能源、科学研究等各个领域的广泛使用已使设计水平发生了质的飞跃。
国际上早在 60 年代初就开始投入大量的人力和物力开发有限元分析程序。
“有限单元”是由Clough R W于1960年首次提出的。
但真正的有限元分析软件是诞生于 70 年代初期，随着计算机运算速度的提高，内、外存容量的扩大和图形设备的发展，以及软件技术的进步，发展成为有限元分析与设计软件，但初期其前后处理的能力还是比较弱的，特别是后处理能力更弱。
到 70 年代中期有限元界的先导就在有限元软件中引入了图形技术及交互式操作方式，使有限元的前后处理进入一个崭新的历史阶段。
此时，用户就可以从繁琐的数据中解放出来。
有限元的发展历史和趋势
一、发展历史
1、古代初期
从古代存在已久的古典有限元法源于单元方程理论，其发展溯源可见其有权威。
已有古典有限元技术，曾经是一个古典概率分析方法，并在一系列经典课本中展现出来，如古典电磁学、经典水力学等。
其在结构力学及电磁学等科学领域的应用，极大地推进了科研发展。
2、20世纪初
在20世纪初，有许多科学家把它应用于结构力学及建筑结构设计等方面，如J.H.Argyris在1918年提出的形式框架有限元法，C. Taylor 於1926年提出基于单元分析的结构有限元法，R. Clough在1960年发明的有限元法等。
在此时期，有许多研究者为改善古典有限元技术而努力，提出了许多新的有限元理论，如Galerkin形式有限元法，Ritz形式有限元法，Rayleigh-Ritz有限元法，几何与元素相结合的有限元法等。
3、20世纪60年代
在20世纪60年代，美国工程师B. A. Szabo首先把有限元法用于电磁场的研究，他在1963年出版了第一本专门介绍有限元法的著作《有限元法在电磁场理论中的应用》，在此后又出版了《有限元法的数学原理》（1969年）、《有限元法及其应用》（1972年）等。
20世纪70年代，许多科学家又着手开发新的有限元技术，从而把有限元法应用到各种工程。
有限元的发展历史和趋势
有限元法（Finite-Element Method，以下简称FEM）是现代工程和
科学研究中一种常用的方法，它可以大大提高计算的效率，减轻计算工作，帮助计算者迅速解决复杂的数学问题。
1960年，Timoshenko和Gere在《力学原理》一书中首次提出了有限
元分析的概念，这成为有限元技术的开端。
他们认为，由许多有限尺寸的
单元组成的实体可以被视为由有限多边形尺寸的单元组成，这就被称为有
限元分析，成为20世纪70年代结构力学计算的基础。
随着计算资源的发展，解决复杂结构和场问题的能力也发生了巨大变化。
尤其是在80年代，由于计算的速度和计算量的大幅度增加，有限元
法被广泛应用于航空航天、电力、原子能、汽车等领域，扮演着越来越重
要的角色。
此外，它还用于求解许多复杂的场问题，从而获得了巨大进展。
随着信息技术的发展，芯片技术和并行计算的应用使有限元法取得了
新的发展，目前已经应用于许多领域，比如：土木工程、流体力学、医学
工程、声学、生物工程、材料科学等领域。
有限元分析方法有限元分析（Finite Element Analysis, FEA）是一种数值分析方法，用于解决物理问题的近似解。
它基于将有限元区域（即解释对象）分解成许多简单的几何形状（有限元）并对其进行数值计算的原理。
本文将深入探讨有限元分析的原理、应用和优点。
有限元分析的原理基于弹性力学理论和数值计算方法。
它通过将解释对象分解为有限个简单的几何区域（有限元）和节点，通过节点之间的连接来建立模型。
这些节点周围的解释对象区域称为“单元”，并且通过使用单元的形状函数近似解释对象的形状。
每个单元都有一个与之相连的节点，通过对每个单元的受力进行计算，可以得到整个解释对象的受力分布。
然后，利用一系列运算和迭代，可以计算出解释对象的位移、应力和变形等相关参数。
有限元分析的应用范围广泛，从结构力学、热传导、电磁场分析到流体力学等各个领域。
在结构力学中，它被用于分析各种结构的静力学、动力学和疲劳等性能。
在热传导领域，它可以用于研究物体内部的温度分布和传热性能。
在电磁场分析中，它可用于计算复杂电磁场下的电场、磁场和电磁场耦合问题。
在流体力学中，有限元方法可以解决各种流体流动、热传递和质量转移问题。
有限元分析的优点之一是可以处理各种复杂边界条件和非线性材料特性。
它可以考虑到不同材料的非线性本质，例如弹塑性和接触等问题。
另外，有限元方法还可以适应任意形状和尺寸的几何模型，因此非常适用于复杂工程问题的建模与分析。
有限元分析的使用需要一定的专业知识和经验。
首先，需要将解释对象抽象成几何模型，并进行细分和离散化。
其次，需要选择适当的几何元素和材料模型，以及合适的边界条件和加载方式。
然后，需要定义求解器和数值方法，并使用计算机程序对模型进行计算。
最后，需要对结果进行后处理和验证，以确保其准确性和可靠性。
总的来说，有限元分析是一种强大的工程分析工具，在解决各种物理问题方面有广泛的应用。
它通过将复杂的问题简化为简单的有限元模型，通过数值计算的方法获得近似解。
有限元分析是对于结构力学分析迅速发展起来的一种现代计算方法。
它是50年代首先在连续体力学领域--飞机结构静、动态特性分析中应用的一种有效的数值分析方法，随后很快广泛的应用于求解热传导、电磁场、流体力学等连续性问题。
有限元分析软件目前最流行的有：ANSYS、ADINA、ABAQUS、MSC四个比较知名比较大的公司。
常见软件有限元分析软件目前最流行的有：ANSYS、ADINA、ABAQUS、MSC四个比较知名比较大的公司，其中ADINA、ABAQUS在非线性分析方面有较强的能力目前是业内最认可的两款有限元分析软件，ANSYS、MSC进入中国比较早所以在国内知名度高应用广泛。
目前在多物理场耦合方面几大公司都可以做到结构、流体、热的耦合分析，但是除ADINA以外其它三个必须与别的软件搭配进行迭代分析，唯一能做到真正流固耦合的软件只有ADINA。
软件对比ANSYS是商业化比较早的一个软件，目前公司收购了很多其他软件在旗下。
ABAQUS专注结构分析目前没有流体模块。
MSC是比较老的一款软件目前更新速度比较慢。
ADINA是在同一体系下开发有结构、流体、热分析的一款软件，功能强大但进入中国时间比较晚市场还没有完全铺开。
结构分析能力排名：1、ABAQUS、ADINA、MSC、ANSYS流体分析能力排名：1、ANSYS、ADINA、MSC、ABAQUS耦合分析能力排名：1、ADINA、ANSYS、MSC、ABAQUS性价比排名：最好的是ADINA，其次ABAQUS、再次ANSYS、最后MSC ABAQUS软件与ANSYS软件的对比分析1．在世界范围内的知名度两种软件同为国际知名的有限元分析软件，在世界范围内具有各自广泛的用户群。
ANSYS 软件在致力于线性分析的用户中具有很好的声誉，它在计算机资源的利用，用户界面开发等方面也做出了较大的贡献。
ABAQUS软件则致力于更复杂和深入的工程问题，其强大的非线性分析功能在设计和研究的高端用户群中得到了广泛的认可。
有限元⽅法的发展及应⽤有限元⽅法的发展及应⽤摘要：有限元法是⼀种⾼效能、常⽤的计算⽅法。
有限元法在早期是以变分原理为基础发展起来的，所以它⼴泛地应⽤于以拉普拉斯⽅程和泊松⽅程所描述的各类物理场中。
⾃从1969年以来，某些学者在流体⼒学中应⽤加权余数法中的迦辽⾦法或最⼩⼆乘法等同样获得了有限元⽅程，因⽽有限元法可应⽤于以任何微分⽅程所描述的各类物理场中，⽽不再要求这类物理场和泛函的极值问题有所联系。
基本思想：由解给定的泊松⽅程化为求解泛函的极值问题。
1有限元法介绍1.1有限元法定义有限元法（FEA，Finite Element Analysis）的基本概念是⽤较简单的问题代替复杂问题后再求解。
它是起源于20世纪50年代末60年代初兴起的应⽤数学、现代⼒学及计算机科学相互渗透、综合利⽤的边缘科学。
有限元法的基本思想是将求解域看成是由许多称为有限元的⼩的互连⼦域组成，对每⼀单元假定⼀个合适的(较简单的）近似解，然后推导求解这个域总的满⾜条件(如结构的平衡条件），从⽽得到问题的解。
这个解不是准确解，⽽是近似解，因为实际问题被较简单的问题所代替。
由于⼤多数实际问题难以得到准确解，⽽有限元不仅计算精度⾼，⽽且能适应各种复杂形状，因⽽成为⾏之有效的⼯程分析⼿段。
有限元法最初应⽤在⼯程科学技术中,⽤于模拟并且解决⼯程⼒学、热学、电磁学等物理问题。
1.2有限元法优缺点有限元⽅法是⽬前解决科学和⼯程问题最有效的数值⽅法，与其它数值⽅法相⽐，它具有适⽤于任意⼏何形状和边界条件、材料和⼏何⾮线性问题、容易编程、成熟的⼤型商⽤软件较多等优点。
（1）概念浅显，容易掌握，可以在不同理论层⾯上建⽴起对有限元法的理解，既可以通过⾮常直观的物理解释来理解，也可以建⽴基于严格的数学理论分析。
（2）有很强的适⽤性，应⽤范围极其⼴泛。
它不仅能成功地处理线性弹性⼒学问题、费均质材料、各向异性材料、⾮线性应⽴-应变关系、⼤变形问题、动⼒学问题已及复杂⾮线性边界条件等问题，⽽且随着其基本理论和⽅法的逐步完善和改进，能成功地⽤来求解如热传导、流体⼒学、电磁场等领域的各类线性、⾮线性问题。
有限元法及应用总结有限元法（Finite Element Method，FEM）是一种数学建模方法，用于求解连续介质的力学问题。
它通过将连续介质分割为有限数量的小单元，通过离散化的方式将连续问题转化为离散问题，然后通过数值计算方法进行求解。
有限元法的基本步骤是：建立初始网格、选择合适的单元类型和数学模型、建立有限元方程、求解有限元方程组、计算和评估结果。
1.建立初始网格：将连续介质分割为离散的小单元。
可以根据问题的特点选择不同形状的单元，如三角形、四边形、六边形等。
初始网格的密度应根据问题的要求进行合理的选择。
2.选择合适的单元类型和数学模型：根据问题的情况，选择合适的数学模型，如线性模型、非线性模型、静力学模型、动力学模型等。
同时，根据问题的要求选择合适的单元类型，如三角形单元、四边形单元等。
3.建立有限元方程：根据选择的数学模型，使用变分原理或其他方法建立有限元方程。
有限元方程通常是一个矩阵方程，包含未知变量和已知条件，通过求解该方程可以得到问题的解。
4.求解有限元方程组：将有限元方程组转换为代数方程组，使用数值计算方法求解。
常用的求解方法有直接解法和迭代解法，如高斯消元法、LU分解法、共轭梯度法等。
根据问题的特点选择合适的求解方法。
5.计算和评估结果：得到问题的解后，可以通过计算和评估结果来验证数值解的准确性和可靠性。
常见的评估方法有误差分析、收敛性分析、模型验证等。
有限元法的应用非常广泛，涉及机械、土木、航空航天、电子、生物医学等多个领域。
通过有限元法可以模拟和分析各类结构的力学行为和变形特性，以及流体、热传导等物理问题。
在机械工程中，有限元法可以用于模拟零件的变形、应力和疲劳行为，优化结构设计，确定最佳工艺参数等。
在土木工程中，可以用于模拟建筑物、桥梁、隧道等结构的稳定性和强度，评估结构的安全性。
在航空航天工程中，可以用于模拟飞机、航天器的疲劳和破坏行为，优化材料和结构设计。
在电子工程中，有限元法可以用于模拟芯片、电路板的热分布和应力分布，优化散热和布线设计。
有限元分析总结引言有限元分析（Finite Element Analysis，简称FEA）是一种广泛应用于工程、物理学等领域的计算方法，用于模拟和分析复杂结构的行为。
通过将复杂结构离散为许多小的有限元件，然后利用数值方法求解这些元件的行为，从而得到整个结构的行为情况。
本文将对有限元分析的原理、应用和优缺点进行总结。
有限元分析原理有限元分析的核心思想是将连续结构离散化，并假设每个小元素的行为是线性的。
然后，通过构建结构的刚度矩阵和荷载向量的方程组，利用数值计算方法求解节点的位移和应力分布。
具体的步骤如下：1.确定要分析的结构的几何形状，将其划分为有限数目的小单元，例如三角形或四边形元素。
2.在每个小单元内，选取适当的插值函数来估计位移和应力分布。
3.根据连续性条件，建立整个结构的刚度矩阵。
刚度矩阵的元素代表了各节点的相互作用关系。
4.构建荷载向量，其中包括外界载荷和边界条件。
5.求解线性方程组，得到结构的节点位移和应力分布。
6.进一步分析节点位移和应力数据，得到结构的各种性能指标。
有限元分析应用有限元分析在工程领域有着广泛的应用，例如：•结构强度分析：通过有限元分析可以评估结构在受载情况下的应力和变形情况，以及可能的破坏模式。
•热传导分析：有限元分析可以模拟热传导过程，预测物体内部的温度分布，以及热传导对结构性能的影响。
•流体力学分析：有限元分析可以描述流体的流动行为，例如流体中的速度、压力分布等。
•多物理场耦合分析：如结构与热传导、流体力学等多个物理领域的耦合问题，可以利用有限元分析进行综合分析。
有限元分析优缺点有限元分析作为一种数值计算方法，具有一些明显的优点和缺点：优点：•可以模拟和分析复杂结构的行为，如非线性和非均匀材料，不规则几何形状等。
•可以提供详细的节点位移和应力分布数据，对结构性能进行深入分析。
•可以快速进行多次迭代计算，探索不同设计参数对结构性能的影响。
•可以进行实时动态仿真和优化，为工程设计提供重要的支持。
现代机械设计理论与方法有限元方法学院：机械工程学院日期：2012年12月8日目录摘要 (3)关键词 (3)Abstract (3)Key Words (4)1 有限元方法的国内外研究现状及应用实例 (4)1.1 有限元的发展趋势 (4)1.2 有限元的应用实例 (4)2 有限元方法的分析过程 (5)2.1 有限元分析的三个阶段 (5)2.2 有限元分析的七个步骤 (5)2.3 有限元软件的分析过程 (6)3 参考文献 (8)有限元方法摘要：有限元方法法的基本概念是用较简单的问题代替复杂问题后再求解。
有限元法的基本思想是先化整为零﹑再积零为整，也就是把一个连续体分割成有限个单元；即把一个结构看成由若干通过节点相连的单元组成的整体，先进行单元分析，然后再把这些单元组合起来代表原来的结构进行整体分析。
关键词：有限元方法；单元；节点Finite Element MethodAbstract：The basic concepts of the finite element method is solving complex problems with a simple question instead.The basic idea of the finite element method is dismembered, and then plot the parts into a whole, that is divided a continuum into a finite number of unit; that is to regard a structure as a whole connected by many nodes，first to analysis unit，then analysis the overall combined by these units，which represents the original structure.Key Words：finite element method；unit；node1 有限元方法的国内外研究现状及应用实例“有限单元法”这一名称是克拉夫（Clough）在1960年首先引用的。
它是随着电子计算机的发展而迅速发展起来的一种现代计算方法。
它虽然是50年代首先在连续体力学领域—飞机结构静、动态特性分析中应用过的一种有效的数值分析方法，但是，由于它所依据理论的普遍性，已经能够成功地用来求解其它工程领域中的许多问题[1]。
随后很快广泛的应用于求应力场、位移场、电磁场、温度场、流体场等连续性问题。
涉及了很多的工程学科，如机械设计、声学、电磁学、岩土力学、流体力学等。
在机械工程领域，有限元被广泛的应用于机构、振动和传热问题上。
1.1 有限元的发展趋势纵观当今国际上有限元软件的发展情况，可看出有限元软件的一些发展趋势：与CAD软件的无缝集成；更为强大的网格处理能力；由求解线性问题发展到求解非线性问题；由单一结构场求解发展到耦合场问题的求解；程序面向用户开放性等。
1.2 有限元的应用实例1.2.1地铁振动预测的周期性有限元—边界元耦合模型Jones利用有限元—无限元耦合二维模型计算了铁路隧道内及周围土体的动力响应[2]。
针对地铁列车运行引起的隧道结构和自由场中的振动响应问题，提出了一个在频率—波数域内的三维周期性有限元—边界元耦合的数值模型，此模型中隧道结构采用有限元法计算，自由场采用边界元法模拟。
此模型采用Floquet变换，利用隧道和自由场在隧道轴线方向上的周期性，把无限长的隧道及自由场的网格划分限制在一个基本元内，这样使动力学数值计算的效率大大提高。
利用此模型计算了在隧道底板上施加固定单位谐振荷载情况下隧道—自由场相互作用系统的动力响应，结果表明此模型可应用于地铁列车运行引起的隧道和自由场中的动力响应预测[3]。
1.2.2 永磁直线同步电机解析分析及有限元验证对永磁直线同步电动机具有边端效应、气隙不均匀、气隙磁场分布复杂、永久磁极几何尺寸难以确定的问题，给出了单段永磁直线同步电动机气隙磁场的二维解析分析，讨论了电机的各主要尺寸参数对气隙磁场和性能的影响，提出了永久磁极的设计原则和计算公式，分析了考虑饱和影响、计及边端效应时分段式永磁直线同步电动机的非线性、不对称、变化的自感和互感参数的解析计算方法，得到了定子绕组自感和互感系数随动子位置不同时的变化曲线。
有限元数值计算结果表明，导出的分段式永磁直线同步电动机永久磁极的设计计算公式以及电机变电感参数解析计算公式是适用的[4]。
1.2.3 基于响应面的桥梁有限元模型修正采用试验设计和回归分析方法，以显式的响应面模型逼近特征量与设计参数间复杂的隐式函数关系，得到简化的结构模型(Meta-model)，给出有限元模型修正过程。
针对复杂的土木工程结构，讨论样本选择、修正参数选取以及如何从众多因素中较合理地建立结构的响应面模型。
用数值模拟算例和六跨连续梁桥环境振动试验结果，实现基于响应面模型的土木工程结构有限元模型修正，并与传统的基于灵敏度方法直接对结构有限元模型修正结果进行比较。
结果表明，基于响应面方法的有限元模型修正和验证，能显著提高修正的效率，修正过程计算简洁、迭代收敛快，避开每次迭代都需要进行有限元计算，易于工程实际应用[5]。
2 有限元方法的分析过程2.1 有限元分析的三个阶段前处理阶段：将整体结构或其一部分简化为理想的数学力学模型，用离散化的单元代替连续实体结构或求解区域；主要包括：定义分析的类型、添加材料属性、添加载荷和约束、网格的划分等……分析求解阶段：运用有限元法对结构离散模型进行分析计算，这个过程是由计算机来完成的。
后处理阶段：对计算结果进行分析、整理和归纳。
2.2 有限元分析的七个步骤1、结构力学模型的简化从实际的问题中抽象出力学模型，对实际问题的边界条件、约束条件和外载荷条件进行简化。
抽象简化出来的力学模型应该能尽可能的反映真实的实际问题，合理的模型既能保证计算结构的精度，又不会带来结构上的过分复杂（模型的建立在有限元分析的过程中是一个比较重要的阶段）。
2、结构的离散化所谓结构的离散化就是将连续的结构体划分为有限个单元体以代替原来的结构。
这个过程也就是网格的划分，网格划分是建立有限元模型的中心工作，模型的合理性很大程度上可以通过所划分的网格形式反映出来。
3、位移模式的选择为了能用节点位移表示单元体的位移、应变和应力，在分析时就要对单元体位移的分布进行一定的假设，假设位移是坐标的某种简单函数，这个函数就是位移模式或者位移函数。
一般情况下选择多项式作为位移模式，因为所有的光滑函数的局部都可以用多项式逼近。
4、分析单元的力学特性单元特性的分析包括以下三部分的内容：（1）利用几何方程，用位移模式导出用节点位移表示单元应变的关系式。
（2）利用物理方程，由应变表达式导出用节点位移表示单元应力的关系式。
（3）利用虚功原理建立作用于单元上的节点力和节点位移之间的关系式，也就是单元的刚度方程。
5、计算等效节点力弹性体经过离散后，假定力是通过节点在单元体之间进行传递的。
但是，实际的连续体，力是通过单元的公共边界进行传递的。
因此，作用在单元上的各种力就需要等效移植到节点上去，也就是用等效的节点力来代替单元上的力。
移植的方法是按照虚功等效原则进行的。
6、集合所有单元的刚度方程，建立这个结构的平衡方程这个过程包括两个方面的内容：一是由各个单元的刚度矩阵集合成整个物体的整体刚度矩阵；二是将作用于各单元的等效节点力列阵合成总的载荷列阵。
集合所依据的原则是要求相邻的单元在公共节点处的位移相等。
7、求解未知节点的位移和计算单元应力由集合起来的平衡方程组，解出未知位移。
在线弹性平衡问题中，可以根据方程组的具体特点选择合适的计算方法。
对于非线性问题，则通过一系列的步骤，并逐步修正刚度矩阵或载荷矩阵，才能获得解答。
最后，利用物理方程和求出的节点位移，计算各单元的应力，并加以整理得出所要的结果。
2.3 有限元软件的分析过程用Solidworks软件中的simulation插件可以解决一些简单的有限元问题。
2.3.1 数学模型的建立从实际问题中抽象出数学模型，是一个长、宽、高分别为1000mm、100mm、50mm 的一个长方体。
利用Solidworks软件进行实体建模，选择材料为合金钢，如下图所示：接下来，我们添加静态算例，因为它所承受的载荷是静态的。
2.3.2 添加约束和载荷将实体的左端面固定，并且在最右端添加一个竖直向下的5000N的力。
如下图所示：2.3.3 将实体进行网格划分网格划分后的结果如下：2.3.4 运行求解应力截图位移截图应变截图2.3.5 结果分析对结果进行分析可知，与实际的工程应用实例结果一致。
3 参考文献[1]任中全，寇子明，赵灿等．现代机械设计理论与方法[M]．北京：煤炭工业出版社，2000：24-25.[2]Jones C J C，Wang A，Dawn T M．Modelling propagation of vibration from railway tunnels[A]．Computational Acoustics and its EnvironmentalApplications[c]．Southampton，April 5-7，1995：285～292．[3]刘卫丰，刘维宁等.地铁振动预测的周期性有限元—边界元耦合模型[J].振动工程学报，2009,22(5)：480—485.[4]王淑红，熊光煜等. 永磁直线同步电机解析分析及有限元验证[J].电机与控制学报，2011,15(7)：8—13.[5]任伟新，陈华斌等.基于响应面的桥梁有限元模型修正[J].土木工程学报，2008,41(12)：73—78.“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
