华东师大版八年级数学下册 第18章 平行四边形 单元测试题(无答案)

八年级数学下册第十八章平行四边形章节练习考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF＝6，AB＝5，则AE的长为（）A．4 B．6 C．8 D．102、在平行四边形ABCD中，∠A的平分线把BC边分成长度是3和4的两部分，则平行四边形ABCD周长是（）A．22 B．18 C．22或20 D．18或223、如图，在四边形ABCD中，AB∥CD，添加下列一个条件后，定能判定四边形ABCD是平行四边形的是（）A ．AB ＝BC B ．AC ＝BD C ．∠A ＝∠C D ．∠A ＝∠B4、在平行四边形ABCD 中，45DBC ∠=︒，DE BC ⊥于E ，BF CD ⊥于F ，DE ， BF 相交于H ，BF与AD 的延长线相交于点G ，下面给出四个结论：①BD ；②A BHE ∠=∠；③AB BH =；④BCF DCE ∆≅∆，其中正确的结论是（ ）A ．①②③B ．①②④C ．②③④D ．①②③④5、如图，在平行四边形ABCD 中，已知6cm AD =，4cm AB =，DE 平分ADC ∠交BC 边于点E ，则BE 等于（ ）A ．1cmB ．2cmC ．4cmD ．6cm6、如图，平行四边形ABCD 中，E 、F 分别在边BC 、AD 上，添加条件后不能使AE ＝CF 的是（ ）A ．BE ＝DFB ．AE ∥CFC ．AF ＝AED ．AF ＝EC7、下列命题不正确的是（ ）A ．三边对应相等的两三角形全等B ．若a b =，则22a b =C ．有一组对边平行、另一组对边相等的四边形是平行四边形D ．ABC 的三边为a 、b 、c ，若222a c b -=，则ABC 是直角三角形．8、如图四边形ABCD 的对角线AC ，BD 交于点O ，则不能．．判断四边形ABCD 是平行四边形的是（ ）A ．AB ∥CD ，∠DAC =∠BCAB ．AB =CD ，∠ABO =∠CDOC ．AC =2AO ，BD =2BO D ．AO =BO ，CO =DO9、如图，在平行四边形ABCD 中，∠A +∠C ＝130°，则∠B 的度数为（ ）A ．130°B ．115°C ．105°D ．95°10、如图，在▱ABCD 中，∠B ＝60°，AB ＝BC ，AE ⊥BC 于点E ，连接DE ，交AC 于点G ．以DE 为边作等边△DEF ，连接AF ，交DE 于点N ，交DC 于点M ，且M 为AF 的中点．在下列说法中：①∠EAN ＝45°，②12AE ，③S △AGE ＝S △DGC ，④AF ⊥DE ．正确的个数有（ ）A ．1个B ．2个C ．3个D ．4个第Ⅱ卷（非选择题 70分）二、填空题（10小题，每小题4分，共计40分）1、如图，在ABC 中，2AB AC ==，90BAC ∠=︒，M ，N 为BC 上的两个动点，且MN =AM AN +的最小值是________．2、如图，平行四边形ABCD 中，AC 、BD 交于点O ，分别以点A 和点C 为圆心，大于12AC 的长为半径作弧，两弧相交于M 、N 两点，作直线MN ，交AB 于点E ，交CD 于点F ，连接CE ，若AD ＝6，△BCE 的周长为14，则CD 的长为_________．3、如图，ABCD 中，对角线AC BD 、交于O ，若120,7,10BOC AD BD ∠==︒=，则ABCD S =______．4、在四边形ABCD 中，若AB //CD ，BC _____AD ，则四边形ABCD 为平行四边形．5、在ABCD 中，已知对角线AC BD 、交于点O ，ABO 的周长为17，6AB =，那么对角线AC BD +=_________．6、平行四边形的性质：平行四边形的两组对边分别________；平行四边形的两组对角分别________；平行四边形的对角线________．7、□ABCD 的周长为60cm ，其对角线交于O 点，若△AOB 的周长比△BOC 的周长多10cm ，则AB =_____，BC =_____．8、如图，ABCD 中，90,3,4BAC AB AC ∠=︒==，则BD 的长为_________．9、如图，平面直角坐标系中，有()3,4A ，()6,0B ，()0,0O 三点，以A ，B ，O 三点为顶点的平行四边形的另一个顶点D 的坐标为______．10、如图，平行四边形ABCD 的AB 边在x 轴上，点C 、D 分别在(0)k y x x =>，3(0)y x x-=<的图象上，若平行四边形ABCD 的面积是8，则k 的值为_________．三、解答题（5小题，每小题6分，共计30分）1、如图1，已知点C 的坐标是（，，过点C 分别向x 轴、y 轴作垂线，垂足分别为点B 、点D ，点E 是线段OD 上一点（不与点O 、D 重合），连接BE ，作点O 关于直线BE 的对称点O '，连接CO '，点P 为CO '的中点，连接BP ，延长CO '与BE 的延长线交于点F ，连接DF ．（1）求证：∠PBF =45°；（2）如图2，连接BD ，当点O '刚好落在线段BD 上时，求直线BF 的解析式；（3）在（2）的条件下，在平面内是否存在点M ，使得以M 、O 、O '、F 为顶点的四边形是平行四边形，若存在，请直接写出点M 的坐标；若不存在，请说明理由．2、如图，平行四边形ABCD 中，AC 是它的一条对角线，过B 、D 两点作BH AC ⊥，DG AC ⊥，垂足分别为H 、G ，延长BH 、DG 分别交CD 、AB 于F 、E ．（1）求证：四边形DEBF 是平行四边形；（2）求证：FCH EAG ≅△△．3、已知：如图，E 在ABCD 边BC 的延长线上，且CE BC =．求证：四边形ACED 是平行四边形．4、先判断下列各命题的真假，然后写出它们的逆命题，并判断逆命题的真假：（1）平行四边形相邻的两个角都相等；（2）一组对边平行，另一组对边相等的四边形是平行四边形．5、作图题（1）填空：如果长方形的长为3，宽为2，那么对角线的长为_________．（2）如下图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，以格点为顶点（端点），分别按下列要求画图（不要求写画法和证明，但要标注顶点）．①在图1中，分别画三条线段AB 、CD 、EF ，使AB CD =EF②在图2中，画三角形ABC ，使AB =3、BC =CA③在图3中，画平行四边形ABCD ，使45A ∠=︒，且面积为6．-参考答案-一、单选题1、C【解析】【分析】先证△ABO ≌△AFO 得到OB 的长度，再用勾股定理求AO 的长，再证△AOF ≌△EOB ，从而得到AE =2AO ，即可求得AE 的长．【详解】解：设AG与BF交点为O，如图所示：∵AB=AF,AG平分∠BAD，AO=AO,∴△ABO≌△AFO,∴BO=FO，∠AOB=∠AOF=90º，∵BF＝6BF＝3∴BO=FO=12在Rt△AOB中，由勾股定理得：AO==，4在▱ABCD中，AF∥BE,∴∠FAO=∠BEO又∵BO=FO，∠AOB=∠AOF∴△AOF≌△EOB,∴AO=EO,∴AE=2AO=8，故选C．【点睛】本题考查全等三角形的判定和性质、平行四边形的性质、勾股定理及用尺规作图的方法画角平分线．2、C【解析】【分析】利用平行四边形对边平行得出∠DAE=∠AEB，利用角平分线的定义得出∠BAE=∠DAE，进而得到∠BAE=∠BEA，利用等角对等边，得出AB=BE，通过对BE和EC长度的讨论，利用周长的定义逐个计算即可．【详解】解：在平行四边形ABCD中，AD∥BC，则∠DAE=∠AEB．∵AE平分∠BAD，∴∠BAE=∠DAE，∴∠BAE=∠BEA，∴AB=BE，BC=BE+EC，如图，①当BE=3，EC=4时，平行四边形ABCD的周长为：2（AB+BC）=2（3+3+4）=20．②当BE=4，EC=3时，平行四边形ABCD的周长为：2（AB+BC）=2（4+4+3）=22．故选:C．【点睛】本题考查了平行四边形的性质、角平分线的定义、等腰三角形的判定之等角对等边等内容，解决本题的关键是求出AB的长，本题涉及到的思想为分类讨论的思想．3、C【解析】【分析】利用平行线的判定与性质结合平行四边形的判定得出即可.【详解】∵AB//CD，∴∠B+∠C=180°，当∠A=∠C时，则∠A+∠B=180°，故AD//BC，则四边形ABCD是平行四边形.故选C.【点睛】本题考查了平行四边形的判定，掌握平行四边形的判定是解题的关键．4、A【解析】【分析】先判断△DBE是等腰直角三角形，根据勾股定理可推导得出BD BE，可判断①不正确；根据∠BHE 和∠C都是∠HBE的余角，可得∠BHE=∠C，再由∠A=∠C，可判断②正确；证明△BEH≌△DEC，从而可得BH=CD，再由AB=CD，可判断③正确；利用对应边不等可判断④不正确，据此即可得到选项．【详解】解：∵∠DBC=45°，DE⊥BC于E，∴∠DEB=90°，∠BDE=180°-∠DBE-∠DEB=180°-45°-90°=45°，∴在Rt △DBE 中，BE 2+DE 2=BD 2，∴BD，故①正确；∵DE ⊥BC ，BF ⊥DC ，∴∠HBE +∠BHE =90°，∠C +∠FBC =90°，∴∠BHE 和∠C 都是∠HBE 的余角，∴∠BHE =∠C ，又∵在▱ABCD 中，∠A =∠C ，∴∠A =∠BHE ，故②正确；在△BEH 和△DEC 中，BHE C HEB CED BE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△BEH ≌△DEC （AAS ），∴BH =CD ，∵四边形ABCD 为平行四边形，∴AB =CD ，∴AB =BH ，故③正确；∵BE ＞BH ＞BE =DE ，BC ＞BF ＞BH =DC ，∠FBC =∠EDC ，∴不能得到△BCF ≌△DCE ，故④错误．【点睛】本题考查了平行四边形的性质、等腰直角三角形的判定与性质、勾股定理、全等三角形的判定与性质等，熟练掌握相关性质与定理是解题的关键．5、B【解析】【分析】由平行四边形对边平行根据两直线平行，内错角相等可得EDA DEC ∠=∠，而DE 平分ADC ∠，进一步推出EDC DEC ∠=∠，在同一三角形中，根据等角对等边得CE CD =，则BE 可求解．【详解】解：∵四边形ABCD 是平行四边形，∴6cm BC AD ==，4cm CD AB ==，//AD BC ，∴EDA DEC ∠=∠，又∵DE 平分ADC ∠，∴EDC ADE ∠=∠，∴EDC DEC ∠=∠，∴4cm CD CE AB ===，即()642cm BE BC EC =-=-=．故选：B ．【点睛】本题考查了平行四边形的性质的应用及等腰三角形的判定，理解其性质及等腰三角形的判定是解题关键．6、C【分析】利用平行四边形的性质，依据平行四边形的判定方法，即可得出不能使AE＝CF的条件．【详解】解：A、在▱ABCD中，∴AD∥BC，AD＝BC，∵BE＝DF，∴AF＝CE，∴四边形AECF是平行四边形，∴AE＝CF，故A可以使AE＝CF，不符合题意；B、∵AE∥CF，AF∥CE，∴四边形AECF是平行四边形，∴AE＝CF，故B可以使AE＝CF，不符合题意；C、添加AE＝AF后不能使AE＝CF，故C符合题意；D、∵四边形AECF是平行四边形，∴AE＝CF，故D可以使AE＝CF，不符合题意；故选C．【点睛】本题主要考查了平行四边形的性质定理和判定定理；熟记平行四边形的判定方法是解决问题的关键．7、C【解析】【分析】根据三角形全等的判定定理（SSS 定理）、乘方运算法则、平行四边形的判定、勾股定理的逆定理逐项判断即可得．【详解】解：A 、三边对应相等的两三角形全等，此命题正确，不符题意；B 、若a b =，则22a b =，此命题正确，不符题意；C 、有一组对边平行、另一组对边相等的四边形有可能是等腰梯形，不一定是平行四边形，所以此项命题不正确，符合题意；D 、ABC 的三边为a 、b 、c ，若222a c b -=，即222a b c =+，则ABC 是直角三角形，此命题正确，不符题意；故选：C ．【点睛】本题考查了三角形全等的判定定理、乘方运算法则、平行四边形的判定、勾股定理的逆定理，熟练掌握各定理是解题关键．8、D【解析】【分析】A.证明//AD BC ，即可根据两组对边分别平行的四边形是平行四边形判断；B.证明AB ∥CD ，即可根据有一组对边平行且相等的四边形是平行四边形判断；C. 可根据对角线互相平分的四边形是平行四边形判断；D. 条件不足无法判断；∠DAC=∠BCA∴//AD BC，∴四边形ABCD是平行四边形，故A选项正确，不符合题意；∠ABO=∠CDO//∴AB CD又 AB=CD，∴四边形ABCD是平行四边形，故B选项正确，不符合题意；AC=2AO，BD=2BO,∴==AO CO BO DO∴四边形ABCD是平行四边形，故C选项正确，不符合题意；D. 条件不足无法判断，符合题意；故选D【点睛】本题考查了平行四边形的判定，掌握平行四边形的判定方法是解题的关键．9、B【解析】【分析】由平行四边形ABCD中，若∠A＋∠C＝130°，可求得∠C的度数，继而求得∠B的度数．解：∵四边形ABCD 是平行四边形，∴∠A ＝∠C ，∵∠A ＋∠C ＝130°，∴∠C ＝65°，∴∠B ＝180°−∠C ＝115°．故选：B ．【点睛】此题考查了平行四边形的性质．此题比较简单，根据平行四边形对角相等解答是解此题的关键．10、B【解析】【分析】连接CF ，过点A 作AH ⊥DC 于点H ，首先通过SAS 证明△DAE ≌△DCF ，得AE ＝CF ，∠DAE ＝∠DCF ＝90°，则∠ACF ＝150°，由AC ≠CF ，则∠EAN ≠45°，故①错误；易证△AHM ≌△FCM （AAS ），得HM ＝CM ＝12a ＝12AE ，故②正确；因为AD //BC ，得S △AEC ＝S △DCE ，从而可证③正确；因为△EDF 是等边三角形，若AF ⊥DE ，则AF 垂直平分DE ，则AD ＝AE ，显然AD ≠AE ，故AF 与AD 不垂直，故④错误．【详解】 解：连接CF ，过点A 作AH ⊥DC 于点H ，∵四边形ABCD是平行四边形，∠B＝60°，AB＝BC，∴△ABC、△ADC都是等边三角形，AD//BC，∵AE⊥BC，∴BE＝CE，∠BAE＝∠CAE＝30°，设BE＝CE＝a，则AB＝BC＝AC＝2a，∴AE，∵∠ADC＝∠EDF＝60°，∴∠ADE＝∠CDF，在△DAE和△DCF中，AD CDADE CDF ED FD=⎧⎪∠=∠⎨⎪=⎩，∴△DAE≌△DCF（SAS），∴AE＝CF，∠DAE＝∠DCF，∴∠DCF＝∠DAE＝90°，∴∠ACF＝150°，∵AC≠CF，∴∠CAF≠∠CFA≠15°，∴∠EAN≠45°，故①错误；∵∠AHM＝∠FCM＝90°，MA＝MF，∠AMH=∠FMC，∴△AHM≌△FCM（AAS），∴HM＝CM＝12a，＝12AE，故②正确；∵AD//BC，∴S△AEC＝S△DCE，∴S△AEC−S△GCE＝S△DCE−S△GCE，即S△AGE＝S△DGC，故③正确；∵△EDF是等边三角形，若AF⊥DE，则AF垂直平分DE，则AD＝AE，显然AD≠AE，故AF与AD不垂直，故④错误；∴正确的是②③，一共2个，故选：B．【点睛】本题是四边形的综合题，主要考查了等边三角形的判定与性质、三角形全等的判定与性质，以及线段垂直平分线的性质等知识，通过作辅助线，构造出△DAE≌△DCF是解题的关键．二、填空题1【解析】【分析】过点A作AD//BC，且AD＝MN，连接MD，则四边形ADMN是平行四边形，作点A关于BC的对称点A′，连接AA′交BC于点O，连接A′M，三点D、M、A′共线时，AM AN最小为A′D的长，利用勾股定理求A′D的长度即可解决问题．【详解】解：过点A作AD//BC，且AD＝MN，连接MD，则四边形ADMN 是平行四边形，∴MD ＝AN ，AD ＝MN ，作点A 关于BC 的对称点A ′，连接A A ′交BC 于点O ，连接A ′M ，则AM ＝A ′M ，∴AM ＋AN ＝A ′M ＋DM ，∴三点D 、M 、A ′共线时，A ′M ＋DM 最小为A ′D 的长，∵AD //BC ，AO ⊥BC ，∴∠DA A '＝90°，∵2AB AC ==，90BAC ∠=︒，，∴BC＝BO＝CO ＝AO∴AA '=在Rt△AD A '中，由勾股定理得：A 'D =∴AM AN +【点睛】本题主要考查了等腰三角形的性质，平行四边形的判定与性质，勾股定理等知识，构造平行四边形将AN转化为DM是解题的关键．2、8【解析】【分析】根据题意可知用MN垂直平分AC，则EA=EC，利用等线段代换得到△BCE的周长=AB+BC，然后根据平行四边形的性质AD＝BC可确定答案．【详解】∵四边形ABCD为平行四边形，∴AD＝BC，由题可知，MN是AC的垂直平分线，∴CE=AE，∴△BCE的周长=BC+CE+BE=BC+AB=14，∵BC=AD=6，∴CD=AB=14−6=8．故答案为：8．【点睛】本题考查了垂直平分线的性质、平行四边形的性质，做题的关键是证明EA=EC，将△CDE的周长转化为AB+BC．3、【解析】【分析】过点A 作AE ⊥BD 于E ，设OE ＝a ，则AE ，OA ＝2a ，在直角三角形ADE 中，利用勾股定理可得DE 2+AE 2＝AD 2，进而可求出a 的值，△ABD 的面积可求出，由平行四边形的性质可知：ABCD 的面积＝2S △ABD ，即可求解【详解】解：过点A 作AE ⊥BD 于E ，∵四边形ABCD 是平行四边形， ∴1110522OD BD ==⨯=，∵∠BOC ＝120°，∴∠AOE ＝60°，设OE ＝a ，则AE ，OA ＝2a ，∴DE ＝5+a ，在直角三角形ADE 中，由勾股定理可得DE 2+AE 2＝AD 2，∴（5+a ）2+）2＝72， 解得：32a =，32AE ∴==∴ABCD 的面积＝2S △ABD ＝12102⨯=故答案为：【点睛】本题考查了平行四边形的性质以及勾股定理，解题关键是掌握数形结合思想与方程思想的应用． 4、∥【解析】【分析】根据平行四边形的判定：两组对边分别平行的四边形是平行四边形即可解决问题．【详解】解：根据两组对边分别平行的四边形是平行四边形可知：∵AB //CD ，BC //AD ，∴四边形ABCD 为平行四边形．故答案为：//．【点睛】本题考查了平行四边形的判定，熟练掌握平行四边形的判定方法是解题的关键．5、22【解析】【分析】平行四边形对角线互相平分，△ABO 的周长即为对角线的一半与一边AB 之和，有AB 的长，对角线之和则可解．【详解】 解：如图， ABCD ，11,,22OA OC AC OB OD BD ∴==== ()2,AC BD OA OB ∴+=+∵△ABO的周长为17，AB=6，∴OA+OB=11，∴AC+BD=22．故答案为22．【点睛】本题考查了平行四边形的基本性质，并利用性质解题．平行四边形基本性质：①平行四边形两组对边分别平行；②平行四边形的两组对边分别相等；③平行四边形的两组对角分别相等；④平行四边形的对角线互相平分．6、相等相等互相平分【解析】略7、 20cm 10cm【解析】【分析】根据平行四边形的性质可知，平行四边形的对边相等，平行四边形的对角线互相平分．已知周长为60cm，可以求出一组邻边的和为30cm，△AOB的周长比△BOC的周长多10cm，则AB比BC的值多10cm，则进一步可求出AB，BC的长．【详解】解：∵□ABCD的周长为60cm，AB +BC =30，∵△AOB 的周长比△BOC 的周长多10cm ，∴AB -BC =10，∴3010AB BC AB BC +=⎧⎨-=⎩解得2010AB BC =⎧⎨=⎩故答案为：①20cm ②10cm．【点睛】本题考察了平行四边形的性质，平行四边形的对边相等，平行四边形的对角线互相平分，做题的关键是由一组邻边的和为30cm ，△AOB 的周长比△BOC 的周长多10cm ，列出方程解方程即可．8、【解析】【分析】 利用平行四边形的性质先求解12,,2OA OC OB OD BD ====再利用勾股定理求解,OB 从而可得答案. 【详解】解：,4,ABCD AC =12,,2OA OC OB OD BD ∴====90,3,BAC AB ∠=︒=OB ∴==2BD OB ∴==故答案为：【点睛】本题考查的是平行四边形的性质，勾股定理的应用，掌握平行四边形的对角线互相平分是解题的关键.9、（9，4）、（-3，4）、（3，-4）【解析】【分析】根据平行四边形的性质得出AD=BO =6，AD ∥BO ，根据平行线得出A 和D 的纵坐标相等，根据B 的横坐标和BO 的值即可求出D 的横坐标．【详解】∵平行四边形ABCD 的顶点A 、B 、O 的坐标分别为（3，4）、（6，0）、（0，0），∴AD=BO =6，AD ∥BO ，∴D 的横坐标是3+6=9，纵坐标是4，即D 的坐标是（9，4），同理可得出D 的坐标还有（-3，4）、（3，-4）．故答案为：（9，4）、（-3，4）、（3，-4）．【点睛】本题考查了坐标与图形性质和平行四边形的性质，注意：平行四边形的对边平行且相等． 10、5【解析】【分析】由四边形ABCD 是平行四边形，得到AB ∥CD 则可设C 点坐标为,k a a ⎛⎫ ⎪⎝⎭，则D 点坐标为3,a k k a ⎛⎫- ⎪⎝⎭，得到33a a CD a a k k ⎛⎫=--=+ ⎪⎝⎭，再由=8C ABCD S CD y ⋅=四边形，得到38k a a a k ⎛⎫+= ⎪⎝⎭，由此求解即可． 【详解】 解：∵四边形ABCD 是平行四边形，∴AB ∥CD设C 点坐标为,k a a ⎛⎫ ⎪⎝⎭，则D 点坐标为3,a k k a ⎛⎫- ⎪⎝⎭， ∴33a a CD a a k k ⎛⎫=--=+ ⎪⎝⎭， ∵=8C ABCD S CD y ⋅=四边形， ∴38k a a a k ⎛⎫+= ⎪⎝⎭， ∴38k +=，∴5k =，故答案为：5．【点睛】本题主要考查了反比例函数比例系数的几何意义，平行四边形的性质，解题的关键在于能够熟练掌握反比例函数比例系数的几何意义．三、解答题1、（1）见解析；（2）(18y x =+-（3）存在，M 坐标为（8，4+）或（-4）或（4-． 【解析】【分析】（1）连接O 'B ，由点O 关于直线BE 的对称点O '，得∠OBF =∠O 'BF =12∠OBO '，由△BO 'C 是等腰三角形，点P为CO'的中点，得∠CBP=∠O'BP=12∠CBO'，从而∠PBF'=12∠OBC=45°；（2）连接EO'，设OE=O'E=x，则DE x，在Rt△DOE中，DO'2+O'E2=DE2，可得（2+x2=（x）2，解得x，E（0，，设直线BF的解析式为y=kx+b，将B（0）、E（0，（3）过O'作O'G⊥OB于G，先求出O'、F坐标，设M（a，b），分三种情况：①以MO、O'F为对角线，②以MO'、OF为对角线，③以MF、OO'为对角线，用平行四边形对角线中点重合列方程即可求解．【详解】解：（1）连接O'B，如图：∵C的坐标是（，过点C分别向x轴、y轴作垂线，垂足分别为点B、点D，∴OB=BC∵点O关于直线BE的对称点O'，∴∠OBF=∠O'BF=12∠OBO'，O'B=OB，∴O'B=BC，即△BO'C是等腰三角形，∵点P为CO'的中点，∴∠CBP=∠O'BP=12∠CBO'，∴∠PBF=∠O'BF+∠O'BP=12∠OBO'+12∠CBO'=12（∠OBO'+∠CBO'）=12∠OBC=45°；（2）连接EO'，如图：在Rt △BOD 中，OB =OD ，∴BD ，∵点O 关于直线BE 的对称点O '，∴OE =O 'E ，O 'B =OB ，∠EO 'B =∠EOB =90°，∴∠DOE =90°，DO '=BD -O 'B设OE =O 'E =x ，则DE x ，在Rt △DOE 中，DO '2+O 'E 2=DE 2，∴（2+x 2=（x ）2，解得x∴E （0，，设直线BF 的解析式为y =kx +b ，将B （，0）、E （0，8b b ⎧=+⎪⎨-=⎪⎩，解得18k b ⎧=⎪⎨=-⎪⎩∴直线BF 的解析式为y =（x（3）存在以M 、O 、O '、F 为顶点的四边形是平行四边形，理由如下： 过O '作O 'G ⊥OB 于G ，如图：∵△BOD 是等腰直角三角形，∴△O 'BG 是等腰直角三角形，∵O 'B =OB，∴O 'G =BG =4，∴OG =OB -BG，∴O '（，4），∵C （，，设直线CO '为y =mx +n，则()44m n n⎧=+⎪⎨⎪=+⎩，解得18m n ⎧=⎪⎨=⎪⎩， ∴直线CO '为y =1）x，联立BF 、CO '解析式得()1818y x y x ⎧=+-⎪⎨=+⎪⎩解得4x y ⎧=-+⎪⎨=⎪⎩ ∴F（4-+，设M （a ，b ），以M 、O 、O '、F 为顶点的四边形是平行四边形，分三种情况： ①以MO 、O 'F 为对角线，如图：此时MO 的中点即是O 'F 的中点，而MO 中点为（02a +，02b +），O 'F，∴04404a b ⎧+=-+⎪⎨+=+⎪⎩84a b ⎧=⎪⎨=+⎪⎩，∴M （8，4+）；②以MO '、OF 为对角线，如图：同理可得40440a b ⎧+=-+⎪⎨+=+⎪⎩4a b ⎧=-⎪⎨=⎪⎩，∴M （-，4）；③以MF 、OO '为对角线，如图：同理可得40404a b ⎧-++⎪⎨+=+⎪⎩，解得4a b ⎧=⎪⎨=-⎪⎩∴M （4-）；综上所述，M 坐标为（8，4+-，4）或（4-）．【点睛】本题考查了一次函数的综合应用，涉及轴对称变换、勾股定理应用、平行四边形的判定及性质等知识，解题的关键是灵活运用平行四边形的性质：对角线互相平分列方程组解决问题．2、（1）见解析；（2）见解析【解析】【分析】（1）根据四边形ABCD 是平行四边形，可得//CD AB ，根据BH AC ⊥，DG AC ⊥，可得//DE BF ，即可证明四边形DEBF 是平行四边形；（2）由平行线的性质可得FCH EAG ∠=∠，由（1）可得DF BE =，进而可得CF AE =，根据BH AC ⊥，DG AC ⊥，得90AGE CHF ∠=∠=︒，根据AAS 即可证明FCH EAG △≌△．【详解】证明：（1）∵四边形ABCD 是平行四边形，∴//CD AB ，即//DF BE ，∵BH AC ⊥，DG AC ⊥，∴//DE BF ，∴四边形DEBF 是平行四边形；（2）∵四边形ABCD 是平行四边形，∴AB CD =，//AB CD ，∴FCH EAG ∠=∠，∵四边形DEBF 是平行四边形，∴DF BE =，∴CF AE =，∵BH AC ⊥，DG AC ⊥，∴90AGE CHF ∠=∠=︒，∴()AAS FCH EAG △≌△．【点睛】本题考查了平行四边形的性质与判定，全等三角形的判定，掌握平行四边形的性质与判定是解题的关键．3、见解析【解析】【分析】首先根据平行四边形的性质得到BC =AD ，根据CE BC =进而可得出AD =CE ，结合//AD CE 即可证明．【详解】∵四边形ABCD是平行四边形，∴//AD BC且AD=BC，，又∵CE BC∴AD=CE，AD CE，又∵//AD BC，即//∴四边形ACED是平行四边形．【点睛】此题考查了平行四边形的判定和性质，解题的关键是熟练掌握平行四边形的判定和性质．4、（1）假；相邻两个角相等的四边形是平行四边形；真；（2）假；平行四边形的一组对边平行，另一组对边相等；真【解析】【分析】（1）根据平行四边形的性质定理和判定定理以及逆命题的概念判断；（2）根据平行四边形的性质定理和判定定理判断．【详解】解：（1）平行四边形相邻的两个角都互补，则平行四边形相邻的两个角都相等是假命题，平行四边形相邻的两个角都相等的逆命题是相邻的两个角都相等的四边形是平行四边形，是真命题；（2）一组对边平行，另一组对边相等的四边形是平行四边形或等腰梯形，则一组对边平行，另一组对边相等的四边形是平行四边形是假命题，一组对边平行，另一组对边相等的四边形是平行四边形的逆命题是平行四边形的一组对边平行，另一组对边相等，是真命题．【点睛】本题考查的是命题的真假判断、逆命题的概念，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．5、（1（2）①见解析；②见解析；③见解析【解析】【分析】（1）根据勾股定理计算即可；（2）答案不唯一，根据勾股定理计算画出即可．【详解】（1）∵长方形的长为3，宽为2，（2）只要画图正确可（不唯一）①三条线段AB、CD、EF如图1所示：②三角形ABC如图2所示：③平行四边形ABCD如图3 所示：．【点睛】本题考查了勾股定理，平行四边形的判定和性质，熟练掌握平行四边形的判定与性质是解题的关键．。

华东师大版八年级数学下册第18章《平行四边形》检测试卷一、选择题1、如图，平行四边形ABCD 中，AB=8cm ，AD=12cm ，点P 在AD 边上以每秒1cm 的速度从点A 向点D 运动，点Q 在BC 边上，以每秒4cm 的速度从点C 出发，在CB 间往返运动，两个点同时出发，当点P 到达点D 时停止（同时点Q 也停止），在运动以后，以P 、D 、Q 、B 四点组成平行四边形的次数有（）A. 4次B. 3次C. 2次D. 1次（第1题图） （第2题图） （第12题图） 2、如图，在▱ABCD 中，已知AD=12cm ，AB=8cm ，AE 平分∠BAD 交BC 边于点E ，则CE 的长等于（ ）A ．8cmB ．6cmC ．4cmD ．2cm3、如图，在Rt △ABC 中，∠B=90°，AB=3，BC=4，点D 在BC 上，以AC 为对角线的所有▱ADCE 中，DE 最小的值是（ ）A ．2B ．3C ．4D ．54、在如右图的网格中，以格点A 、B 、C 、D 、E 、F 中的4个点为顶点，你能画出平行四边形的个数为 ( )A ．2个B ．3个C ．4个D ．5个5、已知平行四边形的一边长是14，下列各组数中能分别作为它的两条对角线的是（ ）A ．10与16B ．12与16C ．20与22D ．10与40 6、平行四边形ABCD 与等边三角形AEF 按如图所示的方式摆放，如果∠B ＝45°，则∠BAE 的大小是( )A ．75°B ．80°C ．100°D ．120°7、如图，已知▱ABCD 的两条对角线AC 与BD 交于平面直角坐标系的原点，点A 的坐标为(－2，3)，则点C 的坐标为( )A ．(－3，2)B ．(－2，－3)C ．(3，－2)D ．(2，－3)（第6题图） （第7题图） （第8题图） （第9题图） 8、如图所示，EF 过▱ABCD 的对角线的交点O ，交AD 于点E ，交BC 于点F ，已知AB ＝4，BC ＝5，OE ＝1.5，那么四边形EFCD 的周长是( )A ．10B ．11C ．12D ．13 9、如图，在ABCD 中，点E 在边AD 上，以BE 为折痕，将△ABE 向上翻折，点A 正好落在CD 边上的F 点处，若△FDE 的周长为14，△FCB 的周长为22，则FC 的长度为( ) A ．4 B ．6 C ．5 D ．3二、填空题10、如图，在▱ABCD 中，AD=2AB ，F 是AD 的中点，作CE ⊥AB ，垂足E 在线段AB 上，连接EF 、CF ，则下列结论中一定成立的是 。

华东师大版八年级数学下册第18章平行四边形测试卷（满分150分，考试时间：120分钟）一、选择题(1．在 ABCD中，∠A：∠B =1：2，则∠A的度数是（）A.72°B. 108°C. 120°D. 60°2．下列条件中，不能确定四边形ABCD是平行四边形的是（）A. AB=CD，AD∥BCB. AB=CD，AB∥CDC. AB∥CD，AD∥BCD. AB=CD，AD=BC3. 下列说法中正确的是（）A.有两组对边分别平行的图形是平行四边形B.平行四边形的对边平行且相等C.平行四边形的对角互补，邻角相等D.平行四边形的对角线相等4．如图，在 ABCD中，已知AC=5cm，若△ACD的周长为14cm，则 ABCD的周长为（）A．26cm B．24cm C．20cm D．18cm5．若以A(－0.5,0)，B(2,0)，C(0,1)三点为顶点画平行四边形，则第四个顶点不可能在（）A．第一象限B．第二象限C．第三象限D．第四象限6．如图，在四边形ABCD中，E是BC边的中点，连接DE并延长，交AB的延长线于点F，AB=BF．添加一个条件使四边形ABCD是平行四边形，你认为下面四个条件中可选择的是（）A．AD=BC B．∠F=∠CDFC．∠A=∠C D．CD=BF7．若平行四边形的一边和一条对角线长都是10cm，则另一条边长可以是（）A．10cm B．20cm C．30cm D．40cm8．如图， ABCD中，BC=BD，∠C=72°，则∠ADB的度数是（）A．26°B．34°C．36°D．68°9．在四边形ABCD中：①AB∥CD②AD∥BC③AB=CD④AD=BC，从以上选择两个条件使四边形ABCD为平行四边形的选法共有（）A．3种B．4种C．5种D．6种10.如图，在 ABCD 中，E ，F 是对角线AC 上的两点且AE=CF ，在①BE=DF ；②BE ∥DF ；③AB=DE ；④四边形EBFD 为平行四边形；⑤S△ADE =S △ABE ；⑥AF=CE ，这些结论中正确的个数是（ ）A ．3B ．4C ．5D ．6二、填空题（共6小题，每小题4分，满分24分）11.一个平行四边形的一边长是8，一条对角线长是6，则它的另一条对角线x 的取值范围为 ．12.如图，已知 ABCD 的对角线AC ，BD 交于点O ，且AC =8，BD =10，AB =5，则△OCD 的周长为 ．13.如图，在 ABCD 中，AB =3cm ，BC =5cm ，∠BCD 的平分线交AD 于M ，则AM 的长为________．14.如图， ABCD 的对角线相交于点O ，且AD≠CD ，过点O 作OM ⊥AC ，交AD 于点M ．如果△CDM 的周长为8，那么 ABCD 的周长是 ．15.如图，在 ABCD 中，AB =10，AD =6，AC ⊥BC ．则BD 的长为 ．16.如图，在 ABCD 中，连接BD ，且BD=CD ，过点A 作AM ⊥BD 于点M ，过点D 作DN ⊥AB 于点N ，且DN =3，在DB 的延长线上取一点P 满足∠ABD =∠MAP+∠P AB ，则AP 的长为 ．三、解答题(共9小题，满分86分)17．（8分）如图， ABCD 中，DB=CD ，o70=∠C ，AE ⊥BD 于E ．求BAE ∠的度数.18.（8分）如图， ABCD 的对角线AC ，BD 相交于点O ，EF 过点O 且与AD ，BC 分别相交于点E，F．求证：AE=CF．19．（8分）如图， AECF中，点D、B分别在线段CF、AE的延长线上，且DF=BE．求证：（1）△AFD ≌△CEB；（2）四边形ABCD是平行四边形．20．（8分）如图，已知在△ABC中，D是AB的中点，E是AC上的点，且∠ABE=∠BAC，EF∥AB，DF∥BE，请猜想DF与AE有怎样的关系，并说明理由．21．（8分）已知四边形ABCD的对角线AC与BD交于点O，给出下列四个论断：①OA=OC，②AB=CD，③∠BAD=∠DCB，④AD∥BC．请你从中选择两个论断作为条件，以“四边形ABCD为平行四边形”作为结论，完成下列各题：(1)构造一个真命题，所选条件是；(2)画出图形，并给出证明.22．（10分）如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F，连接DF.（1）试说明：AC=EF ；（2）求证：四边形ADFE 是平行四边形.23.（10分）如图，在 ABCD 中，E 、F 为对角线BD 上的点，且BE ＝DF .小明说：四边形AECF 是平行四边形；小东说：你说得对，若将“E 、F 为对角线BD 上的点”改为“点E 在DB 的延长线上，点F 在BD 的延长线上”，得到的四边形AECF 也是平行四边形；你认为小东的说法有道理吗？请画出图形，并说明理由.24.（12分）如图，在△ABC 中，∠ACB =90°，∠CAB =30°，BC=12AB ，以线段AB 为边向外作等边△ABD ，点F 是线段AD 的中点，连接CF 交线段AB 于点E ．（1）求证：四边形BCFD 为平行四边形；（2）若AB =6，求 BCFD 的面积．25.（14分）如图1，△ABC 和△AED 都是等腰直角三角形，∠BAC =∠EAD =90°，点B 在线段AE 上，点C 在线段AD 上．（1）请直接写出线段BE 与线段CD 的关系： ；（2）如图2，将图1中的△ABC 绕点A 顺时针旋转角α（0＜α＜180°），①（1）中的结论是否成立?若成立，请利用图2证明；若不成立，请说明理由； ②当ED AC 21 时，探究在△ABC 旋转的过程中，是否存在这样的角α，使以A 、B 、C 、D四点为顶点的四边形是平行四边形？若存在，请直接写出角α的度数；若不存在，请说明理由．参考答案一、选择题1．D. 2． A 3．B 4. D 5． C 6. B 7. A 8. C 9.B10. C 二、填空题11.2210<<x 12. 14 13．2 14.16 15.134． 16. 23三.解答题17.解：∵CD DB =∴070=∠=∠C DBC∴040=∠BDC∵四边形ABCD 是平行四边形∴AB ∥CD∴040=∠=∠BDC ABD∵BD AE ⊥∴090=∠AEB∴︒=∠-∠-︒=∠50180AEB ABD BAE18.证明：∵ ABCD 的对角线AC ，BD 交于点O ，∴AO=CO ，AD ∥BC ，∴∠EAC =∠FCO ，∵∠AOE =∠COF∴△AOE ≌△COF ，∴AE=CF ．19.（1）证明：∵四边形AECF是平行四边形，∴AE=CF, AE∥CF, AB∥CD∴∠AFD=∠ECD ∠ECD=∠CEB∴∠AFD=∠CEB又∵DF=BE，∴△AFD≌△CEB；（2）∵四边形AECF是平行四边形，∴AE=CF又∵DF=BEAE+BE=CF+DF即AB=CD∵△AFD≌△CEB；∴AD=BC∴四边形ABCD是平行四边形．20. 解：猜想DF=AE，理由如下：∵EF∥AB，DF∥BE，∴四边形BEFD是平行四边形，∴BE=DF，∵∠ABE=∠BAC，∴BE=AE，∴DF=AE21.解：（1）①④为条件（只提供一种答案）（2））∵AD∥BC，∴∠DAC=∠BCA，∠ADB=∠DBC，又∵OA=OC，∴△AOD≌△COB，∴AD=BC．又∵AD∥BC，∴四边形ABCD为平行四边形．22．证明：∵△ABE .是等边三角形∴AB=BE ,∠ABE =60°∵EF ⊥AB∴∠EFB =90°,03021=∠=∠AEB BEF ∵∠ACB =90°,∠BAC =30°∴∠ACB=∠EFB,∠BAC =∠BEF∴△BAC ≌△BEF∴AC=EF（2）∵△ADC 是等边三角形∴AD=AC , ∠DAC =60°由（1）可知AC=EF ∴AD=EF∵∠DAB =∠DAC +∠BAC =60+30°=90°∴DF ⊥AB 又∵EF ⊥AB∴AD ∥EF∴四边形ADFE 为平行四边形．23.如图，∵四边形ABCD 是平行四边形，∴AB=CD ，AB ∥CD ，∴∠ABD=∠CDB,∴CDB ABD ∠-=∠-00180180∴∠ABE=∠CDF,∵BE=DF∴△ABE ≌△CDF∴AE=CF ,∠AEB=∠CFD,∴AE ∥CF∴四边形AECF 为平行四边形．24.（1）证明：在△ABC 中，∠ACB =90°，∠CAB =30°，∴∠ABC =60°．在等边△ABD 中，AB=AD,∠BAD =60°，∴∠BAD =∠ABC =60°．∴BC ∥FD ，∵E 为AB 的中点，∴DF=12AD ∵BC= 12AB ， ∴BC=DF ．∴四边形BCFD 是平行四边形．（2）解：在Rt △ABC 中，∵AB=6，∴BC=12 AB =3， ∴33362222=-=-=BC AB AC ∴S 平行四边形BCFD=3⨯=．25．解：（1）∵△ABC 和△AED 都是等腰直角三角形，∠BAC =∠EAD =90°， ∴AB=AC ，AE=AD ，∴AE ﹣AB=AD ﹣AC ，∴BE=CD ；（2）①∵△ABC 和△AED 都是等腰直角三角形，∠BAC =∠EAD =90°， ∴AB=AC ，AE=AD ，由旋转的性质可得∠BAE=∠CAD ，在△BAE 与△CAD 中，⎪⎩⎪⎨⎧=∠=∠=CD AE CAD BAE AC AB ,,∴△BAE ≌△CAD （SAS ），∴BE=CD ；②∵以A 、B 、C 、D 四点为顶点的四边形是平行四边形，∴∠ABC =∠ADC =45°，∵AC= 12ED ，∴∠CAD =45°，∴角α的度数是45°．。

华东师大版八年级数学下册第18章平行四边形单元检测卷一、选择题(每小题4分，共28分)1.如图，在平行四边形ABCD中，∠B=80°，AE平分∠BAD交BC于点E，CF∥AE交AD 于点F，则∠1=()A.40°B.50°C.60°D.80°(第1题)(第4题)(第5题)2.平行四边形两邻角的平分线相交所成的角为()A.锐角B.直角C.钝角D.不确定3.在▱ABCD中，AD=3cm，AB=2cm，则▱ABCD的周长等于()A.10 cmB.6 cmC.5 cmD.4 cm4.如图，四边形ABCD是平行四边形，点E在边BC上.如果点F是边AD上的点，那么△CDF 与△ABE不一定全等的条件是()A.DF=BEB.AF=CEC.CF=AED.CF∥AE5.如图，在平行四边形ABCD中，下列各式不一定正确的是()A.∠1+∠2=180°B.∠2+∠3=180°C.∠3+∠4=180°D.∠2+∠4=180°6.如图，在平行四边形ABCD中，AB=3cm，BC=5cm，对角线AC，BD相交于点O，则OA 的取值范围是()A.3cm<OA<5cm ;B.2cm<OA<8cmC.1cm<OA<4cmD.3cm<OA<8cm(第6题)(第7题) (第8题)7.如图所示，四边形ABCD中，AB=CD，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD 于点F，连结AF，CE，若DE=BF，则下列结论：①CF=AE；②OE=OF；③四边形ABCD 是平行四边形；④图中共有四对全等三角形.其中正确结论的个数是()A.4B.3C.2D.1二、填空题(每小题5分，共25分)8.如图，在▱ABCD中，对角线AC，BD相交于点O，若AC=14，BD=8，AB=10，则△OAB 的周长为.9.如图，在平行四边形ABCD中，AB=，AD=4，将平行四边形ABCD沿AE翻折后，点B恰好与点C重合，则折痕AE的长为.(第9题) (第10题)10.如图所示，平行四边形ABCD的周长是18cm，对角线AC，BD相交于点O，若△AOD与△AOB的周长差是5cm，则边AB的长是cm.11.如图，在平行四边形ABCD中，CE是∠DCB的平分线，F是AB的中点，AB=6，BC=4，则AE∶EF∶FB的值是.(第11题)(第12题)12.如图，已知直线a∥b，点A、点C分别在直线a，b上，且AB⊥b，CD⊥a，垂足分别为B，D，有以下五种说法：①点A到直线b的距离为线段AB的长；②点D到直线b的距离为线段CD的长；③a，b两直线之间距离为线段AB的长；④a，b两直线之间距离为线段CD的长；⑤AB=CD，其中正确的有(只填相应的序号).三、解答题(共47分)13.(10分)已知：如图，在四边形ABCD中，AB∥CD，E，F为对角线AC上两点，且AE=CF，DF∥BE.求证：四边形ABCD为平行四边形.14.(12分)如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高.(1)求证：四边形ADEF是平行四边形.(2)求证：∠DHF=∠DEF.15.(12分)如图，在▱ABCD中，点O是对角线AC，BD的交点，点E是边CD的中点，点F在BC的延长线上，且CF=BC，求证：四边形OCFE是平行四边形.16.(13分)嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图的四边形ABCD，并写出了如下不完整的已知和求证.已知，如图在四边形ABCD中，BC=AD，AB=.求证：四边形ABCD是四边形.(1)在方框中填空，以补全已知和求证.(2)按嘉淇的想法写出证明：(3)用文字叙述所证命题的逆命题为.参考答案一、选择题(每小题4分，共28分)1.如图，在平行四边形ABCD中，∠B=80°，AE平分∠BAD交BC于点E，CF∥AE交AD 于点F，则∠1=()A.40°B.50°C.60°D.80°【解析】选B.∵四边形ABCD是平行四边形，∴AD∥BC，∵∠B=80°，∴∠BAD=100°，又∵AE平分∠BAD交BC于点E，∴∠EAD=∠BAD=50°，∵CF∥AE，∴四边形AECF是平行四边形，∴∠1=∠EAD=50°.2.平行四边形两邻角的平分线相交所成的角为()A.锐角B.直角C.钝角D.不确定【解析】选B.▱ABCD的∠DAB的平分线和∠ABC的平分线交于点O，∴∠DAB+∠ABC=180°，∠DAO=∠BAO=∠DAB，∠ABO=∠CBO=∠ABC，∴∠BAO+∠ABO=90°，∴∠AOB=180°-90°=90°.3.在▱ABCD中，AD=3cm，AB=2cm，则▱ABCD的周长等于()A.10 cmB.6 cmC.5 cmD.4 cm【解析】选A.因为平行四边形的对边相等，所以AD=BC=3cm，AB=CD=2cm，所以周长为10 cm.4.如图，四边形ABCD是平行四边形，点E在边BC上.如果点F是边AD上的点，那么△CDF 与△ABE不一定全等的条件是()A.DF=BEB.AF=CEC.CF=AED.CF∥AE【解析】选C.由平行四边形的性质可得AB=CD，AD=BC，∠B=∠D等.A中，DF=BE，∠B=∠D，AB=CD，符合“边角边”定理，△CDF≌△ABE，选项A成立；B中，AF=CE，可得DF=BE，同选项A，选项B成立；C中，CF=AE，∠B=∠D，AB=CD，条件为两边及一边的对角，C 不一定成立；D中，CF∥AE，可得四边形AECF是平行四边形，得AF=CE，所以BE=DF，同选项A，该选项成立.综上所述，选C.5.如图，在平行四边形ABCD中，下列各式不一定正确的是()A.∠1+∠2=180°B.∠2+∠3=180°C.∠3+∠4=180°D.∠2+∠4=180°【解析】选D.由平行四边形的性质及图形可知：∠1和∠2是邻补角，故∠1+∠2=180°，A 正确；因为AD∥BC，所以∠2+∠3=180°，B正确；因为AB∥CD，所以∠3+∠4=180°，C 正确；D.根据平行四边形的对角相等，∠2=∠4，∠2+∠4=180°不一定正确，故选D.6.如图，在平行四边形ABCD中，AB=3cm，BC=5cm，对角线AC，BD相交于点O，则OA 的取值范围是()A.3cm<OA<5cmB.2cm<OA<8cmC.1cm<OA<4cmD.3cm<OA<8cm【解析】选C.在△ABC中，BC-AB<AC<AB+BC，即2cm<AC<8cm，所以1cm<OA<4cm.7.如图所示，四边形ABCD中，AB=CD，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连结AF，CE，若DE=BF，则下列结论：①CF=AE；②OE=OF；③四边形ABCD 是平行四边形；④图中共有四对全等三角形.其中正确结论的个数是()A.4B.3C.2D.1【解析】选B.∵AE⊥BD于点E，CF⊥BD于点F，∴∠DFC=∠BEA=90°.∵DE=BF，∴DF=BE.又∵AB=CD，∴△DFC≌△BEA，∴CF=AE，①正确，∠CDF=∠ABE，∴AB∥C D.又∵AB=CD，∴四边形ABCD是平行四边形，③正确，∴OD=O B.又∵DF=BE，∴OE=OF，②正确，易知图中的全等三角形有：△DFC≌△BEA，△OFC≌△OEA，△AOF≌△COE，△AEF≌△CFE，△ACF≌△CAE，△AOB≌△COD，△AOD≌△COB，△ABD≌△CDB，△ACD≌△CAB，…，故④不正确.综上可知，正确的结论为①②③，共3个.二、填空题(每小题5分，共25分)8.如图，在▱ABCD中，对角线AC，BD相交于点O，若AC=14，BD=8，AB=10，则△OAB 的周长为.【解析】因为平行四边形的对角线互相平分，所以OA=AC=7，OB=BD=4，又因为AB=10，所以△OAB的周长=7+4+10=21.答案：219.如图，在平行四边形ABCD中，AB=，AD=4，将平行四边形ABCD沿AE翻折后，点B恰好与点C重合，则折痕AE的长为.【解析】点B恰好与点C重合，且四边形ABCD是平行四边形，根据翻折的性质，则AE⊥BC，BE=CE=2，在Rt△ABE中，由勾股定理得AE===3.答案：310.如图所示，平行四边形ABCD的周长是18cm，对角线AC，BD相交于点O，若△AOD 与△AOB的周长差是5cm，则边AB的长是cm.【解析】∵四边形ABCD是平行四边形，∴OA=OC，OB=OD，∵△AOD的周长=OA+OD+AD，△AOB的周长=OA+OB+AB，又∵△AOD与△AOB的周长差是5cm，∴AD=AB+5，设AB=x，AD=5+x，则2(x+5+x)=18，解得x=2，即AB=2cm.答案：211.如图，在平行四边形ABCD中，CE是∠DCB的平分线，F是AB的中点，AB=6，BC=4，则AE∶EF∶FB的值是.【解析】∵四边形ABCD是平行四边形，∴∠DCE=∠BE C.∵CE是∠DCB的平分线，∴∠DCE=∠BCE，∴∠CEB=∠BCE，∴BE=BC=4.∵F是AB的中点，AB=6，∴FB=3.∴EF=BE-FB=1，∴AE=AB-BE=2，∴AE∶EF∶FB=2∶1∶3.答案：2∶1∶312.如图，已知直线a∥b，点A、点C分别在直线a，b上，且AB⊥b，CD⊥a，垂足分别为B，D，有以下五种说法：①点A到直线b的距离为线段AB的长；②点D到直线b的距离为线段CD的长；③a，b两直线之间距离为线段AB的长；④a，b两直线之间距离为线段CD的长；⑤AB=CD，其中正确的有(只填相应的序号). 【解析】本题主要考查点到直线的距离和平行线间的距离，①②③④⑤都正确.答案：①②③④⑤三、解答题(共47分)13.(10分)已知：如图，在四边形ABCD中，AB∥CD，E，F为对角线AC上两点，且AE=CF，DF∥BE.求证：四边形ABCD为平行四边形.【证明】∵AB∥CD，∴∠BAE=∠DCF，∵BE∥DF，∴∠BEF=∠DFE，∴∠AEB=∠CF D.在△AEB和△CFD中，∴△AEB≌△CFD，∴AB=C D.又∵AB∥CD，∴四边形ABCD是平行四边形.14.(12分)如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高.(1)求证：四边形ADEF是平行四边形.(2)求证：∠DHF=∠DEF.【证明】(1)∵点D，E分别是AB，BC的中点，∴DE∥AC；同理：EF∥AB，∴四边形ADEF是平行四边形.(2)∵四边形ADEF是平行四边形，∴∠DAF=∠DEF.∵在Rt△AHB中，D是AB中点，∴DH=AB=AD，∴∠DAH=∠DHA，同理：∠F AH=∠FHA，∴∠DAF=∠DHF，∴∠DHF=∠DEF.15.(12分)如图，在▱ABCD中，点O是对角线AC，BD的交点，点E是边CD的中点，点F 在BC的延长线上，且CF=BC，求证：四边形OCFE是平行四边形.【证明】∵四边形ABCD是平行四边形，∴点O是BD的中点.又∵点E是边CD的中点，∴OE是△BCD的中位线，∴OE∥BC，且OE=B C.又∵CF=BC，∴OE=CF.又∵点F在BC的延长线上，∴OE∥CF，∴四边形OCFE是平行四边形.16.(13分)嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图的四边形ABCD，并写出了如下不完整的已知和求证.已知，如图在四边形ABCD中，BC=AD，AB=.求证：四边形ABCD是四边形.(1)在方框中填空，以补全已知和求证.(2)按嘉淇的想法写出证明：(3)用文字叙述所证命题的逆命题为. 【解析】(1)CD平行(2)证明：连结B D.在△ABD和△CDB中，∵AB=CD，AD=CB，BD=DB，∴△ABD≌△CDB，∴∠1=∠2，∠3=∠4，∴AB∥CD，AD∥CB，∴四边形ABCD是平行四边形.(3)平行四边形的对边相等.。

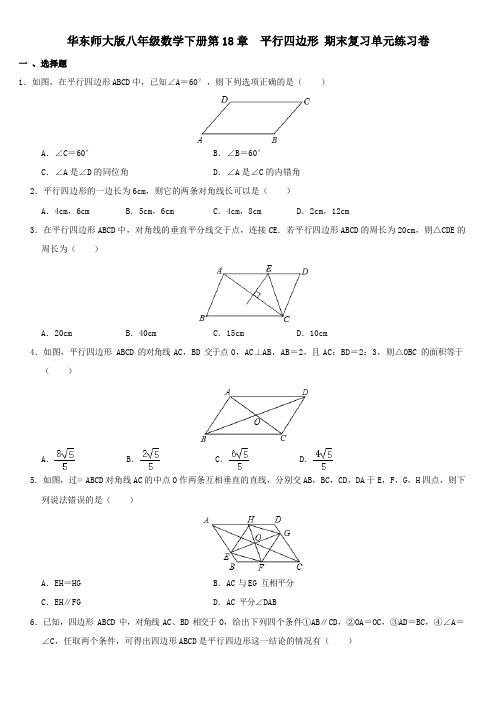
华东师大版八年级数学下册第18 章平行四边形期末复习单元练习卷一、选择题1．如图，在平行四边形ABCD 中，已知∠A＝60°，则下列选项正确的是（）A．∠C＝60°B．∠B＝60°C．∠A是∠D的同位角D．∠A是∠C的内错角2．平行四边形的一边长为6cm，则它的两条对角线长可以是（）A．4cm，6cm B．5cm，6cm C．4cm，8cm D．2cm，12cm3．在平行四边形ABCD 中，对角线的垂直平分线交于点，连接CE．若平行四边形ABCD 的周长为20cm，则△CDE的周长为（）A．20cm B．40cm C．15cm D．10cm4．如图，平行四边形 ABCD 的对角线 AC，BD 交于点 O，AC⊥AB，AB＝2，且 AC：BD＝2：3，则△OBC 的面积等于（）A．B．C．D．5．如图，过▱ABCD 对角线AC 的中点O 作两条互相垂直的直线，分别交AB，BC，CD，DA 于E，F，G，H 四点，则下列说法错误的是（）A．EH＝HG B．AC 与EG 互相平分C．EH∥FG D．AC 平分∠DAB6．已知，四边形 ABCD 中，对角线 AC、BD 相交于 O，给出下列四个条件①AB∥CD，②OA＝OC，③AD＝BC，④∠A＝∠C，任取两个条件，可得出四边形ABCD 是平行四边形这一结论的情况有（）A ．5 种B ．4 种C ．3 种D ．2 种7．如图，在四边形 ABCD 中，对角线 AC ，BD 相交于点 O ，添加下列条件后仍不能判定四边形 ABCD 是平行四边形的是 （ ）A ．AD∥BC，AO ＝COB ．AD ＝BC ，AO ＝OCC ．AD ＝BC ，CD ＝ABD ．S △AO D ＝S △COD ＝S △BOC8．已知△ABC （如图 1），按图 2 图 3 所示的尺规作图痕迹，（不需借助三角形全等）就能推出四边形 ABCD 是平行四边形的依据是（ ）A ．两组对边分别平行的四边形是平行四边形B ．对角线互相平分的四边形是平行四边形C ．一组对边平行且相等的四边形是平行四边形D ．两组对边分别相等的四边形是平行四边形9．如图，平行四边形 ABCD 中，E 、F 分别为边 AB 、DC 的中点，则图中共有平行四边形的个数是（）A ．3 个B ．4 个C ．5 个D ．6 个10．如图，由 25 个点构成的 5×5 的正方形点阵中，横、纵方向相邻的两点之间的距离都是 1 个单位．定义：由点阵中的四个点为顶点的平行四边形叫做阵点平行四边形，图中以 A 、B 为顶点，面积为 4 的阵点平行四边形的个数 有 （ ）A．6 个B．7 个C．9 个D．11 个二、填空题11．▱ABCD 的周长是32cm，∠ABC的平分线交AD 所在直线于点E，且AE：ED＝3：2，则AB 的长为．12．如图，在▱ABCD 中，P 是CD 边上一点，且AP、BP 分别平分∠DAB、∠CBA，若AD＝5，AP＝6，则△APB的面积是．13．如图，四边形ABCD和四边形ACEF都是平行四边形，EF经过点D，若平行四边形ABCD的面积为S1，平行四边形ACEF的面积为S2，则S1与S2的大小关系为S1S2．14．平行四边形ABCD 的周长是30，AC，BD 相交于点O，△OAB的周长比△OBC的周长大3，则AB＝．15．如图，平行四边形ABCD 的对角线AC 与BD 相交于点O，AB⊥AC．若AB＝12，AC＝10，则BD 的长为．16．如图，在▱ABCD 中，∠ABC的平分线BE 交AD 于E，∠BCD的平分线交AD 于点F，BC＝5，AB＝3，则EF 长．17．如图，平行四边形的周长为 20cm，AE⊥BC于E，AF⊥CD于F，AE＝2cm，AF＝3cm，平行四边形 ABCD 的面积为cm2．18．如图，在平行四边形 ABCD 中，点E 在边BC 上，连结AE，EM⊥AE，垂足为 E，交 CD 于点M，AF⊥BC，垂足为 F，BH⊥AE，垂足为 H，交 AF 于点 N，若 AE＝BN，AN＝CE，则下列结论：①∠NBF＝∠MEC；②△NBF≌△EAF；③∠BCD＝150°；④AD＝CM+2CE，其中正确的结论是．（填写所有正确结论的序号）19．如图，现将四根木条钉成的矩形框ABCD 变形为平行四边形木框A'BCD′，且A′D′与CD 相交于CD 边的中点E，若AB＝4，则△ECD′的面积是．20．如图，四边形 ABCD 中，AB＝CD，对角线 AC，BD 相交于点 O，AE⊥BD于点E，CF⊥BD于点F，连接 AF，CE，若DE＝BF，则下列结论：①CF＝AE；②OE＝OF；③图中共有四对全等三角形；④四边形ABCD 是平行四边形；其中正确结论的是．21．如图，四边形ABCD 中，AD∥BC，AD＝3，BC＝8，E 是BC 的中点，点P 以每秒1 个单位长度的速度从A 点出发，沿AD 向点D 运动；点Q 同时以每秒2 个单位长度的速度从点C 出发，沿CB 向点B 运动，点P 停止运动时，点Q 也随之停止运动．当运动时间t＝秒时，以点P，Q，E，D 为顶点的四边形是平行四边形．22．如图，在四边形ABCD 中，AD＝12，对角线AC，BD 交于点O，∠ADB＝90°，OD＝OB＝5，AC＝26，则四边形ABCD 的面积为．三、解答题23．如图，在平行四边形 AFCE 中，D，B 分别是 EC，AF 的中点．求证：BC＝AD．24．如图，在平行四边形 ABCD 中，点 E、F 分别在 AB、CD 上，且ED⊥DB，FB⊥BD．（1）求证：△AED≌△CFB．（2）若∠A＝30°，∠DEB＝45°，DA＝5，求 DF 的长．25．如图，在平行四边形 ABCD 中，点 E 在 AD 上，连接 BE、CE，EB 平分∠AEC．（1）如图 1，判断△BCE 的形状，并说明理由；（2）如图 2，∠A＝90°，BC＝5，AE＝1，求线段 BE 的长．26．如图，在▱ABCD 中，对角线 AC，BD 相交于点 O，以 AC 为斜边的等腰直角三角形 AEC 的边CE，与 AD 交于点 F，连接 OE，使得 OE＝OD．在 AD 上截取 AH＝CD，连接 EH，ED．（1）判断四边形 ABCD 的形状，并说明理由；（2）若 AB＝1，BC＝3，求 EH 的长．27．如图，请在由 32 个边长为 1 的小正三角形组成的网格中，按下列要求作图．且所画图形的顶点都在网格顶点上．（1）在图①中画出一个斜边为 2 的直角三角形；（2）在图②中画出一个面积的菱形；（3）在图②中画出一个面积的平行四边形，28．如图，四边形 ABCD 的对角线 AC、BD 相交于点 O，BO＝DO，点 E、F 分别在AO，CO 上，且BE∥DF，AE＝CF．求证：四边形 ABCD 为平行四边形．29．如图，已知△ABC 是等边三角形，E 为AC 上一点，连接 BE．将 AC 绕点E 旋转，使点 C 落在BC 上的点 D 处，点A 落在BC 上方的点 F 处，连接AF．求证：四边形 ABDF 是平行四边形．30．已知如图，点 C、D 在线段 AF 上，AD＝CD＝CF，∠ABC＝∠DEF＝90°，AB∥EF．（1）若，求BD 的长；（2）求证：四边形 BCED 是平行四边形．31．如图，等边△ABC 的边长为 8，动点 M 从点B 出发，沿B→A→C→B的方向以每秒 3 个单位长度的速度运动，动点N 从点C 出发，沿C→A→B﹣C 的方向以每秒 2 个单位长度的速度运动．（1）若动点 M、N 同时出发，经过几秒第一次相遇？（2）若动点 M、N 同时出发，且其中一点到达终点时，另一点即停止运动．在△ABC 的边上是否存在一点 D，使得以点 A、M、N、D 为顶点的四边形为平行四边形？若存在，求此时运动的时间 t 及点D 的具体位置；若不存在，请说明理由．32．如图，△ABC中，D、E、F 分别在边 BC、AB、AC 上，且DE∥AC，DE＝AF，延长 FD 到G，使 DG＝DF．求证：AG 和DE 互相平分．33．如图，平行四边形 ABCD 中，点 E、F 分别为 BC、AD 的中点，连接 AE、CF、DE．（1）求证：四边形 AECF 为平行四边形；（2）若 DE 平分∠AEC，请直接写出图中线段的长度等于 2BE 的线段．34．已知，如图，在▱ABCD 中，延长 AB 到点E，延长 CD 到点F，使得 BE＝DF，连接 EF，分别交 BC，AD 于点M，N，连接 AM，CN．（1）求证：△BEM≌△DFN；（2）求证：四边形 AMCN 是平行四边形．35．如图，D 是△ABC 的边 AB 上一点，CE∥AB，DE 交 AC 于点 F，若 FA＝FC．（1）求证：四边形 ADCE 是平行四边形；（2）若AE⊥EC，EF＝EC＝5，求四边形 ADCE 的面积．36．在▱ABCD 中，点 E 在 CD 边上，连接 AE、BE，点 F 在 AB 边上，连接 CF、DF，且∠DAE＝∠BCF．（1）如图 1，求证：四边形 DFBE 是平行四边形；（2）如图 2，若 E 是CD 边的中点，连接 GH，在不添加任何字母和辅助线的情况下，请直接写出图中以 GH 为边或以GH 为对角线的所有平行四边形．。

2021-2022学年华师大版八年级数学下册《第18章平行四边形》单元综合练习题（附答案）一．选择题1．下列说法不正确的是（）A．平行四边形对边平行B．两组对边平行的四边形是平行四边形C．平行四边形对角相等D．一组对角相等的四边形是平行四边形2．在▱ABCD中，∠B+∠D＝260°，那么∠A的度数是（）A．130°B．100°C．50°D．80°3．直线a、b、c是三条平行直线．已知a与b的距离为7cm，b与c的距离为3cm，则a 与c的距离为（）A．4cm B．10cm C．3cm D．4cm或10cm 4．如图，在▱ABCD中，E，F是对角线AC上的两点且AE＝CF，在①BE＝DF；②BE∥DF；③AB＝DE；④四边形EBFD为平行四边形；⑤S△ADE＝S△ABE；⑥AF＝CE这些结论中正确的个数是（）A．3B．4C．5D．65．如图，已知AB＝DC，AD＝BC，E，F是DB上两点且AE∥CF，若∠AEB＝115°，∠ADB＝35°，则∠BCF＝（）A．150°B．40°C．80°D．90°6．小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（）A．①，②B．①，④C．③，④D．②，③7．如图，在平面直角坐标系中，以A（﹣1，0），B（2，0），C（0，1）为顶点构造平行四边形，下列各点中不能作为平行四边形顶点坐标的是（）A．（3，1）B．（﹣4，1）C．（1，﹣1）D．（﹣3，1）8．如图，▱ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC＝60°，AB＝BC，连接OE．下列结论：①∠CAD＝30°；②S▱ABCD＝AB•AC；③OB＝AB；④OE＝BC，成立的个数有（）A．1个B．2个C．3个D．4个二．填空题9．如图，在▱ABCD中，BE⊥AB交对角线AC于点E，若∠1＝20°，则∠2的度数为．10．如图，在▱ABCD中，AB＝10，AD＝6，AC⊥BC．则BD＝．11．如图，在▱ABCD中，AB＝3，BC＝5，以点B的圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为．12．如图，在▱ABCD中，E、F分别是AB、DC边上的点，AF与DE相交于点P，BF与CE相交于点Q，若S△APD＝16cm2，S△BQC＝25cm2，则图中阴影部分的面积为cm2．13．如图，在▱ABCD中，AD＝2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是．（把所有正确结论的序号都填在横线上）①∠DCF＝∠BCD；②EF＝CF；③S△BEC＝2S△CEF；④∠DFE＝3∠AEF．14．已知：如图，在▱ABCD中，∠BAD，∠ADC的平分线AE，DF分别与线段BC相交于点E，F，AE与DF相交于点G．若AD＝10，AB＝6，AE＝4，则DF的长为．15．如图，在▱ABCD中，AC，BD相交于点O，点E，F在对角线BD上，有下列条件：①BF＝DE；②AE＝CF；③∠EAB＝∠FCD；④AF∥CE．其中一定能判定四边形AECF是平行四边形的是．16．如图，四边形ABCD中，AD∥BC，AD＝12cm，BC＝15cm，点P自点A向D以1cm/s 的速度运动，到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，直线PQ截原四边形为两个新四边形．则当P，Q同时出发秒后其中一个新四边形为平行四边形．三．解答题17．如图，BD是△ABC的角平分线，点E，F分别在BC，AB上，且DE∥AB，BE＝AF．（1）求证：四边形ADEF是平行四边形；（2）若∠ABC＝60°，BD＝4，求平行四边形ADEF的面积．18．已知：如图，在四边形ABCD中，AB∥CD，E，F为对角线AC上两点，且AE＝CF，DF∥BE．求证：四边形ABCD为平行四边形．19．如图，点B，E，C，F在一条直线上，AB＝DE，AC＝DF，BE＝CF．（1）求证：△ABC≌△DEF；（2）连接AD，求证：四边形ABED是平行四边形．20．如图，四边形ABCD中，∠A＝∠ABC＝90°，AD＝1，BC＝3，E是边CD的中点，连接BE并延长与AD的延长线相交于点F．（1）求证：四边形BDFC是平行四边形；（2）若△BCD是等腰三角形，求四边形BDFC的面积．21．如图，△ABC和△ADE都是等边三角形，点D在BC边上，AB边上有一点F，且BF ＝DC，连接EF、EB．（1）求证：△ABE≌△ACD；（2）求证：四边形EFCD是平行四边形．22．如图，▱ABCD中，BD⊥AD，∠A＝45°，E、F分别是AB，CD上的点，且BE＝DF，连接EF交BD于O．（1）求证：BO＝DO；（2）若EF⊥AB，延长EF交AD的延长线于G，当FG＝1时，求AD的长．参考答案一．选择题1．解：A、正确；B、正确；C、正确；D、一组对角相等而另一组对角不相等的四边形不是平行四边形，故命题错误．故选：D．2．解：如图所示：∵四边形ABCD是平行四边形，∴∠B＝∠D，∠A+∠B＝180°，∵∠B+∠D＝260°，∴∠B＝∠D＝130°，∴∠A的度数是：50°．故选：C．3．解：当直线c在a、b之间时，∵a、b、c是三条平行直线，而a与b的距离为7cm，b与c的距离为3cm，∴a与c的距离＝7cm﹣3cm＝4cm；当直线c不在a、b之间时，∵a、b、c是三条平行直线，而a与b的距离为7cm，b与c的距离为3cm，∴a与c的距离＝7cm+3cm＝10cm，综上所述，a与c的距离为4cm或10cm．故选：D．4．解：∵四边形ABCD是平行四边形∴∠BAE＝∠DCF，AB＝CD（故③不正确），∵AE＝CF，∴△ABE≌△CDF，∴BE＝DF（故①正确），同理：DE＝BF，∴四边形EBFD为平行四边形，∴BE∥DF（故②正确），∵AB＝CD，AD＝BC，AC＝AC，∴△ABC≌△CDA，∴两三角形AC边上的高的相等，∵△ABE，△ADE分别是△ABC与△CDA中的小三角形，且AE＝AE，∴S△ADE＝S△ABE（故⑤正确），∵AE＝CF，∴AF＝CE（故⑥正确），∴正确的有：①②④⑤⑥共5项．故选：C．5．解：∵AB＝DC，AD＝BC，∴四边形ABCD是平行四边形，∴AD∥BC，∴∠CBF＝∠ADE，∵AE∥CF，∴∠CFB＝∠AED，∴△BCF≌△DAE，∴∠BCF＝∠DAE，∵∠AEB＝115°，∠ADB＝35°，∴∠AEB＝∠DAE+∠ADB，∴∠DAE＝∠AEB﹣∠ADB＝115°﹣35°＝80°，故选：C．6．解：∵只有②③两块角的两边互相平行，且中间部分相联，角的两边的延长线的交点就是平行四边形的顶点，∴带②③两块碎玻璃，就可以确定平行四边形的大小．7．解：如图所示：①以AC为对角线，可以画出▱AFCB，F（﹣3，1）；②以AB为对角线，可以画出▱ACBE，E（1，﹣1）；③以BC为对角线，可以画出▱ACDB，D（3，1）；故选：B．8．解：∵四边形ABCD是平行四边形，∴∠ABC＝∠ADC＝60°，∠BAD＝120°，∵AE平分∠BAD，∴∠BAE＝∠EAD＝60°∴△ABE是等边三角形，∴AE＝AB＝BE，∵AB＝BC，∴AE＝BC，∴∠BAC＝90°，∴∠CAD＝30°，故①正确；∵AC⊥AB，∴S▱ABCD＝AB•AC，故②正确，∵AB＝BC，OB＝BD，∴AB≠OB，故③错误；∵CE＝BE，CO＝OA，∴OE＝AB，∴OE＝BC，故④正确．故选：C．二．填空题9．解：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠BAE＝∠1＝20°，∵BE⊥AB，∴∠ABE＝90°，∴∠2＝∠BAE+∠ABE＝110°．故答案为：110°．10．解：∵四边形ABCD是平行四边形，∴BC＝AD＝6，OB＝OD，OA＝OC，∵AC⊥BC，∴AC＝＝8，∴OC＝4，∴OB＝＝2，∴BD＝2OB＝4故答案为：4．11．解：根据作图的方法得：BE平分∠ABC，∴∠ABE＝∠CBE∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC＝5，∴∠AEB＝∠CBE，∴∠ABE＝∠AEB，∴DE＝AD﹣AE＝5﹣3＝2；故答案为：2．12．解：连接E、F两点，∵四边形ABCD是平行四边形，∴AB∥CD，∴△EFC的FC边上的高与△BCF的FC边上的高相等，∴S△EFC＝S△BCF，∴S△EFQ＝S△BCQ，同理：S△EFD＝S△ADF，∴S△EFP＝S△ADP，∵S△APD＝16cm2，S△BQC＝25cm2，∴S四边形EPFQ＝41cm2，故答案为：41．13．解：①∵F是AD的中点，∴AF＝FD，∵在▱ABCD中，AD＝2AB，∴AF＝FD＝CD，∴∠DFC＝∠DCF，∵AD∥BC，∴∠DFC＝∠FCB，∴∠DCF＝∠BCF，∴∠DCF＝∠BCD，故①正确；延长EF，交CD延长线于M，∵四边形ABCD是平行四边形，∴AB∥CD，∴∠A＝∠MDF，∵F为AD中点，∴AF＝FD，在△AEF和△DMF中，，∴△AEF≌△DMF（ASA），∴FE＝MF，∠AEF＝∠M，∵CE⊥AB，∴∠AEC＝90°，∴∠AEC＝∠ECD＝90°，∵FM＝EF，∴FC＝FM，故②正确；③∵EF＝FM，∴S△EFC＝S△CFM，∵MC＞BE，∴S△BEC＜2S△EFC故S△BEC＝2S△CEF错误，即③错误；④设∠FEC＝x，则∠FCE＝x，∴∠DCF＝∠DFC＝90°﹣x，∴∠EFC＝180°﹣2x，∴∠EFD＝90°﹣x+180°﹣2x＝270°﹣3x，∵∠AEF＝90°﹣x，∴∠DFE＝3∠AEF，故④正确．故答案为：①②④．14．解：如图，过点C作CK∥AE交AD于K．在平行四边形ABCD中，AB∥DC，∴∠BAD+∠ADC＝180°．AB＝CD＝6，∵AE，DF分别是∠BAD，∠ADC的平分线，∴∠DAE＝∠BAE＝∠BAD，∠ADF＝∠CDF＝∠ADC．∴∠DAE+∠ADF＝∠BAD+∠ADC＝90°．∴∠AGD＝90°．∵AK∥EC，AE∥CK，∴四边形AECK是平行四边形，∠AGD＝∠KID＝90°，∴AE＝CK＝4，∵∠KDI+∠DKI＝90°，∠CDI+∠DCI＝90°，∠IDK＝∠IDC，∴∠DKI＝∠DCI，∴DK＝DC，∴KI＝CI＝2，∵AD∥BC，∴∠ADF＝∠DFC＝∠CDF，∴CF＝CD，∵CI⊥DF，∴FI＝DI，∵DI＝＝＝4，∴DF＝2DI＝8，∴故答案为8．15．解：①∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，OB＝OD，OA＝OC，∵BF＝DE，∴BF﹣OB＝DE﹣OD，即OF＝OE，∴四边形AECF是平行四边形；③∵AB∥CD，∴∠ABE＝∠CDF，∵∠BAE＝∠DCF，在△ABE和△CDF中，，∴△ABE≌△CDF（ASA），∴BE＝DF，∵AO＝CO，BO＝DO，∴OE＝OF，∴四边形AECF是平行四边形；④∵AF∥CE，∴∠AFB＝∠CED，在△ABF和△CDE中，，∴△ABF≌△CDE（AAS），∴BF＝DE，∴BF﹣OB＝DE﹣OD，即OF＝OE，又∵OA＝OC，∴四边形AECF是平行四边形；②∵AE＝CF，不能判定△ABE≌△CDF，∴不能判定四边形AECF是平行四边形；∴一定能判定四边形AECF是平行四边形的是①③④，故答案为：①③④．16．解：根据题意有AP＝tcm，CQ＝2tcm，PD＝（12﹣t）cm，BQ＝（15﹣2t）cm．①∵AD∥BC，∴当AP＝BQ时，四边形APQB是平行四边形．∴t＝15﹣2t，解得t＝5．∴t＝5s时四边形APQB是平行四边形；②AP＝tcm，CQ＝2tcm，∵AD＝12cm，BC＝15cm，∴PD＝AD﹣AP＝（12﹣t）cm，∵AD∥BC，∴当PD＝QC时，四边形PDCQ是平行四边形．即：12﹣t＝2t，解得t＝4s，∴当t＝4s时，四边形PDCQ是平行四边形．综上所述，当P，Q同时出发4或5秒后其中一个新四边形为平行四边形．故答案是：4或5．三．解答题17．（1）证明：∵BD是△ABC的角平分线，∴∠ABD＝∠DBE，∵DE∥AB，∴∠ABD＝∠BDE，∴∠DBE＝∠BDE，∴BE＝DE；∵BE＝AF，∴AF＝DE；∴四边形ADEF是平行四边形；（2）解：过点D作DG⊥AB于点G，过点E作EH⊥BD于点H，∵∠ABC＝60°，BD是∠ABC的平分线，∴∠ABD＝∠EBD＝30°，∴DG＝BD＝×4＝2，∵BE＝DE，∴BH＝DH＝2，设HE＝x，则BE＝2x，（2x）2﹣x2＝22，解得x＝，∴BE＝2x＝，∴DE＝，∴四边形ADEF的面积为：DE•DG＝．18．证明：∵AB∥CD，∴∠DCA＝∠BAC，∵DF∥BE，∴∠DF A＝∠BEC，∴∠AEB＝∠DFC，在△AEB和△CFD中，∴△AEB≌△CFD（ASA），∴AB＝CD，∵AB∥CD，∴四边形ABCD为平行四边形．19．（1）证明：∵BE＝CF，∴BE+EC＝CF+EC，∴BC＝EF，在△ABC和△DEF中，，∴△ABC≌△DEF（SSS）；（2）证明：由（1）得：△ABC≌△DEF，∴∠B＝∠DEF，∴AB∥DE，又∵AB＝DE，∴四边形ABED是平行四边形．20．（1）证明：∵∠A＝∠ABC＝90°，∴BC∥AD，∴∠CBE＝∠DFE，在△BEC与△FED中，，∴△BEC≌△FED，∴BE＝FE，又∵E是边CD的中点，∴CE＝DE，∴四边形BDFC是平行四边形；（2）①BC＝BD＝3时，由勾股定理得，AB＝＝＝2，所以，四边形BDFC的面积＝3×2＝6；②BC＝CD＝3时，过点C作CG⊥AF于G，则四边形AGCB是矩形，所以，AG＝BC＝3，所以，DG＝AG﹣AD＝3﹣1＝2，由勾股定理得，CG＝＝＝，所以，四边形BDFC的面积＝3×＝3；③BD＝CD时，BC边上的中线应该与BC垂直，从而得到BC＝2AD＝2，矛盾，此时不成立；综上所述，四边形BDFC的面积是6或3．21．证明：（1）∵△ABC和△ADE都是等边三角形，∴AE＝AD，AB＝AC，∠EAD＝∠BAC＝60°，∴∠EAD﹣∠BAD＝∠BAC﹣∠BAD，即：∠EAB＝∠DAC，∴△ABE≌△ACD（SAS）；（2）证明：∵△ABE≌△ACD，∴BE＝DC，∠EBA＝∠DCA，又∵BF＝DC，∴BE＝BF．∵△ABC是等边三角形，∴∠DCA＝60°，∴△BEF为等边三角形．∴∠EFB＝60°，EF＝BF∵△ABC是等边三角形，∴∠ABC＝60°，∴∠ABC＝∠EFB，∴EF∥BC，即EF∥DC，∵EF＝BF，BF＝DC，∴EF＝DC，∴四边形EFCD是平行四边形．22．（1）证明：∵四边形ABCD是平行四边形，∴DC＝AB，DC∥AB，∴∠ODF＝∠OBE，在△ODF与△OBE中∴△ODF≌△OBE（AAS）∴BO＝DO；（2）解：∵BD⊥AD，∴∠ADB＝90°，∵∠A＝45°，∴∠DBA＝∠A＝45°，∵EF⊥AB，∴∠G＝∠A＝45°，∴△ODG是等腰直角三角形，∵AB∥CD，EF⊥AB，∴DF⊥OG，∴OF＝FG，△DFG是等腰直角三角形，∵△ODF≌△OBE（AAS）∴OE＝OF，∴GF＝OF＝OE，即2FG＝EF，∵△DFG是等腰直角三角形，∴DF＝FG＝1，∴DG＝＝DO，∴在等腰Rt△ADB中，DB＝2DO＝2＝AD ∴AD＝2，。

第十八章平行四边形单元测试姓名：班级：学号：成绩：一、选择题1.下列性质中，平行四边形不一定具备的是()A. 邻角互补B. 对角互补C. 对边相等D. 对角线互相平分2.在平行四边形ABCD中，∠A：∠B：∠C：∠D的可能情况是()A. 2：7：2：7B. 2：2：7：7C. 2：7：7：2D. 2：3：4：53.如图，在▱ABCD中，AB=3，BC=5，∠ABC的平分线交AD于点E，则DE的长为()A.5B. 4C. 3D. 24.如图，在平行四边形ABCD中，对角线AC，BD相交于点O，下列结论中不一定正确的是()A.AB=CDB. BO=ODC. ∠BAD=∠BCDD. AB⊥AC5.如图，在平行四边形ABCD中，AC，BD为对角线，BC=6，BC边上的高为4，则图中阴影部分的面积为()A.3B. 6C. 12D. 246.小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是()A. ①，②B. ①，④C. ③，④D. ②，③7.下列条件中，能判定四边形为平行四边形的是()A. 对角线相互垂直B. 对角线互相平分C. 一组对角相等D. 一组对边相等8.如图，EF过▱ABCD对角线的交点O，交AD于E，交BC于F，若▱ABCD的周长为18，OE=1.5，则四边形EFCD的周长为()A. 14B. 13C. 12D. 109.如图，在平行四边形ABCD中，AD=8，点E，F分别是BD，CD的中点，则EF等于()A. 2B. 3C. 4D. 610.如图，▱ABCD的对角线交于点O，且AB=5，△OCD的周长为23，则▱ABCD的两条对角线之和是()A. 18B. 28C. 36D. 4611.如图，▱ABCD的边AB长为4cm，DE平分∠ADC，若∠B=80°，∠DAE=50°，则▱ABCD的周长是()A. 8cmB. 16cmC. 24cmD. 32cm12.如图，点A在双曲线y=2x 上，点B在双曲线y=6x上，且AB//x轴，C、D在x轴上，若四边形ABCD为平行四边形，则它的面积为() A. 6 B. 4 C. 3 D. 2二、填空题13.如图，在四边形ABCD中，AB//CD，请你添加一个条件，使得四边形ABCD成为平行四边形，你添加的条件是．14.已知平行四边形的周长是60cm，长边比短边长5cm，则短边是______cm．15.如图，将平行四边形ABCO放置在平面直角坐标系xOy中，O为坐标原点，若点A的坐标是(6,0)，点C的坐标是(1,4)，则点B的坐标是．16.如图，在平行四边形ABCD中，AC⊥BC，AD=AC=2，则BD的长为．17.如图，在▱ABCD中，对角线AC，BD相交于点O，若DO=1.5cm，AB=5cm，BC=4cm，则▱ABCD的面积为________cm2．18.如图，在周长为20的平行四边形ABCD中，AB<AD，AC与BD交于点O，OE⊥BD，交AD于点E，则△ABE的周长为．19.如图，在▱ABCD中，∠C=43°，过点D作AD的垂线，交AB于点E，交CB的延长线于点F，则∠BEF的度数为．20.如图，在四边形ABCD中，AB=CD，AD//BC，以点B为圆心，BA为半径的圆弧与BC交于点E，四边形AECD是平行四边形，AB=6，则扇形(图中阴影部分)的面积是________．三、解答题21.已知，如图，平行四边形ABCD中，E是BC边的中点，连DE并延长交AB的延长线于点F，求证：AB=BF．22.已知：如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF．求证：(1)△ADF≌△CBE；(2)EB//DF．23.如图，在平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F.求证：(1)AE=CF；(2)四边形AECF是平行四边形．24.如图，在四边形ABCD中，AD//BC，延长BC到E，使CE=BC，连接AE交CD于点F，点F是CD的中点．求证：(1)△ADF≌△ECF．(2)四边形ABCD是平行四边形．25.如图，▱ABCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于M、N．(1)求证：四边形CMAN是平行四边形；(2)已知DE=4，FN=3，求BN的长．∠ADC．26.如图，在四边形ABCD中，AB//DC，DB平分∠ADC，E是CD的延长线上一点，且∠AEC=12(1)求证：四边形ABDE是平行四边形．(2)若DB⊥CB，∠BCD=60°，CD=12，作AH⊥BD于H，求四边形AEDH的周长．答案和解析1.【答案】B【解析】解：A、平行四边形邻角互补，正确，不合题意；B、平行四边形对角不一定互补，错误，符合题意；C、平行四边形对边相等，正确，不合题意．D、平行四边形对角线互相平分，正确，不合题意；故选：B．2.【答案】A【解析】解：∵四边形ABCD是平行四边形，∴∠A=∠C，∠B=∠D，∴∠A：∠B：∠C：∠D的可能情况是2：7：2：7．故选：A．3.【答案】D【解析】解：∵四边形ABCD是平行四边形，∴AD//BC，AD=BC=5，∴∠AEB=∠CBE，∵BE平分∠ABC，∴∠ABE=∠CBE，∴∠ABE=∠AEB，∴AE=AB=3，∴DE=AD−AE=2．故选：D．4.【答案】D【解答】解：∵四边形ABCD是平行四边形，∴AB=CD，BO=OD，∠BAD=∠BCD，∴选项A、B、C正确，D不一定正确．故选D．5.【答案】C【解答】解：通过观察结合平行四边形性质得：S阴影=12×6×4=12．故选：C．6.【答案】D【解答】解：∵只有②③两块角的两边互相平行，且中间部分相连，角的两边的延长线的交点就是平行四边形的顶点，∴带②③两块碎玻璃，就可以确定平行四边形的大小．故选D．7.【答案】B【解答】解：A.对角线互相平分的四边形才是平行四边形，而对角线互相垂直的四边形不一定是平行四边形，故本选项错误；B.对角线互相平分的四边形是平行四边形，故本选项正确；C.两组对角分别相等的四边形是平行四边形，故本选项错误；D.两组对边分别相等的四边形是平行四边形，故本选项错误．故选B．8.【答案】C【解析】解：∵四边形ABCD是平行四边形，周长为18，∴AB=CD，BC=AD，OA=OC，AD//BC，∴CD+AD=9，∠OAE=∠OCF，在△AEO和△CFO中，{∠OAE=∠OCF OA=OC ∠AOE=∠COF ，∴△AEO≌△CFO(ASA)，∴OE=OF=1.5，AE=CF，则EFCD的周长=ED+CD+CF+EF=(DE+CF)+CD+EF=AD+CD+EF=9+3=12．故选：C．9.【答案】C【解答】解：∵四边形ABCD是平行四边形，∴BC=AD=8，∵点E、F分别是BD、CD的中点，∴EF=12BC=12×8=4．故选C．10.【答案】C【解答】解：∵四边形ABCD是平行四边形，∴AB=CD=5，BD=2DO，AC=2OC，∵△OCD的周长为23，∴OD+OC=23−5=18，∵BD=2DO，AC=2OC，∴▱ABCD的两条对角线的和=BD+AC=2(DO+OC)=36．故选C．11.【答案】C【解析】解：∵四边形ABCD是平行四边形，∴AB=CD=4cm，且AD//BC，∴∠ADE=∠CED，又∵DE平分∠ADC，∴∠ADE=∠CDE，∴∠CED=∠CDE，∴CE=CD=4cm，∵AD//BC，∴∠DAE=∠AEB=50°，又∵∠B=80°，∴∠BAE=50°=∠AEB，∴AB=BE=4cm，∴BC=8cm，∴▱ABCD的周长=2(4+8)=24(cm)，故选：C．12.【答案】B【解析】解：∵点A在双曲线y=2x 上，点B在双曲线y=6x上，且AB//x轴，∴设A(2b ,b)，B(6b,b)，则AB=6b −2b，▱ABCD的CD边上高为b，∴S▱ABCD=(6b −2b)×b=6−2=4．故选(B)．13.【答案】AB=CD或AD//BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°(不唯一)【解答】解：∵在四边形ABCD中，AB//CD，∴可添加的条件是：AB=DC，∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)．故答案为AB=CD或AD//BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等．14.【答案】252【解析】解：设短边长为xcm，则长边长为(x+5)cm，∵平行四边形的对边相等，∴2(x+x+5)=60，解得x=252．cm．所以短边是252．故填空答案：25215.【答案】(7,4)【解析】解：∵四边形ABCO是平行四边形，O为坐标原点，点A的坐标是(6,0)，点C的坐标是(1,4)，∴BC=OA=6，6+1=7，∴点B的坐标是(7,4)；故答案为：(7,4)．16.【答案】2√5【解析】解：设AC与BD的交点为O∵四边形ABCD是平行四边形∴AD=BC=2，AD//BCAO=CO=1，BO=DO∵AC⊥BC∴BO=√BC2+CO2=√5∴BD=2√5故答案为2√517.【答案】12【解答】解：∵四边形ABCD是平行四边形，∴BD=2DO=2×1.5=3(cm)，CD=AB=5cm，∵BC=4cm，∴BC2+BD2=CD2，∴∠CBD=90°，即DB⊥BC，∴S▱ABCD=BC·BD=4×3=12(cm2)．故答案为12．18.【答案】10【解答】解：根据平行四边形的对角线互相平分可知OB=OD，又因为OE⊥BD，所以由垂直平分线的性质知BE=DE，所以ΔABE的周长=AB+AE+BE=AB+AE+DE=AB+AD，因为平行四边形的周长是20，所以AB+AD=10，即ΔABE的周长为10．故答案为10．19.【答案】47°【解析】解：∵四边形ABCD是平行四边形，∴∠A=∠C=43°．∵DF⊥AD，∴∠ADE=90°，∴∠AED=90°−43°=47°，∴∠BEF=∠AED=47°．故答案是：47°．20.【答案】6π【解答】解：∵四边形AECD是平行四边形，∴AE=CD，∵AB=BE=CD=6，∴AB=BE=AE，∴△ABE是等边三角形，∴∠B=60°，∴S扇形BAE =60π×62360=6π，故答案为6π．21.【答案】证明：∵E是BC的中点，∴CE=BE，∵四边形ABCD 是平行四边形，∴AB//CD ，AB =CD ，∴∠DCB =∠FBE ，在△CED 和△BEF 中，{∠DCB =∠FBE CE =BE ∠CED =∠BEF, ∴△CED≌△BEF(ASA)，∴CD =BF ，∴AB =BF ．22.【答案】证明：(1)∵AE =CF ，∴AE +EF =CF +FE ，即AF =CE ．又ABCD 是平行四边形，∴AD =CB ，AD//BC ．∴∠DAF =∠BCE ．在△ADF 与△CBE 中{AF =CE ∠DAF =∠BCE AD =CB，∴△ADF≌△CBE(SAS)．(2)∵△ADF≌△CBE ，∴∠DFA =∠BEC ．∴DF//EB ．23.【答案】证明：(1)∵四边形ABCD 是平行四边形． ∴AD//BC ，AD =BC ．∴∠ADE =∠CBF ．∵AE ⊥BD ，CF ⊥BD ，∴∠AED =∠CFB =90°．∵在△ADE 与△CBF 中{∠AED=∠CFB ∠ADE=∠CBF AD=CB，∴△ADE≌△CBF(AAS)，∴AE=CF．(2)∵AE⊥BD，CF⊥BD，∴∠AEF=∠CFE=90°．∴AE//CF．又∵AE=CF，∴四边形AECF是平行四边形．24.【答案】证明：(1)∵AD//BC，∴∠DAF=∠E，∵点F是CD的中点，∴DF=CF，在△ADF与△ECF中，{∠DAF=∠E∠AFD=∠EFC DF=CF,∴△ADF≌△ECF(AAS)；(2)∵△ADF≌△ECF，∴AD=EC，∵CE=BC，∴AD=BC，∵AD//BC，∴四边形ABCD是平行四边形．25.【答案】(1)证明：∵四边形ABCD是平行四边形，∴CD//AB，∵AM⊥BD，CN⊥BD，∴AM//CN，∴CM//AN，AM//CN，∴四边形AMCN是平行四边形；(2)解：∵四边形AMCN是平行四边形，∴CM=AN，∵四边形ABCD是平行四边形，∴CD=AB，CD//AB，∴DM=BN，∠MDE=∠NBF，在△MDE和△NBF中，{∠DEM=∠NFB=90°∠MDE=∠NBFDM=BN,∴△MDE≌△NBF，∴ME=NF=3，BN=DM，在Rt△DME中，∵∠DEM=90°，DE=4，ME=3，∴DM=√DE2+ME2=√32+42=5，∴BN=DM=5．26.【答案】解：(1)∵DB平分∠ADC，∴∠1=∠2=12∠ADC，又∵∠AEC=12∠ADC，∴∠AEC=∠1，∴AE//BD，又∵AB//EC，∴四边形AEDB是平行四边形；(2)∵DB平分∠ADC，∠ADC=60°，AB//EC，∴∠1=∠2=∠3=30°，∴AD=AB，又∵DB⊥BC，∴∠DBC=90°，在Rt△BDC中，CD=12，∴BC=6，DB=6√3，在等腰△ADB中，AH⊥BD，DB=3√3，∴DH=BH=12在Rt△ABH中，∠AHB=90°，∴AH=3，AB=6，∵四边形AEDB是平行四边形，∴AE=BD=6√3，ED=AB=6，∴AE+ED+DH+AH=9√3+9，∴四边形AEDH的周长为9√3+9．。

平行四边形的性质与判定1.有关边角的计算问题角：对角相等、邻角互补、对边平行（内错角、同位角、同旁内角等） 边：对边相等，周长=2×（邻边的和）；面积=底×高（有两组，即等积式）；2.两条对角线分得的四个三角形的周长和面积（主要同底、同高等）判定平行四边形从边看从角看从对角线看从对称性看对边平行对边相等对角相等 邻角互补对角线互相平分中心对称图形三角形全等、等腰三角形、直角三角形等性质ABCD S S S S S 平行四边形414321====；ABCD S S S S 平行四边形21312=+=；ABCD S S S S S 平行四边形214231=+=+4231S S S S ⋅=⋅3.一些常见模型4.解决平行四边形问题，除了平行四边形本身的性质能用外，很多时候还得根据情景借助三角形的知识（三角形全等、等腰三角形、直角三角形等）来求解。

练习：1.如图，在△ABC 中，AB =AC =6，D 是BC 上的点，DF △AB 交AC 于点F ，DE △AC 交AB 于E ，那么四边形AFDE 的周长为( )A . 6B . 12C . 24D . 48两内角平分线 （直角三角形）一内角平分线（等腰三角形） 中点+垂线=垂直平分线（等腰三角形）2.如图，AE △BD ，BE △DF ，AB △CD ，下面给出四个结论：（1）AB =CD ；（2）BE =DF ；（3）S 四边形ABDC =S四边形BDFE；（4）S △ABE =S △DCF .其中正确的有（ ）A .1个B .2个C .3个D .4个3.如图， ABCD 的周长为40，∆BOC 的周长比∆AOB 的周长多4，则AB 的长为（ ） A.4 B. 8 C.12 D.164.平行四边形的边长为5，则它的对角线长可能是（）A. 4和6B. 2和12C. 4和8D. 4和35.如图，将沿对角线AC 折叠，使点B 落在点B′处，若△1=△2=44°，则△B 为（ ） A.66° B.104° C.114° D.124°6.如图，E ，F 分别是□ABCD 的边AD ，BC 上的点，EF ＝6，∠DEF ＝60°，将四边形EFCD 沿EF 翻折，得到四边形EFC ′D ′，ED ′交BC 于点G ，则△GEF 的周长为 （ ）A. 6B. 12C. 18D. 247.在四边形ABCD 中，AB//CD ，要使ABCD 是平行四边形，可添加条件不正确的是（ ） A.AB=CD B.BC//AD C.△A =△C D. BC =AD8.若平行四边形的两条对角线长为6cm 和16cm ，则下列长度的线段可作为平四边形边长的是（ ） A.5cm B.8cm C.12cm D.16cm第3题第2题第1题第5题第6题第7题第9题第10题9.如图，在中，将△ADC 沿AC 折叠后，点D 恰好落在DC 的延长线上的点E 处，若△B=60°，AB=3，则△ADE 的周长为（ ）A.12B.15C.18D.2110. 如图，过☐ABCD 的对角线BD 上一点M 分别作平行四边形两边 的平行线EF 和GH ，那么图中的☐AEMH 的面积1S 与☐MGFC 的面 积2S 的大小关系是( )A.21S S >B.21S S <C.21S S =D.212S S = 11.如图，在平面直角坐标系中，以A （-1,0），B （2,0）， C （0,1）为顶点构造平行四边形，下列不能作为平行四边 形顶点坐标的是（ ）A.（3,1）B.（-4,1）C.（1，-1）D.（-3,1）12.如图，平行四边形ABCD 中，点E . F 分别在BC ，AD 上，当时，四边形AFCE 是平行四边形.13.如图，在☐ABCD 中，△ABC 的平分线BE 交AD 于点E ，AB=5,ED=2,则☐ABCD 的周长为 . 14.如图，在☐ABCD 中，点E 为边CD 上一点，将∆ADE 沿AE 折叠至AD′E 处，AD′与CE 交于点F ，若△B=52°，△DAE=20°，则△FED′的大小为 .15.如图，平行四边形OABC 中的三个顶点分别为（0,0），C （4,0），B （3,3），AB 与y 轴交于点D,△AOC第13题第14题第12题的平分线交AB于点P，则点P的坐标为.16.如图，在☐ABCD中，对角线AC、BD相交于点O，OE△BD交AD于点E，连接BE，若☐ABCD的周长为28，则△ABE的周长为.17.如图，在平行四边形ABCD 中，P 是C D 边上一点，且A P、BP 分别平分△DAB、△CBA，若A D＝5，AP＝6，则△APB 的面积是．18.如图，在中，AE△BC于点E，AF△DC于点F,BC=5，AB=4,AE=3,则AF的长度为.19.如图，平行四边形的周长为20cm，AE△BC 于 E，AF△CD 于 F，AE＝2cm，AF＝3cm，平行四边形ABCD 的面积为cm2．20.如图，平行四边形ABCD的顶点D在平行四边形AEFG的边FG上，点E在平行四边形ABCD的边BC上，CD与EF相交于点H，设△ABE，△ECH，△HFD，△DGA的面积分别为1S，2S，3S，4S，给出下列结论：△4321SSSS+=+；△423SSS+=；△321SSS+=；△AEFGABCDSS平行四边形平行四边形=，其中正确的结论是.第21题第20题第15题第16题第17题第18题第19题第22题21.如图，正比函数x y =与反比例函数xy 1=的图象相交于A 、C 两点，AB△x 轴于点A,CD△x 轴于点D,则四边形ABCD 的形状是 四边形，其面积为 .22.如图，在四边形ABCD 中，AB △CD ，△D =2△B ，若AD =3，AB =5，则CD =______.23.如图，在☐ABCD 中，对角线AC 与BD 相交于点O ，EF 过点O 且与AD ，BC 分别相交于点E ，F ，求证：OE=OF24.如图，在☐ABCD 中，对角线AC 与BD 相交于点O ，E 和F 分别是OA 和OC 的中点，求证：DE=BF25.如图，在平行四边形ABCD中，E，F分别是对角线BD上的两点，且BE=DF．求证：AE=CF．26.如图，在平行四边形ABCD中，延长BA到点E，延长DC到点F，使AE=CF，连接EF，分别交AD、BC于点N、M，连接BN、DM.(1)求证：△ANE△△CMF；(2)求证：四边形BMDN是平行四边形.27.如图，所示，在 ABCD中，点E，F在对角线AC上，且AF=CE.求证：四边形BEDF是平行四边形28.如图，BD是∆ABC的角平分线，点E，F分别在BC，AB上，且DE//AB，BE=AF.求证：四边形ADEF是平行四边形.29.如图，在平行四边形ABCD中，点E，F分别在AB、CD上，AE=CF，连接AF，BF，DE，CE，分别交于H，G .求证：（1）四边形AECF是平行四边形；（2）EF与GH互相平分；30.如图，在☐ABCD中，E是BC的中点，连结AE并延长交DC的延长线于点F.（1）求证：AB=CF；（2）连结DE，若AD=2AB，求证：DE△AF30.如图，在☐ABCD中，△BAD的平分线AE交CD于点F，交BC的延长线于点E.（1）求证：BE=CD；（2）连接BF，若BF△AE，△BEA=60°，AB=4，求平行四边形ABCD的面积.31.如图，在平行四边形ABCD 中，点E 在AD 上，连接BE、CE，EB 平分△AEC．（1）如图1，判断△BCE 的形状，并说明理由；（2）如图2，△A＝90°，BC＝5，AE＝1，求线段BE 的长．32.如图，在四边形ABCD 中，AD//BC,BC=18cm,CD=15cm,AD=10cm,AB=12cm,动点P 、Q 分别从点A ，C 同时出发，点P 以2cm/s 的速度由A 向D 运动，点Q 以3cm/s 的速度由C 向B 运动（当其中一个点停止运动时，另一个点也随之停止运动）.（1）几秒后，四边形ABQP 为平行四边形？并求出此时四边形ABQP 的周长？（2）几秒后，四边形PDCQ 为平行四边形？并求出此时四边形PDCQ 的周长？33.如图，在平面直角坐标系中，直线1l ：621+-=x y 分别与x 轴、y 轴交于点B 、C ，且与直线2l ：x y 21=交于点A ． （1）点A 的坐标是 ；点B 的坐标是 ；点C 的坐标是 ；（2）若D 是线段OA 上的点，且COD ∆的面积为12，求直线CD 的函数表达式；（3）在（2）的条件下，，在平面内是否存在点P ，使以O 、C 、P 、D 为顶点的四边形是平行四边形？若存在，直接写出点P 的坐标；若不存在，请说明理由．34.如图，△ABC是等边三角形，点D是边BC上的一点，以AD为边坐等边三角形ADE，过点C作CF//DE 交AB于点F.（1）若点D是BC边的中点，求证：EF=CD.（2）在（1）的条件下直接写出△AEF和△ABC的面积比；（3）若点D是BC边上除B、C外的任意一点，那么（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；35.如图，在平行四边形ABCD 中，点 E 在边 BC 上，连结AE，EM△AE，垂足为E，交 CD 于点 M，AF△BC，垂足为 F ，BH△AE ，垂足为 H ，交 AF 于点 N ，若 AE ＝BN ，AN ＝CE ，则下列结论：△△NBF ＝△MEC ；△△NBF△△EAF ；△△BCD ＝150°；△AD＝CM+2CE，其中正确的结论是（填写所有正确结论的序号） 1、只要朝着一个方向努力，一切都会变得得心应手。

华师大版八年级下册第１８章平行四边形单元测试题姓名：，成绩：；一、选择题（１２题，共４８分）１、(2015山东济南网评培训)不能判定一个四边形是平行四边形的条件是（Ｂ）A.两组对边分别平行 B. 一组对边平行，另一组对边相等C. 一组对边平行且相等D. 两组对边分别相等２、（2014山东济南，第10题，3分）在□ＡＢＣＤ中，延长AB到E，使BE＝AB，连接DE交BC于F，则下列结论不一定成立的是（Ｄ）A．∠Ｅ＝∠ＣＤＦ B．ＥＦ＝ＤＦ C．第２题第３题第４题３、（2014十堰6．如图，在平行四边形ABCD中，AB=4，BC=6，AC的垂直平分线交AD于点E，则△CDE的周长是（Ｂ）Ａ、７Ｂ、１０Ｃ、１１Ｄ、１２４、（2015四川省绵阳市，7，3分）如图，在四边形ABCD中，对角线AC、BD相交于点E，∠CBD＝90°，BC＝4，BE＝ED＝3，AC＝10，则四边形ABCD的面积为（Ｄ）A．6 B．12 C．20 D．24５、若以A(－0.5,0)，B(2,0)，C(0,1)三点为顶点画平行四边形，则第四个顶点不可能在( Ｄ)A．第一象限 B．第二象限 C．第三象限 D．第四象限６、已知：平行四边形ＡＢＣＤ中，ＡＢ＝１３，ＢＣ＝７，ＡＣ的长为整数，则ＡＣ的最大值为（Ｂ）Ａ、２０Ｂ、１９Ｃ、７Ｄ、６７、( 2015·呼和浩特市初三年级质量普查调研)已知平行四边形ABCD的对角线AC与BD相交于点O，AB⊥AC，若AB=2，AC=8，则对角线BD 长度是（Ａ）A. 45B. 42C. 25D. 22８、（2015天津,第11题3分）（2015天津）如图，已知▱ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′．若∠ADC=60°，∠ADA′=50°，则∠DA′E′的大小为（Ｃ）A．130°B．150°C．160°D．170°９、在平行四边形ＡＢＣＤ中，下列描述正确的是（Ａ）Ａ、对角线交于点Ｏ，则过点Ｏ的直线平分平行四边形的面积Ｂ、∠Ａ：∠Ｂ：∠Ｃ：∠Ｄ＝３：１：１：３Ｃ、对角线是平行四边形的对称轴；Ｄ、ＡＢ＝ＢＣ，ＡＣ＝ＢＤ；１０、（2014浙江湖州，第10题3分）在连接A地与B地的线段上有四个不同的点D、G、K、Q，下列四幅图中的实线分别表示某人从A地到B地的不同行进路线（箭头表示行进的方向），则路程最长的行进路线图是（Ｄ）A．B．C．D．１１、 (2015山东济南一模)如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，四边形ACDE是平行四边形，连结CE交AD于点F，连结BD交CE于点G，连结BE. （1）下列结论中：①CE=BD；②△ADC是等腰直角三角形；③∠ADB=∠AEB；④CD·AE=EF·CG；一定正确的结论有（Ｄ）A．1个 B 2个 C 3个 D．4个１２、 (2015·江苏无锡崇安区·一模) 在面积为60的□ABCD中，过点A作AE⊥直线BC于点E，作AF⊥直线CD于点F，若AB＝10，BC＝12，则CE＋CF的值为 ( Ｄ )A. 22＋11 3B. 22－11 3C. 22＋113或22－11 3D. 22＋113或2＋ 3二、填空题（６题，共２４分）１３、（2015内蒙古赤峰15，3分）如图，四边形ABCD中，AD∥BC，E是DC上一点，连接BE并延长交AD延长线于点F，请你只添加一个条件：BD∥FC 使得四边形BDFC为平行四边形．第１３题第１４题第１６题１４、（2015山东潍坊第二学期期中）以△ABC的顶点A为圆心，以BC长为半径作弧；再以顶点C为圆心，以AB长为半径作弧，两弧交于点D；连结AD、CD．若∠B=65°，则∠ADC的大小为６５度.１５、在平行四边形ＡＢＣＤ中，对角线ＡＣ＝１４，ＢＤ＝８，则边ＡＢ的取值范围是６<AB<22 ，边ＡＤ的取值范围是6<AD<22 。

八年级数学下册《第十八章 平行四边形》单元测试卷及答案（华东师大版）一、选择题1．如图，在平行四边形ABCD 中，下列结论错误的是( )A ．12∠=∠B ．13∠=∠C ．AB CD = D ．BO DO =2．如图，在平面直角坐标系中，ABCD 的顶点A ，B ，D 的坐标分别是(00)(50)(23)，，，，，，则顶点C 的坐标是（ ）A ．(73)，B ．(53)，C ．(37)，D ．(82)，3．在平行四边形ABCD 中，45AB BC ABC ==∠，，的平分线交AD 于点E ，则DE 的长为（ ） A ．4B ．3C ．2D ．14．能判定一个四边形是平行四边形的条件是（ ）A ．一组对边平行，另一组对边相等B ．一组对边平行，一组对角互补C ．一组对角相等，一组邻角互补D ．一组对角相等，另一组对角互补5．如图，下列条件不能判定四边形ABCD 是平行四边形的是（ ）A ．AB//CD ，AD=BCB ．AB=CD ，AD=BC C ．∠ABC=∠ADC ，∠BAD=∠BCDD ．AO=CO ，BO=DO6．如图，在Rt ABC 中90ABC ∠=︒，AB=1，D 是BC 边上一点，将ACD 沿AD 折叠得AED ，连接BE ，若四边形ABED 为平行四边形，则AE 的值是（ ）A 3B ．5C ．2D 57．如图，在ABCD 中，BE 平分ABC ∠交DC 于点E .若60A ︒∠=，则DEB ∠的度数为（ ）A ．130︒B ．125︒C ．120︒D ．115︒8．如图，四边形ABCD 中，AD ＝BC ，下列条件不能判定四边形ABCD 为平行四边形的是( )A ．AD∥BCB ．∥A+∥B ＝180°C ．∥A ＝∥CD ．AB ＝CD9．如图，点A 是直线l 外一点，在l 上取两点B 、C ，分别以A 、C 为圆心，BC AB 、长为半径画弧，两弧交于点D ，分别连接AB AD CD 、、，则四边形ABCD 是平行四边形．其依据是（ ）A ．一组对边平行且相等的四边形是平行四边形B ．两组对边分别相等的四边形是平行四边形C ．两组对边分别平行的四边形是平行四边形D ．一组对边平行，另一组对边相等的四边形是平行四边形10．在四边形ABCD 中，从下面四个条件中选取两个：①AB CD ；②AB CD =；③BC AD ；④BC AD =，能使四边形ABCD 是平行四边形的选法有（ ）A ．3种B ．4种C ．5种D ．6种二、填空题11．已知点O 是平行四边形ABCD 两条对角线的交点，AC ＝12．BC ＝18，OD ＝14，则∥OBC 的周长为 ．12．在ABCD 中，若54A B ∠∠=：：，则C ∠= ︒．13．如图，在ABCD 中，对角线AC ，BD 交于点E ，AC BC ⊥若2AC =，AB=3，则BD = ．14．如图，在ABCD 中，点E ，F 均在AD 边上，BE 平分∥ABC ，CF 平分∥BCD ，如果BE ＝8，CF ＝6，EF ＝2，那么ABCD 的周长等于 ．三、解答题15．如图，在ABCD 中，对角线AC ，BD 交于点O ，点E ，F 分别是OD ，OB 的中点，连接AE ，CF ，求证：AE CF =．16．如图，在ABCD 中13AB =，AD=5，AC BC ⊥求ABCD 的面积．17．如图，在平行四边形ABCD 中，点E 、F 分别在BC 、AD 上，且BE DF =.请判断AE 与CF 的数量关系，并说明理由.18．在平行四边形ABCD 中，点E 、F 是对角线AC 上的两点，且AE ＝CF ，求证：四边形BFDE 是平行四边形．四、综合题19．如图，在四边形ABCD 中908cm 10cm 6cm AD BC B AD BC AB ∠====，，，，，点Q 从点A 出发以1cm/s 的速度向点D 运动，点P 从点B 出发以2cm /s 的速度向点C 运动，P Q ，两点同时出发，当点P 到达点C 时，掉头沿CB 方向继续运动，直至点Q 到达点D ，两点同时停止运动．若设运动时间为s t ．（1）直接写出：AQ = cm ，DQ = cm ；（用含t 的式子表示） （2）当t 为何值时，四边形PQDC 为平行四边形？20．如图，已知平行四边形ABCD ，AC 、BD 相交于点O ，AB=4，AC=6，BD=10．（1）求∥ACD 的度数； （2）求BC 的长.21．如图，已知点E 、F 为∥ABCD 对角线BD 上两点，且BAF DCE ∠=∠，连接AE ，CF ．求证：（1）AF CE =；（2）四边形AECF 为平行四边形．22．如图，点E 为ABCD 的边AD 上的一点，连接EB 并延长，使BF BE =，连接EC 并延长，使CG CE = 连接FG ．H 为FG 的中点，连接DH ，AF ．（1）若70BAE ∠=︒，20DCE ∠=︒ 求DEC ∠的度数； （2）求证：四边形AFHD 为平行四边形；（3）连接EH ，交BC 于点O ，若OC OH =，求证：12OE BC =．答案解析部分1．【答案】B【解析】【解答】解：∵四边形ABCD是平行四边形∴AB∥CD，AB=CD，OB=OD∴∥1=∥2∴ACD正确，B错误；故答案为：B.【分析】利用平行四边形的性质可得AB∥CD，AB=CD，OB=OD，再利用平行线的性质可得∥1=∥2，据此逐一判断即可.2．【答案】A【解析】【解答】解：在平行四边形ABCD中，AB∥CD，AB=CD.∵A（0，0），B(5，0)∴AB=5.∴CD=5.∵D（2，3）∴C的坐标为（7，3）.故答案为：A.【分析】根据平行四边形“对边平行且相等”的性质，对边AB和CD线段长度相等.3．【答案】D【解析】【解答】解：在平行四边形ABCD中，AD∥BC，BC=5∴∥AEB=∥EBC，AD=BC=5∵BE平分∥ABC∴∥ABE=∥EBC∴∥ABE=∥AEB∴AE=AB=4∴DE=AD-AE=5-4=1；故答案为：D.【分析】由平行四边形的性质可得∥AEB=∥EBC，AD=BC=5，结合角平分线的定义可推出∥ABE=∥AEB，可得AE=AB=4，利用DE=AD-AE即可求解.4．【答案】C【解析】【解答】A、根据“一组对边平行，另一组对边相等”不能判定一个四边形是平行四边形，故本选项错误；B、“一组对边平行，一组对角互补”的四边形，也可能是梯形，故本选项错误；C、根据邻角互补，可以判定一组对边平行，再由-组对角相等可以推知另一组邻角互补，则可以判定另一组对边平行，所以由“两组对边互相平行的四边形是平行四边形”可以判定一个四边形是平行四边形故本选项正确；D、根据“一组对角相等，另一组对角互补”不能判定一个四边形是平行四边形，故本选项错误；故答案为：C。