三角模糊数相离度法比较大小Matlab程序及例题

MATLAB数学⼿册教程_第6章__模糊逻辑第6章模糊逻辑6.1 ⾪属函数6.1.1 ⾼斯⾪属函数函数 gaussmf格式 y=gaussmf(x,[sig c])说明⾼斯⾪属函数的数学表达式为：22)c x (e )c ,;x (f σ--=σ，其中c ,σ为参数，x 为⾃变量，sig 为数学表达式中的参数σ。

例6-1>>x=0:0.1:10;>>y=gaussmf(x,[2 5]); >>plot(x,y)>>xlabel('gaussmf, P=[2 5]')结果为图6-1。

0.0.0.0.g a u s s m f, P =[2 5]图6-16.1.2 两边型⾼斯⾪属函数函数 gauss2mf格式 y = gauss2mf(x,[sig1 c1 sig2 c2])说明 sig1、c1、sig2、c2为命令1中数学表达式中的两对参数例6-2>>x = (0:0.1:10)';>>y1 = gauss2mf(x, [2 4 1 8]); >>y2 = gauss2mf(x, [2 5 1 7]); >>y3 = gauss2mf(x, [2 6 1 6]); >>y4 = gauss2mf(x, [2 7 1 5]); >>y5 = gauss2mf(x, [2 8 1 4]);>>plot(x, [y1 y2 y3 y4 y5]);>>set(gcf, 'name', 'gauss2mf', 'numbertitle', 'off');结果为图6-2。

6.1.3 建⽴⼀般钟型⾪属函数函数 gbellmf格式 y = gbellmf(x,params)说明⼀般钟型⾪属函数依靠函数表达式b 2|ac x |11)c ,b ,a ;x (f -+=这⾥x 指定变量定义域范围，参数b 通常为正，参数c 位于曲线中⼼，第⼆个参数变量params 是⼀个各项分别为a ，b 和c 的向量。

matlab数组比较运算Matlab是一种强大的数学计算软件，它提供了丰富的数组比较运算功能。

本文将介绍一些常用的数组比较运算符，并给出一些实际应用的示例。

在Matlab中，数组比较运算符主要包括等于（==）、不等于（~=）、大于（>）、小于（<）、大于等于（>=）和小于等于（<=）等。

这些运算符可以用于比较两个数组的元素，并返回一个逻辑数组作为结果。

逻辑数组中的每个元素代表了对应位置的元素是否满足比较关系。

我们来看一些简单的数组比较运算示例。

假设有两个数组a和b，它们分别如下所示：a = [1, 2, 3, 4, 5];b = [2, 2, 3, 3, 4];我们可以使用等于运算符（==）来比较这两个数组的元素是否相等：result = a == b;运行上述代码后，将得到一个逻辑数组result，其中的元素分别表示对应位置的元素是否相等。

在本例中，result的值为[0, 1, 1, 0, 0]，表示a和b的第2个和第3个元素相等，其他位置的元素不相等。

除了等于运算符，我们还可以使用其他的数组比较运算符。

例如，不等于运算符（~=）可以用来比较两个数组的元素是否不相等：result = a ~= b;运行上述代码后，将得到一个逻辑数组result，其中的元素分别表示对应位置的元素是否不相等。

在本例中，result的值为[1, 0, 0, 1, 1]，表示a和b的第1个、第4个和第5个元素不相等，其他位置的元素相等。

类似地，大于运算符（>）、小于运算符（<）、大于等于运算符（>=）和小于等于运算符（<=）可以用于比较两个数组的元素大小关系。

例如，我们可以使用大于运算符（>）来比较两个数组的对应位置的元素是否满足a中的元素大于b中的元素：result = a > b;运行上述代码后，将得到一个逻辑数组result，其中的元素分别表示对应位置的元素是否满足a中的元素大于b中的元素。

三角分布matlab -回复三角分布，又称为三角概率密度函数，是一种常见的概率分布函数形式。

它的基本形状呈现出一个对称的三角形，因此得名。

三角分布有着许多应用领域，包括统计分析、金融建模、风险评估等等。

在本文中，我们将介绍三角分布的定义、参数、特点以及如何在MATLAB中生成和分析三角分布。

首先，让我们来了解一下三角分布的定义和参数。

三角分布的概率密度函数可以表示为：\[f(x;a,b,c)=\begin{cases}0 & ,x < a \\ \frac{2(x-a)}{(b-a)(c-a)}& ,a \leq x < c \\ \frac{2(b-x)}{(b-a)(b-c)} & ,c \leq x \leq b \\ 0 & ,x > b\end{cases}\]其中，\(a\)、\(b\)和\(c\)是三角分布的参数，且满足\(a < c < b\)。

\(a\)和\(b\)代表了分布的最小值和最大值，而\(c\)代表了最有可能出现的值，也可以看作是众数。

三角分布的特点之一是其形状对称，这意味着分布的左侧和右侧的概率密度函数相等。

此外，三角分布还具有一个重要特点，即它可以根据参数的选择具有不同的形状。

当\(a\)、\(b\)和\(c\)趋近于接近时，三角分布逐渐接近均匀分布。

当\(a\)和\(b\)固定，而\(c\)变化时，三角分布则呈现出不同的峰度。

现在，我们将在MATLAB中使用三角分布生成一些随机变量，并分析其特性。

首先，我们需要使用三角分布函数`trigpdf` 生成随机样本。

matlaba = 0;b = 10;c = 5;n = 1000;生成三角分布的随机样本x = trigpdf(a, b, c, n);在这个例子中，我们选择了\(a=0\)、\(b=10\)和\(c=5\)作为参数的值，同时生成了1000个随机样本。

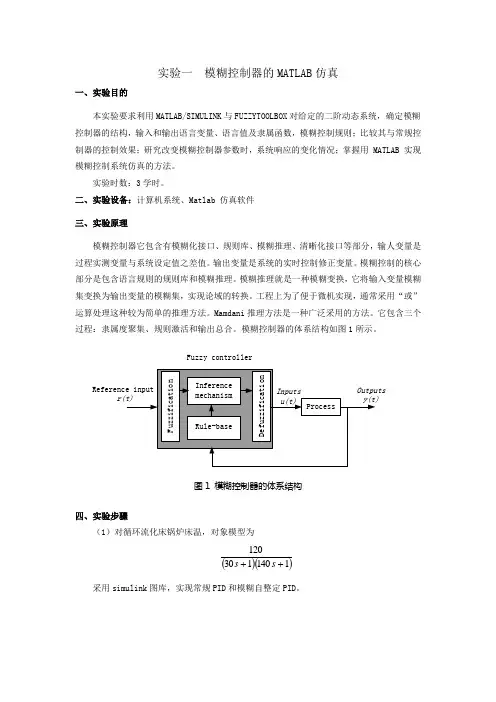
实验一 模糊控制器的MATLAB 仿真一、实验目的本实验要求利用MATLAB/SIMULINK 与FUZZYTOOLBOX 对给定的二阶动态系统，确定模糊控制器的结构，输入和输出语言变量、语言值及隶属函数，模糊控制规则；比较其与常规控制器的控制效果；研究改变模糊控制器参数时，系统响应的变化情况；掌握用 MATLAB 实现模糊控制系统仿真的方法。

实验时数：3学时。

二、实验设备：计算机系统、Matlab 仿真软件 三、实验原理模糊控制器它包含有模糊化接口、规则库、模糊推理、清晰化接口等部分，输人变量是过程实测变量与系统设定值之差值。

输出变量是系统的实时控制修正变量。

模糊控制的核心部分是包含语言规则的规则库和模糊推理。

模糊推理就是一种模糊变换，它将输入变量模糊集变换为输出变量的模糊集，实现论域的转换。

工程上为了便于微机实现，通常采用“或”运算处理这种较为简单的推理方法。

Mamdani 推理方法是一种广泛采用的方法。

它包含三个过程：隶属度聚集、规则激活和输出总合。

模糊控制器的体系结构如图1所示。

图1 模糊控制器的体系结构四、实验步骤（1）对循环流化床锅炉床温，对象模型为()()1140130120++s s采用simulink 图库，实现常规PID 和模糊自整定PID 。

（2）确定模糊语言变量及其论域：模糊自整定PID 为2输入3输出的模糊控制器。

该模糊控制器是以|e|和|ec|为输入语言变量，Kp 、Ki 、Kd 为输出语言变量，其各语言变量的论域如下：误差绝对值：e={0，3，6，10}；误差变化率绝对值：ec={0，2，4，6}；输出Kp：Up={0，0.5，1.0，1.5}；输出Ki：Ui={0，0.002，0.004，0.006}；输出Kd：Ud={0，3，6，9}。

（3）语言变量值域的选取：输入语言变量|e|和|ec|的值域取值“大”(B)、“中”(M)、“小”(s)和“零”(Z) 4种；输出语言变量Kp、Ki、Kd的值域取值为“很大”(VB)、“大”(B)、“中”(M)、“小”(s) 4种。

23.模糊聚类剖析原理及实现聚类剖析，就是用数学方法研究和办理所给定对象，依据事物间的相像性进行区分和分类的过程。

传统的聚类剖析是一种硬区分，它把每个待识其他对象严格地区分到某个类中，拥有非此即彼的性质，这种分类的类型界线是分明的。

跟着模糊理论的成立，人们开始用模糊的方法来办理聚类问题，称为模糊聚类剖析。

因为模糊聚类获得了样本数与各个类其他不确立性程度，表达了样本类属的中介性，即成立起了样本关于类其他不确立性的描绘，能更客观地反应现实世界。

本篇先介绍传统的两种（适合数据量较小情况，及理解模糊聚类原理）：鉴于择近原则、模糊等价关系的模糊聚类方法。

（一）预备知识一、模糊等价矩阵定义 1 设 R=(r ij )n×n为模糊矩阵， I 为 n 阶单位矩阵，若R 知足i)自反性： I≤R （等价于 r ii =1）；ii)对称性： R T=R;则称 R 为模糊相像矩阵，若再知足niii) 传达性： R2≤R（等价于( r ik r kj ) r ij）k1则称 R 为模糊等价矩阵。

定理 1 设 R 为 n 阶模糊相像矩阵，则存在一个最小的自然数k（k<n）, 使得 R k为模糊等价矩阵，且对全部大于k 的自然数 l，恒有R l=R k. R k称为 R 的传达闭包矩阵，记为 t(R).二、模糊矩阵的λ-截矩阵定义 2 设 A=(a ij)n×m为模糊矩阵，对随意的λ∈[0,1], 作矩阵Aa ij( )n m此中，a ij( )1,aij 0,aij称为模糊矩阵 A 的λ-截矩阵。

明显，Aλ为布尔矩阵，且其等价性与与A一致。

意义：将模糊等价矩阵转变为等价的布尔矩阵，能够获得有限论域上的一般等价关系，而等价关系是能够分类的。

所以，当λ在[0,1]上改动时，由 Aλ获得不一样的分类。

若λ1＜λ2,则Aλ1≥Aλ2,进而由Aλ2 确立的分类是由Aλ1 确立的分类的加细。

当λ从 1 递减变化到 0 时，Aλ的分类由细变粗，渐渐合并，形成一个分级聚类树。

三角分布matlab -回复如何在MATLAB中生成三角分布？三角分布是统计学中常用的一种分布形式，它可以用来描述某个随机变量在一个有限范围内取值的概率分布。

在MATLAB中，可以通过以下步骤来生成三角分布。

步骤1：了解三角分布的特点和参数在生成三角分布之前，我们需要先了解三角分布的特点和参数。

三角分布是由三个参数定义的：最小值a、最大值b和峰值处在区间[a, b]中的众数m。

这三个参数决定了分布的形状。

三角分布的概率密度函数如下所示：f(x) = 2(x-a)/(b-a)*(m-a)/(b-a), 若a <= x < m2/(b-a), 若x = m2(b-x)/(b-a)*(b-m)/(b-a), 若m < x <= b其中，a <= x <= b。

步骤2：生成一组随机数使用MATLAB的rand函数可以生成0到1之间的均匀分布的随机数。

我们可以通过如下语句生成一组随机数：x = rand(n,1)其中，n是所需生成的随机数的个数。

这里生成的随机数具有均匀分布。

步骤3：将均匀分布的随机数映射到三角分布上由于三角分布与均匀分布的形状不同，我们需要将均匀分布的随机数映射到三角分布上。

通过线性映射的方法可以实现这一步骤。

具体地，我们可以通过以下公式将均匀分布的随机数映射到三角分布上：y = a + sqrt(u*(b-a)*(m-a))其中，u是0到1之间的均匀分布的随机数。

步骤4：绘制三角分布的图像生成一组符合三角分布的随机数后，我们可以使用MATLAB的histogram函数来绘制三角分布的直方图。

具体的代码如下：histogram(x, 'Normalization', 'pdf')其中，x为生成的符合三角分布的随机数数组。

步骤5：调整参数并进一步优化在实际应用中，我们可能需要调整三角分布的参数以适应具体的情况。

例如，我们可以改变最小值、最大值和众数来改变分布的形状。

matlab如何求解三角函数方程（最新版）目录一、引言二、MATLAB 求解三角函数方程的方法1.使用符号计算函数2.使用 solve 函数3.使用 vpasolve 函数4.使用 fsolve 函数5.使用数值分析算法三、具体示例1.求解带有三角函数的方程组2.求解复杂三角方程四、结论正文一、引言在数学问题中，三角函数方程是一种常见的问题类型。

求解这类问题，我们可以使用 MATLAB 这一强大的数学软件。

MATLAB 提供了多种方法来求解三角函数方程，本文将对这些方法进行详细介绍。

二、MATLAB 求解三角函数方程的方法1.使用符号计算函数在 MATLAB 中，可以使用 symbolic 计算函数来求解三角函数方程。

例如，对于方程 sin(x) = y，可以使用以下命令求解：```matlabsyms x y;eq = sin(x) - y;solve(eq, x)```2.使用 solve 函数solve 函数是 MATLAB 中求解方程的常用函数。

对于三角函数方程，也可以使用 solve 函数求解。

例如，对于方程 sin(x) = y，可以使用以下命令求解：```matlabf = @(x) sin(x) - y;x0 = pi/4;[x, fval] = solve(f, x0)```3.使用 vpasolve 函数vpasolve 函数是 MATLAB 中用于求解带有参数的方程的函数。

对于三角函数方程，可以使用 vpasolve 函数求解。

例如，对于方程 a*sin(x) + b*cos(x) = c，可以使用以下命令求解：```matlabvpasolve("a*sin(x) + b*cos(x) = c", [a, b, c])```4.使用 fsolve 函数fsolve 函数是 MATLAB 中用于求解非线性方程的函数。

对于三角函数方程，可以使用 fsolve 函数求解。

直觉模糊集是模糊数学中的一个重要概念，它通过区间估计的方式描述模糊性，对于一些复杂的实际问题有着重要的应用价值。

在实际问题中，我们经常需要对直觉模糊集进行计算和处理，而Matlab作为一个功能强大的数学计算软件，为我们提供了便利的工具和函数来实现直觉模糊集的计算。

在本文中，我们将介绍在Matlab中如何使用代码来进行直觉模糊集的计算。

1. 定义直觉模糊集我们需要了解直觉模糊集的定义。

直觉模糊集是指在实际问题中，人们在将模糊概念用语言描述时所使用的模糊集合。

它不同于数学中对模糊集的抽象描述，而是基于人们的主观直觉和经验，使用自然语言描述的模糊集合。

“很快”、“比较大”等词语就可以被看作是直觉模糊集的表达。

2. 直觉模糊集的表示在Matlab中，可以使用向量或矩阵来表示直觉模糊集。

对于一个直觉模糊集“很快”，可以使用一个包含速度范围的向量来表示。

假设速度范围为[60, 100]，则可以用Matlab代码表示为：```V = [60, 100];3. 直觉模糊集的运算在Matlab中，可以通过内置函数来对直觉模糊集进行运算。

对于两个直觉模糊集A和B，如果需要计算它们的交集，可以使用Matlab中的min函数来实现。

具体代码如下：```C = min(A, B);```这段代码将直觉模糊集A和B的每个元素分别进行比较，取最小值作为交集C的对应元素。

通过类似的方式，可以实现并集、差集等运算。

4. 直觉模糊集的可视化在实际应用中，通常需要将直觉模糊集进行可视化，以便更直观地理解和分析。

Matlab提供了丰富的绘图函数，可以方便地实现直觉模糊集的可视化。

可以使用plot函数来绘制直觉模糊集的图形，使用fill函数来填充直觉模糊集的范围等。

5. 示例代码下面给出一个简单的示例代码，展示了如何在Matlab中实现直觉模糊集的计算和可视化。

```matlab% 定义直觉模糊集A和BA = [60, 100];B = [80, 120];% 计算交集C = min(A, B);% 可视化x = [A(1), A(2), A(2), A(1)];y = [0, 0, 1, 1];fill(x, y, 'b', 'FaceAlpha', 0.3);hold on;x = [B(1), B(2), B(2), B(1)];fill(x, y, 'r', 'FaceAlpha', 0.3);xlabel('速度');ylabel('隶属度');legend('A', 'B');```通过上面的示例代码，我们可以看到，利用Matlab的强大功能，我们可以轻松地实现直觉模糊集的计算和可视化，为实际问题的分析和处理提供了便利和支持。

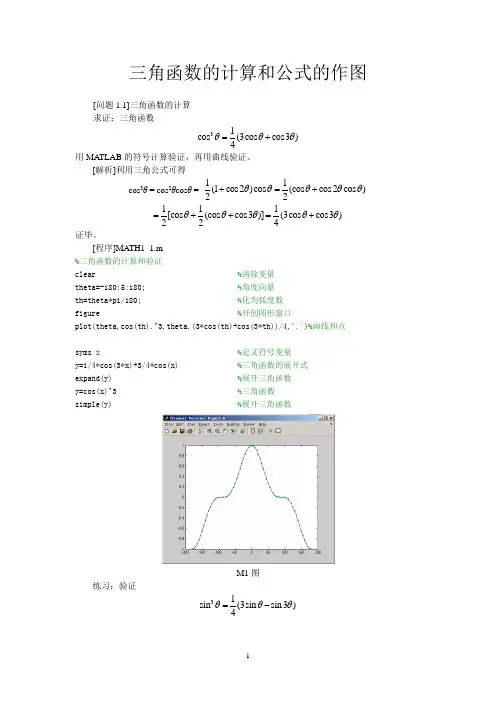
1 三角函数的计算和公式的作图 [问题1.1]三角函数的计算 求证：三角函数

31cos(3coscos3)4

用MATLAB的符号计算验证，再用曲线验证。 [解析]利用三角公式可得

cos3θ = cos2θcosθ = 11(1cos2)cos(coscos2cos)22 111[cos(coscos3)](3coscos3)224

证毕。 [程序]MATH1_1.m %三角函数的计算和验证 clear %清除变量 theta=-180:5:180; %角度向量 th=theta*pi/180; %化为弧度数 figure %开创图形窗口 plot(theta,cos(th).^3,theta,(3*cos(th)+cos(3*th))/4,'.')%画线和点

syms x %定义符号变量 y=1/4*cos(3*x)+3/4*cos(x) %三角函数的展开式 expand(y) %展开三角函数 y=cos(x)^3 %三角函数 simple(y) %展开三角函数

M1图 练习：验证

31sin(3sinsin3)4 2

[问题1.2] 曲线族的画法 根据麦克斯韦速率分布率律，求最概然速率？氧气分子在300K到600K温度区间(温度间隔为100K)，速率分布曲线有什么异同？最概然速率是多少？氢气、氦气、氖气、氮气、氧气和氟气分子的分子量分别为2、4、20、28、32和38，这些气体分子在300K时的速率分布曲线有什么异同？最概然速率是多少？ [解析]麦克斯韦速率分布函数为

23/22()4π()exp()2π2mmvfvvkTkT (1.2.1)

其中，k = 1.38×10-23J/K是玻尔兹兹常数，m是分子质量，v是分子速率。 当v = 0时，f(v) = 0；当v→∞时，f(v)→0。由于f(v)不小于零，因此f(v)必有极大值。令df(v)/dv = 0，即

模糊PID控制器设计和仿真步骤：各变量隶属度函数的确定第一步：各变量隶属度函数的确定1、 用于PID 参数调整的模糊控制器采用二输入三输出的形式。

该控制器是以误差E 和误差变化率EC 作为输入，PID 控制器的三个参数P、I、D 的修正△KP、△KI、△KD 作为输出，如图1；2、 取输入E 和EC 和输出△KP、 △KI、△KD 模糊子集为{NB,NM,NS,ZO,PS,PM,PB}，其论域为[-6,6],量化等级为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}；如图23、 在模糊逻辑工具箱的隶属度函数编辑器中，选择输入量E，EC 隶属函数为高斯型（gaussmf）,输出△KP、△KI、△KD 的隶属函数为三角形（trimf），如图2和3。

图1图2图3第二步：根据图4规则建立模糊规则表，如图5：图4图5第三步：设置参数：与方式与方式 (And method)为min ；或方式（Or method)为max ；推理推理 (Implication)为min ；合成；合成 (Aggregation)为max ；去模糊（Defuzzification)为重心平均法（centroid ）。

）。

第四步：保存该FIS 文件，取名为FuzzyPID.fis第五步：在MA MATLABTLAB 的M 文件编辑器里建立一个名为FuzzyPID.m 的文件，其内容为：martrix=readfis （‘Fuzzypid.fis ’），并运行。

，并运行。

第六步：打开SIMULINK ，新建一个Model ，选择一个Subsystem ，在其中编辑模块，如图6，并设置模糊化因子KE=KEC=0.01，解模糊因子KP=0.5，KI=KD=0.01，并在Fuzzy Logic Controller 模块的Parameters 中输入readfis('FuzzyPID.fis')：图6第七步：返回到新建的Model 中，按照如图7所示建立模糊PID 控制器，其中，控制器，其中，PID PID 初始值为KP0=20，KI0=1.35，KD0=3.7，传递函数为：图7第八步：保存为FuzzyPID.mdl 并运行。

三角分布matlab -回复三角分布是概率论中常见的概率分布之一，它的形状呈现出一个对称的三角形。

在统计学和金融学等领域经常被用来描述随机变量的概率分布。

在本文中，我们将使用MATLAB来分析和绘制三角分布，并探讨其特性和应用。

首先，让我们来回顾一下三角分布的定义和特性。

三角分布，也称为连续型谐波分布，是一种概率密度函数在一个区间上连续变化的分布。

它具有三个参数：a、b和c。

其中a和b是定义分布区间的两个端点，而c是位于a和b之间的三角分布的峰值。

三角分布的概率密度函数可以用以下公式表示：f(x) = 2(x-a)/(b-a)(c-a)，当a<=x<=c,f(x) = 2(b-x)/(b-a)(b-c)，当c<x<=b,f(x) =0，当x<a或x>b.在MATLAB中，我们可以使用`tripdf`函数来计算给定三角分布参数的概率密度函数值。

这个函数的输入参数是一个概率密度函数的x值和三个参数a、b和c。

例如，如果我们想计算x=0.5处的概率密度函数值，可以使用以下代码：MATLABa = 0;b = 1;c = 0.5;x = 0.5;pdf_value = tripdf(x,a,b,c);接下来，我们可以使用MATLAB的`trirnd`函数生成服从三角分布的随机变量。

这个函数的输入参数是随机变量的个数和三个参数a、b和c。

例如，如果我们想生成1000个服从三角分布的随机变量，可以使用以下代码：MATLABa = 0;b = 1;c = 0.5;n = 1000;random_variables = trirnd(a,b,c,n);然后，我们可以使用MATLAB的`histogram`函数来绘制服从三角分布的随机变量的直方图。

直方图是一种用来表示数据分布的图表，它将数据划分为多个间隔，并在每个间隔内绘制相应数据的条形。

以下是绘制三角分布直方图的示例代码：MATLABa = 0;b = 1;c = 0.5;n = 1000;random_variables = trirnd(a,b,c,n);figure;histogram(random_variables, 'Normalization', 'probability'); xlabel('Random variable');ylabel('Probability');title('Triangular Distribution Histogram');在这个示例中，我们指定了`'Normalization'`参数为`'probability'`，以便将数据的频率归一化为概率。

三角分布matlab -回复什么是三角分布？三角分布是统计学中常用的一种连续概率分布模型，它得名于其概率密度函数呈三角形状。

三角分布通常用来描述一个实验结果在一定范围内的可能性分布。

三角分布的概率密度函数形式如下：f(x;a,b,c) = (2*(x-a))/((b-a)*(c-a))，当a <= x < c= (2*(b-x))/((b-a)*(b-c))，当c <= x <= b= 0，其他情况其中，a、b、c分别代表分布的最小值、最大值和众数。

三角分布的特点之一是众数恰好位于最小值和最大值之间。

这使得三角分布在实际应用中得到了广泛的使用。

接下来，我们将一步一步介绍如何在MATLAB中实现三角分布的模拟和分析。

首先，我们需要指定分布的参数：最小值a、最大值b和众数c。

以a=0，b=10，c=5为例。

matlaba = 0;b = 10;c = 5;接下来，我们可以使用"triang"函数来生成三角分布的样本数据。

使用该函数需要指定样本数量和参数a、b、c。

matlabsampleSize = 1000;data = triang(sampleSize, c, (b-a)/(c-a), a);在此示例中，我们生成了1000个三角分布样本。

接下来，我们可以使用直方图可视化生成的数据，并与理论概率密度函数进行比较，以验证我们的模拟结果。

matlabhistogram(data, 'Normalization', 'pdf', 'EdgeColor', 'w')hold onx = a:0.01:b;pdf = zeros(size(x));pdf(x >= a & x < c) = (2*(x(x >= a & x < c)-a))/((b-a)*(c-a));pdf(x >= c & x <= b) = (2*(b-x(x >= c & x <= b)))/((b-a)*(b-c));plot(x, pdf, 'r', 'LineWidth', 2)ylim([0,max(pdf)+0.1])legend('实际数据', '理论概率密度函数')title('三角分布的模拟结果与理论概率密度函数比较')hold off运行上述代码，我们将得到一个包含实际数据直方图和理论概率密度函数的图表。