动车组运行能耗影响因素的量化分析 刘儒奇

轨道列车空气动力学性能研究与分析轨道列车作为现代交通工具的重要组成部分，其空气动力学性能的研究与分析对于提高列车的运行效率、安全性和舒适性具有重要意义。

本文将对轨道列车的空气动力学性能进行深入探讨，包括气动力学特性、阻力与风噪声的产生机理和控制手段等方面。

首先，我们来了解轨道列车的气动力学特性。

轨道列车在高速运行的过程中，会遇到气动力学效应的限制和影响。

气动力学主要涉及列车与空气之间的相互作用，主要表现为气动阻力、气动升力、气动不稳定性等。

气动阻力是指随着列车速度增加，由于列车与空气之间的摩擦而产生的阻碍某物体运动的力。

而气动升力是指在一定的高度和速度下，由于空气的上升和下降运动产生的力。

此外，气动不稳定性会在列车的高速行驶中产生剧烈震动，影响乘客的乘车舒适性和列车的行驶稳定性。

针对轨道列车的气动力学特性，研究人员通过大量的实验和仿真计算，不断优化列车的外形设计和结构，以降低气动阻力、提高运行效率。

一种常见的设计方法是利用流体力学分析软件对列车外形进行优化。

通过改变列车的前后端形状、减小车身侧面投影面积、改善底部流场等手段，可以有效降低气动阻力，提高列车的能效。

此外，列车机车头部的设计也起到了重要的作用。

采用气动优化的机车头部设计减小了空气流动的阻力，进一步降低了气动阻力。

除了气动力学特性，轨道列车的空气动力学性能研究还需要关注阻力与风噪声的产生机理和控制手段。

阻力是列车运行过程中造成能量损耗的主要因素，其中包括气动阻力、摩擦阻力和辐射阻力等。

减小阻力可以降低列车运行过程中的能量消耗，提高能效。

为了降低气动阻力，研究人员采用了一系列的措施，如采用小阻力车体设计、减小车体侧面投影面积、改变车体几何形状等。

风噪声是轨道列车运行过程中一个重要的噪声源，对乘客的舒适性和周围环境的影响较大。

风噪声的产生主要来自列车与周围空气流动之间的相互作用。

研究人员通过在列车车体上装置风噪声控制装置、调整车厢窗户的设计等手段，来减小风噪声对乘客的干扰。

第20卷第6期2020年12月交通运输系统工程与信息Journal of Transportation Systems Engineering and Information TechnologyV ol.20No.6December 2020文章编号：1009-6744(2020)06-0170-08中图分类号：U268.6文献标志码：ADOI:10.16097/ki.1009-6744.2020.06.022城市轨道交通列车追踪间隔与牵引能耗优化高豪，郭进*，张亚东(西南交通大学信息科学与技术学院，成都611756)摘要：针对城市轨道交通高峰小时列车密集追踪运行的特点，将降低列车牵引能耗和提升线路通过能力同时作为优化目标，研究列车运行操纵优化问题.给出移动闭塞条件下列车牵引能耗和最小追踪间隔的计算方式，考虑列车安全、正点运行约束，构建双目标优化模型.结合ε-约束法，提出一种基于动态规划的搜索算法求解模型.以亦庄线为优化算例，求解得到一组列车最优操纵Pareto 解，体现两优化目标之间的均衡关系：列车进站过程采用两次制动操纵策略可有效压缩最小追踪间隔，为弥补两次制动过程额外消耗的运行时间，列车需付出更多的牵引能耗提升进站以前的运行速度以满足正点运行约束.关键词：铁路运输；列车最优操纵；动态规划；列车；最小追踪间隔；节能Optimization of Train Headway and Traction EnergyConsumption in UrbanRail TransitGAO Hao,GUO Jin,ZHANG Ya-dong(School of Information Science and Technology,Southwest Jiaotong University,Chengdu 611756,China)Abstract:Focusing on the characteristics of dense train tracking operation during the peak hour in urban rail transit,this paper takes both reducing traction energy consumption and improving line capacity as objectives in the train driving strategy optimization.The calculation method of traction energy consumption and minimum headway is given under the moving block system.Considering the constraint of safe running and punctual arriving,the two-objective optimization model is constructed.A dynamic programming based approach combined with ε-constraint method is proposed to solve the model.A case study of Yizhuang urban rail line was executed and a set of Pareto solutions were achieved which reflecting the trade-off between those two objectives.The results showed that the multi-step braking strategy during the phase of entering a station can compress the minimum headway effectively.To reduce the increased running time because of the multi-step braking strategy,trains need to improve their velocity before the phase of entering a station to satisfy the constraint of punctual arriving,which consumes more traction energy.Keywords:railway transportation;optimum driving strategy;dynamic programming;train;minimum headway;energy saving0引言随着城市轨道交通大量新建线路投入网络化运营，我国轨道交通客运量增长明显，北京、上海两市日均客运量均已超过1000万人.为满足日益增长的客运需求，以基于通信的列车运行控制(Communication Based Train Control,CBTC)为代表的移动闭塞系统取代了传统固定闭塞系统，并得到广泛应用.利用高精度列车定位、双向大容量车地无线通信等新兴技术，CBTC 系统可以进一步提升高峰小时线路通过能力.据资料统计，2019年收稿日期：2020-07-15修回日期：2020-09-16录用日期：2020-09-17基金项目：国家自然科学基金青年科学基金/Young Scientists Fund of the National Natural Science Foundation of China(61703349).作者简介：高豪(1989-)，男，江苏苏州人，博士生.*通信作者：*******************.cn第20卷第6期城市轨道交通列车追踪间隔与牵引能耗优化全国城市轨道交通高峰小时最小发车间隔平均为290s，进入120s以内的线路共12条.同线路能力一样，列车牵引能耗是制约城市轨道交通可持续发展的关键因素.面向高峰小时多列车密集追踪的运行场景，能耗问题尤为突出.在保证列车安全、正点运行前提下，通过调整列车操纵策略，进一步压缩行车间隔并减少牵引能耗，可有效提升城市轨道交通服务水平和经济效益.针对多列车运行操纵优化问题，国内外学者开展了广泛讨论.Wang[1]面向固定闭塞和移动闭塞系统下的列车追踪运行场景，以最小追踪间隔为约束条件，研究列车运行受扰后的多列车节能操纵优化问题.Ye[2]考虑快慢车越行场景下的列车安全追踪及正点运行约束，通过构建多阶段优化控制模型求解多列车节能操纵最优策略.进一步地，柏赟[3]考虑追踪间隔要求和再生制动能利用，研究以列车净能耗最少为目标的快慢车线路列车协同操纵优化问题.Wang[4]在确保列车运行满足最小追踪间隔的前提下，通过调整各列车的站间运行时间来最大化多列车追踪优化的节能效果.以上文献将最小追踪间隔作为约束条件，研究不同场景下多列车节能驾驶优化问题.优化后的列车运行间隔发生改变，但线路能力并未得到本质提升.Takeuchi[5]将最小追踪间隔作为衡量线路能力的性能指标，分析列车运行速度对最小追踪间隔的影响.陈荣武[6]通过调整车站限速区域及限速值压缩了近6.3%的列车最小追踪间隔.Nakamura[7]指出列车采用多级制动的进站操纵策略可有效压缩最小追踪间隔，并利用遗传算法优化列车进站操纵策略.上述文献将最小追踪间隔作为优化目标，通过调整列车操纵策略提升线路通过能力，却忽略了操纵策略改变带来的牵引能耗增加问题.针对高峰小时地铁列车密集追踪运行的特点，本文同时将降低列车牵引能耗和缩短最小追踪间隔作为优化目标，通过优化列车操纵策略实现列车节能驾驶并提升线路通过能力.首先给出移动闭塞条件下列车牵引能耗和最小追踪间隔的计算方式，在此基础上考虑列车正点运行和线路限速约束，构建双目标优化模型；引入ε-约束法将模型转为单目标形式，并利用动态规划方法作进一步求解.1列车运行性能指标1.1列车牵引能耗对运行过程中的列车进行受力分析，构建基于单质点的列车运动学计算模型，即d v()xd x=u()x-r()xM⋅()1+α⋅v()x(1)r()x=r b()x+r1()x(2) r b()x=M⋅[]a+b⋅v()x+c⋅v2()x(3)r1()x=r g()x+r c()x+r t()x(4)式中：M为列车质量；x为列车位置；v()x为列车速度；α为回转系数；u()x为列车牵引制动力；r()x为列车运行阻力，包括基本阻力r b()x和和附加阻力r1()x；r b()x由戴维斯方程来表示，其系数a、b及c根据列车型号而定；r1()x包括坡道附加阻力r g()x、曲线附加阻力r c()x和隧道附加阻力r t()x.列车以操纵策略U={u()x|u min()x≤u()x≤}u max()x,x∈[0,X]在线路上追踪运行，其中，u max()x 和u min()x分别为列车保证乘客安全、舒适条件下的最大牵引力和最大制动力，X为列车站间运行距离.列车执行U后的牵引能耗E()U和运行时间T()U为E()U=∫0X max[]0,u()x⋅d x(5)T()U=∫0X1v()x⋅d x(6) 1.2最小追踪间隔线路通过能力体现为列车追踪运行过程中最小追踪间隔的倒数[5]，取决于列车在线路最受限制点处的最小安全追踪距离及通过该距离的运行速度[6].移动闭塞系统中，相邻列车的间隔距离必须始终大于最小安全追踪距离.现有CBTC系统均采用不考虑先行列车速度的“硬撞墙”模型来计算最小安全追踪距离，即S min()x a=L react()x a+L eb()x a+L sm+L train(7)L react()x a=T react⋅v()x a(8)L eb()x a=v2()x a2a eb(9)式中：S min()x a为列车在位置x a处的最小安全追踪171交通运输系统工程与信息2020年12月距离；L react()x a为列车在反应时间T react内的走行距离；L eb()x a为列车紧急制动距离；a eb为紧急制动率；L sm为安全余量；L train为列车车长.为简化计算，假设T react、a eb、L sm和L train为固定值.根据列车在通过最小安全追踪距离期间是否停靠站台，将最小追踪间隔的计算分为区间和车站两种模式.图1为区间最小追踪间隔示意，相邻两车以最小安全追踪距离为间隔分别运行至x a和x a+S min()x a处，其中，x a+S min()x a<x S，x S为站台位置.相邻列车沿图中实线所示的运行轨迹连续经过x a的最小时间间隔H min()x a为H min()x a=∫x a x a+S min()x a1v()x⋅d x(10)图1区间最小追踪间隔Fig.1Minimum headway of interstation地铁车站一般不设配线，列车到达车站后需在正线上完成停站作业，且同一时间只允许1列列车进行停站作业.车站最小追踪间隔的计算不考虑存在多配线条件下的列车到达、到通、出发、发通等间隔，如图2所示.相邻两车分别运行至x a和x a+S min()x a处，其中，x a+S min()x a≥x S，列车通过S min()x a期间需经历减速进站、停车和加速出站过程.因此，相邻列车连续经过x a的最小时间间隔H min()x a为H min()x a=T in()x a+T dwell+T out()x a(11)T in()x a=∫x a x S1v()x⋅d x(12)T out()x a=∫x S x a+S min()x a1v()x⋅d x(13)式中：T in()x a、T out()x a分别为列车进站、出站运行时间；T dwell为停站时间.图2车站区域最小追踪间隔Fig.2Minimum headway of station area对于任意位置x a，H min()x a取决于S min()x a和通过S min()x a的列车运行速度.由式(7)~式(9)可知，S min()x a取决于v()x a和x a以前的列车操纵策略有关，通过S min()x a的列车运行速度和x a以后的列车操纵策略有关.因此，操纵策略决定了列车追踪运行过程中可实现的最小追踪间隔.全线列车执行相同U在线路上追踪运行，可实现的最小追踪间隔H()U为列车连续通过最受限制点的最小时间间隔，即H()U=maxx∈[]0,XH min()x(14) 2列车运行性能优化2.1问题描述列车站间运行时间由运行图预先给定，理论上存在无数种操纵策略保证列车安全、正点运行.面向高峰小时地铁列车密集追踪的运行场景，将其中可实现追踪间隔最小且牵引能耗最小的操纵策略作为最优操纵策略.Takeuchi[5]对最小追踪间隔计算进行了灵敏度分析，结果表明，增大列车牵引/制动加速度可有效压缩最小追踪间隔.Liu[8]利用极大值原理推导出连续控制条件下的列车节能驾驶最优控制应包括最大牵引、巡航、惰行和最大制动.上述文献表明，列车最大牵引和最大制动是实现节能驾驶和高效追踪的必要控制条件.因此，本文选择最大牵引、巡航、惰行和最大制动组成列车最优操纵策略的4种控制变量，目标问题转化为寻找这些控制变量之间的组合顺序及其对应的转换点.本文假设列车装备自动驾驶系统，能够在线172第20卷第6期城市轨道交通列车追踪间隔与牵引能耗优化路任意位置实现巡航控制.因现有地铁系统并未完全装备再生制动设备，为不失一般性，再生制动能不在本文考虑范围内.2.2优化模型将U 作为决策变量，将min E ()U 和min H ()U 作为优化目标，设置列车安全、正点运行约束条件，构建双目标优化模型为ìíîïïïïmin E ()U min H ()U s.t.T ()U =T setv ()x <V limit ()x ,x ∈[0,X ](15)式中：V limit ()x 为线路限速条件；T set 为指定站间运行时间.2.3模型求解构建双目标优化模型旨在降低列车牵引能耗的同时压缩列车最小追踪间隔，期望得到一组准确的Pareto 最优解以体现两目标之间的均衡，采用基于动态规划方法的精确算法求解式(15).由于最小追踪间隔指标在动态规划逐段递推过程中并不严格单调，不具备动态规划方法所需的“无后效性”，引入ε-约束法将其转化为约束条件，并将式(15)转化为单目标优化模型，并以Δε为间隔由小到大调整ε参数值后多次利用动态规划方法进行求解.ìíîïïïïmin E ()U s.t .H ()U ≤εT ()U =T setv ()x <V limit ()x ,x ∈[0,X ](16)对式(16)的状态空间进行离散，将列车运行过程在空间域上划分K 个阶段，保证各阶段线路条件不变且各阶段长度不大于Δx .在k 阶段开始位置x k 处，按间隔Δv 划分k 阶段的开始状态集{}s k,i|sk,i=()x k ,i ⋅Δv ,0≤i ⋅Δv ≤Vˉ()x ,i ∈Ν，其中，Vˉ()x 为列车在最速策略下运行至x 处的速度.如图3所示，实线为列车最速运行轨迹，圆点为各阶段开始状态，亦为上一阶段的结束状态.列车运行过程的起点和终点分别记为s 1,0和s K +1,0.动态规划始终运行在基于上述离散划分规则的状态空间内，其优化结果一定能够满足安全运行约束v ()x <V limit ()x.图3模型阶段状态划分示意图Fig.3Stages and vertices of optimization model列车在k 阶段运行时固定采用最大牵引、巡航、惰行和最大制动中的一种工况，将其简记为u k ，列车在相邻阶段的最优控制工况切换还应满足图4所示的接续条件.图4列车控制接续约束Fig.4Train regime switching constraint列车在k 阶段s k,i 处施加u k 后运行至k +1阶段()x k +1,v ′处，()x k +1,v ′有可能不属于已划分的开始状态集，需要对其进行近似处理并修正至s k +1,j 处，其中j =round ()v ′Δv ，将上述状态转移过程简写为s k +1,j =F ()s k,i ,u k (17)列车在s k,i 处施加u k 阶段牵引能耗e ()s k,i ,u k 和运行时间t ()s k,i ,u k 计算为e ()s k,i ,u k =∫x kx k +1max []0,u ()x ⋅d x(18)t ()s k,i ,u k =∫xkx k +11v ()x ⋅d x(19)为获取式(16)在ε参数下的最优操纵策略U *ε，采用后向动态规划的求解方式，从s K +1,0开始逐段向前推进寻找列车在各阶段的最优控制决策173交通运输系统工程与信息2020年12月直至s 1,0.对于阶段k ，将列车从s k,i 运行至s K +1,0的操纵子策略记为U ()s k,i ，其对应的牵引能耗和运行时间分别为E []U () s k,i 和T []U ()s k,i ，下面建立评价U ()s k,i 最优性的过程指标函数.将列车从s 1,0运行至s k,i 处的操纵子策略记为U ()s k,i ，其对应的牵引能耗及运行时间分别记为E []U () s k,i 和T []U ()s k,i .因此，式(16)的优化目标min E ()U 可拆解为min E []U () s k,i 和min E []U ()s k,i .在后向动态规划求解过程中，E []U ()s k,i 无法直接求解得到.列车牵引能耗与运行时间在节能操纵条件下呈反比关系，故min E []U ()s k,i 等效于max T []U () s k,i .因T []U () s k,i +T []U ()s k,i =T set ，故min E []U () s k,i 等效于min T []U ()s k,i .因此，评价U ()s k,i 最优性的过程指标函数为E []U *() s k,i =min u k{}e ()s k,i ,u k +E {}U *éëùû F ()s k,i ,u k (20)T []U *() s k,i =min u k{}t ()s k,i ,u k +T {}U *éëùûF ()s k,i ,u k (21)U ()s k,i 对应的最小追踪间隔H []U () s k,i 应满足ε约束，即H []U ()s k,i ≤ε(22)U ()s k,i 应满足准点运行约束为T min []U () s k,i ≤T []U () s k,i ≤T max []U () s k,i (23)式中：T min []U () s k,i 、T max []U ()s k,i 分别为列车从s k,i 到s K +1,0的最短、最长运行时间.特别的，列车在s 1,0和s K +1,0的准点约束条件为T []U () s 1,0=T min []U () s 1,0=T max []U ()s 1,0=T set (24)T []U () s K +1,0=T min []U () s K +1,0=T max []U ()s K +1,0=0(25)T min []U () s k,i 和T max []U ()s k,i 的计算方法如图5所示.点划线为列车从s k,i 到s K +1,0的最速运行轨迹，其对应的运行时间为T min []U ()s k,i .虚线为列车从s 1,0到s k,i 的最速运行轨迹，其对应的运行时间为T min []U () s k,i ，则T max []U () s k,i =T set -T min []U () s k,i .图5T min []U () s k,i 和T max []U ()s k,i 计算原理Fig.5Calculation principle of T min []U () s k,i and T max []U ()s k,i由于存在2个冲突的过程指标，即式(20)和式(21)，列车从s k,i 处运行至s K +1,0的最优操纵子策略应为一组Pareto 解，记为{}U *w () s k,i ，其中，U *w ()s k,i 为s k,i 处的第w 个最优子策略.动态规划方法从s K +1,0开始逐段向前推进，求解各阶段各状态点的Pareto 最优子操纵策略集直至起点s 1,0.由于准点运行式(24)的限制，s 1,0处的最优操纵策略有且只有一个，为式(16)在ε参数下的最优解，即U *ε=U *1()s 1，0.式(16)的具体求解步骤描述如下：Step 1读入线路数据及列车参数并计算V ˉ()x ，设定模型参数Δx 、Δv 和ε，划分离散状态集合{}s k,i ，设定边界条件E []U *1()s K +1,0=0，T []U *1()s K +1,0=0，令k =K ，完成模型求解初始化.Step 2对于k 阶段所有的s k,i ，遍历4种最优控制工况u k ，获取k +1阶段F ()s k,i ,u k 处的最优子策略集{}U *w éëùûF ()s k,i ,u k .在满足式(22)和式(23)的条件下，将u k 加入{}U *w éëùûF ()s k,i ,u k 生成s k,i 处的可行子策略集{}U ()s k,i .Step 3根据过程指标式(20)和式(21)，对{}U ()s k,i 进行Pareto 占优操作，得到s k,i 的Pareto 最优子策略集{}U *w () s k,i .若k ≠1，则令k =k -1，跳转174第20卷第6期城市轨道交通列车追踪间隔与牵引能耗优化至Step 2；若k =1，输出式(16)的最优解U *ε.3算例分析基于C++开发优化程序，以北京地铁亦庄线为算例，选择文献[2]中线路数据和车辆参数，在此基础上进一步设定，a eb =-1.0m/s 2、L sm =30m 、L train =90m 、T react =0.5s 和T dwell =30s .根据“计算时间—优化效益可接受原则”设置模型参数如下：Δx =10m 、Δv =1km/h 和Δε=0.1，模型参数决定模型的求解精度和求解效率，间隔越小，模型求解精度越高且求解效率越低.以第7区间“万源街—荣京东”为例：首先，令ε=0，不断迭代计算ε=ε+Δε后的式(16)直至获取第1个有效解，该解即为能够实现理论最小追踪间隔的操纵策略U *headway ，令εmin =H ()U *headway ；其次，将ε设置为一个较大的正值后对式(16)进行求解，所得解即为只考虑节能目标的最优操纵策略U *energy ，令εmax =H ()U *energy ；最后，以Δε为间隔在[]εmin ,εmax 内由小到大调整ε参数值，多次求解式(16)，获得一组Pareto 最优解，如图6所示.图6列车最优操纵Pareto 解Fig.6Pareto solution of optimum driving strategy选取ε=70条件下的最优操纵策略U *70，对比U*energy、U *70和U*headway这3种策略下的v ()x 及其对应的H min ()x ，如图7所示.U*energy条件下列车从起点开始最大牵引至A 1，然后以惰行和巡航的组合方式运行至B 1，最后施加最大制动至终点；列车从C 1开始进入车站追踪模式，H min ()x 发生跃变；U *energy的性能指标分别为E ()U*energy=9.8kW ⋅h ，H ()U *energy =77.2s .U *70条件下列车最大牵引至A 2，惰行并巡航至B -2后开始施加第1次最大制动至C 2，然后惰行至B 2后施加第2次最大制动至终点；由于提前制动，列车在C 2处才进入车站追踪模式，其性能指标为E ()U *70=10.7kW∙h，H ()U *70=70.0s .同U *70一样，U *headway 在B -3处提前制动，采用两次制动的进站模式分别经过了A 3-B -3-C 3-B 3点，列车自C 3开始进入车站追踪模式，性能指标为E ()U *headway =13.0kW∙h ，H ()U *headway =67.1s .相较于U *energy，U *70和U *headway 在进站过程中执行两次制动策略，压缩了列车最小追踪间隔，为弥补两次制动进站过程中额外消耗的运行时间，U *70和U *headway 提升了进站以前的运行速度，额外增加了牵引能耗.图7U *energy 、U *70和U *headway 的列车运行轨迹及最小时间间隔Fig.7Train trajectory and minimum time separation ofU *energy ,U *70and U *headway列车进站操纵策略变化本质上影响的是车站追踪模式下T in ()x 和T out ()x ，从而改变H min ()x .U *energy 、U *70和U *headway 策略下的T in ()x 和T out ()x 随v ()x 的变化趋势如图8所示.上述操纵策略在车站追踪模式下的运行过程均包含1次惰行和1次最大制动.随着列车向终点运行，3种操纵策略对应的175交通运输系统工程与信息2020年12月T out()x从0开始递增并分别在列车进站的制动初始点B1、B2和B3处达到极大值，T in()x呈递减趋势并在终点处减为0.由于不同操纵策略下T in()x和T out()x存在差异，U*energy条件下的H min()x呈先增后减趋势，在B1处达到极大值；U*70和U*headway条件下，H min()x分别在C2和C3处达到极大值.图8车站追踪模式下列车运行轨迹及相关时间间隔Fig.8Train trajectory and related time separation under station tracking mode 计算全线13个站间的最优操纵Pareto解，选取各站间的U*headway与U*energy进行比较，如表1所示.与U*energy相比，列车在U*headway下的全线通行能力提升了17.0%，牵引总能耗增加了19.3%.各站间的U*headway均采用两次制动的进站策略且第2次制动的进站初速度都为23.0km/h，各站间U*headway的最小追踪间隔均达到约67s的极小值.各站间的U*energy都采用一次制动进站策略，其最小追踪间隔的大小与列车进站制动初速度正相关.不失一般性，图9以第2区间和第4区间为例，描绘U*headway和U*energy策略下v(x)和H min(x)来进一步印证上述结论.表1列车操纵策略优化结果Table1Optimaziton results of drivingstrategy176第20卷第6期城市轨道交通列车追踪间隔与牵引能耗优化图9U *headway 和U *energy 的列车运行轨迹及最小时间间隔Fig.9Train trajectory and minimu time separation of U *headway 和U *energy4结论列车操纵策略决定了列车在线路上运行的牵引能耗和可实现的最小追踪间隔.列车采用两次制动的进站策略可以有效压缩最小追踪间隔，但需要消耗更多的牵引能耗.列车最小追踪间隔和进站制动初速度正相关且存在极小值.相较于只考虑节能目标的最优操纵策略，追踪间隔压缩后的最优操纵策略最多可提升17.0%的线路通过能力，同时也增加了19.3%的牵引能耗.运营商可权衡地铁高峰小时服务水平和运营成本的实际需求，利用本文方法获得列车追踪运行最优操纵策略，具有一定实际意义.随着再生制动设备在城市轨道交通系统的应用普及，考虑再生制动能利用的列车运行能耗和追踪间隔多目标优化问题有待进一步讨论.参考文献：[1]WANG Y,DE SCHUTTER B,VAN DEN BOOM T J J,et al.Optimal trajectory planning for trains under fixed and moving signaling systems using mixed integer linear programming[J].Control Engineering Practice,2014,22:44-56.[2]YE H,LIU R.A multiphase optimal control method for multi-train control and scheduling on railway lines[J].Transportation Research Part B:Methodological,2016,93:377-393.[3]柏赟,于昭,贾文峥,等.考虑追踪安全的地铁快慢车协同操纵节能优化[J].交通运输系统工程与信息,2019,19(3):126-133.[BAI Y,YU Z,JIA W Z,et al.Cooperative control of express/local metro trains for energy saving considering the safe headway[J].Journal of Transportation Systems Engineering and Information Technology,2019,19(3):126-133.][4]WANG P,GOVERDE R M P.Multi-train trajectory optimization for energy-efficient timetabling[J].European Journal of Operational Research,2019,272(2):621-635.[5]TAKEUCHI H,GOODMAN C J,SONE S.Moving block signalling dynamics:Performance measures and re-starting queued electric trains[J].IEE Proceedings-electric Power Applications,2003,150(4):483-492.[6]陈荣武,诸昌钤,刘莉.CBTC 系统列车追踪间隔计算及优化[J].西南交通大学学报,2011,46(4):579-585.[CHEN R W,ZHU C Q,LIU L.Calculation and optimization of train headway in CBTC system[J].Journal of Southwest Jiaotong University,2011,46(4):579-585.]下转第204页177交通运输系统工程与信息2020年12月Influences of traffic flow characteristics on accidentseverity on secondary roads[J].China Journal ofHighway and Transport,2020,33(2):135-145.] [9]吴琴,施欣,陶学宗.海事事故严重性影响因素及影响程度识别[J].交通运输系统工程与信息,2019,19(1):189-195.[WU Q,SHI X,TAO X Z.Identifying the factors and their impact levels on severity of maritime traffic accidents[J].Journal of Transportation Systems Engineering and Information Technology,2019,19(1): 189-195.]上接第177页[7]NAKAMURA H.Analysis of minimum train headway ona moving block system by genetic algorithm[J].WITTransactions on the Built Environment,1998,37:1013-1022.[8]LIU R R,GOLOVITCHER I M.Energy-efficientoperation of rail vehicles[J].Transportation ResearchPart A:Policy and Practice,2003,37(10):917-932.上接第183页[2]李军,邓红平.基于公交IC卡数据的乘客出行分类研究[J].重庆交通大学学报(自然科学版),2016,35(6):109-114.[LI J,DENG H P.Classification ofpassenger's travel behavior based on IC card data[J].Journal of Chongqing Jiaotong University(NaturalSciences),2016,35(6):109-114.][3]何兆成,余畅,许敏行.考虑出行模式和周期性的公交出行特征分析[J].交通运输系统工程与信息,2016,16(6):135-141.[HE Z C,YU C,XU M X.Analyzingmethods of residents'travel characteristics consideringtravel patterns and periodicity[J].Journal ofTransportation Systems Engineering and InformationTechnology,2016,16(6):135-141.][4]GOULET-LANGLOIS G,KOUTSOPOULOS H N,ZHAO Z,et al.Measuring regularity of individual travelpatterns[J].IEEE Transactions on IntelligentTransportation Systems,2017,19(5):1583-1592. [5]翁剑成,王昌,王月玥,等.基于个体出行数据的公共交通出行链提取方法[J].交通运输系统工程与信息,2017,17(3):67-73.[WENG J C,WANG C,WANG YY,et al.Extraction method of public transit trip chainsbased on the individual riders'data[J].Journal ofTransportation Systems Engineering and InformationTechnology,2017,17(3):67-73.][6]ZOU Q,YAO X,ZHAO P,et al.Detecting home locationand trip purposes for cardholders by mining smart cardtransaction data in Beijing subway[J].Transportation,2018,45(3):919-944.[7]PEI J,HAN J,MORTAZAVI-ASL B,et al.Miningsequential patterns by pattern-growth:The prefixspanapproach[J].IEEE Transactions on Knowledge and DataEngineering,2004,16(11):1424-1440.204。

考虑车轮谐波磨耗的动车组车轴疲劳寿命随着高速列车运行速度的不断提高,轮轨间各种随机激励引起的轮轨振动加剧。

为保证列车安全平稳运行,作为列车主要承载部件的车轴,它的性能良好与否直接关系到列车的行车安全。

因此,国内外学者关于车轴疲劳寿命做了大量的研究工作,并取得了一定的成果。

田合强等［1］以中国某型高速动车组车轴为研究对象,分别基于日本JIS E 4501 标准和欧洲EN 13104 标准对车轴强度进行计算,并与有限元仿真计算结果进行对比分析。

陆超等［2］分别基于欧洲EN 13104 标准和有限元法对出口哈萨克斯坦的动车组动力车轴进行应力计算,并校核各截面处的疲劳强度。

随着对车轴强度研究的不断深入,国内外学者［3-5］认为车轴的疲劳强度不能按无限寿命设计和计算,因为对于车轴这类高周疲劳构件,其疲劳强度会随着应力循环次数的增加而降低,计算应力时应考虑各种随机激励的影响。

于是,国内外学者开始借助于有限元软件和动力学软件,并结合有限寿命理论进行车轴疲劳寿命的估算,其研究成果具有很高的工程应用价值。

如赵利华等［6］运用SIMPACK 软件建立多刚体车辆动力学模型,结合ANSYS 软件计算车轴危险点的应力时间历程,基于线性累积损伤理论计算车轴的疲劳寿命。

曹建国等［7］运用SIMPACK 软件建立动车组整车动力学模型,并计算车轴的载荷时间历程,结合ANSYS 和FE-SAFE 软件计算车轴的疲劳寿命。

POKORNÝ P 等［8］对实测载荷时间历程下车轴的残余疲劳寿命进行了研究。

随着高速列车车轮多边形问题的日益凸显,尤其是德国ICE高速列车脱轨,研究表明事故的原因是由于多边形橡胶弹性车轮的接触载荷过大、导致车轮轮辋疲劳断裂造成的［9］,引起了众学者的高度关注。

之后,对车轮多边形最主要表现形式的车轮谐波磨耗的研究众多,但大部分皆为车辆—轨道耦合动力系统下的振动特性研究,鲜有车轮谐波磨耗下车轴疲劳寿命的研究。

基于RAMS的动车组牵引供能系统可靠性分析摘要：高速动车组列车作为当下最流行的出行交通工具，给人们的生活工作带来了许多便利。

随着科学技术的发展，越来越多的高新技术集中与动车组列车上，如自动诊断、信息化控制等，为动车组车辆运行安全帮助。

利用动车组实时故障数据，完成动车组列车的RAMS分析研究，能够更加系统的对整车情况进行系统的认知。

本文基于RAMS研究现状分析动车组牵引供能系统的可靠性。

关键词：动车组；RAMS；牵引供能系统1.研究背景随着我国经济的快速发展，轨道行业也在突飞猛进。

截止到2018年，我国拥有铁路客车约73000辆，其中动车组列车约2935组23480辆。

动车组列车运行速度快，运行里程长，运行环境更为恶劣，所以保证动车组列车的运行安全至关重要。

动车组列车是当今科学技术的代表，集机械、电气、网络、牵引、制动、通信等高新技术于一体，装备设计各类系统及复杂的设备，各专业要求严格系统十分复杂，对于可靠性的管理成为确保车辆安全运行的关键。

本文针对动车组牵引供能系统，完成RAMS可靠性指标分析，构建合理的故障管理和处理流程。

2.RAMS研究现状RAMS于1999年在欧洲标准中最先体现，指代的是可靠性，可用性，维修性以及安全性，而我国结合国内技术发展现状，制定符合我国发展现状的国家标准GB/T21562-2008，明确RAMS为轨道交通——可靠性，可用性，可维修性和安全性规范及示例。

可靠性指的是在规定时间和条件下，产品能过够完成规定功能的能力，主要元素包括产品，规定条件，规定时间，规定功能和能力。

可用性是指在某时刻，可维修产品具备或保持规定功能的能力。

可用性指标主要通过可用度表述，包含固有可用度、达到可用度、使用可用度和正点率等。

维修性理论的发展阶段主要是从故障后改善处理的“事后维修”到故障前的“预防性维修”，我国动车组列车普遍采用预防性周期性维修与特殊故障集中维修结合的方式完成。

安全性顾名思义指的是不引起人身物质的重大损伤。

高速动车组运行性能与乘坐舒适度的关系研究引言动车组的运行性能和乘坐舒适度主要按运行稳定性、运行安全性、轮轴横向力和运行平稳性来评定。

运行稳定性包括线性稳定性和非线性稳定性（又称为横向运动稳定性或蛇行运动稳定性）。

运行安全性分别按脱轨系数、轮重减载率、倾覆系数、轮轴（横向）力来评定。

本文以引进西门子的CRH3动车组动为例，进行力学仿真计算分析和说明。

所计算分析内容涵盖了CRH3动车组的运行稳定性、安全性、平稳性、轮轴横向力和轮轨关系等方面的内容。

1、运行安全性1.1、脱轨系数在《铁道车辆动力性能评定和试验鉴定规范》（以下简写为GB5599-85）中定义为：爬轨侧车轮作用于钢轨上的横向力Q与其作用与钢轨上的垂向力P的比值。

即：脱轨系数=Q/P≤0.8由于在西门子的UIC518标准中采用Y表示横向力，Q表示垂向力，因而西门子公司在概念中采用了欧洲习惯的表达方式，即用Y/Q代替Q/P表示脱轨系数。

1.2、减载率GB5599-85中定义为：轮重减载量Δp与该轴平均静轮重p的比值；即：轮重减载率=Δp/p，其中：Δp=pd-p，pd是动态下的实测轴重。

按规定：当速度≤160km/h时，轮重减载率≤0.65；当速度≥160km/h时，轮重减载率按准静态和动态两种工况考察。

其中，准静态轮重减载率是只考察准静力作用下的减载率，其限值：=0.65（准静态）。

西门子概念中采用了欧洲习惯的表示方法:△Q/Q0=0.65。

动态轮重减载率是同时考察动态作用下的减载率，其限值：=0.80（动态）。

西门子概念中的表达方式为：△Q/Q0 =0.80。

1.3、倾覆系数按GB5599-85《铁道车辆动力学性能评定和试验鉴定规范》规定：倾覆系数D=Pd/Pet<0.8。

2、运行稳定性运行稳定性主要考察非线性稳定性，即横向运动稳定性（或者说蛇行运动稳定性），考核对象为构架的横向加速度，其限值为连续6个周期8～10m/s2(0.5～10Hz，见图1)。

高速铁路动车组气动性能分析与优化研究随着我国高速铁路建设的不断发展，动车组已经成为了我国铁路承载大容量客流的主力车型之一。

作为现代高速铁路的主要技术支撑之一，高速动车组的设计和制造已经走在了全球前沿。

但是，高速动车组的气动性能对于安全性、舒适性及通行效率均有着至关重要的作用。

因此，在高速动车组的设计中，气动性能的分析与优化显得尤为重要。

本文将从高速动车组的气动性能分析入手，探讨高速动车组的气动性能分析与优化的研究。

一、高速动车组气动性能分析的研究现状高速动车组的气动性能分析是动车组研究的一个重要方向，它能够为高速动车组设计提供重要的理论依据。

目前，国内外对高速动车组的气动性能分析研究已经取得了很多进展。

其中，流场模拟、列车模型试验及实车试验是常用的三种研究方法。

1.流场模拟流场模拟是利用计算流体力学（CFD）方法对高速动车组进行气动性能分析的一种研究方法。

CFD方法是一种能够数值模拟物理流动的计算方法，该方法研究精度高、计算效率高、成本低廉等优点。

目前，CFD方法已经成为高速动车组气动性能分析的主要手段。

在流场模拟中，工程师可以通过计算机模拟得到动车组的速度场、压力场、流线和阻力等信息。

通过对这些数据进行分析，可以得到动车组的气动性能，并通过优化设计来改善气动性能。

2.列车模型试验列车模型试验是高速动车组气动性能分析的常用方法之一。

该方法利用减小比例的列车模型来进行气动试验，评估列车空气动力学特性和空气动力学性能。

这种试验可以为动车组设计提供重要的实验数据。

在列车模型试验中，工程师可以通过对列车模型进行实际试验来获取动车组的阻力、气动升力、稳定性等数据，然后通过实验数据的分析，对动车组的设计进行优化。

3.实车试验实车试验是高速动车组气动性能分析的一种重要方法。

利用实车试验，可以对动车组的实际运行情况进行观测和记录，并获得动车组在不同工况下的动态气动数据。

通过根据实车试验数据计算出动车组不同工况下的阻力、气动升力等指标，然后通过数据分析，进行动车组气动性能的优化。

钢轨打磨对动车组异常抖动影响研究随着我国经济飞速发展，城市间交通运输需求量越来越大。

《中长期铁路网规划》对我国铁路未来发展进行了规划，目标在2020年达到12万km以上的铁路运营里程，通过建立省会城市和大中城市之间的快速客运通道、“四纵四横”等客运系统来满足日益增长的客运需求[1]。

随着人们生活水平的提升，旅客对于客车的运行时间、乘坐舒适性及安全性也提出了越来越高的要求，因此客运专线成为旅客运输的最佳选择[2]。

但随着运营里程的增加，在客运专线上运营的动车组车辆逐渐出现异常振动现象，该现象也成为工务和车辆部门急需解决的问题。

摘星楼筑在谷中央最高的石峰顶上，稍逊于此峰的另外两座石峰与之鼎足而三，峰顶分别筑有觅星殿与赏星居，风和日丽的晴天，夕阳沉没之前，便是将最后一片暮色铺展在摘星楼、觅星殿、赏星居蓝绿的琉璃飞檐上，令平素朴实无华的檐角在此一刻，闪闪发光，好像是由黄金铸就。

Orlova等[3]针对严重的轮缘磨耗及车辆装载工况下出现的振动加速度偏大等现象，通过MEDYNA程序对车辆计算模型进行优化，并提出了较优的车辆悬挂参数。

Johnsson等[4]为得到最佳车辆运行性能并尽可能地减小轮轨磨耗，通过Gensys软件建立车辆系统动力学模型，基于多目标优化理论优化了车辆系统中悬挂参数阻尼，整体提升了车辆的运行性能。

张剑等[5]基于60 kg/m钢轨廓形，以LMA踏面为研究对象，改进了其主要工作面，使轮轨间发生一定横移时的轮轨匹配关系趋于优化，从而改善了车辆的运行性能。

乔红刚等[6]通过线路测试、抗蛇行减振器台架性能测试及动力学仿真进行分析，得出动车组异常抖动的原因。

许自强[7]对动车组横向稳定性进行了研究，得出不同速度级的车轮踏面服役等效锥度建议限制。

郝宏志等[8]通过对兰新二线运营动车组异常抖动区间线路进行调研，从车轮踏面、车辆平稳性和振动测试等方面展开分析，提出车轮镟修和钢轨打磨的建议周期。

以上研究结果基于车辆悬挂结构设计及车轮型面设计，其对车辆运行品质的提升做出了卓越贡献，但对于实际磨耗状态轮轨匹配的分析及从钢轨型面设计出发的研究较少，且没有对打磨前后车辆的运行性能进行跟踪分析。

科技资讯2017 NO.09SCIENCE & TECHNOLOGY INFORMATION工 程 技 术85科技资讯 SCIENCE & TECHNOLOGY INFORMATION 1 研究背景地铁方便市民出行的同时其背后运营成本压力一直高居不下,根据轨道交通行业经验,地铁电费约占运营成本的30%,而牵引能耗约占地铁系统电能消耗的50%。

地铁电价一般参照工商业用电执行,费用较高,表1列出部分城市地铁电价制定情况。

地铁牵引能耗的影响因素较多,运行模式与能耗有着密不可分的关系。

该文结合东莞、深圳、郑州等城市既有地铁线路运行情况,从运行管理的角度开展因素分析,暂未考虑列车编组、车辆选型、运营里程等要素变化的影响。

文中的牵引能耗指列车在运用中的能耗,并未特别区分出空调的能耗。

2 主要因素分析2.1 载客量一般来说地铁载客量越大,整车的牵引能耗越大。

如果单纯从减少单列车载客量的角度出发,可通过增加上线列车数量来实现,但同时上线列车数量变多成本也会相应提高,与上述的初衷背道而驰。

另一方面载客量也非绝对可控因素,特别是像深圳地铁这样高强度运营的地铁系统,必须尽全力及时满足市民的出行需求。

从整体经济效益来看,用尽可能少的车运送最多的旅客是比较理想的方案。

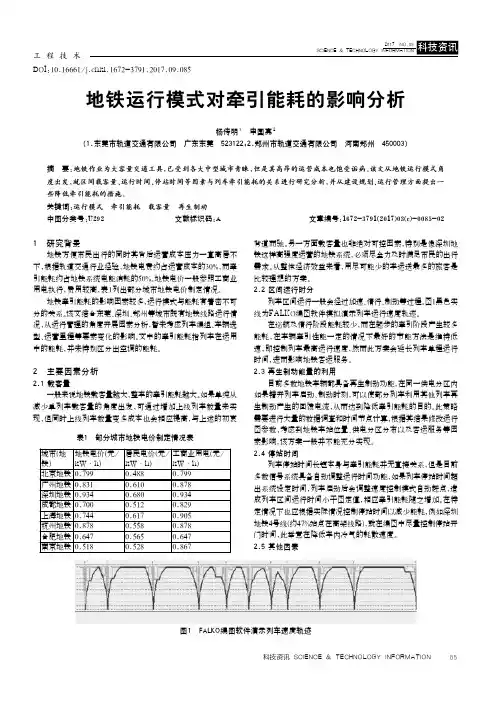
2.2 区间运行时分列车区间运行一般会经过加速、惰行、制动等过程。

图1黑色实线为FALKO编图软件模拟演示列车运行速度轨迹。

在巡航及惰行阶段能耗较少,而在起步的牵引阶段产生较多能耗,在车辆牵引性能一定的情况下最好的节能方法是维持低速,即控制列车最高运行速度,然而此方案会延长列车单程运行时间,进而影响地铁客运服务。

2.3 再生制动能量的利用目前多数地铁车辆都具备再生制动功能,在同一供电分区内如果错开列车启动、制动时刻,可以使部分列车利用其他列车再生制动产生的回馈电流,从而达到降低牵引能耗的目的。

此策略需要进行大量的数据调查和时间节点计算,根据其结果修改运行图参数,考虑到地铁车站位置、供电分区分布以及客运服务等因素影响,该方案一般并不能充分实现。

地铁能耗分析摘要：随着城市化进程的加快和交通需求的日益增长，地铁作为一种高效、环保的城市公共交通工具，其能源消耗问题受到了广泛关注。

本文旨在对地铁系统的能耗进行深入分析，为节能减排和可持续发展提供理论依据和实践指导。

首先，本文回顾了地铁系统的基本构成及其运行特点，并概述了当前地铁能耗研究的现状。

通过收集实际运营数据，本文分析了不同因素如车辆设计、运行速度、气候条件等对地铁能耗的影响。

此外，文中还探讨了节能技术的应用现状与潜力，包括牵引系统优化、能量回收系统、绿色建筑材料。

最后，本文提出了一系列针对地铁能耗降低的策略与建议，并对未来研究方向进行了展望。

本研究不仅有助于提高地铁运营的能效，也对于推动城市交通的绿色发展具有重要意义。

关键词：地铁能耗；能效优化；数据分析；节能策略1地铁系统概述1.1地铁的历史与发展自1863年世界上第一条地铁——伦敦地铁开通以来，地铁作为城市公共交通的重要组成部分，在全球范围内得到了迅速发展。

地铁的发展历程反映了人类对高效率城市交通需求的不断增长以及对环境保护意识的提升。

从最初的蒸汽动力到现在的电力驱动，地铁技术的进步极大地推动了城市交通的现代化。

1.2地铁系统的组成现代地铁系统通常由轨道线路、车辆、车站、信号系统、电力供应系统等部分组成。

轨道线路是地铁行驶的基础设施，车辆是承载乘客的主体，车站则是乘客进出的节点，信号系统确保行车安全和效率，电力供应系统则为整个地铁系统的运行提供动力。

2地铁能耗的特点2.1能源消耗的主要环节地铁系统的能源消耗主要集中在以下几个方面：列车牵引、车站设备运行、照明系统、空调通风系统以及电梯等辅助设施。

其中，列车牵引是最大的能耗环节，它直接关系到列车的加速、减速和正常运行。

2.2影响能耗的关键因素影响地铁能耗的因素众多，包括列车的设计参数（如重量、空气动力学特性）、运行模式（如速度、停站频率）、乘客流量、线路条件（如坡度、曲线半径）以及车站的设计（如站台长度、深度）。