大学物理第三版试题

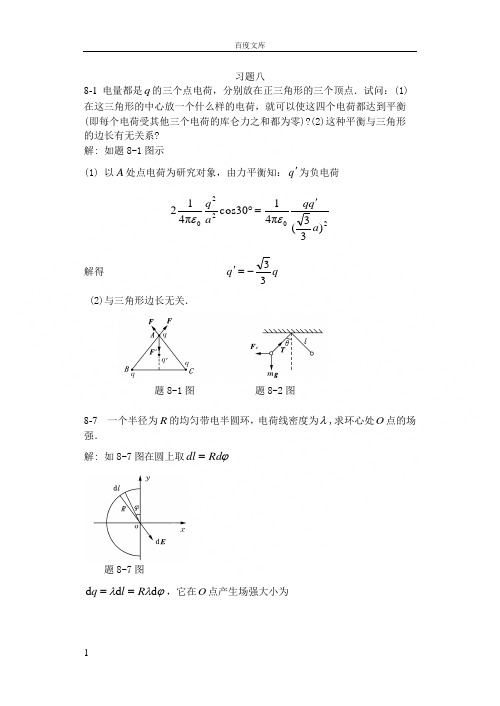
习题八8-1 电量都是q的三个点电荷，分别放在正三角形的三个顶点．试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解: 如题8-1图示(1) 以A处点电荷为研究对象，由力平衡知：q'为负电荷2220)33(π4130cosπ412aq qaq'=︒εε解得qq33-='(2)与三角形边长无关．题8-1图题8-2图8-7 一个半径为R的均匀带电半圆环，电荷线密度为λ,求环心处O点的场强．解: 如8-7图在圆上取ϕRddl=题8-7图ϕλλddd Rlq==，它在O点产生场强大小为20π4d d RR E εϕλ=方向沿半径向外 则 ϕϕελϕd sin π4sin d d 0RE E x ==ϕϕελϕπd cos π4)cos(d d 0RE E y -=-=积分RR E x 000π2d sin π4ελϕϕελπ==⎰0d cos π400=-=⎰ϕϕελπRE y∴ RE E x 0π2ελ==，方向沿x 轴正向．8-11 半径为1R 和2R (2R ＞1R )的两无限长同轴圆柱面，单位长度上分别带有电量λ和-λ,试求:(1)r ＜1R ；(2) 1R ＜r ＜2R ；(3) r ＞2R 处各点的场强．解: 高斯定理0d ε∑⎰=⋅q S E s取同轴圆柱形高斯面，侧面积rl S π2= 则 rl E S E Sπ2d =⋅⎰对(1) 1R r <0,0==∑E q(2) 21R r R << λl q =∑∴ rE 0π2ελ=沿径向向外(3) 2R r >=∑q∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电，电荷的面密度分别为1σ和2σ，试求空间各处场强．解: 如题8-12图示，两带电平面均匀带电，电荷面密度分别为1σ与2σ，两面间， n E)(21210σσε-= 1σ面外， n E )(21210σσε+-= 2σ面外， n E)(21210σσε+= n：垂直于两平面由1σ面指为2σ面．题8-16图8-16 如题8-16图所示，在A ，B 两点处放有电量分别为+q ,-q 的点电荷，AB 间距离为2R ，现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点，求移动过程中电场力作的功． 解: 如题8-16图示0π41ε=O U 0)(=-RqR q 0π41ε=O U )3(R qR q -Rq 0π6ε-= ∴ Rqq U U q A o C O 00π6)(ε=-=8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R ．试求环中心O 点处的场强和电势． 解: (1)由于电荷均匀分布与对称性，AB 和CD 段电荷在O 点产生的场强互相抵消，取θd d R l =则θλd d R q =产生O 点Ed 如图，由于对称性，O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E yR 0π4ελ=［)2sin(π-2sin π-］R0π2ελ-=(2) AB 电荷在O 点产生电势，以0=∞U⎰⎰===AB200012ln π4π4d π4d R R x x x x U ελελελ同理CD 产生 2ln π402ελ=U 半圆环产生 0034π4πελελ==R R U∴ 0032142ln π2ελελ+=++=U U U U O 8-22 三个平行金属板A ，B 和C 的面积都是200cm 2，A 和B 相距4.0mm ，A与C 相距2.0 mm ．B ，C 都接地，如题8-22图所示．如果使A 板带正电3.0×10-7C ，略去边缘效应，问B 板和C 板上的感应电荷各是多少?以地的电势为零，则A 板的电势是多少?解: 如题8-22图示，令A 板左侧面电荷面密度为1σ，右侧面电荷面密度为2σ题8-22图(1)∵ AB AC U U =，即 ∴ AB AB AC AC E E d d = ∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A=得 ,32S q A =σ Sq A 321=σ而 7110232-⨯-=-=-=A C q S q σC C10172-⨯-=-=S q B σ(2) 301103.2d d ⨯===AC AC AC A E U εσV 8-23 两个半径分别为1R 和2R （1R ＜2R )的同心薄金属球壳，现给内球壳带电+q ，试计算：(1)外球壳上的电荷分布及电势大小；(2)先把外球壳接地，然后断开接地线重新绝缘，此时外球壳的电荷分布及电势；*(3)再使内球壳接地，此时内球壳上的电荷以及外球壳上的电势的改变量．解: (1)内球带电q +；球壳内表面带电则为q -,外表面带电为q +，且均匀分布，其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R R qrr q r E U εε (2)外壳接地时，外表面电荷q +入地，外表面不带电，内表面电荷仍为q -．所以球壳电势由内球q +与内表面q -产生：0π4π42020=-=R q R q U εε8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳，介质相对介电常数为r ε，金属球带电Q ．试求： (1)电介质内、外的场强； (2)电介质层内、外的电势；(3)金属球的电势．解: 利用有介质时的高斯定理∑⎰=⋅q S D Sd(1)介质内)(21R r R <<场强303π4,π4rrQ E r r Q D r εε ==内; 介质外)(2R r <场强303π4,π4r r Q E r Qr D ε ==外(2)介质外)(2R r >电势rQE U 0rπ4r d ε=⋅=⎰∞外 介质内)(21R r R <<电势2020π4)11(π4R Q R r qr εεε+-=)11(π420R r Qr r -+=εεε(3)金属球的电势r d r d 221⋅+⋅=⎰⎰∞R R R E E U 外内⎰⎰∞+=22220π44πdr R R Rr r Qdrr Q εεε)11(π4210R R Qr r-+=εεε 8-28 如题8-28图所示，在平行板电容器的一半容积内充入相对介电常数为rd r d ⋅+⋅=⎰⎰∞∞rrE E U 外内r ε的电介质．试求：在有电介质部分和无电介质部分极板上自由电荷面密度的比值．解: 如题8-28图所示，充满电介质部分场强为2E ，真空部分场强为1E，自由电荷面密度分别为2σ与1σ 由∑⎰=⋅0d q S D得11σ=D ，22σ=D而 101E D ε=,202E D r εε=d21U E E == ∴r D D εσσ==1212题8-28图 题8-29图8-29 两个同轴的圆柱面，长度均为l ，半径分别为1R 和2R (2R ＞1R )，且l >>2R -1R ，两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时，求：(1)在半径r 处(1R ＜r ＜2R ＝，厚度为dr ，长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量；(2)电介质中的总电场能量； (3)圆柱形电容器的电容．解: 取半径为r 的同轴圆柱面)(S则 rlD S D S π2d )(=⋅⎰当)(21R r R <<时，Q q =∑∴ rlQD π2=(1)电场能量密度 22222π82l r Q D w εε== 薄壳中 rlrQ rl r l r Q w W εευπ4d d π2π8d d 22222=== (2)电介质中总电场能量⎰⎰===211222ln π4π4d d R R VR R l Q rl r Q W W εε (3)电容：∵ CQ W 22=∴ )/ln(π22122R R lW Q C ε== 习题九9-8 在真空中，有两根互相平行的无限长直导线1L 和2L ，相距0.1m ，通有方向相反的电流，1I =20A,2I =10A ，如题9-8图所示．A ，B 两点与导线在同一平面内．这两点与导线2L 的距离均为5.0cm ．试求A ，B 两点处的磁感应强度，以及磁感应强度为零的点的位置．题9-8图解：如题9-8图所示,A B方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B在2L 外侧距离2L 为r 处则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r mT9-11 氢原子处在基态时，它的电子可看作是在半径a =0.52×10-8cm 的轨道上作匀速圆周运动，速率v =2.2×108cm ·s -1．求电子在轨道中心所产生的磁感应强度和电子磁矩的值．解：电子在轨道中心产生的磁感应强度3004aav e B πμ ⨯= 如题9-11图，方向垂直向里，大小为134200==a evB πμ T 电子磁矩m P在图中也是垂直向里，大小为242102.92-⨯===eva a T e P m π 2m A ⋅ 题9-11图 题9-12图9-12 两平行长直导线相距d =40cm ，每根导线载有电流1I =2I =20A ，如题9-12图所示．求：(1)两导线所在平面内与该两导线等距的一点A 处的磁感应强度；(2)通过图中斜线所示面积的磁通量．(1r=3r =10cm,l=25cm)．解：(1) 5210104)2(2)2(2-⨯=+=dIdIBAπμπμT方向⊥纸面向外(2)取面元rlS dd=6121110102.23ln31ln23ln2])(22[1211-+⨯=πμ=πμ-πμ=-πμ+πμ=⎰l Il Il IldrrdIrIrrrΦWb9-13 一根很长的铜导线载有电流10A，设电流均匀分布.在导线内部作一平面S，如题9-13图所示．试计算通过S平面的磁通量(沿导线长度方向取长为1m的一段作计算)．铜的磁导率μμ=.解：由安培环路定律求距圆导线轴为r处的磁感应强度⎰∑μ=⋅lIlBd222RIrrBμπ=∴22RIrBπμ=题 9-13 图磁通量602)(1042-===⋅=Φ⎰⎰πμπμIdrRIrS dB RsmWb题9-15图9-15 题9-15图中所示是一根很长的长直圆管形导体的横截面，内、外半径分别为a ,b ，导体内载有沿轴线方向的电流I ，且I 均匀地分布在管的横截面上．设导体的磁导率0μμ≈，试证明导体内部各点)(b r a << 的磁感应强度的大小由下式给出：r a r a b IB 22220)(2--=πμ解：取闭合回路r l π2= )(b r a <<则 ⎰π=⋅lr B l B 2d2222)(a b Ia r I ππππ--=∑∴ )(2)(22220a b r a r I B --=πμ 9-16 一根很长的同轴电缆，由一导体圆柱(半径为a )和一同轴的导体圆管(内、外半径分别为b ,c )构成，如题9-16图所示．使用时，电流I 从一导体流去，从另一导体流回．设电流都是均匀地分布在导体的横截面上，求：(1)导体圆柱内(r ＜a ),(2)两导体之间(a ＜r ＜b )，（3）导体圆筒内(b ＜r ＜c )以及(4)电缆外(r ＞c )各点处磁感应强度的大小解： ⎰∑μ=⋅LI l B 0d(1)a r < 2202RIr r B μπ=202R IrB πμ=(2) b r a << I r B 02μπ=rIB πμ20=(3)c r b << I bc b r I r B 0222202μμπ+---= )(2)(22220b c r r c I B --=πμ (4)c r > 02=r B π0=B题9-16图题9-17图题9-21图9-21 边长为l =0.1m 的正三角形线圈放在磁感应强度B =1T 的均匀磁场中，线圈平面与磁场方向平行.如题9-21图所示，使线圈通以电流I =10A ，求： (1)线圈每边所受的安培力； (2)对O O '轴的磁力矩大小；(3)从所在位置转到线圈平面与磁场垂直时磁力所作的功．解： (1) 0=⨯=B l I F bcB l I F ab⨯= 方向⊥纸面向外，大小为866.0120sin ==︒IlB F ab NB l I F ca⨯=方向⊥纸面向里，大小866.0120sin ==︒IlB F ca N(2)IS P m =B P M m⨯= 沿O O '方向，大小为221033.443-⨯===B l I ISB M m N ⋅(3)磁力功 )(12ΦΦ-=I A∵ 01=Φ B l 2243=Φ ∴221033.443-⨯==B l IA J9习题十10-1 一半径r =10cm 的圆形回路放在B =0.8T 的均匀磁场中．回路平面与B垂直．当回路半径以恒定速率tr d d =80cm ·s -1收缩时，求回路中感应电动势的大小．解: 回路磁通 2πr B BS m ==Φ感应电动势大小40.0d d π2)π(d d d d 2====trr B r B t t m Φε V 10-2 一对互相垂直的相等的半圆形导线构成回路，半径R =5cm ，如题10-2图所示．均匀磁场B =80×10-3T ，B 的方向与两半圆的公共直径(在Oz 轴上)垂直，且与两个半圆构成相等的角α 当磁场在5ms 内均匀降为零时，求回路中的感应电动势的大小及方向．解: 取半圆形cba 法向为i， 题10-2图则 αΦcos 2π21B R m =同理，半圆形adc 法向为j，则αΦcos 2π22B R m=∵ B 与i 夹角和B 与j夹角相等，∴ ︒=45α则 αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tBR t m αεV方向与cbadc 相反，即顺时针方向．题10-4图10-4 如题10-4图所示，载有电流I 的长直导线附近，放一导体半圆环MeN 与长直导线共面，且端点MN 的连线与长直导线垂直．半圆环的半径为b ，环心O 与导线相距a ．设半圆环以速度v 平行导线平移．求半圆环内感应电动势的大小和方向及MN 两端的电压 N M U U -．解: 作辅助线MN ，则在MeNM 回路中，沿v方向运动时0d =m Φ ∴ 0=MeNM ε 即 MN MeN εε= 又∵ 0cos d ln 02a bMN a bIv a bvB l a bμεππ+--==<+⎰所以MeN ε沿NeM 方向，大小为ba ba Iv -+ln20πμ M 点电势高于N 点电势，即ba ba Iv U U N M -+=-ln20πμ 题10-5图10-5如题10-5所示，在两平行载流的无限长直导线的平面内有一矩形线圈．两导线中的电流方向相反、大小相等，且电流以tId d 的变化率增大，求： (1)任一时刻线圈内所通过的磁通量；(2)线圈中的感应电动势． 解: 以向外磁通为正则 (1)]ln [lnπ2d π2d π2000dad b a b Ilr l r Ir l r Iab b ad d m +-+=-=⎰⎰++μμμΦ(2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε10-6 如题10-6图所示，用一根硬导线弯成半径为r 的一个半圆．令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转．整个电路的电阻为R ．求：感应电流的最大值．题10-6图解: )cos(2π02ϕωΦ+=⋅=t r B S B m∴ Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε ∴ RBfr R I m22π==ε 10-7 如题10-7图所示，长直导线通以电流I =5A ，在其右方放一长方形线圈，两者共面．线圈长b =0.06m ，宽a =0.04m ，线圈以速度v =0.03m ·s -1垂直于直线平移远离．求：d =0.05m 时线圈中感应电动势的大小和方向．题10-7图解: AB 、CD 运动速度v方向与磁力线平行，不产生感应电动势． DA 产生电动势⎰==⋅⨯=AD I vb vBb l B v d2d )(01πμεBC 产生电动势)(π2d )(02d a Ivbl B v CB+-=⋅⨯=⎰με∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad d Ibv μεεε V 方向沿顺时针．10-8 长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动．已知导轨处于均匀磁场B 中，B 的方向与回路的法线成60°角(如题10-8图所示)，B的大小为B =kt (k 为正常)．设t =0时杆位于cd 处，求：任一时刻t 导线回路中感应电动势的大小和方向．解: ⎰==︒=⋅=22212160cos d klvt lvkt Blvt S B mΦ∴ klvt tm-=-=d d Φε 即沿abcd 方向顺时针方向．题10-8图10-9 一矩形导线框以恒定的加速度向右穿过一均匀磁场区，B的方向如题10-9图所示．取逆时针方向为电流正方向，画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0)．解: 如图逆时针为矩形导线框正向，则进入时0d d <Φt,0>ε； 题10-9图(a)题10-9图(b) 在磁场中时0d d =tΦ,0=ε； 出场时0d d >tΦ，0<ε，故t I -曲线如题10-9图(b)所示. 题10-10图10-10 导线ab 长为l ，绕过O 点的垂直轴以匀角速ω转动，aO =3l磁感应强度B 平行于转轴，如图10-10所示．试求： （1）ab 两端的电势差； （2）b a ,两端哪一点电势高?解: (1)在Ob 上取dr r r +→一小段 则 ⎰==320292d l Ob l B r rB ωωε 同理 ⎰==302181d l Oa l B r rB ωωε ∴ 2261)92181(l B l B Ob aO ab ωωεεε=+-=+= (2)∵ 0>ab ε 即0<-b a U U ∴b 点电势高．题10-11图10-11 如题10-11图所示，长度为b 2的金属杆位于两无限长直导线所在平面的正中间，并以速度v平行于两直导线运动．两直导线通以大小相等、方向相反的电流I ，两导线相距2a ．试求：金属杆两端的电势差及其方向． 解：在金属杆上取r d 距左边直导线为r ，则ba b a Iv r r a r Iv l B v ba ba BAAB -+-=-+-=⋅⨯=⎰⎰+-ln d )211(2d )(00πμπμε∵ 0<AB ε ∴实际上感应电动势方向从A B →，即从图中从右向左， ∴ ba ba Iv U AB -+=ln0πμ 题10-12图10-12 磁感应强度为B的均匀磁场充满一半径为R 的圆柱形空间，一金属杆放在题10-12图中位置，杆长为2R ，其中一半位于磁场内、另一半在磁场外．当tBd d ＞0时，求：杆两端的感应电动势的大小和方向．解： ∵ bc ab ac εεε+=tBR B R t t ab d d 43]43[d d d d 21=--=-=Φε=-=tabd d 2Φεt BR B R t d d 12π]12π[d d 22=-- ∴ tB R R acd d ]12π43[22+=ε∵0d d >tB∴ 0>ac ε即ε从c a →10-13 半径为R 的直螺线管中，有dtdB＞0的磁场，一任意闭合导线abca ，一部分在螺线管内绷直成ab 弦，a ,b 两点与螺线管绝缘，如题10-13图所示．设ab =R ，试求：闭合导线中的感应电动势． 解：如图，闭合导线abca 内磁通量)436π(22R R B S B m -=⋅= Φ∴ tB R R i d d )436π(22--=ε ∵0d d >tB∴0<i ε，即感应电动势沿acba ，逆时针方向．题10-13图题10-14图∴ 题10-15图 10-15 一无限长的直导线和一正方形的线圈如题10-15图所示放置(导线与线圈接触处绝缘)．求：线圈与导线间的互感系数．解： 设长直电流为I ，其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2aaIa r r Ia μμΦ∴ 2ln π2012aI M μΦ==10-16 一矩形线圈长为a =20cm ，宽为b =10cm ，由100匝表面绝缘的导线绕成，放在一无限长导线的旁边且与线圈共面．求：题10-16图中(a)和(b)两种情况下，线圈与长直导线间的互感．解：(a)见题10-16图(a)，设长直电流为I ，它产生的磁场通过矩形线圈的磁通为2ln π2d 2πd 020)(12Ia r r Ia S B bb S μμΦ⎰⎰==⋅= ∴ 6012108.22ln π2-⨯===a N I N M μΦ H (b)∵长直电流磁场通过矩形线圈的磁通012=Φ，见题10-16图(b) ∴ 0=M题10-16图题10-17图10-20 一无限长圆柱形直导线，其截面各处的电流密度相等，总电流为I ．求：导线内部单位长度上所储存的磁能．解：在R r <时 20π2R I B r μ=∴ 4222002π82Rr I B w m μμ== 取 r r V d π2d =(∵导线长1=l )则 ⎰⎰===R R m I R r r I r r w W 00204320π16π4d d 2μμπ。

第一章运动的描述1-1 ｜｜与有无不同?和有无不同? 和有无不同?其不同在哪里?试举例说明．解：（1）是位移的模，是位矢的模的增量，即，；（2）是速度的模，即.只是速度在径向上的分量.∵有（式中叫做单位矢），则式中就是速度径向上的分量，∴不同如题1-1图所示.题1-1图(3)表示加速度的模，即，是加速度在切向上的分量.∵有表轨道节线方向单位矢），所以式中就是加速度的切向分量.(的运算较复杂，超出教材规定，故不予讨论)1-2 设质点的运动方程为=()，=()，在计算质点的速度和加速度时，有人先求出r＝，然后根据 =，及＝而求得结果；又有人先计算速度和加速度的分量，再合成求得结果，即=及=你认为两种方法哪一种正确？为什么？两者差别何在？解：后一种方法正确.因为速度与加速度都是矢量，在平面直角坐标系中，有，故它们的模即为而前一种方法的错误可能有两点，其一是概念上的错误，即误把速度、加速度定义作其二，可能是将误作速度与加速度的模。

在1-1题中已说明不是速度的模，而只是速度在径向上的分量，同样，也不是加速度的模，它只是加速度在径向分量中的一部分。

或者概括性地说，前一种方法只考虑了位矢在径向（即量值）方面随时间的变化率，而没有考虑位矢及速度的方向随间的变化率对速度、加速度的贡献。

1-3 一质点在平面上运动，运动方程为=3+5, =2+3-4.式中以 s计，,以m计．(1)以时间为变量，写出质点位置矢量的表示式；(2)求出=1 s 时刻和＝2s 时刻的位置矢量，计算这1秒内质点的位移；(3)计算＝0 s时刻到＝4s时刻内的平均速度；(4)求出质点速度矢量表示式，计算＝4 s 时质点的速度；(5)计算＝0s 到＝4s 内质点的平均加速度；(6)求出质点加速度矢量的表示式，计算＝4s 时质点的加速度(请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式)．解：（1）(2)将,代入上式即有(3)∵∴(4)则(5)∵(6)这说明该点只有方向的加速度，且为恒量。

习题1616・1・如图所示，金属圆环半径为/?,位于磁感应强度为P的均匀磁场中，圆环平面与磁场方向垂直。

当圆环以恒定速度▽在环所在平面内运动时，求环中的感应电动势及环上位于与运动方向垂直的直径两端〃间的电势差。

解：(1)由法拉第电磁感应定律考虑到圆环内的磁通量不变，所以，环中的感dtr u ——(2)利用：8ah= £ (vxB)-dl ,有：£ah = Bv・2R = 2BvR。

【注：相同电动势的两个电源并联，并联后等效电源电动势不变】16-2.如图所示，长直导线屮通有电流/ = 5.0/1,在与其相距d = 0.5cm 处放有一矩形线圈，共1000匝，设线圈长/ = 4.0cm ,宽a = 2.0cm。

不计线圈口感，若线圈以速度v = 3.0cm/s沿垂直于长导线的方向向右运动，线圈中的感生电动势多大？解法一：利用法拉第电磁感应定律解决。

首先用［fp•〃二工/求出电场分布，易得:则矩形线圈内的磁通量为:rh s = -N有:dxdt八=1.92x107 V。

2 兀（d + a）解法二：利用动生电动势公式解决。

由击j〃二“0工/求出电场分布，易得:“（）/ 17tr考虑线圈框架的两个平行长直导线部分产生动生电动势,近端部分：®=NBJv,远端部分：E2=NB2I V,吗丄—丄”心2兀 ' d d + a 27ld（d 十= l・92xlOP。

16・3・如图所示，长直导线屮通有电流强度为/的电流，长为/的金属棒必与长直导线共面且垂直于导线放置，其。

端离导线为d,并以速度E平行于长直导线作匀速运动，求金属棒中的感应电动势£并比较4、5的电势大小。

解法一：利用动生电动势公式解决：d£ = (yxBydl如力,171 r"o" dr“0以［〃 + /------ ——= -------- In -----17C r 2兀 d由右手定则判定：u（l>u ho解法二：利用法拉第电磁感应定律解决。

大学物理实验第三版答案择题，书本已给出）习题一1-6 ｜?r｜与?r 有无不同?drdrdvdv和有无不同? 和有无不同?其不同在哪里?dtdtdtdt试举例说明．解：（1）???r是位移的模，?r是位矢的模的增量，即?r?r2?r1，?r?r2?r1；（2）dsdrdr是速度的模，即. ?v?dtdtdtdr只是速度在径向上的分量. dt?（式中r?叫做单位矢）∵有r?rr，则式中?drdrdr??r ?rdtdtdtdr就是速度径向上的分量， dt∴drdr与不同如题1-1图所示.dtdt题1-6图?dvdv?dv(3)表示加速度的模，即a?，是加速度a在切向上的分量.dtdtdt∵有v?v?(?表轨道节线方向单位矢），所以????dvdv?d????v dtdtdtdv就是加速度的切向分量. dt???d??dr与(?的运算较复杂，超出教材规定，故不予讨论) dtdt式中1-7 设质点的运动方程为x=x(t)，y=y(t)，在计算质点的速度和加速度时，有人先求drd2r出r＝x?y，然后根据v =，及a＝2而求得结果；又有人先计算速度和加速度dtdt22的分量，再合成求得结果，即?dx??dy?=?????及a=dt???dt?22?d2x??d2y???dt2?????dt2?? 你认为两种方法哪一种????22正确？为什么？两者差别何在？???解：后一种方法正确.因为速度与加速度都是矢量，在平面直角坐标系中，有r?xi?yj，??drdx?dy??v??i?jdtdtdt?222??dy?drdxa?2?2i?2jdtdtdt故它们的模即为?dx??dy?22v?vx?vy???????dt??dt?22x2y22?d2x??d2y?a?a?a???dt2?????dt2??????2而前一种方法的错误可能有两点，其一是概念上的错误，即误把速度、加速度定义作drv?dtd2ra?2dtdrdrd2r与2误作速度与加速度的模。

习题22.1 选择题(1) 一质点作匀速率圆周运动时，(A)它的动量不变，对圆心的角动量也不变。

(B)它的动量不变，对圆心的角动量不断改变。

(C)它的动量不断改变，对圆心的角动量不变。

(D)它的动量不断改变，对圆心的角动量也不断改变。

[答案：C](2) 质点系的内力可以改变(A)系统的总质量。

(B)系统的总动量。

(C)系统的总动能。

(D)系统的总角动量。

[答案：C](3) 对功的概念有以下几种说法：①保守力作正功时，系统内相应的势能增加。

②质点运动经一闭合路径，保守力对质点作的功为零。

③作用力与反作用力大小相等、方向相反，所以两者所作功的代数和必为零。

在上述说法中：(A)①、②是正确的。

(B)②、③是正确的。

(C)只有②是正确的。

(D)只有③是正确的。

[答案：C]2.2填空题(1) 某质点在力i x F )54(+=（SI ）的作用下沿x 轴作直线运动。

在从x=0移动到x=10m的过程中，力F 所做功为 。

[答案：290J ](2) 质量为m 的物体在水平面上作直线运动，当速度为v 时仅在摩擦力作用下开始作匀减速运动，经过距离s 后速度减为零。

则物体加速度的大小为 ，物体与水平面间的摩擦系数为 。

[答案：22;22v v s gs](3) 在光滑的水平面内有两个物体A 和B ，已知m A =2m B 。

（a ）物体A 以一定的动能E k 与静止的物体B 发生完全弹性碰撞，则碰撞后两物体的总动能为 ；（b ）物体A 以一定的动能E k 与静止的物体B 发生完全非弹性碰撞，则碰撞后两物体的总动能为 。

[答案：2;3k k E E ]2.3 在下列情况下，说明质点所受合力的特点：（1）质点作匀速直线运动；（2）质点作匀减速直线运动；（3）质点作匀速圆周运动；（4）质点作匀加速圆周运动。

解：（1）所受合力为零；（2）所受合力为大小、方向均保持不变的力，其方向与运动方向相反；（3）所受合力为大小保持不变、方向不断改变总是指向圆心的力；（4）所受合力为大小和方向均不断变化的力，其切向力的方向与运动方向相同，大小恒定；法向力方向指向圆心。

10.1选择题(D) 回路L 上各点的H 仅与回路L 包围的电流有关。

［答案：C ］(2)对半径为R 载流为I 的无限长直圆柱体，距轴线 r 处的磁感应强度 B ()(A) 内外部磁感应强度 B 都与r 成正比；(B) 内部磁感应强度 B 与r 成正比，外部磁感应强度 B 与r 成反比； (C) 内外部磁感应强度 B 都与r 成反比；(D) 内部磁感应强度 B 与r 成反比，外部磁感应强度 B 与r 成正比。

［答案：B ］(3) 质量为m 电量为q 的粒子，以速率 v 与均匀磁场B 成B 角射入磁场，轨迹为一螺旋 线，若要增大螺距则要()(A ) 增加磁场B ； (B )减少磁场B ； ( C )增加B 角；(D )减少速率V 。

［答案：B ］(4) 一个100匝的圆形线圈，半径为5厘米，通过电流为 0.1安，当线圈在1.5T 的磁场中从9=0的位置转到180度(B 为磁场方向和线圈磁矩方向的夹角)时磁场力做功为() (A) 0.24J ； (B ) 2.4J ; ( C ) 0.14J ; ( D ) 14J 。

［答案：A ］10.2填空题(1)边长为a 的正方形导线回路载有电流为I ，则其中心处的磁感应强度习题10(1) 对于安培环路定理的理解,(A) 若环流等于零，则在回路 (B) 若环流等于零，则在回路(C) 若环流等于零，则在回路 正确的是： L 上必定是 H 处处为零;L 上必定不包围电流；L 所包围传导电流的代数和为零; ［答案:，方向垂直正方形平面(2)计算有限长的直线电流产生的磁场 理求得(填能或不能)。

［答案：能，不能］用毕奥——萨伐尔定律，而 用安培环路定(3)电荷在静电场中沿任一闭合曲线移动一周，电场力做功为 闭合曲线移动一周，磁场力做功为 ______ 。

［答案：零，正或负或零］____ 。

电荷在磁场中沿任(4)两个大小相同的螺线管一个有铁心一个没有铁心，当给两个螺线管通以 ___ 电流时,管内的磁力线 H 分布相同，当把两螺线管放在同一介质中， 管内的磁力线H 分布将［答案：相同，不相同］10.3在同一磁感应线上，各点 B 的数值是否都相等？为何不把作用于运动电荷的磁力方向 定义为磁感应强度B 的方向？解：在同一磁感应线上，各点 B 的数值一般不相等•因为磁场作用于运动电荷的磁力方向 不仅与磁感应强度 B 的方向有关，而且与电荷速度方向有关，即磁力方向并不是唯一由磁10.4 (1)在没有电流的空间区域里，如果磁感应线是平行直线，磁感应强度 B 的大小在沿磁感应线和垂直它的方向上是否可能变化 (即磁场是否一定是均匀的)?(2)若存在电流，上述结论是否还对？解:(1)不可能变化，即磁场一定是均匀的•如图作闭合回路abed 可证明B 1B 2B dl B-|da B 2 beI 0abedB 1 B 2(2)若存在电流，上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线，但B 方向相反，即B 1B 2.10.5 用安培环路定理能否求有限长一段载流直导线周围的磁场 ？答：不能，因为有限长载流直导线周围磁场虽然有轴对称性，但不是稳恒电流，安培环路 定理并不适用.10.6在载流长螺线管的情况下， 我们导出其内部 B °nl ,外面B =0,所以在载流螺线管 外面环绕一周(见题10.6图)的环路积分■■- L B 外• d l =0但从安培环路定理来看，环路 L 中有电流I 穿过，环路积分应为LB 外• d |=01这是为什么？场决定的，所以不把磁力方向定义为B 的方向.题10.3图2B S 2 0onl ,B 外 0有一个假设的前提， 即每匝电流均垂直于螺线管轴线. 这时图中环路L 上就一定没有电流通过，即也是 L B 外dl 0 I 0，与■l B 外 dl 0 dl 0是不矛盾的•但这是导线横截面积为零，螺距为零的理想模型•实际上以上假设并不真实存在，所以使得穿过L 的电流为I ，因此实际螺线管若是无限长时，只是B 外的轴向分量为零，而垂直于轴的圆周方向分量 B 丛，r 为管外一点到螺线管轴2 r的距离.10.7如果一个电子在通过空间某一区域时不偏转，能否肯定这个区域中没有磁场 ？如果它发生偏转能否肯定那个区域中存在着磁场？解：如果一个电子在通过空间某一区域时不偏转， 不能肯定这个区域中没有磁场，也可能存在互相垂直的电场和磁场， 电子受的电场力与磁场力抵消所致. 如果它发生偏转也不能肯定那个区域存在着磁场，因为仅有电场也可以使电子偏转.10.8 已知磁感应强度 B 2.0Wb ・m 2的均匀磁场，方向沿x 轴正方向，如题9-6图所示.试 ⑵ 通过图中befe 面的磁通量；(3)通过图中aefd 面的磁通量.(1)通过abed 面积的磁通是1 B 2.0 0.3 0.40.24 Wb⑵ 通过befe 面积S 2的磁通量(3)通过aefd 面积S 3的磁通量解：我们导出B 内求：(1)通过图中abed 面的磁通量; 题10.6 图解：如题10.8图所示题10.8图0 I 1 0 1 2B A0112 (0.1 0.05)B B2 (0.1 0.05)20.0551.33 10 T4B S 32 0.3 0.5 cos 2 0.3 0.5 —0.24 Wb (或 0.24 Wb )流，l 1=20A, l 2=10A ，如题10.10图所示.A , B 两点与导线在同一平面内.这两点与导线L 2的距离均为5.0cm .试求A , B 两点处的磁感应强度，以及磁感应强度为零的点的位置.■题 10.10 图解：如题10.10图所示,B A 方向垂直纸面向里10.9 如题10.9图所示,AB 、CD 为长直导线,BC为圆心在O 点的一段圆弧形导线，其半径为R .若通以电流 I ，求O 点的磁感应强度. 解：如题 10.9图所示,O 点磁场由AB 、BC 、CD 三部分电流产生•其中AB 产生 B 1 0CD 产生B 2』，方向垂直向里12RCD 段产生B 3—°^(sin90sin 60 )/ R 4 -2-），方向向里 210.10 在真空中,B 3hR (1i 3 6)，方向向里.有两根互相平行的无限长直导线 ，相距0.1m ，通有方向相反的电题10.9图O11 =20A题10.12图⑵设B 0在L 2外侧距离L 2为r 处I_[_2 2 (r 0.1)2 rr 0.1 m|2产生B 2方向纸面向里 打(2)1B 21 210.12 在一半径R =1.0cm 的无限长半圆柱形金属薄片中，自上而下地有电流 1=5.0 A 通过，电流分布均匀.如题10.12图所示•试求圆柱轴线任一点P 处的磁感应强度.则解得10.11如题10.11图所示，两根导线沿半径方向引向铁环上的 源相连•已知圆环的粗细均匀，求环中心O 的磁感应强度.A ,B 两点，并在很远处与电解：如题10.11图所示，圆心O 点磁场由直电流 A 和B 及两段圆弧上电流|1与|2所产生，但A 和B 在O 点产生的磁场为零。

篇一：大学物理学北京邮电·第3版.修订版下册习题答案习题99.3 电量都是q的三个点电荷，分别放在正三角形的三个顶点．试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解: 如题9.3图示(1) 以A处点电荷为研究对象，由力平衡知：q?为负电荷1q212cos304π?0a24π?0qq?(2a)3解得q?3q 3(2)与三角形边长无关．题9.3图题9.4图9.4 两小球的质量都是m，都用长为l的细绳挂在同一点，它们带有相同电量，静止时两线夹角为2? ,如题9.4图所示．设小球的半径和线的质量都可以忽略不解: 如题9.4图示Tcosmg??q2 ?TsinF?1e?4π?0(2lsin?)2?解得 q?2lsin?40mgtan? 9.5 根据点电荷场强公式E?q40r2，当被考察的场点距源点电荷很近(r→0)时，则场强→∞，这是没有物理意义的，对此应如何理解??解: E?q4π?0r2?r0仅对点电荷成立，当r?0时，带电体不能再视为点电荷，再用上式求场强是错误的，实际带电体有一定形状大小，考虑电荷在带电体上的分布求出的场强不会是无限大．19.6 在真空中有A，B两平行板，相对距离为d，板面积为S，其带电量分别为+q和-q．则这两板之间有相互作用力f，有人说f=q240d2,又有人说，因为qq2，所以f=．试问这两种说法对吗?为什么? f到底应等于f=qE,E0S?0S多少?解: 题中的两种说法均不对．第一种说法中把两带电板视为点电荷是不对的，第二种说法把合场强E?q看成是一个带电板在另一带电板处的场强也是不对?0Sq2?0S的．正确解答应为一个板的电场为E?，另一板受它的作用力q2，这是两板间相互作用的电场力． f?q?2?0S2?0Sq9.7 长l=15.0cmAB上均匀地分布着线密度?=5.0x10-9C·m-1荷．试求：(1)在导线的延长线上与导线B端相距a1=5.0cm处P点的场强；(2)在导线的垂直平分线上与导线中点相距d2=5.0cm 处Q解：如题9.7图所示(1) 在带电直线上取线元dx，其上电量dq在P点产生场强为dEP?1?dx24π?0(a?x)?EPdEP?4π?0?l2l?2dx题9.7图 2(a?x)??1[?]ll4π?0a?a?221??lπ?0(4a2?l2)2用l?15cm，5.0?10?9C?m?1, a?12.5cm代入得EP?6.74?102N?C?1方向水平向右(2)dEQ?1?dx方向如题9.7图所示 224π?0x?d2由于对称性?dEQx?0，即EQ只有y分量，l∵ dEQy1?dx?4π?0x2?d22d2x?d222EQydEQyld24π?2?l2l?2dx(x2?d22)32??l2π?0l?4d222以5.0?10?9C?cm?1, l?15cm,d2?5cm代入得EQ?EQy?14.96?102N?C?1，方向沿y轴正向9.8 一个半径为R的均匀带电半圆环，电荷线密度为?,求环心处O点的场强．解: 如9.8图在圆上取dl?Rd?题9.8图dqdl?R?d?，它在O点产生场强大小为dE??Rd?方向沿半径向外4π?0R2则 dEx?dEsin?sin?d?4π?0Rcos?d? 4π?0R3dEy?dEcos(?)?积分Ex?sin?d4π?0R2π?0REycos?d0 4π?0R∴ E?Ex??，方向沿x轴正向．2π?0R9.9 均匀带电的细线弯成正方形，边长为l，总电量为q．(1)求这正方形轴线上离中心为r处的场强E；(2)证明：在rl处，它相当于点电荷q产生的场强E解: 如9.9图示，正方形一条边上电荷?q在P点产生物强dEP方向如图，大小为 4dEP?cos?1?cos?2?4π?0r2?lr2?l22l42∵ cos?1?cos?2cos?1∴ dEP??4π?0r2?l42lr2?l22?dEP在垂直于平面上的分量dEdEPcos? ∴dE?l4π?0r2?l42rr2?l22r2?l424题9.9图由于对称性，P点场强沿OP方向，大小为EP?4?dE4?lr4π?0(r2?ll)r2?4222∵∴ EP?q 4lqr4π?0(r2?ll)r2?4222方向沿OP9.10(1)点电荷q位于一边长为a的立方体中心，试求在该点电荷电场中穿过立方体的一个面的电通量；(2)如果该场源点电荷移动到该立方体的一个顶点上，这时穿过立方体各面的电通量是多少?q解: (1)由高斯定理E?dS?s?0立方体六个面，当q在立方体中心时，每个面上电通量相等∴各面电通量?e?q． 6?0(2)电荷在顶点时，将立方体延伸为边长2a的立方体，使q处于边长2a的立方体中心，则边长2a的正方形上电通量?e?q 6?0q， 24?0对于边长a的正方形，如果它不包含q所在的顶点，则?e?如果它包含q所在顶点则?e?0．如题9.10图所示．题9.10图9.11 均匀带电球壳内半径6cm，外半径10cm，电荷体密度为2×10?5C·m-3求距球心5cm，8cm ,12cm 各点的场强．5篇二：大学物理学(第三版)上课后习题答案第一章运动的描述｜与有无不同?1-1 ｜和有无不同? 和有无不同?其不同在哪里?试举例说明．解：（1）是位移的模，是位矢的模的增量，即，（2）是速度的模，即.只是速度在径向上的分量.∵有（式中叫做单位矢），则式中就是速度径向上的分量，∴不同如题1-1图所示.题1-1图(3)表示加速度的模，即，是加速度在切向上的分量.∵有表轨道节线方向单位矢），所以式中就是加速度的切向分量.(的运算较复杂，超出教材规定，故不予讨论)；1-2 设质点的运动方程为=()，=()，在计算质点的速度和加速度时，有人先求出r＝，然后根据=，及＝计算速度和加速度的分量，再合成求得结果，即而求得结果；又有人先=及=你认为两种方法哪一种正确？为什么？两者差别何在？解：后一种方法正确.因为速度与加速度都是矢量，在平面直角坐标系中，有，故它们的模即为而前一种方法的错误可能有两点，其一是概念上的错误，即误把速度、加速度定义作其二，可能是将误作速度与加速度的模。

习题55.1选择题(1)一物体作简谐振动，振动方程为)2cos(πω+=t A x ，则该物体在0=t 时刻的动能与8/T t =（T 为振动周期）时刻的动能之比为： (A)1：4 （B ）1：2 （C ）1：1 (D) 2：1[答案：D](2)弹簧振子在光滑水平面上作简谐振动时，弹性力在半个周期内所作的功为 (A)kA 2 (B) kA 2/2 (C) kA 2//4 (D)0[答案：D](3)谐振动过程中，动能和势能相等的位置的位移等于 (A)4A ±(B) 2A± (C) 23A±(D) 22A ± [答案：D]5.2 填空题(1)一质点在X 轴上作简谐振动，振幅A ＝4cm ，周期T ＝2s ，其平衡位置取作坐标原点。

若t ＝0时质点第一次通过x ＝－2cm 处且向X 轴负方向运动，则质点第二次通过x ＝－2cm 处的时刻为____s 。

[答案：23s ](2)一水平弹簧简谐振子的振动曲线如题5.2(2)图所示。

振子在位移为零，速度为－ωA 、加速度为零和弹性力为零的状态，对应于曲线上的____________点。

振子处在位移的绝对值为A 、速度为零、加速度为－ω2A 和弹性力为－KA 的状态，则对应曲线上的____________点。

题5.2(2) 图[答案：b 、f ； a 、e](3)一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点，已知周期为T ，振幅为A 。

(a)若t=0时质点过x=0处且朝x 轴正方向运动，则振动方程为x=___________________。

(b) 若t=0时质点过x=A/2处且朝x 轴负方向运动，则振动方程为x=_________________。

[答案：cos(2//2)x A t T ππ=-； cos(2//3)x A t T ππ=+]5.3 符合什么规律的运动才是谐振动?分别分析下列运动是不是谐振动： (1)拍皮球时球的运动；(2)如题5.3图所示，一小球在一个半径很大的光滑凹球面内滚动(设小球所经过的弧线很 短)．题5.3图 题5.3图(b)解：要使一个系统作谐振动，必须同时满足以下三个条件：一 ，描述系统的各种参量，如质量、转动惯量、摆长……等等在运动中保持为常量；二，系统是在自己的稳定平衡位置附近作往复运动；三，在运动中系统只受到内部的线性回复力的作用． 或者说，若一个系统的运动微分方程能用0d d 222=+ξωξt描述时，其所作的运动就是谐振动．(1)拍皮球时球的运动不是谐振动．第一，球的运动轨道中并不存在一个稳定的平衡位置； 第二，球在运动中所受的三个力：重力，地面给予的弹力，击球者给予的拍击力，都不是线性回复力．(2)小球在题5.3图所示的情况中所作的小弧度的运动，是谐振动．显然，小球在运动过程中，各种参量均为常量；该系统(指小球凹槽、地球系统)的稳定平衡位置即凹槽最低点，即系统势能最小值位置点O ；而小球在运动中的回复力为θsin mg -，如题5.3图(b)中所示，因S ∆＜＜R ，故RS∆=θ→0，所以回复力为θmg -.式中负号，表示回复力的方向始终与角位移的方向相反．即小球在O 点附近的往复运动中所受回复力为线性的．若以小球为对象，则小球在以O '为圆心的竖直平面内作圆周运动，由牛顿第二定律，在凹槽切线方向上有θθmg tmR -=22d d令Rg=2ω，则有 222d 0d tθωθ+=5.4 弹簧振子的振幅增大到原振幅的两倍时，其振动周期、振动能量、最大速度和最大加速度等物理量将如何变化？解：弹簧振子的振动周期、振动能量、最大速度和最大加速度的表达式分别为222122,m m T E kA v A a Aππωωω===== 所以当振幅增大到原振幅的两倍时，振动周期不变，振动能量增大为原来的4倍，最大速度增大为原来的2倍，最大加速度增大为原来的2倍。

---○---○------○---○---……… 评卷密封线…………… 密封线内不要答题，密封线外不准填写考生信息，违者考试成绩按0分处理…………… 评卷密封………线 ………中南大学考试试卷2019 ~2020 学年二学期 大学物理 Ⅲ 课程 时间100分钟 72学时，4.5学分，闭卷，总分100分，占总评成绩 70 %题 号一二三（1） 三（2） 三（3）合计得 分评卷人 复查人一、选择题（共30分，每小题3分）1． 水在粗细均匀虹吸管中流动时，如图中四点的压强关系是（A ）4321P P P P === （B ）4321P P P P <<< （C ）3241P P P P =>= （D ）4321P P P P <==［ ］ 2．某元素的特征光谱中含有波长分别为1λ＝450 nm 和2λ＝750 nm (1 nm ＝10-9 m)的光谱线。

在光栅光谱中，这两种波长的谱线有重叠现象，重叠处2λ的谱线的级数将是 (A) 2 ，3 ，4 ，5 ．．．．．． (B) 2 ，5 ，8 ，11．．．．．． (C) 2 ，4 ，6 ，8 ．．．．．． (D) 3 ，6 ，9 ，12．．．．．． ［ ］得 分 评卷人3．图中MN 为某理想气体的绝热曲线，ABC 是任意过程，箭头方向表示过程进行的方向，ABC 过程结束后气体的温度和吸收的热量为（A ）温度升高，吸热为正 （B ）温度升高，吸热为负（C ）温度降低，吸热为正 （D ）温度降低，吸热为负［ ］4．一简谐波沿x 轴正方向传播，t = T /4时的波形曲线如图所示．若振动以余弦函数表示，且此题各点振动的初相取-π 到π 之间的值，则 (A) O 点的初相为00=φ (B) 1点的初相为π-=211φ (C) 2点的初相为π=2φ (D) 3点的初相为π-=213φ ［ ］5．用单色光垂直照射在观察牛顿环的装置上．如图，当平凸透镜垂直向上缓慢平移而远离平面玻璃时，可以观察到这些环状干涉条纹（Ａ）向右平移 （Ｂ）向中心收缩 （Ｃ）向外扩张 （D ）向左平移6．一定量理想气体保持压强不变，则气体分子的平均碰撞频率z 和平均自由程λ与气体温度T 的关系为（A ）z 正比于T /1，λ正比于T （B ）z 正比于T ，λ正比于1/T（C ）z 正比于T ，λ正比于1/T （D ）z 与T 无关，λ正比于TxO 1u y 234空气单色光7．一金属球壳的内外半径分别为R 1和R 2，其中心放一点电荷q ，则金属球壳的电势为（A ）104/R q πε（B ）204/R q πε （C ）()120///8q R q R πε+（D ）)(2210R R q +πε8．如图所示，四分之一圆形线圈半径为R ，通有电流I ，在均匀磁场B 的作用下，从图示位置转过30°时，它所受磁力矩的大小与方向分别为 （A ）82IB R π，沿图面竖直向下 （B ）82IBR π，沿图面竖直向上（C ）832IB R π，沿图面竖直向下 （D ）832IB R π，沿图面竖直向上 9．一艘以0.9c 的速率离开地面的宇宙飞船，以相对于自己0.8c 的速率向前发射一枚导弹，则该导弹相对于地球的速率为（A ）1.7c （B ）0.988c （C ）0.1c （D ）0.357c10．一个电子的运动速度为v =0.99c ，则该电子的动能E k 为（电子的静止能量为0.51Mev ） （A ）3.5Mev （B ）4.0Mev （C ）3.1Mev （D ）2.5Mev二、填空题（共40分）1．（本题6分）一横波沿绳子传播时的波动方程为：),410cos(1.0x t S ππ-= 式中：s 、x 以米计，t 以秒计。

⼤学物理学_第3版（课后答案）__习题⼆习题⼆2-1 ⼀细绳跨过⼀定滑轮，绳的⼀边悬有⼀质量为1m 的物体，另⼀边穿在质量为2m 的圆柱体的竖直细孔中，圆柱可沿绳⼦滑动．今看到绳⼦从圆柱细孔中加速上升，柱体相对于绳⼦以匀加速度a '下滑，求1m ，2m 相对于地⾯的加速度、绳的张⼒及柱体与绳⼦间的摩擦⼒(绳轻且不可伸长，滑轮的质量及轮与轴间的摩擦不计)．解：因绳不可伸长，故滑轮两边绳⼦的加速度均为1a ，其对于2m 则为牵连加速度，⼜知2m 对绳⼦的相对加速度为a '，故2m 对地加速度，由图(b)可知，为a a a '-=12 ①⼜因绳的质量不计，所以圆柱体受到的摩擦⼒f 在数值上等于绳的张⼒T ，由⽜顿定律，有111a m T g m =- ②222a m g m T =- ③联⽴①、②、③式，得2121211212212211)2()()(m m a g m m T f m m a m g m m a m m a m g m m a +'-==+'--=+'+-=讨论 (1)若0='a ，则21a a =表⽰柱体与绳之间⽆相对滑动．(2)若g a 2='，则0==f T ，表⽰柱体与绳之间⽆任何作⽤⼒，此时1m , 2m 均作⾃由落体运动．题2-1图2-2 ⼀个质量为P 的质点，在光滑的固定斜⾯（倾⾓为α）上以初速度0v 运动，0v 的⽅向与斜⾯底边的⽔平线AB 平⾏，如图所⽰，求这质点的运动轨道．解: 物体置于斜⾯上受到重⼒mg ，斜⾯⽀持⼒N .建⽴坐标：取0v⽅向为X 轴，平⾏斜⾯与X 轴垂直⽅向为Y 轴.如图2-2.题2-2图X ⽅向： 0=x F t v x 0= ①Y ⽅向： y y ma mg F ==αsin ②0=t 时 0=y 0=y vt g y α=由①、②式消去t ，得220sin 21x g v y ?=α2-3 质量为16 kg 的质点在xOy 平⾯内运动，受⼀恒⼒作⽤，⼒的分量为x f ＝6N ，y f ＝-7 N ，当t ＝0时，==y x 0，x v ＝-2 m ·s -1，y v ＝0．求当t ＝2 s 时质点的 (1)位⽮；(2)速度．解：2s m 83166-?===m f a x x 2s m 167-?-==m f a y y(1)--?-=?-=+=?-=?+-=+=20101200s m 872167s m 452832dt a v v dt a v v y y y x x x于是质点在s 2时的速度1s m 8745-?--=ji v(2)m874134)167(21)4832122(21)21(2t a i t a t v r y x --=?-+??+?-=++=2-4 质点在流体中作直线运动，受与速度成正⽐的阻⼒kv (k 为常数)作⽤，t =0时质点的速度为0v ，证明(1) t 时刻的速度为v ＝t mk ev )(0-；(2) 由0到t 的时间内经过的距离为x ＝(k m v 0)［1-t m ke )(-］；(3)停⽌运动前经过的距离为)(0k m v ；(4)证明当k m t =时速度减⾄0v 的e 1，式中m 为质点的质量．答: (1)∵t v m kv a d d =-= 分离变量，得m t k v v d d -= 即-=v v t m tk v v 00d dmkt e v v -=ln ln 0∴tm k e v v -=0(2)---===tttm k m ke k mv t ev t v x 000)1(d d(3)质点停⽌运动时速度为零，即t →∞，故有='00d k m v t ev x tm k(4)当t=k m时，其速度为e v e v ev v kmm k 0100===-?-即速度减⾄0v 的e 1.2-5 升降机内有两物体，质量分别为1m ，2m ，且2m ＝21m ．⽤细绳连接，跨过滑轮,绳⼦不可伸长，滑轮质量及⼀切摩擦都忽略不计，当升降机以匀加速a ＝21g 上升时，求：(1) 1m 和2m 相对升降机的加速度．(2)在地⾯上观察1m ，2m 的加速度各为多少?解: 分别以1m ,2m 为研究对象，其受⼒图如图(b)所⽰．(1)设2m 相对滑轮(即升降机)的加速度为a '，则2m 对地加速度a a a -'=2；因绳不可伸长，故1m 对滑轮的加速度亦为a '，⼜1m 在⽔平⽅向上没有受牵连运动的影响，所以1m 在⽔平⽅向对地加速度亦为a '，由⽜顿定律，有)(22a a m T g m -'=-a m T '=1题2-5图联⽴，解得g a ='⽅向向下 (2) 2m 对地加速度为22ga a a =-'= ⽅向向上1m 在⽔⾯⽅向有相对加速度，竖直⽅向有牵连加速度，即牵相绝a a a+=' ∴ gg g a a a 25422221=+=+'=arctan ==，左偏上．2-6⼀质量为m 的质点以与地的仰⾓θ=30°的初速0v 从地⾯抛出，若忽略空⽓阻⼒，求质点落地时相对抛射时的动量的增量．解: 依题意作出⽰意图如题2-6图题2-6图在忽略空⽓阻⼒情况下，抛体落地瞬时的末速度⼤⼩与初速度⼤⼩相同，与轨道相切斜向下, ⽽抛物线具有对y 轴对称性，故末速度与x 轴夹⾓亦为o30，则动量的增量为0v m v m p -=?由⽮量图知，动量增量⼤⼩为0v m ，⽅向竖直向下．2-7 ⼀质量为m 的⼩球从某⼀⾼度处⽔平抛出，落在⽔平桌⾯上发⽣弹性碰撞．并在抛出1 s ，跳回到原⾼度，速度仍是⽔平⽅向，速度⼤⼩也与抛出时相等．求⼩球与桌⾯碰撞过程中，桌⾯给予⼩球的冲量的⼤⼩和⽅向．并回答在碰撞过程中，⼩球的动量是否守恒? 解: 由题知，⼩球落地时间为s 5.0．因⼩球为平抛运动，故⼩球落地的瞬时向下的速度⼤⼩为g gt v5.01==，⼩球上跳速度的⼤⼩亦为g v 5.02=．设向上为y 轴正向，则动量的增量12v m v m p-=?⽅向竖直向上，⼤⼩ mgmv mv p =--=?)(12碰撞过程中动量不守恒．这是因为在碰撞过程中，⼩球受到地⾯给予的冲⼒作⽤．另外，碰撞前初动量⽅向斜向下，碰后末动量⽅向斜向上，这也说明动量不守恒．2-8 作⽤在质量为10 kg 的物体上的⼒为i t F)210(+=N ，式中t 的单位是s ，(1)求4s 后，这物体的动量和速度的变化，以及⼒给予物体的冲量．(2)为了使这⼒的冲量为200 N ·s ，该⼒应在这物体上作⽤多久，试就⼀原来静⽌的物体和⼀个具有初速度j6-m ·s -1的物体,回答这两个问题．解: (1)若物体原来静⽌，则it i t t F p t10401s m kg 56d )210(d -??=+==,沿x 轴正向，i p I im p v11111+-=+-=-=t t tF v m t m F v m p v m p 000000d )d (,于是 ??==-=?t p t F p p p 0102d, 同理， 12v v=,12I I = 这说明，只要⼒函数不变，作⽤时间相同，则不管物体有⽆初动量，也不管初动量有多⼤，那么物体获得的动量的增量(亦即冲量)就⼀定相同，这就是动量定理． (2)同上理，两种情况中的作⽤时间相同，即+=+=tt t t t I 0210d )210(亦即 0200102=-+t t 解得s 10=t ，(s 20='t 舍去)2-9 ⼀质量为m 的质点在xOy 平⾯上运动，其位置⽮量为j t b i t a rωωsin cos +=求质点的动量及t ＝0 到ωπ2=t 时间内质点所受的合⼒的冲量和质点动量的改变量．解: 质点的动量为)cos sin (j t b i t a m v m pωωω+-==将0=t 和ωπ2=t 分别代⼊上式，得j b m pω=1,i a m p ω-=2,则动量的增量亦即质点所受外⼒的冲量为)(12j b i a m p p p I+-=-=?=ω2-10 ⼀颗⼦弹由枪⼝射出时速率为1试计算⼦弹⾛完枪筒全长所需时间；(2)求⼦弹所受的冲量．(3)求⼦弹的质量．解: (1)由题意，⼦弹到枪⼝时，有0)(=-=bt a F ,得b a t =(2)⼦弹所受的冲量-=-=t bt at t bt a I 0221d )(将b at =代⼊，得b a I 22=(3)由动量定理可求得⼦弹的质量0202bv a v I m ==2-11 ⼀炮弹质量为m ，以速率v 飞⾏，其内部炸药使此炮弹分裂为两块，爆炸后由于炸药使弹⽚增加的动能为T ，且⼀块的质量为另⼀块质量的k 倍，如两者仍沿原⽅向飞⾏，试证其速率分别为v +m kT 2, v -km T 2证明: 设⼀块为1m ，则另⼀块为2m ，21km m =及m m m =+21于是得1,121+=+=k mm k km m ①⼜设1m 的速度为1v , 2m 的速度为2v ，则有2222211212121mv v m v m T -+=②2211v m v m mv += ③联⽴①、③解得12)1(kv v k v -+= ④将④代⼊②，并整理得21)(2v v km Tv v 21±= 将其代⼊④式，有m kT v v 22±=⼜，题述爆炸后，两弹⽚仍沿原⽅向飞⾏，故只能取km Tv v m kT v v 2,221-=+=证毕．2-12 设N 67j i F -=合．(1) 当⼀质点从原点运动到m 1643k j i r ++-=时，求F所作的功．(2)如果质点到r 处时需0.6s ，试求平均功率．(3)如果质点的质量为1kg ，试求动能的变化．解: (1)由题知，合F 为恒⼒，∴ )1643()67(k j i j i r F A++-?-=?=合J 452421-=--=(2) w756.045==?=t A P(3)由动能定理，J45-==?A E k2-13 以铁锤将⼀铁钉击⼊⽊板，设⽊板对铁钉的阻⼒与铁钉进⼊⽊板内的深度成正⽐，在铁锤击第⼀次时，能将⼩钉击⼊⽊板内1 cm ，问击第⼆次时能击⼊多深，假定铁锤两次打击铁钉时的速度相同．解: 以⽊板上界⾯为坐标原点，向内为y 坐标正向，如题2-13图，则铁钉所受阻⼒为题2-13图ky f -=第⼀锤外⼒的功为1A==-='=s s ky ky y f y f A 1=21222221d y k ky y ky A ②由题意，有2)21(212kmv A A === ③即 222122k k ky =- 所以， 22=y于是钉⼦第⼆次能进⼊的深度为cm 414.01212=-=-=?y y y2-14 设已知⼀质点(质量为m )在其保守⼒场中位⽮为r 点的势能为nP r k r E /)(=, 试求质点所受保守⼒的⼤⼩和⽅向．解:1d )(d )(+-==n r nkr r E r F⽅向与位⽮r的⽅向相反，即指向⼒⼼．2-15 ⼀根劲度系数为1k 的轻弹簧A 的下端，挂⼀根劲度系数为2k 的轻弹簧B ，B 的下端⼀重物C ，C 的质量为M ，如题2-15图．求这⼀系统静⽌时两弹簧的伸长量之⽐和弹性势能之⽐．解: 弹簧B A 、及重物C 受⼒如题2-15图所⽰平衡时，有题2-15图Mg F F B A ==⼜ 11x k F A ?=22x k F B ?= 所以静⽌时两弹簧伸长量之⽐为1221k k x x =??11121212k kx k x k E E p p =??=2-16 (1)试计算⽉球和地球对m 物体的引⼒相抵消的⼀点P ，距⽉球表⾯的距离是多少?地球质量5.98×1024kg ，地球中⼼到⽉球中⼼的距离3.84×108m ，⽉球质量7.35×1022kg ，⽉球半径1.74×106m ．(2)如果⼀个1kg 的物体在距⽉球和地球均为⽆限远处的势能为零，那么它在P 点的势能为多少? 解: (1)设在距⽉球中⼼为r 处地引⽉引F F =，由万有引⼒定律，有()22r R mM Gr mM G-=地⽉经整理，得RM M M r ⽉地⽉+==2224221035.71098.51035.7?+??81048.3??m 1032.386= 则P 点处⾄⽉球表⾯的距离为m 1066.310)74.132.38(76?=?-=-=⽉r r h(2)质量为kg 1的物体在P 点的引⼒势能为()r R M GrM G E P ---=地⽉()724111083.34.381098.51067.61083.31035.71067.6?-??--=- J 1028.16=2-17 由⽔平桌⾯、光滑铅直杆、不可伸长的轻绳、轻弹簧、理想滑轮以及质量为1m 和2m 的滑块组成如题2-17图所⽰装置，弹簧的劲度系数为k ，⾃然长度等于⽔平距离BC ，2m 与桌⾯间的摩擦系数为µ，最初1m 静⽌于A 点，AB ＝BC ＝h ，绳已拉直，现令滑块落下1m ,求它下落到B 处时的速率．解: 取B 点为重⼒势能零点，弹簧原长为弹性势能零点，则由功能原理，有])(21[)(21212212l k gh m v m m gh m ?+-+=-µ式中l ?为弹簧在A 点时⽐原长的伸长量，则 h BC AC l )12(-=-=? 联⽴上述两式，得()()212221122m m kh gh m m v +-+-=µ题2-17图2-18 如题2-18图所⽰，⼀物体质量为2kg ，以初速度0v＝3m ·s -1从斜⾯A 点处下滑，它与斜⾯的摩擦⼒为8N ，到达B 点后压缩弹簧20cm 后停⽌，然后⼜被弹回，求弹簧的劲度系数和物体最后能回到的⾼度．解: 取⽊块压缩弹簧⾄最短处的位置为重⼒势能零点，弹簧原长处为弹性势能零点。