最新北师大版八年级数学(下册)【第一章三角形的证明】测试题【1】

北师大版八年级下册数学第一章三角形的证明评卷人得分一、单选题1．等腰三角形的两边长分别为3和6，则这个等腰三角形的周长为（）A．12B．15C．12或15D．182．如图，在△ABC和△DEC中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是A．BC=EC，∠B=∠E B．BC=EC，AC=DCC．BC=DC，∠A=∠D D．∠B=∠E，∠A=∠D3．下列命题的逆命题是真命题的是（）A．如果a＞0，b＞0，则a+b＞0B．直角都相等C．两直线平行，同位角相等D．若a=b，则|a|=|b|4．如图一艘轮船由海平面上A地出发向南偏西40°的方向行驶40海里到达B地，再由B 地向北偏西20°的方向行驶40海里到达C地，则A、C两地相距（）A．30海里B．40海里C．50海里D．60海里5．如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP的长不可能是()A．3.5B．4.2C．5.8D．76．如图，以∠AOB的顶点O为圆心，适当长为半径画弧，交OA于点C，交OB于点D．再分别以点C、D为圆心，大于12CD的长为半径画弧，两弧在∠AOB内部交于点E，过点E作射线OE，连接CD．则下列说法错误的是A．射线OE是∠AOB的平分线B．△COD是等腰三角形C．C、D两点关于OE所在直线对称D．O、E两点关于CD所在直线对称7．如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC＝24，DE＝4，AB ＝7，则AC长是（）A．3B．4C．6D．58．如图，长方体的底面边长分别为2cm和3cm，高为6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈达到点B，那么所用细线最短需要（）A．11cm B．C．（）cm D．（cm评卷人得分二、填空题9．已知等腰三角形的一个底角为70°，则它的顶角为_______.10．用反证法证明“一个三角形不可能有两个直角”时，第一步应假设：_______________________；11．如图，已知OC平分∠AOB，CD∥OB，若OD＝6cm，则CD的长为________cm.12．如图，△ABC中，AB+AC=6cm，BC的垂直平分线l与AC相交于点D，则△ABD的周长为___cm．13．如图，在长方形ABCD中，AB＝2，BC＝3，对角线AC的垂直平分线分别交AD，BC 于点E，F，连接CE，则CE的长为________．14．如图，∠AOB=60°，C是BO延长线上的一点，OC=10cm，动点P从点C出发沿CB 以2cm/s的速度移动，动点Q从点O发沿OA以1cm/s的速度移动，如果点P、Q同时出发，用t（s）表示移动的时间，当t=时，△POQ是等腰三角形．评卷人得分三、解答题15．如图，Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于E，若AC=6，BC=8，CD=3．（1）求DE的长；（2）求△ADB的面积．16．如图，AD为△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF交AD于点O．(1)求证：AD垂直平分EF；(2)若∠BAC=60 ，写出DO与AD之间的数量关系，不需证明．17．如图，在等边三角形ABC中，D是AB边上的动点，以CD为一边，向上作等边三角形EDC，连接AE.(1)△DBC和△EAC全等吗？请说出你的理由；(2)试说明AE∥BC.18．如图，在△ABC中，∠A=90º，∠B=30º，AC=6厘米，点D从点A开始以1厘米/秒的速度向点C运动，点E从点C开始以2厘米/秒的速度向点B运动，两点同时运动，同时停止，运动时间为t秒；过点E作EF//AC交AB于点F；（1）当t为何值时，△DEC为等边三角形？（2）当t为何值时，△DEC为直角三角形？（3）求证：DC=EF；参考答案1．B【解析】试题分析：根据题意，要分情况讨论：①、3是腰；②、3是底．必须符合三角形三边的关系，任意两边之和大于第三边．解：①若3是腰，则另一腰也是3，底是6，但是3+3=6，∴不构成三角形，舍去．②若3是底，则腰是6，6．3+6＞6，符合条件．成立．∴C=3+6+6=15．故选B．考点：等腰三角形的性质．2．C【解析】试题分析：根据全等三角形的判定方法分别进行判定：A、已知AB=DE，加上条件BC=EC，∠B=∠E可利用SAS证明△ABC≌△DEC，故此选项不合题意；B、已知AB=DE，加上条件BC=EC，AC=DC可利用SSS证明△ABC≌△DEC，故此选项不合题意；C、已知AB=DE，加上条件BC=DC，∠A=∠D不能证明△ABC≌△DEC，故此选项符合题意；D、已知AB=DE，加上条件∠B=∠E，∠A=∠D可利用ASA证明△ABC≌△DEC，故此选项不合题意．故选C．3．C【解析】【分析】先写出每个命题的逆命题，再进行判断即可．【详解】解：A．逆命题为：如果a+b＞0，则a＞0，b＞0，是假命题；B．逆命题为：相等的角是直角，是假命题；C．逆命题为：同位角相等，两直线平行，是真命题；D．逆命题为：若|a|=|6|，则a=6，是假命题．故选C．【点睛】此题考查了命题与定理，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题．正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．4．B【解析】【分析】由已知可得△ABC是等边三角形，从而不难求得AC的距离．【详解】由题意得∠ABC=60°，AB=BC=40∴△ABC是等边三角形∴AC=AB=40海里．故选B．5．D【解析】【详解】解：根据垂线段最短，可知AP的长不可小于3∵△ABC中，∠C=90°，AC=3，∠B=30°，∴AB=6，∴AP的长不能大于6．≤≤∴3PA6故选D．6．D【解析】试题分析：A、连接CE、DE，根据作图得到OC=OD，CE=DE．∵在△EOC与△EOD中，OC=OD，CE=DE，OE=OE，∴△EOC≌△EOD（SSS）．∴∠AOE=∠BOE，即射线OE是∠AOB的平分线，正确，不符合题意．B、根据作图得到OC=OD，∴△COD是等腰三角形，正确，不符合题意．C、根据作图得到OC=OD，又∵射线OE平分∠AOB，∴OE是CD的垂直平分线．∴C、D两点关于OE所在直线对称，正确，不符合题意．D、根据作图不能得出CD平分OE，∴CD不是OE的平分线，∴O、E两点关于CD所在直线不对称，错误，符合题意．故选D．7．D【解析】【分析】作DF⊥AC于F，如图，根据角平分线定理得到DE＝DF＝4，再利用三角形面积公式和S△ADB＋S△ADC ＝S△ABC得到12×4×7＋12×4×AC＝24，然后解一次方程即可．【详解】作DF⊥AC于F，如图，∵AD是△ABC中∠BAC的角平分线，DE⊥AB，DF⊥AC，∴DE＝DF＝4，∵S△ADB＋S△ADC＝S△ABC，∴12×4×7＋12×4×AC＝24，∴AC＝5，故选：D．【点睛】本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等，三角形的面积公式等知识，解题的关键是学会添加常用辅助线，学会利用面积法构建方程解决问题，属于中考常考题型．8．B【解析】要求所用细线的最短距离，需将长方体的侧面展开，进而根据“两点之间线段最短”得出结果．解：将长方体展开,连接AB′，则AB′最短.∵AA′=3+2+3+2=10cm，A′B′=6cm，∴AB=故选B..9．40°【解析】∵等腰三角形的一个底角为70°∴顶角=180°−70°×2=40°.故答案为40°10．在一个三角形中，有两个角是直角【解析】【详解】用反证法证明命题“在一个三角形中，不能有两个内角为直角”时，应假设“在一个三角形中，可以有两个内角为直角”．故答案为：在一个三角形中，可以有两个内角为直角．【点睛】反证法：第一步应假设假设结论不成立.11．6cm【解析】∵OC平分∠AOB，∴∠AOC=∠BOC；又∵CD∥OB，∴∠C=BOC，∴∠C=∠AOC；∴CD=OD=6cm.故答案为6cm.点睛：本题考查了等腰三角形的判定定理和性质定理以及平行线的性质，角平分线的定义，注意等腰三角形的判定定理：等角对等边，出现角平分线和平行线容易出现等腰三角形. 12．6【解析】【详解】∵l垂直平分BC，∴DB=DC．∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=6cm13．13 6【解析】EF垂直且平分AC，故AE=EC，AO=OC．所以△AOE≌△COE．设CE为x．则DE=AD-x，CD=AB=2．根据勾股定理可得x2=（3-x）2+22解得CE=13/6．14．103s@10s【解析】根据等腰三角形的判定，分两种情况：（1）当点P在线段OC上时；（2）当点P在CO的延长线上时．分别列式计算即可求．解：分两种情况：（1）当点P在线段OC上时，设t时后△POQ是等腰三角形，有OP=OC﹣CP=OQ，即10﹣2x=x，解得，x=103s；（2）当点P在CO的延长线上时，此时经过CO时的时间已用5s，有OQ=OP，即2（x﹣5）=x，解得，x=10s故填103s或10s．15．（1）DE=3；（2）ADB S 15∆=.【解析】【分析】（1）根据角平分线性质得出CD=DE ，代入求出即可；（2）利用勾股定理求出AB 的长，然后计算△ADB 的面积.【详解】（1）∵AD 平分∠CAB ，DE ⊥AB ，∠C=90°，∴CD=DE ，∵CD=3，∴DE=3；（2）在Rt △ABC 中，由勾股定理得：AB 10===，∴△ADB 的面积为ADB 11S AB DE 1031522∆=⋅=⨯⨯=.16．（1）见解析；（2）14DO AD =【解析】试题分析：（1）由AD 为△ABC 的角平分线，得到DE=DF ，推出∠AEF 和∠AFE 相等，得到AE=AF ，即可推出结论；（2）由已知推出∠EAD=30°，得到AD=2DE ，在△DEO 中，由∠DEO=30°推出DE=2DO ，即可推出结论．试题解析：（1）∵AD 为△ABC 的角平分线，DE ⊥AB ，DF ⊥AC ，∴DE=DF ，∠AED=∠AFD=90°，∴∠DEF=∠DFE ，∴∠AEF=∠AFE ，∴AE=AF ，∴点A 、D 都在EF 的垂直平分线上，∴AD 垂直平分EF ．（2）14DO AD =，理由：∵∠BAC=60°，AD 平分∠BAC ，∴∠EAD=30°，∴AD=2DE，∠EDA=60°，∵AD⊥EF，∴∠EOD=90°，∴∠DEO=30°∴DE=2DO，∴AD=4DO，∴14 DO AD.【点睛】本题主要考查了角平分线的性质，线段垂直平分线的性质，含30°角的直角三角形的性质等知识点，解此题的关键是（1）证AE=AF和DE=DF；（2）证AD=2DE和DE=2DO．17．(1)△DBC和△EAC全等，理由见解析；（2）见解析【解析】【分析】(1)要证两个三角形全等，已知的条件有AC=BC，CE=CD，我们发现∠BCD和∠ACE都是60°减去一个∠ACD，因此两三角形全等的条件就都凑齐了(SAS)；(2)要证AE∥BC，关键是证∠EAC=∠ACB，由于∠ACB=∠ACB，那么关键是证∠EAC=∠ACB，根据(1)的全等三角形，我们不难得出这两个角相等，也就得出了证平行的条件．【详解】解：(1)△DBC和△EAC全等．理由：∵△ABC和△EDC都是等边三角形，∴∠ACB＝60°，∠DCE＝60°，AC＝BC，DC＝EC，∴∠BCD＝60°－∠ACD，∠ACE＝60°－∠ACD，∴∠BCD＝∠ACE.在△DBC和△EAC中，∵BC＝AC，∠BCD＝∠ACE，DC＝EC，∴△DBC≌△EAC(SAS)．(2)∵△DBC≌△EAC，∴∠EAC＝∠B＝60°.又∵∠ACB＝60°，∴∠EAC＝∠ACB，∴AE∥BC.故答案为：(1)△DBC和△EAC全等，理由见解析；(2)见解析.【点睛】本题考查了全等三角形的判定与性质及等边三角形的性质．18．（1）当t为2时，△DEC为等边三角形；（2）当t为1.2或3时，△DEC为直角三角形；（3）见解析【解析】【分析】(1)根据等边三角形的性质得到EC=DC，列方程得到t=2；(2)根据直角三角形的性质得到CE=12DC，列方程得到t=1.2，根据直角三角形的性质还可得到12CE＝DC，列方程得到t=3；(3)根据直角三角形的性质得到BC=12cm，于是得到DC=(6-t)cm，BE=(12-2t)cm，根据平行线的性质得到∠A=∠BFE=90°，由直角三角形的性质得到EF=12BE=12(12-2t)=(6-t)cm，即可得到结论；【详解】解：由题意得AD＝t cm，CE＝2t cm.(1)若△DEC为等边三角形，则EC＝DC，∴2t＝6－t，解得t＝2，∴当t为2时，△DEC为等边三角形．(2)若△DEC为直角三角形，当∠CED＝90°时，∵∠B＝30°，∴∠ACB＝60°，∴∠CDE＝30°，∴CE＝12DC，∴2t＝12(6－t)，解得t＝1.2；当∠CDE＝90°时，同理可得∠CED＝30°，∴12CE＝DC，∴12×2t＝6－t，∴t＝3，∴当t为1.2或3时，△DEC为直角三角形．(3)证明：∵∠A＝90°，∠B＝30°，AC＝6cm，∴BC＝12cm，∴DC＝(6－t)cm，BE＝(12－2t)cm.∵EF∥AC，∴∠BFE＝∠A＝90°.∵∠B＝30°，∴EF＝12BE＝12(12－2t)＝(6－t)cm，∴DC＝EF.故答案为(1)2；(2)1.2或3；(3)证明见解析【点睛】本题考查了等边三角形的判定和性质、直角三角形的判定和性质.。

北师大版八年级下册第一章三角形的证明测试题一．选择题（共10小题）1、等腰三角形的一个角是80°，则它顶角的度数是（）A.80°B.80°或20°C.80°或50°D.20°2．一个等腰三角形的两边长分别为3，6，则它的周长为（）A．9 B．12 C．15 D．12或153．如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（）A．50°B．51°C．51.5°D．52.5°4．一个等腰三角形一边长为4cm，另一边长为5cm，那么这个等腰三角形的周长是（）A．13cm B．14cm C．13cm或14cm D．以上都不对5．如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为（）A．44°B．66°C．88°D．92°6．如图所示，底边BC为2，顶角A为120°的等腰△ABC中，DE垂直平分AB于D，则△ACE的周长为（）A．2+2B．2+C．4 D．37．如图，∠B=∠C，∠1=∠3，则∠1与∠2之间的关系是（）A．∠1=2∠2 B．3∠1﹣∠2=180°C．∠1+3∠2=180° D．2∠1+∠2=180°8．如图在等腰△ABC中，其中AB=AC，∠A=40°，P是△ABC内一点，且∠1=∠2，则∠BPC等于（）A．110°B．120°C．130°D．140°9．如图，在△ABC中，AB=AC，BD=CE，BE=CF，若∠A=50°，则∠DEF=（）A．55°B．60°C．65°D．70°10．如图所示，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC=4cm²，则S阴影等于（）A．2cm²B．1cm²C．cm²D．cm²二．填空题（共5小题）11．等边三角形是一个轴对称图形，它有______条对称轴．12．等腰三角形一腰上的高与另一腰的夹角为48°，则该等腰三角形的底角的度数为______．13．在等腰△ABC中，AB=AC，AC腰上的中线BD将三角形周长分为15和21两部分，则这个三角形的底边长为______.14．等腰三角形的一个内角为70°，它一腰上的高与底边所夹的度数为______．15．如图，已知：∠MON=30°，点A1、A2、A3 在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=a，则△A6B6A7的边长为______．三．解答题（共8小题）16．如图，在△ABC中，AB=AC，AD是BC边上的中线，AE⊥BE于点E，且BE=．求证：AB平分∠EAD．17．如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．求证：△OAB是等腰三角形．18．如图，已知△ABC中，AB=BD=DC，∠ABC=105°，求∠A，∠C度数．19．如图，在△ABC中，AB=AC，AB的垂直平分线交AB于点N，交BC的延长线于点M，若∠A=40°．（1）求∠NMB的度数；（2）如果将（1）中∠A的度数改为70°，其余条件不变，再求∠NMB的度数；（3）你发现∠A与∠NMB有什么关系，试证明之．20．如图，在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE∥AC，交AB于E．求证：△BDE是等腰三角形．21．如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DE⊥AB于点E，DF ⊥AC于点F．求证：△ABC是等腰三角形．22．如图，在△ABC中，AB=AC，AD是BC边上的中线，BE⊥AC于点E．求证：∠CBE=∠BAD．23．如图，在△ABC中，AB=AC，D是BC上任意一点，过D分别向AB，AC引垂线，垂足分别为E，F，CG是AB边上的高．（1）当D点在BC的什么位置时，DE=DF？并证明．（2）DE，DF，CG的长之间存在着怎样的等量关系？并加以证明：（3）若D在底边BC的延长线上，（2）中的结论还成立吗？若不成立，又存在怎样的关系？北师大版八年级下册第一章三角形的证明测试题参考答案与试题解析一．选择题（共10小题）1、等腰三角形的一个角是80°，则它顶角的度数是（）【解答】解：①80°角是顶角时，三角形的顶角为80°，②80°角是底角时，顶角为180°﹣80°×2=20°，综上所述，该等腰三角形顶角的度数为80°或20°．故选B．2．一个等腰三角形的两边长分别为4，8，则它的周长为（）A．12 B．16 C．20 D．16或20【解答】解：①当4为腰时，4+4=8，故此种情况不存在；②当8为腰时，8﹣4＜8＜8+4，符合题意．故此三角形的周长=8+8+4=20．故选C．3．如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（）A．50°B．51°C．51.5°D．52.5°【解答】解：∵AC=CD=BD=BE，∠A=50°，∴∠A=∠CDA=50°，∠B=∠DCB，∠BDE=∠BED，∵∠B+∠DCB=∠CDA=50°，∴∠B=25°，∵∠B+∠EDB+∠DEB=180°，∴∠BDE=∠BED=（180°﹣25°）=77.5°，∴∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°，故选D．4．一个等腰三角形一边长为4cm，另一边长为5cm，那么这个等腰三角形的周长是（）A．13cm B．14cm C．13cm或14cm D．以上都不对【解答】解：当4cm为等腰三角形的腰时，三角形的三边分别是4cm，4cm，5cm符合三角形的三边关系，∴周长为13cm；当5cm为等腰三角形的腰时，三边分别是，5cm，5cm，4cm，符合三角形的三边关系，∴周长为14cm，故选C5．如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为（）A．44°B．66°C．88°D．92°【解答】解：∵PA=PB，∴∠A=∠B，在△AMK和△BKN中，∴△AMK≌△BKN，∴∠AMK=∠BKN，∵∠MKB=∠MKN+∠NKB=∠A+∠AMK，∴∠A=∠MKN=44°，∴∠P=180°﹣∠A﹣∠B=92°，故选：D．6．如图所示，底边BC为2，顶角A为120°的等腰△ABC中，DE垂直平分AB于D，则△ACE的周长为（）A．2+2B．2+C．4 D．3【解答】解：过A作AF⊥BC于F，∵AB=AC，∠A=120°，∴∠B=∠C=30°，∴AB=AC=2，∵DE垂直平分AB，∴BE=AE，∴AE+CE=BC=2，∴△ACE的周长=AC+AE+CE=AC+BC=2+2，故选：A．7．如图，∠B=∠C，∠1=∠3，则∠1与∠2之间的关系是（）A．∠1=2∠2 B．3∠1﹣∠2=180°C．∠1+3∠2=180° D．2∠1+∠2=180°【解答】解：∵∠1=∠3，∠B=∠C，∠1+∠B+∠3=180°，∴2∠1+∠C=180°，∴2∠1+∠1﹣∠2=180°，∴3∠1﹣∠2=180°．故选B．8．如图在等腰△ABC中，其中AB=AC，∠A=40°，P是△ABC内一点，且∠1=∠2，则∠BPC等于（）A．110°B．120°C．130°D．140°【解答】解：∵∠A=40°，∴∠ACB+∠ABC=180°﹣40°=140°，又∵∠ABC=∠ACB，∠1=∠2，∴∠PBA=∠PCB，∴∠1+∠ABP=∠PCB+∠2=140°×=70°，∴∠BPC=180°﹣70°=110°．故选A．9．如图，在△ABC中，AB=AC，BD=CE，BE=CF，若∠A=50°，则∠DEF=（）A．55°B．60°C．65°D．70°【解答】解：∵AB=AC，∴∠B=∠C，在△DBE和△ECF中，∴△DBE≌△ECF（SAS），∴∠EFC=∠DEB，∵∠A=50°，∴∠C=（180°﹣50°）÷2=65°，∴∠CFE+∠FEC=180°﹣65°=115°，∴∠DEB+∠FEC=115°，∴∠DEF=180°﹣115°=65°．故选：C．10．如图所示，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC=4cm2，则S阴影等于（）A．2cm2 B．1cm2 C．cm2 D．cm2【解答】解：根据三角形的面积公式，知：等底等高的两个三角形的面积相等．即有：S阴影=S△BCE=S△ABC=1cm2．故选：B．二．填空题（共10小题）11．等边三角形是一个轴对称图形，它有 3 条对称轴【解答】解：等边三角形是轴对称图像，它有三个顶点，所以对应3条对称轴故答案为：312．等腰三角形一腰上的高与另一腰的夹角为48°，则该等腰三角形的底角的度数为69°或21°．【解答】解：分两种情况讨论：①若∠A＜90°，如图1所示：∵BD⊥AC，∴∠A+∠ABD=90°，∵∠ABD=48°，∴∠A=90°﹣48°=42°，∵AB=AC，∴∠ABC=∠C=（180°﹣42°）=69°；②若∠A＞90°，如图2所示：同①可得：∠DAB=90°﹣48°=42°，∴∠BAC=180°﹣42°=138°，∵AB=AC，∴∠ABC=∠C=（180°﹣138°）=21°；综上所述：等腰三角形底角的度数为69°或21°．故答案为：69°或21°．13．在等腰△ABC中，AB=AC，AC腰上的中线BD将三角形周长分为15和21两部分，则这个三角形的底边长为16或8．【解答】解：∵BD是等腰△ABC的中线，可设AD=CD=x，则AB=AC=2x，又知BD将三角形周长分为15和21两部分，∴可知分为两种情况①AB+AD=15，即3x=15，解得x=5，此时BC=21﹣x=21﹣5=16；②AB+AD=21，即3x=21，解得x=7；此时等腰△ABC的三边分别为14，14，8．经验证，这两种情况都是成立的．∴这个三角形的底边长为8或16．故答案为：16或8．14．等腰三角形的一个内角为70°，它一腰上的高与底边所夹的度数为35°或20°．【解答】解：在△ABC中，AB=AC，①当∠A=70°时，则∠ABC=∠C=55°，∵BD⊥AC，∴∠DBC=90°﹣55°=35°；②当∠C=70°时，∵BD⊥AC，∴∠DBC=90°﹣70°=20°；故答案为：35°或20°．15．如图，已知：∠MON=30°，点A1、A2、A3 在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=a，则△A6B6A7的边长为32a ．【解答】解:∵△A1B1A2是等边三角形∴∠B1A1A2＝60°，A1B1＝B1A2＝A1A2∵∠MON=30°∴∠OB1A1=30°（三角形的一个外角等于和它不相邻的两个外角和∠OB1A1=∠B1A1A2－∠MON）∴OA1=A1B1（等边对等角）∴OA1=A1A2=a同理，根据∠MON=∠OB2A2，可得：A2A3=A2B2=OA1＋A1A2=2A1A2=2a同理，可推出：A3A4=2A2A3=4a同理，可推出：A4A5=2A3A4=8a同理，可推出：A5A6=2A4A5=16a同理，可推出：A6A7=2A5A6=32a 即题目所求另外我们不难发现，第n个（△A1B1A2为第一个）等边三角形的边长为AnAn+1=(2^n-1)a 注：2的n-1次方倍的a三．解答题（共8小题）16．如图，在△ABC中，AB=AC，AD是BC边上的中线，AE⊥BE于点E，且BE=．求证：AB平分∠EAD．【解答】证明：∵AB=AC，AD是BC边上的中线，∴BD=BC，AD⊥BC，∵BE=BC，∴BD=BE，∵AE⊥BE，∴AB平分∠EAD．17．如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．求证：△OAB是等腰三角形．【解答】证明：∵AC⊥BC，BD⊥AD∴∠D=∠C=90°，在Rt△ABD和Rt△BAC中，，∴Rt△ABD≌Rt△BAC（HL），∴∠DBA=∠CAB，∴OA=OB，即△OAB是等腰三角形．另外一种证法：证明：∵AC⊥BC，BD⊥AD∴∠D=∠C=90°在Rt△ABD和Rt△BAC中∴Rt△ABD≌Rt△BAC（HL）∴AD=BC，在△AOD和△BOC中，∴△AOD≌△BOC（AAS），∴OA=OB，即△OAB是等腰三角形．18．如图，已知△ABC中，AB=BD=DC，∠ABC=105°，求∠A，∠C度数．【解答】解：∵AB=BD，∴∠BDA=∠A，∵BD=DC，∴∠C=∠CBD，设∠C=∠CBD=x，则∠BDA=∠A=2x，∴∠ABD=180°﹣4x，∴∠ABC=∠ABD+∠CDB=180°﹣4x+x=105°，解得：x=25°，所以2x=50°，即∠A=50°，∠C=25°．19．如图，在△ABC中，AB=AC，AB的垂直平分线交AB于点N，交BC的延长线于点M，若∠A=40°．（1）求∠NMB的度数；（2）如果将（1）中∠A的度数改为70°，其余条件不变，再求∠NMB的度数；（3）你发现∠A与∠NMB有什么关系，试证明之．【解答】解：（1）∵在△ABC中，AB=AC，∠A=40°，∴∠ABC=∠ACB=70°，∵AB的垂直平分线交AB于点N，交BC的延长线于点M，∴MN⊥AB，∴∠NMB=90°﹣∠ABC=20°；（2）∵在△ABC中，AB=AC，∠A=70°，∴∠ABC=∠ACB=55°，∵AB的垂直平分线交AB于点N，交BC的延长线于点M，∴MN⊥AB，∴∠NMB=90°﹣∠ABC=35°；（3）∠NMB=∠A．理由：∵在△ABC中，AB=AC，∴∠ABC=∠ACB=，∵AB的垂直平分线交AB于点N，交BC的延长线于点M，∴MN⊥AB，∴∠NMB=90°﹣∠ABC=∠A．20．如图，在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE∥AC，交AB于E．求证：△BDE是等腰三角形．【解答】解：（1）∵AD平分∠BAC，DE∥AC，∴∠EAD=∠CAD，∠EDA=∠CAD，∴∠EAD=∠EDA，∵BD⊥AD，∴∠EBD+∠EAD=∠BDE+∠EDA∴∠EBD=∠BDE，∴DE=BE，∴△BDE是等腰三角形．21．如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DE⊥AB于点E，DF ⊥AC于点F．求证：△ABC是等腰三角形．【解答】证明：∵AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，∴DE=DF，在Rt△BDE和Rt△CDF中，，∴Rt△BDE≌Rt△CDF（HF），∴∠B=∠C，∴△ABC为等腰三角形．22．如图，在△ABC中，AB=AC，AD是BC边上的中线，BE⊥AC于点E．求证：∠CBE=∠BAD．【解答】证明：∵AB=AC，AD是BC边上的中线，BE⊥AC，∴∠CBE+∠C=∠CAD+∠C=90°，∠CAD=∠BAD，∴∠CBE=∠BAD．23．如图，在△ABC中，AB=AC，D是BC上任意一点，过D分别向AB，AC引垂线，垂足分别为E，F，CG是AB边上的高．（1）当D点在BC的什么位置时，DE=DF？并证明．（2）DE，DF，CG的长之间存在着怎样的等量关系？并加以证明：（3）若D在底边BC的延长线上，（2）中的结论还成立吗？若不成立，又存在怎样的关系？【解答】解：（1）当点D在BC的中点时，DE=DF，理由如下：∵D为BC中点，∴BD=CD，∵AB=AC，∴∠B=∠C，∵DE⊥AB，DF⊥AC，∴∠DEB=∠DFC=90°，在△BED和△CFD中，∴△BED≌△CFD（AAS），∴DE=DF．（2）DE+DF=CG．证明：连接AD，则S△ABC=S△ABD+S△ACD，即AB•CG=AB•DE+AC•DF，∵AB=AC，∴CG=DE+DF．（3）当点D在BC延长线上时，（1）中的结论不成立，但有DE﹣DF=CG．理由：连接AD，则S△ABD=S△ABC+S△ACD，即AB•DE=AB•CG+AC•DF∵AB=AC，∴DE=CG+DF，即DE﹣DF=CG．同理当D点在CB的延长线上时，则有DE﹣DF=CG，说明方法同上．。

第一章三角形的证明专项测试题(一)一、单项选择题（本大题共有15小题，每小题3分，共45分）1、如图，在中，已知，的平分线交于点．若，则点到的距离是（）.A.B.C.D.2、在中，，则，为（）.的垂直平分线交于点，交于点，且A.B.C.D.无法确定3、下列说法中，不正确的是（）.A.线段有1条对称轴B.等边三角形有条对称轴C.角只有1条对称轴D.底与腰不相等的等腰三角形只有一条对称轴4、如图，是（）平分，，，垂足分别为，．下列结论中不一定成立的A.B.C.D.平分垂直平分5、若点在线段A.B.无法确定C.D.6、如图，是的依据是（）的垂直平分线上，，则().内一点，且点到的距离，则A.B.C.D.7、如图，中，，，则（）A.B.C.D.8、到三角形三个顶点的距离都相等的点是这个三角形的（）A.三条高的交点B.三条角平分线的交点C.三条中线的交点D.三条边的垂直平分线的交点9、如图，公路，则互相垂直，公路两点间的距离为（）的中点与点被湖隔开．若测得的长为A.B.C.D.10、某一实验装置的截面图如图所示，上方装置可看做一长方形，其侧面与水平线的夹角为，下方是一个直径为，高为的圆柱形容器，若使容器中的液面与上方装置相接触，则容器中液体的高度至少应为（）A.B.C.D.11、如图，若要用“”证明，则还需补充条件（）A.B.或C.且D.以上都不对12、使两个直角三角形全等的条件是（）A.一个锐角对应相等B.两个锐角对应相等C.一条边对应相等D.两条边对应相等13、已知直角三角形的周长为，斜边上的中线长为．则直角三角形的面积为（）A.B.C.D.14、如图，在中，，平分，于．如果，那么等于（）A.B.C.D.和15、如图，中、平分、，过作直线平行于，交、于、，当的位置及大小变化时，线段的大小关系是（）A.不能确定B.C.D.二、填空题（本大题共有5小题，每小题5分，共25分）16、等腰三角形两腰上的高相等，这个命题的逆命题是_________________________，这个逆命题是________命题.17、如图，已知PE⊥OA，PF⊥OB，且PE=PF，则点P的位置在________上.18、如图，在中，于，点为的中点，，则线段的长等于．，为圆心，大于19、如图，在中，，平分，交于点，若，则．20、如图，点在直线上，按如下步骤作图：①以点为圆心，任意长为半径作圆弧，交于点，；②分别以点的长为半径作圆弧，两弧相交于点；③作直线，连结，，若，则的大小为度．三、解答题（本大题共有3小题，每小题10分，共30分）21、如图，在中，，是上一点，，过点作的垂线交于点.求证：.22、如图，在中，．，是边上的中线，于点，求证：23、如图，的长．中，，是的高，，求第一章三角形的证明专项测试题(一)答案部分一、单项选择题（本大题共有15小题，每小题3分，共45分）1、如图，在中，已知，的平分线交于点．若，则点到的距离是（）.A.B.C.D.【答案】C【解析】解：过点作，交于点，则的长度即为点到直线的距离.，，是的平分线，且，，，已知，.即点到的距离为.故正确答案应选：.2、在中，，的垂直平分线交于点，交于点，且，则为（）.A.B.C.D.无法确定【答案】B【解析】解：如图所示.，且平分，，是等腰三角形，，，，，而，且，，解得.故正确答案是：.3、下列说法中，不正确的是（）.A.线段有1条对称轴B.等边三角形有条对称轴C.角只有1条对称轴D.底与腰不相等的等腰三角形只有一条对称轴【答案】A【解析】解：线段本身所在的直线为线段的条对称轴，线段的垂直平分线为线段的另1条对称轴，所以线段有条对称轴，本说法错误；等边三角形的条高线（或条角平分线）为等边三角形的条对称轴，本说法正确；角的平分线把角一分为二，故角的平分线只有条，本说法正确；底与腰不相等的三角形，顶角的平分线把三角形一分为二，所以底与腰不相等的三角形只有条对称轴，本说法正确.故正确的答案是：线段有1条对称轴.4、如图，平分，，，垂足分别为，．下列结论中不一定成立的是（）A.B.平分C.D.垂直平分【答案】D【解析】解：平分，，，，第一选项正确；在和中，，，，，故第二、三选项正确；由等腰三角形三线合一的性质，垂直平分，不一定垂直平分，故本选项错误5、若点在线段的垂直平分线上，，则().A.B.无法确定C.D.【答案】C【解析】解：因为线段垂直平分线的点到线段两端点的距离相等，所以，所以.故答案为：.6、如图，是内一点，且点到的距离，则的依据是（）A.B.C.D.【答案】A【解析】解：，，，又，为公共边，．7、如图，中，，，则（）A.B.C.D.【答案】A【解析】解：，，，．8、到三角形三个顶点的距离都相等的点是这个三角形的（）A.三条高的交点B.三条角平分线的交点C.三条中线的交点D.三条边的垂直平分线的交点【答案】D【解析】解：到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点．9、如图，公路，则互相垂直，公路两点间的距离为（）的中点与点被湖隔开．若测得的长为A.B.C.D.【答案】D【解析】解：在中，，为的中点，．10、某一实验装置的截面图如图所示，上方装置可看做一长方形，其侧面与水平线的夹角为，下方是一个直径为，高为的圆柱形容器，若使容器中的液面与上方装置相接触，则容器中液体的高度至少应为（）A.B.C.D.【答案】A【解析】解：如图，圆桶放置的角度与水平线的夹角为，依题意得是一个斜边为的等腰直角三角形，此三角形中斜边上的高为斜边的一半，即，水深至少应为．11、如图，若要用“”证明，则还需补充条件（）A.B.或C.且D.以上都不对【答案】B【解析】解：从图中可知为和的斜边，也是公共边．根据“”定理，证明，还需补充一对直角边相等，即或．12、使两个直角三角形全等的条件是（）A.一个锐角对应相等B.两个锐角对应相等C.一条边对应相等D.两条边对应相等【答案】D【解析】解：一个锐角对应相等，利用已知的直角相等，可得出另一组锐角相等，但不能证明两三角形全等，故错误；两个锐角相等，那么也就是三个对应角相等，但不能证明两三角形全等，故错误；一条边对应相等，再加一组直角相等，不能得出两三角形全等，故错误；证全等；若一直角边对应相等，一斜边对两条边对应相等，若是两条直角边相等，可利用应相等，也可证全等，故正确．，斜边上的中线长为．则直角三角形的面积为（）13、已知直角三角形的周长为A.B.C.D.【答案】C【解析】解：，是斜边上的中线，，，，由勾股定理得：，，，．14、如图，在中，，平分，于．如果，那么等于（）A.B.C.D.【答案】C【解析】解：，，，，，，平分，，．15、如图，中、平分、，过作直线平行于，交、于、，当的位置及大小变化时，线段和的大小关系是（）A.不能确定B.C.D.【答案】D【解析】解：由平分得，，，，，，是等腰三角形，，同理可得，，（是等腰三角形），．二、填空题（本大题共有5小题，每小题5分，共25分）16、等腰三角形两腰上的高相等，这个命题的逆命题是_________________________，这个逆命题是________命题.【答案】如果一个三角形两边上的高相等，那么这个三角形是等腰三角形；真.【解析】解：命题“等腰三角形两腰上的高相等”的逆命题是“如果一个三角形两边上的高相等，那么这个三角形是等腰三角形”．它是真命题，可用证明，得到两角相等．17、如图，已知PE⊥OA，PF⊥OB，且PE=PF，则点P的位置在________上.【答案】的平分线【解析】解：由题意知，到角的两边的距离相等的点在角的平分线上，故答案为：的平分线.18、如图，在中，于，点为的中点，，则线段的长等于．【答案】8【解析】解：于，点为的中点，，在中，．19、如图，在中，，平分，交于点，若，则．【答案】14【解析】解：，，平分，，．，为圆心，大于20、如图，点在直线上，按如下步骤作图：①以点为圆心，任意长为半径作圆弧，交于点，；②分别以点的长为半径作圆弧，两弧相交于点；③作直线，连结，，若，则的大小为度．【答案】40【解析】解：由题意可得：故垂直平分．，则，，三、解答题（本大题共有3小题，每小题10分，共30分）21、如图，在中，，是上一点，，过点作的垂线交于点.求证：.【解析】证明：...在和，中.，..，（三线合一）..22、如图，在中，．，是边上的中线，于点，求证：【解析】证明：，是边上的中线，，，，23、如图，的长．．中，，是的高，，求【解析】解：如图，在中，，是高，在直角在直角，中，中，，，．的长为．。

一、选择题1．如图的网格中，每个小正方形的边长为1，A ，B ，C 三点均在格点上，结论错误的是（ ）A ．AB=25B ．∠BAC=90°C ．ABC S 10=D ．点A 到直线BC 的距离是22．如图，点A 为MON ∠的角平分线上一点，过A 点作一条直线分别与MON ∠的边OM ON 、交于,B C 两点，点P 为BC 的中点，过P 作BC 的垂线交OA 的延长线于点D ，连接DB DC 、，若130MON ∠=︒，则BDC ∠=（ ）A ．70︒B ．60︒C ．50︒D ．40︒3．如图，在ABC 中，点A 、B 、C 的坐标分别为(,0)m 、(0,2)和(5,3)，则当ABC 的周长最小时，m 的值为（ ）A ．0B ．1C ．2D ．34．如图，平面直角坐标系中，O 是坐标原点，点A （3，2），点P （m ，0），若△POA 是等腰三角形，则m 可取的值最多有（ ）A ．2个B ．3个C ．4个D ．5个5．如图，已知等边,2ABC AB =，点D 在AB 上，点F 在AC 的延长线上，BD CF DE BC =⊥，于点,E FG BC ⊥于,G DF 交BC 于点P ，则下列结论中：①BE CG =；②EDP GFP ≌；③60EDP ∠=︒；④1EP =．一定正确的是（ ）A ．①B ．②④C ．①②③D ．①②④ 6．如图所示，O 为直线AB 上一点，OC 平分∠AOE ，∠DOE =90°，则①∠AOD 与∠BOE 互为余角；②OD 平分∠COA ；③若∠BOE =56°40'，则∠COE =61°40'；④∠BOE =2∠COD ．结论正确的个数为（ ）A ．4B ．3C ．2D ．17．下列四组线段中，不能组成直角三角形的是（ ）A ．5a =，12b =，13c =B ．6a =，8b =，10c =C ．7a =，24b =，25c =D ．8a =，12b =，15c =8．如图所示，在ABC 中，90BAC ∠=︒，30ACB ∠=︒，AD BC ⊥于D ，BE 是ABC ∠的平分线，且交AD 于P ，如果1AP =，则AC 的长为（ ）A ．1B ．2C ．3D ．49．如图，等腰ABC 中，10AB AC ==，12BC =，点D 是底边BC 的中点，以A 、C 为圆心，大于12AC 的长度为半径分别画圆弧相交于两点E 、F ，若直线EF 上有一个动点P ，则线段PC PD +的最小值为（ ）A ．6B ．8C ．10D ．1210．如图，ABC 中，AB 的垂直平分线分别交AB 、BC 于点D 、E ，AC 的垂直平分线分别交AC 、BC 于点F 、G ，若100BAC ∠=︒，则EAG ∠的度数是（ ）A ．10°B ．20°C ．30°D ．40°11．如图，在ABC 中，ED //BC ，ABC ∠和ACB ∠的平分线分别交ED 于点F 、G ，若2FG =，6ED =，则DB EC +的值为（ ）A ．3B ．4C ．5D ．9 12．如图，每个小正方形的边长都相等，A ，B ，C 是小正方形的顶点，则ABC ∠的度数为（ ）A ．45︒B ．50︒C ．55︒D ．60︒二、填空题13．如图所示，有n +1个边长为1的等边三角形，点A 、C 1、C 2、C 3、…、C n 都在同一条直线上，若记△B 1C 1D 1的面积为S 1，△B 2C 2D 2的面积为S 2，△B 3C 3D 3的面积为S 3，…，△B n C n D n 的面积为S n ，则（1）S 1＝_____；（2）S n ＝_____．14．如图在第一个△A1BC 中，∠B ＝40°，A 1B ＝BC ，在边A 1B 上任取一点D ，延长CA 1到A 2，使A 1A 2＝A 1D ，得到第二个△A 1A 2D ，再在边A 2D 上任取一点E ，延长A 1A 2到A 3，使A 2A 3＝A 2E ，得到第3个△A 2A 3E……如此类推，可得到第n 个等腰三角形．则第n 个等腰三角形中，以An 为顶点的内角的度数为_____________．15．如图，已知△ABC 是等边三角形，AQ=PQ ，PR=PS ，PR ⊥AB 于点R ，PS ⊥AC 于点S ，有以下四个结论：①点P 在∠BAC 的平分线上；②△BRP ≌△QSP ；③QP ∥AR ；④△PQC 是等边三角形，其中正确的有______个．16．如图，在ABC 中，,45,,AB AC BAC AD BE =∠=︒是ABC 的高，点Р是直线AD 上一动点，当PC PE +最小时，则BPC ∠为______度．17．如图，在第1个1A BC 中，36B ∠=︒，1A B CB =；在边1A B 上任取一点D ，延长1CA 到2A ，使121A A A D =，得到第2个12A A D ；在边2A D 上任取一点E ，延长12A A 到3A ，使232A A A E =，得到第3个23A A E △，…按此做法继续下去，第2021个三角形的底角度数是________________．18．如图，在△ABC 中，∠BAC 的平分线交BC 于点D ，过点D 作DE ⊥AC ，DF ⊥AB ，垂足分别为E 、F ，下面四个结论：①∠AFE=∠AEF ；②AD 垂直平分EF ；③BFDCED S BF S CE ∆∆=；④EF//BC ；一定成立的结论是______（请将正确结论的序号填在横线上）19．如图，30,AOB OC ︒∠=为AOB ∠内部一条射线，点P 为射线OC 上一点，6OP=，点,M N 分别为,OA OB 边上动点，则MNP △周长的最小值为______．20．如图，点M 是等边△ABC 的边BC 的中点，AB =4，射线CD BC ⊥于点C ，点P是射线CD 上一动点，点N 是线段AB 上一动点，当MP +NP 的值最小时，则AN 长为____．三、解答题21．在平面直角坐标系中，坐标轴上的三个点(),0A a ，()0,B b ，(),0C c ()0,0a b <>满足()210c a b -++=，F 为射线BC 上的一个动点．（1）c 的值为______，ABO ∠的度数为______．（2）如图()a ，若AF BC ⊥，且交OB 于点E ，求证：OE OC =．（3）如图()b ，若点F 运动到BC 的延长线上，且2FBO FAO ∠=∠，O 在AF 的垂直平分线上，求ABF 的面积．22．如图，已知：AD 是∠BAC 的平分线，AB ＝BD ，过点B 作BE ⊥AC ，与AD 交于点F ． （1）求证：AC ∥BD ；（2）若AE ＝2，AB ＝3，BF ＝355，求△ABF 中AB 边上的高．23．如图，四边形ABCD ，BC ∥AD ，P 为CD 上一点，PA 平分∠BAD 且BP ⊥AP ， （1）若∠BAD=80°，求∠ABP 的度数；（2）求证：BA=BC+AD ；（3）设BP=3a ，AP=4a ，过点P 作一条直线，分别与AD ，BC 所在直线交于点E ，点F ．若AB=EF ，求AE 的长（用含a 的代数式表示）24．如图，在△ABC中，AC=BC，∠ACB=90°，延长CA至点D，延长CB至点E，使AD=BE，连接AE，BD，交点为O．（1）求证：OB=OA；（2）连接OC，若AC=OC，则∠D的度数是度．25．如图，△ABC是等边三角形，点D在BC的延长线上，连接AD，以AD为边作等边△ADE，连接CE．（1）求证BD＝CE；（2）若AC+CD＝2，则四边形ACDE的面积为．26．如图，点D是△ABC内部的一点，BD＝CD，过点D作DE⊥AB，DF⊥AC，垂足分别为E、F，且BE＝CF．（1）求证：∠DBE＝∠DCF；（2）求证：△ABC为等腰三角形．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】根据勾股定理以及其逆定理和三角形的面积公式逐项分析即可得到问题答案．【详解】解：AB=22242025+==，故选项A 正确，不符合题意；∵AC ＝22125+=，BC 2234255=+==，∴22252025AC AB BC +=+==，∴△ACB 是直角三角形，∴∠CAB=90°，故选项B 正确，不符合题意；S △ABC 111442421345222=⨯-⨯⨯-⨯⨯-⨯⨯=，故选项C 错误，符合题意； 点A 到直线BC 的距离25525AC AB BC ===，故选项D 正确，不符合题意； 故选：C ．【点睛】本题考查了勾股定理以及逆定理的运用，在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么 222+=a b c ．熟记勾股定理的内容是解题得关键．2．C解析：C【分析】过D 作DE ⊥OM 于E ，DF ⊥ON 于F ，求出∠EDF ，根据角平分线性质求出DE=DF ，根据线段垂直平分线性质求出BD=CD ，证Rt △DEB ≌Rt △DFC ，求出∠EDB=∠CDF ，推出∠BDC=∠EDF ，即可得出答案．【详解】解：如图：过D 作DE ⊥OM 于E ，DF ⊥ON 于F ，则∠DEB=∠DFC=∠DFO=90°，∵∠MON=130°，∴∠EDF=360°-90°-90°-130°=50°，∵DE ⊥OM ，DF ⊥ON ，OD 平分∠MON ，∴DE=DF ，∵P 为BC 中点，DP ⊥BC ，∴BD=CD，在Rt△DEB和Rt△DFC中，DB DC DE DF=⎧⎨=⎩，∴Rt△DEB≌Rt△DFC（HL），∴∠EDB=∠CDF，∴∠BDC=∠BDF+CDF=∠BDF+∠EDB=∠EDF=50°．故选：C．【点睛】本题考查了全等三角形的性质和判定，角平分线性质，线段垂直平分线性质的应用，能正确作出辅助线是解此题的关键，注意：线段垂直平分线上的点到线段两个端点的距离相等，角平分线上的点到角的两边的距离相等．3．C解析：C【分析】做出B关于x轴对称点为B′，连接B′C，交x轴于点A'，此时ABC的周长最小，由等腰直角三角形的性质可求∠OB'A'=∠OA'B'=45°，可求OB'=OA'=1，即可求解．【详解】解：如图所示，做出B关于x轴对称点为B′，连接B′C，交x轴于点A'，此时△ABC周长最小过点C作CH⊥x轴，过点B'作B'H⊥y轴，交CH于H，∵B（0，2），∴B′（0，-2），∵C（5，3），∴CH= B′H=5，∴∠CB'H=45°，∴∠BB' A'=45°，∴∠OB'A'=∠OA'B'=45°，∴OB'=OA'=2，则此时A'坐标为（2，0）．m 的值为2．故选：C ．【点睛】此题考查了轴对称-最短路径问题，考查了轴对称的性质，等腰直角三角形的性质等知识，根据已知得出A 点位置是解题关键．4．C解析：C【分析】分两种情况分析：①以点OP 为底，②OP 为腰，讨论点P 的个数，再求出m 的值即可.【详解】解：由点P （m ，0）知点P 在x 轴上，分两种情况：当OP 为底时，以A 点为圆心OA 为半径画圆，交x 轴于点P ，以OA=AP 为腰，点P 的坐标为m=2×3=6，当OP 为腰时，以O 为圆心，OA 长为半径，画圆交x 轴于两点P ，点P 在y 轴左侧或右侧，OP=OA=222313+=，∴m=13±，点P 在y 轴右侧，以OA 为底，作AO 的垂直平分线交x 轴与P ，过A 作AB ⊥x 轴，OP=AP=()2223m +-，则m=()2223m +-，解得m=136，综上，共有4个点P ，即m 有4个值，故选择：C.【点睛】本题考察等腰三角形的性质，解题时分两种情况进行讨论，注意以点A 、O 为顶角顶点时应以点为圆心画弧线，避免有遗漏．5．D【分析】由等边三角形的性质可以得出△DEB ≌△FGC ，就可以得出BE ＝CG ，DE ＝FG ，就可以得出△DEP ≌△FGP ，得出∠EDP ＝∠GFP ，EP ＝PG ，得出PC ＋BE ＝PE ，就可以得出PE ＝1，从而得出结论．【详解】解：∵△ABC 是等边三角形，∴AB ＝BC ＝AC ，∠A ＝∠B ＝∠ACB ＝60°．∵∠ACB ＝∠GCF ，∵DE ⊥BC ，FG ⊥BC ，∴∠DEB ＝∠FGC ＝∠DEP ＝90°．在△DEB 和△FGC 中，DEB FGC GCF A BD CF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DEB ≌△FGC （AAS ），BE ＝CG ，DE ＝FG ，故①正确；在△DEP 和△FGP 中，DEP FGP DPE FPG DE FG ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DEP ≌△FGP （AAS ），故②正确；∴PE ＝PG ，∠EDP ＝∠GFP≠60°，故③错误；∵PG ＝PC ＋CG ，∴PE ＝PC ＋BE ．∵PE ＋PC ＋BE ＝2，∴PE ＝1，故④正确．∴正确的有：①②④．故选D ．【点睛】本题考查了等边三角形的性质的运用，全等三角形的判定及性质的运用，解答时证明三角形全等是关键．6．B解析：B【分析】由平角的定义与90DOE ∠=︒，即可求得AOD ∠与∠BOE 互为余角；又由角平分线的定义，可得22AOE COE AOC ∠=∠=∠，即可求得2BOE COD ∠=∠，若5640BOE ∠=︒'，则6140COE ∠=︒'．解：90DOE ∠=︒，90COD COE ∴∠+∠=︒，90EOB DOA ∴∠+∠=︒，故①正确； OC 平分AOE ∠，22AOE COE AOC ∴∠=∠=∠；1801802BOE AOE COE ∴∠=︒-∠=︒-∠，90COD COE ∠=︒-∠，2BOE COD ∴∠=∠，90AOD BOE ∠=︒-∠，故②不正确，④正确；若5640BOE ∠=︒'，180AOE BOE ∠+∠=︒，11(180)(1805640)614022COE BOE ∴∠=︒-∠=︒-︒'=︒'． 故③正确；∴①③④正确．故答案为：B ．【点睛】此题考查了平角的定义与角平分线的定义．题目中要注意各角之间的关系，解题时要仔细识图．7．D解析：D【分析】根据勾股定理的逆定理，只要判断两个较小的数的平方和是否等于最长边的平方即可．【详解】A.∵52+122=132，∴此三角形是直角三角形，不符合题意；B.∵62+82=100=102，∴此三角形是直角三角形，不符合题意；C.∵72+242=625=252，∴此三角形是直角三角形，不符合题意；D.∵82+122=208≠152，∴此三角形不是直角三角形，符合题意；故选：D ．【点睛】本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．8．C解析：C【分析】由三角形的内角和定理和等腰三角形的性质，得到AP=BP=AE=PE=1，CE=BE=2，即可求出AC 的长度．解：∵在ABC 中，90BAC ∠=︒，30ACB ∠=︒，∴60ABC ∠=︒，∵AD BC ⊥于D ，BE 是ABC ∠的角平分线，∴30ABP DBP BAP ∠=∠=∠=︒，∴1AP BP ==，∵90BAC ∠=︒，30ACB ∠=︒，∴60EAP AEP ∠=∠=︒，∴△APE 是等边三角形，∴AP=BP=AE=PE=1，∵30DBP C ∠=∠=︒，∴CE=BE=1+1=2，∴213AC CE AE =+=+=；故选：C ．【点睛】本题考查了等边三角形的判定和性质，等腰三角形的性质，三角形的内角和定理，解题的关键是熟练掌握所学的知识，正确的进行解题．9．B解析：B【分析】由作法知EF 是AC 的垂直平分线，可得AP=CP ，线段PC PD +的最小就是PA+PD ，当A 、P 、D 三点共线时最短，由点D 是底边BC 的中点，可BD=CD =6，由AB=AC ，可得AD BC ⊥，在Rt △ABD 中，由勾股定理得：8即可．【详解】解：连结PA ，由作法知EF 是AC 的垂直平分线，∴AP=CP ，∴PC+PD=PA+PD ，线段PC PD +的最小就是PA+PD ，当A 、P 、D 三点共线时最短，∵点D 是底边BC 的中点，∴BD=CD=11BC=12=622⨯， ∵AB=AC ，∴AD BC ⊥，在Rt △ABD 中，由勾股定理得：8=，（PC+PD ）最小=（PA+PD ）最小=AD=8．故选择：B．【点睛】本题考查垂直平分线的性质，等腰三角形的三线合一性质，勾股定理，掌握垂直平分线的性质，等腰三角形的三线合一性质，勾股定理，关键是利用垂直平分线将PC转化为PA，找到P、A、D三点共线时最短．10．B解析：B【分析】根据三角形内角和定理求出∠C＋∠B，根据线段的垂直平分线的性质得到EA＝EB，根据等腰三角形的性质得到∠EAB＝∠B，同理，∠GAC＝∠C，计算即可．【详解】解：∵∠BAC＝100°，∴∠C＋∠B＝180°−100°＝80°，∵DE是AB的垂直平分线，∴EA＝EB，∴∠EAB＝∠B，同理：∠GAC＝∠C，∴∠EAB＋∠GAC＝∠C＋∠B＝80°，∴∠EAG＝100°−80°＝20°，故选B．【点睛】本题考查的是线段的垂直平分线的性质和等腰三角形的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．11．B解析：B【分析】根据平行线的性质和等腰三角形的判定证得EG＝EB，DF＝DC即可求得结果．【详解】解：∵ED∥BC，∴∠DFB＝∠FBC，∠EGC＝∠GCB，∵∠DBF＝∠FBC，∠ECG＝∠GCB，∴∠DFB＝∠DBF，∠ECG＝∠EGC，∴BD＝DF，CE＝GE，∵FG＝2，ED＝6，∴DB＋EC＝DF＋GE＝ED−FG＝6−2＝4，故选：B．【点睛】本题考查等腰三角形的判定和性质、角平分线的定义，平行线的性质等知识，解题的关键是等腰三角形的证明．12．A解析：A【分析】由勾股定理及其逆定理可得三角形ABC是等腰直角三角形，从而得到∠ABC 的度数．【详解】解：如图，连结AC，由题意可得：2222221310,125,125,AB AC BC+==+==+=∴AC=BC，222AB AC BC=+，∴△ABC是等腰直角三角形，∴∠ABC=∠BAC=45°，故选A ．【点睛】本题考查勾股定理的应用，熟练掌握勾股定理及其逆定理、等腰直角三角形的性质是解题关键．二、填空题13．【分析】首先求出S1S2S3…探究规律后即可解决问题【详解】解：如图过点B作BE⊥AC1于点E∵△ABC1是等边三角形AB=AC1=BC1=1∴AE=∴∴由题意可知=…所以∵∴故答案为：【点睛】本题解析：3834(1)nn+【分析】首先求出S1，S2，S3，…，探究规律后即可解决问题．【详解】解：如图，过点B 作BE ⊥AC 1于点E ，∵△ABC1是等边三角形，AB=AC1=BC1=1∴AE=12， ∴22221312BE AB AE ⎛⎫=-=-= ⎪⎝⎭∴1113312AC B S ∆=⨯=由题意可知，11111111122B C D AC B AC B S S S S ∆∆∆====133248⨯=， 222211121233B C D AC B AC B S S S S ∆∆∆===， 333321131344B C D AC B AC B S S S S ∆∆∆===， …， 所以111n AC B n S S n ∆=+， ∵111331224AC B S ∆=⨯⨯=， ∴3n n S = 33n 【点睛】本题考查了等边三角形的性质，三角形的面积等知识，解题的关键是学会从特殊到一般的探究方法，学会利用规律解决问题，属于中考常考题型．14．【分析】根据等腰三角形的性质可求出△CBA1的底角的度数再根据三角形外角的性质及等腰三角形的性质可求出△DA1A2的底角的度数同理可求出△EA2A3△FA3A4…底角的度数再找出其规律即可得出第n 个 解析：11702n -︒⨯【分析】根据等腰三角形的性质，可求出 △CBA 1 的底角的度数，再根据三角形外角的性质及等腰三角形的性质，可求出 △DA 1A 2 的底角的度数．同理可求出 △EA 2A 3 、 △FA 3A 4 …底角的度数．再找出其规律即可得出第n 个三角形中以 An 为顶点的底角度数．【详解】在 △CBA 1 中， ∠B=40° ， A 1B=CB ，∴ ∠BA 1C=∠BCA 1=（180°−40°)÷2=70° ，又∵ A 1A 2=A 1D ， ∠BA 1C 是 △A 1A 2D 的外角．∴ ∠DA 2A 1=∠A 2DA 1=12∠BA 1C=12×70° ． 同理可得：∠EA 3A 2=∠A 3EA 2=12∠DA 2A 1=12×12×70°=(12)2×70° ， ∠FA 4A 3=∠A 4FA 3=12∠EA 3A 2=(12)3×70°， 综上可知规律：第n 个三角形中以 An 为顶点的底角度数是：112n -×70° ， 故答案为 70° ×112n -． 【点睛】本题考查等腰三角形和三角形外角的性质，求出 ∠DA 2A 1 、 ∠EA 3A 2 、 ∠FA 4A 3 的度数，找出其规律是解答本题的关键． 15．4【分析】根据角平分线的判定定理可知①正确；根据等腰三角形的性质角平分线的性质可得所以内错角相等所以所以为等边三角形所以可判断③④正确再根据①③④的结论易证②正确【详解】点P 在的平分线上故①正确；A解析：4【分析】根据角平分线的判定定理可知①正确；根据等腰三角形的性质，角平分线的性质，可得APQ QAP ∠=∠，QAP BAP ∠=∠，所以APQ BAP ∠=∠，内错角相等，所以//QP AR ，所以60BAC C ∠=∠=︒，PCQ △为等边三角形，所以可判断③④正确，再根据①③④的结论易证②正确．【详解】,,PR PS PR AB PS AC =⊥⊥90PRB PSQ ∴∠=∠=︒∴点P 在BAC ∠的平分线上，故①正确；PQ AQ =APQ QAP ∴∠=∠AP 平分BAC ∠QAP BAP ∴∠=∠APQ BAP ∴∠=∠//QP AR ∴，故③正确； ABC 为等边三角形60B C BAC ∴∠=∠=∠=︒//QP AR60BAC PQS ∴∠=∠=︒PQC ∴是等边三角形，故④正确；∴在BRP △和QSP 中B PQS PRB PSQ PR PS ∠=∠⎧⎪∠=∠⎨⎪=⎩∴BRP △≌QSP 故②正确综上所述①②③④都正确故答案为：4.【点睛】本题考查了等边三角形的性质，全等三角形的判定，角平分线的性质定理，解题关键是灵活运用所学知识解决问题．16．【分析】连接PC 只要证明PB=PC 即可推出PC+PE=PB+PE 可得PBE 共线时PC+PE 的值最小最小值为BE 的长度从而结合等腰三角形的性质求解【详解】解：如图连接PC ∵AB=ACAD ⊥BC ∴BD=解析：135【分析】连接PC ，只要证明PB=PC ，即可推出PC+PE=PB+PE ，可得P 、B 、E 共线时，PC+PE 的值最小，最小值为BE 的长度，从而结合等腰三角形的性质求解．【详解】解：如图，连接PC ，∵AB=AC ，AD ⊥BC ，∴BD=CD ，∴PB=PC ，∴PC+PE=PB+PE ，又∵BE ⊥AC∴P 、B 、E 共线时，PC+PE 的值最小为BE 的长，∵AB=AC ，∠BAC=45°，BE ⊥AC∴∠ABC=∠ACB=67.5°，∠ABE=45°∴∠PBC=∠PCB=67.5°-45°=22.5°∴∠BPC=180°-22.5°×2=135°故答案为：135．【点睛】本题考查轴对称-最短路线问题，等腰三角形的性质、线段的垂直平分线的性质等知识，解题的关键是灵活运用所学知识解决问题．17．【分析】先根据等腰三角形的性质求得的度数再根据三角形一个外角等于与其不相邻的两个内角和分别求出的度数找出规律即可得到第个三角形中以为顶点的底角度数【详解】解：在中是的外角同理得第个三角形中以为顶点的 解析：20201722⎛⎫⨯ ⎪⎝⎭︒【分析】 先根据等腰三角形的性质求得1BA C ∠的度数，再根据三角形一个外角等于与其不相邻的两个内角和，分别求出213243DA A EA A FA A ∠∠∠、、的度数，找出规律即可得到第n 个三角形中以n A 为顶点的底角度数．【详解】解：在1CBA 中，136,B A B CB ∠=︒=1180722B BAC ︒-∠∴∠==︒ 1211,A A AD BA C =∠是12A A D 的外角，211117222DA A BAC ∴∠=∠=⨯︒ 同理得2321()722EA A ∠=⨯︒， 3431()722FA A ∠=⨯︒ ∴第n 个三角形中以n A 为顶点的底角度数是11()722n -⨯︒ ∴第2021个三角形的底角度数是：20201()722⨯︒，故答案为：20201()722⨯︒．【点睛】 本题考查等腰三角形的性质、三角形的外角性质、规律型—图形的变化类等知识，是重要考点，难度一般，掌握相关知识是解题关键．18．①②③【分析】由三角形ABC 中∠BAC 的平分线交BC 于点D 过点D 作DE ⊥ACDF ⊥AB 根据角平分线的性质可得DE=DF ∠ADE=∠ADF 然后根据全等三角形的性质可得AF=AE 继而证得①∠AFE=∠A解析：①②③【分析】由三角形ABC 中，∠BAC 的平分线交BC 于点D ，过点D 作DE ⊥AC ，DF ⊥AB ，根据角平分线的性质，可得DE=DF ，∠ADE=∠ADF ，然后根据全等三角形的性质，可得AF=AE ，继而证得①∠AFE=∠AEF ；又由线段垂直平分线的判定，可得②AD 垂直平分EF ；然后利用三角形的面积公式求解即可得③BFD CED S BF S CE ∆∆=，EF 平行BC 不能判断，于是可得④ ． 【详解】解：①∵三角形ABC 中，∠BAC 的平分线交BC 于点D ，DE ⊥AC ，DF ⊥AB ，∴∠ADE=∠ADF ，DF=DE ，∵AD=AD ，∴Rt △ADF ≌Rt △ADE （HL ），∴AF=AE ，∴∠AFE=∠AEF ，故正确；②∵DF=DE ，AF=AE ，∴点D 在EF 的垂直平分线上，点A 在EF 的垂直平分线上，∴AD 垂直平分EF ，故正确；③∵12BFD DF S BF ∆=•，S △CDE =12CE DE •，DF=DE ， ∴BFD CED S BF S CE∆∆=；故正确； ④∵∠EFD 不一定等于∠BDF ，∴EF 不一定平行BC ．故错误．故答案为：①②③．【点睛】此题考查了角平分线的性质、线段垂直平分线的性质以及等腰三角形的性质．此题难度适中，注意掌握数形结合思想的应用．19．6【分析】作点P 关于OA 的对称点P1点P 关于OB 的对称点P2连结P1P2与OA 的交点即为点M 与OB 的交点即为点N 则此时MN 符合题意求出线段P1P2的长即可【详解】解：作点P 关于OA 的对称点P1点P 关解析：6【分析】作点P关于OA的对称点P1，点P关于OB的对称点P2，连结P1P2，与OA的交点即为点M，与OB的交点即为点N，则此时M、N符合题意，求出线段P1P2的长即可．【详解】解：作点P关于OA的对称点P1，点P关于OB的对称点P2，连结P1P2与OA的交点即为点M，与OB的交点即为点N，△PMN的最小周长为PM＋MN＋PN＝P1M＋MN＋P2N＝P1P2，即为线段P1P2的长，连结OP1、OP2，则OP1＝OP2＝OP＝6，又∵∠P1OP2＝2∠AOB＝60°，∴△OP1P2是等边三角形，∴P1P2＝OP1＝6，即△PMN的周长的最小值是6．故答案是：6．【点睛】本题考查了等边三角形的性质和判定，轴对称−最短路线问题的应用，关键是确定M、N的位置．20．1【分析】作点M关于直线CD的对称点G过G作于N交CD与P再根据等边三角形的性质计算即可；【详解】作点M关于直线CD的对称点G过G作于N交CD与P∵△ABC是等边三角形AB=4∴AB=BC=AC=4解析：1【分析】⊥于N，交CD与P，再根据等边三角形作点M关于直线CD的对称点G，过G作GN AB的性质计算即可；【详解】⊥于N，交CD与P，作点M关于直线CD的对称点G，过G作GN AB∵△ABC是等边三角形，AB=4，∴AB=BC=AC=4，30G ∠=︒，∵M 是BC 的中点，∴2BM CM CG ===，∴6BG =，在Rt △BNG 中，30G ∠=︒，6BG =，∴3BN =，∴431AN =-=；故答案是1．【点睛】本题主要考查了轴对称最短路径问题，准确计算是解题的关键．三、解答题21．（1）1； 45°；（2）见解析；（3）94【分析】（1）根据非负数的性质可求得c 的值，得到OA=OB ，即可求得∠ABO 的度数；（2）证明△AOE ≅△BOC 即可证明OE OC =； （3）连结OF ，过点F 作FG x ⊥轴，垂足为点G ，根据线段垂直平分线的性质得到OA=OF ，证明∠OBC=30°，根据直角三角形的性质、三角形的面积公式计算，得到答案．【详解】（1）∵()210c a b -++=，∴10c -=，0a b +=，∴1c =，∵A(a ，0)， B(0，b)，∴OA=OB ，∵∠AOB=90°，∴△AOB 是等腰直角三角形，∴∠ABO=45°，故答案为：1；45°；（2）∵AF BC ⊥，∴90AOE BFE ∠=∠=︒，∵AEO BEF ∠=∠，∴OBC OAE ∠=∠，由（1）得：OA=OB ，在AOE △和BOC 中， AO BO AOE BOC OBC OAE =⎧⎪∠=∠⎨⎪∠=∠⎩，∴AOE BOC ≅△△(AAS)，∴OE OC =；（3）连结OF ，过点F 作FG x ⊥轴，垂足为点G ，∵O 在AF 的垂直平分线上∴AO OF =，∴OAF OFA x ∠=∠=，∴2GOF OAF OFA x ∠=∠+∠=∵22FBO FAO x ∠=∠=，OB OA OF ==，∴2OFC OBF x ∠=∠=，∴4BCO COF OFB x ∠=∠+∠=，∵90OBC OCB ∠+∠=︒，∴690x =，解得15x =，∴230OBC GOF x ∠=∠==︒，∵1c =，∴C(1，0)，1OC =，∵90BOC ∠=°，30OBC ∠=︒，∴22BC OC ==，22OB BC OC 3=-= ∴3OA OF OB === 同理可得：32FG =， ∴31AC AO OC =+= ∴)11119331333222244ABF ACB ACF S S S AC FG AC OB =+=⋅+⋅==+△△△ 【点睛】本题考查了全等三角形的判定和性质、线段垂直平分线的性质、等腰直角三角形的性质、含30度角的直角三角形的性质、三角形的面积计算，掌握全等三角形的判定定理和性质定理是解题的关键．22．（1）见解析；（2）△ABF 中AB 边上的高为255 【分析】 （1）根据角平分线的定义、等腰三角形的性质得到∠CAD ＝∠BDA ，根据平行线的判定定理证明即可；（2）作FG ⊥AB 于G ，根据勾股定理求出BE ，进而求出FE ，根据角平分线的性质定理解答即可．【详解】（1）证明：∵AD 是∠BAC 的平分线，∴∠CAD ＝∠BAD ，∵AB ＝BD ，∴∠BDA ＝∠BAD ，∴∠CAD ＝∠BDA ，∴AC ∥BD ；（2）解：作FG ⊥AB 于G ，在Rt △ABE 中，AE ＝2，AB ＝3，∴BE 2222325AB AE =-=-=，∴FE ＝BE ﹣BF 3255555=-=， ∵AD 是∠BAC 的平分线，BE ⊥AC ，FG ⊥AB ，∴FG ＝FE 255=，即△ABF 中AB 边上的高为255．【点睛】本题考查的是角平分线的性质、等腰三角形的性质，勾股定理,掌握角的平分线上的点到角的两边的距离相等是解题的关键．23．（1）∠ABP=50°；（2）见解析；（3）①EA=52a 或EA=3910a 【分析】（1）由PA 平分∠BAD 且BP ⊥AP ，∠BAD=80°，在Rt APB ∆中即可求得．（2）延长BP 交AD 延长线于H ，可得AB=AH ，可证△BCP ≌△HDP ，可得BC=DH ，从而结论可证．（3）过点P 作一条直线，分别与AD ，BC 所在直线交于点E ，点F ．若AB=EF ，可能有两种情况，延长BP 交AE 延长线于H ，每种情况都可依据角平分线的性质，过P 点分别做PI 和PG 垂直于AB 和AH ，则PI=PG ；然后通过解直角三角形即可求解．【详解】解：（1）∵PA平分∠BAD且∠BAD=80°，∴∠BAP=∠DAP=40°；又∵∠BPA=90°∴∠ABP+∠BAP=90°，故∠ABP=50°．（2）延长BP交AD延长线于H，∵PA平分∠BAD，∴∠BAP=∠DAP而∠BPA=90°=∠HPA，∴∠ABP=∠AHP，∴AB=AH；∵AP⊥BH，∴BP=PH；∵BC//AH，∴∠PBC=∠H；而∠BPC=∠HPD；∴△BCP≌△HDP（ASA）；∴BC=DH，故AB=AH=AD+DH=AD+BC．（3）①延长BP交AE延长线于H，过P点分别做PI和PG垂直于AB和AH，则PI=PG；易得△BFP≌△HEP，∴ BP=HP=3a，FP=EP=12 EF；在直角三角形ABP中，BP2+AP2=AB2；∴ AB=5a，EP=52a；∵在直角三角形ABP中AB PI BP AP⋅=⋅，∴ PI=125a=PG；在直角三角形EPG中，GP2+EG2=EP2，∴ EG=710a；在直角三角形HPG中，GP2+HG2=HP2，∴ GH=95a；∴ EH=52a；∴ EA=AH-EH=52a．②延长BP交AE延长线于H，过P点分别做PI和PG垂直于AB和AH，由①得GH=95a，EG=710a；∴ EH=1110a；∴ EA=3910a．【点睛】本题主要考查了角平分线的性质，全等三角形的判定及性质，解直角三角形，解题的关键是准确作出辅助线．24．（1）见解析；（2）22.5【分析】（1）根据全等三角形的判定和性质得出△ABD≌△BAE，进而得出OB=OA；（2）根据全等三角形的判定和性质以及三角形内角和解答．【详解】证明：（1）∵AC=BC，∠ACB=90°，∴∠ABC=∠BAC=45°．∴∠EBA=∠DAB=135°．在△ABD与△BAE中，135BE AD EBA DAB AB AB =⎧⎪∠=∠=︒⎨⎪=⎩，∴△ABD ≌△BAE （SAS ），∴∠DBA=∠EAB ，∴OB=OA ；（2）由（1）得：OB=OA ，在△OBC 与△OAC 中，OB OA OC OC BC AC =⎧⎪=⎨⎪=⎩，∴△OBC ≌△OAC （SSS ），∴∠OCB=∠OCA=12∠ACB=12×90°=45°， ∵AC=BC ，AC=OC ，∴OC=BC ， ∴∠CBO=∠COB 1801804567.522OCB ︒︒︒︒-∠-===， 在Rt △BCD 中，∠D=180°-90°-∠CBO=22.5°．故答案为：22.5．【点睛】本题考查了全等三角形的判定和性质，等腰三角形的判定和性质，关键是根据全等三角形的判定和性质解答．25．（1）详见解析；（23【分析】（1）由题意可以得到△ABD ≌△ACE ，从而得到BD=CE ；（2）分别过E 作AC 、CD 的垂线EM 、EN ，由（1）及勾股定理可以求得EM 、EN 的值，然后根据三角形面积计算方法及AC+CD=2可以得到四边形ACDE 的面积 ．【详解】证明：（1）∵△ABC 和△ADE 为等边三角形，∴AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE ＝60°，∴∠BAD ＝∠CAE ，在△ABD 和△ACE 中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩, ∴△ABD ≌△ACE （SAS ），∴BD ＝CE ；（2）∵△ABD ≌△ACE ，∴∠ACE ＝∠ABD ＝60°，∴∠DCE ＝180°﹣∠ACE ﹣∠ACB ＝180°﹣60°﹣60°＝60°，过点E 作EM ⊥AC 于M ，过E 作EN ⊥BC ，交BC 延长线于N ，∴EM ＝EN ，∵CE ＝BD ＝AC +CD ＝2，∴EM ＝EN 3∴ACE DCE ACDE S S S =+四边形1122AC EM CD EN =⨯+⨯ ()1132322EM AC CD =+== 3【点睛】本题考查四边形的综合应用，熟练掌握等边三角形的性质、三角形全等的判定及应用、勾股定理、三角形面积的计算方法及角平分线的性质是解题关键．26．(1)见解析(2)见解析【分析】（1）根据HL 可证明Rt △DBE ≌Rt △DCF ；（2）由全等三角形的性质得出∠EBD ＝∠FCD ，由等腰三角形的性质得出∠DBC ＝∠DCB ，则可得出结论．【详解】证明：（1）∵DE ⊥AB ，DF ⊥AC ，∴∠BED ＝∠CFD ＝90°．在Rt △BDE 和Rt △CDF 中，BE CF BD CD =⎧⎨=⎩， ∴Rt △BDE ≌Rt △CDF （HL ）；（2）∵Rt △DBE ≌Rt △DCF ，∴∠EBD ＝∠FCD ，∵BD ＝CD ，∴∠DBC ＝∠DCB ，∴∠DBC ＋∠EBD ＝∠DCB ＋∠FCD ，即∠ABC ＝∠ACB ，∴AB ＝AC ．【点睛】本题考查全等三角形的判定和性质，等腰三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．。

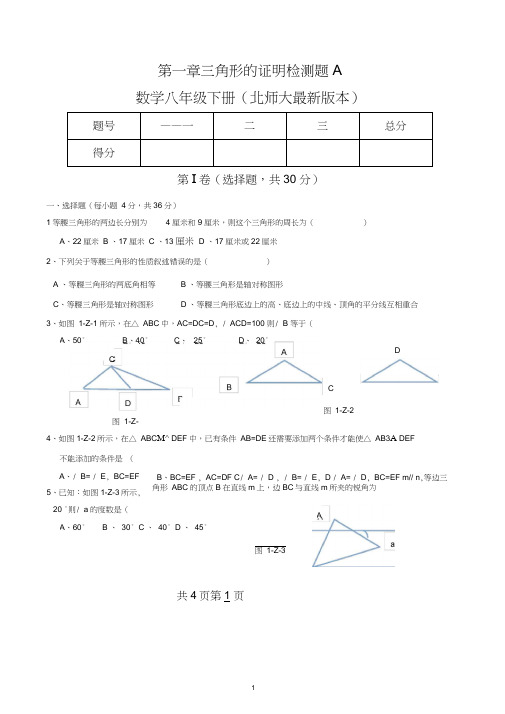
第一章三角形的证明检测题A 数学八年级下册（北师大最新版本）题号——一二三总分得分第I 卷（选择题，共30 分）一、选择题（每小题 4分，共36分） 1等腰三角形的两边长分别为4厘米和9厘米，则这个三角形的周长为（）A 、22厘米B 、17厘米C 、13厘米D 、17厘米或22厘米 2、下列关于等腰三角形的性质叙述错误的是（ ）A 、等腰三角形的两底角相等B 、等腰三角形是轴对称图形C 、等腰三角形是轴对称图形D 、等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合3、如图 1-Z-1 所示，在△ ABC 中，AC=DC=D , / ACD=100 则/ B 等于（4、如图1-Z-2所示，在△ ABC M^ DEF 中，已有条件 AB=DE 还需要添加两个条件才能使△ AB3A DEF不能添加的条件是 （ B 、BC=EF , AC=DF C / A= / D , / B= / E , D / A= / D , BC=EF m// n ,等边三角形 ABC 的顶点B 在直线m 上，边BC 与直线m 所夹的锐角为共4页第1 页图 1-Z-2A 、/ B= / E , BC=EF 5、已知：如图1-Z-3所示, 20 °则/ a 的度数是（ A 、60°B 、 30°C 、 40°D 、 45°图 1-Z-3A 、50°C 、 25°D 、 20°CC 图 1-Z-1B 、40°DA形是等腰三角形，则满足条件的点P 共有（A 、2个B 、3个第口卷（非选择题，共二、填空题（每小题4分，共24分）10、如图1-Z-8所示，已知△ ABC 是等边三角形，AD // BC , CD 丄 AD ，垂足为 D , E 为 AC 的中点，AD=DE=6cm, 则 Z ACD= _________ ° , AC= ______________ cm , / DAC=° ,△ ADE 是一三角形6、如图1-Z-4所示，在△ ABC 中, / ABC 和/ ACB 的平分线交于点 E ,过点E 作MN // BC 交AB 于M , 交AC 于N ， 若BM+CN=9，则线段 MN 的长为（A CC图 1-Z-57、如图 1-Z-5 所示，在△ ABC 中, CD 平分 / ABC , / A=80 ，/ ACB=60 °，那么/ BDC=(A 、80°B 、90° 100 ° 、110 ° 8、如图 1-Z-6 所示，在Rt △ ABC 中, / C=90。

第一章 三角形的证明班级：___________________________姓名：___________________________作业导航1.等腰、等边、直角三角形的性质2.反证法一、填空题1.在等腰三角形中顶角为40°时底角等于_________，一个底角为50°，则顶角等于_________.2.由在同一三角形中“等角对等边”“等边对等角”两个定理我们可以联想到大边对_________，大角对_________.3.等腰三角形的两边分别是7 cm 和3 cm ，则周长为_________.4.一个等边三角形的角平分线、高、中线的总条数为_________.5.等腰三角形的一边长为23，周长为43+7，则此等腰三角形的腰长为_________.6.等边三角形两条中线相交所成的锐角的度数为_________.7.如图1，D 在AC 上，且AB =BD =DC ，∠C =40°，则∠A =_________，∠ABD =_________.图1 图28.如图2，Rt △ABC 中，∠ACB =90°，点D 在AB 上，且AD =AC ，若∠A =40°，则 ∠ACD =_________，∠DCB =_________，若∠A =α，则∠BCD =_________，由此我们可得出∠BCD 与∠A 的关系是∠BCD =_________.9.△ABC 中，若∠A =∠B =21∠C ，则此三角形为_________三角形. 10.Rt △ABC 中，∠C =90°，∠CAB =60°，AD 平分∠CAB ，点D 到AB 的距离是3.8 cm ，则BC =_________ cm.11.△ABC 中，∠BAC =90°，∠B =60°，AD ⊥BC 于D ，AE 是斜边上的中线，若DB =4，则AB =_________，BC =_________.二、选择题12.给出下列命题，正确的有（ ）①等腰三角形的角平分线、中线和高重合； ②等腰三角形两腰上的高相等； ③等腰三角形最小边是底边；④等边三角形的高、中线、角平分线都相等；⑤等腰三角形都是锐角三角形A.1个B.2个C.3个D.4个13.若等腰△ABC 的顶角为∠A ，底角为∠B =α，则α的取值范围是（ ）A.α＜45°B.α＜90°C.0°＜α＜90°D.90°＜α＜180°14.下列命题，正确的有（ ）①三角形的一条中线必平分该三角形的面积；②直角三角形中30°角所对的边等于另一边的一半；③有一边相等的两个等边三角形全等；④等腰三角形底边上的高把原三角形分成两个全等的三角形 A.1个 B.2个 C.3个 D.4个15.若三角形的一边等于另一边的一半，那么这边所对的角度为（ ）A.30°B.45°C.60°D.无法确定16.如果三角形一边的中线和这边上的高重合，则这个三角形是（ ）A.等边三角形B.等腰三角形C.锐角三角形D.钝角三角形17.△ABC 中， AB =AC ， CD 是△ABC 的角平分线， 延长BA 到E 使DE =DC ， 连结EC ， 若 ∠E =51°，则∠B 等于（ ）A.60°B.52°C.51°D.78°18.在△ABC 中∠A ∶∠B ∶∠C =1∶2∶3，CD ⊥AB 于D 点，AB =a ，则BD 的长为（ ）A.2aB.3aC.4aD.以上都不对19.在直角三角形中，一条边长为a ，另一条边长为2a ，那么它的三个内角的比为（ ）A.1∶2∶3B.2∶2∶1C.1∶1∶2D.以上都不对三、解答题20.如图3，在AB =AC 的△ABC 中，D 点在AC 边上，使BD =BC ，E 点在AB 边上，使AD =DE =EB ，求∠ED B.图321.如图4，AB =CD ，AD =BC ，EF 经过AC 的中点O ，分别交AB 和CD 于E 、F ，求证：OE =OF .图422.如图5，在△ABC 中，AB =AC ，D 是AB 上一点，DE ⊥BC ，E 是垂足，ED 的延长线交CA 的延长线于点F ，求证：AD =AF .图523.你以前证过的结论，有的是否可以用反证法证明，试试看.参考答案三角形的证明一、1.70° 80° 2.大角 大边 3.17 cm 4.3条 5.27 +3 6.60° 7.80° 20° 8.70° 20° 2 21∠A 9.等腰直角 10.11.4 11.8 16 二、12.B 13.C 14.C 15.D 16.B 17.B 18.C 19.D三、20.解：设∠BDE =x ∵BE =DE ∴∠EBD =∠EDB =x则∠AED =∠EDB +∠EBD =2x又∵AD =DE ∴∠A =∠AED =2x又∠BDC =∠A +∠ABD =3x又∵BD =BC ，∴∠C =∠BDC =3x又∵AB =AC ，∴∠ABC =∠C =3x根据三角形内角和定理3x +3x +2x =180°∴x =22.5°21.证明：在△ABC 和△CDA 中∵AB =CD ，BC =AD ，AC =AC∴△ABC ≌△CDA ，∴∠1=∠2在△AOE 和△COF 中∵∠1=∠2，OA =OC ，∠3=∠4∴△AOE ≌△COF ，∴OE =OF .22.证明：∵AB =AC ，∴∠B =∠C ，∴EF ⊥BC ，∴∠FEB =∠FEC =90°， ∴∠B +∠BDE =∠C +∠F =90°，∴∠BDE =∠F ，∵∠BDE =∠FDA∴∠F =∠FDA ，∴AD =AF .23.略。

【北师大版八年级数学（下）单元测试卷】第一章：三角形的证明一.选择题：（每小题3分共30分）1．等腰三角形两边长分别为4和9,则该三角形第三边的长为（ ）A ．4B ．9C ．4或9D ．大于5且小于132．如图,在ABC 中,90ACB ∠=︒,CD 是高,30A ∠=︒,若3BD a =,则AD 的长度为（ ）A ．6aB ．9aC ．12aD ．15a3．如图,在ABC 中,DE 是AC 的垂直平分线,若ABC 的周长为19cm ,ABD △的周长为13cm ,则AE 的长为（ ）A ．2cmB ．3cmC ．4cmD ．6cm4．如图,在Rt ABC △中,90C ∠=︒,30B ∠=︒,点D 是AB 的中点,ED AB ⊥于点D,交BC 于点E,连接AE ,若2DE =,则BC 的值是（ ）A ．3B ．4C ．5D ．65．如图,在△ABC 中,∠C=90°,∠B=15°,AB 的垂直平分线交BC 于D,交AB 于E,若DB=10cm,则CD 的长为（ ）6．如图,点C 为∠AOB 的角平分线l 上一点,D,E 分别为OA,OB 边上的点,且CD ＝CE,作CF ⊥OA,垂足为F,若OF ＝5,则OD+OE 的长为（ ）A ．10B ．11C ．12D ．157．如图,等腰三角形ABC 的底边BC 长为4,面积是18,腰AC 的垂直平分线EF 分别交AC 、AB 边于点E 、F ．若点D 为BC 的中点,点M 为线段EF 上一动点,则CDM 周长的最小值为（ ）A ．6B ．8C ．9D ．118．如图,ABC 中,AB BC =,点D 在AC 上,BD BC ⊥．设BDC α∠=,ABD β∠=,则下列关系式正确的是（ ）A ．3180αβ+=︒B ．2180αβ+=︒C ．3180αβ-=︒D ．290αβ-=︒9．如图,已知等边ABC 和等边ADE ,其中点A 、D 、B 在同一条直线上,连接BE 交AC 于点M ,连接DC 交AE 于点N ,BE 和DC 交于点P ,则下列结论中：（1）MN BD ∥；（2）60BPC ∠=︒；（3）DN DE =；（4）BAM CAN ≅△△．正确的个数有（ ）A ．1个B ．2个C ．3个D ．4个侧作等边△ADE 和等边△ADF,分别和AB,AC 交于点G,H,连接GH ．若∠BOC=120°,AB=a,AC=b,AD=c ．则下列结论中正确的个数有（ ）①∠BAC=60°；②△AGH 是等边三角形；③AD 与GH 互相垂直平分；④()12ABC S a b c =+△． A ．1个 B ．2个 C ．3个 D ．4个 二.填空题:（每小题3分共15分）11．在ABC 中,AB AC =,64BAC ∠=︒,BAC ∠的角平分线与AB 的垂直平分线交于点O ,将C ∠沿EF 折叠,点C 与点O 恰好重合,则CFO ∠的度数为__________．12．如图,已知CD 是△ABC 的角平分线,DE ⊥BC,垂足为E,若AC ＝4,BC ＝10,△ABC 的面积是14,则DE ＝_____．13．如图,1230∠=∠=︒,A B ∠=∠,AE BE =,点D 在边AC 上,AE 与BD 相交于点O,则∠C 的度数为______．14．如图,在等腰△ABC 中,AB=AC=10,BC=16,AD 是BC 边上的中线且AD=6,F 是AD 上的动点,E 是AC 边上的动点,则CF+EF 的最小值等于______．15．如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD ⊥BC 于点D,点P 是BA 延长线上一点,点O 是线段AD 上一点,OP=OC,下面结论：①∠ACO=15°；②∠APO+∠DCO=30°；③△OPC 是等边三角形；④AC=AO+AP ； 其中正确的有 ______（填上所有正确结论的序号）．三.解答题:(共55分)16．(5分)如图,在ABC 和ADE 中,AB AC =,AD AE =,90BAC DAE ∠=∠=︒．BD ,CE 相交于点F ．BD ,AC 相交于点M ．(1)求证：BD CE =；(2)求BFC ∠的度数．17．(8分)如图,在ABC 中,60ACB ∠=︒,点D 在AC 上,BC CD =,以AB 为边向左侧作等边三角形ABE ,连ED ．(1)求证：ABC EBD ≌△△； (2)过点B 作BF ED ⊥于点F ,2DF =,求BD 的长．18．(8分)点C 、D 都在线段AB 上,且AD ＝BC,AE ＝BF,∠A ＝∠B,CE 与DF 相交于点G ．(1)求证∠E ＝∠F ；(2)若CE ＝10,DG ＝4,求 EG 的长．19．(8分)在平面直角坐标系中,等腰直角△ABC 顶点A 、C 分别在y 轴、x 轴上,且∠ACB=90°,AC=BC ．(1)如图1,当A(0,−2),C(1,0),点B 在第四象限时,求点B 的坐标．(2)如图2,当点C 在x 轴正半轴上运动,点A(0,a)在y 轴正半轴上运动,点B(m,n)在第四象限时,作BD ⊥y 轴于点D,求a,m,n 之间的关系．20．(8分)如图,在Rt ABC 中,90BAC ∠=︒,AB AC =,AD 是BC 的中线,AE BF =．(1)求证：DE DF =(2)DEF 是什么形状的三角形？请说明理由．连接AD,作∠ADE ＝40°,DE 交线段AC 于E ．(1)当∠BDA ＝115°时,∠EDC ＝______,∠DEC ＝_____；(2)当DC 等于多少时,△ABD ≌△DCE,请说明理由；(3)在点D 的运动过程中,△ADE 的形状可以是等腰三角形吗？若可以,请直接写出∠BDA 的度数．若不可以,请说明理由．22．(9分)如图,在平面直角坐标系中,直线()140y x m m=-+>分别与x 轴,y 轴交于A,B 两点,把线段(1)当54m 时,求点C的坐标；(2)当m值发生变化时,△BOC的面积是否保持不变？若不变,计算其大小；若变化,请说明理由；(3)当S△AOB=2S△BOC时,在x轴上找一点P,使得△PAB是等腰三角形,求满足条件的所有P点的坐标．。

北师大版八年级下册数学第一章三角形的证明单元测试题一．选择题（共12小题）1．如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC=7，DE=2，AB=4，则AC长是（）A．3B．4C．6D．52．如图，锐角三角形ABC中，直线L为BC的中垂线，直线M为∠ABC的角平分线，L与M相交于P点．若∠A=60°，∠ACP=24°，则∠ABP的度数为何？（）A．24 B．30 C．32 D．363．已知等腰三角形的两边长分別为a、b，且a、b满足+（2a+3b﹣13）2=0，则此等腰三角形的周长为（）A．7或8 B．6或1O C．6或7 D．7或104．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是（）A．2.5 B．C．D．25．如图，△ABC中，DE是AC的垂直平分线，AE=4cm，△ABD的周长为14cm，则△ABC的周长为（）A．18cm B．22cm C．24cm D．26cm6．如图，在△ABC，∠C=90°，∠B=15°，AB的中垂线DE交BC于D，E为垂足，若BD=10cm，则AC等于（）A．10cm B．8cm C．5cm D．2.5cm7．如图，已知OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（）A．2B．C．D．8．如图，△ABC中，∠B=40°，AC的垂直平分线交AC于D，交BC于E，且∠EAB：∠CAE=3：1，则∠C等于（）A．28°B．25°C．22.5°D．20°9．若一个等腰三角形至少有一个内角是88°，则它的顶角是（）A．88°或2°B．4°或86°C．88°或4°D．4°或46°10．如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为（）A．3B．3.5 C．2.5 D．2.811．如图，在Rt△ABC中，∠ACB=30°，CD=4，BD平分∠ABC，交AC于点D，则点D到BC的距离是（）A．1B．2C．D．12．如图，在△ABC中，∠ACB=100°，AC=AE，BC=BD，则∠DCE的度数为（）A．20°B．25°C．30°D．40°二．填空题（共6小题）13．如图，在△ABC中，∠C=90°，AB=10，AD是△ABC的一条角平分线．若CD=3，则△ABD的面积为_________．14．如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC于E，交BC的延长线于F，若∠F=30°，DE=1，则BE的长是_________．15．如图，△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E，若∠BAC=70°，则∠CAE=_________．16．如图，△ABC的三边AB、BC、CA长分别为40、50、60．其三条角平分线交于点O，则S△ABO：S△BCO：S△CAO= _________．17．在△ABC中，已知AB=AC，DE垂直平分AC，∠A=50°，则∠DCB的度数是_________．18．如图，在菱形ABCD中，∠ADC=72°，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则∠CPB= _________度．三．解答题（共12小题）19．如图，已知DE是AC的垂直平分线，AB=10cm，BC=11cm，求△ABD的周长．20．如图，D为△ABC边BC延长线上一点，且CD=CA，E是AD的中点，CF平分∠ACB交AB于点F．求证：CE⊥CF．21．如图，在四边形ABCD中，∠B=∠D=90°，∠C=60°，BC=4，CD=3，求AB的长．22．如图，Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于E，若AC=6，BC=8，CD=3．（1）求DE的长；（2）求△ADB的面积．23．如图，已知△ABC和△ABD均为直角三角形，其中∠ACB=∠ADB=90°，E为AB的中点，求证：CE=DE．24．如图所示，在△ABC中，BC＞AC，点D在BC上，且DC=AC，∠ACB的平分线CF交AD于点F．点E是AB的中点，连接EF．（1）求证：EF∥BC；（2）若△ABD的面积是6，求四边形BDFE的面积．25．如图，四边形ABCD中，AD∥BC，∠A=90°，BD=BC，CE⊥BD于点E．求证：AD=BE．26．已知；如图，在△ABC中，AB=BC，∠ABC=90度．F为AB延长线上一点，点E在BC上，BE=BF，连接AE、EF和CF．（1）求证：AE=CF；（2）若∠CAE=30°，求∠EFC的度数．27．如图，在△ABC中，AB≠AC，∠BAC的外角平分线交直线BC于D，过D作DE⊥AB，DF⊥AC分别交直线AB，AC于E，F，连接EF．（1）求证：EF⊥AD；（2）若DE∥AC，且DE=1，求AD的长．28．如图，Rt△ABC中，∠C=90°，AC=6，∠A=30°，BD平分∠ABC交AC于点D，求点D到斜边AB的距离．29．如图，在△ABC中，∠CAB=90°，AB=3，AC=4，AD是∠CAB的平分线，AD交BC于D，求BD的长．30．如图，四边形ABCD中，AB=BC，AB∥CD，∠D=90°，AE⊥BC于点E，求证：CD=CE．参考答案与试题解析一．选择题（共12小题）1．如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC=7，DE=2，AB=4，则AC长是（）A．3B．4C．6D．5考点：角平分线的性质．专题：几何图形问题．分析：过点D作DF⊥AC于F，根据角平分线上的点到角的两边距离相等可得DE=DF，再根据S△ABC=S△ABD+S△ACD列出方程求解即可．解答：解：如图，过点D作DF⊥AC于F，∵AD是△ABC中∠BAC的角平分线，DE⊥AB，∴DE=DF，由图可知，S△ABC=S△ABD+S△ACD，∴×4×2+×AC×2=7，解得AC=3．故选：A．点评：本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质是解题的关键．2．如图，锐角三角形ABC中，直线L为BC的中垂线，直线M为∠ABC的角平分线，L与M相交于P点．若∠A=60°，∠ACP=24°，则∠ABP的度数为何？（）A．24 B．30 C．32 D．36考点：线段垂直平分线的性质．分析：根据角平分线的定义可得∠ABP=∠CBP，根据线段垂直平分线上的点到两端点的距离相等可得BP=CP，再根据等边对等角可得∠CBP=∠BCP，然后利用三角形的内角和等于180°列出方程求解即可．解答：解：∵直线M为∠ABC的角平分线，∴∠ABP=∠CBP．∵直线L为BC的中垂线，∴BP=CP，∴∠CBP=∠BCP，∴∠ABP=∠CBP=∠BCP，在△ABC中，3∠ABP+∠A+∠ACP=180°，即3∠ABP+60°+24°=180°，解得∠ABP=32°．故选：C．点评：本题考查了线段垂直平分线上的点到两端点的距离相等的性质，角平分线的定义，三角形的内角和定理，熟记各性质并列出关于∠ABP的方程是解题的关键．3．已知等腰三角形的两边长分別为a、b，且a、b满足+（2a+3b﹣13）2=0，则此等腰三角形的周长为（）A．7或8 B．6或1O C．6或7 D．7或10考点：等腰三角形的性质；非负数的性质：偶次方；非负数的性质：算术平方根；解二元一次方程组；三角形三边关系．分析：先根据非负数的性质求出a，b的值，再分两种情况确定第三边的长，从而得出三角形的周长．解答：解：∵|2a﹣3b+5|+（2a+3b﹣13）2=0，∴，解得，当a为底时，三角形的三边长为2，3，3，则周长为8；当b为底时，三角形的三边长为2，2，3，则周长为7；综上所述此等腰三角形的周长为7或8．故选：A．点评：本题考查了非负数的性质、等腰三角形的性质以及解二元一次方程组，是基础知识要熟练掌握．4．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是（）A．2.5 B．C．D．2考点：直角三角形斜边上的中线；勾股定理；勾股定理的逆定理．专题：几何图形问题．分析：连接AC、CF，根据正方形性质求出AC、CF，∠ACD=∠GCF=45°，再求出∠ACF=90°，然后利用勾股定理列式求出AF，再根据直角三角形斜边上的中线等于斜边的一半解答即可．解答：解：如图，连接AC、CF，∵正方形ABCD和正方形CEFG中，BC=1，CE=3，∴AC=，CF=3，∠ACD=∠GCF=45°，∴∠ACF=90°，由勾股定理得，AF===2，∵H是AF的中点，∴CH=AF=×2=．故选：B．点评：本题考查了直角三角形斜边上的中线等于斜边的一半的性质，正方形的性质，勾股定理，熟记各性质并作辅助线构造出直角三角形是解题的关键．5．如图，△ABC中，DE是AC的垂直平分线，AE=4cm，△ABD的周长为14cm，则△ABC的周长为（）A．18cm B．22cm C．24cm D．26cm考点：线段垂直平分线的性质．分析：根据线段垂直平分线上的点到线段两端点的距离相等可得AD=CD，然后求出△ABD的周长=AB+BC，再求出AC的长，然后根据三角形的周长公式列式计算即可得解．解答：解：∵DE是AC的垂直平分线，∴AD=CD，∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC，∵AE=4cm，∴AC=2AE=2×4=8cm，∴△ABC的周长=AB+BC+AC=14+8=22cm．故选B．点评：本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，求出△ABD的周长=AB+BC是解题的关键．6．如图，在△ABC，∠C=90°，∠B=15°，AB的中垂线DE交BC于D，E为垂足，若BD=10cm，则AC等于（）A．10cm B．8cm C．5cm D．2.5cm考点：线段垂直平分线的性质；勾股定理．专题：探究型．分析：连接AD，先由三角形内角和定理求出∠BAC的度数，再由线段垂直平分线的性质可得出∠DAB的度数，根据线段垂直平分线的性质可求出AD的长及∠DAC的度数，最后由直角三角形的性质即可求出AC的长．解答：解：连接AD，∵DE是线段AB的垂直平分线，BD=15，∠B=15°，∴AD=BD=10，∴∠DAB=∠B=15°，∴∠ADC=∠B+∠DAB=15°+15°=30°，∵∠C=90°，∴AC=AD=5cm．故选C．点评：本题考查的是直角三角形的性质及线段垂直平分线的性质，熟知线段垂直平分的性质是解答此题的关键．7．如图，已知OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（）A．2B．C．D．考点：角平分线的性质；含30度角的直角三角形；直角三角形斜边上的中线；勾股定理．分析：由OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，易得△OCP是等腰三角形，∠COP=30°，又由含30°角的直角三角形的性质，即可求得PE的值，继而求得OP的长，然后由直角三角形斜边上的中线等于斜边的一半，即可求得DM的长．解答：解：∵OP平分∠AOB，∠AOB=60°，∴∠AOP=∠COP=30°，∵CP∥OA，∴∠AOP=∠CPO，∴∠COP=∠CPO，∴OC=CP=2，∵∠PCE=∠AOB=60°，PE⊥OB，∴∠CPE=30°，∴CE=CP=1，∴PE==，∴OP=2PE=2，∵PD⊥OA，点M是OP的中点，∴DM=OP=．故选：C．点评：此题考查了等腰三角形的性质与判定、含30°直角三角形的性质以及直角三角形斜边的中线的性质．此题难度适中，注意掌握数形结合思想的应用．8．如图，△ABC中，∠B=40°，AC的垂直平分线交AC于D，交BC于E，且∠EAB：∠CAE=3：1，则∠C等于（）A．28°B．25°C．22.5°D．20°考点：线段垂直平分线的性质．专题：计算题．分析：设∠CAE=x，则∠EAB=3x．根据线段的垂直平分线的性质，得AE=CE，再根据等边对等角，得∠C=∠CAE=x，然后根据三角形的内角和定理列方程求解．解答：解：设∠CAE=x，则∠EAB=3x．∵AC的垂直平分线交AC于D，交BC于E，∴AE=CE．∴∠C=∠CAE=x．根据三角形的内角和定理，得∠C+∠BAC=180°﹣∠B，即x+4x=140°，x=28°．则∠C=28°．故选A．点评：此题综合运用了线段垂直平分线的性质、等腰三角形的性质以及三角形的内角和定理．9．若一个等腰三角形至少有一个内角是88°，则它的顶角是（）A．88°或2°B．4°或86°C．88°或4°D．4°或46°考点：等腰三角形的性质．分析：分88°内角是顶角和底角两种情况讨论求解．解答：解：88°是顶角时，等腰三角形的顶角为88°，88°是底角时，顶角为180°﹣2×88°=4°，综上所述，它的顶角是88°或4°．故选C．点评：本题考查了等腰三角形的两底角相等的性质，难点在于要分情况讨论．10．如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为（）A．3B．3.5 C．2.5 D．2.8考点：线段垂直平分线的性质；勾股定理；矩形的性质．专题：计算题．分析：根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AE=CE，设CE=x，表示出ED的长度，然后在Rt△CDE中，利用勾股定理列式计算即可得解．解答：解：∵EO是AC的垂直平分线，∴AE=CE，设CE=x，则ED=AD﹣AE=4﹣x，在Rt△CDE中，CE2=CD2+ED2，即x2=22+（4﹣x）2，解得x=2.5，即CE的长为2.5．故选：C．点评：本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，勾股定理的应用，把相应的边转化为同一个直角三角形的边是解题的关键．11．如图，在Rt△ABC中，∠ACB=30°，CD=4，BD平分∠ABC，交AC于点D，则点D到BC的距离是（）A．1B．2C．D．考点：角平分线的性质；含30度角的直角三角形；勾股定理．分析：根据直角三角形两锐角互余求出∠ABC=60°，再根据角平分线的定义求出∠ABD=∠DBC=30°，从而得到∠DBC=∠ACB，然后利用等角对等边的性质求出BD的长度，再根据直角三角形30°角所对的直角边等于斜边的一半求出AD，过点D作DE⊥BC于点E，然后根据角平分线上的点到角的两边的距离相等解答即可．解答：解：∵Rt△ABC中，∠ACB=30°，∴∠ABC=60°，∵BD平分∠ABC，∴∠ABD=∠DBC=30°，∴∠DBC=∠ACB，∴BD=CD=4，在Rt△ABD中，∵∠ABD=30°，∴AD=BD=×4=2，过点D作DE⊥BC于点E，则DE=AD=2．故选B．点评：本题考查了角平分线上的点到角的两边的距离相等的性质，30°角所对的直角边等于斜边的一半的性质，以及等角对等边的性质，小综合题，但难度不大，熟记各性质是解题的关键．12．如图，在△ABC中，∠ACB=100°，AC=AE，BC=BD，则∠DCE的度数为（）A．20°B．25°C．30°D．40°考点：等腰三角形的性质．专题：几何图形问题．分析：根据此题的条件，找出等腰三角形，找出相等的边与角度，设出未知量，找出满足条件的方程．解答：解：∵AC=AE，BC=BD∴设∠AEC=∠ACE=x°，∠BDC=∠BCD=y°，∴∠A=180°﹣2x°，∠B=180°﹣2y°，∵∠ACB+∠A+∠B=180°，∴100+（180﹣2x）+（180﹣2y）=180，得x+y=140，∴∠DCE=180﹣（∠AEC+∠BDC）=180﹣（x+y）=40°．故选D．点评：根据题目中的等边关系，找出角的相等关系，再根据三角形内角和180°的定理，列出方程，解决此题．二．填空题（共6小题）13．如图，在△ABC中，∠C=90°，AB=10，AD是△ABC的一条角平分线．若CD=3，则△ABD的面积为15．考点：角平分线的性质．专题：几何图形问题．分析：要求△ABD的面积，现有AB=7可作为三角形的底，只需求出该底上的高即可，需作DE⊥AB于E．根据角平分线的性质求得DE的长，即可求解．解答：解：作DE⊥AB于E．∵AD平分∠BAC，DE⊥AB，DC⊥AC，∴DE=CD=3．∴△ABD的面积为×3×10=15．故答案是：15．点评：此题主要考查角平分线的性质；熟练运用角平分线的性质定理，是很重要的，作出并求出三角形AB边上的高时解答本题的关键．14．如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC于E，交BC的延长线于F，若∠F=30°，DE=1，则BE的长是2．考点：含30度角的直角三角形；线段垂直平分线的性质．分析：根据同角的余角相等、等腰△ABE的性质推知∠DBE=30°，则在直角△DBE中由“30度角所对的直角边是斜边的一半”即可求得线段BE的长度．解答：解：∵∠ACB=90°，FD⊥AB，∴∠ACB=∠FDB=90°，∵∠F=30°，∴∠A=∠F=30°（同角的余角相等）．又∵AB的垂直平分线DE交AC于E，∴∠EBA=∠A=30°，∴直角△DBE中，BE=2DE=2．故答案是：2．点评：本题考查了线段垂直平分线的性质、含30度角的直角三角形．解题的难点是推知∠EBA=30°．15．如图，△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E，若∠BAC=70°，则∠CAE=55°．考点：角平分线的性质．分析：首先过点E作EF⊥BD于点F，作EG⊥AC于点G，作EH⊥BA于点H，由△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E，易证得AE是∠CAH的平分线，继而求得答案．解答：解：过点E作EF⊥BD于点F，作EG⊥AC于点G，作EH⊥BA于点H，∵△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E，∴EH=EF，EG=EF，∴EH=EG，∴AE是∠CAH的平分线，∵∠BAC=70°，∴∠CAH=110°，∴∠CAE=∠CAH=55°．故答案为：55°．点评：此题考查了角平分线的性质与判定．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．16．如图，△ABC的三边AB、BC、CA长分别为40、50、60．其三条角平分线交于点O，则S△ABO：S△BCO：S△CAO= 4：5：6．考点：角平分线的性质．专题：压轴题．分析：首先过点O作OD⊥AB于点D，作OE⊥AC于点E，作OF⊥BC于点F，由OA，OB，OC是△ABC的三条角平分线，根据角平分线的性质，可得OD=OE=OF，又由△ABC的三边AB、BC、CA长分别为40、50、60，即可求得S△ABO：S△BCO：S△CAO的值．解答：解：过点O作OD⊥AB于点D，作OE⊥AC于点E，作OF⊥BC于点F，∵OA，OB，OC是△ABC的三条角平分线，∴OD=OE=OF，∵△ABC的三边AB、BC、CA长分别为40、50、60，∴S△ABO：S△BCO：S△CAO=（AB•OD）：（BC•OF）：（AC•OE）=AB：BC：AC=40：50：60=4：5：6．故答案为：4：5：6．点评：此题考查了角平分线的性质．此题难度不大，注意掌握辅助线的作法，注意数形结合思想的应用．17．在△ABC中，已知AB=AC，DE垂直平分AC，∠A=50°，则∠DCB的度数是15°．考点：线段垂直平分线的性质；等腰三角形的性质．分析：由DE垂直平分AC，∠A=50°，根据线段垂直平分线的性质，易求得∠ACD的度数，又由AB=AC，可求得∠ACB的度数，继而可求得∠DCB的度数．解答：解：∵DE垂直平分AC，∴AD=CD，∴∠ACD=∠A=50°，∵AB=AC，∠A=50°，∴∠ACB=∠B==65°，∴∠DCB=∠ACB﹣∠ACD=15°．故答案为：15°．点评：此题考查了线段垂直平分线的性质与等腰三角形的性质．此题比较简单，注意数形结合思想的应用．18．如图，在菱形ABCD中，∠ADC=72°，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则∠CPB= 72度．考点：线段垂直平分线的性质；菱形的性质．专题：计算题．分析：欲求∠CPB，可根据菱形、线段垂直平分线的性质、对称等方面去寻求解答方法．解答：解：先连接AP，由四边形ABCD是菱形，∠ADC=72°，可得∠BAD=180°﹣72°=108°，根据菱形对角线平分对角可得：∠ADB=∠ADC=×72°=36°，∠ABD=∠ADB=36度．EP是AD的垂直平分线，由垂直平分线的对称性可得∠DAP=∠ADB=36°，∴∠PAB=∠DAB﹣∠DAP=108°﹣36°=72度．在△BAP中，∠APB=180°﹣∠BAP﹣∠ABP=180°﹣72°﹣36°=72度．由菱形对角线的对称性可得∠CPB=∠APB=72度．点评：本题开放性较强，解法有多种，可以从菱形、线段垂直平分线的性质、对称等方面去寻求解答方法，在这些方法中，最容易理解和表达的应为对称法，这也应该是本题考查的目的．灵活应用菱形、垂直平分线的对称性，可使解题过程更为简便快捷．三．解答题（共12小题）19．如图，已知DE是AC的垂直平分线，AB=10cm，BC=11cm，求△ABD的周长．考点：线段垂直平分线的性质．分析：先根据线段垂直平分线的性质得出AD=CD，故可得出BD+AD=BD+CD=BC，进而可得出结论．解答：解：∵DE垂直平分，∴AD=CD，∴BD+AD=BD+CD=BC=11cm，又∵AB=10cm，∴△ABD的周长=AB+BC=10+11=21（cm）．点评：本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．20．如图，D为△ABC边BC延长线上一点，且CD=CA，E是AD的中点，CF平分∠ACB交AB于点F．求证：CE⊥CF．考点：等腰三角形的性质．专题：证明题．分析：根据三线合一定理证明CF平分∠ACB，然后根据CF平分∠ACB，根据邻补角的定义即可证得．解答：证明：∵CD=CA，E是AD的中点，∴∠ACE=∠DCE．∵CF平分∠ACB，∴∠ACF=∠BCF．∵∠ACE+∠DCE+∠ACF+∠BCF=180°，∴∠ACE+∠ACF=90°．即∠ECF=90°．∴CE⊥CF．点评：本题考查了等腰三角形的性质，顶角的平分线、底边上的中线和高线、三线合一．21．如图，在四边形ABCD中，∠B=∠D=90°，∠C=60°，BC=4，CD=3，求AB的长．考点：含30度角的直角三角形；相似三角形的判定与性质．专题：计算题．分析：延长DA，CB，交于点E，可得出三角形ABE与三角形CDE相似，由相似得比例，设AB=x，利用30角所对的直角边等于斜边的一半得到AE=2x，利用勾股定理表示出BE，由BC+BE表示出CE，在直角三角形DCE中，利用30度角所对的直角边等于斜边的一半得到2DC=CE，即可求出AB的长．解答：解：延长DA，CB，交于点E，∵∠E=∠E，∠ANE=∠D=90°，∴△ABE∽△CDE，∴=，在Rt△ABE中，∠E=30°，设AB=x，则有AE=2x，根据勾股定理得：BE==x，∴CE=BC+BE=4+x，在Rt△DCE中，∠E=30°，∴CD=CE，即（4+x）=3，解得：x=，则AB=．点评：此题考查了相似三角形的判定与性质，含30度直角三角形的性质，熟练掌握相似三角形的判定与性质是解本题的关键．22．如图，Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于E，若AC=6，BC=8，CD=3．（1）求DE的长；（2）求△ADB的面积．考点：角平分线的性质；勾股定理．分析：（1）根据角平分线性质得出CD=DE，代入求出即可；（2）利用勾股定理求出AB的长，然后计算△ADB的面积．解答：解：（1）∵AD平分∠CAB，DE⊥AB，∠C=90°，∴CD=DE，∵CD=3，∴DE=3；（2）在Rt△ABC中，由勾股定理得：AB===10，∴△ADB的面积为S△ADB=AB•DE=×10×3=15．点评：本题考查了角平分线性质和勾股定理的运用，注意：角平分线上的点到角两边的距离相等．23．如图，已知△ABC和△ABD均为直角三角形，其中∠ACB=∠ADB=90°，E为AB的中点，求证：CE=DE．考点：直角三角形斜边上的中线．专题：证明题．分析：由于AB是Rt△ABC和Rt△ABD的公共斜边，因此可以AB为媒介，再根据斜边上的中线等于斜边的一半来证CE=ED．解答：证明：在Rt△ABC中，∵E为斜边AB的中点，∴CE=AB．在Rt△ABD中，∵E为斜边AB的中点，∴DE=AB．∴CE=DE．点评：本题考查的是直角三角形的性质：在直角三角形中，斜边上的中线等于斜边的一半．24．如图所示，在△ABC中，BC＞AC，点D在BC上，且DC=AC，∠ACB的平分线CF交AD于点F．点E是AB的中点，连接EF．（1）求证：EF∥BC；（2）若△ABD的面积是6，求四边形BDFE的面积．考点：等腰三角形的性质；三角形中位线定理；相似三角形的判定与性质．专题：几何综合题．分析：（1）在等腰△ACD中，CF是顶角∠ACD的平分线，根据等腰三角形三线合一的性质知F是底边AD的中点，由此可证得EF是△ABD的中位线，即可得到EF∥BC的结论；（2）易证得△AEF∽△ABD，根据两个相似三角形的面积比（即相似比的平方），可求出△ABD的面积，而四边形BDFE的面积为△ABD和△AEF的面积差，由此得解．解答：（1）证明：∵在△ACD中，DC=AC，CF平分∠ACD；∴AF=FD，即F是AD的中点；又∵E是AB的中点，∴EF是△ABD的中位线；∴EF∥BC；（2）解：由（1）易证得：△AEF∽△ABD；∴S△AEF：S△ABD=（AE：AB）2=1：4，∴S△ABD=4S△AEF=6，∴S△AEF=1.5．∴S四边形BDFE=S△ABD﹣S△AEF=6﹣1.5=4.5．点评：此题主要考查的是等腰三角形的性质、三角形中位线定理及相似三角形的判定和性质．25．如图，四边形ABCD中，AD∥BC，∠A=90°，BD=BC，CE⊥BD于点E．求证：AD=BE．考点：直角三角形全等的判定；全等三角形的性质．专题：证明题．分析：此题根据直角梯形的性质和CE⊥BD可以得到全等条件，证明△ABD≌△BCE，然后利用全等三角形的性质证明题目的结论．解答：证明：∵AD∥BC，∴∠ADB=∠DBC．∵CE⊥BD，∴∠BEC=90°．∵∠A=90°，∴∠A=∠BEC．∵BD=BC，∴△ABD≌△BCE．∴AD=BE．点评：本题考查了直角三角形全等的判定及性质；此题把全等三角形放在梯形的背景之下，利用全等三角形的性质与判定解决题目问题．26．已知；如图，在△ABC中，AB=BC，∠ABC=90度．F为AB延长线上一点，点E在BC上，BE=BF，连接AE、EF和CF．（1）求证：AE=CF；（2）若∠CAE=30°，求∠EFC的度数．考点：等腰三角形的性质；全等三角形的判定与性质．专题：计算题；证明题．分析：根据已知利用SAS判定△ABE≌△CBF，由全等三角形的对应边相等就可得到AE=CF；根据已知利用角之间的关系可求得∠EFC的度数．解答：（1）证明：在△ABE和△CBF中，∵，∴△ABE≌△CBF（SAS）．∴AE=CF．（2）解：∵AB=BC，∠ABC=90°，∠CAE=30°，∴∠CAB=∠ACB=（180°﹣90°）=45°，∠EAB=45°﹣30°=15°．∵△ABE≌△CBF，∴∠EAB=∠FCB=15°．∵BE=BF，∠EBF=90°，∴∠BFE=∠FEB=45°．∴∠EFC=180°﹣90°﹣15°﹣45°=30°．点评：此题主要考查了全等三角形的判定方法及等腰三角形的性质等知识点的掌握情况；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．27．如图，在△ABC中，AB≠AC，∠BAC的外角平分线交直线BC于D，过D作DE⊥AB，DF⊥AC分别交直线AB，AC于E，F，连接EF．（1）求证：EF⊥AD；（2）若DE∥AC，且DE=1，求AD的长．考点：角平分线的性质；全等三角形的判定与性质；线段垂直平分线的性质．专题：几何综合题；压轴题．分析：（1）根据AD是∠EAF的平分线，那么DE=DF，如果证得EA=FA，那么我们就能得出AD是EF的垂直平分线，那么就证得EF⊥AD了．因此证明EA=FA是问题的关键，那么就要先证得三角形AED和AFD全等．这两个三角形中已知的条件有∠EAD=∠FAD，一条公共边，一组直角，因此两三角形全等，那么就可以得出EA=AF了．（2）要求AD的长，在直角三角形AED中，有了DE的值，如果知道了∠ADE或∠EAD的度数，那么就能求出AD了．如果DE∥AC，那么∠EAC=90°，∠EAD=45°，那么在直角三角形AED中就能求出AD的长了．解答：（1）证明：∵AD是∠EAF的平分线，∴∠EAD=∠DAF．∵DE⊥AE，DF⊥AF，∴∠DEA=∠DFA=90°又AD=AD，∴△DEA≌△DFA．∴EA=FA∵ED=FD，∴AD是EF的垂直平分线．即AD⊥EF．（2）解：∵DE∥AC，∴∠DEA=∠FAE=90°．又∠DFA=90°，∴四边形EAFD是矩形．由（1）得EA=FA，∴四边形EAFD是正方形．∵DE=1，∴AD=．点评：本题考查了全等三角形的判定，角平分线的性质，线段垂直平分线的性质等知识点．本题中利用全等三角形得出线段相等是解题的关键．。

北师大版八年级下册数学第一章三角形的证明评卷人得分一、单选题1．如图，OP 平分∠AOB ，PC ⊥OA 于C ，PD ⊥OB 于D ，则PC 与PD 的大小关系是（）A ．PC ＞PDB ．PC ＝PD C ．PC ＜PD D ．不能确定2．如图，已知在△ABC ，AB ＝AC ．若以点B 为圆心，BC 长为半径画弧，交腰AC 于点E ，则下列结论一定正确的是（）A ．AE ＝ECB ．AE ＝BEC ．∠EBC ＝∠BACD ．∠EBC ＝∠ABE3．已知ABC ∆三边的垂直平分线的交点在ABC ∆的边上，则ABC ∆的形状为（）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定4．如图,点C 是△ABE 的BE 边上一点,点F 在AE 上,D 是BC 的中点,且AB=AC=CE,给出下列结论:①AD ⊥BC;②CF ⊥AE;③∠1=∠2;④AB+BD=DE,其中正确的结论有()A ．1个B ．2个C ．3个D ．4个5．如图，∠ACB=90°，CD ⊥AB ，则∠1与∠B 的关系是（）A．互余B．互补C．相等D．不确定6．等腰三角形的两边长分别为3和6，则这个等腰三角形的周长为（）A．12B．15C．12或15D．187．若等边△ABC的边长为2cm，那么△ABC的面积为（）A32B．2cm C．3cm2D．4cm28．如图，在△ABC中，AC=4cm，线段AB的垂直平分线交AC于点N，△BCN的周长是7cm，则BC的长为（）A．1cm B．2cm C．3cm D．4cm9．在等边三角形所在平面内找出一个点，使它与三角形中的任意两个顶点所组成的三角形都是等腰三角形，这样的点一共有（）A．1个B．4个C．7个D．10个10．如图，在△ABC中，BC=8，AB的中垂线交BC于D，AC的中垂线交BC于E，则△ADE 的周长等于（）A．8B．4C．12D．16评卷人得分二、填空题11．已知等腰三角形的一个外角是70°，则它顶角的度数为．12．如图，已知△ABC 中，AB=AC ，AB 边上的垂直平分线DE 交AC 于点E ，D 为垂足，若∠ABE ：∠EBC=2：1，则∠A=__________．13．如图，在△ABC 中，AB=AC ，D 为BC 中点，∠BAD=36°，则∠BAC 的度数为________，∠C 的度数为________．14．如图所示，AB=AD ，AD ∥BC ，∠BDC=90°，∠ABC=∠DCB ，则∠ADB 等于________度．15．如图，△ABC 的三边AB 、BC 、CA 长分别是20、30、40，其三条角平分线将△ABC 分成三个三角形，则ABO S ：BCO S ：CAO S 等于__________．16．在等腰△ABC 中，AD ⊥BC 交直线BC 于点D ，若AD =12BC ，则△ABC 的顶角的度数为_____．17．如图∠AOP=∠BOP=15°，PC ∥OA ，PD ⊥OA ，若PC=6，则PD 等于________.18．如图，已知点P是∠AOB角平分线上的一点，∠AOB=60°，PD⊥OA，M是OP的中点，DM=4cm，如果点C是OB上一个动点，则PC的最小值为________cm．评卷人得分三、解答题19．如图，点D，E在△ABC的边BC上，AB=AC，BD=CE．求证：AD=AE．20．如图，A，E，F，C在一条直线上，AE＝CF，过E，F分别作DE⊥AC，BF⊥AC，若AB＝CD，试证明BD平分EF．21．如图，△ABC的高BD与CE相交于点O，OD=OE，AO的延长线交BC于点M，请你从图中找出几对全等的直角三角形，并说明理由．22．如图：AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，连接E、F，求证：AD 是EF 的垂直平分线．23．如图所示，ABC ∆是边长为1的等边三角形，BDC ∆是顶角120BDC ∠=︒的等腰三角形，以D 为顶点作一个60︒的角，角的两边交AB 、AC 于M 、N ，连结MN ，求AMN ∆周长.24．如图，在△ABC 中，点D 是AB 的中点，点F 是BC 延长线上一点，连接DF ，交AC 于点E ，连接BE ，∠A=∠ABE ．（1）求证：DF 是线段AB 的垂直平分线；（2）当AB=AC ，∠A=46°时，求∠EBC 及∠F 的度数．25．如图，在△ABC 中，∠ACB=90°，AC=BC ，AE 是BC 边的中线，过点C 作CF ⊥AE ，垂足为点F ，过点B 作BD ⊥BC 交CF 的延长线于点D ．（1）试证明：AE=CD ；（2）若AC=12cm ，求线段BD 的长度．26．如图，等边△ABC中，AO是∠BAC的角平分线，D为AO上一点，以CD为一边且在CD下方作等边△CDE，连接BE．（1）求证：△ACD≌△BCE．（2）延长BE至Q，P为BQ上一点，连接CP、CQ使CP=CQ=5，若BC=6，求PQ的长．27．如图，已知在△ABC中，AB=AC=10cm，BC=8cm，D为AB中点，设点P在线段BC 上以3cm/秒的速度由B点向C点运动，点Q在线段CA上由C点向A点运动.（1）若Q点运动的速度与P点相同，且点P，Q同时出发，经过1秒钟后△BPD与△CQP 是否全等，并说明理由；（2）若点P，Q同时出发，但运动的速度不相同，当Q点的运动速度为多少时，能在运动过程中有△BPD与△CQP全等？（3）若点Q以（2）中的速度从点C出发，点P以原来的速度从点B同时出发，都是逆时针沿△ABC的三边上运动，经过多少时间点P与点Q第一次在△ABC的哪条边上相遇？参考答案1．B【解析】主要应用到全靠等三角形的判定、性质及应用．通过AAS来证明△OCP和△ODP全等即可．证明：∵OP平分∠AOB∴∠AOP=∠BOP∵PC⊥OA于C，PD⊥OB于D∴∠OCP=∠ODP=90°又∵OP=OP∴△OCP≌△ODP(AAS)∴PC＝PD点评：此题主要考查学生对全等三角形判定的应用，及对角平分线的理解．2．C【解析】解：∵AB=AC，∴∠ABC=∠ACB．∵以点B为圆心，BC长为半径画弧，交腰AC于点E，∴BE=BC，∴∠ACB=∠BEC，∴∠BEC=∠ABC=∠ACB，∴∠BAC=∠EBC．故选C．点睛：本题考查了等腰三角形的性质，当等腰三角形的底角对应相等时其顶角也相等，难度不大．3．B【解析】【分析】根据三角形三边垂直平分线概念即可解题.【详解】解,由三角形的垂直平分线可知,锐角三角形三边的垂直平分线的交点在△ABC的内部,直角三角形三边的垂直平分线的交点在△ABC的斜边上,钝角三角形三边的垂直平分线的交点在△ABC的外部.故选B.【点睛】本题考查了三角形垂直平分线的概念,属于简单题,熟悉概念是解题关键.4．B【解析】【分析】根据所给条件利用三线合一性质即可证明①正确,进而证明④正确,即可解题.【详解】①∵D是BC的中点，AB=AC，∴AD⊥BC，故①正确；②∵F在AE上，不一定是AE的中点，AC=CE，∴无法证明CF⊥AE，故②错误；③无法证明∠1=∠2，故③错误；④∵D是BC的中点，∴BD=DC，∵AB=CE，∴AB+BD=CE+DC=DE，故④正确．故其中正确的结论有①④．故选B.【点睛】本题考查三角形的性质和证明,中等难度,找到等腰三角形利用三线合一性质是解题关键. 5．C【分析】根据直角三角形得∠A+∠B=90°,根据CD ⊥AB ，得∠1+∠A=90°,利用同角的余角相等即可得到∠1=∠B.【详解】解：∵∠ACB=90°，∴∠A+∠B=90°,∵CD ⊥AB ，∴∠1+∠A=90°,∴∠1=∠B （同角的余角相等）,故选C【点睛】本题考查了三角形的证明,用到了同角的余角相等,属于简单题,熟悉直角三角形的性质是解题关键.6．B【解析】试题分析：根据题意，要分情况讨论：①、3是腰；②、3是底．必须符合三角形三边的关系，任意两边之和大于第三边．解：①若3是腰，则另一腰也是3，底是6，但是3+3=6，∴不构成三角形，舍去．②若3是底，则腰是6，6．3+6＞6，符合条件．成立．∴C=3+6+6=15．故选B ．考点：等腰三角形的性质．7．A【解析】【分析】根据等边三角形面积公式S=23a 4,即可解题.解：∵△ABC为等边三角形,边长=2,,∴S=224故选A【点睛】本题考查求等边三角形的面积,属于简单题,熟悉等边三角形面积公式是解题关键.8．C【解析】试题分析：∵MN是线段AB的垂直平分线，∴AN=BN，∵△BCN的周长是7cm，∴BN+NC+BC=7（cm），∴AN+NC+BC=7（cm），∵AN+NC=AC，∴AC+BC=7（cm），又∵AC=4cm，∴BC=7﹣4=3（cm）．故选C．考点：线段垂直平分线的性质．9．D【解析】解：如图，①内部一个，是三角形的中心P，②外面有九个，在直线AP上有三个点，，，满足A=AB，A=AB，B=AB，同理，在直线BP上有三个点，在直线CP上有三个点，满足条件．共有10个点．故选D．10．A【解析】∵AB的中垂线交BC于D，AC的中垂线交BC于E，∴DA=DB，EA=EC，则△ADE的周长=AD+DE+AE=BD+DE+EC=BC=8，故选A．11．110°【解析】试题分析：三角形内角与相邻的外角和为180°，三角形内角和为180°，等腰三角形两底角相等，110°只可能是顶角．解：等腰三角形一个外角为70°，那相邻的内角为110°，三角形内角和为180°，如果这个内角为底角，内角和将超过180°，所以110°只可能是顶角．故答案为110°．考点：等腰三角形的性质．12．45°【解析】∵AB=AC，∴∠ABC=∠C，∵E在线段AB的垂直平分线上，∴EA=EB，∴∠ABE=∠A=2∠EBC，∴∠ABC=∠ABE+∠EBC=∠A+12∠A，∵∠A+∠ABC+∠C=180°，∴∠A+2(∠A+12∠A)=180°，∴∠A=45°，故答案为：45°. 13．72°54°【解析】根据已知证明△ABC为等腰三角形,利用三线合一性质即可解题.【详解】解：∵AB=AC，D为BC中点，∴∠BAD=∠CAD,AD⊥BC（三线合一）,∵∠BAD=36°，∴∠BAC=72°,∠C=90°-36°=54°.【点睛】本题考查三角形的证明,三线合一的性质,属于简单题,熟悉三线合一的性质是解题关键. 14．30【解析】【分析】根据已知证明三角形ABD为等腰三角形,利用AD∥BC得∠ABD=∠ADB=∠DBC,根据∠BDC=90°得到∠DCB与∠DBC互余,等量代换角即可解题.【详解】解：∵AB=AD，AD∥BC，∴∠ABD=∠ADB=∠DBC,又∠ABC=∠DCB，∴∠DCB=2∠DBC,∵∠BDC=90°，即∠DCB+∠DBC=90°,∴∠DBC=30°,∴∠ADB=30°.【点睛】本题考查了简单的三角证明,平行线性质,直角三角形性质,中等难度,等量代换角是解题关键. 15．2：3：4.【解析】【分析】由角平分线的性质可得，点O到三角形三边的距离相等，即三个三角形的AB、BC、CA的高相等，利用面积公式即可求解．解：过点O 作OD ⊥AC 于D ，OE ⊥AB 于E ，OF ⊥BC 于F ，∵O 是三角形三条角平分线的交点，∴OD=OE=OF ，∵AB=20，BC=30，AC=40，∴ABO S ：BCO S ：CAO S =2：3：4．故答案为2：3：4．16．30°或150°或90°【解析】试题分析：分两种情况；①BC 为腰，②BC 为底，根据直角三角形30°角所对的直角边等于斜边的一半判断出∠ACD =30°，然后分AD 在△ABC 内部和外部两种情况求解即可．解：①BC 为腰，∵AD ⊥BC 于点D ，AD =12BC ，∴∠ACD =30°，如图1，AD 在△ABC 内部时，顶角∠C =30°，如图2，AD 在△ABC 外部时，顶角∠ACB =180°﹣30°=150°，②BC 为底，如图3，∵AD⊥BC于点D，AD=12BC，∴AD=BD=CD，∴∠B=∠BAD，∠C=∠CAD，∴∠BAD+∠CAD=12×180°=90°，∴顶角∠BAC=90°，综上所述，等腰三角形ABC的顶角度数为30°或150°或90°．故答案为30°或150°或90°．点睛：本题考查了含30°交点直角三角形的性质，等腰三角形的性质，分类讨论是解题的关键．17．3【解析】【详解】试题分析：过P作PE⊥OB于E，根据角平分线的性质可得PE=PD，在求得∠BCP=30°，在Rt△ECP中，根据30°的锐角所对的直角边等于斜边的一半即可求得PD的长．试题解析：过P作PE⊥OB于E，∵PD⊥OA，PE⊥OB，∠AOP=∠BOP=15°，∴∠BOA=30°，PE=PD，∵PC∥OA，∴∠BOA=∠BCP=30°，又△ECP为直角三角形，且PC=6，∴PE=3，PD=3．考点：角平分线的性质；特殊直角三角形的性质．18．4【分析】根据角平分线的定义可得1AOP AOB 302∠== ，再根据直角三角形的性质求得1PD OP 42==，然后根据角平分线的性质和垂线段最短得到答案．【详解】P 是AOB ∠角平分线上的一点，AOB 60 ∠=，1AOP AOB 302∠∠∴== ，PD OA ⊥ ，M 是OP 的中点，DM 4cm =，OP 2DM 8∴==，1PD OP 42∴==， 点C 是OB 上一个动点，PC ∴的最小值为P 到OB 距离，PC ∴的最小值PD 4==，故答案为4．【点睛】本题考查了角平分线上的点到角的两边距离相等的性质，直角三角形的性质，熟记性质并作出辅助线构造成直角三角形是解题的关键．19．利用等腰三角形的性质得到∠B=∠C ，然后证明△ABD ≌△ACE 即可证得结论．【解析】分析：证明：∵AB=AC ，∴∠B=∠C ．在△ABD 与△ACE 中，∵AB AC{B C BD EC=∠=∠=，∴△ABD ≌△ACE （SAS ）．∴AD=AE ．20．详见解析.【解析】根据已知条件证明AB=CD,AF=CF ，证明Rt △ABF ≌Rt △CDE （HL ）,得BF ＝DE,进而证明△BFG ≌△DEG （AAS ），即可证明.【详解】证明∵DE ⊥AC ，BF ⊥AC ，∴∠DEG ＝∠BFE ＝90°,∵AE ＝CF ，AE ＋EF ＝CF ＋EF,即AF ＝CE ．在Rt △ABF 和Rt △CDE 中，AB=CD,AF=CF ，∴Rt △ABF ≌Rt △CDE （HL ），∴BF ＝DE ．在△BFG 和△DEG 中，∠BFG=∠DEG,∠BGF=∠DGE ，BF=DE∴△BFG ≌△DEG （AAS ），∴FG ＝EG ，即BD 平分EF【点睛】本题考查了三角形全等的判定与性质,中等难度,将中点问题转化成证明全等问题是解题关键.21．△ADO ≌△AEO ，△DOC ≌△EOB ，△COF ≌△BOF ，△ACF ≌△ABF ，△ADB ≌△AEC ，△BCE ≌△CBD ．理由见解析.【解析】试题分析：△ADO ≌△AEO ，△DOC ≌△EOB ，△COF ≌△BOF ，△ACF ≌△ABF ，△ADB ≌△AEC ，△BCE ≌△CBD ，利用全等三角形的判定可证明，做题时，要结合已知条件与三角形全等的判定方法逐个验证．试题解析：△ADO ≌△AEO ，△DOC ≌△EOB ，△COF ≌△BOF ，△ACF ≌△ABF ，△ADB ≌△AEC ，△BCE ≌△CBD ．理由如下：在△ADO 与△AEO 中，∠ADO =∠AEO =90°，OA OA OD OE =⎧⎨=⎩，∴△ADO ≌△AEO （HL ），∴∠DAO =∠EAO ，AD =AE ，在△DOC 与△EOB 中，90ODC OEB OD OE DOC EOB∠=∠=︒⎧⎪=⎨⎪∠=∠⎩，∴△DOC ≌△EOB （ASA ），∴DC =EB ，OC =OB ，∴DC +AD =EB +AE ，即AC =AB ，∵∠DAO =∠EAO ，∴AM ⊥BC ，CM =BM ，在△COF 与△BOF 中，∠OMC =∠OMB =90°，OC OB OM OM=⎧⎨=⎩，∴△COF ≌△BOF （HL ），在△ACF 与△ABF 中，∠AFC =∠AFB =90°，AC ABAM AM =⎧⎨=⎩，∴△ACF ≌△ABF （HL ），在△ADB 与△AEC 中，AD AEDAB EAC AB AC=⎧⎪∠=∠⎨⎪=⎩，∴△ADB ≌△AEC （SAS ），在△BCE 与△CBD 中，∠BEC =∠CDB =90°，BC CB BE CD=⎧⎨=⎩，∴△BCE ≌△CBD （HL ）．22．详见解析.【解析】【分析】根据垂直证明Rt △AED ≌Rt △AFD （HL ），即可解题.【详解】证明：∵AD 是∠BAC 的平分线，DE ⊥AB ，DF ⊥AC ，∴DE=DF ，∠AED=∠AFD=90°，在Rt △AED 和Rt △AFD 中∵AD AD DE DF =⎧⎨=⎩，∴Rt △AED ≌Rt △AFD （HL ），∴AE=AF ，∵AD 是∠BAC 的平分线，∴AD 是EF 的垂直平分线【点睛】本题考查了全等三角形的判定,属于简单题,将垂直平分线问题转换为全等问题是解题关键.23．△AMN 的周长为2．【解析】【分析】根据已知条件得△CDE ≌△BDM ，再利用DE=DM ，MDE EDN 60∠∠==︒证明△DMN ≌△DEN ，得到对应边相等即可解题.【详解】如图，延长NC 到E ，使CE=BM ，连接DE ，∵△ABC 为等边三角形，△BCD 为等腰三角形，且∠BDC=120°，∴∠MBD=∠MBC+∠DBC=60°+30°=90°，∠DCE=180°﹣∠ACD=180°﹣∠ABD=90°，又∵BM=CE ，BD=CD ，∴△CDE ≌△BDM ，∴∠CDE=∠BDM ，DE=DM ，∠NDE=∠NDC+∠CDE=∠NDC+∠BDM=∠BDC ﹣∠MDN=120°﹣60°=60°，∵在△DMN 和△DEN 中，60DM DE MDE EDN DN DN =⎧⎪∠=∠=︒⎨⎪=⎩，∴△DMN ≌△DEN ，∴MN=NE=CE+CN=BM+CN ，∴△AMN 的周长=AM+AN+MN=AM+AN+NC+BM=AB+AC=1+1=2，故△AMN 的周长为2．【点睛】本题考查等边三角形的性质与应用,截长补短的数学方法,中等难度,作辅助线证明全等是解题关键.24．（1）见解析；（2）∠EBC =21°，∠F=23°．【解析】试题分析：(1)、根据题意得出AE=BE ，然后结合AD=BD 得出答案；(2)、根据等腰三角形的性质得出∠ABC=∠ACB=67°，根据∠EBC=∠ABC ﹣∠ABE 和∠F=90°﹣∠ABC 得出角度．试题解析：(1)、证明：∵∠A=∠ABE ，∴EA=EB ，∵AD=DB ，∴DF 是线段AB 的垂直平分线；(2)、解：∵∠A=46°，∴∠ABE=∠A=46°，∵AB=AC ，∴∠ABC=∠ACB=67°，∴∠EBC=∠ABC ﹣∠ABE=21°，∠F=90°﹣∠ABC=23°．25．（1）证明见解析（2）BD=6cm ．【解析】【分析】（1）证两条线段相等，通常用全等，本题中的AE 和CD 分别在三角形AEC 和三角形CDB 中，在这两个三角形中，已经有一组边相等，一组角相等了，因此只需再找一组角即可利用角角边进行解答；（2）由（1）得BD=EC=12BC=12AC ，且AC=12cm ，即可求出BD 的长．【详解】（1）∵DB ⊥BC ，CF ⊥AE ，∴∠DCB+∠D=∠DCB+∠AEC=90°，∴∠D=∠AEC ，又∵∠DBC=∠ECA=90°，且BC=CA ，∴△DBC ≌△ECA （AAS ），∴AE=CD ；（2）因为△ACE ≌△CBD ，所以BD =CE ，因为CE=12BC=12AC=12×12=6cm ，所以BD =6cm ．【点睛】本题考查了全等三角形的判定与性质，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．26．（1）详见解析；（2）PQ=8.【解析】【分析】（1）根据等边三角形得∠ACD=∠BCE,即可证明△ACD ≌△BCE （SAS ）,（2）过C 作CH ⊥BQ ，垂足为H ，由角平分线得到∠CAD=12∠BAC=30°,通过（1）得∠CAD=∠CBH=30°,根据30°角所对直角边等于斜边一半求出CH=3,勾股定理得HQ=4,三线合一性质即可求出PQ=8.【详解】（1）证明：∵△ABC,△CDE 均为等边三角形，∴∠ACB=∠DCE=60°，∴∠ACB-∠DCO=∠DCE-∠DCO,即∠ACD=∠BCE ，在△ACD 和△BCE 中，AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△BCE （SAS ）（2）解：∵等边△ABC 中，AO 平分∠BAC ，∴∠CAD=12∠BAC=30°.如下图，过C 点作CH ⊥BQ ，垂足为H ，由（1）知△ACD≌△BCE,则∠CAD=∠CBH=30°,∴CH=12BC=3,∴在Rt△CHQ中，HQ=4(勾股定理)，又∵CP=CQ，CH⊥PQ，∴PH=HQ（三线合一）∴PQ=8.【点睛】本题主要考查三角形的证明,包括特殊直角三角形,等腰三角形的性质,中等难度,熟悉特殊三角形的性质是解题关键.27．（1）详见解析；（2）154cm/秒；（3）803秒在AB边相遇.【解析】【分析】（1）求出BD,CP,根据全等三角形的判定即可,（2）由全等推出时间t,在利用CQ=BD求出Q的速度即可,（3）求出Q的运动路程,根据△ABC的三边长度即可确定Q的位置.【详解】（1）解：∵t=1秒，∴BP=CQ=3×1=3cm，∵AB=10cm，点D为AB的中点，∴BD=5cm．又∵PC=BC﹣BP，BC=8cm，∴PC=8﹣3=5cm，∴PC=BD．又∵AB=AC，∴∠B=∠C，在△BPD和△CQP中，BC BD B C BP CQ=⎧⎪∠=∠⎨⎪=⎩∴△BPD≌△CQP（SAS）．（2）解：∵v P≠v Q，∴BP≠CQ，又∵△BPD≌△CPQ，∠B=∠C，则BP=PC=4cm，CQ=BD=5cm，∴点P，点Q运动的时间t=BP433=秒，∴v Q=CQ5154t43==cm/秒；（3）设经过x秒后点P与点Q第一次相遇，由题意，得154x=3x+2×10，解得x=803．∴点P共运动了803×3=80cm．∴80=56+24=2×28+24，∴点P、点Q在AB边上相遇，∴经过803秒点P与点Q第一次在边AB上相遇．【点睛】本题考查了全等三角形中的动点问题,难度较大,证明三角形全等,利用全等三角形的性质是解题关键.。

第一章 三角形的证明单元测试一、选择题(每题3分,共30分)1、△ABC 中，AB = AC ，BD 平分∠ABC 交AC 边于点D ，∠BDC = 75°，则∠A 的度数为（ ）A 35°B 40°C 70°D 110°2、适合条件∠A =∠B =31∠C 的三角形一定是（ ）A 锐角三角形B 钝角三角形C 直角三角形D 任意三角形3、用两个全等的直角三角形拼下列图形：①平行四边形（不包含菱形、矩形、正方形）；②矩形；③正方形；④等腰三角形，一定可以拼成的图形是（ ）A ①②④B ②④C ①④D ②③④4、已知△ABC 中，AB ＝AC ，AB 的垂直平分线交AC 于D ，△ABC 和△DBC 的周长分别是60 cm 和38 cm ，则△ABC 的腰和底边长分别为 ( ) A 24 cm 和12 cm B 16 cm 和22 cm C 20 cm 和16 cm D 22 cm 和16 cm5、如图，△ABC 中，AC ＝BC ，直线l 经过点C ，则 ( ) A l 垂直AB B l 平分AB C l 垂直平分AB D 不能确定6、三角形中，若一个角等于其他两个角的差，则这个三角形是 ( ) A 钝角三角形 B 直角三角形 C 锐角三角形 D 等腰三角形7、已知等腰三角形的两边长分别为6㎝、3㎝，则该等腰三角形的周长是( ) A 9㎝B 12㎝C 12㎝或者15㎝D 15㎝8、如图，已知在△ＡＢＣ中，ＡＢ＝ＡＣ，Ｄ为ＢＣ上一点，ＢＥ＝ＣＤ，ＣＦ＝ＢＤ，那么∠ＥＤＦ等于（ ）Ａ 90°－∠Ａ Ｂ 90°－21∠Ａ Ｃ 45°－21∠Ａ Ｄ 180°－∠Ａ9、一个正方形和一个等腰三角形有相等的周长，已知等腰三角形有两边长分别为5.6 cm和13.2 cm，则这个正方形的面积为（）Ａ 64 cm２Ｂ 48 cm２Ｃ 36 cm２Ｄ 24 cm２10、如图，等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE的度数是（）A 45°B 55°C 60°D 75°二、填空题（每小题3分，共30分）1、“直角三角形两条直角边的平方和等于斜边的平”的方逆定理是2、等腰三角形的腰长为2cm，面积等于1cm2，则它的顶角的度数为 .3、如图，在Rt△ABC中，∠B=90°，∠A=40°，AC的垂直平分线MN与AB相交于D点，则∠BCD的度数是 .4、等腰三角形一腰上的高与另一腰的夹角为30°，腰长为a，则其底边上的高是 .5、正三角形的边长为a，则它的面积为．6、在△ABC中，AB=AC，∠A＝58°，AB的垂直平分线交AC于N，则∠NBC = .7、在直角三角形中，如果一个锐角为30°，而斜边与较小直角边的和为12，那么斜边长为．8、已知：如图，AB＝AC，FD⊥BC于D，DE⊥AB于E，若∠AFD＝145°，则∠EDF＝．9、在等腰三角形ABC中，AB=AC=5，BC=6，D是BC上一点，作DE⊥AB，DF⊥AC，则DE+DF= ．10、如图，一张直角三角形的纸片，象图中那样折叠，使A与B重合，∠B=30°，AC=3，则折痕DE等于．三、解答题(本题共8个小题，共60分)1、（7分）已知：如图，等腰三角形ABC 中，AC ＝BC ，∠ACB ＝90°，直线l 经过点C(点A 、B 都在直线l 的同侧)，AD ⊥l ，BE ⊥l ，垂足分别为D 、E ．求证：△ADC ≌△CEB.2、（7分）用反证法证明一个三角形中不能有两个角是直角．3、（8分）如图，在△ABC 中，AD 是高，CE 是中线，DC=BE ，DG ⊥CE 于G ．求证：①G 是CE 的中点． ②∠B=2∠BCE ．4、（7分）在四边形ABCD 中，AC 平分∠BAD ，过C 作CE ⊥AB 于E ，且AE ＝21（AB ＋AD ），求∠ABC ＋∠ADC 的度数．ABCDEGABCED5、（7分）如图，△ABC 中，E 是BC 边上的中点，DE ⊥BC 于E ，交∠BAC 的平分线AD 于D ，过D 作DM ⊥AB 于M ，作DN ⊥AC 于N ，试证明：BM ＝CN ．6、（7分）已知：如图，在Rt △ABC 中，∠ACB=90°，AC=BC ，点D 是BC 的中点，CE ⊥AD ，垂足为点E ，BF//AC 交CE 的延长线于点F ． 求证：AC=2BF ．7、（7分）在△ABC 中，AB ＝AC ，D 是AB 上一点，E 是AC 延长线上一点，且BD ＝CE ． 求证：DM ＝EM ．ABC DMNEBFABCDE8、（10分）已知：如图，在Rt△ABC中，∠C＝90°，沿过B点的一条直线BE折叠这个三角形，使C点与AB边上的一点D重合．(1)当∠A满足什么条件时，点D恰为AB的中点?写出一个你认为适当的条件，并利用此条件证明D为AB的中点；(2)在(1)的条件下，若DE＝1，求△ABC的面积．参考答案一、选择题1、B2、B3、A4、D5、D6、B7、D8、B9、A 10、C二、填空题1、如果三角形的两边的平方和等于第三边的平方，那么这个三角形是直角三角形2、30°或150°3、10°4、32a 5、234a 6、3°7、 6 8、55° 9、24510、1三、解答题(本题共8个小题，共60分) 1、略 2、略3、提示：连结DE ，由直角三角形斜边中线等于斜边的一半易证．4、提示：过C 点作AD 的延长线的垂线，垂足为F ．利用角平分线的性质和AE=21（AB+AD ）可知BE=DF ，CF=CE ，再由△CDF ≌CBE 即得． 5、提示：连结BD 、CD 利用角平分线和中垂线的性质证△BDM ≌CDN ． 6、提示：证△ACD ≌CBF ．7、提示：过D 点作AC 的平行线（或者过E 点作AB 的平行线）利用三角形全等可证．8、（1）∠A = 30°；证明略（2）△ABC。