第六章 动量

[课时作业·巩固提升] 精选名校试题 考点全面覆盖一、选择题1．人从高处跳到低处时，为了安全，一般都是前脚掌先着地，并在着地的过程中屈腿下蹲，这是为了( )A ．使人的动量变化量变得更小B ．减小人脚所受的冲量C ．延长人体速度变化所经历的时间，从而减小地面对人脚的作用力D ．增大人对地的压强，使人站立得更稳，起到安全作用解析：人在和地面接触时，人的速度减为零，由动量定理可知(F －mg )t ＝m Δv ，而脚尖着地屈腿下蹲可以增加人着地的时间，由公式可知可以减小人脚受到地面的冲击力，故C 正确，A 、B 、D 错误．答案：C2．(2020·安徽阜阳第三中学模拟)2019年阜阳三中科学晚会中，科技制作社团表演了“震撼动量球”实验．为感受碰撞过程中的力，在互动环节，表演者将球抛向观众，假设质量约为3 kg 的超大气球以2 m/s 的速度竖直下落到手面，某观众双手上推，使气球以原速度大小竖直向上反弹，作用时间为0.2 s ．忽略气球所受浮力及空气阻力，g 取10 m/s 2.则观众双手受的压力为( )A ．30 NB ．60 NC ．90 ND ．120 N解析：取竖直向下为正方向，对大气球由动量定理有(mg －F )·Δt ＝m v ′－m v ，代入数据解得F ＝90 N ，故C 正确．答案：C3．(2020·山西晋城高三模拟)太空中的尘埃对飞船的碰撞会阻碍飞船的飞行，质量为M 的飞船飞入太空尘埃密集区域时，需要开动引擎提供大小为F 的平均推力才能维持飞船以恒定速度v 匀速飞行．已知尘埃与飞船碰撞后将完全黏附在飞船上，则在太空尘埃密集区域单位时间内黏附在飞船上尘埃的质量为( )A ．M ＋F vB.F v －MC ．M －F v D.F v解析：设单位时间内黏附在飞船上尘埃的质量为m .以单位时间内黏附在飞船上的尘埃为研究对象，根据动量定理有Ft ＝m v －0，其中t ＝1 s ，可得m ＝F v ，D 正确．答案：D4．为估算池中睡莲叶面承受雨滴撞击产生的平均压强，小明在雨天将一圆柱形水杯置于露台，测得1小时内杯中水位上升了45 mm.查询得知，当时雨滴竖直下落速度约为12 m/s ，据此估算该压强约为(设雨滴撞击睡莲后无反弹，不计雨滴重力，雨水的密度为1×103 kg/m 3)( )A ．0.15 PaB ．0.54 PaC ．1.5 PaD ．5.4 Pa解析：设雨滴受到睡莲叶面的平均作用力为F ，在Δt 时间内有质量为Δm 的雨水的速度由v ＝12 m/s 减为零．以向上的方向为正方向，对这部分雨水应用动量定理有F Δt ＝0－(－Δm v )＝Δm v ，得到F ＝Δm Δtv .设水杯横截面积为S ，对水杯里的雨水，在Δt 时间内水面上升Δh ，则有Δm ＝ρS Δh ，得F ＝ρS v Δh Δt .压强p ＝F S ＝ρv Δh Δt ＝1×103×12×45×10－33 600Pa ＝0.15 Pa ，故选A.答案：A5．(多选)一质量为m ＝60 kg 的运动员从下蹲状态竖直向上跳起，经t ＝0.2 s ，以大小v ＝1 m/s 的速度离开地面，取重力加速度g ＝10 m/s 2，在这0.2 s 内 ( )A ．地面对运动员的冲量大小为180 N·sB ．地面对运动员的冲量大小为60 N·sC ．地面对运动员做的功为30 JD ．地面对运动员做的功为零解析：起跳后人的速度由原来的零变为v ，设向上为正方向，由动量定理可得I －mgt ＝m v －0，故地面对人的冲量为I ＝m v ＋mgt ＝60×1 N·s ＋600×0.2 N·s ＝180 N·s ，故A 正确，B 错误；人在跳起时，地面对人的支持力竖直向上，在跳起过程中，在支持力方向上没有位移，所以地面对运动员的支持力不做功，故C 错误，D 正确．答案：AD6．如图所示，AB 为固定的光滑圆弧轨道，O 为圆心，AO 水平，BO 竖直，轨道半径为R ，将质量为m 的小球(可视为质点)从A 点由静止释放，在小球从A 点运动到B 点的过程中( )A ．小球所受合力的冲量方向为弧中点指向圆心B ．小球所受支持力的冲量为0C ．小球所受重力的冲量大小为m 2gRD ．小球所受合力的冲量大小为m 2gR解析：小球受到竖直向下的重力和垂直切面指向圆心的支持力，所以合力不指向圆心，故合力的冲量也不指向圆心，故A 错误；小球的支持力不为零，作用时间不为零，故支持力的冲量不为零，故B 错误；小球在运动过程中只有重力做功，所以根据机械能守恒可得mgR ＝12m v 2B ，故v B ＝2gR ，根据动量定理可得I 合＝Δp ＝m v B ＝m 2gR ，故C 错误，D 正确． 答案：D7．(多选)(2017·高考全国卷Ⅲ)一质量为2 kg 的物块在合外力F 的作用下从静止开始沿直线运动．F 随时间t 变化的图线如图所示，则( )A ．t ＝1 s 时物块的速率为1 m/sB ．t ＝2 s 时物块的动量大小为4 kg·m/sC ．t ＝3 s 时物块的动量大小为5 kg·m/sD ．t ＝4 s 时物块的速度为零解析：由动量定理有Ft ＝m v ，解得v ＝Ft m ，t ＝1 s 时物块的速率v ＝Ft m＝1 m/s ，A 正确；F -t 图线与时间轴所围面积表示冲量，所以t ＝2 s 时物块的动量大小为p ＝2×2 kg·m/s ＝4 kg·m/s ，B 正确；t ＝3 s 时物块的动量大小为p ′＝(2×2－1×1) kg·m/s ＝3 kg·m/s ，C 错误；t ＝4 s 时物块的动量大小为p ″＝(2×2－1×2) kg·m/s ＝2 kg·m/s ，速度不为零，D 错误．答案：AB二、非选择题8．如图所示，由喷泉中喷出的水柱把一个质量为M 的垃圾桶倒顶在空中，水以速率v 0、恒定的质量增率(即单位时间喷出的质量)Δm Δt从地下射向空中．求垃圾桶可停留的最大高度．(设水柱喷到桶底后以相同的速率反弹，重力加速度为g )解析：设垃圾桶可停留的最大高度为h ，并设水柱到达h 高处的速度为v t ，则v 2t －v 20＝－2gh得v 2t ＝v 20－2gh由动量定理得，在极短时间Δt 内，水受到的冲量为F Δt ＝2(Δm Δt·Δt )v t 解得F ＝2Δm Δt ·v t ＝2Δm Δtv 20－2gh据题意有F ＝Mg联立解得h ＝v 202g －M 2g 8(Δt Δm)2 答案：v 202g －M 2g 8(Δt Δm)2。

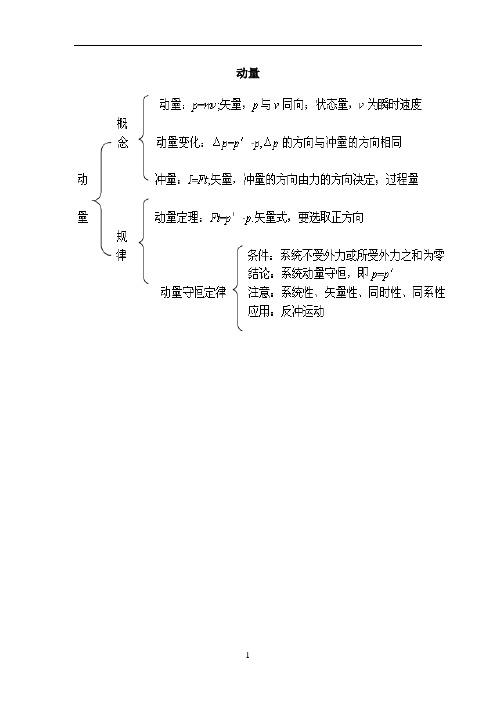
第1讲动量、冲量、动量定理板块一主干梳理·夯实基础【知识点1】动量Ⅱ1．定义：运动物体的质量m和它的速度v的乘积m v叫做物体的动量。

动量通常用符号p 来表示，即p＝m v。

2．单位：在国际单位制中，动量的单位是千克米每秒，符号为kg·m/s。

说明：动量既有大小，又有方向，是矢量。

我们讲物体的动量，是指物体在某一时刻的动量，动量的方向与物体瞬时速度的方向相同。

有关动量的运算，一般情况下用平行四边形定则进行运算。

如果物体在一条直线上运动，则选定一个正方向后，动量的运算就可以转化为代数运算。

3．动量的三个性质(1)动量具有瞬时性。

物体的质量是物体的固有属性，是不发生变化的，而物体的速度是与时刻相对应的，由动量的定义式p＝m v可知，动量是一个状态量，具有瞬时性。

(2)动量具有相对性。

选用不同的参考系时，同一运动物体的动量可能不同，通常在不说明参考系的情况下，指的是物体相对于地面的动量。

在分析有关问题时要先明确相应的参考系。

(3)矢量性。

动量是矢量，方向与速度的方向相同，遵循矢量运算法则。

【知识点2】动量的变化Ⅱ1．因为p＝m v是矢量，只要m的大小、v的大小和v的方向三者中任何一个发生变化，动量p就发生了变化。

2．动量的变化量Δp是矢量，其方向与速度的改变量Δv的方向相同。

3．动量的变化量Δp的大小，一般用末动量p′减去初动量p进行计算，也称为动量的增量。

即Δp＝p′－p，此式为矢量式，若p′、p不在同一直线上，则要用平行四边形定则(或矢量三角形定则)求矢量差；若在同一直线上，则应先规定正方向，再用正、负表示p、p′的方向，最后用Δp＝p′－p＝m v′－m v进行代数运算。

【知识点3】动量、动能、动量变化量的比较Ⅱ【知识点4】冲量、动量定理Ⅱ1．冲量(1)定义：力和力的作用时间的乘积。

(2)表达式：I＝Ft。

单位：牛秒(N·s)。

(3)矢量性：冲量是矢量，它的方向由力的方向决定。

一、选择题1．一个质量是5 kg的小球以5 m/s的速度竖直落到地板上，随后以3 m/s的速度反向弹回，若取竖直向下的方向为正方向，则小球动量的变化量是() A．10 kg·m/s B．－10 kg·m/sC．40 kg·m/s D．－40 kg·m/s答案：D2．关于冲量，以下说法正确的是()A．只要物体受到了力的作用，一段时间内物体受到的总冲量就一定不为零B．物体所受合外力的冲量小于物体动量的变化C．冲量越大的物体受到的动量越大D．如果力是恒力，则其冲量的方向与该力的方向相同解析：合外力的冲量等于动量的变化，如果动量的变化为零，则合外力的冲量为零，所以物体所受外力的合冲量可能为零，故A错误；由动量定理可知物体所受合外力的冲量等于物体动量的变化，故B错误；冲量越大，动量的变化量越大，动量不一定大，故C错误；如果力是恒力，则冲量的方向就是该力的方向，故D正确．答案：D3．(2018·湖北黄冈质检)一小球从水平地面上方无初速释放，与地面发生碰撞后反弹至速度为零，假设小球与地面碰撞没有机械能损失，运动时的空气阻力大小不变，下列说法正确的是()A．上升过程中小球动量改变量等于该过程中空气阻力的冲量B．小球与地面碰撞过程中，地面对小球的冲量为零C．下落过程中小球动能的改变量等于该过程中重力做的功D．从释放到反弹至速度为零过程中小球克服空气阻力做的功等于重力做的功解析：根据动量定理可知，上升过程中小球动量改变量等于该过程中重力和空气阻力的合力的冲量，选项A错误；小球与地面碰撞过程中，由动量定理得：Ft－mgt ＝m v 2－(－m v 1)，可知地面对小球的冲量Ft 不为零，选项B 错误；下落过程中小球动能的改变量等于该过程中重力和空气阻力做功代数和，选项C 错误；由能量守恒关系可知，从释放到反弹至速度为零过程中小球克服空气阻力做的功等于重力做的功，选项D 正确；故选D.答案：D4．(2018·湖北部分重点中学模拟)质量为m 的运动员从下蹲状态竖直向上起跳，经过时间t ，身体伸直并刚好离开地面，离开地面时速度为v .在时间t 内( )A ．地面对他的平均作用力为mgB ．地面对他的平均作用力为m v tC ．地面对他的平均作用力为m (v t －g )D ．地面对他的平均作用力为m (g ＋v t )解析：人的速度原来为零，起跳后变化v ，则由动量定理可得：(F －mg )t ＝m v ；故地面对人的平均作用力为F ＝m (g ＋v t )，故D 正确．答案：D5.将一个质量为m 的小木块放在光滑的斜面上，使木块从斜面的顶端由静止开始向下滑动，滑到底端总共用时t ，如图所示，设在下滑的前一半时间内木块的动量变化为Δp 1，在后一半时间内其动量变化为Δp 2，则Δp 1∶Δp 2为( )A ．1∶2B ．1∶3C ．1∶1D ．2∶1解析：木块在下滑的过程中，一直受到的是重力与斜面支持力的作用，二力的合力大小恒定为F ＝mg sin θ，方向也始终沿斜面向下．由动量定理可得Δp 1∶Δp 2＝(F ·t 1)∶(F ·t 2)＝(mg sin θ·12t )∶(mg sin θ·12t )＝1∶1.故选项C 正确．答案：C6．(多选)光滑水平地面上，A 、B 两物体质量都为m ，A 以速度v 向右运动，B 原来静止，左端有一轻弹簧，如图所示，当A 撞上弹簧，弹簧被压缩最短时( )A ．A 、B 系统总动量仍然为m vB ．A 的动量变为零C ．B 的动量达到最大值D ．A 、B 的速度相等解析：系统水平方向动量守恒，A 正确；弹簧被压缩到最短时A 、B 两物体具有相同的速度，D 正确，B 错误；但此时B 的速度并不是最大的，因为弹簧还会弹开，故B 物体会进一步加速，A 物体会进一步减速，C 错误．答案：AD7.如图，质量为M 的小船在静止水面上以速率v 0向右匀速行驶，一质量为m 的救生员站在船尾，相对小船静止．若救生员以相对水面速率v 水平向左跃入水中，则救生员跃出后小船的速率为( )A ．v 0＋m M vB ．v 0－m M vC ．v 0＋m M (v 0＋v )D ．v 0＋m M (v 0－v )解析：设水平向右为正方向，根据动量守恒定律，对救生员和船有(M ＋m )v 0＝－m v ＋M v x ，解得v x ＝v 0＋m M (v 0＋v )，选项C 正确．答案：C二、非选择题8.如图所示，光滑水平面上停放一个木箱和小车，木箱质量为m ，小车和人总质量为M ，M ∶m ＝4∶1，人以速率v 沿水平方向将木箱推出，木箱被挡板以原速率反弹回来以后，人接住木箱再以同样大小的速率v 第二次推出木箱，木箱又被原速反弹……，问人最多能推几次木箱？解析：选木箱、人和小车组成的系统为研究对象，取向右为正方向．设第n 次推出木箱后人与小车的速度为v n ，第n 次接住后速度为v n ′，则由动量守恒定律可知：第一次推出后有：0＝M v 1－m v ，则v 1＝m v M第一次接住后有：M v 1＋m v ＝(M ＋m )v 1′第二次推出后有：(M ＋m )v 1′＝M v 2－m v ，则v 2＝3m v M第二次接住后有：M v 2＋m v ＝(M ＋m )v 2′……第n －1次接住：M v n －1＋m v ＝(M ＋m )v n －1′第n 次推出：(M ＋m )v n －1′＝M v n －m v即v n ＝(2n －1)M m v设最多能推N 次，推出后有{v N ≥v v N －1＜v 即(2N －1)m v M ≥v ，且[2(N －1)－1]m v M＜v 所以12(M m ＋1)≤N ＜12(M m ＋1)＋1将M m ＝4代入，可得：2.5≤N ＜3.5因为N 取整数，故N ＝3.答案：3。

- 1 - 动量 - 1 - 冲量和动量 一、单项选择题(共23题，合计44分) 1.从同一高度以相同速率分别抛出质量相同的三个小球，一球竖直上抛，一球竖直下抛，一球平抛，则： A．三球落地时动量相同 B．三球落地时动量不相同 C．从抛出到落地过程，三球受到的冲量相同 D．从抛出到落地过程，三球受到的冲量不相同 2.一个质量是0.05 kg的网球，以20 m/s的水平速度飞向球拍，被球拍打击后，反向水平飞回，飞回的速度的大小也是20 m/s．设网球被打击前的动量为p，被打击后的动量为p′，取打击后飞回的方向为正方向，关于网球动量变化的下列计算式，正确的是： A．p′－p=1 kg·m/s－(－1kg·m/s)=2kg·m/s． B．p－p′=－1kg·m/s－1kg·m/s=－2kg·m/s． C．p′－p=－1kg·m/s－1kg·m/s=－2kg·m/s． D．p－p′=1 kg·m/s－1kg·m/s=0． 3.竖直上抛一小球，小球又落回地面，空气阻力大小不变，则在此过程中： A．重力冲量为零 B．空气阻力冲量为零 C．空气阻力做功为零 D．上升过程比下降过程动量增量数值大 4.竖直上抛一质量为m的小球，经t秒小球重新回到抛出点，若取向上为正方向，那么小球的动量变化为： A．－mgt B．mgt C．0 D．－mgt/2 5.质量为m的物体做竖直上抛运动，从开始抛出到落回抛出点用时间为t，空气阻力大小恒为f。规定向下为正方向，在这过程中物体动量的变化量为： A．(mg+f)t B．mgt C．(mg-f)t D．以上结果全不对 6.某物体在水平桌面上，受到一个推力F作用时间t后，物体没有移动，则F的冲量为： A．0 B．Ft C．mgt D．无法计算 7.质量为m的物体放在光滑水平地面上，在与水平方向成θ角的恒定推力F作用下，由静止开始运动，在时间t内推力的冲量和重力的冲量大小分别为： A．Ft；0 B．Ftcosθ；0 C．Ft；mgt D．Ftcosθ；mgt 8.玻璃杯从同一高度落下掉在石头上比掉在草地上容易碎是由于玻璃杯与石头撞击过程中： A．玻璃杯的动量较大 B．玻璃杯受到的冲量较大 C．玻璃杯的动量变化较快 D．玻璃杯的动量变化较大 9.如图所示，质量为2kg的物体A静止在光滑的水平面上，与水平方向成300角的恒力F=3N作用于该物体，历时10s，则： A．力的冲量大小为零 B．力F对物体的冲量大小为30Ns

动量6.1动量和冲量动量定理一、考点聚焦动量冲量动量定理Ⅱ级要求二、知识扫描1．动量：运动物体的质量和速度的乘积叫做物体的动量，即P = mv．动量是矢量，其方向与速度方向相同．它的单位是kg·m/s．两动量相同，必是它们大小相等，且方向相同．动量和动能都是状态量．质量为m的物体，动量大小为P，动能为E k ，它们的关系是P2=2mE k．2．冲量：力和力的作用时间的乘积称为力F的冲量．即I = Ft．冲量是矢量，若在时间t内，F方向恒定，则它的方向与F方向相同，它的单位是N·s．3．动量定理动量定理的内容是物体的动量增量等于物体所受外力的总冲量，表达式为ΔP = Σ I．在恒力作用的条件下，动量定理可由牛顿第二定律推导出来，其简要过程为ΣFt = mv2 －mv1，即ΔP = Σ I．注意：（1）在物体受变力作用时动量定理仍然成立．但此时不可用F·t表示冲量，动量定理可表达为ΣI = ΔP．（2）动量定理中的速度通常均指以地面为参照系的速度．三、好题精析例1．从塔顶以相同速率抛出A、B、C三小球，A竖直上抛，B平抛，C竖直下抛．另有D球从塔顶起自由下落，四小球质量相同，落到同一水平面上．则（）A．落地时动能相同的小球是A、B、CB．落地时动量相同的小球是A、B、CC．从离开塔顶到落地过程中，动能增量相同的小球只有A、B、CD．从离开塔顶到落地过程中，动量增量相同的小球是B、D〖解析〗四个小球在运动过程中机械能均守恒．抛出时动能相同的小球，机械能相同，落地时它们机械能一定也相同，即落地时动能相同，故A对．动量是矢量，落地时B的速度方向与A、C不同，故B的动量与A、C不同，B错．四小球运动过程中的动能增量均为ΔE K = mgh，均相同，C错．小球运动过程中的动量增量为ΔP= mg · t，只有B、D运动时间相同，故D对．〖点评〗（1）动量是矢量，质量相同的物体，速率相等，动能相同．但因方向可能不同，故动量可能不相同．（2）本题中，物体只受重力作用，动能增量等于重力所做功，它与轨迹是直线还是曲线无关，当小球的部分路径重复时（如A球）仍可只计起终点高度差去计算重力的功．小球动量增量等于重力的冲量，它也与轨迹是直线还是曲线无关，但路径重复时，所经时间仍要计为重力作用的时间．例2．如图6－1－1所示，质量为m 的物体，由静止开始从A 点沿斜面从h 1高处下滑到地面，随后又沿另一斜面上滑到h 2高处B 点停止．若在B 点给物体一瞬时冲量，使物体B 点沿原路返回A 点，需给物体的最小冲量的大小是多少？〖解析〗物体从A 运动到B ，克服摩擦力做的功为)(21h h mg E W p f -=∆=物体要从B 返回A ，必需的最小动能为)(221h h mg W E E f p k -=+∆=∆根据mp E k 22=，所以最小冲量的大小为 )(2221h h g m mE p p I k -===∆= 〖点评〗注意动能与动量大小之间的关系，mp E k 22=。