下载文档原格式
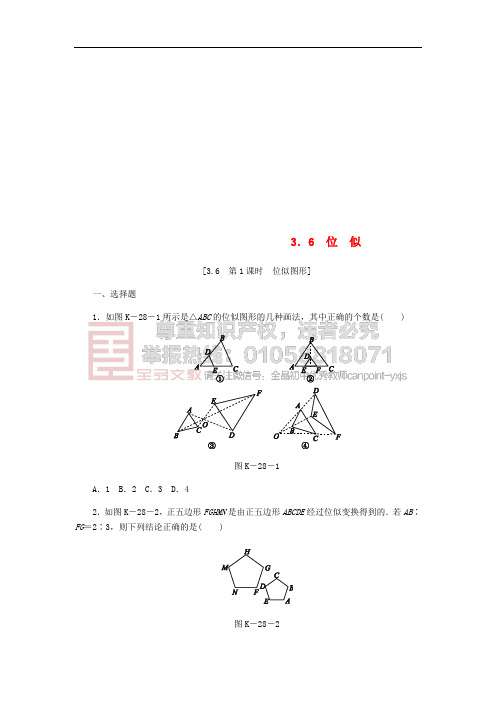
3．6 位似[3.6 第1课时位似图形]一、选择题1．如图K－28－1所示是△ABC的位似图形的几种画法，其中正确的个数是( )图K－28－1A．1 B．2 C．3 D．42．如图K－28－2，正五边形FGHMN是由正五边形ABCDE经过位似变换得到的．若AB∶FG＝2∶3，则下列结论正确的是( )图K－28－2A ．2DE ＝3MNB ．3DE ＝2MNC ．3∠A ＝2∠FD ．2∠A ＝3∠F3.如图K －28－3，D ，E ，F 分别是OA ，OB ，OC 的中点，下面的说法中： ①△ABC 与△DEF 是位似图形； ②△ABC 与△DEF 的相似比为1∶2； ③△ABC 与△DEF 的周长之比为2∶1； ④△ABC 与△DEF 的面积之比为4∶1. 正确的是( )图K －28－3A ．①②③B ．①③④C ．①②④D ．②③④ 二、填空题4．如图K －28－4，已知△EFH 和△MNK 是位似图形，那么其位似中心是点________．(填“A ”“B ”“C ”或“D ”)图K －28－45．2017·兰州如图K －28－5，四边形ABCD 与四边形EFGH 位似，位似中心是点O ，OEOA＝35，则FGBC＝________．图K －28－5三、解答题6．如图K －28－6，在8×6的网格图中，每个小正方形的边长均为1，点O 和△ABC 的顶点均为小正方形的顶点．(1)以O 为位似中心，在网格图中画出将△ABC 缩小为原来的12得到的△A ′B ′C ′；(2)连接(1)中的AA ′，求四边形AA ′C ′C 的周长(结果保留根号).链接听课例2归纳总结图K －28－67已知△ABC 是正三角形，正方形EFPN 的顶点E ，F 在边AB 上，顶点N 在边AC 上． (1)如图K －28－7，在正三角形ABC 及其内部，以点A 为位似中心，画出正方形EFPN 的位似正方形E ′F ′P ′N ′，且使正方形E ′F ′P ′N ′的面积最大(不写画法，但要保留画图痕迹)；(2)若正三角形ABC 的边长为3＋2 3，则(1)中画出的正方形E ′F ′P ′N ′的边长为多少？图K－28－71．[解析] C 利用位似图形的画法：①确定位似中心；②分别连接位似中心和能代表原图的关键点并延长(或反向延长)；③根据位似比，确定能代表所作的位似图形的关键点；④顺次连接上述各点，得到放大或缩小的图形．由位似图形的画法可得①②③中所作图形都是△ABC 的位似图形，故选C .2．[答案] B 3．答案] B 4．[答案] B[解析] 如图，∵△EFH 和△MNK 是位似图形，连接FN ，HK 交于点B ，故点B 是其位似中心．5．[答案] 35[解析] ∵四边形ABCD 与四边形EFGH 位似，∴△OEF ∽△OAB ，△OFG ∽△OBC ， ∴OE OA ＝OF OB ＝35，∴FG BC ＝OF OB ＝35.故答案为35. 6．解：(1)如图所示：(2)如图，AA ′＝CC′＝2.在Rt △OA ′C ′中，OA ′＝OC′＝2.得A′C′＝2 2；同理可得AC ＝4 2， ∴四边形AA′C′C 的周长＝4＋6 2 .7解：(1)如图所示，正方形E′F′P′N′即为所求．(2)设正方形E′F′P′N′的边长为x.∵△ABC为正三角形，∴由直角三角形中30°角所对的直角边等于斜边的一半和勾股定理易得AE′＝BF′＝33x.∵E′F′＋AE′＋BF′＝AB，∴x＋33x＋33x＝3＋2 3，解得x＝3.∴正方形E′F′P′N′的边长为3.。
