求解电场强度13种方法(附例题)

求电场强度的几种常用方法（1）电荷法：即在特定点、场中，用电荷的量和作用原理推求电场强度。

（2）量子力学法：即利用量子力学方法，由量子力学方程解得电场强度。

（3）电流法：即用电流的量和作用原理推求电场强度。

（4）电压法：用电压和静电力的量和作用原理推求电场强度。

（5）数值法：即通过数值计算机模拟和求解电场中的电场强度和电势分布。

2、按计算作用机分类：（1）电阻法：即用电阻和电压的量和变化原理推求电场强度。

（2）电容法：用电容的量和变化原理推求电场强度。

（3）磁力法：用磁力的量和变化原理推求电场强度。

（4）电路法：即用电路的量和变化原理推求电场强度。

（5）电磁学分析法：通过电磁学分析对电场强度和电场静势进行推求和分析。

二、常用的电场强度方法1、电荷法：电荷法是现代电场理论中应用最广泛的方法，它基于两个基本假设：一是电场强度是由放电体所产生的；二是空间任意两点间的电势差即可定义场中电场强度。

由此可见，电荷法的核心就是关于电场强度与电势之间的关系，也即求出电荷分布形式，使它满足Gauss定律（特别是关于场强场态的求解），就可以推出电场强度。

2、量子力学法：量子力学法是利用量子力学方程（如Schrdinger方程）或者Dirac方程）来求得一个电场强度。

量子力学法计算精度比较高，但是由于量子力学方程的复杂性，它的计算量也比较大，常用的解决方法是用蒙特卡罗法（Monte Carlo）来处理。

3、数值法：数值法也是现代电场理论中一种常用的计算电场强度的方法，它利用数值计算机模拟和求解电场中的电场强度和电势分布，可以用很多种数值法进行求解，比如有静电场的快速多体算法（FAST），费米子蒙特卡罗法（FPMC），康拉德方法（Conrad），Boltzmann方法（Boltzmann）等。

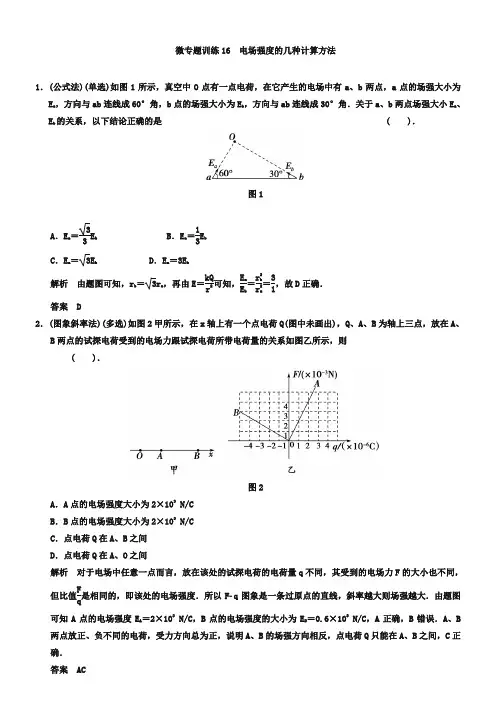
微专题训练16 电场强度的几种计算方法1．(公式法)(单选)如图1所示，真空中O 点有一点电荷，在它产生的电场中有a 、b 两点，a 点的场强大小为E a ，方向与ab 连线成60°角，b 点的场强大小为E b ，方向与ab 连线成30°角．关于a 、b 两点场强大小E a 、E b 的关系，以下结论正确的是( )．图1A ．E a ＝33E bB ．E a ＝13E bC ．E a ＝3E bD ．E a ＝3E b解析 由题图可知，r b ＝3r a ，再由E ＝kQ r 2可知，E a E b ＝r 2b r 2a ＝31，故D 正确．答案 D2．(图象斜率法)(多选)如图2甲所示，在x 轴上有一个点电荷Q(图中未画出)，Q 、A 、B 为轴上三点，放在A 、B 两点的试探电荷受到的电场力跟试探电荷所带电荷量的关系如图乙所示，则( )．图2A ．A 点的电场强度大小为2×103N/C B ．B 点的电场强度大小为2×103 N/C C ．点电荷Q 在A 、B 之间 D ．点电荷Q 在A 、O 之间解析 对于电场中任意一点而言，放在该处的试探电荷的电荷量q 不同，其受到的电场力F 的大小也不同，但比值Fq 是相同的，即该处的电场强度．所以F­q 图象是一条过原点的直线，斜率越大则场强越大．由题图可知A 点的电场强度E A ＝2×103N/C ，B 点的电场强度的大小为E B ＝0.6×103N/C ，A 正确，B 错误．A 、B 两点放正、负不同的电荷，受力方向总为正，说明A 、B 的场强方向相反，点电荷Q 只能在A 、B 之间，C 正确． 答案 AC3．(叠加法)(多选)如图3所示，在x 轴坐标为＋1的点上固定一个电荷量为4Q 的正点电荷，坐标原点O 处固定一个电荷量为Q 的负点电荷，那么在x 坐标轴上，电场强度方向沿x 轴负方向的点所在区域应是( )．图3A ．(0,1)B ．(－1,0)C ．(－∞，－1)D ．(1，＋∞)解析 在区域(0,1)中4Q 和－Q 的电场的电场强度方向都向左，合场强仍向左，A 对；在－Q 左侧距－Q 为x 处场强为零，由k Q x 2＝k4Q＋2得x ＝1，所以区域(－∞，－1)内合场强向左，C 对．答案 AC4．(叠加法)(单选)如图4所示，中子内有一个电荷量为＋2e 3的上夸克和两个电荷量为－e3的下夸克，3个夸克都分布在半径为r 的同一圆周上，则3个夸克在其圆心处产生的电场强度大小为( )图4A.ker2B.ke3r 2C.ke9r2D.2ke 3r2 解析 位于同一圆周上A 、B 、C 处的三个夸克在圆心产生的电场的场强大小分别为：E A ＝k 2e3r 2，方向沿AO 指向O ，E B ＝k e 3r 2，方向沿BO 指向B ，E C ＝k e3r2，方向沿CO 指向C ，由矢量合成法则可得，圆心处的场强大小为k e r 2.答案 A5．(对称法)(单选)如图5所示，有一带电荷量为＋q 的点电荷与均匀带电圆形薄板相距为2d ，此点电荷到带电薄板的垂线通过板的圆心．若图中a 点处的电场强度为零，则图中b 点处的电场强度大小是( )．图5A ．k q 9d 2＋k q d 2B ．k q 9d 2－k qd2C ．0D ．k qd2解析 点电荷在a 点产生的电场强度大小E ＝k qd 2，方向向左，由题意，带电薄板在a 点产生的电场强度大小E 1＝k q d 2，方向向右．根据对称性，带电薄板在b 点产生的电场强度大小E 2＝k qd 2，方向向左，点电荷在b 点产生的电场强度大小E 3＝kq9d 2，方向向左，根据电场强度的叠加原理，E b ＝E 2＋E 3，可知A 正确．答案 A6．(平衡法)一根绝缘细线的一端分别固定在天花板上的P 、Q 点，另一端分别拴有质量均为m ＝0.12 kg 的带电小球A 和B ，其中A 球带正电，电荷量为q ＝3×10－6C ，B 球带负电，与A 球带电荷量相同．A 、B 之间用第三根线连接起来．在水平向左的匀强电场作用下，A 、B 保持静止，悬线仍处于竖直方向，且A 、B 间细线恰好伸直．(静电力常量`k ＝9×109N·m 2/C 2)图6(1)求此匀强电场的电场强度E 的大小．(2)现将PA 之间的线烧断，由于有空气阻力，A 、B 球最后达到新的平衡位置．求此时细线QB 所受的拉力T 的大小，并求出A 、B 间细线与竖直方向的夹角θ.(3)求A 球的电势能与烧断前相比改变了多少(不计B 球所带电荷对匀强电场的影响)．解析 (1)B 球水平方向合力为零，所以q B E ＝k qq B L 2，可得E ＝k q L 2＝9×109×3×10－60.32N/C ＝3×105N/C.(2)两球及细线最后位置如图所示，利用整体法可得T＝2mg＝2×0.12×10 N＝2.4 N因为小球受力平衡，所以qE＝mgtan θ，代入数据，可得θ＝37°.(3)A球克服电场力做功W＝qEL(1－sin θ)＝3×10－6×3×105×0.3×(1－0.6)J＝0.108 J，所以A球的电势能增加了0.108 J.答案(1)3×105 N/C (2)2.4 N 37°(3)0.108 J。

补偿法求电场强度例题
（实用版）
目录
1.补偿法求电场强度的概念和原理
2.补偿法的具体步骤和计算方法
3.补偿法在求解电场强度例题中的应用
正文
一、补偿法求电场强度的概念和原理
补偿法是一种求解电场强度的数值方法，它是基于电场线的切线方向与场强方向相切的原理，通过在场强方向上积分电场线的数量来求解场强。

其基本思想是在某一区域内，通过虚拟位移的方式，使电场线与位移方向垂直，从而达到求解电场强度的目的。

二、补偿法的具体步骤和计算方法
1.首先确定需要求解的电场区域，并在该区域内选取一个虚拟的位移方向。

2.通过计算电场线在这个虚拟位移方向上的分量，得到电场强度在该方向上的数值。

3.在整个区域内积分电场强度的分量，得到电场强度的总值。

4.最后，通过总值除以积分面积，就可以得到该区域内的电场强度。

三、补偿法在求解电场强度例题中的应用
假设有一个点电荷 Q，位于原点，我们需要求解距离原点为 r 的球
面上的电场强度。

1.首先，我们选取一个从球心到球面上任意一点的位移方向。

2.然后，我们计算电场线在这个位移方向上的分量，由于电场线的方
向与位移方向垂直，所以电场强度在这个方向上的分量就等于电荷 Q 除以位移的距离。

3.接着，我们在整个球面上积分电场强度的分量，由于球面的面积为4πr^2，所以电场强度的总值就等于 Q 乘以 4πr^2 除以位移的距离。

4.最后，我们用电场强度的总值除以积分面积，就可以得到距离原点为 r 的球面上的电场强度，即 E=Q/(4πε_0r^2)，其中ε_0 为真空介电常数。

静电场点点清专题3 电场强度的几种计算方法一 知能掌握（一）电场强度的三个计算公式（二）电场强度的求解方法1.基本公式法：定义式法、点电荷电场强度公式法、匀强电场公式法、场强有三个公式：E ＝F q 、E ＝k Q r2、E ＝Ud，在一般情况下可由上述公式计算场强， 2.矢量叠加法：电场强度是矢量，叠加时应遵从平行四边形定则，分析电场的叠加问题的一般步骤是： (1)确定分析计算场强的空间位置；(2)分析该处有几个分电场，先计算出各个分电场在该点的电场强度的大小和方向； (3)依次利用平行四边形定则求出矢量和．但在求解带电圆环、带电平面等一些特殊带电体产生的场强时，上述公式无法直接应用。

这时，如果转换思维角度，灵活运用补偿法叠加、微元法叠加、对称法叠加、等效法等巧妙方法，可以化难为易。

（1）直接叠加：（2）叠加中的对称性思想：对称法实际上就是根据某些物理现象、物理规律、物理过程或几何图形的对称性进行解题的一种方法，利用此法分析解决问题可以避免复杂的数学演算和推导，直接抓住问题的实质，有出奇制胜之效。

利用空间上对称分布的电荷形成的电场具有对称性的特点，使复杂电场的叠加计算问题大为简化．例如：如图9，均匀带电的34球壳在O 点产生的场强，等效为弧BC 产生的场强，弧BC 产生的场强方向，又等效为弧的中点M 在O 点产生的场强方向．①微元对称叠加：微元法就是将研究对象分割成若干微小的的单元，或从研究对象上选取某一“微元”加以分析，从而可以化曲为直，使变量、难以确定的量转化为常量、容易确定的量。

将带电体分成许多元电荷，每个元电荷看成点电荷，先根据库仑定律求出每个元电荷的场强，再结合对称性和场强叠加原理求出合场强．可将带电圆环、带电平面等分成许多微元电荷，每个微元电荷可看成点电荷，再利用公式和场强叠加原理求出合场强。

②分段对称③利用已知的对称结论等量同种、等量异种电场强度的对称性（3）叠加中的等效思想：“等效替代”方法，是指在效果相同的前提下，从A 事实出发，用另外的B 事实来代替，必要时再由B 而C ……直至实现所给问题的条件，从而建立与之相对应联系，得以用有关规律解之。

电场强度的几种求法一． 公式法1．qFE =是电场强度的定义式：适用于任何电场，电场中某点的场强是确定值，其大小和方向与试探电荷无关，试探电荷q 充当“测量工具”的作用。

2．2rk QE =是真空中点电荷电场强度的决定式，E 由场源电荷Q 和某点到场源电荷的距离r 决定。

3．dUE =是场强与电势差的关系式，只适用于匀强电场，注意式中的d 为两点间的距离在场强方向的投影。

二．对称叠加法当空间的电场由几个点电荷共同激发的时候，空间某点的电场强度等于每个点电荷单独存在时所激发的电场在该点的场强的矢量和，其合成遵守矢量合成的平行四边形定则。

例：如图，带电量为+q 的点电荷与均匀带电。

例：如图，带电量为+q 的点电荷与均匀带电薄板相距为2d ，点电荷到带电薄板的垂线通过板的几何中心，如图中a 点处的场强为零，求图中b 点处的场强多大？例：一均匀带负电的半球壳，球心为O 点，AB 为其对称轴，平面L 垂直AB 把半球壳一分为二，L 与AB 相交于M 点，对称轴AB 上的N 点和M 点关于O 点对称。

已知一均匀带电球壳内部任一点的电场强度为零，点电荷q 在距离其为r 处的电势为rqk=ϕ。

假设左侧部分在M 点的电场强度为E 1，电势为1ϕ；右侧部分在M 点的电场强度为E 2，电势为2ϕ；整个半球壳在M 点的电场强度为E 3，在N 点的电场强度为E 4，下列说法中正确的是（ ） A ．若左右两部分的表面积相等，有E 1＞E 2，1ϕ＞2ϕ B ．若左右两部分的表面积相等，有E 1＜E 2，1ϕ＜2ϕC ．只有左右两部分的表面积相等，才有E 1＞E 2，E 3=E 4D ．不论左右两部分的表面积是否相等，总有E 1＞E 2，E 3=E 4 答案：D例：ab 是长为L 的均匀带电细杆，P1、P2是位于ab 所在直线上的两点，位置如图所示．ab 上电荷产生的静电场在P1处的场强大小为E 1，在P2处的场强大小为E2。

电场强度习题1. 导言电场强度是描述电场在一点的作用力的物理量。

在计算电场强度时，我们需要考虑电荷的大小、位置以及介质的性质。

本文将通过一些典型的电场强度习题，帮助读者理解电场强度的概念并掌握计算方法。

2. 电场强度的定义电场强度 $\\mathbf{E}$ 由公式 $\\mathbf{E} =\\dfrac{\\mathbf{F}}{q}$ 给出，其中 $\\mathbf{F}$ 是电荷q在电场中受到的力。

3. 电场强度的计算方法对于不同的电荷分布情况，电场强度的计算方法也有所不同。

下面将介绍几种常见的计算电场强度的方法。

3.1 点电荷产生的电场强度对于一个点电荷q，离它距离为q的位置，它产生的电场强度可以通过公式 $E =\\dfrac{1}{4\\pi\\epsilon_0}\\dfrac{Q}{r^2}$ 计算得到。

其中 $\\epsilon_0$ 是真空介电常数。

3.2 均匀带电细线产生的电场强度假设有一条长度为q的均匀带电细线，总电荷为q。

现在要计算离线上距离为q的位置处的电场强度。

首先，将细线分为无数小段，每段的长度为qq，电荷为qq。

则这一小段所产生的电场强度为 $dE =\\dfrac{1}{4\\pi\\epsilon_0}\\dfrac{dq}{r^2}$，其中q是距离这一小段的距离。

对于整个细线上的每一小段，其电荷元素$dq = \\dfrac{Q}{L}dx$，所以有 $dE =\\dfrac{1}{4\\pi\\epsilon_0}\\dfrac{Q}{L}\\dfrac{dx}{r^2}$。

最后，再对整个细线上的每一小段电场强度积分，即可得到离线上距离为q处的电场强度q。

3.3 均匀带电平面产生的电场强度假设有一块面积为q，电荷密度为 $\\sigma$ 的均匀带电平面。

要计算距平面距离为q处的电场强度。

我们可以将平面划分为无数小块，每块面积为qq。

每块小面积产生的电场强度为 $dE = \\dfrac{1}{4\\pi\\epsilon_0}\\dfrac{\\sigma dA}{r^2}$，其中q是距离这一小块面积的距离。

补偿法求电场强度例题
（原创版）
目录
1.补偿法求电场强度的概念和原理
2.补偿法的具体应用步骤
3.补偿法求电场强度的例题解析
4.补偿法求电场强度的注意事项
正文
一、补偿法求电场强度的概念和原理
补偿法求电场强度是一种基于电场线的物理方法，通过在空间中设置一个测试电荷，观察其在电场中的受力情况，从而推算出电场强度。

其原理基于库仑定律，即电场强度与电荷之间的作用力成正比。

通过这种方法，可以较为直观地描绘出电场的强度和方向。

二、补偿法的具体应用步骤
补偿法求电场强度的具体应用步骤可以分为以下几个步骤：
1.选择一个合适的测试电荷，通常选择一个体积小、质量轻的点电荷。

2.在需要求解电场强度的位置放置测试电荷，并观察其在电场中的受力情况。

3.根据库仑定律，计算出电场强度与测试电荷之间的作用力。

4.通过比例关系，求解出电场强度。

三、补偿法求电场强度的例题解析
假设在一个空间中，存在一个点电荷 Q，我们在距离其 r 的位置放置一个测试电荷 q，观察其在电场中的受力情况。

根据库仑定律，可以得到电场强度 E 与电荷 Q 和测试电荷 q 之间的关系：E = k * Q / r^2，
其中 k 为库仑常数。

四、补偿法求电场强度的注意事项
在使用补偿法求电场强度时，需要注意以下几点：
1.测试电荷的选择应尽量小，以减小对电场线的影响。

2.在放置测试电荷时，应选择一个合适的位置，以便观察其在电场中的受力情况。

3.在计算电场强度时，要准确地测量出测试电荷的受力情况，以及其与电荷 Q 之间的距离。

高中物理静电场和电场问题解题方法静电场和电场问题是高中物理中的重要内容，也是学生们常常感到困惑的部分。

在解题过程中，正确的方法和技巧是非常关键的。

本文将介绍一些解决静电场和电场问题的方法，并通过具体的题目进行说明，帮助高中学生和他们的父母更好地理解和应用这些知识。

一、电场强度的计算方法电场强度是描述电场强弱的物理量，它的计算方法是通过库仑定律得到的。

库仑定律表明，两个点电荷之间的电场强度与它们之间的距离和电荷量的乘积成正比。

因此，我们可以通过以下公式计算电场强度：E = k * Q / r²其中，E表示电场强度，k是库仑常数，Q是电荷量，r是距离。

例如，有一个电荷量为2μC的点电荷，距离它0.5m处的电场强度是多少？根据公式，我们可以计算得到：E = (9 * 10^9 N·m²/C²) * (2 * 10^-6 C) / (0.5m)² = 72 N/C所以，距离该点电荷0.5m处的电场强度为72 N/C。

二、电场线的绘制方法电场线是描述电场分布的图形，它可以帮助我们更直观地理解电场的性质。

在绘制电场线时，我们需要遵循以下规则：1. 电场线的方向是电场强度的方向，即从正电荷指向负电荷。

2. 电场线的密度表示电场强度的大小，密集的电场线表示电场强度大，稀疏的电场线表示电场强度小。

3. 电场线不能相交，因为在交叉点上存在两个不同的电场强度方向，这是不符合物理规律的。

例如，有两个相同大小的正电荷，它们之间的距离为1m，如何绘制它们的电场线？首先，我们可以根据库仑定律计算出两个电荷产生的电场强度大小，然后根据规则绘制电场线。

假设电荷量为Q，距离为r，电场强度为E，我们可以得到：E = k * Q / r²由于两个电荷相同，所以它们产生的电场强度大小相等。

假设它们的电荷量为2μC，距离为1m，我们可以计算得到：E = (9 * 10^9 N·m²/C²) * (2 * 10^-6 C) / (1m)² = 18 N/C接下来，我们可以根据这个电场强度大小绘制电场线。

例谈电场强度的求解方法孙永福甘肃省永昌县第四中学物理组 甘肃 永昌737200电场强度是静电场中极其重要的概念，也是历年高考考查的重点内容。

电场强度的求解方法可以分为两大类：基本方法和特殊方法。

一 基本方法，就是利用电场强度的基本公式来求解电场强度，这三个公式的形式及适用条件分别如下。

1qF E =，此式是电场强度的定义式，适用于一切电场。

22rQ k E =，此式是点电荷场强的决定式，可求出点电荷在任意一点的电场强度。

3dU E =，此式是匀强电场中电场强度与电势差的关系式，定量的计算只适用于匀强电场。

二 特殊方法 1微元法微元法就是将研究对象分割成无数个非常微小的单元，或从研究对象上选取某一“微元”加以分析，从而可以化曲为直，使变量、难以确定的量为常量、容易确定的量。

例1：如图1所示，均匀带点圆环所带正电荷量为Q ,半径为R ,圆心为O ,P 为垂直于圆环平面对称轴上的一点，OP=L.试求P 点的场强。

解析：设想将圆环等分为n 个小段，当n 相当大时，每一小段都可以看作点电荷。

其所带电荷量为nQ q =，由点电荷场强公式可求得每一点电荷在P 点处的场强)(2222L R n Q k nr Q k r q kE +===由对称性可知，每一小段带电环在P 处的场强E 的垂直于轴向的分量y E 相互抵消，而E的轴向分量XE 之和即为带电圆环在P 处的场强E P .图123222222)()(.)(cos L R kQL L R LL R n nkQ nE nE E X P +=++===θ点评：严格的说，微分法是利用微积分的思想处理物理问题的一种思想方法，对考生来说有一定的难度，但是在高考题中也时而出现，所以，在复习过程中要进行该方法的思维训练，以适应高考的要求。

2补偿法（添补法）求解物理问题，要根据问题给出的条件建立相对应的物理模型。

但有时由题给条件建立模型不是一个完整的模型，这时需要给原来的问题补充一些条件，组成一个完整的新模型。

一．必会的基本方法：1．运用电场强度定义式求解例1.质量为m 、电荷量为q 的质点，在静电力作用下以恒定速率v 沿圆弧从A 点运动到B 点,，其速度方向改变的角度为θ（弧度），AB 弧长为s ，求AB 弧中点的场强E 。

2．运用电场强度与电场差关系和等分法求解例2．如图1-1所示，在平面直角坐标系中，有方向平行于坐标平面的匀强电场，其中坐标原点O 处的电势为0V ，点A 处的电势为6V ，点B 处的电势为3V ，则电场强度的大小为AA ．200/V m B．/mC ．100/V m D．/m3．运用“电场叠加原理”求解例3如右图2， M 、N 和P 是以MN 为直径的半圈弧上的三点，O 点为半圆弧的圆心，60MOP ∠=︒．电荷量相等、符号相反的两个点电荷分别置于M 、N 两点，这时O 点电场强度的大小为1E ；若将N 点处的点电荷移至P则O 点的场场强大小变为2E ，1E 与2E 之比为BA ．1:2B ．2:1 C． D． 二．必备的特殊方法：4．运用平衡转化法求解例4．一金属球原来不带电，现沿球的直径的延长线放置一均匀带电的细杆MN ，如图3所示。

金属球上感应电荷产生的电场在球内直径上a 、b 、c 三点的场强大小分别为E a 、E b 、E c ，三者相比（ ）A ．E a 最大B ．E b 最大C ．E c 最大D ．E a = E b = E c图3N图25．运用“对称法”（又称“镜像法”）求解例5．如图4，一半径为R 的圆盘上均匀分布着电荷量为Q 的电荷，在垂直于圆盘且过圆心c 的轴线上有a 、 b 、d 三个点，a 和b 、b 和c 、 c 和d 间的距离均为R ，在a 点处有一电荷量为q (q>O)的固定点电荷.已知b 点处的场强为零，则d 点处场强的大小为(k 为静电力常量)A.kB. kC. kD. k点评：对称法是利用带电体电荷分布具有对称性，或带电体产生的电场具有对称性的特点来求合电场强度的方法。

求电场强度的六种特殊方法一、镜像法（对称法）镜像法实际上就是根据某些物理现象、物理规律、物理过程或几何图形的对称性进行解题的一种方法，利用此 法分析解决问题可以避免复杂的数学演算和推导，直接抓住问题的实质，有出奇制胜之效例1. （2005年上海卷4题）如图1,带电量为+q 的点电荷与均匀带电薄板相距为 2d , 点电荷到带电薄板的垂线通过板的几何中心.若图中a 点处的电场强度为零，根据对称性，带电薄板在图中b 点处产生的电场强度大小和方向如何？（静电力恒量为k ）ffli二、微元法微元法就是将研究对象分割成若干微小的的单元，或从研究对象上选取某一 “微元”加以分析，从而可以化曲 为直，使变量、难以确定的量转化为常量、容易确定的量。

例2.如图2所示，均匀带电圆环所带电荷量为Q,半径为R 圆心为0, P 为垂直于圆环平面的称轴上的一点， 01 L ,试求P 点的场强。

三、等效替代法“等效替代”方法，是指在效果相同的前提下， 直至实现所给问题的条件，从而建立与之相对应联系， 替代数个分力（分运动）；等效电阻、等效电源等。

例3.如图3所示，一带正Q 电量的点电荷 垂直距离为为d,试求A 与板MN 的连线中点C 处的电场强度.4 ---- © C A四、补偿法求解物理问题，要根据问题给出的条件建立起物理模型。

但有时由题给条件建立模型不是一个完整的模型，这 时需要给原来的问题补充一些条件，组成一个完整的新模型。

这样，求解原模型的问题就变为求解新模型与补充条 件的差值问题。

从A 事实出发，用另外的B 事实来代替，必要时再由B 而C 得以用有关规律解之。

如以模型代实物，以合力（合运动）A,与一块接地的长金属板 MN 组成一系统，点电荷 A 与板MN 间的 M例4.如图5所示，用长为L的金属丝弯成半径为r的圆弧，但在 A B之间留有宽度为于r，将电量为Q的正电荷均为分布于金属丝上，求圆心处的电场强度。

针对训练2:如图所示，一半径为R 的圆盘上均匀分布着电荷量为 的轴线上有a 、b 、d 三个点，a 和b 、b 和c 、c 和d 间的距离均为 固定点电荷。