单件作业排序问题的基于lingo软件解法(含代码)

L下面看一个稍微复杂一点儿的例子。

例4.13 职员时序安排模型一项工作一周7天都需要有人（比如护士工作），每天（周一至周日）所需的最少职员数为20、16、13、16、19、14和12，并要求每个职员一周连续工作5天，试求每周所需最少职员数，并给出安排。

注意这里我们考虑稳定后的情况。

model:sets:days/mon..sun/: required,start;endsetsdata:!每天所需的最少职员数;required = 20 16 13 16 19 14 12;enddata!最小化每周所需职员数;min=@sum(days: start);@for(days(J):@sum(days(I) | I #le# 5:start(@wrap(J+I+2,7))) >= required(J));end计算的部分结果为Global optimal solution found at iteration: 0Objective value: 22.00000Variable Value Reduced CostREQUIRED( MON) 20.00000 0.000000REQUIRED( TUE) 16.00000 0.000000REQUIRED( WED) 13.00000 0.000000REQUIRED( THU) 16.00000 0.000000REQUIRED( FRI) 19.00000 0.000000REQUIRED( SAT) 14.00000 0.000000REQUIRED( SUN) 12.00000 0.000000START( MON) 8.000000 0.000000START( TUE) 2.000000 0.000000START( WED) 0.000000 0.3333333START( THU) 6.000000 0.000000START( FRI) 3.000000 0.000000START( SAT) 3.000000 0.000000START( SUN) 0.000000 0.000000从而解决方案是：每周最少需要22个职员，周一安排8人，周二安排2人，周三无需安排人，周四安排6人，周五和周六都安排3人，周日无需安排人。

零件加工排序的单目标非线性整数规划模型摘要本文讨论了总加工时间最短情况下零件加工排序的单目标非线性规划问题。

首先，分析题目给出的数据，可以发现各零件模型在各设备上的加工时间上有差异，那么我们就得出零件模型之间在加工时存在等待时间。

对于等待时间，我们分两种情况进行了讨论：当 i 零件模型完成上一工序的总时间大于或等于（1i -）工件完成下一工序的总时间，此时i 零件模型不需要等待（1i -）零件模型而立即就进入下一工序，此时不需要考虑等待时间；反之，则考虑等待时间。

其次，我们通过对各个零件模型（排序后）完成某项特定工序所需总时间进行求和可以得到整个加工任务所需要的总时间，其各工件的总时间包括零件在设备上的加工时间和加工其他零件时的等待时间。

基于以上分析，我们以最佳排序下总加工时间最短为目标，以零件排序前后所占的位置为约束条件，建立非线性整数规划模型，运用LINGO 编程求解得到最佳加工排序为：4--5--10--1--9--7--8--2--3--6；最短加工总时间为：168分钟本文的主要优点是：在模型的建立过程中，先针对C1、C2工序之间关于总生产时间进行讨论，在得到关于C2工序时间最短的加工顺序模型后进行递推，从而清晰、简洁的求出这10种零件模型总加工时间最短的加工顺序；考虑到实际应用，我们对模型进行了推广，使该模型能够更广的解决多种零件在多道设备生产中的加工排序问题。

主要缺点是：为了方便模型的建立，我们提出了一些有悖于实际的理想化假设，可能会造成小部分结果的细微偏差，但不影响整体结果。

关键词：加工排序；单目标非线性规划；优化算法；0-1变量一、 问题提出某塑料厂要加工十个零件模型(编号为1，2，…，10 ),这些零件模型必须依次通过3个设备C1,C2,C3，每个设备一次只能加工一个零件，其加工时间见表1.1（表详见附录一）(单位：分钟)。

试建立模型求出使总加工时间最短的加工顺序。

二、 模型假设1、假设每个工人都是熟练工人，每个零件在设备上加工的时间是固定不变的，不会应工人的技术水平而改变。

第4讲 Lingo 软件入门司守奎烟台市，海军航空工程学院数学教研室Email ：sishoukui@4.1 初识Lingo 程序Lingo 程序书写实际上特别简捷，数学模型怎样描述，Lingo 语言就对应地怎样表达。

首先介绍两个简单的Lingo 程序。

例4.1 求解如下的线性规划问题：121212112max726450,128480,s.t.3100,,0z x x x x x x x x x =++≤⎧⎪+≤⎪⎨≤⎪⎪≥⎩ Lingo 求解程序如下max =72*x1+64*x2; x1+x2<=50;12*x1+8*x2<=480; 3*x1<=100;说明：Lingo 中默认所有的变量都是非负的，在Lingo 中就不需写出对应的约束。

例4.2 抛物面22y x z +=被平面1=++z y x 截成一椭圆，求原点到这椭圆的最短距离。

该问题可以用拉格朗日乘子法求解。

下面我们把问题归结为数学规划模型，用Lingo 软件求解。

设原点到椭圆上点),,(z y x 的距离最短，建立如下的数学规划模型：⎩⎨⎧+==++++.,1s.t.min 22222y x z z y x z y xLingo 求解程序如下： min =(x^2+y^2+z^2)^(1/2); x+y+z=1; z=x^2+y^2;@free (x); @free (y);说明：Lingo 中默认所有变量都是非负的，这里y x ,的取值是可正可负的，所以使用Lingo 函数free 。

例4.3 求解如下的数学规划模型：⎪⎪⎩⎪⎪⎨⎧==∑∑∑===.,1s.t.min9912100100110012i ii i i ix x x x用Lingo 求解上述数学规划问题，使用集合和函数比较方便，使用集合的目的是为了定义向量，集合使用前，必须先定义；Lingo 程序中的标量不需要定义，直接使用即可。

sets :var/1..100/:x; endsetsmin =@sqrt (@sum (var(i):x(i)^2)); @sum (var(i):x(i))=1;x(100)=@sum (var(i)|i#le#99:x(i)^2); @for (var(i)|i#le#99:@free (x(i)));说明：如果不使用集合和函数，全部使用标量x1,x2,…,x100，最后一个约束就要写99遍，@free(x1); …; @free (x99)。

lingo软件使用教程一般来说，一个优化模型将由以下三部分组成：1. 目标函数（Objective Function）：要达到的目标。

2. 决策变量（Decision variables）：每组决策变量的值代表一种方案。

在优化模型中需要确定决策变量的最优值，优化的目标就是找到决策变量的最优值使得目标函数取得最优。

3. 约束条件（Constraints）：对于决策变量的一些约束，它限定决策变量可以取的值。

在写数学模型时，一般第一行是目标函数，接下来是约束条件，再接着是一些非负限制等。

在模型窗口输入如下代码:Max = 2*x1+3*x2;X1+2*x2<=8;4*x1<16;4*x2<12;注意：1.每一个lingo表达式最后要跟一个分号;2.多数电脑中没有符号，lingo中<=代替；为了方便可以用<代替小于等于，用>代替大于等于。

3.我们可以添加一些注释，增加程序的可读性。

注释以一个！（叹号必须在英文状态下输入，它会自动变为绿色）开始，以；（分号）结束。

4．Lingo中不区分变量名的大小写。

变量名必须以字母（A-Z）开头，后面的字符可以是字母、数字、下划线。

变量名不能超过32个字符。

Lingo程序的一些规则：1. 在Lingo中最开始都是“MAX=”或者“MIN=”开始表示求目标函数的最大或者最小值。

2. 变量和它前面的系数之间要用“*”连接，中间可以有空格。

3. 变量名不区分大小写，但必须以字母开始，不超过32个字符。

4. 数学表达式结束时要用分号“；”表示结束。

表达式可以写在多行上，但是表达式中间不能用分号。

5. 在电脑系统中一般没有“小于等于”符号，在Lingo采用“<=”来表示“小于等于”，用“>=”表示“大于等于”。

小于等于也可以用更简单的“<”表示，大于等于用“>”表示。

集合段：在我们已经得到的程序里有一些量没有定义，如WAREHOUSES( I)，DEMAND( J)， LINKS( I, J)。

LINGO 使用教程LINGO 是用来求解线性和非线性优化问题的简易工具。

LINGO 内置了一种建立最优化模型的语言，可以简便地表达大规模问题，利用LINGO 高效的求解器可快速求解并分析结果。

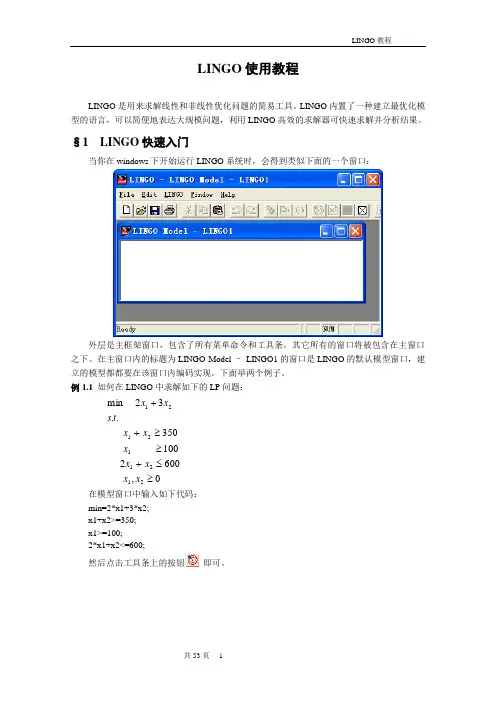
§1 LINGO 快速入门当你在windows 下开始运行LINGO 系统时，会得到类似下面的一个窗口：外层是主框架窗口，包含了所有菜单命令和工具条，其它所有的窗口将被包含在主窗口之下。

在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口，建立的模型都都要在该窗口内编码实现。

下面举两个例子。

例1.1 如何在LINGO 中求解如下的LP 问题：,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x x在模型窗口中输入如下代码： min=2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。

例1.2 使用LINGO软件计算6个发点8个收点的最小费用运输问题。

产销单位运价如下表。

model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));!这里是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮即可。

LINGO 使用教程LINGO 是用来求解线性和非线性优化问题的简易工具。

LINGO 内置了一种建立最优化模型的语言，可以简便地表达大规模问题，利用LINGO 高效的求解器可快速求解并分析结果。

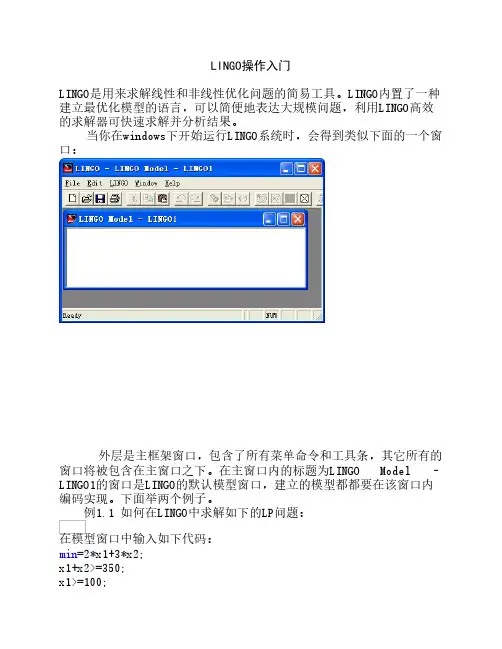
§1 LINGO 快速入门当你在windows 下开始运行LINGO 系统时，会得到类似下面的一个窗口：外层是主框架窗口，包含了所有菜单命令和工具条，其它所有的窗口将被包含在主窗口之下。

在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口，建立的模型都都要在该窗口内编码实现。

下面举两个例子。

例1.1 如何在LINGO 中求解如下的LP 问题：,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x x在模型窗口中输入如下代码： min=2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。

例1.2 使用LINGO软件计算6个发点8个收点的最小费用运输问题。

产销单位运价如下表。

model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));!这里是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮即可。

LINGO使⽤教程（⼀）LINGO是⽤来求解线性和⾮线性优化问题的简易⼯具。

LINGO内置了⼀种建⽴最优化模型的语⾔，可以简便地表达⼤规模问题，利⽤LINGO ⾼效的求解器可快速求解并分析结果。

1.LINGO快速⼊门当你在windows下开始运⾏LINGO系统时，会得到类似下⾯的⼀个窗⼝：外层是主框架窗⼝，包含了所有菜单命令和⼯具条，其它所有的窗⼝将被包含在主窗⼝之下。

在主窗⼝内的标题为LINGO Model – LINGO1的窗⼝是LINGO的默认模型窗⼝，建⽴的模型都都要在该窗⼝内编码实现。

下⾯举两个例⼦。

例1.1 如何在LINGO中求解如下的LP问题：在模型窗⼝中输⼊如下代码：min=2*x1+3*x2;x1+x2>=350;x1>=100;2*x1+x2<=600;然后点击⼯具条上的按钮即可。

例1.2 使⽤LINGO软件计算6个发点8个收点的最⼩费⽤运输问题。

产销单位运价如下表。

使⽤LINGO软件，编制程序如下：model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!⽬标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));!这⾥是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击⼯具条上的按钮即可。

LINGO 使用教程LINGO 是用来求解线性和非线性优化问题的简易工具。

LINGO 内置了一种建立最优化模型的语言，可以简便地表达大规模问题，利用LINGO 高效的求解器可快速求解并分析结果。

§1 LINGO 快速入门当你在windows 下开始运行LINGO 系统时，会得到类似下面的一个窗口：外层是主框架窗口，包含了所有菜单命令和工具条，其它所有的窗口将被包含在主窗口之下。

在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口，建立的模型都都要在该窗口内编码实现。

下面举两个例子。

例1.1 如何在LINGO 中求解如下的LP 问题：0,6002100350..32min212112121≥≤+≥≥++x x x x x x x t s x x在模型窗口中输入如下代码：min =2*x1+3*x2;x1+x2>=350;x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。

例1.2 使用LINGO 软件计算6个发点8个收点的最小费用运输问题。

产销单位运价如model :!6发点8收点运输问题;sets :warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min =@sum (links: cost*volume);!需求约束;@for (vendors(J):@sum (warehouses(I): volume(I,J))=demand(J));!产量约束;@for (warehouses(I):@sum (vendors(J): volume(I,J))<=capacity(I));!这里是数据;data :capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮 即可。