2019秋北师大版八年级数学上册课件：第五章复习课(共29张PPT)

且∠BDC＝90°(勾股定理逆定理)．
(2)解：设 AD＝x，则 AC＝x＋9. ∵AB＝AC，∴AB＝x＋9.
∵∠BDC＝90°，∴∠ADB＝90°，
∴AB2＝AD2＋BD2(勾股定理)， 即(x＋9)2＝x2＋122，解得 x＝72， ∴AC＝72＋9＝225， ∴S△ABC＝12AC·BD＝75.
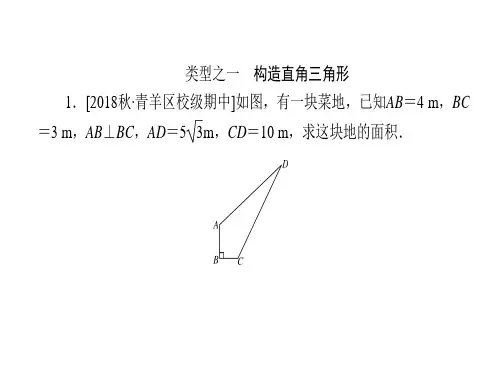
2.如图，在△ABC中，已知AB＝AC，D是AC上的一点，CD ＝9，BC＝15，BD＝12. (1)证明：△BCD是直角三角形； (2)求△ABC的面积．
(1)证明：∵CD＝9，BD＝12， ∴CD2＋BD2＝81＋144＝225. ∵BC＝15，BC2＝225，∴CD2＋BD2＝BC2， ∴△BCD 是直角三角形，
解：如图，在 Rt△ABC 中， ∵BC＝20 尺，AC＝5×3＝15 尺， 且 AB2＝BC2＋AC2， ∴AB2＝202＋152＝252. ∴AB＝25 尺，即葛藤的长为 25 尺．
∴AC2＋BC2＝AB2，∴△ABC 是直角三角形． (2)解：S 阴影＝SRt△ABC－SRt△ACD＝12×10×24－12×8×6＝96.
9．我国古代有这样一道数学题：“枯木一根直立地上，高2 丈，周3尺，有葛藤自根缠绕而上，5周而达其顶．问葛藤之 长几何？”这里1丈＝10尺，葛藤之长指它的最短长度．解 题时，枯木视为圆柱(如图)，周3尺指圆柱底面周长3尺．求 葛藤的长．
解：由题意得 OB＝12×1.5＝18(海里)，OA＝16×1.5＝24(海里)， ∵AB＝30 海里，又 182＋242＝302， 即 OB2＋OA2＝AB2，
∴∠AOB＝90°. ∵∠DOA＝40°，∴∠BOD＝50°.
故另一艘舰艇的航行方向是北偏西 50°.
【例2】如图，∠ABC＝90°，AB＝6 cm，AD＝24 cm，BC＋ CD＝34 cm，C是直线l上一动点，请你探索当C离B多远时， △ACD是一个以CD为斜边的直角三角形？

(4－t)2，解得t＝
25 8
.③当CO＝OM时，M与A点重合，∴t＝8.综上所述，
当△COM是等腰三角形时，t的值为5或285或8 .
参考答案
点击进入答案PPT链接
点击进入答案word链接
解：(1)∵AC＝8 cm，BC＝6 cm，∠ACB＝90°，∴AB＝ BC2＋AC2
＝10
cm.∵O为AB的中点，∴AO＝
Hale Waihona Puke 1 2AB＝5cm.由∠AMO＝∠AOM知，
AO＝AM，∴AM＝5 cm，∴CM＝3 cm，∴t＝3. (2)①当CO＝CM时，CM＝5 cm，∴t＝5.②当MC＝MO时，t2＝32＋
解：(1)如答图所示． (2)MN＝M′N′＝ 92＋62＝3 13， MN′＝ 82＋72＝ 113， M′N＝ 102＋52＝5 5， 则实际最短的路径为 113厘米．
类型之六 勾股定理的综合问题 10．如图，在△ABC中，∠ACB＝90°，BC＝6 cm，AC＝8 cm，点O 为AB的中点，连接CO.点M在CA边上，从点C以1 cm/秒的速度沿CA向点 A运动，设运动的时间为t秒． (1)当∠AMO＝∠AOM时，求t的值； (2)当△COM是等腰三角形时，求t的值．
为等腰直角三角形，∴BE＝CE＝
1 2
BC.由勾股定理得AB2＋AC2＝BC2，AE2
＝AB2－BE2＝AC2－CE2，AD2＝AE2＋ED2，∴2AD2＝2AE2＋2ED2＝AB2－ BE2＋(BD－BE)2＋AC2－CE2＋(CE－CD)2＝AB2＋AC2＋BD2＋CD2－
2BD×BE－2CD×CE＝AB2＋AC2＋BD2＋CD2－2×12BC×BC＝BD2＋CD2， 即BD2＋CD2＝2AD2.

（结
11．计算：
巩固提高
12．计算：
巩固提高
巩固提高
13．实数a、b、c在数轴上的位置如图所示，化简：
解：由数轴可得：c＜a＜0＜b， 则a﹣b＜0，a+c＜0，c﹣b＜0，﹣2b＜0， 原式=|a﹣b|﹣|a+c|+|c﹣b|﹣|﹣2b| =b﹣a+a+c+b﹣c﹣2b =0
巩固提高
14.已知x=2+ ，y=2﹣ ，求x2+y2﹣3xy﹣5x+5y
的被开方
2．若 m=1 ，n=2
变式练习
都是最简二次根式，则 ．
例3.计算：
精典范例
解：（1）原式=2﹣1+3=4；
3．计算：
变式练习
巩固提高
4．在式子 中，二次根式有（C ）
A．2个 B．3个 C．4个 D．5个 5．二次根式 中，是最简二次根式的个数有（B） A．1个 B．2个 C．3个 D．4个
的值．
解：∵x=2+ ，y=2﹣ ， ∴x﹣y=2 ，xy=1， ∴x2+y2﹣3xy﹣5x+5y =（x﹣y）2﹣xy﹣5（x﹣y） =（2 ）2﹣1﹣5×2 =11﹣10 ．
15．当x=
巩固提高
时，求代数式 的值．
巩固提高
6．已知
是整数，正整数n的最小值为（C ）
A．0 B．1 C．6 D．36
7．当1＜a＜2时，代数式
+|1﹣a|的值
是（B ）
A．﹣1 B．1 C．2a﹣3 D．3﹣2a
8．当x= -5 时，
既是最简二次
根式，被开方数又相同．
巩固提高
9．观察分析下列数据：

解：(1)∵a，b 满足 a－4＋|b－6|＝0， ∴a－4＝0，b－6＝0， 解得 a＝4，b＝6， ∴点 B 的坐标是(4，6)． (2)∵点 P 从原点出发，以每秒 2 个单位长度的速度沿着 O→C→B→A→O 的线路移动，∴2×4＝8. ∵OA＝4，OC＝6，∴当点 P 移动 4 秒时，在线段 CB 上，离点 C 的距离是 8－6＝2，即当点 P 移动 4 秒时，此时点 P 在线段 CB 上，离点 C 的距离是 2 个 单位长度，点 P 的坐标是(2，6)．
C．(－2，4)
D．(2，－4)
3．[2018·北京]如图是老北京城一些地点的分布示意图．在图中，分别以正东、 正北方向为 x 轴、y 轴的正方向建立平面直角坐标系，有如下四个结论：
①当表示北京天安门的点的坐标为(0，0)，表示广安门的点的坐标为(－6， －3)时，表示左安门的点的坐标为(5，－6)；
A．2 017 C．2 019
B．2 018 D．2 020
12．[2017·奉节期中]如图，在平面直角坐标系中，每个小方格都是边长为 1 的正 方形．
(1)写出图中从原点 O 出发，按箭头所指方向先后经过的 A，B， C，D，E 这几点的坐标；
(2)按图中所示规律，找到下一个点 F 的位置并写出它的坐标．
x 轴对称，并写出△A′B′C′三顶点的坐标； (3)若 M(x，y)是△ABC 内部任意一点，请直接写出这点在
△A′B′C′内部的对应点 M′的坐标．
解：(1)描点如答图所示． (2)如答图所示，△A′B′C′即为所求．
A′(－2，－1)，B′(3，－1)，C′(2，－3)； (3)M′(x，－y)．
解：(1)A(1，0)，B(1，2)，C(－2，2)，D(－2，－2)，E(3，－2)． (2)F(3，4)．