教案《生活中的平移》李荣章

《生活中的平移》说课稿【教材分析】一、教材的地位和作用“生活中的平移”是北师大版数学八年级上册第三章图形的平移与旋转的第一节，本节课对图形变换的学习具有承上启下的作用．学生在前面已学习了轴对称及轴对称图形，在此基础上还将学习生活中的旋转与设计图案等内容．同轴对称一样，平移也是现实生活中广泛存在的现象，它不仅是探索图形变换的一些性质的必要手段，而且也是解决现实世界中的具体问题的重要工具．二、教学目标（一）知识与技能通过具体实例认识平移，理解平移的基本内涵，理解平移前后两个图形对应线段平行且相等、对应角相等、对应点所连的线段平行且相等的性质．（二）过程与方法经历观察、分析、操作、欣赏以及抽象、概括等过程，经历探索图形平移基本性质的过程以及与他人合作交流的过程，进一步发展空间观念，增强审美意识．（三）情感与态度①通过自己身边“平移”的实例，感受“生活中处处有数学”，激发学生学习数学的兴趣．②通过欣赏生活中平移图形，使学生感受数学美，体会美的价值所在，进而追求美并创造美．三、教学重点和难点教学重点是探索图形平移的概念和基本性质．教学难点是图形平移的基本性质的探索与理解．【学情分析】1.学生的年龄特征和认知特征八年级学生思维活跃，对新事物满怀探求欲望，并具备了一定的合作学习能力．2.学生已具备的知识和技能学生在小学已经初步认识了平移，并且对生活中的平移现象有一些感性的认识，同时已经具有线段相等、平行线的判定和轴对称等知识储备，能在教师的引导下发现问题，通过自主学习、相互交流、师生互动获取知识．3.学生有待于提高的知识和技能但学生的分析能力以及抽象概括能力仍有待提高，因此本节课的设计利用学生已掌握的知识，通过对学生已知生活中平移现象的观察、分析，引导学生归纳出平移的概念，进而研究平移的性质和应用，从而使学生的分析能力和抽象概括能力有所提高．【教法学法】教学方法①创设问题情境：营造和谐的教学氛围，激发学生的学习兴趣，激发求知欲望．②采用引导探究法：逐步呈现教学信息，突出教师的主导作用和学生的主体作用；突出独立性、又体现合作性．学习方法学生采用自主探究和合作交流相结合的方法：通过学生自主学习、交流，师生互动，生生互动，让学生自主获取知识．【教学过程】（一）创设情境，引入新课．先让学生欣赏郑州市的古建筑“黄河博物馆”，讲解这座百年建筑具有很高的文物价值，但是在道路改造计划中，“黄河博物馆”正好在规划范围内，进而设置悬念：怎样才能既保住这座古建筑，又不影响道路的改造呢？工程人员经过冥思苦想，最后决定通过平移把博物馆移走。

初中数学八年级上册《生活中的平移》说课稿初中数学八年级上册《生活中的平移》说课稿一、说教材(一)教材的地位和作用今天我说课的内容是北师大版数学八年级上册第三章图形的平移与旋转的第一节《生活中的平移》。

学生在前面已学习了轴对称及轴对称图形,在此基础上还将学习生活中的旋转与旋转设计图案等内容。

同轴对称一样,平移也是现实生活中广泛存在的现象,是现实世界运动变化的最简捷的形式之一,它不仅是探索图形变换的一些性质的必要手段,而且也是解决现实世界中的具体问题以及进行数学交流的重要工具。

为综合运用几种变换(平移,旋转,轴对称,相似等)进行图案设计打下基础。

《生活中的平移》对图形变换的学习具有承上启下的作用。

(二)教学目标根据上述教材分析,以及新课程标准，考虑到学生已有的认知结构、心理特征,制定如下教学目标知识目标：通过具体实例认识平移,理解平移的基本内涵,理解平移前后两个图形对应点连线平行且相等,对应线段平行且相等,对应角相等的性质。

能力目标：通过探究归纳平移的定义,特征,性质,积累数学活动经验,提高学生的科学思维能力.情感目标：经历观察,分析,操作,欣赏以及抽象,概括等过程,经历探索图形平移基本性质的过程以及与他人合作交流的过程,进一步发展空间观念,增强审美意识.(三)教学重点与难点平移是现实生活中广泛存在的现象,它不仅是探索图形变换的一些性质的.必要手段,而且也是解决现实世界中的具体问题以及进行数学交流的重要工具。

探索平移的基本性质,认识平移在现实生活中的广泛应用是学习本节内容的重点。

平移特征的获得过程,教科书中仅用了一段文字,很少的篇幅,对于这个特征,不是要学生死记硬背,而是要学生具备一定的探究归纳能力,对八年级的学生来说,有一定的难度,因此本课的难点是平移特征的探索及理解。

上面是对教材的地位与作用、教学目标以及教学重难点的分析，接下来我将说说学情：二、说学情1.学生已经学习学习了轴对称及轴对称图形，对图形的变换已经有了了解，有了一定的学习基础。

第三章图形的平移与旋转1．生活中的平移教学目标通过具体实例认识平移，理解平移的基本内涵，理解平移前后两个图形对应点连线平行且相等、对应线段和对应角分别相等的性质。

教学过程创设情境1.引入问题，出现课题：请你判断：小明跟着妈妈乘观光电梯上楼，一会儿，小明兴奋地大叫起来：“妈妈！妈妈！你看我长高了！我比对面的大楼还要高！”小明说的对吗？为什么？2.接触平移现象：（1）电视机在传送带上移动的过程。

（2）手扶电梯上人的移动的过程。

问题：①你能发现传送带上的电视机、手扶电梯上的人在平移前后什么没有改变，什么发生了改变吗？②在传送带上，如果电视机的某一按键向前移动了80cm，那么电视机的其它部位（如屏幕左上角的图标）向什么方向移动？移动了多少距离？③如果把移动前后的同一台电视机屏幕分别记为四边形和四边形（多媒体演示书上的图3-2），那么四边形与四边形的形状、大小是否相同？平移前后两个图形的形状和大小没有改变，位置发生了改变。

活动探究活动一：探求平移的定义根据上述分析，你能说明什么样的图形运动称为平移？“一个物体沿着某个方向移动一定的距离”平移定义：在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移。

平移不改变图形的形状和大小。

活动二：探究平移的性质演示图形的平移过程，让学生通过对图形平移现象的观察，探索其中的性质。

同学们通过刚才的观察，总结出一个结论，即：“图形的位置改变了，但形状和大小没有改变”。

现在我们一起来探索：平移前后对应点、对应线段以及对应角之间在做怎样的变化。

教师提出问题：想一想：（1）在上图中，线段AE，BF，CG，DH有怎样的位置关系？（2）图中每对对应线段之间有怎样的位置关系？（3）图中有哪些相等的线段、相等的角？学生归纳总结，教师板书平移的性质：经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等。

例题讲解例1 如图所示，△ABE沿射线XY的方向平移一定距离后成为△CDF。

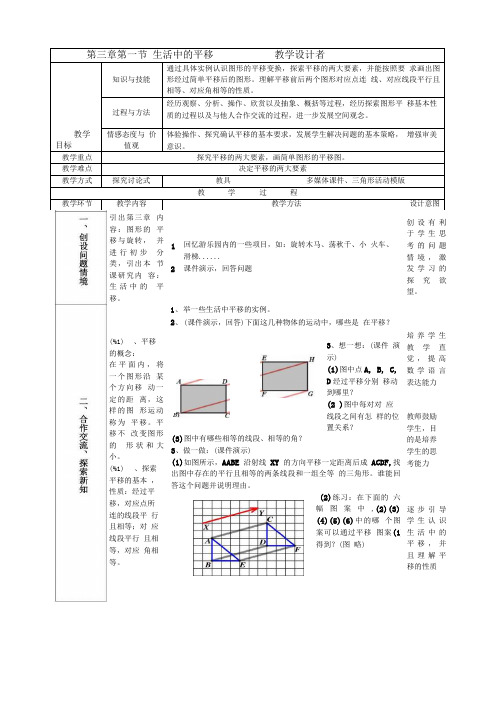
第三章第一节生活中的平移教学设计者教学目标知识与技能通过具体实例认识图形的平移变换，探索平移的两大要素，并能按照要求画出图形经过简单平移后的图形。

理解平移前后两个图形对应点连线、对应线段平行且相等、对应角相等的性质。

过程与方法经历观察、分析、操作、欣赏以及抽象、概括等过程，经历探索图形平移基本性质的过程以及与他人合作交流的过程，进一步发展空间观念。

情感态度与价值观体验操作、探究确认平移的基本要求，发展学生解决问题的基本策略，增强审美意识。

教学重点探究平移的两大要素，画简单图形的平移图。

教学难点决定平移的两大要素教学方式探究讨论式教具多媒体课件、三角形活动模版教学过程教学环节教学内容教学方法设计意图引出第三章内容：图形的平移与旋转，并进行初步分类，引出本节课研究内容：生活中的平移。

(%1)、平移的概念：在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移。

平移不改变图形的形状和大小。

(%1)、探索平移的基本，性质：经过平移，对应点所连的线段平行且相等；对应线段平行且相等，对应角相等。

12回忆游乐园内的一些项目，如：旋转木马、荡秋千、小火车、滑梯......课件演示，回答问题1、举一些生活中平移的实例。

2、(课件演示，回答)下面这几种物体的运动中，哪些是在平移？B3、想一想：(课件演示)(1)图中点A, B, C,D经过平移分别移动到哪里？(2 )图中每对对应线段之间有怎样的位置关系？(3)图中有哪些相等的线段、相等的角？3、做一做：(课件演示)(1)如图所示，AABE沿射线XY的方向平移一定距离后成ACDF,找出图中存在的平行且相等的两条线段和一组全等的三角形。

谁能回答这个问题并说明理由。

(2)练习：在下面的六幅图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到？(图略)创设有利于学生思考的问题情境，激发学习的探究欲望。

培养学生教学直觉，提高数学语言表达能力教师鼓励学生，目的是培养学生的思考能力逐步引导学生认识生活中的平移，并且理解平移的性质。

《生活中的平移》教学案例一、教学目标1．通过欣赏、观察、操作、分析及抽象、概括等过程，经历探索图形平移基本性质的过程以及与他人合作交流的过程，进一步发展空间观念，增强审美意识。

2．通过具体实例认识平移，理解平移的基本内涵，理解平移前后两个图形对应点所连线段平行且相等、对应线段和对应角分别相等的性质。

二、教学内容分析1．设计意图分析《生活中的平移》是华师大版八年级数学上册第15章《平移与旋转》的第一节，它对图形变换的学习具有承上启下的作用。

学生在前面已学习了轴对称及轴对称图形。

在此基础上还将学习生活中的旋转与旋转设计图案等内容。

同轴对称一样，平移也是现实生活中广泛存在的现象，是现实世界运动变化最简捷的形式之一，它不仅是探索图形变换性质的必要手段，而且也是解决现实世界中具体问题以及进行数学交流的重要工具。

重点探索平移的基本性质，认识平移在现实生活中的广泛应用是本节内容的学习重点。

2．设计思路分析设计思路分为三个层次：第一层次：第二层次：从特例出发研究平移的基本性质；第三层次：在应用中，进一步深化学生对平移变换的理解和认识。

3．教学中应注意的问题在教学中，教师要引导学生充分挖掘和利用现实生活中大量存在的平移现象，并对其中的一些共性特征加以分析，总结。

同时，充分利用相对真实的情境以及现实生活中大量存在的典型图形和平移进行教学，尽可能全面地体现教学素材的现实性和问题的挑战性。

三、学校及学生状况分析本节课授课班级共有40名学生，授课地点多媒体教室，该班是学校对初中七年级所有学生在进行入学情况调查后，根据学生的学业成绩、兴趣特长以及性格特征平行分班组成的一个班级。

该班学生性格活泼好动，热爱动手操作，对新教材有较强的适应性。

四、教学过程设计1．创设情境，引入新课（1）回忆校园内的一些运动现象，如开关中的校门、升降国旗、荡秋千……引入本章内容——图形的平移与旋转。

（图1）图1（由学生很熟悉的生活经历引入，让学生在轻松、愉快的心情下开始学习。

初中数学八年级上册《生活中的平移》说课稿第1篇：初中数学八年级上册《生活中的平移》说课稿一、说教材(一)教材的地位和作用今天我说课的内容是北师大版数学八年级上册第三章图形的平移与旋转的第一节《生活中的平移》。

学生在前面已学习了轴对称及轴对称图形,在此基础上还将学习生活中的旋转与旋转设计图案等内容。

同轴对称一样,平移也是现实生活中广泛存在的现象,是现实世界运动变化的最简捷的形式之一,它不仅是探索图形变换的一些*质的必要手段,而且也是解决现实世界中的具体问题以及进行数学交流的重要工具。

为综合运用几种变换(平移,旋转,轴对称,相似等)进行图案设计打下基础。

《生活中的平移》对图形变换的学习具有承上启下的作用。

(二)教学目标根据上述教材分析,以及新课程标准，考虑到学生已有的认知结构、心理特征,制定如下教学目标知识目标：通过具体实例认识平移,理解平移的基本内涵,理解平移前后两个图形对应点连线平行且相等,对应线段平行且相等,对应角相等的*质。

能力目标：通过探究归纳平移的定义,特征,*质,积累数学活动经验,提高学生的科学思维能力.情感目标：经历观察,分析,*作,欣赏以及抽象,概括等过程,经历探索图形平移基本*质的过程以及与他人合作交流的过程,进一步发展空间观念,增强审美意识.(三)教学重点与难点平移是现实生活中广泛存在的现象,它不仅是探索图形变换的一些*质的必要手段,而且也是解决现实世界中的具体问题以及进行数学交流的重要工具。

探索平移的基本*质,认识平移在现实生活中的广泛应用是学习本节内容的重点。

平移特征的获得过程,教科书中仅用了一段文字,很少的篇幅,对于这个特征,不是要学生死记硬背,而是要学生具备一定的探究归纳能力,对八年级的学生来说,有一定的难度,因此本课的难点是平移特征的探索及理解。

上面是对教材的地位与作用、教学目标以及教学重难点的分析，接下来我将说说学情：二、说学情1.学生已经学习学习了轴对称及轴对称图形，对图形的变换已经有了了解，有了一定的学习基础。

3．1 生活中的平移邓宏书一、教材分析：和轴对称一样，平移也是现实生活中广泛存在的现象，是现实世界运动变化的最简捷的形式之一。

探索平移的基本性质，认识和欣赏平移在现实生活中的广泛运用，是第三学段学习的主要目标。

学生在七年级下学期已经学习了“生活中的轴对称”，初步积累了一定的图形变换的数学活动经验，在此基础上，教材提供了电梯、传送带上的电视机、老井上的辘轳等图片，目的是使学生从这些生活图形中抽象出它们的共同特征。

教材在安排上通过学生观察图片，鼓励学生探索平移现象的共同特征，动手操作、亲自实验，体验数学活动的乐趣。

教材给学生自主探索留有很大的空间，学生可以充分发挥现象，以促进学生对平移的体验和理解。

二、教学目标：1、知识和技能目标：（1）通过学生观察生活中平移的例子，认识图形的平移变换，探索它的基本性质，理解“对应点所连的线段平行且相等”以及“对应线段平行且相等，对应角相等”等基本性质。

（2）能按要求作出简单的平面图形平移后的图形。

（3）认识和欣赏平移变换在现实生活中应用，使学生初步感受利用平移的性质进行图案设计。

2、过程与方法目标（1）经历探索图形平移的特征的过程，体验和感受图形平移的主要特征。

（2）经历观察、实践、验证等数学学习的活动，培养学生初步的数学推理能力。

（3）使学生在探索与创造的数学学习活动中，学会与人合作、与人交流。

3、情感与态度目标：（1）通过收集自己身边“平移”的实例，感受“生活处处有数学”，激发学生学习数学的兴趣。

（2）通过欣赏生活中平移图形与学生自己设计平移图案，使学生感受数学美，体会美的价值所在，进而追求美并创造美。

三、教学重点和难点：1、教学重点：探索图形平移的主要特征和基本性质。

2、教学难点：从生活中的平移现象中概括出平移的特征。

四、教学方法：采用自主探究式的教学方法，本着贯彻启发性、直观性、理论联系实际的教学原则，体现以教师为主导，学生为主体的教学思想，确定本节课的教学方法如下：①采用引导发现法：逐步呈现教学信息，突出教师的主导作用和学生的主体作用；突出独立性、又体现合作性。

《生活中的平移》教学设计推荐理由：本教学设计的课堂实录获2012年全国青年教师初中数学课堂教学竞赛一等奖。

推荐人：莲湖进校郑小瑛一、教材的地位和作用本课是第三学段“空间与图形”中内容，学生在前面已学习轴对称及轴对称图形的基础上，认识图形的平移并不困难。

而学好平移能为综合运用几种变换(平移,旋转,轴对称,相似等)进行图案设计打下基础。

平移在图形变换的学习中具有承上启下的作用。

二、教学目标，重难点教学目标：1，借助具体情境图形，理解平移的基本内涵，理解平移性质，并能初步运用平移的定义和性质解决问题2，通过观察，发现和实践操作等活动，经历感受，认识，意义建构，概括并应用，体会知识发生发展的全过程。

提高学生的探究能力和方法。

3，在生活情境中发现数学问题，通过合作交流探索，感受生活中的数学，体会数学的实用价值，提高学数学用数学的意识。

教学重点：理解平移内涵，平移的性质并能初步应用教学难点：（1）、探索平移的性质（2）、利用平移的有关概念和基本性质解决问题。

三、学情分析1. 学生对平移有所了解，但大都是通过直观感知，操作得到的。

此部分的学习让学生通关观察，操作，归纳平移的定义与性质。

使学生经历从感性认识到数学描述的学习全过程。

2. 学生在“生活中的轴对称”学习中，初步积累了一定的图形变换的数学活动经验，已经具备一定的归纳和表达的能力。

四．教学过程：环节一：创设情境，点明课题。

情景设置：观看发射火箭视频问题：火箭的位置发生了怎样的变化？学生活动：观看视频，初步感知生活中的平移设计意图：通过视频激发学生的学习欲望，明确“这样”的运动叫做平移运动，导入新课。

环节二：探索交流，获取新知第一部分：归纳平移的定义情景设置：观察生活中平移运动视频。

问题： 1.这些平移运动具有哪些共同点？2.根据这些特征，请你用自己的语言归纳平移的定义？学生活动：观察思考，初步感知，发现视频中运动的共同点，并用自己的语言归纳平移定义设计意图：数学来源于实际生活，利用视频使学生初步感受平移现象，并引导学生观察平移运动共同点，明确具有“图形”“同一方向”“一定距离”的特征的运动叫平移。