裂项相消法

裂项相消万能公式有哪些裂项法，这是分解与组合思想在数列求和中的具体应用。

是将数列中的每项（通项）分解，然后重新组合，使之能消去一些项，最终达到求和的目的。

通项分解（裂项）倍数的关系。

通常用于代数，分数，有时候也用于整数。

裂项相消万能公式有哪些1裂项相消的公式1/n(n+1)=1/n-1/(n+1)1/(2n-1)(2n+1)=1/2[1/(2n-1)-1/(2n+1)]1/n(n+1)(n+2)=1/2[1/n(n+1)-1/(n+1)(n+2)]1/(√daoa+√b)=[1/(a-b)](√a-√b)n·n!=(n+1)!-n!2裂项法求和（1）1/[n(n+1)]=（1/n）- [1/(n+1)]（2）1/[(2n-1)(2n+1)]=1/2[1/(2n-1)-1/(2n+1)]（3）1/[n(n+1)(n+2)]=1/2{1/[n(n+1)]-1/[(n+1)(n+2)]}（4）1/(√a+√b)=[1/(a-b)](√a-√b)（5）n·n!=(n+1)!-n!（6）1/[n(n+k)]=1/k[1/n-1/(n+k)]（7）1/[√n+√（n+1）]=√（n+1）-√n（8）1/（√n+√n+k）=（1/k）·[√（n+k）-√n]3数列求和的常用方法1、分组法求数列的和：如an=2n+3n2、错位相减法求和：如an=n·2^n3、裂项法求和：如an=1/n(n+1)4、倒序相加法求和：如an= n5、求数列的最大、最小项的方法：①an+1-an=……如an= -2n2+29n-3②(an>0) 如an=③an=f(n) 研究函数f(n)的增减性如an= an^2+bn+c(a≠0)6、在等差数列中,有关Sn 的最值问题——常用邻项变号法求解：(1)当a1>0,d<0时，满足{an}的项数m使得Sm取最大值.(2)当a1<0,d>0时，满足{an}的项数m使得Sm取最小值. 7、对于1/n+1/(n+1)+1/(n+2)……+1/(n+n)的算式同样适用。

裂项相消法求和公式
裂项相消法是数学中常用的一种方法，用于简化求和式。

它通
常用于对称性比较明显的求和式，可以通过将求和式中的相邻项相减，从而简化问题。

裂项相消法常用于数学和物理中的求和问题，
下面我将从数学和物理两个方面来介绍裂项相消法的求和公式。

在数学中，裂项相消法可以用于简化一些复杂的求和式，特别
是在级数求和的过程中。

一个常见的裂项相消法求和公式是对称式
的求和。

比如，对于等差数列$a_1, a_2, a_3, ..., a_n$，我们可
以利用裂项相消法将求和式简化为$\frac{1}{2}(a_1+a_n)n$。

这个
公式的推导过程就是利用了裂项相消法，通过将数列的首尾项相加，次首尾项相加，依次类推，最终得到简化后的形式。

在物理中，裂项相消法同样有着重要的应用。

比如在物理中的
力学问题中，特别是涉及到质心的问题中，裂项相消法可以帮助简
化力矩的求和问题。

通过将作用在质点上的力分解成对称的部分，
然后利用裂项相消法简化力矩的表达式，从而简化了问题的求解过程。

总的来说，裂项相消法是一种非常有用的数学方法，它可以帮
助简化复杂的求和式，特别是对称性比较明显的求和式。

在数学和物理问题中都有着重要的应用。

通过合理运用裂项相消法，可以简化问题、加快计算速度，是数学和物理学习中的重要工具之一。

裂项相消法的八种优势和劣势优势1. 简单易懂：裂项相消法是数学中的一种简单方法，容易理解和掌握。

简单易懂：裂项相消法是数学中的一种简单方法，容易理解和掌握。

2. 节省时间：使用裂项相消法可以简化复杂的运算，从而节省时间和精力。

节省时间：使用裂项相消法可以简化复杂的运算，从而节省时间和精力。

3. 解决方程：裂项相消法在解决一元方程中非常有效，可以帮助我们快速求解未知数。

解决方程：裂项相消法在解决一元方程中非常有效，可以帮助我们快速求解未知数。

4. 适用广泛：无论是在代数、几何还是微积分中，裂项相消法都可以广泛应用。

适用广泛：无论是在代数、几何还是微积分中，裂项相消法都可以广泛应用。

5. 提高精度：裂项相消法可以准确计算并求解问题，提高结果的精度和准确性。

提高精度：裂项相消法可以准确计算并求解问题，提高结果的精度和准确性。

6. 启发思考：使用裂项相消法不仅可以解决具体问题，还能培养逻辑思维和数学推理能力。

启发思考：使用裂项相消法不仅可以解决具体问题，还能培养逻辑思维和数学推理能力。

7. 避免错误：裂项相消法可以帮助我们避免犯错，尤其在复杂运算中更具优势。

避免错误：裂项相消法可以帮助我们避免犯错，尤其在复杂运算中更具优势。

8. 拓展应用：裂项相消法可以作为解决其他数学问题的基础，其技巧和思路可以迁移到其他领域。

拓展应用：裂项相消法可以作为解决其他数学问题的基础，其技巧和思路可以迁移到其他领域。

劣势1. 有限适用性：虽然裂项相消法适用于很多问题，但并非所有问题都能通过该方法解决。

有限适用性：虽然裂项相消法适用于很多问题，但并非所有问题都能通过该方法解决。

2. 要求基础知识：使用裂项相消法需要一定的数学基础知识，对一些初学者来说可能难以理解。

要求基础知识：使用裂项相消法需要一定的数学基础知识，对一些初学者来说可能难以理解。

3. 繁琐步骤：在复杂的问题中，裂项相消法可能需要进行繁琐的步骤和计算，增加了解题的难度。

错位相减法和裂项相消法错位相减法和裂项相消法是初中数学中常见的两种解题方法。

这两种方法都是通过将原式子变形，使得原本难以计算的式子简化、易于计算。

下面将详细介绍这两种方法。

一、错位相减法1.1 定义错位相减法又称交错相减法，是一种用于解决一些复杂的多项式运算的方法。

它的核心思想是将一个多项式拆分成两个部分，然后交错地进行相减运算，从而达到简化计算的目的。

1.2 原理假设有一个多项式a(x)，它可以被拆分成两个部分：奇数项和偶数项。

a(x) = a(奇)(x) + a(偶)(x)那么我们可以利用下面这个公式来计算a(x)：a(x) = a(奇)(x) - a(偶)(x)这个公式就是错位相减法的核心公式。

通过使用这个公式，我们可以将一个复杂的多项式简化为两个较为简单的多项式之差。

在实际应用中，我们通常会选择拆分出来奇数项或者偶数项较少的那个部分作为a(奇)(x)或者a(偶)(x)，以达到简化计算的目的。

1.3 例子下面我们来看一个例子，假设有一个多项式：a(x) = x^4 - 3x^3 + 2x^2 - x + 1我们可以将它拆分成两个部分：a(奇)(x) = x^4 - 2x^2 + 1a(偶)(x) = 3x^3 - x然后，我们可以利用错位相减法的公式来计算a(x)：a(x) = a(奇)(x) - a(偶)(x)= (x^4 - 2x^2 + 1) - (3x^3 - x)= x^4 - 3x^3 + 2x^2 - x + 1通过使用错位相减法，我们将原本较为复杂的多项式简化为了两个较为简单的多项式之差，从而达到了简化计算的目的。

二、裂项相消法2.1 定义裂项相消法又称因式分解法，是一种用于解决一些复杂方程或者不等式问题的方法。

它的核心思想是将原方程或者不等式中出现的一些复杂项分解成一些简单项之积，并利用这些简单项之间相互抵消或者合并来达到简化计算的目的。

2.2 原理裂项相消法的原理可以用下面这个例子来说明。

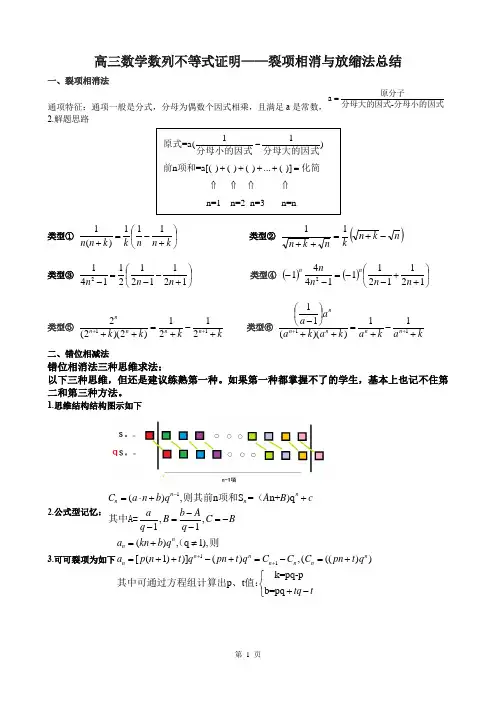
高三数学数列不等式证明——裂项相消与放缩法总结一、裂项相消法通项特征：通项一般是分式，分母为偶数个因式相乘，且满足a是常数，a-=原分子分母大的因式分母小的因式2.解题思路类型①⎪⎭⎫⎝⎛+-=+knnkknn111)(1类型②()nknknkn-+=++11类型③⎪⎭⎫⎝⎛+--=-121121211412nnn类型④()()⎪⎭⎫⎝⎛++--=--121121114412nnnn nn类型⑤kkkk nnnnn+-+=++++112121)2)(2(2类型⑥kakakakaaannnnn+-+=++⎪⎭⎫⎝⎛-++1111))((11二、错位相减法错位相消法三种思维求法：以下三种思维，但还是建议练熟第一种。

如果第一种都掌握不了的学生，基本上也记不住第二和第三种方法。

1.思维结构结构图示如下2.公式型记忆：1(),n S=n+)q,,11n nn nC a n b q A B ca b AB C Bq q-=⋅++-==---则其前项和（其中A=3.可可裂项为如下11(),q1),[(1))](),((())k=pq-pp tb=pqnnn n nn n n na knb qa p n t q pn t q C C C pn t qtq t++=+≠=++-+=-=+⎧⎨+-⎩（则其中可通过方程组计算出、值：11=a()n=a[( )( )( )...( )]n=1 n=2 n=3 n=n-++++=⇑⇑⇑⇑原式分母小的因式分母大的因式前项和化简放缩模型——平方型与指数型证明下列不等式：1、、2、)(21......31211222*∈<++++Nnn3、)(471......31211222*∈<++++Nnn4、)(351......31211222*∈<++++Nnn)(21)12()12(1......751531311*∈<+⨯-++⨯+⨯+⨯NnnnnnS + + +...+n=1 n=2 n=3 n=nqS + + +...+q-=⇑⇑⇑⇑=①②①的基础上左右同时乘，即在①式中指数加1①②代入通项公式，等差数列当等比数列的系数在n-+k( )=+k( )=-S=--n得（1q)S①中的第一项指数函数相加②的最后一项①中的第一项等比求和公式②的最后一项化简两边同时除以（1q)即得平方型：分母是两项积可放缩到裂项相消模型指数型：可放缩为等比模型5、)(45)12(1......51311222*∈<-++++N n n6、),2(32121......121121121432*∈≥<-++-+-+-N n n n7、)(23231......231231231332211*∈<-++-+-+-N n nn8、)(342 (3232221211)432*+∈<-++-+-+-N n n n n一、单选题1．已知数列{}n a 的首项是11a =，前n 项和为n S ，且()1231n n S S n n N *+=++∈，设()2log 3n n c a =+，若存在常数k ，使不等式()()116n nc k n N n c *-≥∈+恒成立，则k 的取值范围为（ ） A ．1,9⎡⎫+∞⎪⎢⎣⎭B ．1,16⎡⎫+∞⎪⎢⎣⎭C ．1,25⎡⎫+∞⎪⎢⎣⎭D ．1,36⎡⎫+∞⎪⎢⎣⎭2．已知数列{}n a 的首项是11a =，前n 项和为n S ，且1231n n S S n +=++（*N n ∈），设()2log 3n n c a =+，若存在常数k ，使不等式()116n n c k n c -≥+（*N n ∈）恒成立，则k 的最小值为（ ）A ．19B ．116C ．125D ．136二、填空题3．已知数列{}n a 中，112a =，()1n n n n a a a +-=，*n ∈N ，数列11n n a a +⎧⎫⎨⎬⋅⎩⎭的前n 项和为n S .若对于任意的*n ∈N ，不等式n S t <恒成立，则实数t 的取值范围是________.4．已知首项为1的数列{}n a 的前n 项和为n S ，且()12n n nS n S +=+，数列2112n n n n a a a +++⎧⎫⎨⎬⎩⎭的前n 项和为n T ，若()110n n T λ++-⋅>，且λ∈Z ，则λ=___________.三、解答题5．已知数列{}n a 中11a =，)2n a n =≥.(1)求{}n a 的通项公式；(2)若21n n c a -=，数列1n c ⎧⎫⎨⎬⎩⎭的前n 项和为n T ，证明：21211n n n a T a +--<≤.6．已知数列{}n a 满足1222n n a a a a =-，*n N ∈．(1)证明：数列11n a ⎧⎫⎨⎬-⎩⎭是等差数列，并求数列{}n a 的通项公式；(2)记12n n T a a a =，*n N ∈，22212n n S T T T =++．证明：当*n N ∈时，11243n n S a +>-．7．已知函数()()3log 1(0)1x f x x x +=>+的图像上有一点列()()*,n n n P x y n N ∈，点n P 在x 轴上的射影是(),0n n Q x ，且(1322n n x x n -=+≥，且)*1,2n N x ∈=.(1)求证：{}1n x +是等比数列，并求数列{}n x 的通项公式；(2)对任意的正整数n ，当[]1,1m ∈-吋，不等式239181n y t mt <-+恒成立，求实数t 的取值范围；(3)设四边形11n n n n P Q Q P ++的面积是n T ，求证：1211132nT T nT +++<.8．已知正项数列{}n a 的首项11a =，前n 项和nS 满足)2n a n ≥. (1)求数列{}n a 的通项公式；(2)记数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为n T ，若对任意的*N n ∈，不等式24n T a a <-恒成立，求实数a 的取值范围.9．已知数列{}n a 满足11a =，且11n n a a n +-=+,n S 是1n a ⎧⎫⎨⎬⎩⎭的前n 项和.(1)求n S ；(2)若n T 为数列2n S n ⎧⎫⎪⎪⎛⎫⎨⎬ ⎪⎝⎭⎪⎪⎩⎭的前n 项和，求证：232n nT n >>+.10．已知数列{}n a 的前n 项和为n S ，11a =，22a =，且214n n n S S a ++=+． (1)求n a ；(2)求证：121112111n a a a +++<+++．11．已知数列{}n a 的前n 项和为n S ，13a =，24a =，()112322n n n S S S n +-+=-≥. (1)证明：数列{}2n a -是等比数列，并求数列{}n a 的通项公式；(2)记112n n n n b a a -+=，数列{}n b 的前n 项和为n T ，证明：11123n T≤<.12．证明：135212462n n -⨯⨯⨯⋯⨯13．已知数列{}n a 是等差数列，23a =，数列{}n b 是等比数列，18b =，公比3q >，且3q a =，2213b a a =.(1)求{}n a ，{}n b 的通项公式； (2)设24log n n n b c a =，n *∈N ，求证：1212nc c c ++⋅⋅⋅+<.14．已知各项为正的数列{}n a 满足：113a =，()*134N n n n a a n a +=∈+． (1)设0a >，若数列1log 1a n a ⎧⎫⎛⎫⎪⎪+⎨⎬ ⎪⎪⎪⎝⎭⎩⎭是公差为2的等差数列，求a 的值；(2)设数列1n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为n S ，证明4543n S n ≤<+．参考答案：1、 通项公式为： ()()⎪⎭⎫⎝⎛+--=+-=1211212112121n n n n a n2、通项公式为： ()⎪⎭⎫ ⎝⎛--=-<=≥n n n n n a n n 111111,22 3、通项公式为： ⎪⎭⎫ ⎝⎛+--=-<=≥111121111,222n n n n a n n 4、通项公式为： ⎪⎭⎫ ⎝⎛+--=-<==≥1211212144441,2222n n n n n a n n 5、通项公式为： ()⎪⎭⎫⎝⎛--=-<+-=-=≥n n n n n n n a n n 111414411441121,2222 6、通项公式为：()11111123121211221221121,2---++⋅=≤≤=-=-<-=≥n n n n n n n a a a n 7、通项公式为：11313231231--=⋅-<-=n n n n n n a 8、通项公式为：nn n n n nn n n n a n 2222,21<-+=-=≥+ 1．C 【详解】由1231n n S S n +=++，则当2n ≥时，得123(1)1n n S S n -=+-+， 两式相减得123n n a a +=+，变形可得：132(3)n n a a ++=+，又134a +=，122123116a a S S +==+⨯+=，所以25a =，2132(3)a a +=+， ∴数列{}3n a +是以4为首项、2为公比的等比数列，故113422n n n a -++=⨯=，所以2log (3)1n n c a n =+=+，所以2111116(16)(16)(1)17168172517n n c n n n c n n n n n n -===≤=++++++++， 当且仅当4n =时等号成立，故125k ≥.故选：C. 2．C 【详解】当2n ≥ 时，由1231n n S S n +=++可得-123-2n n S S n =+，两式相减得：123n n a a +=+ ，即132(3)n n a a ++=+，而134a +=，2121224,5a a S S a +==+=， 故2132(3)a a +=+ ，所以{3}n a + 是以134a +=为首项，2q为公比的等比数列，则11342,23n n n n a a -++=⨯=- ，故()122log 3log 21n n n c a n +=+==+，所以()111616(16)(1)17n n c n n c n n n n -==+++++，而16N ,8n n n*∈+≥ ，当且仅当4n = 时取等号， 故()11116162517n n c n c n n-=≤+++，当且仅当4n = 时取等号， 所以若存在常数k ，使不等式()116n n c k n c -≥+（*N n ∈）恒成立，则k 的最小值为125，故选：C 3．[)4,+∞【详解】由()1n n n n a a a +-=得11n n a n a n++=，则有 312412321234112321n n n n a a a a a n n a a a a a n n ----⨯⨯⨯⨯⨯=⨯⨯⨯⨯⨯--，化简得1n a n a =，即2n n a =， 所以1114114()1(1)122n n n n a a n n n n +===-+⋅++⨯， 所以111114(1)4(11)4223341111111n S n n n n n ---=-+-+-+++=-++<， 所以不等式n S t <恒成立，则有4t ≥.故答案为：[)4,+∞ 4．0【详解】由()12n n nS n S +=+，得()1()2n n n n S a n S ++=+， 即12n n na S +=，当1n =时，2122a S ==，21021a a -=；可知当2n ≥时，12n n na S +=，()112n n n a S --=， 两式相减整理，得101n na a n n，所以n a n ⎧⎫⎨⎬⎩⎭是以1为首项，0为公差的等差数列，所以1na n=，n a n =，所以()()21111211221221n n n n n n n a n a a n n n n ++++++==-⋅⋅+⋅⋅+，所以()12231111111()()()21222223221n n n T n n +=-+-+⋅⋅⋅+-⨯⨯⨯⨯⋅⋅+()111221n n +=-⋅+， ()110n n T λ++-⋅>等价于()()11111212n n n λ++-⋅>-⋅+；当n 是正奇数时，()111212n n λ+>-⋅+，因为()12111132122228n n +-≤-⨯=-⋅+，所以38λ>-； 当n 是正偶数时，()111221n n λ+<-⋅+，因为()1311111122122324n n +-≥-=⋅+⨯，所以1124λ<； 综上所述，λ的取值范围为311824λ-<<，则整数λ的值为0.故答案为：0. 5．(1)n a =证明见解析【解析】(1)将)2n a n =≥两边同时平方，整理得()22112n n a a n --=≥， 所以数列{}2n a 是首项为211a =，公差为1的等差数列，所以()2111n a n n =+-⨯=.由题知0n a >，所以n a(2)因为n a =21n n c a -==1n c =. 先证21n n T a -≤：当1n =时，11a =，11T =，满足21n n T a -≤； 当2n ≥时，1n c ==所以)(21112n n T n a -<++++-==.故21n n T a -≤得证.再证211n n T a+>-：因为1nc ==>=所以)(211211n n T n a +>++++==-.故不等式21211nn n a Ta +--<≤成立.【点睛】关键的点睛：本题考查等差数列的证明，以及放缩法证明不等式，本题的第二问的难点是对通项公式的放缩，放缩后，再进行裂项相消法求和，1n c==<=1n c ==>= 6．(1)证明见解析；()*12n n a n N n +=∈+(2)证明见解析 【解析】(1)当1n =时，1122a a =-，123a =，当2n ≥时，1222n n a a a a =-；121122n n a a a a --=- 相除得11(2)1n n n a a n a --=≥-，整理为：1111(2)111n n n n a n a a a -==-≥---，即1111(2)11n n n a a --=≥--， 11n a ⎧⎫∴⎨⎬-⎩⎭为等差数列，公差1d =，首项为1131a =-；所以()13121n n n a =+-=+-，整理为：()*12n n a n N n +=∈+，经检验，符合要求. (2)由（1）得：()*12n n a n N n +=∈+．1222n n T a a a n ==+， 2244114(2)(2)(3)23n T n n n n n ⎛⎫∴=>=- ⎪+++++⎝⎭，22212111112441342333n n S T T T n n n ⎛⎫⎛⎫∴=++>-++-=-- ⎪ ⎪+++⎝⎭⎝⎭，112224333n n n S a n ++∴>-=-+， 所以，当*n N ∈时，11243n n S a +>-．7．(1)证明见解析，31nn x =-(2)()(),22,∞∞--⋃+(3)证明见解析【解析】(1)因为2n ≥，且*1,32n n n N x x -∈=+，所以()1131n n x x -+=+，即1131n n x x -+=+（常数）； 因为113x +=，所以{}1n x +是首项为3，公比为3的等比数列，所以11333n n n x -+=⨯=，即31n n x =-；数列{}n x 的通项公式为31n n x =-.(2)由题可知()()3*log 10,1n n nn x y xn N x +=>∈+，由（1）可得3log 3033n n n n n y ==>，所以1113n ny n y n ++=<，即1n n y y +<，数列{}n y 为单调递减数列.所以n y 最大值为113y =；因为当[]1,1m ∈-吋，不等式239181n y t mt <-+恒成立，所以29180t mt ->恒成立.所以2291809180t t t t ⎧->⎨+>⎩，解得2t <-或2t >.所以t 的取值范围为()(),22,∞∞--⋃+.(3)四边形11n n n n P Q Q P ++的面积是()()114123n n n n n y y x x n T +++-+==.因为()()331134111n n n n n n ⎛⎫<=- ⎪+++⎝⎭，所以1211111111111313122233411n T T nT n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++<-+-+-++-=- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦. 因为*n ∈N，所以13313311n n ⎛⎫-=-< ⎪++⎝⎭；所以121113.2nT T nT +++<8．(1)21n a n =-；(2)1a ≤-或2a ≥.【解析】(1)当2n ≥时，n a=∴1nn S S --=1=1=， 所以数列是首项为1，公差为1n ，又由n a 121n n n =+-=-（2n ≥），当1n =时，11a =也适合，所以21n a n =-. (2)∴()()()111111221212121n n a a n n n n +==--+-+，∴11111111111233521212212n T n n n ⎛⎫⎛⎫=-+-++-=-< ⎪ ⎪-++⎝⎭⎝⎭， 又∴对任意的*N n ∈，不等式24n T a a <-恒成立，，∴22a a ≤-，解得1a ≤-或2a ≥.即所求实数a 的范围是1a ≤-或2a ≥. 9．(1)21n nS n =+(2)证明见解析 【解析】(1)∴11n n a a n +-=+，∴212a a -=，323a a -=，…1n n a a n --= 由上述1n -个等式相加得12n a a n -=++，∴()1122n n n a a n +=+++=， ∴11121n a n n ⎛⎫=- ⎪+⎝⎭，11111122121223111n n S n n n n ⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪+++⎝⎭⎝⎭.(2)令()()22221441112n n S b n n n n n ⎛⎫⎛⎫⎛⎫===>⎪ ⎪ ⎪++++⎝⎭⎝⎭⎝⎭， ∴11111111244233412222n n T n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫>-+-++-=-= ⎪ ⎪ ⎪ ⎪⎢⎥++++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦， 又因为()22221411441111n n S b n n n n n n n ⎛⎫⎛⎫⎛⎫⎛⎫===<=- ⎪ ⎪ ⎪ ⎪++++⎝⎭⎝⎭⎝⎭⎝⎭，且11b =∴11111111414143323341211n T n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫<+-+-++-=+-=-< ⎪ ⎪ ⎪ ⎪⎢⎥+++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，综上，232nn T n >>+，得证. 10．(1)()12n n a n -*=∈N (2)证明见解析【解析】(1)解：由214n n n S S a ++=+得24n n a a +=． 所以，当()21n k k *=-∈N 时，21214k k a a +-=，所以数列{}21k a -是首项为11a =，公比为4的等比数列， 故11211414k k k a a ---=⨯=⨯，即()211222122k k k a ----==． 当()2n k k *=∈N 时，则2224k k a a +=，所以，数列{}2k a 是首项为22a =，公比为4的等比数列，所以，1121224242k k k k a a ---=⨯=⨯=．所以()12n n a n -*=∈N ．(2)证明：由（1）知11111212n n n a --⎛⎫=< ⎪+⎝⎭，所以0121121111111111221111122221122nn n a a a -⎛⎫- ⎪⎛⎫⎛⎫⎛⎫⎛⎫⎝⎭+++<++++=<= ⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭⎝⎭--.故原不等式成立.11．(1)证明见解析，122n n a -=+(2)证明见解析【解析】(1)解：当2n ≥时，由11232n n n S S S +-+=-可变形为()1122n n n n S S S S +--=--， 即122n n a a +=-，即()1222n n a a +-=-，所以()12222n n a n a +-=≥-，又因为13a =，24a =，可得1221,22a a -=-=，所以21222a a -=-，所以数列{}2n a -是以1为首项，2为公比的等比数列，所以122n n a --=，所以数列{}n a 的通项公式为122n n a -=+.(2)解：由122n n a -=+，可得()()11111221122222222n n n n nn n n n b a a ----+===-++++， 所以123n n T b b b b =+++⋅⋅⋅+1111111111134466102222322n n n-=-+-+-+⋅⋅⋅+-=-+++，因为1022n >+，所以1113223n -<+，即13n T <，又因为()11322n f n =-+，n *∈N 单调递增， 所以()()111212212n T b ≥==++，所以11123n T ≤<. 12．证明见解析 【详解】证明：212221n n n n -<+，∴135212452246235721n nn n -⨯⨯⨯⋯⨯<⨯⨯⨯⋯⨯+．213521135212421()()()24622462352121n n n n n n n --∴⨯⨯⨯⋯⨯<⨯⨯⨯⋯⨯⨯⨯⨯⋯⨯=++．∴135212462n n -⨯⨯⨯⋯⨯()f x x x -，x ∈当4π，∴cos cos 4x π>∴()10f x x '->()f x x x ∴-在上递增，()(0)0f x f ∴>=x x >，=∴综上：135212462n n -⨯⨯⨯⋯⨯< 13．(1)1n a n =+ ，212n n b +=(2)证明见解析【解析】(1)由题意，数列{}n a 是等差数列，23a =，数列{}n b 是等比数列，18b =，公比3q >， 设{}n a 的公差为d ，由()()23833q d q d d =+⎧⎪⎨=-⋅+⎪⎩可得()()()28333d d d +=-+，∴3d =-或1d =±，33q d =+>，∴1d =，∴4q =可得：()()223211n a a n d n n =+-=+-⨯=+, 11211842n n n n b b q --+==⨯=.(2)()()()()2124443log 2212221111n n n n c n n n n +++==<=++++ 且()()()3112n n n n +>++∴()()()()()21112112n c n n n n n n n <=-+++++∴()()()121111111122323341122n c c c n n n n ++⋅⋅⋅+<-+-+⋅⋅⋅+-<⨯⨯⨯⨯+++，故不等式得证. 14．(1)2(2)证明见解析 【解析】(1)因为()*134N n n n a a n a +=∈+，所以111141n n a a +⎛⎫+=+ ⎪⎝⎭等式两边同时取以a 为底的对数可得111log 1log 1log 4a a a n n a a +⎛⎫⎛⎫+=++⎪ ⎪⎝⎭⎝⎭，()*N n ∈又数列1log 1a n a ⎧⎫⎛⎫⎪⎪+⎨⎬ ⎪⎪⎪⎝⎭⎩⎭是公差为2的等差数列可知log 42a =，即2a =(2)由（1）可知数列11n a ⎧⎫+⎨⎬⎩⎭是公比为4的等比数列，可得11111414n n n a a -⎛⎫+=+= ⎪⎝⎭，可得数列{}n a 的通项公式为()*1N 14n n a n =∈- 记1n n n a b a +=可求得其通项公式为()1*4141N n n n b n +-=∈- 显然{}n b 为正项数列，因此()11*N 5n S S b n ≥==∈另一方面，构造数列{}n c 满足()*N 4n n c b n =-∈可得其通项公式为()*1N 34n n c n =∈- 注意到1113134414n n n n c ---⎛⎫=≤ ⎪⋅+-⎝⎭，记{}n c 的前n 项和为n T ，可得11441314n n T -≤<-， 而由于4n n c b =-，因此()*4N n n T S n n =-∈，从而443n S n <+，综上所述，4543n S n ≤<+.。

裂项相消法求数列Sn
预备知识
•
1.等差数列Sn公式：
Sn
(a1
an) n 2
na1
n(n 1) 2
d
• 2.等比数列Sn公式： S n
a 1 (1 q n ) 1 q
(n为求和项数)
题型：把数列的通项拆成两项之差（即数列的每一项都按此法拆 成两项之差），在求和时一些正负项相互抵消，于是前n项的和变 成首尾若干项之和，这一求和方法称为裂项相消法。 最常见的情况是数列的各项由一个等差数列乘等差数列再取倒数 组成时，求它和可采用错位相减法。
• 例如:
• 步骤如下： （1）将通项公式拆成“正-负”的形式； （2）写出前n项和的表达式； （3）将各式相加，即可转化为有限项的和.
例题：
已Байду номын сангаас数列
an
(2n
1 1) (2n
1)
, 求Sn
课后练习与反思

数列裂项相消法的八大类型
裂项相消法的八大类型：等差型、无理行、指数型、对数型、三角函数型、阶乘和组合数公式型、抽象型、混合型。

裂项相消法是将数列中的每项（通项）分解，然后重新组合，使之能消去一些项，最终达到求和的目的。

比如1/[n(n+1)]=（1/n）-[1/(n+1)]、1/[(2n-1)(2n+1)]=1/2[1/(2n-1)-1/(2n+1)]。

裂项相消法是分解与组合思想在序列求和中的具体应用。

它是将序列中的每一个项（总项）进行分解，然后重新组合，使之剔除一些项，最终达到求和的目的。

一般项分解的倍数关系（分项）。

通常用于代数、分数，有时也用于整数。

这种变形的特点是，原数列的每一项被拆成两项后，中间的大部分项目会相互抵消。

只剩下几项了。

等差数列裂项相消公式等差数列裂项相消公式，这可是数学学习中的一个重要知识点呢！咱先来说说啥是等差数列。

比如说，1，3，5，7，9 这一组数，每两个相邻的数之间的差值都一样，都是 2，这就是等差数列。

那裂项相消公式又是啥呢？咱举个例子，有一个等差数列 1/(1×2) + 1/(2×3) + 1/(3×4) +... + 1/(n×(n + 1)) ，这时候裂项相消公式就派上用场啦。

咱们把每一项拆开，1/(1×2) 可以写成 1 - 1/2 ，1/(2×3) 可以写成 1/2 - 1/3 ，1/(3×4) 可以写成 1/3 - 1/4 ，以此类推。

这样一来，原来的式子就变成了 (1 - 1/2) + (1/2 - 1/3) + (1/3 - 1/4) +... + (1/n - 1/(n + 1)) 。

你瞧，中间的那些项是不是都能消掉？最后就剩下 1 - 1/(n + 1) ，等于 n/(n + 1) 。

还记得我之前教过的一个学生小明吗？刚开始他怎么都搞不明白这个裂项相消公式，那眉头皱得哟，都能夹死一只苍蝇。

我就给他一步一步地拆解，从最基础的等差数列讲起，再到裂项的原理。

我让他自己动手去算几个例子，一开始他总是出错，不是这里漏了一项，就是那里符号搞错了。

但这孩子有股子不服输的劲儿，一直埋头苦算。

后来啊，他终于搞明白了，那高兴的样子，就跟中了大奖似的，还到处跟同学炫耀自己学会了这个厉害的公式。

再来说说这公式在解题中的妙处。

比如有一道题，求数列 1/(2×5) +1/(5×8) + 1/(8×11) +... + 1/((3n - 1)×(3n + 2)) 的前 n 项和。

这时候咱们就可以用裂项相消公式啦，把每一项拆成 1/3 × (1/(2 - 5) - 1/(5 - 8)) 这样的形式，然后再按照前面的方法进行相消，答案很快就能算出来。

高中数学裂项相消法例题【引言】在高中数学的学习过程中，学生们常常会遇到复杂数学题，其中裂项相消法是一种有效的解题方法。

通过这种方法，可以将复杂的数学问题简化，进而提高解题效率。

本文将详细介绍裂项相消法的基本概念、应用步骤，并通过实例进行讲解。

【裂项相消法的基本概念】裂项相消法，顾名思义，就是将一个复杂的项分解成若干个部分，并在计算过程中使部分相互抵消，从而简化问题。

这种方法主要适用于求和、求积、求极值等问题。

它基于一个重要的数学原理：部分之和等于整体。

【裂项相消法的应用步骤】在使用裂项相消法解题时，一般遵循以下步骤：1.观察题目，判断是否适用裂项相消法；2.将复杂项分解成若干个部分；3.分析各部分之间的关系，找出相互抵消的部分；4.进行抵消计算，简化问题；5.根据简化后的式子，求解原问题。

【高中数学裂项相消法例题解析】例题1：求和问题已知数列{an}满足：an = n^2 - 3n + 2，求前n项和。

解：首先，将an分解成部分，得到an = (n - 1)(n - 2)。

接下来，观察前n项和的公式，可以发现相邻两项可以相互抵消。

S_n = a1 + a2 + a3 + ...+ an= (1*2) + (2*3) + (3*4) + ...+ (n*(n+1))= (1*2 + 2*3 + 3*4 + ...+ n*(n+1))将上式中的相邻项进行抵消，得到：S_n = (1*2 - 2*1) + (2*3 - 3*2) + (3*4 - 4*3) + ...+ (n*(n+1) -(n+1)*n)= 1 + 3 + 5 + ...+ (2n-1)最后，根据等差数列求和公式，求得前n项和：S_n = n*(1 + 2n - 1)/2 = n^2例题2：求极值问题求函数f(x) = x^3 - 6x^2 + 9x - 1的极值。

解：首先，将f(x)分解成部分，得到：f(x) = x^3 - 6x^2 + 9x - 1= x^3 - 4x^2 - 2x^2 + 9x - 1接下来，找出相互抵消的部分：f(x) = (x^3 - 4x^2) - (2x^2 - 9x) - 1然后，求解简化后的函数的极值。

差比数列求和裂项相消差比数列是一种数列,其中的每一项都是前两项的差或比。

差比数列的通项公式可以用来求出数列的前几项和。

差比数列求和裂项相消法是一种求差比数列和的方法,它通过将数列的前几项相加,并使用裂项公式求出数列的通项公式,然后使用通项公式求出数列的和。

举个例子,假设我们要求的是以2为公差的等差数列的前5项和。

我们可以将数列的前几项相加,得到：2 + 4 + 6 + 8 + 10 = 30然后使用裂项公式求出数列的通项公式,即：a + (n-1)d = 30其中a是数列的第一项,n是数列的项数,d是数列的公差。

在这个例子中,a=2,n=5,d=2。

将这些值代入公式中得到：2 + (5-1)2 = 30解得：2 + 8 = 3010 = 30显然,这个结果是不正确的,说明我们没有正确地求出数列的通项公式。

总之,差比数列求和裂项相消法是一种求差比数列和的方法,它通过将数列的前几项相加,并使用裂项公式求出数列的通项公式,然后使用通项公式求出数列的通项公式来求出数列的和。

差比数列的通项公式为：S = (a1 + an) * n / 2其中S是数列的和,a1是数列的第一项,an是数列的最后一项,n是数列的项数。

在这个例子中,a1=2,an=10,n=5。

将这些值代入公式中得到：S = (2 + 10) * 5 / 2S = 12 * 5 / 2S = 60 / 2S = 30这样我们就正确地求出了以2为公差的等差数列的前5项和。

总之,差比数列的通项公式是一种有效的求数列和的方法,它可以帮助我们快速求出数列的和,而无需手动求和。

2 + 1 + 2 + 3),
所以 2Tn= 2 + 3 + 2 + 1 − 3-1,
所以 2Tn- +1 = 2 + 3 + 2 + 1 − 3-1- 2 + 1 = 2 + 3 − 3-1,
当 n≥3 时, 2 + 3 − 3-1≥ 2 × 3 + 3 − 3-1=3- 3-1=2- 3>0,
-1
-2
又
2
·…·
1
+1

-1
4
3
·a1=
×
×
×…× 2 × 1 ·a1(n≥2),
-1
-2 -3
(+1)×
(+1)
a1=1,∴an= 2×1 ×1= 2 (n≥2).
又当 n=1 时,a1=1 也符合上式,
(+1)
∴an= 2 .
①
②
1
2
1
1
(2)证明 由(1)知, = (+1)=2 - +1 ,
1 + 3 + 1 + 6 = 20,
则
9×8
91 + 2 = 27(1 + ),
21 + 9 = 20,
1 = 1,
即
解得
181 = 9,
= 2,
所以 an=a1+(n-1)d=1+2(n-1)=2n-1.
(2)证明 bn=
2
+2 +
2( 2+3- 2-1)
4
+1
1
.
4

数列裂项相消法数列是数学中一个重要的概念，它是按照一定的规律排列成一列数的集合。

在数学中，数列不仅仅是一些数的简单排列，它更是我们探索抽象、递推的一个途径，也是一些数学问题解决的基础。

在数学中，数列裂项相消法是一种简便的数学工具，它充分利用数列的性质，将数列通过裂项相消的方式，简化和加速计算过程。

本文将从数列基础认识入手，详细介绍数列裂项相消法的原理和应用，希望能为学生和教师提供一些帮助。

一、数列的基础认识1、数列的定义按照一定规律排列成一列数的集合称为数列。

2、数列的表示形式数列一般表示为a1, a2, a3, ……,an (n为自然数) 或 {an}。

3、数列的通项公式我们可以通过观察数列的规律，利用代数方法推出数列的通项公式，通项公式是数列中每一项的公式。

4、数列的性质数列有许多重要的性质，主要包括公差、公比和递推公式等。

二、裂项相消法的原理数列裂项相消法是一种计算数列的方法，它的基本原理是：利用数列中相邻项的差或比，裂项相消，简化计算过程。

an - a(n-1) = f(n) - f(n-1)a(n-1) - a(n-2) = f(n-1) - f(n-2)……a2 - a1 = f(2) - f(1)如果把所有式子加起来，就可以得到：利用裂项相消法，可以得到：an = （a1 + an）/2 + （n - 1）/2 * d这个公式可以用于计算等差数列的前n项和。

例如，有一个公差为3，首项为1的等差数列，前5项和为？根据上面的公式，可以得到：5 * （1 + 5*3）/2 = 40。

因此，该等差数列的前5项和为40。

an / a(n-1) = q由此可以得到等比数列的求和公式：当q ≠ 1 时：a1 = 1，q = 2，n = 4。

斐波那契数列是一种非常特殊的数列，它的前两项都是1，每一项都是前两项之和。

1,1,2,3,5,8,13,21,34……an = （1/√5）*（（（1+√5）/2）^n -（（1-√5）/2）^n）∑（k=1 to n）a(k) = a(n+2) - 1。

裂项相消法公式求和公式在数学中，求和公式是一个非常基础的概念，它用于将一系列的数值相加，得到它们的总和。

裂项相消法是求和公式的一种常见方法，在这种方法中，我们通过将相邻的项相减，以消去一些项，从而简化求和公式。

本文将详细介绍裂项相消法的公式和使用方法。

裂项相消法公式裂项相消法公式是一个非常重要的求和公式，它可以用来求解一些较为复杂的求和问题。

这个公式的具体形式如下：$$\sum_{i=1}^{n}a_i=\frac{1}{2}\left[\sum_{i=1}^{n}(a_i+a_{n-i+1})-\sum_{i=1}^n(a_i-a_{n-i+1})\right]$$这个公式看起来比较复杂，但实际上它非常简单。

其中，$\sum_{i=1}^{n}a_i$表示从1到n的所有$a_i$的和，而$\sum_{i=1}^{n}(a_i+a_{n-i+1})$和$\sum_{i=1}^{n}(a_i-a_{n-i+1})$分别表示将$a_i$和$a_{n-i+1}$相加和相减后的总和。

根据裂项相消法的原理，这两个总和相减后，可以得到原始的$a_i$的和。

使用裂项相消法求和使用裂项相消法求和的具体方法非常简单，只需要按照公式进行计算即可。

以下是一个具体的例子：$$\sum_{i=1}^{5}i^3$$我们可以使用裂项相消法来计算这个求和式。

首先，我们可以将这个求和式写成两个总和的形式：$$\begin{aligned}\sum_{i=1}^{5}i^3&=\frac{1}{2}\left[\sum_{i =1}^{5}(i^3+(6-i)^3)-\sum_{i=1}^{5}(i^3-(6-i)^3)\right]\\&=\frac{1}{2}\left[\sum_{i=1}^{5}(i^3+(6-i)^3)-\sum_{i=1}^{5}(2i^3-3i^2\times6+3i\times36-2\times6^3)\right]\end{aligned}$$然后，我们可以使用简单的代数运算来计算这两个总和：$$\begin{aligned}&\sum_{i=1}^{5}(i^3+(6-i)^3)=2\times\sum_{i=1}^{5}(i^3+108-18i^2)\\=&2\times(\sum_{i=1}^{5}i^3+540-18\sum_{i=1}^{5}i^2)\\=&2\times(1^3+2^3+3^3+4^3+5^3 +540-18\times(1^2+2^2+3^2+4^2+5^2))\\=&2\times(1+8+27+6 4+125+540-18\times55)\\=&2\times(775)=1550\end{aligned}$$$$\begin{aligned}&\sum_{i=1}^{5}(2i^3-3i^2\times6+3i\times36-2\times6^3)=2\times\sum_{i=1}^{5}(2i^3-18i^2+108i-216)\\=&2\times(2\times1^3-18\times1^2+108\times1-216+2\times2^3-18\times2^2+108\times2-216+2\times3^3-18\times3^2+108\times3-216\\&+2\times4^3-18\times4^2+108\times4-216+2\times5^3-18\times5^2+108\times5-216)\\=&2\times(-740)=-1480\end{aligned}$$然后，我们将这两个总和相减并除以2，即可得到答案：$$\frac{1550-(-1480)}{2}=1515$$因此，$\sum_{i=1}^{5}i^3=1515$。

分数裂项相消法公式一、分数裂项相消法的基本类型及公式。

（一）分母为两个连续自然数相乘的形式。

1. 裂项公式。

- 对于(1)/(n(n + 1))，可以裂项为(1)/(n)-(1)/(n + 1)。

- 例如：(1)/(2×3)=(1)/(2)-(1)/(3)，(1)/(3×4)=(1)/(3)-(1)/(4)等。

2. 证明。

- (1)/(n)-(1)/(n + 1)=(n+1 - n)/(n(n + 1))=(1)/(n(n + 1))。

（二）分母为两个相差d（d为常数）的自然数相乘的形式。

1. 裂项公式。

- 对于(1)/(n(n + d))，可以裂项为(1)/(d)((1)/(n)-(1)/(n + d))。

- 例如：当d = 2时，(1)/(3×5)=(1)/(2)((1)/(3)-(1)/(5))。

2. 证明。

- (1)/(d)((1)/(n)-(1)/(n + d))=(1)/(d)×(n + d - n)/(n(n + d))=(1)/(n(n + d))。

（三）分母为三个连续自然数相乘的形式。

1. 裂项公式。

- 对于(1)/(n(n + 1)(n+2))，可以裂项为(1)/(2)[(1)/(n(n + 1))-(1)/((n + 1)(n+2))]。

- 例如：(1)/(1×2×3)=(1)/(2)((1)/(1×2)-(1)/(2×3))。

2. 证明。

- (1)/(2)[(1)/(n(n + 1))-(1)/((n + 1)(n + 2))]=(1)/(2)×((n + 2)-n)/(n(n +1)(n+2))=(1)/(n(n + 1)(n+2))。

二、分数裂项相消法的应用示例。

（一）求和。

1. 例1：求S=(1)/(1×2)+(1)/(2×3)+(1)/(3×4)+·s+(1)/(99×100)的值。