期末复习题——简谐振动2

高二物理简谐运动练习题1、一简谐振子沿x 轴振动，平衡位置在坐标原点。

0t =时刻振子的位移0.1m x =-；4s 3t =时刻0.1m x =；4s t =时刻0.1m x =。

该振子的振幅和周期可能为A ．0. 1 m ，8s 3B ．0.1 m, 8sC ．0.2 m ，8s 3D ．0.2 m ，8s2、某质点做简谐运动，其位移随时间变化的关系式为x ＝Asin 4t π，则质点（ ）A.第1 s 末与第3 s 末的位移相同B.第1 s 末与第3 s 末的速度相同C.3 s 末至5 s 末的位移方向都相同D.3 s 末至5 s 末的速度方向都相同 3、描述简谐运动特征的公式是x=.自由下落的篮球经地面反弹后上升又落下.若不考虑空气阻力及在地面反弹时的能量损失,此运动（填“是”或“不是”）简谐运动.4、某质点做简谐运动，其位移随时间变化的关系式为x ＝5sin 4t π（cm ），则下列关于质点运动的说法中正确的是 ( )A ．质点做简谐运动的振幅为10cmB ．质点做简谐运动的周期为4sC ．在t = 4 s 时质点的速度最大D ．在t = 4 s 时质点的加速度最大5、在竖直平面内，有根光滑金属杆弯成如图所示形状，相应的曲线方程为y ＝A cos x 。

将一个光滑小环在该金属杆上，并从x ＝0，y ＝A 处以某一初速沿杆向＋x 方向运动，运动过程中 （ ）yA EO B D x CA ．小环在B 点加速度为零 B ．小环在B 点和D 点速度最大C ．小环在C 点速度最大D ．小环在C 点和E 点加速度大小相等、方向相反6、一弹簧振子做简谐运动，周期为T ，下列说法正确的是．( )A ．若t 时刻和(t +△t )时刻振子对平衡位置的位移大小相等，方向相同，则△t 一定等于T 的整数倍B ．若t 时刻和(t +△t )时刻振子运动速度大小相等，方向相反，则△t 一定等于2T的整数倍 C ．若△t =4T，则t 和(t +△t )两时刻，振子的位移大小之和一定等于振幅 D ．若△t ＝2T，则在t 时刻和(t +△t )时刻振子速度的大小一定相等7、水平弹簧振子做简谐运动的周期为T ，振子在t 1时刻的动量为p 、动能为q ，下列说法正确的是 （ ）A ．如果振子在t 2时刻的动量也为p ，则（t 2－t 1）的最小值为TB ．如果振子在t 2时刻的动能也为q ，则（t 2－t 1）的最小值为TC ．在半个周期的时间内，弹簧的弹力的冲量一定为零D ．在半个周期的时间内，弹簧的弹力的功一定为零8、如图所示，一个弹簧振子在A 、B 两点间做简谐运动，O 点为平衡位置，下列说法中正确．．的有( )A ．它在A 、B 两点时动能为零B ．它经过O 点时加速度方向要发生变化C ．它远离O 点时作匀减速运动D ．它所受回复力的方向总跟它偏离平衡位置的位移方向相反9、光滑的水平面上放有质量分别为m 和m 21的两木块，下方木块与一劲度系数为k 的弹簧相连，弹簧的另一端固定在墙上，如图所示。

高考物理专题复习：简谐运动一、单选题1．如图甲所示，弹簧振子以O点为平衡位置，在A、B两点之间做简谐运动，取向右为正方向，振子的位移x随时间t的变化如图乙所示，下列说法正确的是（）A．t=0.2 s时，振子在O点右侧6 cm处B．t=0.6 s和t=1.4 s时，振子的速度完全相同C．t=0.8 s时，振子的速度方向向左D．t=0.4 s到t=0.8 s的时间内，振子的位移和速度都逐渐减小2．振动物体偏离平衡位置后，所受到的使它回到平衡位置的力，叫回复力，关于简谐运动的回复力，下列说法正确的是（）A．可以是恒力B．可以是方向不变而大小变化的力C．可以是大小不变而方向变化的力D．一定是变力3．一个质点做简谐运动，它的振动图像如图中的曲线部分所示，则（）A．有向线段OA是质点在t1时刻的位移B．有向线段OA在t轴上的投影是质点在t1时刻的位移C．有向线段OA在x轴上的投影是质点在t1时刻的位移D．有向线段OA的斜率是质点在t1时刻的瞬时速率4．下列有关简谐运动的说法中正确的是（）A．振子振动过程中位移不变B．经过一个周期振子完成一次全振动C．一分钟内完成全振动的次数，叫简谐运动的频率D．从某位置出发，到下次经过该位置就完成一次全振动5．如图所示，表示一物体做简谐运动的位移与时间关系图像，关于物体的速度、位移、加速度和能量等，下列说法正确的是（）A．0.2至0.3秒时间内，位移增大速度减小B．0.2至0.3秒时间内，速度减小加速度减小C．0.3至0.4秒时间内，位移与速度方向相同D．0.3至0.4秒时间内，势能增加动能减少6．如图是一物体振动的位移-时间图像，下列说法正确的是（）A．振幅是6cmB．周期是0.2sC．频率是0.4HzD．初相是π rad7．关于简谐运动，下列说法正确的是（）A．物体在一个位置附近的往复运动称为简谐运动B．由于做简谐运动的物体受回复力作用，所以简谐运动一定是受迫振动C．如果物体的位移与时间关系图像是一条余弦曲线，则物体做的是简谐运动D．如果物体的位移与时间关系图像是一条正弦曲线，则物体做的可能不是简谐运动8．一个质点以O为中心做简谐运动，位移随时间变化的图象如图所示．a、b、c、d表示质点在不同时刻的相应位置，且b、d关于平衡位置对称，则下列说法正确的是（）A ．质点做简谐运动的方程为sin2x A t π=B ．质点在位置b 与位置d 时相对平衡位置的位移大小相等，方向相同C ．质点在位置b 与位置d 时速度大小相等，方向相同D ．质点从位置a 运动到b 和从位置b 运动到c 的过程中平均速度相同 二、多选题9．某质点做简谐运动，其位移随时间变化的关系式为x =A sin 4πt ，则该质点（ ） A ．第1s 末与第2s 末的位移相同 B ．第1s 末与第3s 末的速度方向相反 C ．3s 末至5s 末的位移方向都相反 D ．3s 末至5s 末的速度方向都相同 E.3s 末至5s 末的速度方向都相反10．如图，轻弹簧上端固定，下端连接一小物块，物块沿竖直方向做简谐运动。

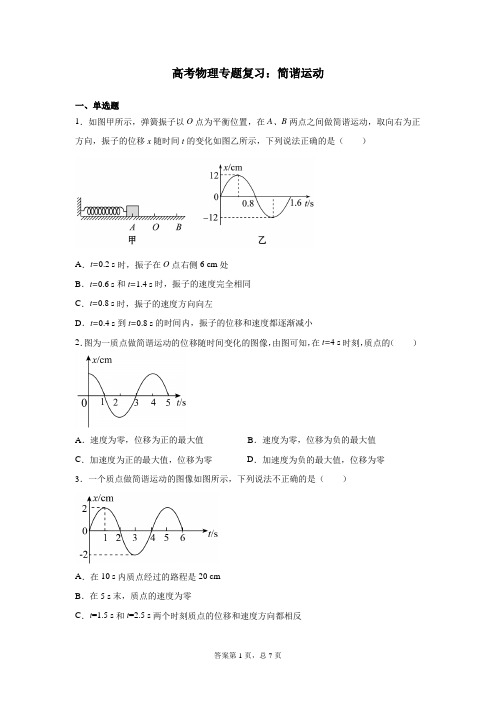
高考物理专题复习：简谐运动一、单选题1．如图甲所示，弹簧振子以O点为平衡位置，在A、B两点之间做简谐运动，取向右为正方向，振子的位移x随时间t的变化如图乙所示，下列说法正确的是（）A．t=0.2 s时，振子在O点右侧6 cm处B．t=0.6 s和t=1.4 s时，振子的速度完全相同C．t=0.8 s时，振子的速度方向向左D．t=0.4 s到t=0.8 s的时间内，振子的位移和速度都逐渐减小2．图为一质点做简谐运动的位移随时间变化的图像，由图可知，在t=4 s时刻，质点的（）A．速度为零，位移为正的最大值B．速度为零，位移为负的最大值C．加速度为正的最大值，位移为零D．加速度为负的最大值，位移为零3．一个质点做简谐运动的图像如图所示，下列说法不正确的是（）A．在10 s内质点经过的路程是20 cmB．在5 s末，质点的速度为零C．t=1.5 s和t=2.5 s两个时刻质点的位移和速度方向都相反D ．t =1.5 s 和t =4.5 s cm4．某弹簧振子沿x 轴的简谐运动图像如图所示，下列描述正确的是（ ）A ．1s t =时，振子的速度为零B ．2s t =时，振子的速度为负，但不是最大值C ．3s t =时，振子的速度为负的最大值D ．4s t =时，振子的速度为正，但不是最大值 5．如图所示，弹簧振子在M 、N 之间做简谐运动。

以平衡位置O 为原点，建立Ox 轴，向右为x 轴正方向。

若振子位于N 点时开始计时，则其振动图像为（ ）A ．B ．C ．D ．6．一做简谐运动的弹簧振子，其质量为m ，最大速率为v 0。

若从某时刻算起，在半个周期内，合外力（ ） A ．做功一定为0 B ．做功一定不为0C ．做功一定是12mv 02D ．做功可能是0到12mv 02之间的某一个值7．如图所示，物体A 置于物体B 上，一轻质弹簧一端固定，另一端与B 相连，在弹性限度范围内，A 和B 一起在光滑水平面上做往复运动（不计空气阻力），两者保持相对静止。

简谐振动训练一、单选题1．一简谐运动的振动图像如图所示，下列说法正确的是（ ）A ．质点在0和0.8s 时刻具有正向的最大速度B ．质点在0.2s 时刻具有负向的最大加速度C ．在0~0.4s 内，质点的加速度方向始终指向x 轴负方向D ．在0.2s~0.4s 内，质点的加速度方向和速度方向相同2．如图所示是一单摆做阻尼振动的x t -图像，则此单摆的摆球在图中P 与N 时刻的（ ）A ．速率P N V V >B ．重力势能PP PN E E <C ．机械能P N E E <D ．受到的拉力P N F F =3．惠更斯利用单摆的等时性原理制成了第一座摆钟。

如图甲所示为日常生活中我们能见到的一种摆钟，图乙为摆钟的结构示意图，圆盘固定在摆杆上，螺母可以沿摆杆上下移动，摆钟的摆动可看作是单摆，下列说法正确的是（ ）A ．在山脚走时准的摆钟，在山顶仍能走准B ．若将摆钟的摆角由3°增加到5°（不计空气阻力），单摆的周期减小C ．走时准确的摆钟，调节螺母向下移动，摆钟仍能走准D ．将摆钟由赤道移到北极，单摆振动周期减小4．在飞机的发展史中，工程师们为了解决飞机飞上天空后抖动厉害的问题，创造性地在飞机机翼前缘处安装一个配重杆。

在飞机机翼前缘处安装配重杆的主要目的是（ ）A ．改变机翼的固有频率B ．加大飞机的惯性C ．使机翼更加牢固D ．使机体更加平衡5．物体做简谐运动，振幅为0.8cm ，周期为0.5s ，计时开始时具有负向最大加速度，它的位移公式是（ ） A ．3m sin 810(4)2x t ππ-=⨯+ B ．3810sin(2)m 2x t ππ-=⨯+ C ．3410sin(4)m 2x t ππ-=⨯- D ．3410sin(2)m 2x t ππ-=⨯-6．放在光滑水平面上的弹簧振子作简谐振动，振子的质量为m ，振子运动中的最大速度为v 。

以下说法中不正确的是（ ）A ．从某时刻算起，在14周期内弹力做的功可能为零 B ．从某时刻算起，在14周期内弹力做的功可能为零到212mv 之间的某一个值 C ．从某时刻算起，在12周期内弹力的冲量一定为零 D ．从某时刻算起，在14周期内弹力的冲量可能是0到mv 之间的某一个值 7．如图所示是用来测量各种发动机转速的转速计原理图。

机械振动期末考试题及答案一、选择题（每题2分，共20分）1. 简谐振动的周期与振幅无关，这是由哪个定律决定的？A. 牛顿第二定律B. 牛顿第三定律C. 胡克定律D. 能量守恒定律答案：C2. 下列哪个不是阻尼振动的特点？A. 振幅逐渐减小B. 频率逐渐增大C. 能量逐渐减少D. 振幅随时间呈指数衰减答案：B3. 一个物体做自由振动，若其振幅逐渐减小，这表明振动受到了：A. 阻尼B. 共振C. 强迫振动D. 非线性振动答案：A4. 质点的振动方程为 \( y = A \sin(\omega t + \phi) \)，其中\( \omega \) 表示：A. 振幅B. 频率C. 角频率D. 相位答案：C5. 弹簧振子的振动周期与下列哪个参数无关？A. 弹簧的劲度系数B. 振子的质量C. 振子的振幅D. 振子的初始相位答案：C6. 阻尼振动的振幅随时间呈指数衰减，其衰减速率与什么有关？A. 振幅大小B. 阻尼系数C. 振动频率D. 振动周期答案：B7. 以下哪个不是振动系统的自由度？A. 1B. 2C. 3D. 无穷大答案：D8. 共振现象发生在以下哪种情况下？A. 系统固有频率等于外部激励频率B. 系统阻尼系数最大C. 系统振幅最小D. 系统能量最大答案：A9. 以下哪个是简谐振动的特有现象？A. 振幅不变B. 频率不变C. 能量不变D. 周期不变答案：A10. 一个物体在水平面上做简谐振动，其振动能量主要由以下哪两个因素决定？A. 振幅和频率B. 振幅和阻尼系数C. 阻尼系数和频率D. 振幅和劲度系数答案：A二、填空题（每空2分，共20分）11. 简谐振动的周期公式为 \( T = \frac{2\pi}{\omega} \)，其中\( \omega \) 为________。

答案：角频率12. 当外部激励频率接近系统的________时，系统将产生共振现象。

答案：固有频率13. 阻尼振动的振幅随时间的变化规律可表示为 \( A(t) = A_0 e^{-\beta t} \)，其中 \( \beta \) 为________。

高中物理简谐运动试题及答案一、选择题1. 一个质点做简谐运动，其振动方程为x=Asin(ωt+φ)，其中A=0.2m，ω=2πrad/s，φ=π/3。

则该质点振动的周期为（）。

A. 0.5sB. 1sC. 2sD. 5s答案：B解析：根据振动方程x=Asin(ωt+φ)，周期T=2π/ω，代入ω=2πrad/s，可得T=2π/(2π)=1s。

2. 一个弹簧振子做简谐运动，其振幅为0.1m，周期为2s。

则该振子振动的角频率为（）。

A. π/2 rad/sB. π rad/sC. 2π rad/sD. 4π rad/s答案：B解析：根据周期T=2π/ω，代入T=2s，可得ω=2π/T=2π/2=πrad/s。

3. 一个质点做简谐运动，其振动方程为x=Asin(ωt+φ)，其中A=0.2m，ω=2πrad/s，φ=π/3。

则该质点振动的最大加速度为（）。

A. 0.4π m/s²B. 0.8π m/s²C. 1.6π m/s²D. 3.2π m/s²答案：C解析：根据简谐运动的加速度公式a=-Aω²sin(ωt+φ)，当sin(ωt+φ)=1时，a取最大值，即a_max=Aω²。

代入A=0.2m，ω=2πrad/s，可得a_max=0.2×(2π)²=1.6π m/s²。

4. 一个弹簧振子做简谐运动，其振幅为0.1m，周期为2s。

则该振子振动的最大速度为（）。

A. 0.1π m/sB. 0.2π m/sC. 0.4π m/sD. 0.8π m/s答案：C解析：根据简谐运动的速度公式v=Aωsin(ωt+φ)，当sin(ωt+φ)=1时，v取最大值，即v_max=Aω。

代入A=0.1m，ω=π rad/s，可得v_max=0.1×π=0.4π m/s。

二、填空题5. 一个质点做简谐运动，其振动方程为x=Asin(ωt+φ)，其中A=0.2m，ω=2πrad/s，φ=π/3。

机械振动期末试题及答案1. 选择题1.1 哪种情况下，系统的振动是简谐振动？A. 有耗尽能量的情况B. 存在非线性的力恢复系统中C. 无外部干扰D. 系统的振幅随时间而增长答案：C1.2 振动系统达到稳态的条件是：A. 初始位移为零B. 扰动力为零C. 初始速度为零D. 振幅随时间减小答案：B1.3 一个简谐振动的周期与振幅的关系是：A. 周期与振幅无关B. 周期与振幅成正比C. 周期与振幅成反比D. 周期与振幅正弦相关答案：A2. 判断题2.1 简谐振动的周期和角频率之间满足正比关系。

A. 对B. 错答案：B2.2 简谐振动的中心力是恒力。

A. 对B. 错答案：A2.3 当振动系统有阻尼情况时，振幅会随时间增大。

A. 对B. 错答案：B3. 简答题3.1 什么是简谐振动？它的特点是什么？答案：简谐振动是指振动系统在没有外力干扰的情况下，其平衡位置附近以某一频率固定幅度上下振动的现象。

它的特点包括振动周期与振幅无关，且系统的振动可由正弦或余弦函数进行描述。

3.2 请简要说明受迫振动的原理。

答案：受迫振动是指振动系统在外力作用下的振动。

外力的频率与系统的固有频率相近或相等时，会发生共振现象。

在共振时，外力的能量会以最大幅度传递给振动系统，导致振动幅度增大。

4. 计算题4.1 一个弹簧振子平衡位置附近的势能函数为U(x) = 4x^2 + 3，求振子的振动周期。

答案：根据简谐振动的势能函数表达式，势能函数为U(x) =1/2kx^2，其中k为弹簧的劲度系数。

将已知的势能函数与标准表达式进行比较，可得4x^2 = 1/2kx^2，解得k = 8。

由振动周期公式T =2π√(m/k)，代入m和k的值，可计算出振子的振动周期。

5. 算法题设计一个程序，计算一个简谐振动系统的振动频率和振幅，并将结果打印输出。

// 输入参数float k; // 弹簧的劲度系数float m; // 系统的质量// 计算振动频率float omega = sqrt(k / m);// 计算振幅float A = 1; // 假设振幅为1// 打印输出结果print("振动频率：", omega);print("振幅：", A);经过以上计算，我们可以得到一个简谐振动系统的振动频率和振幅。

简谐振动一、基本要求1、掌握简谐振动的定义，描述简谐振动的各物理量及其相互关系，会根据定义来判断一各物体的运动是不是简谐振动。

2、掌握简谐振动的旋转矢量表示法。

3、掌握简谐振动的基本特征，能根据一定的初始条件写出简谐振动的运动方程。

4、掌握同方向频率的两个简谐振动的合成，了解相互垂直同频率的简谐振动的合成。

二、主要内容1、简谐振动的表达式（运动方程） cos()x A t ωϕ=+三个特征量：振幅A ，决定与振动的能量；角频率ω，决定于振动系统的固有属性； 初相位ϕ，决定于振动系统初始时刻的状态。

简谐运动可以用旋转矢量来表示。

2、振动的相位：()t ωϕ+两个振动的相差：同相2k ϕπ∆=，反相(21)k ϕπ∆=+3、简谐振动的运动微粉方程：2220d x x dtω+=4、简谐振动的实例弹簧振子：220,2d x k x T dt m π+==单摆小角度振动：220,2d g T dt l θθ+==LC振荡：2210,2d q q T dt LCπ+== 5、简谐振动的能量：222111()222k P dx E E E m kx kA dt =+=+= 6、两个简谐振动的能量（1）同方向同频率的简谐振动的合成合振动是简谐振动，合振动的振幅和初相位由下式决定A =11221122sin sin tan cos cos A A A A ϕϕϕϕϕ+=+（2）相互垂直的两个同频率的简谐振动的合成合运动的轨迹一般为椭圆，其具体形状决定于两个分振动的相差和振幅。

当2k ϕπ∆=或(21)k π+时，合运动的轨迹为直线，这时质点在做简谐振动。

三、习题与解答1、两个质点各自作简谐振动，它们的振幅相同、周期相同。

第一个质点的振动方程为)cos(1ϕω+=t A x 。

某时刻当第一个质点正在平衡位置向负方向运动时，第二个质点正在最大位移处。

则第二个质点的振动方程为：（ B ）（A ）)2cos(2πϕω++=t A x （B ）)2cos(2πϕω-+=t A x（C ）)23cos(2πϕω-+=t A x （D ）)cos(2πϕω++=t A x 2、一物体做简谐振动，振幅为A ，在起始时刻质点的位移为2A-且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为：（ D ）3、一质点作简谐振动，振动方程)cos(ϕω+=t A x ，当时间 t =T/4 时，质点的速度为：( C )（A ） ϕωsin A - (B) ϕωsin A （C ）ϕωcos A - （D ）ϕωcos A4、一质点作谐振动，周期为T ，当它由平衡位置向 x 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为（ A ）（A ）T /6（B ）T /12 （C）T /4 （D ）T /85、有两个沿x 轴做简谐运动的质点，其频率、振幅皆相同，当第一个质点自平衡位置向负方向运动时，第二个质点在处（A 为振幅）也向负方向运动，则两者的相位差（12ϕϕ-）为：（ C ）2Ax -=（A ）2π （B ）32π （C ）6π （D ）65π6、质量为10×10－3 kg 的小球与轻弹簧组成的系统，按20.1cos(8)3x t ππ=+(SI)的规律做谐振动，求：(1)振动的周期、振幅、初位相及速度与加速度的最大值；(2)最大的回复力、振动能量、平均动能和平均势能，在哪些位置上动能与势能相等？ (3)t 2＝5 s 与t 1＝1 s 两个时刻的位相差. 解：(1)设谐振动的标准方程为)cos(0φω+=t A x ，则知：3/2,s 412,8,m 1.00πφωππω===∴==T A 又 πω8.0==A v m 1s m -⋅ 51.2=1s m -⋅2.632==A a m ω2s m -⋅(2) N 63.0==ma F mJ 1016.32122-⨯==m mv E J 1058.1212-⨯===E E E k p当p k E E =时，有p E E 2=， 即)21(212122kA kx ⋅= ∴ m 20222±=±=A x (3) ππωφ32)15(8)(12=-=-=∆t t7、一个沿x 轴做简谐振动的弹簧振子，振幅为A ，周期为T ，其振动方程用余弦函数表出.如果t ＝0时质点的状态分别是：(1)x 0＝－A ；(2)过平衡位置向正向运动；(3)过2Ax =处向负向运动； (4)过x =处向正向运动.试求出相应的初位相，并写出振动方程.解：因为 ⎩⎨⎧-==000sin cos ϕωϕA v A x将以上初值条件代入上式，使两式同时成立之值即为该条件下的初位相．故有)2cos(1πππϕ+==t T A x)232cos(232πππϕ+==t T A x)32cos(33πππϕ+==t T A x)452cos(454πππϕ+==t T A x8、一质量为10×10－3 kg 的物体做谐振动，振幅为24 cm ，周期为4.0 s ，当t ＝0时位移为＋24 cm.求：(1)t ＝0.5 s 时，物体所在的位置及此时所受力的大小和方向； (2)由起始位置运动到x ＝12 cm 处所需的最短时间； (3)在x ＝12 cm 处物体的总能量. 解：由题已知 s 0.4,m 10242=⨯=-T A ∴ 1s rad 5.02-⋅==ππωT又，0=t 时，0,00=∴+=ϕA x 故振动方程为m )5.0cos(10242t x π-⨯=(1)将s 5.0=t 代入得0.17m m )5.0cos(102425.0=⨯=-t x πN102.417.0)2(10103232--⨯-=⨯⨯⨯-=-=-=πωxm ma F方向指向坐标原点，即沿x 轴负向． (2)由题知，0=t 时，00=ϕ，t t =时 3,0,20πϕ=<+=t v A x 故且 ∴ s 322/3==∆=ππωϕt (3)由于谐振动中能量守恒，故在任一位置处或任一时刻的系统的总能量均为J101.7)24.0()2(10102121214223222--⨯=⨯⨯⨯===πωA m kA E9、有一轻弹簧，下面悬挂质量为1.0 g 的物体时，伸长为4.9 cm.用这个弹簧和一个质量为8.0 g 的小球构成弹簧振子，将小球由平衡位置向下拉开1.0 cm 后，给予向上的初速度v 0＝5.0 cm·s －1，求振动周期和振动表达式. 解：由题知12311m N 2.0109.48.9100.1---⋅=⨯⨯⨯==x g m k 而0=t 时，-12020s m 100.5m,100.1⋅⨯=⨯-=--v x ( 设向上为正)又 s 26.12,51082.03===⨯==-ωπωT m k 即 m102)5100.5()100.1()(22222220---⨯=⨯+⨯=+=∴ωv x A45,15100.1100.5tan 022000πφωϕ==⨯⨯⨯=-=--即x v ∴ m )455cos(1022π+⨯=-t x10、图为两个谐振动的x －t 曲线，试分别写出其谐振动方程.题10图解：由题10图(a)，∵0=t 时，s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ 即 1s rad 2-⋅==ππωT故 m )23cos(1.0ππ+=t x a 由题10图(b)∵0=t 时，35,0,2000πϕ=∴>=v A x 01=t 时，35,0,2000πϕ=∴>=v A x又 ππωϕ253511=+⨯=∴ πω65=故 m t x b )3565cos(1.0ππ+=11、有两个同方向、同频率的简谐振动，其合成振动的振幅为0.20 m ，位相与第一振动的位相差为6π，已知第一振动的振幅为0.173 m ，求第二个振动的振幅以及第一、第二两振动的位相差.解：由题意可做出旋转矢量图如下． 由图知01.02/32.0173.02)2.0()173.0(30cos 222122122=⨯⨯⨯-+=︒-+=A A A A A ∴ m 1.02=A 设角θ为O AA 1，则θcos 22122212A A A A A -+=即 01.0173.02)02.0()1.0()173.0(2cos 2222122221=⨯⨯-+=-+=A A A A A θ 即2πθ=，这说明，1A 与2A 间夹角为2π，即二振动的位相差为2π.12、试用最简单的方法求出下列两组谐振动合成后所得合振动的振幅：(1)125cos(3),375cos(3);3x t cm x t cm ππ⎧=+⎪⎪⎨⎪=+⎪⎩(2)125cos(3),345cos(3).3x t cm x t cm ππ⎧=+⎪⎪⎨⎪=+⎪⎩解： (1)∵ ,233712πππϕϕϕ=-=-=∆ ∴合振幅 cm 1021=+=A A A (2)∵ ,334πππϕ=-=∆∴合振幅 0=A13、一质点同时参与两个在同一直线上的简谐振动，振动方程为120.4cos(2),650.3cos(2).6x t m x t m ππ⎧=+⎪⎪⎨⎪=-⎪⎩试分别用旋转矢量法和振动合成法求合振动的振幅和初相，并写出谐振动方程. 解：∵ πππϕ=--=∆)65(6 ∴ m 1.021=-=A A A 合3365cos 3.06cos 4.065sin3.06sin4.0cos cos sin sin tan 22122211=+-⨯=++=ππππϕϕϕϕφA A A A ∴ 6πϕ=其振动方程为m )62cos(1.0π+=t x14、若简谐运动方程为0.10cos(200.25)()x t m ππ=+，求：（1）振幅、频率、角频率、周期和初相；（2）2t s =时的位移、速度和加速度。