北京2020高考理科数学总复习空间中的平行与垂直学生版
- 格式:docx
- 大小:362.54 KB
- 文档页数:9

规范答题示例2 空间中的平行与垂直典例2 (14分)如图,四棱锥P —ABCD 的底面为正方形,侧面PAD ⊥底面ABCD ,PA ⊥AD ,E ,F ,H 分别为AB ,PC ,BC 的中点.(1)求证:EF ∥平面PAD ; (2)求证:平面PAH ⊥平面DEF .审题路线图 (1)条件中各线段的中点――→设法利用中位线定理取PD 的中点M ――→考虑平行关系长度关系 平行四边形AEFM ―→AM ∥EF ――→线面平行的判定定理EF ∥平面PAD (2)平面PAD ⊥平面ABCDPA ⊥AD―――→面面垂直的性质PA ⊥平面ABCD ―→PA ⊥DE ――――――――→正方形ABCD 中E ,H 为AB ,BC 中点DE ⊥AH ――――→线面垂直的判定定理DE ⊥平面PAH ――――→面面垂直的判定定理平面PAH ⊥平面DEF规 范 解 答·分 步 得 分构 建 答 题 模 板证明 (1)取PD 的中点M ,连结FM ,AM .∵在△PCD 中,F ,M 分别为PC ,PD 的中点,∴FM ∥CD 且FM =12CD .∵在正方形ABCD 中,AE ∥CD 且AE =12CD ,∴AE ∥FM 且AE =FM , ∴四边形AEFM 为平行四边形, ∴AM ∥EF ,4分∵EF ⊄平面PAD ,AM ⊂平面PAD , ∴EF ∥平面PAD .7分(2)∵侧面PAD ⊥底面ABCD ,PA ⊥AD , 侧面PAD ∩底面ABCD =AD ,PA ⊂平面PAD , ∴PA ⊥底面ABCD ,∵DE ⊂底面ABCD ,∴DE ⊥PA . ∵E ,H 分别为正方形ABCD 边AB ,BC 的中点, ∴Rt△ABH ≌Rt△DAE ,则∠BAH =∠ADE ,∴∠BAH +∠AED =90°,∴DE ⊥AH ,10分∵PA ⊂平面PAH ,AH ⊂平面PAH ,PA ∩AH =A ,∴DE ⊥平面PAH , ∵DE ⊂平面EFD ,∴平面PAH ⊥平面DEF .14分 第一步找线线:通过三角形或四边形的中位线、平行四边形、等腰三角形的中线或线面、面面关系的性质寻找线线平行或线线垂直. 第二步找线面:通过线线垂直或平行,利用判定定理,找线面垂直或平行;也可由面面关系的性质找线面垂直或平行. 第三步找面面:通过面面关系的判定定理,寻找面面垂直或平行. 第四步写步骤:严格按照定理中的条件规范书写解题步骤.评分细则 (1)第(1)问证出AE ∥FM 且AE =FM 给2分;通过AM ∥EF 证线面平行时,缺1个条件扣1分;利用面面平行证明EF ∥平面PAD 同样给分;(2)第(2)问证明PA ⊥底面ABCD 时缺少条件扣1分;证明DE ⊥AH 时只要指明E ,H 分别为正方形边AB ,BC 的中点得DE ⊥AH 不扣分;证明DE ⊥平面PAH 只要写出DE ⊥AH ,DE ⊥PA ,缺少条件不扣分.跟踪演练2 (2018·江苏南京外国语学校模拟)如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1,点M,N分别为A1B和B1C1的中点.(1)求证:MN∥平面A1ACC1;(2)求证:平面A1BC⊥平面MAC.证明(1)连结B1M,AC1,在三棱柱ABC-A1B1C1中,AA1∥BB1,AA1=BB1,所以四边形ABB1A1为平行四边形,因为M为A1B的中点,所以M为AB1的中点.又因为N为B1C1的中点,所以MN∥AC1.因为AC1⊂平面A1ACC1,MN⊄平面A1ACC1,所以MN∥平面A1ACC1.(2)因为AB=AA1,点M为A1B的中点,所以AM⊥A1B.在直三棱柱ABC-A1B1C1中,AA1⊥平面ABC,因为AC⊂平面ABC,所以AA1⊥AC.因为∠BAC=90°,即AB⊥AC,又AB∩AA1=A,AB,AA1⊂平面ABB1A1,所以AC⊥平面ABB1A1,因为A1B⊂平面ABB1A1,所以AC⊥A1B.因为AM∩AC=A,AM,AC⊂平面MAC,所以A1B⊥平面MAC,因为A1B⊂平面A1BC,所以平面A1BC⊥平面MAC.。


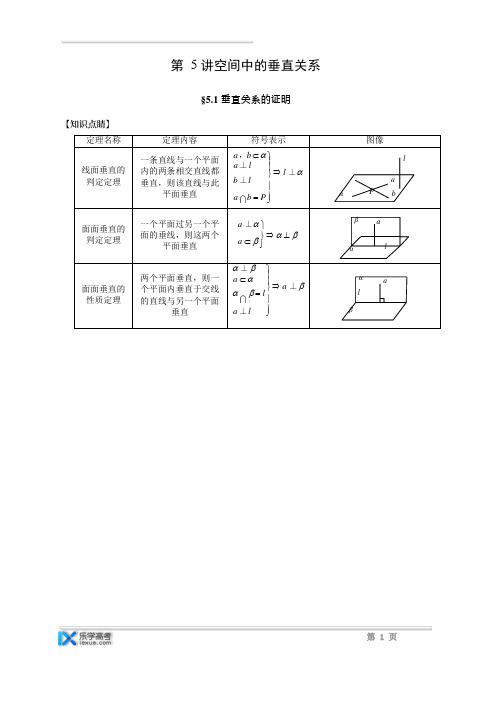
第 5 讲空间中的垂直关系§5.1 垂直关系的证明定理名称定理内容符号表示图像线面垂直的判定定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直a ,b ⊂α⎫a ⊥l ⎪ ⎪⇒ l ⊥αb ⊥l⎬⎪a b =P ⎪⎭laαP b面面垂直的判定定理一个平面过另一个平面的垂线,则这两个平面垂直a ⊥α⎫a ⊂β⎬⇒ α⊥β⎭βaαl面面垂直的性质定理两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直α⊥β⎫a ⊂α⎪ ⎪⇒ a ⊥βαβ=l ⎬⎪a ⊥l ⎪⎭αalβB【例1】 A -BCDE AB ⊥BCDEABC DE ⊥AEAEC D【例2】2019ABCD -A1B1C1D1ABCD E AA1BE ⊥EC1BE ⊥ EB1C1.【例3】2018 P -ABCD ABCD PAD ⊥ ABCD PA ⊥PD PA =PD E F AD PBPE ⊥BCPAB ⊥PCDCD ⊥【例4】2019 P -ABCD ABCD∆PCDPAC ⊥ PCD PA ⊥CD PA ⊥ PCD【例5】AB ⊥BC SA ⊥ABC AM ⊥SB AN ⊥SCSSC ⊥MNCABNM【例6】2019 ABCD ABC AC ⊥BCABC E BDDA ⊥【例7】2019A1A =A1C =AC E, FABC -A1B1C1AC, A1B1A1A CC1⊥ABCEF ⊥BC∠ABC = 90︒【例8】2019 P -ABCD ABCD AD / /BC AB ⊥AD AD = 2AB = 2BC = 2∆PCD PC ⊥AC E PAAC ⊥BE .AE BC【习题1】2018 ABCD E, F AD, BC DF ABFD .C P PF ⊥BF PEF ⊥【习题2】2018 2 ABCD CDC D AMD ⊥BMC∆DFCM CDE CD【习题3】2019 P -ABCDPAC∠ABC = 60︒PAB ⊥PAEPA ⊥ABCD ABCD【习题4】2019 ABC -EFG ABC ⊥BCGF CB = 2GF BF =CF AB ⊥CG .BD ⊥OB1D【习题5】P △ABC PO ⊥ABC O PA ⊥BCAOP PC ⊥ABPPB ⊥ACA CB【习题6】在长方体ABCD -A1B1C1D1 中,点E, F 分别在AA1, CC1 上,且B1E ⊥A1B ,B1F ⊥BC1 ,求证:BD1⊥面B1EF .D1 C1A1FE CABC ⊥。


北京2020高考理科数学总复习空间中的平行与垂直学生版题型一空间位置关系的判断
【题型要点】
(1)解决空间线面位置关系的判断问题常有以下方法:①根据空间线面垂直、平行关系的判定定理和性质定理逐项判断来解决问题;②必要时可以借助空间几何模型,如从长方体、四面体等模型中观察线面位置关系,并结合有关定理来进行判断.
(2)熟练掌握立体几何的三种语言——符号语言、文字语言以及图形语言的相互转换,是解决此类问题的关键.
【例1】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是()
【例2】.如图,平面α⊥平面β,α∩β=直线l, A,C是α内不同的两点,B,D是β内不同的两点,
且A,B,C,D∉直线l, M,N分别是线段AB,CD的中点.下列判断正确的是()
A.当CD=2AB时,M,N两点不可能重合
B.M,N两点可能重合,但此时直线AC与l不可能相交
C.当AB与CD相交,直线AC平行于l时,直线BD可以与l相交
D.当AB,CD是异面直线时,直线MN可能与l平行
题组训练一空间位置关系的判断
1.设四棱锥P-ABCD的底面不是平行四边形,用平面α去截此四棱锥,使得截面四边形是平行四边形,则这样的平面α()
A.有无数多个B.恰有4个
C.只有1个D.不存在
2.已知m,l是直线,α,β是平面,给出下列命题:
①若l垂直于α,则l垂直于α内的所有直线
②若l平行于α,则l平行于α内的所有直线
③若l⊂β,且l⊥α,则α⊥β
④若m⊂α,l⊂β,且α∥β,则m∥l
其中正确的命题的个数是()
A.4B.3C.2D.1
题型二平行与垂直的证明与体积
【题型要点】
(1)平行关系及垂直关系的转化
空间平行、垂直关系证明的主要思想是转化,即通过判定、性质定理将线线、线面、面面之间的平行、垂直关系相互转化.
(2)数学思想
①本例在证明线线垂直、线面平行时,采用了转化与化归思想.
②利用转化与化归思想还可以解决本专题中的线面其他位置关系.
(3)求解多面体的体积问题,如最值问题、高的问题、点面距离的问题,一般利用公式法、等体积法、
割补法、函数与方程的思想求解.
【例2】如图,四棱锥P -ABCD 中,侧面P AD 为等边三角形且垂直于底面ABCD ,AB =BC =1
2AD ,
∠BAD =∠ABC =90°.
(1)证明:直线BC ∥平面P AD ;
(2)若△P AD 面积为27,求四棱锥P -ABCD 的体积.
题组训练二 平行与垂直的证明与体积
如图,平面ABCD ⊥平面ADEF ,四边形ABCD 为菱形,四边形ADEF 为矩形, M ,N 分别是EF ,BC 的中点, AB =2AF , ∠CBA =60°.
①求证: DM ⊥平面MNA ;
②若三棱锥A -DMN 的体积为3
3
,求MN 的长.
题型三 空间几何中的翻折问题
【题型要点】
翻折问题的注意事项
1.画好两图:翻折之前的平面图形与翻折之后形成的几何体的直观图.
2.把握关系:即比较翻折前后的图形,准确把握平面图形翻折前后的线线关系,哪些平行与垂直的关系不变,哪些平行与垂直的关系发生变化,这是准确把握几何体结构特征,进行空间线面关系逻辑推理的基础.
3.准确定量:即根据平面图形翻折的要求,把平面图形中的相关数量转化为空间几何体的数学特征,这是准确进行计算的基础.
【例3】已知长方形ABCD中,AD=2,AB=2,E为AB的中点.将△ADE沿DE折起到△PDE,得到四棱锥P-BCDE,如图所示.
(1)若点M为PC的中点,求证:BM∥平面PDE;
(2)当平面PDE⊥平面BCDE时,求四棱锥P-BCDE的体积;
(3)求证:DE⊥PC.
题组训练三空间几何中的翻折问题
如图(1),在五边形ABCDE中,ED=EA,AB∥CD,CD=2AB,∠EDC=150°.如图(2),将△EAD沿AD折到△P AD的位置,得到四棱锥P-ABCD.点M为线段PC的中点,且BM⊥平面PCD.
(1)求证:平面P AD ⊥平面ABCD ;
(2)若四棱锥P -ABCD 的体积为23,求四面体BCDM 的体积.
【专题训练】 一、选择题
1.已知m, n 是两条不同的直线,α,β是两个不同的平面,给出下列四个命题,错误的命题是( ) A .若m ∥α, m ∥β, α∩β=n ,则m ∥n B .若α⊥β, m ⊥α, n ⊥β,则m ⊥n C .若α⊥β, α⊥γ, β∩γ=m ,则m ⊥α D .若α∥β, m ∥α,则m ∥β
2.在棱长为2的正方体ABCD -A 1B 1C 1D 1中,M 是棱A 1D 1的中点,过C 1,B ,M 作正方体的截面,则这个截面的面积为( )
A.352
B.358
C.92
D.98
3.已知长方体ABCD -A 1B 1C 1D 1中,B 1C ,C 1D 与底面ABCD 所成的角分别为60°和45°,则异面直线B 1C 和C 1D 所成角的余弦值为( )
A.
6
4
B.14
C.
26
D.
36
4.如图,在多面体ABCDEFG 中,平面ABC ∥平面DEFG ,AC ∥GF ,且
△ABC 是边长为2的正三角形,四边形DEFG 是边长为4的正方形,M ,N 分别
为AD ,BE 的中点,则MN 等于( )
A.7 B .4 C.19
D .5
5.如图所示,侧棱与底面垂直,且底面为正方形的四棱柱ABCD —A 1B 1C 1D 1中,AA 1=2,AB =1,M ,N 分别在AD 1,BC 上移动,且始终保持MN ∥平面DCC 1D 1,设BN =x ,MN =y ,则函数y =f (x )的图象大致是( )
6.在四棱锥S -ABCD 中,底面ABCD 是平行四边形,M 、N 分别是SA ,BD 上的点.
①若SM MA =DN
NB ,则MN ∥面SCD ;
②若SM MA =NB
DN
,则MN ∥面SCB ;
③若面SDA ⊥面ABCD ,且面SDB ⊥面ABCD ,则SD ⊥面ABCD .其中正确的命题个数是( ) A .0 B .1 C .2 D .3 二、填空题
7.正方体ABCD -A 1B 1C 1D 1中,E 为线段B 1D 1上的一个动点,则下列结论中正确的是________(填序号).
①AC ⊥BE ;②B 1E ∥平面ABCD ;③三棱锥E -ABC 的体积为定值;④直线B 1E ⊥直线BC 1.
8.表面积为60π的球面上有四点S,A,B,C,且△ABC是等边三角形,球心O到平面ABC的距离为3,若平面SAB⊥平面ABC,则棱锥S-ABC体积的最大值为________.
9.如图,在长方体ABCD-A1B1C1D1中,AA1=6,AB=3,AD=8, 点M是棱AD 的中点,N在棱AA1上,且满足AN=2NA1,P是侧面四边形ADD1A1内一动点(含边界),若C1P∥平面CMN,则线段C1P长度的最小值是________.
10.如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE 翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:
①|BM|是定值;
②点M在某个球面上运动;
③存在某个位置,使DE⊥A1C;
④存在某个位置,使MB∥平面A1DE.
其中正确的命题是________.
三、解答题
11.如图,四面体ABCD中,△ABC是正三角形,AD=CD.
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
12.如图,矩形AB′DE(AE=6,DE=5),被截去一角(即△BB′C),AB=3, ∠ABC=135°,平面P AE⊥
平面ABCDE, P A +PE =10.
(1)求五棱锥P -ABCDE 的体积的最大值; (2)在(1)的情况下,证明: BC ⊥PB .
13.如图,四边形ABCD 为菱形,G 为AC 与BD 的交点,BE ⊥平面ABCD .
(1)证明:平面AEC ⊥平面BED ;
(2)若∠ABC =120°,AE ⊥EC ,三棱锥E -ACD 的体积为63
,求该三
棱锥的侧面积.
14.如图(1),在正△ABC 中,E ,F 分别是AB ,AC 边上的点,且BE =AF =2CF .点P 为边BC 上的点,将△AEF 沿EF 折起到△A 1EF 的位置,使平面A 1EF ⊥平面BEFC ,连接A 1B ,A 1P ,EP ,如图(2)所示.
(1)求证:A 1E ⊥FP ;
(2)若BP =BE ,点K 为棱A 1F 的中点,则在平面A 1FP 上是否存在过点K 的直线与平面A 1BE 平行,若存在,请给予证明;若不存在,请说明理由.。