球轴承与钢球轴承动力学特性对比分析

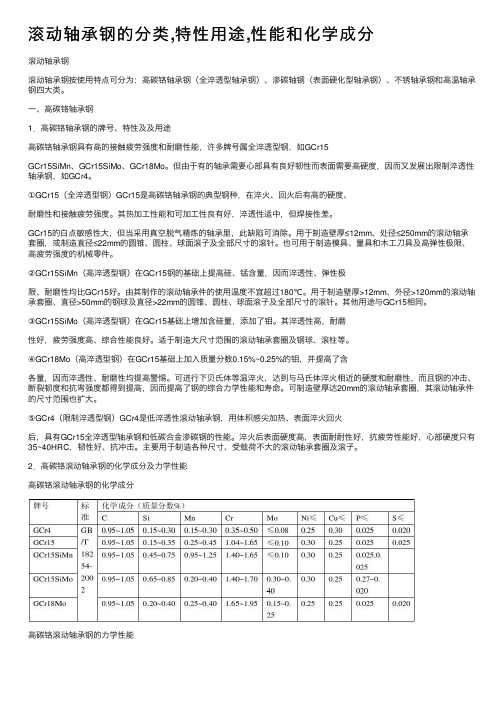
滚动轴承钢的分类,特性⽤途,性能和化学成分滚动轴承钢滚动轴承钢按使⽤特点可分为：⾼碳铬轴承钢（全淬透型轴承钢）、渗碳轴钢（表⾯硬化型轴承钢）、不锈轴承钢和⾼温轴承钢四⼤类。

⼀、⾼碳铬轴承钢1．⾼碳铬轴承钢的牌号、特性及及⽤途⾼碳铬轴承钢具有⾼的接触疲劳强度和耐磨性能，许多牌号属全淬透型钢，如GCr15GCr15SiMn、GCr15SiMo、GCr18Mo。

但由于有的轴承需要⼼部具有良好韧性⽽表⾯需要⾼硬度，因⽽⼜发展出限制淬透性轴承钢，如GCr4。

①GCr15（全淬透型钢）GCr15是⾼碳铬轴承钢的典型钢种，在淬⽕、回⽕后有⾼的硬度、耐磨性和接触疲劳强度。

其热加⼯性能和可加⼯性良有好，淬透性适中，但焊接性差。

GCr15的⽩点敏感性⼤，但当采⽤真空脱⽓精炼的轴承⾥，此缺陷可消除。

⽤于制造壁厚≤12mm、处径≤250mm的滚动轴承套圈，或制造直径≤22mm的圆锥、圆柱、球⾯滚⼦及全部尺⼨的滚针。

也可⽤于制造模具、量具和⽊⼯⼑具及⾼弹性极限、⾼疲劳强度的机械零件。

②GCr15SiMn（⾼淬透型钢）在GCr15钢的基础上提⾼硅、锰含量，因⽽淬透性、弹性极限、耐磨性均⽐GCr15好。

由其制作的滚动轴承件的使⽤温度不宜超过180℃。

⽤于制造壁厚>12mm、外径>120mm的滚动轴承套圈、直径>50mm的钢球及直径>22mm的圆锥、圆柱、球⾯滚⼦及全部尺⼨的滚针。

其他⽤途与GCr15相同。

③GCr15SiMo（⾼淬透型钢）在GCr15基础上增加含硅量，添加了钼。

其淬透性⾼，耐磨性好，疲劳强度⾼、综合性能良好。

适于制造⼤尺⼨范围的滚动轴承套圈及钢球、滚柱等。

④GCr18Mo（⾼淬透型钢）在GCr15基础上加⼊质量分数0.15%~0.25%的钼，并提⾼了含各量，因⽽淬透性、耐磨性均提⾼警惕。

可进⾏下贝⽒体等温淬⽕，达到与马⽒体淬⽕相近的硬度和耐磨性，⽽且钢的冲击、断裂韧度和抗弯强度都得到提⾼，因⽽提⾼了钢的综合⼒学性能和寿命。

一种基于变恢复系数的接触碰撞力模型王旭鹏;张艳;吉晓民;马尚君;佟瑞庭【摘要】为了有效描述机械系统中的接触-碰撞现象,在考虑材料屈服强度和初始碰撞速度的基础上,提出一种变恢复系数模型,进而建立了一种改进的、变恢复系数的接触-碰撞模型;随后,分别以轴-轴承、球-球以及平面曲柄滑块机构为例,通过大量数值模拟和实验测试,以及二者间的对比分析,对改进模型的有效性、准确性进行了验证.研究结果表明,改进的模型能够更加准确的描述间隙铰链处的接触碰撞效应,以及间隙铰链对机械系统动态特性的影响规律.【期刊名称】《振动与冲击》【年(卷),期】2019(038)005【总页数】5页(P198-202)【关键词】变恢复系数;接触碰撞力模型;间隙铰链;动态特性【作者】王旭鹏;张艳;吉晓民;马尚君;佟瑞庭【作者单位】西安理工大学工业设计系,西安710048;西安理工大学工业设计系,西安710048;西安理工大学工业设计系,西安710048;西北工业大学陕西省机电传动与控制工程实验室,西安710072;西北工业大学陕西省机电传动与控制工程实验室,西安710072【正文语种】中文【中图分类】O313.4接触碰撞现象在机械系统中是非常普遍的[1]，比如相邻连接件之间的铰链连接处，因相对运动、加工、装配及其使用过程的摩擦磨损等原因导致存在间隙，而间隙正是接触碰撞的根源[2]。

接触碰撞势必会引起机械系统动态性能、精度、可靠性及寿命等技术指标的下降[3]。

要研究接触碰撞现象及其对机械系统动态性能的影响，首先应建立可用来准确描述接触碰撞效应的接触碰撞力模型。

为此，从20世纪70年代开始，国内外研究者建立了一系列接触碰撞力模型。

作为研究接触碰撞现象的奠基者，Hertz最先提出了一种非线性接触碰撞力模型[4]，但是，Hertz接触理论的应用条件为：接触体具有非协调几何外形，且接触面为平面。

因此，Hertz接触碰撞力模型具有一定的局限性。

Ciavarella等[5]在对Persson接触模型改进的基础上，提出了另外一种适用于接触半径非常小且接触半角足够大工况下的接触碰撞力模型，但该模型同样具有局限性，仅适用于小间隙的接触碰撞。

高速轴承动力学有限元分析方法张利;祁华铭;徐娟;吉智军【摘要】高速轴承是高速列车安全运行的重要部件,轴承运转过程中的动态特性直接影响轴承的使用寿命,采用最小部件之间创建面面接触的方式,建立高速轨道客车用双列圆锥滚子轴承的三维虚拟样机模型,利用ANSYS/LS-DYNA分别研究客车直线匀速行驶和额定速度下以最小转弯半径行驶两种工况下轴承运转过程的动态接触特性,得到轴承的速度特性、加速特性以及滚子承载分布状况、接触单元法向作用力时间历程变化曲线以及保持架的振动曲线,研究结论可以为高速轴承设计过程中模型构建方案的合理确定提供参考.【期刊名称】《图学学报》【年(卷),期】2015(036)004【总页数】5页(P546-550)【关键词】动力学;虚拟样机;ANSYS/LS-DYNA;高速轴承【作者】张利;祁华铭;徐娟;吉智军【作者单位】合肥工业大学机械与汽车工程学院,安徽合肥230009;合肥工业大学机械与汽车工程学院,安徽合肥230009;合肥工业大学安全关键工业测控技术教育部工程研究中心,安徽合肥230009;洛阳轴研科技股份有限公司,河南洛阳471039;洛阳轴研科技股份有限公司,河南洛阳471039【正文语种】中文【中图分类】TH133.3高速铁路客运是未来铁路客运发展的方向，随着铁路运行的不断提速，性能良好的高速轴承将大量应用。

提高轴承的性能与寿命，对提高整车的动力性、安全性和操纵稳定性起着至关重要的作用，因此分析轴承运转中各部件速度、加速度和位移量、应力等的变化和分布情况，并根据受力情况判断易发生疲劳破坏和失效的部位而指导设计过程[1-5]，优化结构参数就显得尤为重要。

通常轴承是在动态载荷工况下工作，滚动轴承的动态接触特性是轴承组件间的复杂动力学行为和接触力学行为的综合体现[3]。

近年来，有关机械零部件间动态接触特性的研究已成为轴承数值分析领域的研究热点。

在滚动轴承运转过程中的动态接触特性数值仿真分析领域已有许多研究。

1、什么是调心滚子轴承？调心滚子轴承有两列滚子，主要承受径向载荷，同时也能承受任一方向的轴向载荷。

有高的径向载荷能力，特别适用于重载或振动载荷下工作，但不能承受纯轴向载荷。

该类轴承外圈滚道是球面形，故其调心性能良好，能补偿同轴度误差。

有两列对称型球面滚子，外圈有一条共用的球面滚道，内圈有两条与轴承轴线倾斜一角度的滚道，具有良好的调心性能，当轴受力弯曲或安装不同心时轴承仍可正常使用，调心性随轴承尺寸系列不同而异，一般所允许的调心角度为1~2.5度，该类型轴承的负荷能力较大，除能承受径向负荷外轴承还能承受双向作用的轴向负荷，具有较好的抗冲击能力，一般来说调心滚子轴承所允许的工作转速较低。

2、调心滚子轴承和调心球轴承有什么区别？从外观上看：调心球轴承有两列钢球，内圈有两条滚道，外圈滚道为内球面型，具有自动调心的性能。

可以自动补偿由于轴的挠曲和壳体变形产生的同轴度误差，适用于支承座孔不能保证同轴度的部件中。

该种轴承主要承受径向载荷，在承受径向载荷的同时，亦可承受少量的轴向载荷，通常不用于承受纯轴向载荷，如承受纯轴向载荷，只有一列钢球受力调心滚子轴承具有两列滚子，主要用于承受径向载荷，同时也能承受任一方向的轴向载荷。

该种轴承径向载荷能力高，特别适用于重载或震动载荷下工作，但不能承受纯轴向载荷；调心性能良好，能补偿同轴度误差。

简单地说，二者的共同点和不同点：共同点：都是调心的、都是双排的不同点：调心滚子轴承的滚动体是：滚子调心球轴承的滚动体是：球不同环境下使用的也不一样，调心滚子轴承承载大于调心球轴承。

3、调心滚子轴承和调心球轴承应用在哪些设备？调心球轴承适用于承受重载荷与冲击载荷、精密仪表、低噪音电机、汽车、摩托车、冶金、轧机、矿山、石油、造纸、水泥、榨糖等行业及一般机械等。

调心滚子轴承适用于承受重载荷与冲击载荷，广泛应用于冶金、轧机、矿山、石油、造纸、水泥、榨糖等行业。

4、经常看到轴承后缀是CC、CA、E、M、MA、MB，有什么区别？在全球，每个大的生产厂家都会有自己的专用代号，就比如说的CC、CA、E、M、MA、MB，其中CC、CA、E是SKF集团对他们的产品所定义的代号名称。

第３４卷第２３期中国机械工程V o l ．３４㊀N o ．２３２０２３年１２月C H I N A M E C HA N I C A LE N G I N E E R I N Gp p．２７９４Ｇ２８０４四点接触球轴承钢球Ｇ沟道多点接触成因分析王亚涛１㊀邱㊀明１,２㊀张家铭１㊀王会杰１１．河南科技大学机电工程学院,洛阳,４７１００３２．河南科技大学机械装备先进制造河南省协同创新中心,洛阳,４７１００３摘要:针对四点接触球轴承钢球与沟道间发生多点接触引起轴承过早失效的问题,以Q J ２１４四点接触球轴承为研究对象,建立了钢球Ｇ沟道接触模型,分析了结构参数及工况参数变化时钢球Ｇ沟道发生多点接触的成因.研究结果表明,内外圈沟道曲率半径系数或内外垫片厚度的增大可使钢球Ｇ沟道接触状态由三点接触转变为两点接触,再转变为三点接触;恒定转速时,轴向载荷的减小可使钢球Ｇ沟道接触状态由两点接触转变为三点接触;转速及轴向载荷均恒定时,径向载荷的增大可使部分钢球Ｇ沟道接触状态由两点接触转变为三点接触,再转变为四点接触.研究成果为避免四点接触球轴承在运转过程中发生多点接触而引起的猫眼圈磨损失效提供了参考.关键词:四点接触球轴承;多点接触;结构参数;工况参数;磨损失效中图分类号:T H １３３．３D O I :１０．３９６９/j ．i s s n ．１００４ １３２X．２０２３．２３．００３开放科学(资源服务)标识码(O S I D ):C a u s eA n a l y s i s o n M u l t i Ｇp o i n tC o n t a c t b e t w e e nS t e e l B a l l a n dR a c e w a y of F o u r Ｇp o i n tC o n t a c t B a l l B e a r i n gs WA N G Y a t a o １㊀Q I U M i n g １,２㊀Z H A N GJ i a m i n g １㊀WA N G H u i ji e １１．C o l l e g e o fM e c h a n i c a l a n dE l e c t r i c a l E n g i n e e r i n g ,H e n a nU n i v e r s i t y o f S c i e n c e a n dT e c h n o l o g y ,L u o y a n g,H e n a n ,４７１００３２．C o l l a b o r a t i v e I n n o v a t i o nC e n t e r o fM a c h i n e r y a n dE q u i p m e n tA d v a n c e d M a n u f a c t u r i n g ofH e n a n P r o v i n c e ,H e n a nU n i v e r s i t y o f S c i e n c e a n dT e c h n o l o g y ,L u o y a n g,H e n a n ,４７１００３A b s t r a c t :A i m i n g a t t h e p r o b l e m s o f p r e m a t u r e b e a r i n g f a i l u r e c a u s e db y m u l t i Ｇpo i n t c o n t a c t s b e Ｇt w e e n t h e s t e e l b a l l a n d t h e r a c e w a y o f f o u r Ｇp o i n t c o n t a c t b a l l b e a r i n g s ,t a k i n g Q J ２１４f o u r Ｇpo i n t c o n Ｇt a c t b a l l b e a r i n g s a s t h e r e s e a r c ho b j e c t ,t h eb a l l a n dt h e r a c e w a y co n t a c tm o d e l sw e r ee s t a b l i s h e d ,a n d t h e c a u s e s o fm u l t i Ｇp o i n t c o n t a c t s b e t w e e n t h e b a l l a n d t h e r a c e w a y w e r e a n a l y z e dw h e n t h e s t r u c Ｇt u r a l p a r a m e t e r s a n dw o r k i n g c o n d i t i o n p a r a m e t e r sw e r e c h a n g e d ．T h e r e s u l t s s h o wt h a tw i t h t h e i n Ｇc r e a s e o f t h e c o e f f i c i e n t o f i n n e r a n do u t e r r a c e w a ygr o o v e c u r v a t u r e r a d i u so r t h e t h i c k n e s so f i n n e r a n do u t e r g a s k e t ,t h e c o n t a c t s t a t e b e t w e e n t h e b a l l a n d t h e r a c e w a y m a y b e c h a n g e d f r o mt h r e e Ｇpo i n t c o n t a c t t o t w o Ｇp o i n t c o n t a c t ,a n d t h e nt o t h r e e Ｇp o i n t c o n t a c t ．A t c o n s t a n t s p e e dc o n d i t i o n ,w i t ht h e r e d u c t i o no f a x i a l l o a d ,t h e c o n t a c t s t a t e b e t w e e n t h e b a l l a n d t h e r a c e w a y m a y b e c h a n ge df r o mt w o Ｇp o i n t c o n t a c t t o t h r e e Ｇp o i n t c o n t a c t ．W h e n t h e r o t a t i o n a l s pe e d a n d t h e a x i a l l o a d a r e c o n s t a n t ,t h e i n Ｇc r e a s e of r a d i a l l o a d sm a y m a k e t h e c o n t a c t s t a t e o f s o m e s t e e l b a l l s a n d t h e r a c e w a y c h a n ge f r o mt w o Ｇp o i n t c o n t a c t t o t h r e e Ｇp o i n t c o n t a c t ,a n d t h e n t o f o u r Ｇp o i n t c o n t a c t ．T h e r e s e a r c h f i n d i n g sm a y pr o v i d e r e f e r e n c e f o r a v o i d i n g t h e c a t ̓s e y e r i n g w e a r f a i l u r e c a u s e db y m u l t i Ｇp o i n t c o n t a c t d u r i n g t h e r u n n i n g o f f o u r Ｇp o i n t c o n t a c t b a l l b e a r i n gs ．K e y wo r d s :f o u r Ｇp o i n t c o n t a c tb a l lb e a r i n g ;m u l t i Ｇp o i n t c o n t a c t ;s t r u c t u r a l p a r a m e t e r ;w o r k i n g c o n d i t i o n p a r a m e t e r ;w e a r f a i l u r e收稿日期:２０２３０６２６基金项目:国家自然科学基金(５２２７５１８６)０㊀引言四点接触球轴承被广泛应用于航空航天㊁船舶㊁汽车等多种场合,在这些场合中轴承的服役工况复杂㊁服役环境恶劣㊁故障率较高且损伤模式多种多样[１Ｇ２].其中,多点接触致使四点接触球轴承产生猫眼圈磨损,是引发轴承早期失效的重要因素之一.近年来,针对滚动轴承接触特性,国内外学者以圆锥滚子轴承[３]㊁圆柱滚子轴承[４]和角接触球轴承[５]为对象开展了大量的研究,但上述轴承不存在多点接触问题.对于涉及多点接触问题的三点接触球轴承,H AM R O C K 等[６]分析了双半外圈三点接触球轴承的载荷分布及寿命特性;彭城等[７]分析了设计接触角及运行参数对三点接触球轴承打滑率的影响.对于涉及多点接触问题的四点接触球轴承,研究主要分布在轴承振动[８]㊁旋转４９７２精度[９]㊁刚度[１０]㊁套圈柔性化[１１]㊁摩擦磨损[１２Ｇ１６]㊁稳定性[１７Ｇ２０]方面.在轴承多点接触方面,俞加欣[２１]仅探讨了静态条件下避免三点接触的临界条件.文献检索可知,关于动态条件下四点接触球轴承多点接触问题的研究还鲜有报道.然而,多点接触产生的磨损失效又是此类轴承常见的故障模式,故有必要深入地研究多点接触产生的原因或条件,为避免四点接触球轴承多点接触引发的猫眼圈磨损失效提供参考.鉴于此,本文针对四点接触球轴承,建立了其钢球Ｇ沟道接触模型,并对比求解特定工况下的轴承接触载荷与已有文献的相应结果,验证了所建模型的正确性.以Q J２１４四点接触球轴承为研究对象,重点讨论了内圈沟道曲率半径系数㊁外圈沟道曲率半径系数㊁内圈垫片厚度㊁外圈垫片厚度结构参数变化和转速㊁轴向载荷㊁径向载荷等工况参数变化时钢球Ｇ沟道间发生多点接触的成因.１㊀四点接触球轴承钢球Ｇ沟道接触模型的建立㊀㊀为了探明诱导四点接触球轴承发生多点接触的原因,需先建立钢球Ｇ沟道接触模型.模型由两部分组成:一部分是钢球中心与内外沟道曲率中心几何关系分析;另一部分是钢球及内圈的受力分析.１．１㊀四点接触球轴承几何关系分析四点接触球轴承的内外套圈沟道均为 桃形 ,轴承需要在钢球Ｇ沟道两点接触的情况下才能正确发挥作用,如图１a所示.四点接触球轴承在实际工作过程中,钢球理应与其中一个半内圈沟道以及与此半内圈呈对角位置的外圈沟道分离,如果未分离,则钢球与沟道会出现多点接触现象,发生三点接触或四点接触,如图１b㊁图１c所示.轴承发生多点接触时,钢球会在低受载套圈的沟道上出现严重的滑动,导致轴承早期失效[２２].(a)两点接触㊀㊀(b)三点接触㊀㊀(c)四点接触图１㊀四点接触球轴承钢球Ｇ沟道接触状态F i g．１㊀B a l lＧr a c e w a y c o n t a c t s t a t e o f f o u rＧp o i n t c o n t a c tb a l l b e a r i n g s垫片角αs是四点接触球轴承的重要结构参数,如图２a所示,它与垫片厚度g有关,表达式为αs i(e)＝a r c s i n(g i(e)２r i(e)－D w)(１)式中,下标i(e)表示轴承内(外)圈;r为沟道曲率半径, r＝f D w;f为曲率半径系数;D w为钢球直径.垫片角的影响使得四点接触球轴承的原始接触角α０与一般角接触球轴承不同,如图２b所示,表达式为α０＝a r c c o s(A－[S d＋２(h i＋h e)]/２－ηi－ηeA)(２)式中,A为内外沟道曲率中心的初始距离;S d为径向装配游隙;h i(e)为内(外)沟道沟尖到钢球表面的距离,见图２c;η为去除垫片后沟道沟尖与未去除垫片的沟道沟底的距离.(a)垫片角(b)原始接触角(c)沟尖Ｇ球面距离图２㊀四点接触球轴承结构F i g．２㊀F o u rＧp o i n t c o n t a c t b a l l b e a r i n g s s t r u c t u r e四点接触球轴承在运转过程中,受外力向量F＝(F x,F y,F z,M y,M z)的作用,轴承内圈相对于外圈产生相对位移d＝(δx,δy,δz,θy,θz),钢球中心O b j和内沟道左沟曲率中心O i l㊁内沟道右沟曲率中心O i r分别变化到Oᶄb j㊁Oᶄi l㊁Oᶄi r,导致轴承内外沟道的曲率中心不在同一条直线上,受载前后钢球中心与内外沟道沟曲率中心相对位置如图３所示.变形后内圈沟道曲率中心相对外圈沟道曲率中心之间的轴向距离A１j㊁径向距离A２j为A１(２)j＝(r i＋r e－D w)s i nα０＋Δ１(２)j(３)式中,Δ１(２)j为内沟道曲率中心在变形前后沿轴向(径向)位移.钢球与内外圈接触角可表示为s i nαi l j＝A１j－X１jr i－D w/２＋δi l j(４)s i nαi r j＝X１j－A１j＋g i c o s(θz c o sφj＋θy s i nφj)r i－D w/２＋δi r j(５)s i nαe l j＝g e－X１jr e－D w/２＋δe l j(６)s i nαe r j＝X１jr e－D w/２＋δe r j(７)５９７２四点接触球轴承钢球Ｇ沟道多点接触成因分析 王亚涛㊀邱㊀明㊀张家铭等图３㊀钢球中心与内外沟道沟曲率中心位置关系F i g．３㊀R e l a t i o nb e t w e e n t h e c e n t e r o f s t e e l b a l l a n d t h ec u r v a t u r e c e n t e r o f i n n e r a n do u t e r t r e n c h e s式中,下标l㊁r表示左㊁右沟道;φj＝２π(j－１)/Z为第j 个钢球的角位置;Z为钢球数量.钢球与内外圈左右沟道的接触变形分别为δi l j＝[(A１j－X１j)２＋(A２j－X２j)２]１/２－(r i－D w２)(８)δi r j＝[(X１j－A１j＋g i c o s(θy s i nφj＋θz c o sφj))２＋(A２j－X２j－g i s i n(θy s i nφj＋θz c o sφj))２]１/２－(r i－D w２)(９)δe l j＝[X２２j＋(g e－X１j)２]１/２－(r e－D w２)(１０)δe r j＝(X２２j＋X２１j)１/２－(r e－D w２)(１１)式中,X１(２)j为变形后钢球中心与外圈沟道曲率中心的轴向(径向)距离.１．２㊀钢球和内圈受力分析轴承在运转过程中,钢球不仅受到内外沟道作用力,还受到离心力和陀螺力矩的作用,对钢球进行受力分析,如图４所示.图４㊀钢球受力分析F i g．４㊀F o r c e a n a l y s i s o f s t e e l b a l l钢球Ｇ沟道接触载荷Q为Q i(e)l(r)j＝K i(e)l(r)jδ１．５i(e)l(r)j(１２)式中,下标i(e)l(r)j表示第j个钢球与内(外)圈左(右)沟道的接触位置;K为套圈接触变形系数.根据钢球局部受力平衡条件,钢球受力平衡方程可表示为Q i l j s i nαi l j－Q i r j s i nαi r j＋Q e l j s i nαe l j－Q e r j s i nαe r j＋M g j D w(λi l j c o sαi l j＋λi r j c o sαi r j－λe l j c o sαe l j－λe r j c o sαe r j)＝０(１３) Q i l j c o sαi l j＋Q i r j c o sαi r j－Q e l j c o sαe l j－Q e r j c o sαe r j＋M g jD w(－λi l j s i nαi l j＋λi r j s i nαi r j－λe l j s i nαe l j＋λe r j s i nαe r j)＋F c j＝０(１４)式中,λi l j㊁λi r j㊁λe l j㊁λe r j分别为内圈和外圈滚道控制参数,研究采用外滚道控制,取λi l j＝λi r＝０,λe l j＝λe r＝２;F c j㊁M g j分别为钢球受到的离心力和陀螺力矩,具体计算方法见文献[１０].在对钢球分析的基础上,对轴承内圈进行受力分析,根据牛顿运动定律,内圈平衡方程可表示为F＋ðZ j＝１R j Q i j＝０(１５)式中,Q i j为作用在轴承内圈上的外力向量;R j为坐标变换矩阵.综上,轴承几何变形关系式(３)和式(８)~式(１１)㊁钢球受力式(１３)~式(１４)㊁内圈受力式(１５)共同构造出四点接触球轴承钢球Ｇ沟道接触模型.２㊀模型求解方法及验证２．１㊀模型求解方法采用分块法与牛顿Ｇ拉夫逊法对上述四点接触球轴承钢球Ｇ沟道接触模型进行求解,求解流程如图５所示.首先输入四点接触球轴承的基本结构参数及载荷等参数,并给出内圈位移迭代初值;其次给定局部变量X１j㊁X２j对钢球平衡方程进行循环迭代计算,直到所有钢球完成迭代计算;然后将钢球局部平衡方程的计算结果代入内圈平衡方程中进行迭代求解,并对内圈广义位移进行修正,当全局误差满足收敛判据时结束迭代运算;最后输出四点接触球轴承内圈位移㊁接触载荷等性能参数.２．２㊀模型验证为了验证所建立的四点接触球轴承钢球Ｇ沟道接触模型的正确性,选取已经公开发表并且被后续许多文献[１０,１４]引用对比的N A S A技术报告[６]中的结果作为参考数据进行比较.在与参考数据中所用轴承结构参数(表１)及工况参数保持６９７２ 中国机械工程第３４卷第２３期２０２３年１２月上半月图５㊀求解流程图F i g．５㊀S o l u t i o n f l o wc h a r t一致的条件下,对比模型计算与参考数据中的钢球Ｇ沟道接触载荷,如图６所示.表１㊀文献轴承结构参数T a b．１㊀S t r u c t u r a l p a r a m e t e r s o f b e a r i n g f r o mr e f e r e n c e s结构参数数值轴承内径d(mm)１５０轴承外径D(mm)２２５钢球直径D w(mm)２２．２３０内圈沟道曲率半径系数f i０．５４０外圈沟道曲率半径系数f e０．５２０外圈垫片厚度g e(mm)０．２５４㊀㊀由图６可知,通过模型计算得到的钢球Ｇ沟道接触载荷与文献结果吻合良好,且误差绝对值最大不超过６．４％,验证了四点接触球轴承钢球Ｇ沟道接触模型的正确性.为对四点接触球轴承钢球Ｇ沟道多点接触成因进行分析,选取型号为Q J２１４的四点接触球轴承为对象,其主要结构参数如表２所示.３㊀模型求解结果与讨论在四点接触球轴承运转过程中,钢球Ｇ沟道的受载情况分为主要承受载荷的呈对角位置的两个主接触区,如图１a所示,以及对面位置的两个副接触区,如图１c所示.根据第１节建立的钢球Ｇ沟道接触模型所得到的接触载荷来判断主副接触区钢球Ｇ沟道接触点数量Zᶄ及轴承是否发生多点接触,进而分析结构参数和工况参数变化时钢球Ｇ沟道发生多点接触的成因.(a)F x＝４４４８N(b)F x＝１３３４５N图６㊀钢球Ｇ沟道接触载荷对比验证F i g．６㊀C o m p a r i s o na n d v e r i f i c a t i o no f b a l lＧr a c e w a yc o n t a c t l o a d表２㊀Q J２１４轴承结构参数T a b．２㊀S t r u c t u r a l p a r a m e t e r s o f Q J２１４b e a r i n g结构参数数值轴承内径d(mm)７０轴承外径D(mm)１２５钢球数量Z１５内圈沟道曲率半径系数f i０．５１７外圈沟道曲率半径系数f e０．５２９内圈垫片厚度g i(mm)０．２９８外圈垫片厚度g e(mm)０．５０８３．１㊀结构参数变化时钢球Ｇ沟道多点接触成因分析为探究内圈沟道曲率半径系数㊁外圈沟道曲率半径系数㊁内圈垫片厚度㊁外圈垫片厚度结构参数变化时钢球Ｇ沟道发生多点接触的成因,根据Q J２１４型四点接触球轴承产品提供的转速㊁载荷等数据,选取转速n＝１００００r/m i n㊁轴向载荷F x＝１５k N㊁径向载荷F z＝５k N作为基础工况进行分析.３．１．１㊀内圈沟道曲率半径系数变化时钢球Ｇ沟道多点接触成因分析图７给出了基础工况下钢球Ｇ沟道接触载荷随内圈沟道曲率半径系数的变化曲线.从图７中可以看出,随着内圈沟道曲率半径系数的增大,内外沟道主接触区钢球Ｇ沟道接触载荷逐渐增大,但７９７２四点接触球轴承钢球Ｇ沟道多点接触成因分析 王亚涛㊀邱㊀明㊀张家铭等(a )f i ＝０．５１２(b )f i ＝０．５１７(c )f i ＝０．５２２(d )f i ＝０．５２７图７㊀钢球Ｇ沟道接触载荷随内圈沟道曲率半径系数变化曲线F i g ．７㊀V a r i a t i o n c u r v e o f b a l l Ｇr a c e w a y c o n t a c t l o a dw i t h c o e f f i c i e n t o f c u r v a t u r e r a d i u s o f t h e i n n e r r i n g gr o o v e 各角位置处钢球Ｇ沟道接触点数量(接触区内钢球Ｇ沟道间存在接触载荷的钢球数量)未发生变化,均为１５个.后续讨论中主接触区钢球Ｇ沟道接触点数量具有与此相同的规律,因此文中不再赘述.内沟道副接触区钢球Ｇ沟道接触载荷随着内圈沟道曲率半径系数的增大逐渐减小为０,外沟道副接触区反之,且同一内圈沟道曲率半径系数下副接触区最多只有一个沟道存在接触载荷,说明钢球与沟道至多发生三点接触,同时表明钢球与内沟道发生第三点接触逐渐转变为钢球与外沟道发生第三点接触.此过程中,副接触区钢球Ｇ沟道接触点数量依次为１２㊁０㊁１５㊁１５,在内圈沟道曲率半径系数为０．５１７附近,钢球Ｇ沟道接触状态发生转变.根据上述分析,细化内圈沟道曲率半径系数为０．５１２~０．５２２,直接分析钢球Ｇ沟道接触点数量Z ᶄ的变化规律,如图８所示.当内圈沟道曲率半径系数f i ＜０．５１６时,部分钢球与内沟道发生三点接触;当内圈沟道曲率半径系数f i 为０．５１６~０．５１７时,副接触区钢球Ｇ沟道接触点数量为０,钢球Ｇ沟道由三点接触转变为两点接触;当内圈沟道曲率系数f i ＞０．５１７时,部分钢球与沟道再转变为三点接触状态,此时三点接触的位置发生在外沟道.图８㊀不同内圈沟道曲率半径系数下副接触区钢球Ｇ沟道接触点数量F i g ．８㊀N u m b e r o f b a l l Ｇr a c e w a y c o n t a c t p o i n t s i n t h e s e c o n d a r y co n t a c t z o n e u n d e r d i f f e r e n t i n n e r g r o o v e c u r v a t u r e r a d i u s c o e f f i c i e n t s３．１．２㊀外圈沟道曲率半径系数变化时钢球Ｇ沟道多点接触成因分析图９给出了基础工况下钢球Ｇ沟道接触载荷随外圈沟道曲率半径系数的变化曲线.随着外圈沟道曲率半径系数的增大,外沟道副接触区钢球Ｇ沟道接触载荷逐渐减小,接触点数量从１５个逐渐减少至０个;内沟道副接触区反之,接触点数量从０个逐渐增加至１５个;在外圈沟道曲率半径系数为０．５２９附近,钢球Ｇ沟道接触状态发生转变.通过进一步细化外圈沟道曲率半径系数区间０．５２４~０．５３４来探究钢球Ｇ沟道多点接触演变规８９７２ 中国机械工程第３４卷第２３期２０２３年１２月上半月(a)f e＝０．５２４(b)f e＝０．５２９(c)f e＝０．５３４(d)f e＝０．５３９图９㊀钢球Ｇ沟道接触载荷随外圈沟道曲率半径系数变化曲线F i g．９㊀V a r i a t i o n c u r v e o f b a l lＧr a c e w a y c o n t a c t l o a dw i t h c o e f f i c i e n t o f c u r v a t u r e r a d i u s o f t h e o u t e r r i n g g r o o v e 律及成因,如图１０所示.当外圈沟道曲率半径系数f e＜０．５２９时,钢球与外沟道的密合度变大,导致部分钢球与外沟道发生三点接触;当外圈沟道曲率半径系数f e增大至０．５２９~０．５３２时,钢球Ｇ沟道转变为两点接触;当外圈沟道曲率半径系数f e＞０．５３２时,钢球与外沟道密合度变小,相对来说,增大了钢球与内沟道的密合度,此时部分钢球与内沟道发生三点接触.图１０㊀不同外圈沟道曲率半径系数下副接触区钢球Ｇ沟道接触点数量F i g．１０㊀N u m b e r o f b a l lＧr a c e w a y c o n t a c t p o i n t s i n t h es e c o n d a r y c o n t a c t z o n e u n d e r d i f f e r e n t c o e f f i c i e n t o fc u r v a t u r e r ad i u s o f t he o u t e r r i n g g r o o v e ３．１．３㊀内圈垫片厚度变化时钢球Ｇ沟道多点接触成因分析图１１给出了基础工况下钢球Ｇ沟道接触载荷随内圈垫片厚度的变化曲线.由图１１可知,副接触区钢球Ｇ沟道接触点数量随着内圈垫片厚度的增大先减少后增加,数量依次为１５㊁１５㊁０㊁５;在内圈垫片厚度为０．２９８mm附近,钢球Ｇ沟道接触状态发生转变.根据上述分析,过大或过小的内圈垫片厚度均会导致轴承发生三点接触,在内圈垫片厚度０．２４８~０．３４８mm区间内进一步分析发生转变的临界值,如图１２所示.当内圈垫片厚度g i＜０．２８８mm时,钢球与外沟道发生三点接触;当内圈垫片厚度g i为０．２８８~０．３２８mm时,钢球Ｇ沟道由三点接触转变为两点接触;当内圈垫片厚度g i 增大至０．３２８mm时,钢球与内沟道发生三点接触.３．１．４㊀外圈垫片厚度变化时钢球Ｇ沟道多点接触成因分析图１３给出了基础工况下钢球Ｇ沟道接触载荷随外圈垫片厚度的变化曲线.从图１３中可以看出,随着外圈垫片厚度的增大,副接触区钢球Ｇ沟道接触点数量先减少后增加,数量依次为６㊁０㊁０㊁１５,轴承在此过程中至多发生三点接触,位置分别在内沟道㊁外沟道上.细化外圈垫片厚度区间０．４２８~０．５２８mm,寻找使钢球Ｇ沟道接触状态发生转变的诱因,如图１４所示,当外圈垫片厚度g e＜０．４４８mm时,由两９９７２四点接触球轴承钢球Ｇ沟道多点接触成因分析 王亚涛㊀邱㊀明㊀张家铭等(a)g i＝０．１９８mm(b)g i＝０．２４８mm(c)g i＝０．２９８mm(d)g i＝０．３４８mm图１１㊀钢球Ｇ沟道接触载荷随内圈垫片厚度变化曲线F i g．１１㊀V a r i a t i o n c u r v e o f b a l lＧr a c e w a y c o n t a c t l o a dw i t h t h i c k n e s s o f t h e i n n e r r i n g g a s k e t段圆弧曲线组成的外桃形沟道的坡度变得平缓,内沟道的坡度相对变得陡峭,钢球与内沟道发生三点接触;当外圈垫片厚度g e增大为０．４４８~０．５１８mm时,钢球Ｇ沟道转变为两点接触;当外圈图１２㊀不同内圈垫片厚度下副接触区钢球Ｇ沟道接触点数量F i g．１２㊀N u m b e r o f b a l lＧr a c e w a y c o n t a c t p o i n t s i n t h es e c o n d a r y c o n t a c t z o n e u n d e r d i f f e r e n t t h i c k n e s so f t h e i n n e r r i n g g a s k e t垫片厚度g e＞０．５１８mm时,由两段圆弧曲线组成的外圈桃形沟道的坡度变得陡峭,导致钢球由两点接触再转变为与外沟道的三点接触状态.３．２㊀工况参数变化时钢球Ｇ沟道多点接触成因分析在３．１节选用工况的基础上,通过进一步改变转速和载荷条件来分析轴向载荷㊁联合载荷作用后四点接触球轴承钢球Ｇ沟道发生多点接触的诱因,轴承结构参数如表２所示.３．２．１㊀轴向载荷变化时钢球Ｇ沟道多点接触成因分析图１５计算了轴承在转速n为１００００r/m i n,轴向载荷F x为５~２０k N的工况下钢球Ｇ沟道接触载荷.由图１５可知,在相同的转速条件下,副接触区钢球Ｇ沟道接触载荷随着轴向载荷的增大而减小,接触点数量依次为１５㊁１５㊁０㊁０;钢球Ｇ沟道接触状态在轴向载荷为１０~１５k N间转变.由图１５可知,较小的轴向载荷更易导致多点接触情况的发生,通过二分法对区间进行细化寻找轴向载荷临界值.当轴向载荷F x＞１１．５６２５k N 时,内外圈在轴向方向上位移量增加,钢球与沟道仅在呈对角位置的主接触区接触,钢球Ｇ沟道由三点接触转变为两点接触.３．２．２㊀联合载荷作用下径向载荷变化时钢球Ｇ沟道多点接触成因分析在转速n为１００００r/m i n,轴向载荷F x为１５k N工况的基础上,分析径向载荷F z为２~１４k N时钢球Ｇ沟道间接触载荷的变化规律,如图１６所示.由图１６可知,在相同的转速及轴向载荷条件下,外内沟道副接触区钢球Ｇ沟道最大接触载荷随着径向载荷的增大而增大,接触点数量分别为０㊁０㊁５㊁１１和０㊁０㊁０㊁３.００８２ 中国机械工程第３４卷第２３期２０２３年１２月上半月(a )g e ＝０．４０８mm㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀(b )g e ＝０．４５８mm (c )g e ＝０．５０８mm㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀(d )g e ＝０．５５８mm 图１３㊀钢球Ｇ沟道接触载荷随外圈垫片厚度变化曲线F i g １３㊀V a r i a t i o n c u r v e o f b a l l Ｇr a c e w a y c o n t a c t l o a dw i t h t h i c k n e s s o f t h e o u t e r r i n g ga s k et 图１４㊀不同外圈垫片厚度下副接触区钢球Ｇ沟道接触点数量F i g ．１４㊀N u m b e r o f b a l l Ｇr a c e w a y c o n t a c t p o i n t s i n t h e s e c o n d a r y co n t a c t z o n e u n d e r d i f f e r e n t t h i c k n e s s o f t h e o u t e r r i n g ga s k e t ㊀㊀利用二分法逼近接触状态转变的临界点,当径向载荷F z ＞６．６２５k N 时,钢球Ｇ沟道由两点接触变为三点接触,当径向载荷F z ＞１２k N 时,径向载荷驱使钢球与内外沟道主接触区㊁副接触区同时接触,钢球Ｇ沟道由三点接触再转变为四点接触.３．２．３㊀工况参数耦合下钢球Ｇ沟道多点接触成因分析为了讨论转速㊁轴向载荷变化对轴承钢球Ｇ沟道多点接触成因的影响,计算了轴承在转速n 为２０００~１２０００r /m i n ㊁轴向载荷F x 为３~１８k N的工况条件下钢球Ｇ沟道接触点总数量Z ᵡ,如图１７所示.由图１７可知,钢球Ｇ沟道接触点总数量随着转速的降低或轴向载荷的增大而减少,且钢球Ｇ沟道接触点总数量最多为４５个,由上文可知此过程钢球Ｇ沟道仅由三点接触转变为两点接触.图１８考虑了转速㊁轴向载荷和径向载荷变化对四点接触球轴承钢球Ｇ沟道多点接触成因的综合影响,给出了在转速n 为２０００~１００００r /m i n㊁轴向载荷F x 为３~１５k N ㊁径向载荷F z 为３~１５k N 的工况下钢球Ｇ沟道接触点总数量.如图１８所示,钢球Ｇ沟道接触点总数量随着转速的降低,或轴向载荷的增大,或径向载荷的减小而减少,且总数量最多为４９个,大于两点接触状态下的３０个和三点接触状态下最多的接触点总数量４５个,表明钢球Ｇ沟道接触状态在两点接触㊁三点接触和四点接触之间转变.４㊀结论(１)在转速n 为１００００r /m i n㊁轴向载荷F x 为１５k N ㊁径向载荷F z 为５k N 的基础工况下,当内圈沟道曲率半径系数f i ＜０．５１６或f i ＞０．５１７时,钢球Ｇ沟道接触状态由两点接触转变为三点接触;当外圈沟道曲率半径系数f e ＜０．５２９或f e ＞０．５３２时,钢球Ｇ沟道接触状态由两点接触转变为１０８２ 四点接触球轴承钢球Ｇ沟道多点接触成因分析 王亚涛㊀邱㊀明㊀张家铭等(a)F x＝５k N(b)F x＝１０k N(c)F x＝１５k N(d)F x＝２０k N图１５㊀钢球Ｇ沟道接触载荷随轴向载荷变化曲线F i g．１５㊀V a r i a t i o n c u r v e o f b a l lＧr a c e w a y c o n t a c t l o a dw i t ha x i a l l o a d三点接触;当内圈垫片厚度g i＜０．２８８mm或g i＞０．３２８mm时,钢球Ｇ沟道接触状态由两点接触转变为三点接触;当外圈垫片厚度g e＜０．４４８m m 或g e＞０．５１８mm时,钢球Ｇ沟道接触状态由两点(a)F z＝２k N(b)F z＝６k N(c)F z＝１０k N(d)F z＝１４k N图１６㊀钢球Ｇ沟道接触载荷随径向载荷变化曲线F i g．１６㊀V a r i a t i o n c u r v e o f b a l lＧr a c e w a y c o n t a c t l o a dw i t h r a d i a l l o a d接触转变为三点接触,且钢球与沟道三点接触的位置会在内外沟道之间转变.２０８２ 中国机械工程第３４卷第２３期２０２３年１２月上半月图１７㊀转速㊁轴向载荷作用下钢球Ｇ沟道接触点总数量F i g ．１７㊀T o t a l n u m b e r o f b a l l Ｇr a c e w a y co n t a c t p o i n t s u n d e r r o t a t i o n a l s pe e da n da x i a l l o ad 图１８㊀转速㊁轴向载荷和径向载荷作用下钢球Ｇ沟道接触点总数量F i g ．１８㊀T o t a l n u m b e r o f b a l l Ｇr a c e w a y co n t a c t s u n d e r r o t a t i o n a l s pe e d ,a x i a l l o a da n d r a d i a l l o a d (２)轴承发生多点接触的钢球数量随着转速的降低或轴向载荷的增大或径向载荷的减小而减少.(３)在转速及轴向载荷作用下,钢球Ｇ沟道接触状态仅在两点接触和三点接触之间转变,转速n 为１００００r /m i n 的工况下,当轴向载荷F x ＞１１．５６２５k N 时,钢球Ｇ沟道接触状态由三点接触转变为两点接触;在转速㊁轴向载荷和径向载荷作用下,钢球Ｇ沟道接触状态会在两点接触㊁三点接触和四点接触之间转变.在转速n 为１００００r /m i n ,轴向载荷F x 为１５k N 工况条件下,当径向载荷F z ＞６．６２５k N 时,钢球Ｇ沟道接触状态由两点接触转变为三点接触,当径向载荷F z ＞１２k N 时,钢球Ｇ沟道接触状态由三点接触转变为四点接触.(４)研究揭示了结构参数及工况参数变化时钢球Ｇ沟道发生多点接触的成因,为避免四点接触球轴承在运转过程中发生多点接触而引起的猫眼圈磨损失效提供了参考.参考文献:[１]㊀何加群．中国战略性新兴产业研究与发展:高端轴承[M ]．北京:机械工业出版社,２０１９．H EJ i a q u n ．R&Do fC h i n a ̓sS t r a t e g i cN e wI n d u s Ｇt r i e s :H i g h Ｇe n d B e a r i n g s [M ]．B e i j i n g :C h i n a M a Ｇc h i n eP r e s s ,２０１９．[２]㊀HA R R I ST A ,K O T Z A L A S M N．R o l l i n g B e a r i n gA n a l y s i s Ｇ２V o l u m e S e t [M ]．B o c a R a t o n :C R C P r e s s ,２００６．[３]㊀王彦伟,罗继伟,陈立平．圆锥滚子轴承接触分析[J ]．华中科技大学学报(自然科学版),２００７,３５(９):１９Ｇ２１．WA N G Y a n w e i ,L U OJ i w e i ,C H E N L i p i n g．A n a l Ｇy s i s o f t h eC o n t a c t so fT a p e rR o l l e rB e a r i n gs [J ]．J o u r n a lo f H u a z h o n g U n i v e r s i t y o f S c i e n c e a n d T e c h n o l o g y (N a t u r a lS c i e n c e E d i t i o n ),２００７,３５(９):１９Ｇ２１．[４]㊀史修江,王黎钦．基于拟动力学的航空发动机主轴滚子轴承热弹流润滑分析[J ]．机械工程学报,２０１６,５２(３):８６Ｇ９２．S H IX i u j i a n g ,WA N G L i q i n ．T E H L A n a l y s i s o f A e r o Ｇe n g i n e M a i n s h a f t R o l l e r B e a r i n g B a s e d o n Q u a s i Ｇd y n a m i c s [J ]．J o u r n a lo f M e c h a n i c a l E n gi Ｇn e e r i n g,２０１６,５２(３):８６Ｇ９２．[５]㊀张进华,方斌,朱永生,等．基于球Ｇ滚道非完全接触状态下的球轴承载荷分布计算及刚度特性研究[J ]．机械工程学报,２０２０,５６(９):７３Ｇ８３．Z HA N GJ i n h u a ,F A N G B i n ,Z HU Y o n g s h e n g,e t a l ．I n v e s t i g a t i o no f t h eL o a dD i s t r i b u t i o na n dS t i f f Ｇn e s s C h a r a c t e r i s t i c o f B a l l B e a r i n g un d e r B a l l Ｇr a c e w a y S e p a r a t i o n C o n d i t i o n [J ]．J o u r n a lo f M e Ｇc h a n i c a l E n g i n e e r i n g,２０２０,５６(９):７３Ｇ８３．[６]㊀HAM R O C KBJ ,A N D E R S O N WJ ．A r c h e d Ｇo u t e r Ｇr a c eB a l l Ｇb e a r i n g A n a l y s i s C o n s i d e r i n g C e n t r i f u g a l F o r c e s ,T N D Ｇ６７６５[R ]．C l e v e l a n d ,O h i o :N a t i o n a l A e r o n a u t i c s a n dS pa c eA d m i n i s t r a t i o n ,１９７２．[７]㊀彭城,曹宏瑞,朱玉彬,等．三点接触球轴承打滑动力学分析与验证[J ]．机械工程学报,２０２３,５９(１):１２３Ｇ１３０．P E N GC h e n g ,C A O H o n gr u i ,Z HU Y u b i n ,e ta l ．D y n a m i cA n a l y s i sa n d V e r i f i c a t i o no nS k i d d i n g Be Ｇh a v i o rof T h r e e Ｇp o i n t C o n t a c t B a l l B e a r i n gs [J ]．J o u r n a l o f M e c h a n i c a lE n g i n e e r i n g ,２０２３,５９(１):１２３Ｇ１３０．[８]㊀田凯文,邱明,王东峰．动力传动机构四点接触球轴承的振动特性分析[J ]．振动与冲击,２０２３,４２(４):３９Ｇ４７．T I A N K a i w e n ,Q I U M i n g ,WA N G D o n g f e n g ．A n a l y s i so fV i b r a t i o nC h a r a c t e r i s t i c so fF o u r Ｇpo i n t C o n t a c tB a l lB e a r i n g sf o rP o w e rT r a n s m i s s i o n [J ]．J o u r n a lo f V i b r a t i o n a n d S h o c k ,２０２３,４２(４):３０８２ 四点接触球轴承钢球Ｇ沟道多点接触成因分析 王亚涛㊀邱㊀明㊀张家铭等３９Ｇ４７．[９]㊀陈月,邱明,杜辉,等．机器人用四点接触球轴承旋转精度影响因素[J]．中国机械工程,２０２０,３１(１４):１６７８Ｇ１６８５．C H E N Y u e,Q I U M i n g,D U H u i,e t a l．F a c t o r s I nＧf l u e n c i ng R o t a t i o n A c c u r a c y o fF o u rＧp o i n tC o n t a c tB a l l B e a r i n g s f o rR o b o t s[J]．C h i n a M e c h a n i c a lE nＧg i n e e r i n g,２０２０,３１(１４):１６７８Ｇ１６８５．[１０]㊀R I V E R A G,T O N G V,HO N G S．C o n t a c tL o a da n dS t i f f n e s so fF o u rＧp o i n tC o n t a c tB a l lB e a r i n g su n d e rL o a d i n g[J]．I n t e r n a t i o n a l J o u r n a lo fP r e c iＧs i o n E n g i n e e r i n g a n d M a n u f a c t u r i n g,２０２２,２３(６):６７７Ｇ６８７．[１１]㊀L A C R O I X S,NÉL I A S D,L E B L A N C A．F o u rＧp o i n tC o n t a c tB a l l B e a r i n g M o d e lw i t hD e f o r m a b l eR i n g s[J]．J o u r n a lo fT r i b o l o g y,２０１３,１３５(３):３１４０２．[１２]㊀C H E N L,X I A X,Z H E N G H,e ta l．F r i c t i o n T o r q u eB e h a v i o ra saF u n c t i o no fA c t u a lC o n t a c tA n g l e i nF o u rＧp o i n tＧc o n t a c tB a l lB e a r i n g[J]．A pＧp l i e d M a t h e m a t i c sa n d N o n l i n e a rS c i e n c e s,２０１６,１(１):５３Ｇ６４．[１３]㊀HA L P I NJD,T R A N A N．A nA n a l y t i c a lM o d e l o fF o u rＧp o i n tC o n t a c tR o l l i n g E l e m e n tB a l lB e a rＧi n g s[J]．J o u r n a lo f T r i b o l o g y,２０１６,１３８(３):３１４０４．[１４]㊀L E B L A N C A,N E L I A SD．B a l lM o t i o na n dS l i dＧi n g F r i c t i o ni na F o u rＧc o n t a c tＧp o i n tB a l lB e a r i n g[J]．J o u r n a l o fT r i b o l o g y,２００７,１２９(４):８０１Ｇ８０８．[１５]㊀L I N B,D U A N M,O KWU D I R E C E,e ta l．A S i m p l i f i e dA n a l y t i c a lM o d e l o fR o l l i n g/S l i d i n g B eＧh a v i o r a n dF r i c t i o n i nF o u rＧp o i n tＧc o n t a c t B a l l B e a rＧi n g sa n dS c r e w s[C]ʊP r o c e e d i n g so ft h e A S M E２０１７I n t e r n a t i o n a l M e c h a n i c a l E n g i n e e r i n g C o nＧg r e s s a n dE x p o s i t i o n．T a m p a:A m e r i c a nS o c i e t y o fM e c h a n i c a l E n g i n e e r s,２０１７:５８３７０．[１６]㊀MAS,L IW,Y A N K,e t a l．AS t u d y o n t h eD yＧn a m i cC o n t a c tF e a t u r eo fF o u rＧc o n t a c tＧp o i n tB a l lB e a r i n g[J]．M e c h a n i c a lS y s t e m sa n dS i g n a lP r oＧc e s s i n g,２０２２,１７４:１０９１１１．[１７]㊀刘少军,路春雨．直升机高速四点接触球轴承接触疲劳可靠性评估方法[J]．航空动力学报,２０１７,３２(１):１３０Ｇ１３７．L I US h a o j u n,L U C h u n y u．C o n t a c tF a t i g u eR e l i aＧb i l i t y A s s e s s m e n t M e t h o d o f H i g h S p e e d F o u rP o i n tＧc o n t a c tB a l l B e a r i n g o fH e l i c o p t e r[J]．J o u rＧn a l o fA e r o s p a c eP o w e r,２０１７,３２(１):１３０Ｇ１３７．[１８]㊀L IK,T A N G W．L o a dＧd i s p l a c e m e n tR e l a t i o n s h i p M o d e l a n dM e a s u r e m e n t o f D e e p G r o o v e B a l l B e a rＧi n g a n d４Ｇp o i n t C o n t a c t B a l l B e a r i n g[J]．J o u r n a l o fM e c h a n i c a lS c i e n c e a n d T e c h n o l o g y,２０２１,３５:３０４５Ｇ３０５８．[１９]㊀Y A O T,WA N GL,L I U X,e t a l．M u l t i b o d y D yＧn a m i c sS i m u l a t i o no fT h i nＧw a l l e dF o u rＧp o i n tC o nＧt a c tB a l lB e a r i n g w i t hI n t e r a c t i o n so fB a l l s,R i n gR a c e w a y sa n d C r o w nＧt y p e C a g e[J]．M u l t i b o d yS y s t e m D y n a m i c s,２０２０,４８:３３７Ｇ３７２．[２０]㊀L IY,L IW,Z HU Y,e t a l．D y n a m i cP e r f o r m a n c eA n a l y s i s o fC a g e i nF o u rＧp o i n tC o n t a c tB a l lB e a rＧi n g[J]．L u b r i c a n t s,２０２２,１０(７):１４９．[２１]㊀俞加欣．避免三点接触临界条件的探讨[J]．轴承,１９９３(１２):６Ｇ９．Y U J i a x i n．D i s c u s s i o n o f C r i t i c a lC o n d i t i o n sf o rA v o i d i n g T h r e eＧp o i n tC o n t a c t[J]．B e a r i n g,１９９３(１２):６Ｇ９．[２２]㊀焦育洁．航空发动机主轴轴承可靠性技术研究[D]．合肥:合肥工业大学,２００４．J I A O Y u j i e．R e s e a r c h o n R e l i a b i l i t y T e c h n o l o g yf o r M a i n S h a f tB e a r i ng so f A i r c r a f tE n g i n e[D]．H e f e i:H e f e iU n i v e r s i t y o fT e c h n o l o g y,２００４．(编辑㊀袁兴玲)作者简介:王亚涛,男,１９９９年生,硕士研究生.研究方向为滚动轴承设计与性能分析.EＧm a i l:w a n g y a t a o h k d＠１６３．c o m.邱㊀明(通信作者),女,１９６９年生,教授㊁博士研究生导师.研究方向为轴承设计与性能分析.EＧm a i l:q i u m i n g６９＠１２６．c o m.４０８２中国机械工程第３４卷第２３期２０２３年１２月上半月。

滚动轴承的刚度分析方法与试验测定任红军【摘要】本文基于Hertz接触理论建立轴承零件模型,在分析轴承零件受力的基础上,给出了轴承内部零件相互作用的具体表达式,分析了轴承载荷(轴向、径向、力矩载荷)对轴承接触应力和接触变形的影响,获得了滚动轴承整体五自由度刚度矩阵的表达形式.在滚动轴承加载试验台上,通过测量不同载荷作用下轴承的轴向位移与径向位移,获得了轴承的刚度特性,与轴承刚度理论计算结果对比,验证模型正确性.【期刊名称】《动力学与控制学报》【年(卷),期】2018(016)006【总页数】6页(P575-580)【关键词】滚动轴承;刚度分析;Hertz接触;位移【作者】任红军【作者单位】辽宁科技大学机械工程与自动化学院,鞍山 114051【正文语种】中文引言滚动轴承的刚度分析是进行轴承设计与优化的基础,对于分析滚动轴承-转子系统的动力学特性具有重要意义,主要涉及滚动体与滚道间的弹性接触问题和轴承整体变形与平衡问题.面向工程设计需求,如何方便有效地确定轴承刚度十分重要. Stribeck[1]首先通过大量试验对钢球及滚道的弹、塑性接触问题进行了研究,确定球轴承的许用接触载荷,给出了球轴承在径向外载荷作用下滚动体最大接触载荷的经验计算公式.Sjovall[2]和Lundberg[3]进行了径向、轴向载荷以及弯矩载荷的滚动轴承滚动体变形与载荷分布规律研究,给出了滚动轴承在联合载荷作用下的套圈位移及载荷分布的计算方法.此外,目前有限元方法广泛应用于滚动轴承刚度分析中,包括计算轴承刚度[4]、接触应力[5,6]、变形[7],有限元模型中可以考虑轴承、轴以及轴承支承结构[8,9].采用有限元法对轴承组件整体分析,存在节点数量与计算精度的矛盾,一般情况下计算量大且费时.对于高速运行下的滚动体等零件惯性力影响,其计算精度更不能满足.Jones[10]假定滚动体与滚道之间的切向接触问题符合Coulomb摩擦定律,并采用滚道控制理论作为滚动体的运动边界条件.Jedrzejewski和Kwasny[11]考虑滚动体离心力、陀螺力矩对接触角影响,建立角接触球轴承力学模型,分析了离心力和陀螺力矩效应对轴承刚度及变形的影响.Noel等[12]在Jones模型基础上提出五自由度角接触球轴承刚度矩阵计算方法.Yi等[13]研究不同轴向预紧力、转速条件下角接触球轴承刚度,并通过试验测量内圈、外圈的位移验证模型准确性.赵春江等[14]研究高速条件下角接触球轴承钢球的陀螺力矩和外部负载以及摩擦系数的关系. 本文基于Hertz接触理论,系统给出了滚动轴承力学模型的建立方法,获得滚动轴承五自由度刚度模型的解析表达式,为滚动轴承的动力学分析与优化设计奠定基础.1 滚动轴承的力学分析滚动轴承的力学模型如图1所示,在该模型中,不计轴承的质量,轴承座及其基础视为刚性,轴承外圈全约束固定,内圈与转轴过盈配合.建立固定坐标系为OXYZ,其坐标原点O为固定点,位于滚动轴承外圈中心点处,X为轴向坐标,Y、Z为径向坐标.作用在滚动轴承上的外载荷和相应的滚动轴承的弹性变形分别为:图1 滚动轴承简化力学模型示意图Fig.1 Simplified mechanical model of rolling bearing假设滚动轴承共有m个滚动体(在这里指滚珠个数).每个滚珠与内外圈接触并相互作用,存在力平衡关系.其力学模型如图2所示.图2 单个滚珠受力学模型图Fig.2 Mechanical model of one ball设滚珠与内外圈的接触满足Hertz接触应力理论,第j个滚珠对轴承内圈沿法线方向的接触力Qj与其变形δj之间的关系为：(1)其中,Kn为滚珠与内外圈之间总的载荷-变形系数(单位N/mn),n是接触指数,对于滚珠轴承可以设为n=1.5.在安装预紧力作用下,产生变形后的滚珠与内外圈的变形示意如图3所示.图中αj 为受负荷后的接触角,为受负荷后内圈沟曲率的中心位置.因外圈固定,受负荷后外圈沟曲率的中心位置仍在Oo处.Aj为和Oo之间的距离,δj为第j个滚珠在接触法向方向上的总接触变形量,δxj为滚珠在轴向的弹性变形量,δrj为滚珠在径向的弹性变形量.图3 滚珠与内外圈的相对变形示意图Fig.3 Relative deformation of inner and outer raceway and ball第j个滚珠在轴向的弹性变形量δxj和在径向的弹性变形量δrj与滚珠轴承的位移q之间的关系如图4所示,其中,总接触变形量δj的两个方向上的分量分别为：δxj=δx+Rj(φysinφj-φzcosφj)(2)δrj=δycosφj+δzsinφj(3)其中,Rj为内滚道沟曲率中心轨迹半径,φj为第j个滚珠的位置角.图4 第j个滚珠与内外圈的相对变形示意图Fig.4 Inner and outer raceway andjth ball deformation式(1)中的滚珠与内外圈之间总载荷-变形系数Kn,是由内圈和外圈的载荷-变形系数Ki、Ko综合求得,即：(4)其中,滚珠内圈和外圈的载荷-变形系数Ki、Ko的计算式为(5)其中,分别是滚珠与内滚道和外滚道的相对趋近量常数,η为综合弹性常数,滚珠与内外套圈接触的曲率和这样,在得到式(1)中的一个滚珠与内外圈之间的载荷-变形系数Kn和接触变形量δj 后,即可得到其弹性接触作用力Qj.2 滚动轴承刚度矩阵的推导滚动轴承的整体载荷-位移关系具有如下关系.即将上面得到的任意位置角φj处的任一滚珠j的弹性接触作用力Qj按轴承总体5个自由度方向进行分解,得:Fxj=QjsinαjFyj=QjcosαjcosφjFzj=QjcosαjsinφjMyj=RjQjsinαjsinφjMzj=-RjQjsinαjcosφj(6)将轴承所有滚珠的接触力进行求和,再根据滚动轴承内圈的平衡条件, 即作用在轴承上的外力与所有钢球对内圈的作用力平衡,可得如下轴承整体平衡方程：(7)在受小载荷作用时,滚珠与套圈之间的接触变形一般是微米级的.在微小变形情况下,滚动轴承各方向上的刚度可近似为线性刚度,即滚动轴承的外载荷与轴承位移之间的关系可记为F=Kq(8)其中K为滚动轴承刚度矩阵,为5×5阶的矩阵,其定义为:(9)其中Kij是刚度矩阵元素,是外载荷分量对弹性位移分量的偏导数.若忽略交叉刚度,只考虑5个方向的主刚度,滚动轴承刚度矩阵K可记为：(10)在已知轴承外载荷F的情况下,通过求解式(10)组成的非线性方程组,得出该轴承载荷作用下的轴承位移提供求得的位移向量估算轴承刚度矩阵元素Kij,进而确定刚度矩阵K.3 结果与分析3.1 轴承参数以71807AC角接触球轴承为例加以分析,所采用轴承的内外圈及滚动体所采用的材料均为GCr15轴承钢,轴承基本参数如表1所示.表1 71807AC角接触球轴承基本参数Table 1 Basic parameters of angular contact ball bearings 71807ACParameterValueDiameter of inner ringDi35.0mmDiameter of outer ring Do47.0mmBall diameter D3.14mmCo ntact angle25°Width7mmCount of ball m25Load-deformation index n3/2Young′s modulus2.07e11 PaPoisson′s ratio0.3Load deformation coefficient1.0649e10 N/mnAxial preload1000N3.2 轴承刚度测试滚动轴承刚度测试试验台如图5所示.被测滚动轴承安装在轴上,其内圈与轴过盈配合,外圈固定在轴承支座上.加载装置分别位于轴向和径向两个方向上,通过力传感器数显装置读取施加的载荷大小,数显千分表分别位于滚动轴承左端轴向方向和靠近轴承的转轴水平方向,用以近似轴承的轴向和径向位移.图5 滚动轴承性能测试原理性试验器Fig.5 Test rig for performances of ball bearing3.3 测试结果对比分析将试验结果与仿真分析的计算结果进行比较.图6表示了不同轴向负荷作用下,轴承的轴向变形情况.图6 不同轴向载荷作用下轴承的轴向位移Fig.6 Axial displacement of ball bearing vs. axial preload由图6可以看出,试验具有很好的重复性,四次测试的结果基本一致.此外,仿真分析结果与试验测试结果在趋势上表现出一致性.轴承轴向测试刚度和仿真计算的轴承轴向刚度比较如图7所示.由图7可以看出,在给定的轴向载荷范围内(500～3500N),试验所得的轴承轴向刚度出现波动,仿真分析结果随着轴向载荷的增大而增大.测试所得轴向刚度较小,由于考虑了试验装置中轴、轴承座和轴承的串联后的刚度.在固定的轴向预载(2800N)条件下,不同径向载荷作用下,轴承的径向位移变化规律和径向刚度变化,分别如图8和9所示.图7 不同轴向载荷作用下轴承的轴向刚度Fig.7 Axial stiffness of ball bearing vs. axial preload图8 不同径向载荷作用下轴承径向位移Fig.8 Radial displacement of ball bearing vs. radial preload图9 不同径向载荷作用下轴承径向刚度Fig.9 Radialstiffness of ball bearing vs. radial preload由图8可以看出,试验具有良好的重复性,六次测试的结果基本一致.此外,仿真分析结果与试验测试结果在趋势上表现出一致性,随着径向载荷的增大,径向位移均呈线性增大趋势.由图9可以看出,在给定的径向载荷范围内(500～3000N),试验所得的轴承径向刚度呈现先减小后增大的趋势,仿真分析结果随着轴向载荷的增大而增大.试验测试所得轴承刚度较小,由于该刚度为考虑了试验装置中轴、轴承座和轴承的串联后的综合刚度.该试验测试结果与仿真分析结果在整体趋势上表现出了相似性,一定程度上验证了仿真计算模型的有效性.4 结论(1)本文给出了小变形下,基于Hertz接触理论滚动轴承五自由度刚度矩阵的计算方法；(2)轴承内圈位移整体上随着载荷的增大而呈线性增大；(3)利用刚度模型获得的理论分析结果与试验测试结果在趋势上表现出良好的一致性.参考文献【相关文献】1Stribeck R. Ball bearings for various loads. Trans ASME, 1907,29:420～4632Sjoväll H. The load distribution within ball and roller bearings under given exte rnal radial and axial load. Teknisk Tidskrift, Mek, 1933,19(3):72～753Lundberg G, Palmgren A. Dynamic capacity of roller bearings. Journal of Applied Mechanics-Transactions of the ASME, 1949,16(2):165～1724Guo Y, Parker R G. Stiffness matrix calculation of rolling element bearings using a finite element/contact mechanics model. Mechanism and Machine Theory, 2012,51(5):32～45 5Lostado R, García R E, Martinez R F. Optimization of operating conditions for a double-row tapered roller bearing. International Journal of Mechanics and Materials in Design, 2016, 12(3): 1～216Lostado R, Martinez R F, Donald B J M. Determination of the contact stresses in double-row tapered roller bearings using the finite element method, experimental analysis and analytical models. Journal of Mechanical Science and Technology, 2015,29(11):4645～46567Nataraj C, Harsha S P. The effect of bearing cage run-out on the nonlinear dynamics of a rotating shaft. Communications in Nonlinear Science and Numerical Simulation,2008,13(4):822～8388Cao L, Brouwer M D, Sadeghi F, et al. Effect of housing support on bearing dynamics. Journal of Tribology, 2015,138(1):0111059George B, Prasad N S. Finite element analysis of squirrel cage ball bearingsfor gas turbine engines. Defence Science Journal, 2007,57(2):165～17110 Jones A. Ball motion and sliding friction in ball bearings. Journal of Basic Engineering, 1959,81(3):1～1211 Jedrzejewski J, Kwasny W. Modelling of angular contact ball bearings and axial displacements for high-speed spindles. CIRP Annals-Manufacturing Technology, 2010,59(1):377～38212 Noel D, Ritou M, Furet B, et al. Complete analytical expression of the stiffness matrix of angular contact ball bearings. Journal of Tribology, 2013,135(4):04110113 Yi D, Yang Y, Zhuo X, et al. An improved dynamic model for angular contact ball bearings under constant preload. Journal of the Chinese Institute of Engineers,2016,39(8):900～90614 Zhao C, Yu X, Huang Q, et al. Analysis on the load characteristics and coefficient offriction of angular contact ball bearing at high speed. Tribology International, 2015,87:50～56。

角接触球轴承保持架柔性多体动力学分析
姚廷强;谢伟;谭阳
【期刊名称】《中国机械工程》
【年(卷),期】2014(025)001
【摘要】考虑套圈、钢球和保持架的结构弹性变形与动态接触关系,建立了角接触球轴承柔性多体接触动力学有限元仿真模型.在不同引导游隙、转速和径向力下,运
用ANSYS/LS-DYNA仿真分析了角接触球轴承的动力学性能,以及保持架的动态冲击应力和稳定性.计算讨论了角接触球轴承的动态接触应力,获得了保持架的角速度、动态冲击应力、质心运动轨迹等仿真结果,它们与理论计算结果具有较好的一致性.
结果表明,球轴承运动速度的变化对保持架的动态冲击应力和稳定性的影响较大.【总页数】6页(P117-122)
【作者】姚廷强;谢伟;谭阳
【作者单位】昆明理工大学,昆明,650093;昆明理工大学,昆明,650093;昆明理工大学,昆明,650093
【正文语种】中文
【中图分类】TH133.33;O313.7
【相关文献】
1.球轴承柔性多体动力学分析与接触振动研究 [J], 姚廷强;迟毅林;王立华;黄亚宇
2.角接触球轴承多体动力学分析 [J], 产文兵;姚廷强
3.角接触球轴承保持架动力学分析 [J], 邓四二;郝建军;滕弘飞;高银涛
4.角接触球轴承柔性多体接触动力学分析 [J], 姚廷强;谭阳;王里达
5.高速角接触球轴承保持架柔体动力学分析 [J], 邓四二;谢鹏飞;杨海生;高银涛因版权原因，仅展示原文概要，查看原文内容请购买。

陶瓷球轴承与钢球轴承的区别陶瓷球轴承与钢球轴承是两种常见的轴承类型，它们在材质、结构和性能等方面存在一些区别。

下面将就这些方面进行详细的比较，以帮助我们更好地理解陶瓷球轴承和钢球轴承的不同。

1. 材质陶瓷球轴承的最大特点是采用陶瓷材料制作，常用的陶瓷材料有硅酸盐陶瓷、氧化铝陶瓷和氮化硅陶瓷等。

这些材料具有低密度、高硬度、高强度、低热膨胀系数、高温耐受力强等特点，使得陶瓷球轴承具备更好的耐磨性和高速运转能力。

相比之下，钢球轴承的球体和内外圈均由钢材制成，其特点是强度高、坚固耐用。

2. 密封性陶瓷球轴承由于材料的特性，具有良好的密封性能，陶瓷材料的低摩擦系数可以减少泄漏和干涉，从而使密封效果更佳。

而钢球轴承一般需要额外的密封装置来增强其密封性。

3. 耐腐蚀性陶瓷材料具有良好的耐腐蚀性，能够抵抗酸、碱等腐蚀性介质的侵蚀，因此陶瓷球轴承在恶劣的工作环境中表现更出色。

而钢球轴承在腐蚀性介质中容易出现腐蚀、生锈等问题。

4. 温度特性陶瓷材料具有优异的高温特性，能够在高温环境下工作，并保持较低的热膨胀系数。

相比之下，钢球轴承的温度特性较差，容易受热膨胀的影响，从而影响其使用寿命。

5. 润滑要求陶瓷球轴承材料表面光滑，在很多情况下可以忽略润滑要求，减小了维护成本。

而钢球轴承需要在运转时添加润滑剂，以减少摩擦和磨损。

6. 重量陶瓷材料的密度低于钢材，因此陶瓷球轴承相对钢球轴承具备更轻的重量。

在需要减轻设备负担、提高运转效率的场合，采用陶瓷球轴承能够有效地实现这一目标。

7. 噪音和振动陶瓷球轴承由于材质的特点，表现出较低的噪音和振动水平。

相比之下，钢球轴承在高速运转时容易产生噪音和振动，影响使用效果和舒适性。

综上所述，陶瓷球轴承和钢球轴承具有不同的材质、结构和性能特点。

作为技术的进步，陶瓷轴承在一些特定的应用领域表现得更出色，如高速运转、高温环境、腐蚀性介质等。

但由于其生产成本较高，陶瓷轴承在一些一般性应用中难以替代传统的钢球轴承。