2015春北师大七年级下册数学《2.2 探索直线平行的条件》习题3

《探究直线平行的条件》习题一、选择题1．如图，直线AB ，CD 被直线EF 所截，以下判断中不正确的选项是( )A.∠3=∠6B.∠2=∠6C.∠1 和∠4 是内错角D.∠3 和∠5 是同位角2．如图，以下四组角中是同位角的是( )A.∠1 与∠7B.∠3 与∠5C.∠4 与∠5D.∠2 与∠63．如图，此中内错角的对数是( )A.5B.2C.3D.44．∠1 和∠2 是直线AB ，CD 被直线EF 所截而形成的内错角，那么∠1 和∠2 的大小关系是( )A.∠1=∠2B.∠1＞∠2C.∠1＜∠2D.没法确立5．如图，在以下条件中，能判断AD ∥BC 的是( )A.∠DAC= ∠BCAB.∠DCB+ ∠ABC=180°C.∠ABD= ∠BDCD.∠BAC= ∠ACD6．如图，在平移三角尺画平行线的过程中，原因是( )A.两直线平行，同位角相等B.两直线平行，内错角相等C.同位角相等，两直线平行D.内错角相等，两直线平行二、填空题7．如图，按角的地点关系填空：∠A 与∠2 是_____．8．如图，∠B 的同位角是_____．9．如图，以下条件中：①∠B+∠BCD=18°0 ；②∠1=∠2；③∠3=∠4；④∠B=∠5；则必定能判断AB ∥CD 的条件有_____(填写全部正确的序号)．10．如图：已知：∠1=105°，∠2=105°，则_____∥_____．三、解答题11．如图，∠1和∠2是哪两条直线被哪一条直线所截形成的？它们是什么角？∠1和∠3是哪两条直线被哪一条直线所截形成的？它们是什么角？12．如图，直线AB，CD订交于点O．写出∠1，∠2，∠3，∠4中每两个角之间的地点关系．13．如图，直线AB，CD订交于O，∠AOD+∠C=180°，直线AB与CE必定平行吗？试着说明你的原因．14．如图：已知∠1和∠D互余，CF⊥DF，试证明AB∥CD．15．如图，△ABC中，∠ACB=90°，CD⊥AB，点D为垂足，点E，F分别在AC．AB边上，且∠AEF=∠B．求证：EF∥CD．参照答案一、选择题1．答案：B分析：【解答】A、依据对顶角相等可得∠3=∠6，故此选项不合题意；B、∠2 和∠6 是同位角，不必定相等，故此选项切合题意；C、∠1 和∠4 是内错角，故此选项不合题意；D、∠3 和∠5 是同位角，故此选项不合题意；应选：B．【剖析】依据对顶角相等，三线八角同位角、内错角或同旁内角定义进行剖析．2．答案：D分析：【解答】依据同位角、邻补角、对顶角的定义进行判断，A、∠1 与∠7 不是同位角，故A 错误；B、∠3 与∠5 是内错角，故B 错误；C、∠4 与∠5 是同旁内角，故C 错误；D、∠2 与∠6 是同位角，故D 正确．应选：D．【剖析】同位角就是：两个角都在截线的同旁，又分别处在被截的两条直线同侧的地点的角．3．答案：D分析：【解答】以下图，是内错角的有：∠ 2 与∠3；∠1 与∠3；∠ 2 与∠4；∠ 1 与∠4．应选D．【剖析】内错角就是：两个角都在截线的异侧，又分别处在被截的两条直线之间的角．4．答案：D分析：【解答】由于两直线的地点关系不确立，因此∠ 1 和∠2 的大小关系也没法确立．应选D．【剖析】从两直线能否平行的角度考虑．5．答案：A分析：【解答】A、∵∠DAC= ∠BCA ，∴AD ∥BC（内错角相等，两直线平行）．故本选项正确；B、依据“∠DCB+ ∠ABC=180°”只好判断“DC∥AB”，而非AD ∥BC．故本选项错误；C、依据“∠ABD= ∠BDC”只好判断“DC∥AB”，而非AD ∥BC．故本选项错误；D、依据“∠BAC= ∠ACD”只好判断“DC∥AB”，而非AD ∥BC．故本选项错误；应选 A ．【剖析】依据各选项中各角的关系及利用平行线的判断定理，分别剖析判断AD、BC 能否平行即可．6．答案：C分析：【解答】∵∠DPF=∠BMF∴AB ∥CD（同位角相等，两直线平行）．应选C．【剖析】由题意联合图形可知∠DPF=∠BMF ，从而得出同位角相等，两直线平行．二、填空题7．答案：同旁内角分析：【解答】依据图形，∠ A 与∠2 是同旁内角．【剖析】依据两直线被第三条直线所截，在截线的同一侧，被截线的同一方向的两个角是同位角；在截线的双侧，被截线的内部的两个角是内错角；在截线的同一侧，被截线的内部的两个角是同旁内角，联合图形找出即可．8．答案：∠ECD，∠ACD分析：【解答】∠ B 的同位角是∠ECD ，∠ACD ，【剖析】依据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，而且在第三条直线（截线）的同旁，进行剖析可得答案．9．答案：①③④分析：【解答】①∵∠B+∠BCD=18°0 ，∴AB ∥CD；②∵∠1=∠2，∴AD ∥CB；③∵∠3=∠4，④∵∠B=∠5，【剖析】依据平行线的判断方法：同旁内角互补，两直线平行可得①能判断AB ∥CD；依据内错角相等，两直线平行可得③能判断AB ∥CD；依据同位角相等，两直线平行可得④能判断AB ∥CD．10．答案：a b分析：【解答】∵∠1=105°，∠2=105°，∴∠1=∠2，∴a∥b．【剖析】依据角度相等获得∠1=∠2，再依据同位角相等，两直线平行解答．三、解答题11．答案：∠1 和∠2 是直线EF、DC 被直线AB 所截形成的同位角，∠1 和∠3 是直线AB 、CD 被直线EF 所截形成的同位角．分析：【解答】∠ 1 和∠2 是直线EF、DC 被直线AB 所截形成的同位角，∠ 1 和∠3 是直线AB 、CD 被直线EF 所截形成的同位角．【剖析】依据同位角的观点作答．正确辨别同位角、内错角、同旁内角的重点，是弄清哪两条直线被哪一条线所截．也就是说，在鉴别这些角以前，要弄清哪一条直线是截线，哪两条直线是被截线．12．答案：∠1 和∠3 是对顶角；∠1 和∠2 是邻补角，∠2 与∠3 是邻补角；∠1 和∠ 4 是同位角，∠ 2 与∠4 是同旁内角，∠ 3 与∠ 4 是内错角．分析：【解答】∠ 1 和∠ 3 是对顶角；∠ 1 和∠ 2 是邻补角，∠ 2 与∠3 是邻补角；∠1 和∠ 4 是同位角，∠ 2 与∠4 是同旁内角，∠ 3 与∠ 4 是内错角．【剖析】联合图形，依据同位角、内错角、同旁内角和对顶角、邻补角的定义求解．正确识别同位角、内错角、同旁内角的重点，是弄清哪两条直线被哪一条线所截．也就是说，在辨别这些角以前，要弄清哪一条直线是截线，哪两条直线是被截线．13．答案：看法答过程．分析：【解答】直线AB 与CE 必定平行．原因以下：∵∠AOD+ ∠C=180°，而∠AOD= ∠BOC，∴∠BOC+ ∠C=180°，∴AB ∥CE．(word完整版)北师大七年级下2.2《探索直线平行的条件》习题含详细答案【剖析】依据对顶角相等获得∠AOD= ∠BOC，又∠AOD+ ∠C=180°，则有∠BOC+ ∠C=180°，依据同旁内角互补，两直线平行即可获得AB ∥CE.14．答案：看法答过程．分析：【解答】∵CF⊥DF ，∴∠C+∠D=90°，又∠1 和∠D 互余，即∠1+∠D=90°，∴∠1=∠C，∴AB ∥CD．【剖析】经过∠ D 中间量的转变，获得∠1=∠C，从而可得出平行．15．答案：看法答过程．分析：【解答】证明：∵∠ACB=90°，∴∠B+∠A=90°，∵CD⊥AB ，∴∠ADC=9°0 ，∴∠A+∠ACD=9°0 ，∴∠B=∠ACD ，∵∠AEF= ∠B，∴∠AEF= ∠ACD ，∴EF∥CD．【剖析】第一依据直角三角形的性质可得∠B+ ∠A=90°，再依据CD⊥AB 可得∠A+ ∠ACD=90°，从而获得∠B=∠ACD ，而后在证明∠AEF= ∠ACD ，可证明EF∥CD．1 / 11。

数学北师大版七年级下册《探索直线平行的条件》同步练习《2.2 探索直线平行的条件》同步练习3一、判断题（1）同位角一定相等；（）（2）两条直线被三条直线所截，如果同错角相等，则这两条直线平行；（）（3）长方形对边互相平行；（）（4）如图，如果?=∠45A ，要使AB a //，则必须有?=∠451．（）二、填空题1．如图，21l l 、和3l 相交，1∠和2∠是______角，1∠和3∠是______角，2∠和3∠是______角，2∠和4∠是______角．2．如图，直线AB 、CD 、GH 相交于M 点，EF 、GH 相交于N 点，则和ENG ∠是同位角的有_____________________，和E N G ∠是内错角的有_________，和EN G ∠是同旁内角的有____________________．3．如果两条直线被第三条直线所截，要使这两条直线平行，角的条件必须有________或__________或________．4．如图：C ∠的同位角是______，B ∠的内错角是______，EAC ∠的同旁内角是______．三、解答题1．如图：?=∠+∠∠=∠∠=∠18031,42,41，找出其中互相平行的直线，并说明理由．2．如图，已知DE 平分AF BDF ,∠平分BAC ∠，且21∠=∠，试说明AC DF //．3．在同一平面内，垂直于同一直线的两条直线平行吗？如果平行请说明理由．参考答案一、判断题（1）× （2）√ （3）√ （4）√二、填空题1．（1）同位，对顶，内错，同旁内2．GMC ∠和BMN AMG ∠∠,和CMN DMN ∠∠,和AMN ∠3．内错角相等、同位角相等、同旁内角互补4．C ∠∠∠,2,1三、解答题1．b a n m l // //// 理由（略）2．说明：因为22,12∠=∠∠=∠BAC BDF ，又因为21∠=∠，所以BAC BDF ∠=∠，所以AC DF //，根据是同位角相等，两直线平行．3．平行，根据是同位角都是直线，或内错角都是直角，即相等，两直线平行，或根据同旁内角都是直角所以互补，故两直线平行．。

北师大版七年级数学下册 2.2《探索直线平行的条件》同步测试北师大版七年级数学下册2.2探索直线平行的条件同步测试一、单选题1．如图，用两个相同的三角板按照如图所示的方式作平行线，能解释其中道理的是( ) A. 同位角相等，两直线平行 B. 内错角相等，两直线平行C. 同旁内角互补，两直线平行D. 以上都不对第1题图第3题图第4题图第5题图2．若直线a∥b，b∥c，则a∥c的依据是( )A. 平行公理B. 等量代换C. 等式的性质D. 平行于同一条直线的两条直线互相平行3．如图，下列能判定AB∥EF的条件有（）①∠B+∠BFE=180°②∠1=∠2③∠3=∠4④∠B=∠5．A. 1个B. 2个C. 3个D. 4个4．如图，直线AB，CD被直线EF所截，∠1=55°，下列条件中能判定AB∥CD的是（）A. ∠2=35° B. ∠2=45° C. ∠2=55° D. ∠2=125°5．如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（）A. ∠3=∠AB. ∠1=∠2C. ∠D=∠DCED. ∠D+∠ACD=180°6．已知如图直线a，b被直线c所截，下列条件能判断a∥b的是（）A. ∠1=∠2B. ∠2=∠3C. ∠1=∠4D. ∠2+∠5=180°第6题图第7题图第8题图第9题图7．如下图，在下列条件中，能判定AB//CD的是（）A. ∠1=∠3B. ∠2=∠3C. ∠1=∠4D. ∠3=∠48．如图所示，“过点P画直线a的平行线b”的作法的依据是（）A. 内错角相等，两直线平行B. 同位角相等，两直线平行C. 两直线平行，内错角相等D. 两直线平行，同位角相等9．如图所示,若∠1与∠2互补,∠2与∠4互补,则()A. l3∥l4l2∥l5 C. l1∥l5 D. l1∥l210．如图所示，下列说法正确的是（）A. 若∠3＝∠5，则CD∥EFB. 若∠2＝∠6，则CD∥EFC. 若∠4＝∠3，则CD∥EFD. 若∠1＝∠6，则GH∥AB第10题图第11题图第12题图11．如图所示，要得到DE∥BC，则需要条件（）A. CD⊥AB，GF⊥ABB. ∠4＋∠5＝180°C. ∠1＝∠3D. ∠2＝∠312．在下列条件中，不能判定AB DF的是（）A. 2180A∠+∠=︒ B. 3A∠=∠ C. 14∠=∠ D. 1A∠=∠二、填空题13．如图，已知∠B＝40°，要使AB∥CD，需要添加一个条件，这个条件可以是___．第13题图第14题图第15题图第16题图14．如图，若AB⊥BC，BC⊥CD，则直线AB与CD的位置关系是______．15．如图，PC∥AB，QC∥AB，则点P，C，Q在一条直线上．理由是____________________ 16．如图，两直线a．b被第三条直线c所截，若∠1=50°，∠2=130°，则直线a．b的位置关系是____________ ．17．如图，下列条件中：①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5；则一定能判定AB∥CD的条件有_____(填写所有正确的序号)．第17题图第18题图18.已知：如图，∠EAD=∠DCF，要得到AB∥CD，则需要的条件________．（填一个你认为正确的条件即可）三、解答题19．如图所示，EF⊥BD，垂足为E，∠1＝50°，∠2＝40°，试判断AB与CD是否平行，并说明理由．20．如图，一条直线分别与直线BE、直线CE、直线CF、直线BF相交于点A，G，D，H且∠1=∠2，∠B=∠C（1）找出图中相互平行的线，说说它们之间为什么是平行的；（2）证明：∠A=∠D．21．将一副三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．求证：CF//AB22．如图，在ΔABC中，CD是高，点E、F、G分别在BC、AB、AC上且EF⊥AB，∠1=∠2，试判断DG与BC的位置关系，并说明理由.23．如图，已知∠ADE=∠B，∠1=∠2，那么CD与FG平行吗？说明理由．24．如图，已知∠1=50°，∠2=50°，∠3=130°，找出图中的平行线，并说明理由；25．已知：如图：∠1=∠2，∠3+∠4= 180°；确定直线a，c的位置关系，并说明理由；解：a c；理由：∵∠1=∠2（）,∴ a // ( )；∵∠3+∠4= 180°（）,∴ c // ( )；∵ a // ,c // ,∴// ( )参考答案及解析1．B【解析】如图：∵∠ABD=∠BAC=30°,根据内错角相等两直线平行，可得AC∥BD.故选：B. 点睛：本题主要考查平行线的判定，解题的关键是：对顶角相等两直线平行这一判定定理的理解和掌握.2．D【解析】因为直线a∥b,b∥c,所以a∥c的依据是平行于同一条直线的两条直线互相平行,故选D.3．C【解析】①∠B+∠BFE=180°，根据同旁内角互补，两直线平行得出AB∥EF；②∠1=∠2，根据内错角相等，两直线平行，得出//DE BF；③∠3=∠4,根据内错角相等，两直线平行，得出AB∥EF；④∠B=∠5，根据同位角相等，两直线平行，得出AB∥EF；故选C.4．C【解析】试题分析：A、由∠3＝∠2＝35°，∠1＝55°推知∠1≠∠3，故不能判定AB∥CD，故本选项错误；B、由∠3＝∠2＝45°，∠1＝55°推知∠1≠∠3，故不能判定AB∥CD，故本选项错误；C、由∠3＝∠2＝55°，∠1＝55°推知∠1＝∠3，故能判定AB∥CD，故本选项正确；D、由∠3＝∠2＝125°，∠1＝55°推知∠1≠∠3，故不能判定AB∥CD，故本选项错误；故选：C．点睛：本题考查了平行线的判定定理，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．5．B【解析】试题解析：B, 12,∠=∠AB∴∥.CD(内错角相等，两直线平行).故选B.6．A【解析】试题解析：∵∠1=∠2，∴a∥b；故选A．7．C【解析】根据平行线的判定，可由∠2=∠3，根据内错角相等，两直线平行，得到AD∥BC，由∠1=∠4，得到AB∥CD.故选：C.8．A 【解析】如图所示，根据图中直线a、b被c所截形成的内错角相等，可得依据为内错角相等，两直线平行．故选：A.点睛：本题考查的是平行线的判定定理，即内错角相等，两直线平行．比较简单．9．D【解析】因为∠1与∠2互补，∠2与∠4互补，可知∠1+∠2=180°，∠2+∠4=180°，所以∠1=∠4，根据内错角相等，两直线平行可得l1∥l2，故选D.10．C【解析】解：∠4和∠3是直线EF和CD被直线GB所截形成的内错角，所以∠4＝∠3时，CD∥EF．故选C．11．C【解析】解：∠1和∠3是直线DE和BC被直线CD所截形成的内错角，所以要得到DE∥BC，需∠1＝∠3．故选C．12．D【解析】∵∠A+∠2=180°，∴AB∥FD，故A选项能判定；∵∠A=∠3，∴AB∥FD，故B选项能判定；∵∠1=∠4，∴AB∥FD，故C选项能判定；∵∠1=∠A，∴ED∥FC，故D选项不能判定.故选D.点睛：掌握平行线的判定定理.13．∠BED＝40°【解析】当∠B=∠BED时,AB∥CD，所以添加∠BED=40°时,可得到AB∥CD.故答案为∠BED=40°.14．AB∥CD【解析】∵AB⊥BC，BC⊥CD，∴∠ABC=∠BCD=90°，∴AB∥CD，故答案为AB∥CD.15．经过直线外一点，有且只有一条直线与这条直线平行【解析】∵PC∥AB,QC∥AB,∵PC和CQ都过点C,∴P,C,Q在一条直线上（过直线外一点有且只有一条直线和已知直线平行）,故答案为:过直线外一点有且只有一条直线平和已知直线平行．16．a∥b．【解析】因为∠2=130°，所以∠3=50°，∠1=50°,所以a∥b．故答案为a∥b．17．①③④【解析】试题解析：①∵∠B+∠BCD=180°，∴AB∥CD；②∵∠1=∠2，∴AD∥CB；③∵∠3=∠4，∴AB∥CD；④∵∠B=∠5，∴AB∥CD考点：平行线的判定．18．答案不唯一，如∠EAD=∠B【解析】如图，∵∠EAD=∠DCF，即∠1=∠3，而想要AB//CD，则需∠2=∠3，∴只要添加条件∠1=∠2即可，即∠EAD=∠B.故答案为∠EAD=∠B（答案不唯一）19．AB与CD平行，理由见解析.【解析】试题分析：首先根据垂直的定义求出∠D的度数，再根据同位角相等，证明两直线平行．试题解析：AB与CD平行．理由：∵EF⊥BD，∴∠FED＝90°，∴∠D＝90°－∠1＝40°，∴∠2＝∠D，∴AB∥CD.20．（1）CE∥BF，AB∥CD．理由见解析.（2）证明见解析.【解析】试题分析：（1）根据同位角相等，两直线平行可得CE∥FB，进而可得∠C=∠BFD，再由条件∠B=∠C可得∠B=∠BFD，从而可根据内错角相等，两直线平行得AB∥CD；（2）根据（1）可得AB∥CD，再根据两直线平行，内错角相等可得∠A=∠D．试题解析：（1）CE∥BF，AB∥CD．理由：∵∠1=∠2，∴CE∥FB，∴∠C=∠BFD，∵∠B=∠C，∴∠B=∠BFD，∴AB∥CD；（2）由（1）可得AB∥CD，∴∠A=∠D．21．详见解析.【解析】试题分析：利用三角板角的大小关系证明∠1=∠3=45°，所以内错角相等，两直线平行.试题解析：∵CF平分∠DCE，∴∠1=∠2=12∠DCE，∵∠DCE=90°，∴∠1=45°，∵∠3=45°，∴∠1=∠3，∴AB∥CF（内错角相等，两直线平行）；22．见解析【解析】试题分析：DG∥BC，由EF⊥AB，CD⊥AB，可得EF∥CD，所以∠2=∠DCB，因为∠1=∠2，所以∠DCB=∠1，所以DG∥BC.试题解析：DG∥BC，理由如下：∵EF⊥AB，CD⊥AB，∴EF∥CD，∴∠2=∠DCB，∵∠1=∠2，∴∠DCB=∠1，∴DG∥BC.点睛：掌握平行线的性质及判定方法.23．CD∥FG，理由见解析.【解析】试题分析：先由∠ADE=∠B可得DE∥BC，进而得出∠1=∠DCB，又因为∠1=∠2，所以∠2=∠DCB，即可证明CD∥FG.试题解析：CD∥FG；证明：∵∠ADE=∠B，∴DE∥BC，∴∠1=∠DCB，∵∠1=∠2，∴∠2=∠DCB，∴CD∥FG.点睛：掌握平行线的性质定理和判定定理.24．AC//OB，OA//BC【解析】试题分析：证明如下：如图所示，因为∠1=∠2，由“同位角相等，两直线平行”，可得AC//O B。

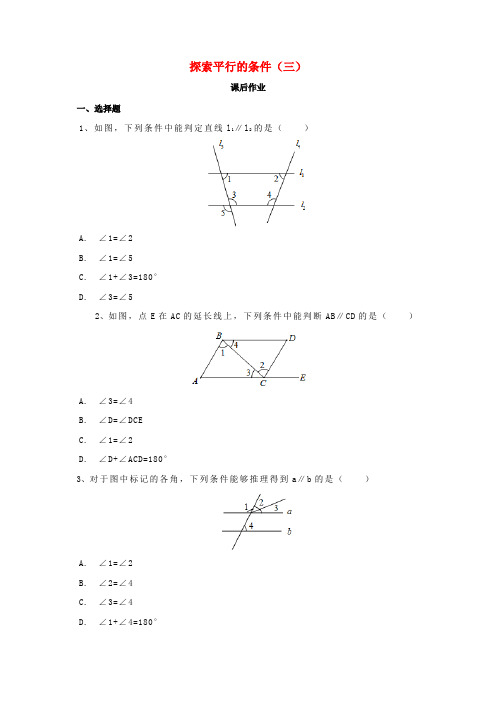
探索平行的条件（三）
课后作业
一、选择题
1、如图，下列条件中能判定直线l1∥l2的是（）
A. ∠1=∠2
B. ∠1=∠5
C. ∠1+∠3=180°
D. ∠3=∠5
2、如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（）
A. ∠3=∠4
B. ∠D=∠DCE
C. ∠1=∠2
D. ∠D+∠ACD=180°
3、对于图中标记的各角，下列条件能够推理得到a∥b的是（）
A. ∠1=∠2
B. ∠2=∠4
C. ∠3=∠4
D. ∠1+∠4=180°
4、如图所示，已知∠1=∠2，要使∠3=∠4，只要（）
A. ∠1=∠3
B. ∠2=∠4
C. ∠1=∠4
D. AB∥CD
5、一个弯形管道ABCD的弯角∠A BC=130°，∠BCD=50°，则管道AB与CD的位置关系是（）
A. 平行
B. 垂直
C. 相交但不垂直
D. 无法确定
二、填空题
6、如图，已知C、D、E三点在同一直线上，∠1=105°，∠A=75°．
求证：AB∥CD．
证明一：∵C、D、E三点在同一直线上，
∴∠1+∠2=180°（平角定义），
∵∠1=105°，
∴∠2=75°（），
又∵∠A=75°，
∴∠2=∠A，
∴AB∥CD ．
证明二：∵C、D、E三点在同一直线上，
∴∠1和∠A是直线AB和直线CD被直线AD所截得到的同旁内角（同旁内角定义），又∵∠A=75°，∠1=105°，。

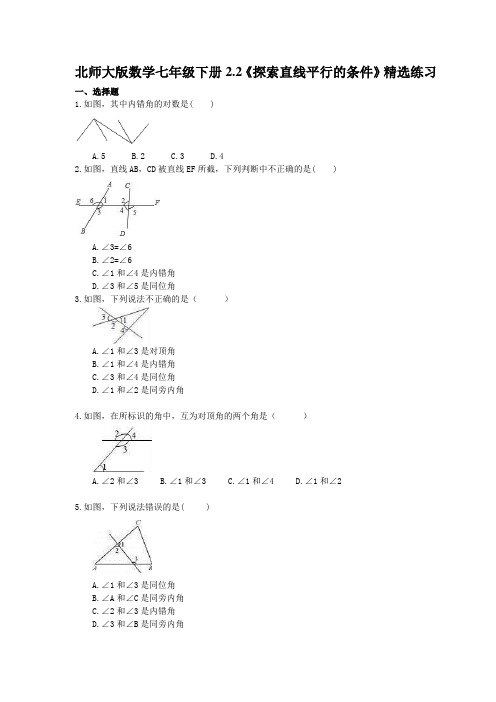
北师大版数学七年级下册2.2《探索直线平行的条件》精选练习一、选择题1.如图，其中内错角的对数是( )A.5B.2C.3D.42.如图，直线AB，CD被直线EF所截，下列判断中不正确的是( )A.∠3=∠6B.∠2=∠6C.∠1和∠4是内错角D.∠3和∠5是同位角3.如图，下列说法不正确的是（）A.∠1和∠3是对顶角B.∠1和∠4是内错角C.∠3和∠4是同位角D.∠1和∠2是同旁内角4.如图，在所标识的角中，互为对顶角的两个角是（）A.∠2和∠3B.∠1和∠3C.∠1和∠4D.∠1和∠25.如图，下列说法错误的是( )A.∠1和∠3是同位角B.∠A和∠C是同旁内角C.∠2和∠3是内错角D.∠3和∠B是同旁内角6.如图所示，∠1与∠2不是同位角的是( )7.如图，在下列条件中，能判断AD∥BC的是( )A.∠DAC=∠BCAB.∠DCB+∠ABC=180°C.∠ABD=∠BDCD.∠BAC=∠ACD8.下列说法正确的是( ).A.不相交的两条直线即平行B.过一点有且只有一条直线与已知直线平行C.与同一条直线相交的两直线相交D.若a∥b，b∥c，则a∥b∥c.9.过直线l外一点P作直线l的平行线，下列尺规作图中错误的是（）A. B. C. D.10.如图，AB∥CD，EF∥GH，且∠1=50°，下列结论错误的是( )A.∠2=130°B.∠3=50°C.∠4=130°D.∠5=50°11.下列图形中，已知∠1=∠2,则可得到AB∥CD的是 ( )12.设a,b,c是三条不同的直线，则在下面四个命题中，正确的有( )①如果a与b相交，b与c相交，那么a与c相交；②如果a与b平行，b与c平行，那么a与c平行；③如果a与b垂直，b与c垂直，那么a与c垂直；④如果a与b平行，b与c相交，那么a与c相交.A.4个B.3个C.2个D.1个二、填空题13.如图，按角的位置关系填空：∠A与∠2是_____.14.如图，写出图中的一对内错角 .15.如图，用给定的∠1至∠5完成填空：∠1与是同位角，∠2与是内错角.16.如图，∠ABC与是同位角；∠ADB与是内错角；∠ABC与是同旁内角.17.如图，下列条件中：①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5；则一定能判定AB∥CD的条件有_____(填写所有正确的序号).18.看图填理由：∵直线AB，CD相交于O,（已知）∴∠1与∠2是对顶角∴∠1=∠2（___________________）∵∠3+∠4=180°（已知）∠1+∠4=180°（__________________）∴∠1=∠3（__________________）∴CD//AB（__________________）三、解答题19.如图，∠1和∠2是哪两条直线被哪一条直线所截形成的？它们是什么角？∠1和∠3是哪两条直线被哪一条直线所截形成的？它们是什么角？20.如图，BE是AB的延长线，指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的？它们是什么角？（1）∠A和∠D；（2）∠A和∠CBA；（3）∠C和∠CBE.21.如图：已知∠1和∠D互余，CF⊥DF，试证明AB∥CD.22.如图所示,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,试说明DA⊥AB.23.如图,已知CD⊥DA，DA⊥AB,∠1=∠2,问直线DE与AF是否平行？为什么？24.如图,已知∠1＋∠2=180°,∠DEF=∠A,试判断∠ACB与∠DEB的大小关系，并证明.参考答案25.答案为：D26.答案为：B27.答案为：D28.答案为：A29.答案为：A；30.答案为：B；31.答案为：A32.答案为：D；33.答案为：D.34.答案为：C；35.B36.C37.答案为：同旁内角38.答案为：∠FAC与∠DBA39.答案为：∠4，∠140.答案为：∠EAD，∠DBC，∠EAD，∠DAB，∠BCD.41.答案为：①③④42. 答案为：对顶角相等；平角定义；同角的补角相等；同位角相等，两直线平行．43.解：∠1和∠2是直线EF、DC被直线AB所截形成的同位角，∠1和∠3是直线AB、CD被直线EF所截形成的同位角.44.解：（1）∠A和∠D是由直线AE、CD被直线AD所截形成的，它们是同旁内角；（2）∠A和∠CBA是由直线AD、BC被直线AE所截形成的，它们是同旁内角；（3）∠C和∠CBE是由直线CD、AE被直线BC所截形成的，它们是内错角. 45.解：∵CF⊥DF，∴∠C+∠D=90°，又∠1和∠D互余，即∠1+∠D=90°，∴∠1=∠C，∴AB∥CD.46.证明：∵DE平分∠ADC,CE平分∠BCD,∴∠1=∠ADC,∠2=∠BCD.∵∠1+∠2=90°,∴∠ADC+∠BCD=180°,∴AD∥BC,∴∠A+∠B=180°.∵CB⊥AB,∴∠B=90°,∴∠A=90°,∴DA⊥AB.47.【解答】解：DE∥AF，理由如下：∵CD⊥DA，DA⊥AB，∴∠CDA=∠DAB=90°，∴CD∥AB，∵∠1=∠2，∴∠CDA﹣∠1=∠DAB﹣∠2，∴∠3=∠4，∴DE∥AF．48.解：∠ACB与∠DEB相等，理由如下：证明：∵∠1+∠2=180°（已知），∠1+∠DFE=180°（邻补角定义），∴∠2=∠DFE（同角的补角相等），∴AB∥EF（内错角相等两直线平行），∴∠BDE=∠DEF（两直线平行，内错角相等），∵∠DEF=∠A（已知），∴∠BDE=∠A（等量代换），∴DE∥AC（同位角相等两直线平行），∴∠ACB=∠DEB（两直线平行，同位角相等）．。

2.2探索直线平行的条件一、单选题1.已知直线AB 及一点P ，要过点P 作一直线与AB 平行，那么这样的直线( ) A.有且只有一条 B.有两条C.不存在D.不存在或者只有一条2.有下列语句：①不相交的两条直线叫平行线；②在同一平面内，两条直线的位置关系只有两种：相交和平行； ③如果线段AB 和线段CD 不相交，那么直线AB 和直线CD 平行； ④如果两条直线都和第三条直线平行，那么这两条直线平行； ⑤过一点有且只有一条直线与已知直线平行. 正确的个数是( ) A.1B.2C.3D.43.如图所示，以下几种说法，其中正确的个数是( ) ①3∠和4∠是同位角；②6∠和7∠是同位角； ③4∠和5∠是内错角；④2∠和5∠是同旁内角 ⑤2∠和7∠是同位角；⑥1∠和2∠是同位角A.3B.4C.5D.6 4.如图，下列条件能判定直线12//l l 的是( )A.12∠=∠B.15∠=∠C.13180∠+∠=︒D.35∠=∠5.如图，下列选项中，不可以得到12//l l 的是( )A.12∠=∠B.23∠=∠C.35∠=∠D.34180∠+∠=︒6.如图，直线,a b 被直线c 所截，下列条件中，不能判定//a b 的是( )A.24∠=∠B.14180∠+∠=︒C.54∠=∠D.13∠=∠7.如图，下列条件不能判定//AB CD 的是( )A.B DCE ∠=∠B.A ACD ∠=∠C.180B BCD ∠+∠=︒D.A DCE ∠=∠8.如图，分别将木条,a b 与木条c 钉在一起，若150280∠=︒∠=︒，，要使木条a 与b 平行，则木条a 需要顺时针转动的最小度数为( )A.30°B.50°C.80°D.130°9.如图，下列条件不能判定直线12//l l 的是( )A.13∠=∠B.14∠=∠C.23180∠+∠=︒D.35∠=∠二、填空题10.如图，2∠的内错角是 ，3∠与B ∠是 角，B ∠的同旁内角是 .11.小友把一副三角板摆放在桌面上，如图所示，其中边,BC DF 在同一条直线上，可以得到_______//______，依据是___________.12.如图，已知//175a b ∠=︒，，则2∠=________．三、解答题13.如图，直线AB 和CD 被直线MN 所截.（1）如图①，EG 平分,BEF F ∠平分DFE ∠（平分的是一对同旁内角），则1∠与2∠满足时，//AB CD ；（2）如图②，EG 平分,MEB FH ∠平分DFE ∠（平分的是一对同位角），则1∠与2∠满足时，//AB CD ；（3）如图③，EG 平分,AEF F ∠平分DFE ∠（平分的是一对内错角），则1∠与2∠满足什么条件时，//AB CD ？为什么？参考答案1.答案：D解析：当点P 在直线AB 上时，这样的直线不存在；当点P 在直线AB 外时，这样的直线只有一条. 2.答案：A解析：①不相交的两条直线叫平行线，必须是在同一平面内，故错误；②在同一平面内，不重合的两条直线的位置关系只有两种：相交和平行，故错误； ③线段AB 和线段CD 不相交，直线AB 和直线CD 不一定平行，故错误；④在同一平面内，如果两条直线都和第三条直线平行，那么这两条直线平行，故正确； ⑤过直线外一点有且只有一条直线与已知直线平行，故错误，故选A. 3.答案：B解析：根据同位角、内错角、同旁内角的特征可知，3∠和4∠是同位角，1∠和2∠是同位角，4∠和5∠是内错角，2∠和5∠是同旁内角，6∠和7∠不是同位角，2∠和7∠不是同位角则正确的为③④①，共4个，故选B4.答案：C解析：1∠与3∠是直线12l l ，被3l 所截而成的同旁内角，当13180∠+∠=︒时，12//l l 5.答案：C解析：A 项，12∠∠=，12//l l ∴（同位角相等，两直线平行）； B 项1223l l ∠=∠∴，，（内错角相等，两直线平行）； C 项，由35∠=∠不能判定12l l ； D 项，1234180l l ∠+∠=∴，（同旁内角互补，两直线平行）6.答案：D解析：选项A 符合同位角相等，两直线平行；选项B 符合同旁内角互补，两直线平行；选项C 符合内错角相等，两直线平行；只有选项D 不能判定直线a 与b 平行. 7.答案：D解析：由B DCE ∠=∠，根据同位角相等，两直线平行，即可判定//AB CD . 由A ACD ∠=∠，根据内错角相等，两直线平行，即可判定//AB CD . 由180B BCD ∠+∠=︒，根据同旁内角互补，两直线平行，即可判定//AB CD . 故A,B,C 不符合题意，故选D. 8.答案：A 解析：如图.当150AOB ∠=∠=︒时，//OA b ，∴要使木条a 与b 平行，木条a 需要顺时针转动的最小度数为805030︒-︒=︒.故选A. 9.答案：A解析：A 项，13∠=∠，不能判定直线12//l l ，故此选项符合题意；B 项，14∠=∠，根据内错角相等，两直线平行，可判定直线12//l l ，故此选项不合题意；C 项，23180∠+∠=︒，根据同旁内角互补，两直线平行，可判定直线12//l l ，故此选项不合题意；D 项，35∠=∠，根据同位角相等，两直线平行，可判定直线12//l l ，故此选项不合题意.故选A. 10.答案：C ∠ 内错 1∠或DAB ∠或C ∠解析：2∠和C ∠在被截线AD 和BC 的内部，截线AC 的两侧，故2∠的内错角是C ∠；3∠与B ∠在被截线AE 和BC 的内部，截线AB 的两侧，故3∠与B ∠是内错角；B ∠的同旁内角是1∠或DAB ∠或C ∠11.答案：AC DE ；；内错角相等，两直线平行解析：由90ACB EDF ∠=∠=︒可以得到//AC DE ，依据是内错角相等，两直线平行. 12.答案：105°解析：18075105︒-︒=︒ 13.答案：（1）1290∠+∠=︒. （2）12∠=∠.（3）12∠=∠.理由：EG 平分,AEF FH ∠平分DFE ∠， 21,22,12,,//.AEF DFE AEF DFE AB CD ∴∠=∠∠=∠∠=∠∴∠=∠∴。

探索平行的条件（三）课后作业一、选择题1、如图，下列条件中能判定直线ll 〃12的是（ ）A. Z1 = Z2B. Z1 = Z5C. Z l + Z3 = 180°D. Z3=Z52、如图，点E 在AC 的延长线上，下列条件屮能判断AB 〃CD 的是（）A. Z3=Z4B. ZD=ZDCEC. Z 1 = Z2D.ZD+ZACD 二 180° A. Z1 = Z2B. Z2 = Z4C. Z3 = Z4D. Z1 + Z4 二180。

3、对于图中标记的各角, 下列条件能够推理得到3〃b 的是（DA. Z1 = Z3B. Z2 二Z4C. Z1 = Z4D. AB/7CD5、系是（A. 平行B. 垂直C. 相交但不垂直D. 无法确定二、填空题6、如图，己知C、E三点在同一直线上，Zl = 105° , ZA=75° •求证：AB/7CD.证明一：TC、D、E三点在同一直线上,••• Z 1+ Z2 二180。

（平角定义）,一个弯形管道ABCD的弯角ZABC二130。

, ZBCD二50。

,则管道AB与CD的位置关••• Z 2=75 °(又V ZA=75° ,••• Z2=ZA,••• AB // CD ____________________________ .证明二：VC. D、E三点在同一直线上，・・・Z1和ZA是直线AB和直线CD被直线AD所截得到的同旁内角（同旁内角定义）,又••• ZA=75° , Zl = 105° ,・・・ ZA+Z 1 = 75° +105° =180° ,A AB//CD _____________________________________7、如图，两直线a, b被第三条直线c所截，若Zl=50° , Z2 = 130°,则直线a, b的位置关系是________________ .8、如图所示，已知Z1二Z2,则再添上条件_____________________ 可使AB〃CD・9、如图所示，若Z1二ZC二60° , ZD二120。

2.2探索直线平行的条件练习题一、选择题1．如图，下列说法中不正确的是（）A．∠1和∠3是同旁内角B．∠2和∠3是内错角C．∠2和∠4是同位角D．∠3和∠5是对顶角2．如图，下列四个条件中，能判断DE∥AC的是（）A．∠3＝∠4 B．∠1＝∠2 C．∠EDC＝∠EFC D．∠ACD＝∠AFE 3．如图，下列条件：①∠1＝∠3；②∠2+∠4＝180°；③∠4＝∠5；④∠2＝∠3；⑤∠6＝∠2+∠3，其中能判断直线l1∥l2的有（）A．5 个B．4 个C．3 个D．2 个4．如图，能判断AB∥CE的条件是（）A．∠A＝∠ACE B．∠A＝∠ECD C．∠B＝∠BCA D．∠B＝∠ACE 5．如图，下列条件中，一定能判断AB∥CD的是（）A．∠2＝∠3 B．∠1＝∠2 C．∠4＝∠5 D．∠3＝∠4 6．如图，在下列给出的条件中，不能判定AC∥DE的是（）A．∠1＝∠A B．∠A＝∠3 C．∠3＝∠4 D．∠2+∠4＝180°7．如图，有以下四个条件：①∠B+∠BCD＝180°，②∠1＝∠2，③∠3＝∠4，④∠B＝∠5，其中能判定AB∥CD的条件的个数有（）A．1 B．2 C．3 D．48．如图所示，直线a，b与直线c相交，给出下列条件：①∠1＝∠2；②∠3＝∠6；③∠4+∠7＝180°；④∠5+∠3＝180°．其中能判断a∥b的是（）A．①②③④B．①③④C．①③D．②④二、填空题9．如图，按角的位置关系填空：∠A与∠1是；∠A与∠3是；∠2与∠3是．10．如图，∠A＝70°，O是AB上一点，直线OD与AB所夹角∠BOD＝82°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转度．11．如图，点E在AC的延长线上，对于给出的四个条件：（1）∠3＝∠4；（2）∠1＝∠2；（3）∠A＝∠DCE；（4）∠D+∠ABD＝180°．能判断AB∥CD的有个．12．如图，给出了过直线外一点作已知直线的平行线的方法，其依据是．三、解答题13．如图，AE与CD交于点O，∠A＝50°，OC＝OE，∠C＝25°，求证：AB∥CD．14．如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠1＝∠2，∠C＝∠D．求证：AC∥DF．15．填空并完成以下证明：已知，如图，∠1＝∠ACB，∠2＝∠3，FH⊥AB于H，求证：CD⊥AB．证明：FH⊥AB（已知）∴∠BHF＝．∵∠1＝∠ACB（已知）∴DE∥BC（）∴∠2＝．（）∵∠2＝∠3（已知）∴∠3＝．（）∴CD∥FH（）∴∠BDC＝∠BHF＝．°（）∴CD⊥AB．16．如图，已知AF平分∠BAC，DE平分∠BDF，且∠1＝∠2，能判定DF∥AC吗？请说明理由？17．如图，若AB∥CD，∠1＝∠2，∠3＝∠4，AD与BC平行吗？并请说明理由．。

2.2探索直线平行的条件第1课时同位角及平行公理要点感知1.同位角的判定：如图，具有4与这样位置关系的角称为同位角，图中的同位角还有Z3与, Z5 与, Z7 与.2.平行线的判定：两条直线被第三条直线所截，如果同位角,那么这两条直线平行，简称为；同位角,两直线平行.【答案】相等3.平行公理：(1)过直线外一点_________ 直线与这条直线平行.(2)平行于同一条直线的两条直线.【答案】(1)有且只有一条(2)互相平行A./1 = /2B. Z2 = Z6C. Z1 = Z4D. Z3 = Z5 【答案】AA基础训练达标区1.如图，直线AB、被直线EF所截，则ZAMN的同位角是( ).FA. ZCNMB. ZCNFC. ZDNFD. ZDNM【答案】B【答案】D3.如图，下列说法不正确的是（）.A.4与/2是同位角B.N2与Z3是同位角C.Z1与匕3是同位角D.4与Z3不是同位角【答案】C4.如图，可以推理得到AB//CD的条件是（）.A./2,= /RB. Z1 = ZAC. Z3 = ZBD. Z3 = ZA 【答案】C5.下列说法中正确的个数是（）.①过一点一定有一条直线与已知直线平行；②一条直线的平行线有无数条；③两条不相交的直线叫做平行线；④与一条直线平行的直线只有一条A. 0个B. 1个C. 2个D. 3个【答案】B6.如图所示，将一张长方形纸对折两次，则产生的折痕与折痕间的位置关系是（【答案】A 7. 直线/同侧有A 、B 、C 三点，若A 、B 两点确定的直线〈与3、C 两点确定的直线A 都与/平行, 则A 、B 、C 三点,其理论依据是.【答案】共线，过直线处一点有且只有一条直线与这条直线平行.8. 如图，三角形ABC 中，已知ZC = 45° , ZADB = 9Q° ,庞为匕4DB 的平分线，与CA 平行吗？ 说明你的理由.【答案】解：DE//CA.因为ZADB = 90° , QE 平分匕所以ZBDE = -ZADB = 45。