下载文档原格式
磁流体方程组磁流体动力学（Magnetohydrodynamics，简称MHD）是研究导电流体（等离子体、液态金属等）在磁场中运动规律的学科。
磁流体方程组是描述这种物理现象的基础数学工具，它结合了流体动力学和电磁学的原理。
本文旨在深入解析磁流体方程组，探讨其物理背景、数学结构以及在实际应用中的重要性。
一、磁流体方程组的物理背景磁流体动力学起源于19世纪对太阳磁场和地球磁场的研究，后来随着等离子体物理和受控核聚变研究的兴起而得到快速发展。
在高温等离子体中，带电粒子（电子和离子）的运动不仅受到电场力的作用，还受到磁场力的影响。
这些力在宏观尺度上表现为流体的运动和电磁场的变化，磁流体方程组正是描述这种复杂相互作用的数学工具。
二、磁流体方程组的数学结构磁流体方程组通常由以下几个部分组成：1. 连续性方程：描述流体质量守恒的方程，与常规流体动力学中的连续性方程类似。
2. 动量方程：描述流体动量变化的方程，其中包含了磁场对流体动量的影响，即洛伦兹力。
3. 能量方程：描述流体能量守恒的方程，包括热传导、焦耳热等能量转换过程。
4. 麦克斯韦方程组：描述电磁场变化的方程，包括电场和磁场的相互转化以及电荷和电流对电磁场的影响。
在磁流体方程组中，电场和磁场不再是独立的物理量，而是通过流体的运动和电荷分布相互联系。
这使得磁流体方程组成为一个高度非线性且耦合的偏微分方程组，其求解难度远大于常规的流体动力学或电磁学问题。
三、磁流体方程组的求解方法由于磁流体方程组的复杂性和非线性，解析求解通常只适用于一些简单情况。
在实际应用中，数值求解是更为常见的方法。
数值求解磁流体方程组需要借助高性能计算资源，采用适当的数值算法（如有限差分法、有限元法、谱方法等）对空间和时间进行离散化，然后通过迭代方法求解离散后的代数方程组。
在数值求解过程中，需要特别注意以下几个问题：1. 数值稳定性：由于磁流体方程组中存在快速变化的物理过程（如阿尔芬波传播），数值求解时很容易出现数值不稳定现象。
植等离子体物理学
等离子体物理学是研究等离子体性质的物理学分支。
等离子体是物质的第四态，是由电子、离子等带电粒子及中性粒子组成的混合气体，宏观上表现出准中性，即正负离子的数目基本相等，整体上呈现电中性，但在小尺度上具有明显的电磁性质。
等离子体还具有明显的集体效应，带电粒子之间的相互作用是长程库仑作用，单个带电粒子的运动状态受到其它许多带电粒子的影响，又可以产生电磁场，影响其它粒子的运动。
等离子体物理学目的是研究发生在等离子体中的一些基本过程，包括等离子体的运动、等离子体中的波动现象、等离子体的平衡和稳定性、碰撞与输运过程等等。
等离子体物理学具有广阔的应用前景，包括受控核聚变、空间等离子体、等离子体天体物理、低温等离子体等等。
等离子体物理学常用的有单粒子轨道理论、磁流体力学、动理学理论三种研究方法。
单粒子轨道理论不考虑带电粒子对电磁场的作用以及粒子之间的相互作用。
磁流体力学将等离子体作为导电流体处理，使用流体力学和麦克斯韦方程组描述。
这种方法只关注流体元的平均效果，因此是一种近似方法。
动理学理论使用统计物理学的方法，考虑粒子的速度分布函数。
《等离子体动力学》讲义祝大军熊彩东电子科技大学物理电子学院目录第一章：引言§1•1定义§1•2基本特征：§1•3等离子体物理的研究方法第二章：动力论方程§2•1分布函数的引入§2•2普遍的动力论方程§2•3V l a s o v方程的严格导出第三章：V l a s o v方程的求解§3•1几个定义§3•2V l a s o v方程的线性化§3•3平衡态V l a s o v方程的解§3•4线性V l a s o v方程的解——特征线法（未扰轨道法）§3•5等离子体纵振荡——初始扰动的演化——F o u r i e r-L a p l a c e变换法第四章：微观不稳定性§4•1等离子体微观不稳定性概述§4•2静电不稳定性§4•3束——等离子体不稳定性、等离子体尾场加速器中静电波特性第一章 引言§1•1 定义：物质的第四态“等离子体态”：固体（加热）→液体（加热）→气体（输入能量）→电离态。
等离子体是由大量的接近自由运动的带电粒子所组成的系统，在整体上是准中性的，粒子的运动主要由粒子间的电磁相互作用所决定，由于这种作用是库仑长程相互作用（密度足够低，一个邻近粒子所产生的力远小于许多远距离粒子所施的长程库能力），因而使之显示出集体行为（如：各种振荡和波动、不稳定性等）。
§1•2 基本特征：1． 系统的尺度必须远大于德拜长度（Debye Length ）1/20222e i d e i i i e KT T n e T Z n e T ελ⎛⎫= ⎪+∑⎝⎭(1.2.1) 2/120⎪⎪⎭⎫ ⎝⎛=e n KT e e d ελ (1.2.2)推导过程： 真空中一个点电荷q 产生一个电场()E r φ=-∇, ()r φ为电势。
其满足拉普拉斯方程()20r φ∇=，得库仑势()04qr r φπε= (1.2.3)在等离子体内部，电子、离子成份都处于热力学平衡状态下，一个点电荷q 近旁总是异号电荷比同号电荷要多些。
单粒子轨道理论单粒子轨道理论是指将等离子体中的带电粒子独立的处理，忽略它们之间的相互作用，只考虑电磁场对单个带电粒子的作用，不考虑带电粒子运动引起的电磁场变化。
1． 均匀磁场中的带电粒子的回旋运动在处于恒定磁场的空间中，带电粒子的运动方程是d mq dt=⨯vv B (1.1)取B 为z 方向，写成分量形式： x y v v =Ω (1.2) y x v v =-Ω (1.3) 0z v =(1.4)这里Bq mΩ=(1.5)称为回旋频率。
记x y v v iv =+，将(1.3)式乘以i 与(1.2)式相加，得到 v v =-Ω(1.6)其解为i t v ce -Ω=(1.7)其中，积分常数i c v e α-⊥=是复数，可写为模v ⊥和辐角α的形式。
对(1.7)式分别取实部和虚部，得到 cos()x v v t α⊥=Ω+(1.8)sin()y v v t α⊥=-Ω+(1.9),v c 均为积分常数，因此，带电粒子的运动是围绕磁场作以Ω为角频率的回旋运动，也称为Larmor 回旋运动。
其角速度为：z =-ΩΩe(1.10)回旋的半径（也称为Larmor 半径）为：v ρ⊥=Ω(1.11)而在平行于磁场的方向，从(1.4)解得：z v v =(1.12)积分常数v 为平行方向速度的初值，带电粒子速度保持不变。
值得注意的是，回旋频率只与磁场的大小有关，而与回旋粒子的垂直速度或回旋半径无关。
但如果相对论效应不能忽略，则带电粒子的质量会发生变化，回旋频率会随着垂直方向的速度改变。
此时，带电粒子的运动方程为d m q dtγ=⨯vv B (1.13)其中相对论因子12221v c γ-⎛⎫=-⎪⎝⎭(1.14)它只与带电粒子速度的大小有关，与速度的方向无关。
而事实上，只要用v 点乘(1.13)式即可看出：2102d dv dt dt⋅==v v (1.15)即带电粒子速度的大小是常数。
因此在解带电粒子的运动方程时，可以将γ视为常数。
空间等离子体波动研究现状概述及解释说明1. 引言1.1 概述空间等离子体波动是指在太阳系以及宇宙中存在的带电粒子组成的等离子体中传播的波动现象。
空间等离子体波动研究是当前天体物理学、空间科学以及工程技术领域中的重要研究方向之一。
通过深入探索空间等离子体波动的特征、机理以及应用，我们可以更好地理解和解释太阳风、行星际介质和星际介质等天文现象，同时也能为未来开展基础科学研究和应用技术提供有力支撑。
1.2 文章结构本文将首先对空间等离子体波动研究现状进行概述，包括其定义与背景、历史发展以及研究方法和技术。
接着将详细讨论空间等离子体波动的特征以及相关机理解释，包括波动的种类与分类、影响因素分析和实验观测结果总结，以及波动机理的理论解释与模型建立。
然后，我们将探讨空间等离子体波动在科学和工程中的应用前景，包括基础科学研究进展与探索方向、技术应用与市场前景展望，以及对未来发展趋势的预测与思考。
最后，我们将进行总结，阐述本文的观点和主要发现成果，并提出对未来空间等离子体波动研究的意义和重要性进行总结，同时提出对相关领域进一步研究的建议和展望。
1.3 目的本文旨在全面概述空间等离子体波动的研究现状，并深入解释其特征和机理。
通过调查和整理已有的研究成果，我们可以更好地了解空间等离子体波动在太阳系中的分布情况以及其对行星际介质形成和演化过程的影响。
此外，本文还旨在探讨空间等离子体波动在科学和工程中的潜在应用前景，并为未来相关领域的研究提供指导性建议。
2. 空间等离子体波动研究现状2.1 定义与背景空间等离子体波动是指在外层空间（如地球上层大气、太阳附近的等离子体区域）中发生的各种波动现象。
空间等离子体是由高温离子和自由电子构成的带电粒子云，它们受到电磁场和其他因素的影响而产生波动。
2.2 历史发展空间等离子体波动的研究可以追溯到20世纪初，当时科学家们开始观测并记录地球上层大气中的奇异光现象。
随着航天技术的发展，人们能够更加直接地观测和研究太阳附近以及其他星球上的等离子体波动现象。
第四章空间等离子体在地球空间环境中，能量低于100keV（千电子伏）的带电粒子构成空间等离子体。
因其相对于宇宙线和地球辐射带的粒子（通称为高能粒子）能量要低，故有时又称为低能粒子。
它不仅受空间磁场（参见第3章）控制，还受空间电场（参见第3章）支配。
按其能量或温度的不同，又可分为高温等离子体（≥10eV）和冷等离子体（<10eV）两类。
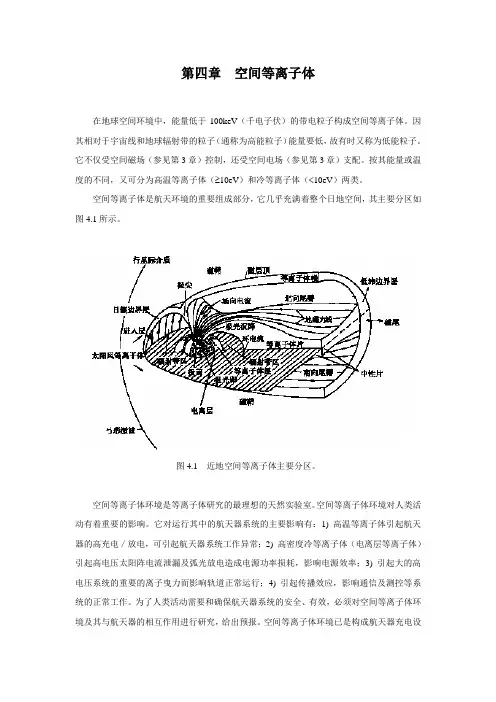
空间等离子体是航天环境的重要组成部分，它几乎充满着整个日地空间，其主要分区如图4.1所示。
图4.1 近地空间等离子体主要分区。
空间等离子体环境是等离子体研究的最理想的天然实验室。
空间等离子体环境对人类活动有着重要的影响。
它对运行其中的航天器系统的主要影响有：1) 高温等离子体引起航天器的高充电／放电，可引起航天器系统工作异常；2) 高密度冷等离子体（电离层等离子体）引起高电压太阳阵电流泄漏及弧光放电造成电源功率损耗，影响电源效率；3) 引起大的高电压系统的重要的离子曳力而影响轨道正常运行；4) 引起传播效应，影响通信及测控等系统的正常工作。
为了人类活动需要和确保航天器系统的安全、有效，必须对空间等离子体环境及其与航天器的相互作用进行研究，给出预报。
空间等离子体环境已是构成航天器充电设计指南或标准的必不可少的重要内容，它是人类航天活动所需要的重要环境。
在研究方法上，有宏观的磁流体力学方法和微观动力论方法两类，具体研究方法的选用取决放研究对象的时间与空间尺度。
由于空间等离子体涉及能量、密度、分布的不同，所处不同区域其它空间环境因素（如电场、磁场、中性粒子、性状等）亦不一样，它涉及很多复杂的运动学及动力学过程，我们只从掌握背景情况的角度出发，给出简况介绍并辅以必要的图表示例。
§4.1 基本的等离子体特征参数和几个重要现象§4.1.1 德拜长度与准中性等离子体中一个带电粒子在周围产生的电位，由放有其它带电粒子影响，不是点电荷的库仑中位，而是德拜电位： 2/12/⎪⎪⎭⎫ ⎝⎛=⋅=-e n T r e CONST V e e D r DκλλλD 就是德拜长度（Debye length ），是德拜电位被屏蔽的距离，也称德拜半径。
