智能车PID的算法推荐

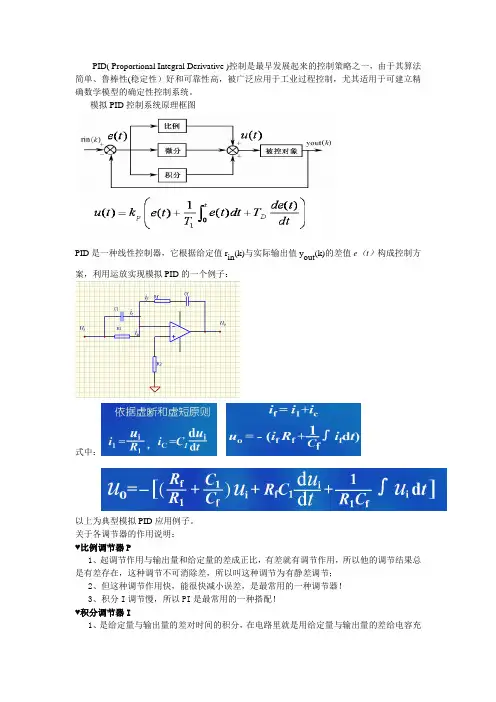
PID( Proportional Integral Derivative )控制是最早发展起来的控制策略之一，由于其算法简单、鲁棒性(稳定性）好和可靠性高，被广泛应用于工业过程控制，尤其适用于可建立精确数学模型的确定性控制系统。

模拟PID控制系统原理框图PID是一种线性控制器，它根据给定值r in(k)与实际输出值y out(k)的差值e（t）构成控制方案，利用运放实现模拟PID的一个例子：式中：以上为典型模拟PID应用例子。

关于各调节器的作用说明：♥比例调节器P1、起调节作用与输出量和给定量的差成正比，有差就有调节作用，所以他的调节结果总是有差存在，这种调节不可消除差，所以叫这种调节为有静差调节；2、但这种调节作用快，能很快减小误差，是最常用的一种调节器！3、积分I调节慢，所以PI是最常用的一种搭配！♥积分调节器I1、是给定量与输出量的差对时间的积分，在电路里就是用给定量与输出量的差给电容充电，只要时间足够长，电容器的电压总会到达给定量，使输出量与给定量的差为零；2、积分调节器是一种无静差调节器，意思是说可调节到给定值，做到精确、准确输出；♥微分控制调节器D1、，这种控制总是以输出量与给定量的差的变化率成正比，差变化越剧烈，调节作用越大，差变化越平稳，调节作用越弱；2、这种微分调节作用，使得输出量平稳而很少波动；3、这种微分调节作用，对输出量的变化、波动产生强烈的阻尼、抑制的作用，就像摩擦力的作用；数字式PID应用：增量式PID的算式为：如果换换成智能车里的方向控制就变为：Pwm_offset=PWMMiddle+PID_P*(error-last_error)+PID_I*(error)+PID_D*(error+pre_error-2*la st_error);其中：error=middle-offset，注意这个公式里的offset应该有正负之分，左右偏移的值互为相反。

这样自然就确定了最后的方向。

智能汽车控制策略及其PID 算法分析作者：王保磊机电1103-11221077目录背景简介一．智能汽车竞赛简介： (1)系统建立二．控制策略： (1)2.1：理论分析 (2)2.2 ： PID 控制规律的离散化 (3)2.3 ： matlab 分析 (4)2.4 ：系统校正 (9)总结三．总结： (14)一．智能汽车竞赛简介。

全国大学生“飞思卡尔”杯智能汽车竞赛是在规定的模型汽车平台上，使用飞思卡尔半导体公司的 8 位、 16 位微控制器作为核心控制模块，通过增加道路传感器、电机驱动电路以及编写相应软件，制作一个能够自主识别道路的模型汽车，按照规定路线行进，以完成时间最短者为优胜。

因而该竞赛是涵盖了控制、模式识别、传感技术、电子、电气、计算机、机械等多个学科的比赛。

摄像头组比赛规则：采用模拟或数字摄像头对赛道信息进行采集，通过硬件二值化并进行软件信息处理，获得赛道信息，采用规定的舵机和电机控制小车的行走。

相同的赛道，竞速，完成赛道时间短的队伍获胜。

下图为赛道示意图和实际赛道照片。

为保证小车一直沿着黑色引导线快速行驶，系统主要的控制对象是小车的转向和车速。

即应使小车在直道上以最快的速度行驶。

在进入弯道的时刻尽快减速，且角度的转向要适合弯道的曲率，确保小车平滑地转弯，并在弯道中保持恒速。

从弯道进入直道时，小车的舵机要转向至中间，速度应该立即得到提升，直至以最大的速度行进。

为实现上述控制思想，我们采用不同的控制方法来控制小车的转角和速度。

下图为小车的实物模型：二．控制策略。

2.1：理论分析：Ov7620 数字摄像头采集到的赛道信息为采集点灰度值，这些灰度值与设定的阀值进行比较转化为二进制信息，利用这些二进制信息可以确定赛道黑线位置，进而确定小车当前位置及理想通过曲线。

求得理想通过曲线上各点的斜率进而确定赛道类型，通过算法控制电机转速，以保证小车安全通过赛道防止侧翻和打滑。

计算小车的当前位置横坐标值即摄像头视野中线与理想通过曲线与横坐标交点的差值。

pid算法公式详解
PID算法，即比例（proportional）、积分（integral）、微分（derivative）控制算法，是一种应用广泛的控制算法。

它结合了比例、积分和微分三种环节于一体，适用于连续系统的控制。

在工业应用中，它是最广泛算法之一，如四轴飞行器、平衡小车、汽车定速巡航、温度控制器等场景均有应用。

PID算法的公式如下：
\[U(t)=K_p e(t)+K_i\int_{0}^{t}e(\tau)d\tau+K_d frac{de(t)}{dt}\]
其中，
-\(U(t)\)是控制器输出的控制信号；
-\(e(t))是控制器输入的误差信号；
-\(K_p\)、\(K_i\)和\(K_d\)是比例、积分和微分系数；
-(\int_{0}^{t}e(\tau)d\tau)是误差信号的累积值，即积分项；
-(\frac{de(t)}{dt}\)是误差信号的变化率，即微分项。

这个公式描述了PID控制器如何根据当前的误差以及过去的误差来计算出控制信号。

比例项反映了当前误差的大小，积分项反映了过去误差的累积，微分项反映了误差变化的趋势。

通过调整这三个参数，可以实现对系统的精确和快速控制。

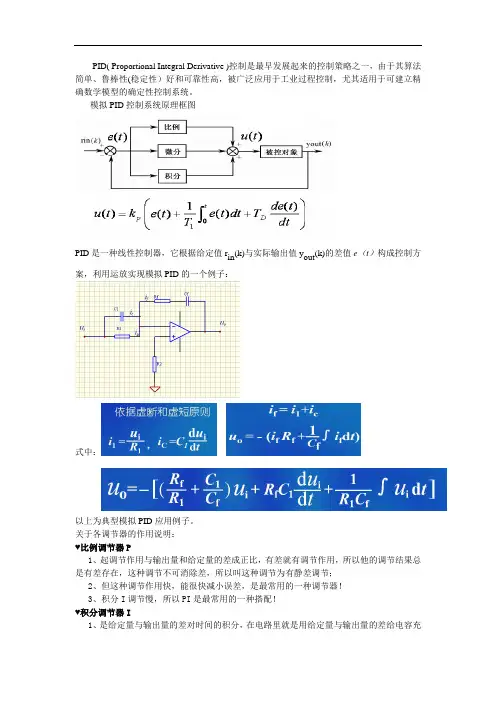
PID( Proportional Integral Derivative )控制是最早发展起来的控制策略之一，由于其算法简单、鲁棒性(稳定性）好和可靠性高，被广泛应用于工业过程控制，尤其适用于可建立精确数学模型的确定性控制系统。

模拟PID控制系统原理框图PID是一种线性控制器，它根据给定值r in(k)与实际输出值y out(k)的差值e（t）构成控制方案，利用运放实现模拟PID的一个例子：式中：以上为典型模拟PID应用例子。

关于各调节器的作用说明：♥比例调节器P1、起调节作用与输出量和给定量的差成正比，有差就有调节作用，所以他的调节结果总是有差存在，这种调节不可消除差，所以叫这种调节为有静差调节；2、但这种调节作用快，能很快减小误差，是最常用的一种调节器！3、积分I调节慢，所以PI是最常用的一种搭配！♥积分调节器I1、是给定量与输出量的差对时间的积分，在电路里就是用给定量与输出量的差给电容充电，只要时间足够长，电容器的电压总会到达给定量，使输出量与给定量的差为零；2、积分调节器是一种无静差调节器，意思是说可调节到给定值，做到精确、准确输出；♥微分控制调节器D1、，这种控制总是以输出量与给定量的差的变化率成正比，差变化越剧烈，调节作用越大，差变化越平稳，调节作用越弱；2、这种微分调节作用，使得输出量平稳而很少波动；3、这种微分调节作用，对输出量的变化、波动产生强烈的阻尼、抑制的作用，就像摩擦力的作用；数字式PID应用：增量式PID的算式为：如果换换成智能车里的方向控制就变为：Pwm_offset=PWMMiddle+PID_P*(error-last_error)+PID_I*(error)+PID_D*(error+pre_error-2*la st_error);其中：error=middle-offset，注意这个公式里的offset应该有正负之分，左右偏移的值互为相反。

这样自然就确定了最后的方向。

PID算法深度技术帖*写给参加飞思卡尔智能车大赛的朋友作者：王玉鹏（郑州轻工业学院）最近很多朋友问我关于PID的算法。

这里我就简单整理了下：PID控制算法是最经典的自动控制算法。

所有《自动控制原理》教材均有大幅篇章介绍。

从数学模型到传递函数，公式推导不厌其烦。

很多‘童鞋’似懂非懂。

下面我就从程序的角度来讲：下面是PID控制系统的原理图PID算法具体分两种：一种是位置式的，一种是增量式的。

在大多数的情况下，执行机构本身没有状态记忆功能，每时每刻都要靠控制信号驱动，如果失去控制信号，执行机构即失去功能。

在这种场合必须采用位置式PID控制算法。

也有一些执行机构具有记忆功能，即使失去驱动信号仍然可以维持原来的状态不变。

例如在用步进电机作为执行机构的自动化控制系统中（数控机床最为典型）下面主要针对位置式PID来讲，以加温设备为例，软件采用uc/os-ii嵌入式操作系统环境//采用位置式PID控制算法的任务函数float Set;//设定值float KP;//比例常数float KI;//积分常数float KD;//微分常数float LE=0;//上次误差float SE;//累计误差void TaskSampleCtrl(void *pdata)//采样控制函数{float now,E,DE,out;//定义临时变量while(1){now=SampleAdc();//传感器采样一次E=Set-now; //计算当前误差SE+=E; //计算当前误差的积分值DE=E-LE; //计算当前误差的微分值out=KP*E //计算比例项+KI*SE //计算积分项+KD*DE; //计算微分项CtrlOut(out); //控制执行机构LE=E; //保存误差值以进行下次计算OSTimeDly(25); //心跳20ms 延时0.5s(采样周期)}}PID参数调节：1.如果被控制对象的温度很快达到设定值，并超过设定值很多才回调（此种称为超调），则应该减小KP和KI，降低控制强度；加大KD，抑止超调。

1.Arduino 智能小车寻迹原理寻迹采用的主要原理就是红外探测法,即利用红外线在不同颜色的物体表面具有不同的反射性质的特点Arduino 单片机就是以是否收到反射回来的红外光为依据来确定黑线的位置和小车的行走路线。

红外探测器探测距离有限，一般最大不应超过15cm。

对于发射和接收红外线的红外探头，可以自己制作或直接采用集成式红外探头2.Arduino 寻迹模块简介3.Arduino pwm 调速4.PID算法5.PID 算法与寻迹6.代码：.#include "pid.h"....#ifdef ARDUINO_DEBUG..int debugLeftSpeed;..int debugRightSpeed;..uint8_t debugIrs = 0;..#endif....const float motorSpeed = 140; //小车输出速度..const int IR_PIN[] = {A0, A1, A2, A3, A4}; //寻迹板引脚定义..const int IN_A1 = 7; //..const int IN_A2 = 6; //..const int IN_B1 = 5; //..const int IN_B2 = 4; //..const int _pwmLeftPin = 10;//左边 pwm 引脚..const int _pwmRightPin = 11;//右边 pwm 引脚..pid_t pid;..float pidValue = 0; //pid 值..bool turnFlag = false;....void setup(void)..{..int i;....//设置引脚功能..pinMode(IN_A1, OUTPUT); ..pinMode(IN_A2, OUTPUT); ..pinMode(IN_B1, OUTPUT); ..pinMode(IN_B2, OUTPUT); ....//设置寻迹板引脚为 INPUT..for (i = 0; i < 5; i++) { .pinMode(IR_PIN[i], INPUT);..}......pid.sampleTime = SAMPLE_TIME;//初始化采样时间..pid.Kp = KP_VALUE;..pid.Ki = KI_VALUE;..pid.Kd = KD_VALUE;..pid.error = 0;..pid.previous_error = 0;....Serial.begin(115200);//设置波特率..delay(5000);//延时 5s....analogWrite(_pwmLeftPin, motorSpeed );.analogWrite(_pwmRightPin, motorSpeed ); ....goForward();//小车向前行驶....return;..}........../**..获取寻迹板红外数据..*/..uint8_t getIrData(void)..{..int i, j;..uint8_t level;..uint8_t temp;..uint8_t irs[9] = {0};....//获取10组数据..for (j = 0; j < 9; j ++) {....for (i = 0; i < 5; i++) {..level = digitalRead(IR_PIN[i]); ..if (level) {..bitSet(irs[j], i);//设置对应位为1 ..} else {..bitClear(irs[j], i);//设置对应为0 .}..}..}....//对所有的数据进行排序..for (i = 0; i < 9 - 1; i ++) {..for (j = 0; j < 9 - i - 1; j ++) { ..if (irs[j] > irs[j + 1]) {..temp = irs[j];..irs[j] = irs[j + 1];..irs[j + 1] = temp;..}..}..}...#ifdef ARDUINO_DEBUG..debugIrs = irs[4];..#endif....//返回中间值..return irs[4];..}..../**..计算误差值..@param irs :获取的寻迹传感器的值..*/..int calcErrorByIrsValue(uint8_t irs) ..{..int curError = pid.error;....switch (irs) {..case B11110: curError = -8; break; ....case B10000:..case B11000: curError = -7; break; ....case B11100: curError = -6; break; ..case B11101: curError = -4; break; ..case B11001: curError = -2; break; ....case B00000:..case B11011: curError = 0; break; ...case B10011: curError = 2; break;..case B10111: curError = 4; break;..case B00111: curError = 6; break;....case B00011:..case B00001: curError = 7; break;....case B01111: curError = 8; break;..case B11111: curError = pid.error > 0 ? 9 : - 9; break; ..}....return curError;..}...../**..排序函数..*/..void _sortData(int *p, int n)..{..int temp;..int i, j;....for (i = 0; i < n - 1; i ++) {..for (j = 0; j < n - i - 1; j ++) { ..if (p[j] > p[j + 1]) {..temp = p[j];..p[j] = p[j + 1];..p[j + 1] = temp;..}..}..}....return;..}....../**..计算误差值..*/..void calcCurrentError(void) ..{..int i;..uint8_t irs;.float sum = 0;..int errorData[10];....//获取 10组数据..for (i = 0; i < 10; i ++) {..irs = getIrData();..errorData[i] = calcErrorByIrsValue(irs); ..}...._sortData(errorData, 10);....for (i = 1; i < 10 - 1; i ++) {..sum += errorData[i];..}...pid.error = sum / 8;....return;..}....void turnRight(void)..{..digitalWrite(IN_A1, LOW); ..digitalWrite(IN_A2, HIGH); ..digitalWrite(IN_B1, HIGH); ..digitalWrite(IN_B2, LOW); ..}....void turnLeft(void)..{..digitalWrite(IN_A1, HIGH); ..digitalWrite(IN_A2, LOW); ..digitalWrite(IN_B1, LOW); ..digitalWrite(IN_B2, HIGH); ..}....void goForward(void)..{..digitalWrite(IN_A1, HIGH); ..digitalWrite(IN_A2, LOW); ..digitalWrite(IN_B1, HIGH); ..digitalWrite(IN_B2, LOW); ..}.../**..小车控制函数..@param pidValue : 计算出来的 pid 值..@param turnFlag : 方向标志..*/..void motorControl(float pidValue, bool turnFlag)..{....int leftMotorSpeed = 0;..int rightMotorSpeed = 0;....//根据 pid 的值调整小车左右电机的速度..leftMotorSpeed = constrain((motorSpeed + pidValue), -255, 255); ..rightMotorSpeed = constrain((motorSpeed - pidValue), -255, 255); ...//当转弯标志被设置时,则需要使用左边与右边的轮子正转与反转来调整,提高调整速度..if (turnFlag) {..//按照较大的 pwm 值进行调整,速度最快,左边速度与右边速度一致..if (abs(leftMotorSpeed) > abs(rightMotorSpeed)) {..leftMotorSpeed = abs(leftMotorSpeed);..rightMotorSpeed = leftMotorSpeed;..} else {..rightMotorSpeed = abs(rightMotorSpeed);..leftMotorSpeed = rightMotorSpeed;..}..} else {..//当速度为正时,则取原值,当速度为负时,则取相反数,保持 pwm 的值为正值..leftMotorSpeed = leftMotorSpeed > 0 ? leftMotorSpeed : -leftMotorSpeed; ..rightMotorSpeed = rightMotorSpeed > 0 ? rightMotorSpeed : -rightMotorSpeed; ..}....analogWrite(_pwmLeftPin, leftMotorSpeed ); ..analogWrite(_pwmRightPin, rightMotorSpeed); ....#ifdef ARDUINO_DEBUG..debugLeftSpeed = leftMotorSpeed ;..debugRightSpeed = rightMotorSpeed;..#endif....return;..}..../***..计算 pid 的值.*/..bool calculatePid(float *pValue)..{..float P = 0;..static float I = 0 ;..float D = 0 ;..static unsigned long lastTime = 0; ..unsigned long now = millis();..int timeChange = now - lastTime; ....//没有到达采样时间..if (timeChange < pid.sampleTime) { ..return false;..}...P = pid.error;//错误值..I = I + pid.error;//积累误差..D = pid.error - pid.previous_error;//计算错误的变化率....*pValue = (pid.Kp * P) + (pid.Ki * I) + (pid.Kd * D) + 1; ..*pValue = constrain(*pValue, -motorSpeed,motorSpeed);....pid.previous_error = pid.error;..lastTime = now;....return true;..}....#if ARDUINO_DEBUG..void print_debug()..{..int i;..String irs2bin = String(debugIrs, 2); ..int len = irs2bin.length();..if (len < 5) {..for (i = 0; i < 5 - len; i++) {..irs2bin = "0" + irs2bin;..}..}....Serial.print("IRS : ");..Serial.print(irs2bin);..Serial.print(" ML:");..Serial.print(debugLeftSpeed);..Serial.print(" MR:");..Serial.print(debugRightSpeed);..Serial.print(" ERROR:");..Serial.print(pid.error, OCT);..Serial.println();..}..#endif..../**..计算运动方向..*/..void calcDirection(void)..{....if (pid.error >= 7 && pid.error <= 9) {..turnLeft();..turnFlag = true;..} else if (pid.error >= -9 && pid.error <= -7) { ..turnRight();..turnFlag = true;..} else {..goForward();..turnFlag = false;..}....return;..}....void loop(void)..{..bool ok;..float pidValue;....//计算错误值..calcCurrentError();..//计算 pid 的值..ok = calculatePid(&pidValue);..if (ok) {..calcDirection();//计算小车运动方向..motorControl(pidValue, turnFlag);//控制电机..}....//delay(500);....#if ARDUINO_DEBUG ..print_debug(); ..delay(1000); ..#endif....return;..}.。

模糊PID控制算法在智能小车中的研究与应用一、本文概述随着科技的快速发展和智能化水平的提高，智能小车在各个领域的应用越来越广泛，如无人驾驶、物流运输、环境监测等。

然而，智能小车的运动控制是一个复杂的问题，需要解决路径规划、避障、速度控制等多个方面的问题。

其中，速度控制是智能小车运动控制的核心问题之一。

传统的PID控制算法在速度控制方面有着广泛的应用，但由于其对于系统参数变化的敏感性，使得其在实际应用中往往难以达到理想的控制效果。

因此，本文提出了一种基于模糊PID控制算法的智能小车速度控制方法，旨在提高智能小车的运动控制精度和稳定性。

本文首先对模糊PID控制算法的基本原理和特点进行了介绍，然后详细阐述了模糊PID控制算法在智能小车速度控制中的应用方法。

在此基础上，通过实验验证了模糊PID控制算法在智能小车速度控制中的有效性和优越性。

本文的研究工作不仅为智能小车的运动控制提供了一种新的方法，同时也为模糊PID控制算法在其他领域的应用提供了有益的参考。

接下来，本文将从模糊PID控制算法的基本原理、智能小车的运动控制模型、模糊PID控制算法在智能小车速度控制中的应用方法、实验结果与分析等方面展开详细的阐述。

二、模糊PID控制算法的基本原理模糊PID控制算法是一种结合了模糊逻辑和传统PID控制算法的控制策略。

该算法利用模糊逻辑处理PID控制中的非线性、不确定性和复杂性问题，从而提高了系统的鲁棒性和控制精度。

模糊逻辑是一种基于模糊集合和模糊推理的控制系统设计方法。

在模糊逻辑中，变量不再局限于具体的数值，而是可以在一定的范围内取任意值，这种变量被称为模糊变量。

模糊逻辑通过模糊集合和模糊运算，能够处理不确定性、非线性和不精确性等问题，使系统更加适应复杂环境。

PID控制算法是一种经典的闭环控制算法，由比例（P）、积分（I）和微分（D）三个部分组成。

PID控制器通过比较实际输出与期望输出的偏差，根据偏差的大小和方向，调整控制量以实现系统的稳定控制。

PID算法原理及调整规律一、PID算法简介在智能车竞赛中，要想让智能车根据赛道的不断变化灵活的行进，PID算法的采用很有意义。

首先必须明确PID算法是基于反馈的。

一般情况下，这个反馈就是速度传感器返回给单片机当前电机的转速。

简单的说，就是用这个反馈跟预设值进行比较，如果转速偏大，就减小电机两端的电压；相反，则增加电机两端的电压。

顾名思义，P指是比例（Proportion），I指是积分（Integral），D指微分（Differential）。

在电机调速系统中，输入信号为正，要求电机正转时，反馈信号也为正（PID算法时，误差=输入-反馈），同时电机转速越高，反馈信号越大。

要想搞懂PID算法的原理，首先必须先明白P,I,D各自的含义及控制规律：比例P：比例项部分其实就是对预设值和反馈值差值的发大倍数。

举个例子，假如原来电机两端的电压为U0，比例P为0.2，输入值是800，而反馈值是1000，那么输出到电机两端的电压应变为U0+0.2*（800-1000）。

从而达到了调节速度的目的。

显然比例P越大时，电机转速回归到输入值的速度将更快，及调节灵敏度就越高。

从而，加大P值，可以减少从非稳态到稳态的时间。

但是同时也可能造成电机转速在预设值附近振荡的情形，所以又引入积分I解决此问题。

积分I：顾名思义，积分项部分其实就是对预设值和反馈值之间的差值在时间上进行累加。

当差值不是很大时，为了不引起振荡。

可以先让电机按原转速继续运行。

当时要将这个差值用积分项累加。

当这个和累加到一定值时，再一次性进行处理。

从而避免了振荡现象的发生。

可见，积分项的调节存在明显的滞后。

而且I值越大，滞后效果越明显。

微分D：微分项部分其实就是求电机转速的变化率。

也就是前后两次差值的差而已。

也就是说，微分项是根据差值变化的速率，提前给出一个相应的调节动作。

可见微分项的调节是超前的。

并且D值越大，超前作用越明显。

可以在一定程度上缓冲振荡。

比例项的作用仅是放大误差的幅值，而目前需要增加的是“微分项”，它能预测误差变化的趋势，这样，具有比例+微分的控制器，就能够提前使抑制误差的控制作用等于零，甚至为负值，从而避免了被控量的严重超调。

1、把I、D调成0 调P给一个较大的值，给一个2米左右的期望值，给好P值后，先空载，如果速度受控，就把车放在跑道上，如果超调，车子就会以大概8m每秒的速度飞奔，如果出现这种情况，就往小调，直到找到临界值，记下那个临界值，做好防撞。

2、P调好后，在临界值的基础上增加百分之30到40，然后调I ，同样的方法I在临界值的基础上增加百分之60到80，然后调D。

3、D只需要微调，慢慢往上加，找到刚好不震荡的那个点就行了。

说明：在调节期间，只用PID什么棒棒，减速程序都先屏蔽了，要不然是看不出效果的。

智能车PID的算法推荐智能车PID控制算法是一种常用的控制算法，它通过不断地调整车辆的控制量来实现目标状态与当前状态之间的误差最小化。

PID算法的名称源于它的三个部分：比例（P）、积分（I）和微分（D），而车辆的控制量则是根据这三个部分的权重参数进行计算。

比例项（P）是通过比较目标状态和当前状态的误差得到的，其控制效果是与误差成比例的。

当误差较大时，比例项会产生较大的输出，有助于加快系统响应速度；而当误差较小时，比例项的输出将减小，以减小振荡。

积分项（I）可以追踪已经发生的误差，得到误差的累积项。

它在误差持续存在时提供控制输出，可以在误差较小或者趋于零时，对系统进行微调以消除持久性误差。

微分项（D）是根据误差的变化率来调整系统的输出。

它可以提供一个反馈信号，预测误差的变化趋势，并制定适当的控制输出来减小误差的变化速度，以克服过冲或振荡的问题。

在实际应用中，选择合适的PID权重参数是非常重要的。

通常的做法是先设置P和D的值，然后逐渐增加I的值直到系统稳定。

这个过程可能需要多次试验和微调，以获得最佳的参数组合。

除了基本的PID算法，还有一些改进的PID算法可供选择，其中一些常用的包括：1.增量PID算法：在每个控制周期中，通过计算误差的变化量来更新控制量，以提高控制系统对于误差变化的敏感性。

2.自适应PID算法：根据系统当前状态和性能，动态调整PID参数，以适应不同的工况和外部扰动。

3.模糊PID算法：结合模糊逻辑和PID算法，通过定义模糊规则来调整PID参数，以更好地适应非线性和不确定性系统。

4.基于模型的PID算法：通过对系统动态建模，根据建模结果自动调整PID参数，以提高系统的控制精度和稳定性。

5.改进的积分项算法：针对积分项可能导致的问题（如积分饱和），进行改进和优化，以避免控制系统出现过度响应或不稳定的情况。

6.鲁棒PID算法：通过考虑外部扰动和模型不确定性，设计具有鲁棒性的PID控制器，以提高系统的抗干扰能力和稳定性。

智能车速度控制pid（电机闭环控制算法）对于智能车的电机闭环控制算法，我之所以标题没有写上智能车电机PID闭环控制算法是因为PID 算法根本就不是特别好的适用于智能车这种变化很快的系统，对于智能车，电机的调速可以说是时时刻刻再进行调速控制的，我上面说描述的经典PID 算法，都是针对一些惰性系统，也就是说是变化比较慢的系统的，所以对于智能车的电机调速采用完完整整的PID 算法，是根本不可取的，及时采用了，你必须要经过一些变换和改进才能使用。

以上的简述只是鄙人自己的看法，如有错误，请各位高手指正。

现在估计您会疑问，PID 不适用于智能车的电机控制，那什么才适用呢？鄙人原来做过智能车，从鄙人本身的理解，P 算法控制电机，也就是比例控制是最好的，反应速度快，控制精度高，不存在积分和微分效应，非常适用于适用于控制周期短的系统，当然，对于一些特殊的逻辑控制算法，可能要采用PD算法，用微分来做补偿，防止震荡和超调。

下面来说下电机控制算法从开始的加入到最终的确定的方法：当然这一切的前提就是安装了编码器，车速有反馈，只有加上编码器，有了反馈，才能组成一个闭环系统。

当然您也可以加上码盘，或者霍尔开关等一切可以返回车速的东西都可以。

（1）首先建议在车速比较慢的时候，采用PID 算法来控制电机，为什么开始要建议您采用PID 呢？主要是为了让您更加深刻理解PID 算法的精髓和调试步骤方法等，有助于以后对控制算法更加深入的研究和书写。

调试PID 三个参数的方法，很多地方都提供了，我在这里简单的说下：首先将ID 参数都变为0，先调整P 比例参数，调整到速度基本上跟您给定的速度差不多，也就是说基本稳定在您给定的脉冲数，当然这个时候会非常的震荡，不要担心，接下来调整I，调整I 的结果就是震荡会消除很多，但是车速会变化缓慢，也就是说会有一些延迟，然后再调整D，调整D 的结果就是增强调节的灵活性和预见性，在给定速度变化的过程中，能够以一个平稳过渡来变换，而且速度可以长时间稳定在给定速度附近，然后PID 三个参数的基本范围就确定了，然后再根据实际的跑车来微调这些参数，当然在您调试PID之前，请仔细阅读PID 理论知识，这样有助于您的调试和理解，。

智能车设计中增量式PID控制算法的运用作者：徐世豪来源：《中国新通信》2017年第02期【摘要】智能车是现代科技研究与发展的重要方向之一，控制系统是智能车研发的关键所在。

本文以增量式PID控制算法作为智能车研究的切入点，通过实验分析得出采用增量式PID控制算法能够起到提升智能车系统控制的目的，提升车辆的运动性能。

【关键词】智能车增量式 PID控制算法一、智能车总体方案设计智能车的运行是基于传感器提前感知到道路的具体情况，进而通过内部控制系统发出相应的指令，做出相应的应对措施，调整行驶状态，达到顺利通过的目的。

综合现有研究，智能车的运行状态如下图1所示：控制器的输入是传感器信息（道路检测传感器和速度传感器信息）；输出是执行器件（舵机和直流电机）的控制参数。

控制器要完成的主要任务有：图像采集、速度测量、图像处理、方向和速度控制。

根据任务需要，控制器中应包含有图像采集模块、引导线提取算法、图像识别算法、脉冲计数模块、定时器模块、速度测量算法、方向控制算法、速度控制算法[1]，如图2所示。

二、智能车的控制算法2.1 PID参数的影响采用比例系数kp的目的，在于通过提升智能车系统的响应速度以提升其调节的精度，但需要合理控制kp的数值，不宜过大和过小。

例如，当kp数值过大，则会加速系统的响应速度，导致超调进而危及到系统的稳定性。

当kp数值过小，则会降低系统的响应速度而调节的精度随之下降，进而导致系统调节的时间被延长，破坏系统的动态性能与静态性能。

在实验过程中，模型车在行驶过程时，随着kp系数增加舵机的反应速度得以提升，模型车在横向转向时，舵机迅速做出反应并及时调整方向。

然而，当模型车处于直线行驶时，因车速较快导致出现控制不灵的问题，表现为：高速行驶过程中，模型车左右晃动难以及时稳定方向，致使直线行驶变成了摇摆不定的曲线。

同时，因方向不定的影响，模型车的速度得不到提升。

积分作用系数ki的作用是消除系统的稳态误差。

智能车的 PID 控制 智能车的转向控制和速度控制是一体的，合理的速度分配以及最优的行驶路线，才能使智能车在最短时间内完成比赛。

从我们开始提速调试的过程中，曲率半径为50cm 的最小弯几乎都会冲出去，究其原因是当初赛道判断出错，入弯时速度调整太迟，当速度调整过来时，车子已经冲出赛道。

经过长期的调试发现，如果在入弯前能及时调整速度，智能车在弯道内可以很好的以比较高的速度行驶，同时可以切线以最优路径行驶以单行黑线点与图像中心的偏差来对转向进行控制。

最终采用了PD 对转向进行控制，P ——某一行的偏差，D ——本次偏差与上一次偏差的差值。

PD 值是我们调好的一组固定值。

只是P 的参考行我们采用的是动态设定，根据我们外部按键设定的速度值的不同，也通过外部按键设定不同的参考行，保证智能车的沿线及切弯。

设定速度低时，参考行设定距车子近的方向，如果此时设定的距车子太远的地方，智能车在过弯道时，很容易切弯过度，行驶出赛道。

当设定速度高时，参考行设定距车子远的方向，这样可以在高速行驶下，使车子提前转弯我们采用的是增量式PID 算法。

PID 控制器原理图如图3.13所示，图3.13 PID 控制器原理框图 图3.13中，r(t)是电动机的速度设定值，c(t)是转速的实际测量值，e(t)是控制器的输入偏差信号，u(t)是控制器的输出控制量，则PID 控制算式如下：公式1其中Kp是比例系数，Ti是积分时间常数，Td是微分时间常数。

把上式离散化处理后得：公式2其中Ts为采样周期。

由于采用的是增量式PID算法，因此PID调节器只需计算出控制量的增量，所以增量式PID控制算式如下：公式3公式4令A=（Kp+Ki+Kd），B=(Kp+2Kd)，C=Kd，则有：公式5我们只需确定上式中的A,B,C三个变量的值，寻找一组最为合适的PID参数，在这里推荐经验调试来确定三个变量的值，先把B,C置0，调参数A，然后在A 的基础上依次来确定B和C。

恩智浦杯全国智能车竞赛之PID调节PID调节是一种经典的控制算法，可以帮助智能车在一定范围内保持目标状态，并且通过不断地调节，使其更加稳定和高效。

在恩智浦杯全国智能车竞赛中，PID调节是必不可少的一项技能，掌握它可以提高竞赛的分数和排名。

PID调节是由三个参数组成的控制算法：比例项（P），积分项（I）和微分项（D）。

通过调节这三个参数，可以获得不同的控制效果。

比例项是最基本的参数，用于控制车辆的响应速度；积分项可以帮助车辆消除系统误差；微分项则可以帮助车辆抑制系统的震荡。

在恩智浦杯全国智能车竞赛中，通常需要使用PID调节来控制小车的速度和位置。

例如，当小车需要按照一定轨迹行驶时，可以通过PID调节控制小车的角速度和轨迹偏差来保持小车在轨迹中间，并且尽可能减小位置误差。

在实际应用中，PID调节还可以应用于自动驾驶汽车、自动控制系统等领域。

为了实现PID调节，需要掌握几个重要的参数：1. P参数（比例项）：该参数控制车辆响应的速度，它直接影响了小车的响应速度和准确性。

当P值增大时，车辆的响应速度增快，但也容易导致车辆震荡和失控。

2. I参数（积分项）：该参数用于消除系统误差。

系统误差是由于传感器等因素引起的小车偏移，通常不能完全通过比例项来校正。

当I值增大时，小车的控制精度会增加，但也容易引起车辆的超调和不稳定性。

3. D参数（微分项）：该参数用于抑制车辆震荡和失控。

当D值增加时，车辆对噪声和干扰的鲁棒性会增强，但也可能导致车辆无法适应快速变化的环境。

当确定了P、I和D参数后，还需要进行参数调节以获得最佳的控制效果。

调节PID参数通常可以使用经验法或自适应算法。

经验法通常需要手动调整参数，但可以根据经验快速缩小参数范围；自适应算法可以自动调整参数，但需要更多的计算资源和时间。

总之，PID调节是智能车竞赛中必不可少的技能之一，可以帮助车辆在规定时间内完成任务并获得高分。

掌握PID调节技能需要不断实践和改进，以便在竞赛中更好地发挥作用。

总所周知，PID算法是个很经典的东西。

而做自平衡小车，飞行器PID是一个必须翻过的坎。

因此本节我们来好好讲解一下PID，根据我在学习中的体会，力求通俗易懂。

并举出PID的形象例子来帮助理解PID。

一、首先介绍一下PID名字的由来：P：Proportion（比例），就是输入偏差乘以一个常数。

I ：Integral（积分），就是对输入偏差进行积分运算。

D：Derivative（微分），对输入偏差进行微分运算。

注：输入偏差=读出的被控制对象的值-设定值。

比如说我要把温度控制在26度，但是现在我从温度传感器上读出温度为28度。

则这个26度就是”设定值“，28度就是“读出的被控制对象的值”。

然后来看一下，这三个元素对PID算法的作用，了解一下即可，不懂不用勉强。

P，打个比方，如果现在的输出是1，目标输出是100，那么P的作用是以最快的速度达到100，把P理解为一个系数即可；而I呢？大家学过高数的，0的积分才能是一个常数，I就是使误差为0而起调和作用；D呢？大家都知道微分是求导数，导数代表切线是吧，切线的方向就是最快到至高点的方向。

这样理解，最快获得最优解，那么微分就是加快调节过程的作用了。

二、然后要知道PID算法具体分两种：一种是位置式的，一种是增量式的。

在小车里一般用增量式，为什么呢？位置式PID的输出与过去的所有状态有关，计算时要对e（每一次的控制误差）进行累加，这个计算量非常大，而明显没有必要。

而且小车的PID控制器的输出并不是绝对数值，而是一个△，代表增多少，减多少。

换句话说，通过增量PID算法，每次输出是PWM要增加多少或者减小多少，而不是PWM的实际值。

所以明白增量式PID 就行了。

三、接着讲PID参数的整定，也就是PID公式中，那几个常数系数Kp，Ti，Td等是怎么被确定下来然后带入PID算法中的。

如果要运用PID，则PID参数是必须由自己调出来适合自己的项目的。

通常四旋翼，自平衡车的参数都是由自己一个调节出来的，这是一个繁琐的过程。

为了实现PID控制所需要的等距离采样，咱们利用了一个按时中断，每2ms进行一次数据采样和PID计算。

与此并行，系统中还设计了一个转速脉冲检测中断，从而实现了转速检测。

为了调试的需要，程序中还在main{}函数中加入了相关的调试代码，这部份代码有最低的优先级，能够在保证不影响控制策略的情形下实现发送调试数据等功能。

检测环节对整个控制系统的质量起到相当重要的作用PID控制调整速度本系统采用的是增量式数字PID控制，通过每一控制周期（10ms）读入脉冲数间接测得小车当前转速vi_FeedBack，将vi_FeedBack与模糊推理取得的小车期望速度vi_Ref比较，由以下公式求得速度误差error1与速度误差率d_error。

error1 = vi_Ref–vi_FeedBack; （公式3）d_error = error1 –vi_PreError; （公式4）公式4中, vi_PreError为上次的速度误差。

考虑到控制周期较长，假设按s 的平均速度计算，则一个控制周期小车可能能够跑过，若是按这种周期用上述PID调节速度，则会致使加速减速均太长的后果，严峻的影响小车的快速性和稳固性。

为了解决那个问题，能够在PID调速控制中加入BANG-BANG控制思想：按照error1的大小，若是正大，则正转给全额占空比；若是负大，则自由停车或给一个反转占空比；不然就采用PID计算的占空比。

PID控制算法为了使赛车光滑得维持在黑线中央，即便赛车的偏移量光滑地维持在0，实用了PID控制算法。

P为比例参数，D为微分参数。

基准值为0，PID输入为水平偏移量X0，PID 输出为转角，转角方向：向左转为正，向右转为负。

P参数在智能车控制器中表示水平误差量的权，D参数在智能车控制器中表示水平误差速度的权。

水平误差量直接反映了赛车偏离黑线的程度，例如赛车偏向黑线的左侧越厉害，则赛车的右转角度将越大。

水平误差量，是PID控制器的P部份。