土力学 第二章 土中的水及其流动
- 格式:ppt
- 大小:1.94 MB
- 文档页数:49

土力学王丽琴西安理工大学土建学院岩土工程研究所王丽琴主讲,1~5,7,10;卓越班作业:P78,1, 2,3,4水工班作业:P46第二章土的渗透性与渗流规律第一节概述第二节土的渗透性第三节二维渗流与流网第四节渗透力和渗透变形王丽琴主讲概 述土颗粒土中水渗流碎散性 三相性孔隙流体流动能量差 渗透性:土具有被水等液体透过的性质。
渗 流:水等液体在土体孔隙中流动的现象。
渗流量渗透变形土石坝防渗斜墙及铺盖浸润线透水层不透水层土石坝坝基坝身渗流渗水压力 扬压力渗流量 渗透变形透水层不透水层基坑板桩墙板桩围护下的基坑渗流渗流量透水层不透水层天然水面水井渗流Q渗流量 原地下水位渗流时地下水位渠道渗流水位渗流滑坡渗流量 渗透变形 渗水压力 渗流滑坡土的渗透性及渗流规律二维渗流及流网 渗透力与渗透变形扬压力 土坡稳定分析挡水建筑物集水建筑物 引水结构物 基坑等地下施工 多雨地区边坡水位第二章土的渗透性与渗流规律第一节概述第二节土的渗透性第三节二维渗流与流网第四节渗透力和渗透变形水往低处流水往高处“跑”速度v压力u 位置:使水流从位置势能高处流向位置势能低处流速:水具有的动能压力:水所具有的压力势能一、渗流中的水头与水力坡降ABL透水层不透水层基坑板桩墙一.渗流中的水头与水力坡降ABLh 1 h 2 z AwA u γwB u γz BΔh基准面gv u z h w22++=γAA u z h γ+=1BB u z h +=212h h h ∆=-wuz h γ+=Lh i ∆=总水头-单位重量水体所具有的能量z :位置水头(势水头) u /γw :压力水头(静水头) v 2/(2g):流速水头(动水头)≈0A 点总水头:B 点总水头:总水头: 水力坡降:水头差(水头损失): 测管水头一.渗流中的水头与水力坡降▪试验前提:层流 ∆h ↑,Q ↑A ↑,Q ↑L ↑,Q ↓Lh AQ ∆∝断面平均流速 水力坡降 AQv =hi ∆=iv ∝1.渗透试验▪试验结果▪试验装置:如图▪试验条件: h 1,A ,L =const ▪量测变量: h 2,V ,t ∆h=h 1-h 2 Q =V /tLVh 1h 2dabc12 Δh土 样2.达西定律 v k i=⋅ 渗透定律v i∝渗透系数k : 反映土的透水性能的比例系数,其大小与土的性质有关。





教学内容设计及安排第一节达西定律【基本内容】渗透——在水位差作用下,水透过土体孔隙的现象。
渗透性——土具有被水透过的性能。
一、达西定律v =ki =k Lh或用渗流量表示为q =vA =kiA式中 v ――渗透速度,cm/s 或m/d ;q ――渗流量,cm 3/s 或m 3/d ;i =h /L ――水力坡降(水力梯度),即沿渗流方向单位距离的水头损失,无因次; h ――试样两端的水头差,cm 或m ; L ――渗径长度;cm 或m ;k ――渗透系数,cm/s 或m/d ;其物理意义是当水力梯度i 等于1时的渗透速度; A ――试样截面积,cm 2或m 2。
【注意】由上式求出的v 是一种假想的平均流速,假定水在土中的渗透是通过整个土体截面来进行的。
水在土体中的实际平均流速要比达西定律采用的假想平均流速大。
二、达西定律的适用范围与起始水力坡降对于密实的粘土:由于结合水具有较大的粘滞阻力,只有当水力梯度达到某一数值,克服了结合水的粘滞阻力后才能发生渗透。
起始水力梯度――使粘性土开始发生渗透时的水力坡降。
(a ) 砂土 (b ) 密实粘土 (c )砾石、卵石粘性土渗透系数与水力坡降的规律偏离达西定律而呈非线性关系,如图(b )中的实线所示,常用虚直线来描述密实粘土的渗透规律。
()b i i k v -= (2-3)式中 i b ――密实粘土的起始水力坡降;对于粗粒土中(如砾、卵石等):在较小的i 下,v 与i 才呈线性关系,当渗透速度超过临界流速v cr 时,水在土中的流动进入紊流状态,渗透速度与水力坡降呈非线性关系,如图(c )所示,此时,达西定律不能适用。
第二节 渗透系数及其确定方法【基本内容】一、渗透试验1.常水头试验常水头试验适用于透水性大(k >10-3cm/s )的土,例如砂土。
常水头试验就是在整个试验过程中,水头保持不变。
试验时测出某时间间隔t 内流过试样的总水量V ,根据达西定律At LhkkiAt qt V === 即 hAtVL k =2.变水头试验粘性土由于渗透系数很小,流经试样的总水量也很小,不易准确测定。



第2章土的渗透性与渗流2.1概述由于土体本身具有连续的孔隙,如果存在水位差的作用时,水就会透过土体孔隙而产生孔隙内的流动,这一现象称为渗透。
土具有被水透过的性能称为土的渗透性。
这里所论及的水是指重力水。
水是在土的孔隙中流动的,本章假定土颗粒骨架形成的孔隙是固定不变的,并且认为,在孔隙中流动的水是具有粘滞性的流体。
也就是说,把土中水的流动,简单地看成是粘滞性的流体在土烧制成的素陶磁管似的刚体的孔隙中流动。
这种思考方法,在被称为达西定律的试验中反映出来。
达西定律是土中水的运动规律的最重要的公式。
这个公式采用了“水是从水头(总水头)高的地方流向低处”这一水流的基本原理。
根据达西定律和连续方程,再考虑边界条件,一般的透水问题都可以得到解决,即可以求出土中水的流量(透水量)及土中水压力的分布。
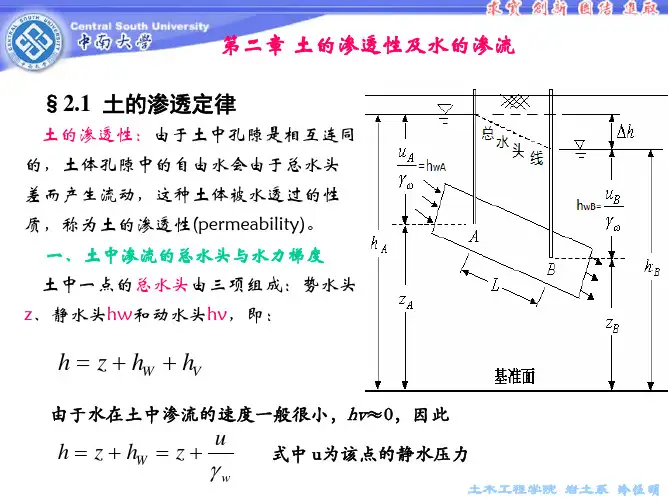
如图2-1 所示为土木、水利工程中典型渗流问题。
此外,土的渗透性的强弱,对土体的固结、强度以及工程施工都有非常重要的影响。
为此,我们必须对土的渗透性质、水在土中的渗透规律及其与工程的关系进行很好的研究,从而给土工建筑物或地基的设计、施工提供必要的资料。
图2-1土木、水利工程中的渗流问题2.2土的渗透性土是由固体相的颗粒、孔隙中的液体和气体三相组成的,而土中的孔隙具有连续的性质,当土作为水土建筑物的地基或直接把它用作水土建筑物的材料时,水就会在水头差作用下从水位较高的一侧透过土体的孔隙流向水位较低的一侧。
渗透:在水头差作用下,水透过土体孔隙的现象。
渗透性:土允许水透过的性能称为土的渗透性。
水在土体中渗透,一方面会造成水量损失,影响工程效益;另一方面将引起土体内部应力状态的变化,从而改变水土建筑物或地基的稳定条件,甚者还会酿成破坏事故。
此外,土的渗透性的强弱,对土体的固结、强度以及工程施工都有非常重要的影响。
2.2.1土的渗透定律地下水在土体孔隙中渗透时,由于渗透阻力的作用,沿程必然伴随着能量的损失。
为了揭示水在土体中的渗透规律,法国工程师达西(H.darcy)经过大量的试验研究,1856年总结得出渗透能量损失与渗流速度之间的相互关系即为达西定律。
Teton 坝损失损失::直接直接800080008000万美元万美元万美元,,起诉55005500起起,2.52.5亿美元亿美元亿美元,,死1414人人,受灾受灾2.52.52.5万万人,6060万亩土地万亩土地万亩土地,,3232公公里铁路原因原因::管涌土坝土坝位于美国位于美国Idaho 州Teton 河上河上,,防洪防洪、、灌溉灌溉、、发电发电、、旅游综合利用旅游综合利用,,装机16MW ,最大坝高126.5m ,坝顶长945m 。
建于建于197219721972--7575年年,75,75年年1111月开始蓄水月开始蓄水月开始蓄水,,7676年春年春洪水期间水位迅速上升洪水期间水位迅速上升,,达1.21.2m/d m/d m/d。
6月5日上午日上午11:5511:5511:55发发生溃坝生溃坝。
下图是现在的景象Teton坝1976年6月5日上午10:30左右,下游坝面有水渗出并带出泥土。
Teton坝1111::0000左右洞口不断扩大并向坝顶靠近,泥水流量增加Teton Teton坝坝11:30洞口继续向上扩大,泥水冲蚀了坝基,主洞的上方又出现一渗水洞。
流出的泥水开始冲击坝趾处的设施。
11:50左右洞口扩大加速,泥水对坝基的冲蚀更加剧烈。
Teton Teton坝坝11:57 坝坡坍塌,泥水狂泻而下Teton Teton坝坝12:00过后坍塌口加宽Teton Teton坝坝洪水扫过下游谷底,附近所有设施被彻底摧毁Teton Teton坝坝失事现场目前的状况Teton Teton坝坝水头梯度又称水力梯度、水力坡降。
三、渗透系数及其确定方法渗透试验渗透试验((室内室内))AtLhk kiAt qt V ===时间t 内流出的水量hAtVL k =1.1.常水头试验常水头试验————整个试验过程中水头保持不变适用于透水性大适用于透水性大((k >10-3cm/s )的土,例如砂土例如砂土。