第11章 反比例函数 单元测评卷(1)

八年级数学下册第11章反比例函数测试卷1 （新版）苏科版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（八年级数学下册第11章反比例函数测试卷1 （新版）苏科版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为八年级数学下册第11章反比例函数测试卷1 （新版）苏科版的全部内容。

第十一章 反比例函数(时间；90分钟 满分:100分）一、填空题(每题2分，共20分) 1．若点(一2，3）在反比例函数ky x=的图象上，则k=_______． 2．函数2y x=-的图象在每个象限内，y 随着x 的减小而_______．3．反比例函数)2my x-=，其图象在一、三象限，则m 的取值范围是_______．4．k y x =的图象是过点(12，一4）的双曲线:则k=_______，图象在第_______象限．5．已知正比例函数y=kx,y 随x 的增大而减小，则对于反比例函数)ky x=，当x 〈0时,y随x 的增大而_______．6．已知A 是函数2y x=-的图象上的点，过A 点作AH ⊥x 轴，垂足为H ，连接OA ，则∆AOH的面积为_______．7．若一次函数)y mx n =+与反比例函数33n m y -=的图象相交于点(12，2)，那么该直线与双曲线的另一交点为_______．8．在平面直角坐标系内，从反比例函数(0)ky k x=>的图象上的一点分别作x 、y 轴的垂线段，与x ,y 轴所围成的矩形面积是12，那么该函数解析式是_______．9．双曲线3y x=在第_______象限内，经过点(一1，_______)． 10．若点A （7，1y ）,B(5，2y ）在反比例函数3y x=-图象上，则1y 、2y 的大小关系是_______;若点C(a,3y )，D （a+1,4y )也在上述函数的图象上，则3y ,4y 的大小关系是_______． 二、选择题(每题3分，共30分）11．下列式子中，表示y 是x 的反比例函数的是 ( )A ．21y x =B ．2x y =C ． 1x y x =+ D ．1xy = 12．反比例函数ky x=的图象经过点（2，7），那么也在该图象上的点是 （ )A ．（1，5)B ．(一7，一2）C ．(3,6）D ．(一5，0） 13．已知反比例函数3m y x+=的图象具有下列特征：在所在象限内，y 的值随x 值的增大而增大,则m 的取值范围是 （ ） A ．m= 一3 B ．m>一3 C ．m<一3 D ．m 〉314．反比例函数,231,,4y y y x x x==-=的共同点是 （ )A ．图象位于同样的象限内B ．自变量的取值范围是全体实数C ．图象在每一象限内，y 随x 的增大而减少D ．图象都不与坐标轴相交15．已知点111222(,),(,)p x y p x y 在双曲线(0)ky k x=>上，若120x x <<，则1y 与2y 的关系为（ )A ．12y y >B ． 12y y <C ．12y y =D ．不能确定16．已知点A （a ，b ）在某一反比例函数的图象上，则下列各点中也在此图象上的是（ ）A ．(,)a b -B ．(,)a b -C ．11,a b ⎛⎫⎪⎝⎭D ．(,)a b --17．如果反比例函数ky x=的图象经过(2,2)-，那么函数y kx k =-的图象一定过 ( ) A ．第一、二、四象限 B ．第二、三、四象限 C ．第一、三、四象限 D ．第一、二、三象限18．某乡的粮食总产量为a （a 为常数)吨，设该乡平均每人占有粮食数为y(吨)，人口数为x ，则y 与x 之间的函数关系图象应为下图所示中的 （ ）19．已知反比例函数257(1)aa y a x --=--的图象位于第一、三象限，则a 的值为 ( )A ．6B ．一1C ．一1或6D ．一6或1第一象 20．如图，点P 、Q 是反比例函数1y x=的图象上在限内的任两点，分别过P 、Q 作x 轴、y 轴的垂线段 PA 、PB 、QC 、QD ，垂足分别为A 、B 、C 、D,又已知线段PA 、QD 相交于点E ，四边形PEDB 、QEAC的面积分别记为S 1、S 2是，则 （ ） A ．S 1>S 2 B ．S 1〈S 2C ．S 1=S 2D ．S 1•S 2的大小不确定 三、解答题(共50分)21．（6分）在直角坐标系中画出函数6y x=的图象．22．(7分）已知正比例函数y kx =与反比例函数3y x=的图象都过点A （m ，1）．求： （1)正比例函数的解析式；(2）正比例函数与反比例函数在图象上的另一个交点坐标．23．（7分)已知反比例函数3y x=及一次函数4y x =-+,求这两个函数图象的交点坐标．24．(7分）一定质量的二氧化碳，当它的体积35V m =时,它的密度32/kg m ρ=．（1)求ρ与V 的函数关系式；（2)求当V=20 m3时,二氧化碳的密度ρ．25．(7分)如图，在∆ABC中,D为AB上一点，DE//BC,延长DE 到F，使DF=BC．设DE=2，BD=3,AD=x，EF=y,求y与x的函数关系式．26．(8分)如图，一次函数y kx b=+的图象与反比例函数myx=的图象交于A、B两点．(1）利用图中条件,求反比例函数和一次函数的解析式;(2）根据图象求出使一次函数的值大于反比例函数的值时,x的取值范围．27．（8分）如图，在平面直角坐标系中，双曲线kyx=过第一象限内一点A,AB x⊥轴,垂足为B,S△AOB=2．（1）求k的值；C，求△ABC的面积．(2）如果直线y x k=+经过点A,与x轴交于点参考答案1．一6 2．减小 3．m 〈2 4．一2 二、四 5．增大 6．1 7．（一1，1) 8．12y x=9．一、二 3 10．y 1>y 2 y 3〈y 4 11．D 12．B 13．C 14．D 15．A 16．D 17．A 8．D 19．B 20．C 21．略22．（1) 13y x = （2）（一3，一1）23．（3，1) （1，3) 24．（1）10V ρ= (2)31/2kg m ρ= 25．6y x=26．（1) 2y x=- 1y x =--(2)当2x <-或01x <<时，一次函数的值大于反比例函数的值．27．（1)k=4 （2）可得A 2,2)，C （一4，0)，6ABCS∴=+。

反比例函数单元测试卷含答案一、选择题1. 反比例函数的一般形式是：A. y = kxB. y = ax + bC. y = k/xD. y = mx + c答案: C2. 当x为0时，反比例函数的值为：A. 0B. 1C. 无定义D. 任意值答案: C3. 若反比例函数的k值为正数，x趋近于无穷大，y会趋近于：A. 正无穷大B. 负无穷大C. 0D. 不存在极限答案: B4. 反比例函数的图像是一条：A. 直线B. 抛物线C. 余弦曲线D. 双曲线答案: D5. 若反比例函数的x值为正数，y值为负数，那么k值是：A. 正数B. 负数C. 零D. 无法确定答案: B二、计算题1. 已知反比例函数y = 5/x，当x = 2时，求y的值。

答案: 2.52. 已知反比例函数y = 3/x，当y = 6时，求x的值。

答案: 0.5三、简答题1. 什么是反比例函数？答案: 反比例函数是一种函数关系，当自变量x的值增大时，因变量y的值会减小，并且二者之间呈现出一种倒数关系。

它的一般形式为y = k/x，其中k为常数。

2. 反比例函数的图像有什么特点？答案: 反比例函数的图像是一条双曲线。

当x趋近于无穷大或无穷小时，函数的值趋近于零。

两支曲线的对称轴为y轴，并在y 轴上有一个渐近线。

3. 如何确定反比例函数的常数k的值？答案: 可以通过已知点的坐标进行求解。

将已知的x和y的值代入反比例函数的一般形式中，解方程得到k的值。

以上就是反比例函数单元测试卷的答案。

希望能对你的学习有所帮助！。

函数y=(x>0)的图像经过该菱形对角线的交点A,且与边BC交于点F.若点D
1.如图11-5-1,过反比例函数y=(x>0)的图像上一点A作AB⊥x轴于点B,连
2.如图11-5-2,点P是反比例函数y=(x>0)图像上的任意一点,过点P分别作两
图11-6-3
24.如图11-6-4,直线y=x+2与双曲线相交于点A(m,3),与x轴交于(2)求点C的坐标,并结合图像写出不等式0<x+m≤的解集.
苏教版八年级下册——第十一章 反比例函数——单元测试卷 基础版
在殿堂和田垄之间，你选择后者，脚踏泥泞，仰首鞠行，在荆棘和贫穷中拓荒。

洒下的汗水，是青春，埋下的种子，叫理想。

∴解得
∴一次函数的表达式为y=x+2. (2)∵将x=0代入y=x+2,得y=2,
∴点C 的坐标为(0,2). ∴S △AOB =S △AOC +S △COB =×2×[2-(-4)]=6.。

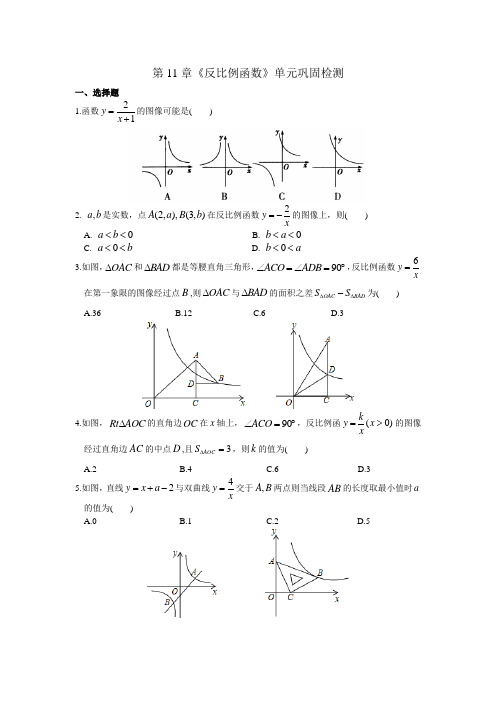
第11章《反比例函数》单元巩固检测一、选择题 1.函数21y x =+的图像可能是( )2. ,a b 是实数，点(2,),(3,)A a B b 在反比例函数2y x=-的图像上，则( ) A. 0a b << B. 0b a << C. 0a b << D. 0b a <<3.如图，OAC ∆和BAD ∆都是等腰直角三角形，90ACO ADB ∠=∠=︒，反比例函数6y x= 在第一象限的图像经过点B ,则OAC ∆与BAD ∆的面积之差OAC BAD S S ∆∆-为( ) A.36 B.12 C.6 D.34.如图，Rt AOC ∆的直角边OC 在x 轴上，90ACO ∠=︒，反比例函(0)ky x x=>的图像 经过直角边AC 的中点D ,且3AOC S ∆=，则k 的值为( )A.2B.4C.6D.3 5.如图，直线2y x a =+-与双曲线4y x=交于,A B 两点则当线段AB 的长度取最小值时a 的值为( )A.0B.1C.2D.56.在平面直角坐标系xOy 中，将一块含有45°角的直角三角板如图放置，直角顶点C 的坐 标为(1,0 )，顶点A 的坐标为(0,2)，顶点B 恰好落在第一象限的双曲线上，现将直角三角 板沿x 轴正方向平移，当顶点A 恰好落在该双曲线上时停止运动，则此时点C 的对应点 C '的坐标为( )A. 3(,0)2B. (2,0)C. 5(,0)2D. (3,0) 二、填空题 7.如图，双曲线(0)ky k x=>与圆O 在第一象限内交于,P Q 两点，分别过,P Q 两点向x 轴 和y 轴作垂线.已知点P 的坐标为(1,3)，则图中阴影部分的面积为 .8.如图，反比例函数(0)ky k x=≠的图像经过,A B 两点，过点A 作AC x ⊥轴，垂足为C ，过点B 作BD x ⊥轴，垂足为D ，连接AO ，连接BO 交AC 于点E ，若OC CD =，四 边形BDCE 的面积为2，则k 的值为 .9.如图，正比例函数1(0)y mx m =>的图像与反比例函数2ky x=的图像交于点(,4)A n 和点,B AM y ⊥轴，垂足为M ，若AMB ∆的面积为8，则满足12y y >的实数x 的取值范围 是 .10.如图，已知点,A C 在反比例函数a y x =的图像上，点,B D 在反比例函数by x=的图像上，0,////a b AB CD x >>轴，,AB CD 在x 轴的两侧，33,42AB CD ==，AB 与CD 间的距离为6，则a b -的值是 .三、解答题11.(6分)已知121,y y y y =-与x 成反比例，2y 与(2x -)成正比例，并且当1x =-时， 15y =-，当2x =时，32y =.求y 与x 之间的函数表达式.12. (8分)如图，一次函数12y x =-+的图像与反比例函数2ky x=的图像相交于,A B 两点， 点B 的坐标为(2,)m m -.(1)求出m 的值并确定反比例函数的表达式; (2)请直接写出当2x m <时，2y 的取值范围.13. (8分)如图，在平面直角坐标系中，一次函数(0)y mx n m =+≠的图像与反比例函数 (0)ky k x=≠的图像交于第一、三象限内的,A B 两点,与y 轴交于点C ，过点B 作 BM x ⊥轴，垂足为2,,8M BM OM OB ==，点A 的纵坐标为4.(1)求该反比例函数和一次函数的表达式; (2)连接MC ，求四边形MBOC 的面积.14.(12分)某汽车的功率P (W)为一定值，汽车行驶时的速度v (m/s)与它所受的牵引力F (N) 之间的函数关系如图所示.(1)这辆汽车的功率是多少?请写出这一函数的表达式; (2)当它所受牵引力为1 200 N 时，汽车的速度为多少? (3)若限定汽车的速度不超过30 m/s ，则F 在什么范围内?15.如图，在平面直角坐标系xOy 中，函数(0)ky x x=>的图像与直线2y x =-交于点 (3,)A m . (1)求,k m 的值;(2)已知点(,)(0)P n n n >，过点P 作平行于x 轴的直线，交直线2y x =-于点M ，过点 P 作平行于y 轴的直线，交函数(0)ky x x=>的图像于点N . ①当1n =时，判断线段PM 与PN 的数量关系，并说明理由; ②若PN PM ≥，结合函数的图像，直接写出n 的取值范围.16.(14分)如图，一次函数y kx b =+与反比例函数ay x=的图像在第一象限交于点(4,3)A ， 与y 轴的负半轴交于点B ,且OA OB =.(1)求一次函数和反比例函数的表达式;(2)已知点C 在x 轴上，且ABC ∆的面积是8，求此时点C 的坐标;(3)反比例函数(16)ay x x=≤≤的图像记为曲线1C ，将V 向左平移2个单位长度，得曲 线2C ，则1C 平移至2C 处所扫过的面积是.【拓展训练】拓展点：1.与反比例函数有关的新定义问题2.四边形与反比例函数结合的规律性问题 1.定义一个新的运算:ab =2()2()a b a b b a b a-+≤⎧⎪+⎨>⎪-⎩，则运算x 2的最小值为( ) A.－3 B.－2 C. 2 D.32.如图，边长为n 的正方形OABC 的边,OA OC 在坐标轴上，点121,,,n A A A -⋅⋅⋅为OA 的n 等 分点，点121,,,n B B B -⋅⋅⋅为CB 的n 等分点，连接112211,,,n n A B A B A B --⋅⋅⋅，分别交双曲线 2(0)n y x x-=>于点121,,,n C C C -⋅⋅⋅.若1515151516C B C A =，则(n n 为正整数)的值为 ()A.15B. 16C. 17D.18 3.点1122(,),(,)A x y B x y 分别在双曲线1y x=-两支上，若120y y +>，则12x x +的取值范围是 .4.如图，函数y x =-的图像是二、四象限的夹角平分线，将y x =-的图像以点O 为中心旋转90°，其与函数1y x=在第一象限的图像交于点A ，再将y x =-的图像向右平移至点 A ，与x 轴交于点B ，则点B 的坐标为 .5.六一儿童节，小文到公园游玩，看到公园的一段人行弯道MN (不计宽度)如图，它与两面 互相垂直的围墙,OP OQ 之向有一块空地(,)MPOQN MP OP NQ OQ ⊥⊥他发现弯道 MN 上任一点到两围墙的垂线段与围墙所围成的矩形的面积都相等，比如: ,,A B C 是弯 道MN 上三点，矩形ADOG 、矩形BEOH 、矩形CFOI 的面积相等.爱好数学的他建立 了平面直角坐标系(如图)，图中三块阴影部分的面积分别记为123,,S S S ，并测得26S = (单位:m 2) , OG GH HI ==. (1)求1S 和3S 的值;(2)设(,)T x y 是弯道MN 上的任一点，写出y 关于x 的函数表达式;(3)公园准备对区域MPOQN 内部进行绿化改造，在横、纵坐标都是偶数的点处种植花木 (区域边界上的点除外)，已知MP =2 m, NQ =3 m.问一共能种植多少棵花木?参考答案1.C2.A3.D4.D5.C6.C7.48. 163- 9. 20x -<<或2x >10.3 11. 34(2)y x x=+- 12. (1) 2m =，反比例函数的表达式28y x=-; (2) 22y <-. 13.(1)反比例函数：4y x=，一次函数的表达式：22y x =+; (2)四边形MBOC 的面积为4.14.(1)汽车的功率是60000W,函数的表达式: 60000v F=; (2)汽车的速度为50m/s' (3) F 应大于等于2000N. 15.(1) 3,1k m ==; (2)①PM PN =;②01n <≤或3n ≥.16.(1)一次函数的表达式：25y x =-，反比例函数的表达式：12y x=; (2)点C 的坐标1(,0)2或9(,0)2; (3)20【拓展训练】1.B2.C3. 120x x +>4.(2,0)5.(1)1S =18,3S =12; (2) 36y x=; (3)一共能种植17棵花木.。

八年级下册数学第11章《反比例函数》单元试卷-2020-2021年苏科版数学一、单选题1．函数()221ay a x -=-是反比例函数，则a 的值是（ ） A ．1- B ．1C ．±1D ．3± 2．已知()()()1231,2,3,A y B y C y -、、都在反比例函数2y x=的图象上，则323y y y 、、的大小关系的是（ ）A ．123y y y >>B ．213y y y >>C ．321y y y >>D ．132y y y >> 3．如图，M 是反比例函数k y x=的图象上的任意一点，MN x ⊥轴于点N ，且MON △的面积为2，则k 的值是（ ）A ．2B ．2-C ．4D ．4-4．若A （x 1，y 1）、B （x 2，y 2）两点在反比例函数y ＝5k x-的图象上，①过点B 作BC ⊥x 轴，C 为垂足，连接OB ．若△BCO 的面积为2，则k ＝9；②若x 1＝2x 2，则2y 1﹣y 2＝0；③若y 1＜0＜y 2，且x 1＞x 2，则k ＞5其中真命题个数是（ ）A ．0B ．1C ．2D ．35．为了响应“绿水青山就是金山银山”的号召，建设生态文明，某工厂自2019年1月开始限产进行治污改造，其月利润y （万元）与月份x 之间的变化如图所示，治污完成前是反比例函数图象的一部分，治污完成后是一次函数图象的一部分，下列选项错误的是（ ）A ．4月份的利润为50万元B ．治污改造完成后每月利润比前一个月增加30万元C ．治污改造完成前后共有3个月的利润低于100万元D ．8月份该厂利润达到200万元6．如图，已知正比列函数y 1＝4x 的图象与反比例函数y ＝4x 的图象相交于A ，B 两点，正比例函数y 2＝kx （k ≠0）的图象与反比例面数y ＝4x的图象相交于C ，D 两点．连接AD ，BD ，BC ，AC ，若四边形ADBC 是矩形，则k 的值是（ ）A ．12B ．14C ．18D ．17．在同一平面直角坐标系中，函数y ＝kx +1（k ≠0）和k y x=（k ≠0）的图象大致是（ ） A ． B ． C ．D ．8．如图，过点O 作直线与双曲线()0k y k x=≠交于A ，B 两点，过点B 作BC x ⊥轴于点C ，作BD y ⊥轴于点D ．在x 轴、y 轴上分别取点E ，F ，使点A ，E ，F 在同一条直线上，且AE AF =．设图中矩形ODBC 的面积为1S ，EOF △的面积为2S ，则1S ，2S 的数量关系是（ ）A ．12S SB ．122S S =C ．123S S =D ．124S S = 9．如图，一次函数()0y kx b k =+≠与反比例函数()0m y m x =≠分别交于,A B 两点，则不等式m kx b x+<的解集是（ ）A ．2x <-B ．4x >C ．2x <-或04x <<D ．24x -<< 10．如图，在平面直角坐标系中，四边形ABCD 是矩形，AD ∥x 轴，且点C 的坐标为1(1,)2-，2AB =，4=AD ．将矩形ABCD 向右平移，得矩形A B C D ''''使点A '，C '恰好同时落在反比例函数(0)ky x x=>的图象上，则反比例函数的解析式为（ ）A ．2y x =B ．5y x =C ．52y x =D ．25y x =二、填空题11．函数5x y x=-中自变量x 的取值范围是__________． 12．已知菱形的面积是12cm 2，菱形的两条对角线长分别为x 和y ，则y 与x 之间的函数关系是________________．13．已知反比例函数(0)a y a x=>的图像上有两点()11,A y ，()22,B y ，那么1y ______2y ．（填“>”或“<”）14．如图，反比例函数y 1＝k x 和一次函数y 2＝ax+b 的图象交于点A （﹣1，2），B （2，﹣1）两点，则当﹣2＜y 1＜y 2＜12时，x 的取值范围为_____．15．点(,)P m n 是函数3y x=-和4y x =+图象的一个交点，则mn n m +-的值为_________． 16．如图，直线2y x =-与反比例函数()0k y x x =>的图象交于点C ，与x 轴交于点A ，过A 作AB x ⊥轴，交反比例函数图象与点B ．若AC BC =，则OBC 的面积为____．17．如图，过y 轴上任意一点p ，作x 轴的平行线，分别与反比例函数4y x =-和2y x =的图象交于A 点和B 点．若C 为x 轴上任意一点，连接AC BC 、，则ABC 的面积为__________．三、解答题18．已知一次函数17y x =-+的图象与反比例函数2k y x=图像交于A 、B 两点、且A 点的横坐标1-，求：（1）反比例函数的解析式．（2）AOB 的面积．（3）直接写出满足12y y <时x 的取值范围．19．已知一次函数()0y kx n k =+≠与反比例函数m y (m 0)x=≠的图象交于点(,2)A a ，()1,3B ．（1）求这两个函效的表达式；（2）直接写出关于x 的不等式m kx n x+≤的解； （3）若点1(2,)P h y -在一次函数y kx n =+的图象上，若点()22,Q h y -在反比例函数m y x=的图象上，12h <，请比较1y 与2y 的大小． 20．(本题满分8分)某气球内充满了一定质量的气体，在温度不变的条件下，气球内气体的压强p (Pa)是气球体积V(m 3)的反比例函数，且当V=1.5m 3时，p =16000Pa ． （1）当V =1.2m 3时，求p 的值：（2）当气球内的气压大于40000Pa 时，气球将爆炸，为确保气球不爆炸，气球的体积应不小于多少?21．实验数据显示，一般成人喝50毫升某品牌白酒后，血液中酒精含量y(毫克/百毫升)与时间x(时)变化的图象，如下图(图象由线段OA 与部分双曲线AB 组成) ．国家规定，车辆驾驶人员血液中的酒精含量大于或等于20（毫克/百毫升）时属于“酒后驾驶”，不能驾车上路．（1）求部分双曲线AB 的函数解析式；（2）参照上述数学模型，假设某驾驶员晚上22：30在家喝完50毫升该品牌白酒，第二天早上7：00能否驾车去上班？请说明理由．22．如图，在平面直角坐标系中，点()A 3,2在反比例函数(0)k y x x=>的图像上，点B 在射线OA 上，BC x ⊥轴，垂足为C ，BC 与反比例函数的图像相交于点D ，连接AC ，AD ．（1）当点B 的横坐标为6时，求线段AD 的长；（2）若52ACD S =△，求点B 的坐标． 23．如图，在平面直角坐标系中，四边形ABCD 为正方形，已知点(6,0),(7,3)A D --，点B 、C 在二象限内．（1）点B 的坐标________；（2）将正方形ABCD 以每秒2个单位的速度沿x 轴向右平移t 秒，若存在某一时刻t ，使在第一象限内点B ，D 两点的对应点B 、D 正好落在某反比例函数的图象上，请求出此时t 的值以及这个反比例函数的解析式；（3）在（2）的情况下，问是否存在y 轴上的点P 和反比例函数图象上的点Q ，使得以P 、Q 、B 、D 四个点为顶点的四边形是平行四边形？若存在，请直接写出符合题意的点P、Q的坐标：若不存在，请说明理由．参考答案1．A解：∵函数()221a y a x -=-是反比例函数，∴10a -≠，221a -=-，解得：a=-1，故选A ．2．A解：∵k =2＞0，∴图象在一、三象限，且在每一象限内y 随x 的增大而减小．∵1＜2，∴y 1＞y 2＞0，∵-3＜0，∴y 3＜0，∴y 1＞y 2＞y 3，3．D解：∵反比例函数的图象在二、四象限，∴k ＜0，∵点M 是该函数图象上一点，S △MON =2，122k ∴=，解得k=4（舍）或-4． 故选：D ．4．B解：∵A （x 1，y 1）、B （x 2，y 2）两点在反比例函数y ＝5k x-的图象上， ∴过点B 作BC ⊥x 轴，C 为垂足，连接OB ．若△BCO 的面积为2，则|k ﹣5|＝2×2，得k ＝9或k ＝1，故①中的命题是假命题；若x 1＝2x 2，则y 2＝2y 1，故2y 1﹣y 2＝0，故②中的命题是真命题；若y 1＜0＜y 2，且x 1＞x 2，则k ﹣5＜0，故k ＜5，故③中的命题是假命题．故选：B ．5．D解：A、设反比例函数的解析式为y=kx，把（1，200）代入得，k=200，∴反比例函数的解析式为：y=200x，当x=4时，y=50，∴4月份的利润为50万元，故此选项正确，不合题意；B、治污改造完成后，从4月到6月，利润从50万到110万，故每月利润比前一个月增加30万元，故此选项正确，不合题意；C、当y=100时，则100=200x，解得：x=2，则只有3月，4月，5月共3个月的利润低于100万元，故此选项正确，不符合题意．D、设一次函数解析式为：y=kx+b，则450 6110 k bk b+⎧⎨+⎩＝＝，解得：3070 kb⎧⎨-⎩＝＝，故一次函数解析式为：y=30x-70，故y=200时，200=30x-70，解得：x=9，则治污改造完成后的第5个月，即9月份该厂利润达到200万元，故此选项不正确，符合题意．故选：C．6．B【详解】解：联立y1＝4x和y＝4x得：144yxy x⎧⎪⎨=⎪⎩＝，解得：14xy⎧⎨=⎩＝或41xy⎧⎨=-⎩＝-，故点A（1，4），联立y2＝kx（k≠0）和y＝4x，同理可得，点C（k，2k），∵四边形ADBC是矩形，故OA＝OC，即（k）2+（2k）2＝12+42，解得：k＝14，故选：B.7．C①当k> 0时，y=kx+1过第一、二、三象限，kyx=过第一、三象限；②当k<0时，y= kx+1过第一、二、四象限，kyx=过第二、四象限，观察图形可知，只有C选项符合题意，故选：C．8．B解：过点A作AM⊥x轴于点M，如图所示．∵AM⊥x轴，BC⊥x轴，BD⊥y轴，∴S矩形ODBC=-k，S△AOM=-12k．∵AE=AF．OF⊥x轴，AM⊥x轴，∴AM=12OF ，ME=OM=12OE ， ∴S △EOF =12OE•OF =4S △AOM =-2k ， ∴2S 矩形ODBC =S △EOF ，即2S 1=S 2．故答案为：2S 1=S 2．9．C解：观察函数图象，发现：当2x <-或04x <<时，一次函数图象在反比例函数图象的下方，∴不等式m kx b x +<的解集是2x <-或04x <<． 故选：C ．10．C 解： 点C 的坐标为1(1,)2-，2AB =，4=AD ， ∴ 55,2A ⎛⎫- ⎪⎝⎭， 设点5'5,2A a ⎛⎫-+ ⎪⎝⎭，1'1,2C a ⎛⎫-+ ⎪⎝⎭， 点'A ，'C 在反比例函数(0)k y xx=>的图象上， ∴ k=()552a -+=()112a -+， 解得，a=6,()151622k ∴=-+=， 52y x ∴= 故选：C ．11．x≠5根据题意得，5−x≠0, 则x≠5.故答案为x≠5.【点睛】本题考查了函数自变量的范围，一般从三个方面考虑：(1)当函数解析式是整式时，自变量可取全体实数；(2)当函数解析式是分式时，分式的分母不能为0；(3)当函数解析式是二次根式时，被开方数非负．12．24y x = 解：由题意得：12xy ＝12，可得：24y x =，故答案为：24y x =．13．>(0)ay a x =>，∴反比例函数的图象在每一个象限内y 随着x 的增大而减小，12<，12y y ∴>，故答案为：>．14．1＜x ＜2解：∵反比例函数y 1＝kx 和一次函数y 2＝ax+b 的图象交于点A （﹣1，2），B （2，﹣1）两点，∴k ＝﹣1×2＝﹣2，∴反比例函数为y ＝﹣2x ，把y ＝﹣2代入求得x ＝1；∴由图可得，当﹣2＜y 1＜y 2＜12时，x 的取值范围是1＜x ＜2，故答案为1＜x ＜2．15．1解：∵点P （m ，n ）是函数3y x =-和y=x+4图象的一个交点， ∴mn=-3，n=m+4，∴n-m=4，∴mn+n-m=-3+4=1，故答案为：1．16．6解：作CD AB ⊥于D ，如图，把0y =代入2y x =-得20x -=，解得2x =，则A 点坐标为(2,0)， 把2x =代入k y x=得2k y =，则B 点坐标为(2,)2k ， CA CB =，AD BD ∴=，C ∴点的纵坐标为4k ， 把4k y =代入k y x=得4x =，则C 点坐标为(4,)4k ， 把(4,)4k C 代入2y x =-得424k -=，解得8k ，B ∴点坐标为(2,4)，C 点坐标为(4,2)，OBC OAB ABC OAC S S S S ∆∆∆∆∴=+-111244(42)22222=⨯⨯+⨯⨯--⨯⨯ 6=．故答案为6．17．3解：设(0,)P b ，直线//AB x 轴，A ∴，B 两点的纵坐标都为b ，而点A 在反比例函数4y x =-的图象上， ∴当y b =，4x b=-，即A 点坐标为4(b -，)b ， 又点B 在反比例函数2y x=的图象上， ∴当y b =，2x b=，即B 点坐标为2(b ，)b ， 246()AB b b b∴=--=， 116322ABC S AB OP b b∴=⋅⋅=⋅⋅=△． 故答案为：3．18．解：（1）把x =-1分别代入y 1=-x +7得y 1=1+7=8，∴A （-1，8），把A （-1，8）代入2k y x =得81k =-， 解得 k =-8，∴反比例函数的解析式为28y x=-；（2）设y =-x +7与y 轴交点为C （0，7）∴OC =7， 联立得78y x y x =-+⎧⎪⎨=-⎪⎩，解得18x y =-⎧⎨=⎩或81x y =⎧⎨=-⎩， ∴B （8，-1），∴S △AOB =S △AOC +S △BOC =11637178222⨯⨯+⨯⨯=； （3）y 1＜y 2时x 的取值范围是-1＜x ＜0或x ＞8．19．解：（1）把()1,3B 代入m y (m 0)x=≠得133m =⨯=， ∴反比例函数解析式为3y x =，把(,2)A a 代入3y x =得23a =，解得32a =，则3(2A ，2)， 把3(2A ，2)，()1,3B 代入y kxb =+得3223k b k b ⎧+=⎪⎨⎪+=⎩，解得25k b =-⎧⎨=⎩， ∴一次函数解析式为25y x =-+；（2）由图可知： 不等式m kx nx +的解集为01x <或32x ； （3）12h <， 322h ∴->， 21y y ∴>．20．（1）20000Pa ；（2）30.6m【详解】解：（1）设函数解析式为P=，∵当V=1．5m 3时，p=16000Pa ，∴k=Vp=24000， ∴，当v=1．2 m 3时，p=20000（Pa ）；（3）∵气球内的气压大于40000Pa 时，气球将爆炸， ∴≤4000，解得：v≥0．6，即气球的体积应不小于0．6m 3．21．解：（1）依题意，直线OA 过1(4，20)，则直线OA 的解析式为80y x =， 当32x =时，120y =，即3(2A ，120)， 设双曲线的解析式为k y x=，将点3(2A ，120)代入得：180k =， 1803()2y x x ∴=； 由180y x =得当20y =时，9x =， 从晚上22:30到第二天早上7:00时间间距为8.5小时，8.59<，∴第二天早上7:00不能驾车去上班．22．（1；（2）（18，12）或18121111⎛⎫ ⎪⎝⎭， 解：（1）将点()A 3,2代入反比例函数(0)k y x x=>中，6k xy == ∴反比例函数解析式为：6y x=设射线OA 的解析式为：y mx = 将点()A 3,2代入y mx =中，32m =，解得：23m =∴射线OA 的解析式为：23y x =在23y x =中，当x =6时，y =4 ∴B 点坐标为（6，4） 在6y x =中，当x =6时，y =1 ∴D 点坐标为（6，1）过点A 作AE ⊥BC∵()A 3,2，B （6，4），D （6，1）∴AE =3，DE =1在Rt △ADE 中，AD =（2）设B 点坐标为（x ，23x ）， ∴D 点坐标为（x ，6x ） ∴165322ACD S x x =⋅-=△ 解得：118x =；21811x = ∴B 点坐标为（18，12）或18121111⎛⎫ ⎪⎝⎭，23．解：（1）如图，过点B、D分别作BH⊥x轴、DG⊥x轴交于点H、G，∵点A（-6，0）、D（-7，3），∴OA=6，OG=7，DG=3，∴AG=OG-OA=1，∵∠DAG+∠BAH=90°，∠DAG+∠GDA=90°，∴∠GDA=∠BAH，又∠DGA=∠AHB=90°，AD=AB，∴△DGA≌△AHB（AAS），∴DG=AH=3，BH=AG=1，∴点B坐标为（-3，1）；（2）由（1）知，B（-3，1），∵D（-7，3）∴运动t秒时，点D'（-7+2t，3）、B'（-3+2t，1），设反比例函数解析式为kyx ，∵点B'，D'在反比例函数图象上，∴k=（-7+2t）×3=（-3+2t）×1，∴9,62t k ==， ∴反比例函数解析式为6y x =； （3）存在，理由：由（2）知，点D '（-7+2t ，3）、B '（-3+2t ，1），92t =， ∴D '（2，3）、B '（6，1），由（2）知，反比例函数解析式为6y x =， 设点6(,)Q m m，点P （0，s ）， 以P 、Q 、B '、D '四个点为顶点的四边形是平行四边形，∴①当PQ 与B 'D '是对角线时， ∴11161(0)(26),()(31)2222m s m +=++=+， ∴138,4m s ==， ∴313(8,),(0,)44Q P ， ②当PB '与QD '是对角线时， ∴11116(06)(2),(1)(3)2222m s m+=++=+， ∴74,2m s ==， ∴37(4,),(0,)22Q P ， ③当PD '与QB '是对角线时， ∴11116(02)(6),(3)(1)2222m s m+=++=+， ∴74,2m s =-=-， ∴37(4,),(0,)22Q P ---， 综上所述：313(8,),(0,)44Q P 或37(4,),(0,)22Q P 或37(4,),(0,)22Q P ---．。

苏科版八年级数学下册第11章《反比例函数》单元测试题满分100分班级:________姓名:________座位:________成绩:________一．选择题（共10小题，满分30分）1．下列函数：①y＝x﹣2，②y＝，③y＝x﹣1，④y＝，y是x的反比例函数的个数有（）A．0个B．1个C．2个D．3个2．若反比例函数y＝（k≠0）的图象经过（2，3），则k的值为（）A．5B．﹣5C．6D．﹣63．若函数y＝（2m﹣1）x是反比例函数，则m的值是（）A．﹣1或1B．小于的任意实数C．﹣1D．14．已知反比例函数y＝2x﹣1，下列结论中，不正确的是（）A．点（﹣2，﹣1）在它的图象上B．y随x的增大而减小C．图象在第一、三象限D．若x＜0时，y随x的增大而减小5．若点A（﹣2020，y1）、B（2021，y2）都在双曲线上，且y1＞y2，则a的取值范围是（）A．a＜0B．a＞0C．D．6．若ab＞0，则一次函数y＝ax﹣b与反比例函数y＝在同一坐标系数中的大致图象是（）A．B．C．D．7．如图，已知A为反比例函数y＝（x＜0）的图象上一点，过点A作AB⊥y轴，垂足为B．若△OAB的面积为1，则k的值为（）A．2B．﹣2C．4D．﹣48．电路上在电压保持不变的条件下，电流I（A）与电阻R（Ω）成反比例关系，I与R的函数图象如图，I关于R函数解析式是（）A．B．C．D．9．如图，正比例函数y＝ax的图象与反比例函数y＝的图象相交于A，B两点，其中点A 的横坐标为2，则不等式ax＜的解集为（）A．x＜﹣2或x＞2B．x＜﹣2或0＜x＜2C．﹣2＜x＜0或0＜x＜﹣2D．﹣2＜x＜0或x＞210．如图，△DEF的三个顶点分别在反比例函数xy＝n与xy＝m（x＞0，m＞n＞0）的图象上，若DB⊥x轴于B点，FE⊥x轴于C点，若B为OC的中点，△DEF的面积为2，则m，n的关系式是（）A．m﹣n＝8B．m+n＝8C．2m﹣n＝8D．2m+n＝3二．填空题（共6小题，满分18分）11．若反比例函数y＝的图象经过点A（﹣3，4）和点B（2，a）两点，则a＝．12．已知点A（2，3）在反比例函数y＝（k≠0）的图象上，当x＞﹣2时，则y的取值范围是．13．课本上，在画图象之前，通过讨论函数表达式中x，y的符号特征以及取值范围，猜想出的图象在第一、三象限．据此经验，猜想函数的图象在第象限．14．如果正比例函数y＝ax（a≠0）与反比例函数y＝（b≠0）的图象有两个交点，其中一个交点的坐标为（﹣3，﹣2）那么另一个交点的坐标为．15．如图，在平面直角坐标系中，BA⊥y轴于点A，BC⊥x轴于点C，函数y＝（x＞0）的图象分别交BA，BC于点D，E，当AD：BD＝1：4且△BDE的面积为3.6时，则k 的值是．16．如图，在反比例函数y＝（x≥0）的图象上，有点P1，P2，P3，P4，…，P n（n为正整数，且n≥1），它们的横坐标依次为1，2，3，4，…，n（n为正整数，且n≥1）．分别过这些点作x轴与y轴的垂线，连接相邻两点，图中所构成的阴影部分（近似看成三角形）的面积从左到右依次为S1，S2，S3，…，S n﹣1（n为正整数，且n≥2），那么S1+S2+S3+S4+S5＝．三．解答题（共6小题，满分52分）17．列出下列问题中的函数关系式，并判断它们是否为反比例函数．（1）某农场的粮食总产量为1 500t，则该农场人数y（人）与平均每人占有粮食量x（t）的函数关系式；（2）在加油站，加油机显示器上显示的某一种油的单价为每升4.75元，总价从0元开始随着加油量的变化而变化，则总价y（元）与加油量x（L）的函数关系式；（3）小明完成100m赛跑时，时间t（s）与他跑步的平均速度v（m/s）之间的函数关系式．18．如图，正比例函数y＝2x的图象与反比例函数y＝的图象交于A，B两点，过点A作AC垂直x轴于点C，连接BC．若△ABC的面积为2．（1）求k的值；（2）直接写出＞2x时，自变量x的取值范围．19．在平面直角坐标系xOy中，函数y＝（x＞0）的图象与直线l1：y＝x+k（k＞0）交于点A，与直线l2：x＝k交于点B，直线l1与l2交于点C．（1）当点A的横坐标为1时，求此时k的值；（2）横、纵坐标都是整数的点叫做整点．记函数y＝（x＞0）的图象在点A、B之间的部分与线段AC，线段BC围成的区域（不含边界）为W．①当k＝3时，结合函数图象，求区域W内的整点个数；②若区域W内只有1个整点，直接写出k的取值范围．20．如图，在平面直角坐标系中，直线y1＝2x﹣2与双曲线y2＝交于A、C两点，AB⊥OA 交x轴于点B，且AB＝OA．（1）求双曲线的解析式；（2）连接OC，求△AOC的面积．21．某气球内充满了一定量的气体，当温度不变时，气球内气体的气压p（kPa）是气体体积V（m3）的反比例函数，其图象如图所示．（1）求这一函数的解析式；（2）当气体体积为1m3时，气压是多少？（3）当气球内的气压大于140kPa时，气球将爆炸，为了安全起见，气体的体积应不小于多少？（精确到0.01m3）22．小明根据学习函数的经验，对函数y＝+1的图象与性质进行了探究．下面是小明的探究过程，请补充完整：（1）函数y＝+1的自变量x的取值范围是；（2）如表列出了y与x的几组对应值，请写出m，n的值：m＝，n＝；x…﹣﹣1﹣023…y…m0﹣1n2…（3）在如图所示的平面直角坐标系中，描全上表中以各对对应值为坐标的点，并画出该函数的图象．（4）结合函数的图象，解决问题：①写出该函数的一条性质：．②当函数值+1＞时，x的取值范围是：．参考答案一．选择题（共10小题）1．【解答】解：①y＝x﹣2，②y＝，③y＝x﹣1，④y＝，y是x的反比例函数的是：②y＝，③y＝x﹣1，共2个．故选：C．2．【解答】解：∵反比例函数y＝（k≠0）的图象经过（2，3），∴k＝2×3＝6，故选：C．3．【解答】解：依题意得：m2﹣2＝﹣1且2m﹣1≠0，解得m＝±1．故选：A．4．【解答】解：A、把（﹣2，﹣1）代入y＝2x﹣1得：左边＝右边，故本选项正确，不符合题意；B、k＝2＞0，在每个象限内，y随x的增大而减小，故本选项错误，符合题意；C、k＝3＞0，图象在第一、三象限内，故本选项正确，不符合题意；D、若x＜0时，y随x的增大而减小，故本选项正确，不符合题意；不正确的只有选项B，故选：B．5．【解答】解：∵点A（﹣2020，y1），B（2021，y2）两点在双曲线y＝上，且y1＞y2，∴3+2a＜0，∴a＜﹣，∴a的取值范围是a＜﹣，故选：D．6．【解答】解：A、根据一次函数可判断a＞0，b＜0，即ab＜0，故不符合题意，B、根据一次函数可判断a＜0，b＞0，即ab＜0，故不符合题意，C、根据一次函数可判断a＜0，b＜0，即ab＞0，根据反比例函数可判断ab＞0，故符合题意，D、根据反比例函数可判断ab＜0，故不符合题意；故选：C．7．【解答】解：∵AB⊥y轴，∴S△OAB＝|k|，∵△OAB的面积为1，∴|k|＝1，∵k＜0，∴k＝﹣2．故选：B．8．【解答】解：∵当R＝20，I＝11时，∴电压＝20×11＝220，∴．故选：A．9．【解答】解：∵正比例函数y＝ax的图象与反比例函数y＝的图象相交于A，B两点，∴A，B两点坐标关于原点对称，∵点A的横坐标为2，∴B点的横坐标为﹣2，∵ax＜，∴在第一和第三象限，正比例函数y＝ax的图象在反比例函数y＝的图象的下方，∴x＜﹣2或0＜x＜2，故选：B．10．【解答】解：设D（a，），则F（2a，），E（2a，），∵S△DEF＝S梯形BCFD﹣S梯形BCED，△DEF的面积为2，∴2＝（+）•a﹣（+），整理得，m﹣n＝8，故选：A．二．填空题（共6小题）11．【解答】解：∵反比例函数y＝的图象经过点A（﹣3，4）和点B（2，a）两点，∴﹣3×4＝2a，解得：a＝﹣6，故答案为：﹣6．12．【解答】解：∵点A（2，3）在反比例函数y＝（k≠0）的图象上，∴k＝2×3＝6，∴y＝，∴图象在一三象限，在每个象限内y随x增大而减小，当x＝﹣2时，y＝＝﹣3，∴当x＞﹣2时，y＜﹣3或y＞0．故答案为：y＜﹣3或y＞0．13．【解答】解：x＞0时，．此时函数在第一象限．x＜0时，．此时函数在第二象限．故函数的图象在第一、二象限．故答案为：一、二．14．【解答】解：由题设知﹣2＝a×（﹣3），（﹣3）×（﹣2）＝b解得a＝，b＝6联立方程组得解得，所以另一个交点的坐标为（3，2）．或：利用正比例函数与反比例函数的图象及其对称性，可知两个交点关于原点对称，因此另一个交点的坐标为（3，2）．故答案为：（3，2）．15．【解答】解：如图，过点D作DF⊥x轴于点F，过点E作EG⊥y轴于点G．设B（5a，b），E（5a，d）．∵AD：BD＝1：4，∴D（a，b）．又∵△BDE的面积为3.6，∴BD＝4a，BE＝b﹣d，∴×4a（b﹣d）＝3.6，∴a（b﹣d）＝1.8，即ab﹣ad＝1.8，∵D，E都在反比例函数图象上，∴ab＝5ad，∴5ad﹣ad＝1.8，解得：ad＝0.45，∴k＝5ad＝2.25．故答案为：2.25．16．【解答】解：当x＝1时，P1的纵坐标为4，当x＝2时，P2的纵坐标为2，当x＝3时，P3的纵坐标为，当x＝4时，P4的纵坐标为1，当x＝5时，P5的纵坐标为…则S1＝×1×（4﹣2）＝1＝2﹣1；S2＝×1×（2﹣）＝＝1﹣；S3＝×1×（﹣1）＝＝﹣；∴S1+S2+S3＝2﹣1+1﹣+﹣＝2﹣＝；S4＝×1×（1﹣）＝＝﹣；…S5＝；∴S1+S2+S3+S4+S5＝2﹣1+1﹣+﹣+﹣+＝2﹣．故答案为．三．解答题（共6小题）17．【解答】解：（1）由平均数，得x＝，即y＝是反比例函数；（2）由单价乘以油量等于总价，得y＝4.75x，即y＝4.75x是正比例函数；（3）由路程与时间的关系，得t＝，即t＝是反比例函数．18．【解答】解：（1）设点A的坐标为（m，n）．∵点A在直线y＝2x上，∴n＝2m．根据对称性可得OA＝OB，∴S△ABC＝2S△ACO＝2，∴S△ACO＝1，∴m•2m＝1，∴m＝1（舍负），∴点A的坐标为（1，2），∴k＝1×2＝2；（2）如图，由点A与点B关于点O成中心对称得点B（﹣1，﹣2）．结合图象可得：不等式＞2x的解集为x＜﹣1或0＜x＜1．19．【解答】解：（1）当x＝1时，y＝＝2，∴A（1，2），把A（1，2）代入y＝x+k中，得2＝+k，∴；（2）①当k＝3时，则直线l1：y＝x+3，与直线l2：x＝3，当x＝3时，y＝x+3＝4，∴C（3，4），作出图象如图1：∴区域W内的整点个数为3；②如图2，当直线l1：y＝x+k过（2，3）点，区域W内只有1个整点，此时，3＝+k，则k＝，当直线l1：y＝x+k过（0，2）点，区域W内没有整点，此时，2＝0+k，则k＝2，∴当2＜k≤时，区域W内只有1个整点，故答案为：2＜k≤．20．【解答】解：（1）作AH⊥OB于H，如图，∵AB⊥OA交x轴于点B，且AB＝OA．∴△OAB为等腰直角三角形，∴OH＝BH＝AH，设A（t，t），把A（t，t）代入y＝2x﹣2得2t﹣2＝t，解得t＝2，∴A（2，2），把A（2，2）代入y2＝得k＝2×2＝4，∴双曲线的解析式为y2＝；（2）当x＝0时，y＝2x﹣2＝﹣2，则一次函数与y轴的交点坐标为（0，﹣2），解方程得或，则C（﹣1，﹣4），∴△AOC的面积＝×（2+1）×2＝3．21．【解答】解：（1）设，由题意知，所以k＝96，故；（2）当v＝1m3时，；（3）当p＝140kPa时，．所以为了安全起见，气体的体积应不少于0.69m3．22．【解答】解：（1）由分式的分母不为0得：x﹣1≠0，∴x≠1；故答案为：x≠1．（2）当x＝﹣1时，y＝+1＝，当x＝时，y＝+1＝3，∴m＝，n＝3，故答案为：，3．（3）如图：（4）①观察函数图象，可知：函数图象经过原点且关于点（1，1）对称，故答案为：函数图象经过原点且关于点（1，1）对称．②观察函数图象，可知：当函数值+1＞时，x的取值范围是1＜x＜3，故答案为：1＜x＜3．。

第十一章《反比例函数》单元测试卷一、选择题一、函数ky x =的图象通过点(12)A -，，则k 的值为（ ） A ．12B ．12-C ．2D ．2-二、已知反比例函数2y x=，下列结论中，不正确．．．的是（ ） A ．图象必通过点(12)，B ．y 随x 的增大而减少C ．图象在第一、三象限内D ．若1x >，则2y <3、用电器的输出功率P 与通过的电流I 、用电器的电阻R 之间的关系是2P I R =，下面说法正确的是（ ）A ．P 为定值，I 与R 成反比例B ．P 为定值，2I 与R 成反比例C ．P 为定值，I 与R 成正比例D ．P 为定值，2I 与R 成正比例4、如图，某反比例函数的图像过点M （2-，1），则此反比例函数表达式为（ A ．2y x =B ．2y x =-C ．12y x= D ．12y x=-五、若反比例函数ky x=的图象通过点(3)m m ，，其中0m ≠，则此反比例函数的图 象在（ ） A ．第一、二象限；B ．第一、三象限 ；C ．第二、四象限； D ．第三、四象限六、已知三角形的面积必然，则它底边a 上的高h 与底边a 之间的函数关系的图象大致是（ ）A ．B ．C ．D ．7、如图，一次函数11y x =-与反比例函数22y x=的图像交于点(21)A ，，(12)B --，，则使12y y > 的x 的取值范围是（ ）A ．2x >B ．2x >或10x -<<C ．12x -<<D ．2x >或1x <-八、已知120k k <<，则函数1y k x =和2k y x=的图象大致是（ ） 九1二11111111三120、已知点A （2，6）、B （3，4）在某个反比例函数的图象上. （1） 求此反比例函数的解析式；（2）若直线mx y =与线段AB 相交，求m 的取值范围.2一、已知正比例函数y kx =的图象与反比例函数5ky x-=（k 为常数，0k ≠）的图象有一个交点的横坐标是2．（1）求两个函数图象的交点坐标；（2）若点11()A x y ，，22()B x y ，是反比例函数5ky x-=图象上的两点，且12x x <，试比较12y y ，的大小．2二、某工厂计划为震区生产A B ，两种型号的学生桌椅500套，以解决1250名学生的学习问题，一套A 型桌椅（一桌两椅）需木材30.5m ，一套B 型桌椅（一桌三椅）需木材30.7m ，工厂现有库存木材3302m ． （1）有多少种生产方案？（2）现要把生产的全数桌椅运往震区，已知每套A 型桌椅的生产本钱为100元，运费2元；每套B 型桌椅的生产本钱为120元，运费4元，求总费用y （元）与生产A 型桌椅x （套）之间的关系式，并肯定总费用最少的方案和最少的总费用．（总费用=生产本钱+运费） （3）按（2）的方案计算，有无剩余木材？若是有，请直接写出用剩余木材再生产以上两种型号的桌椅，最多还能够为多少名学生提供桌椅；若是没有，请说明理由．一一六二11三1解法二：点B -在第四象限， 而反比例函数4y x=的图象在一、三象限． ∴点B -不在4y x =的图象上． 8分 20、解：（1）设所求的反比例函数为xky =，依题意得: 6 =2k，∴k=12．∴反比例函数为xy 12=． （2） 设P （x ，y ）是线段AB 上任一点，则有2≤x≤3，4≤y ≤6．∵m =x y ， ∴34≤m ≤26． 所以m 的取值范围是34≤m ≤3． （8分）2一、解：（1）由题意，得522kk -=， 1分解得1k =．所以正比例函数的表达式为y x =，反比例函数的表达式为4y x=． 解4x x=，得2x =±．由y x =，得2y =±． 所以两函数图象交点的坐标为（2，2），(22)--，．（2）因为反比例函数4y x=的图象别离在第一、三象限内， y 的值随x 值的增大而减小，所以当120x x <<时，12y y >． 当120x x <<时，12y y >．当120x x <<时，因为1140y x =<，2240y x =>，所以12y y <．2二、解：（1）设生产A 型桌椅x 套，则生产B 型桌椅(500)x -套，由题意得0.50.7(500)30223(500)1250x x x x +⨯-⎧⎨+⨯-⎩≤≥ 解得240250x ≤≤因为x 是整数，所以有11种生产方案．。