样本量的确定
1. 二值分布(估计比例时的样本容量)
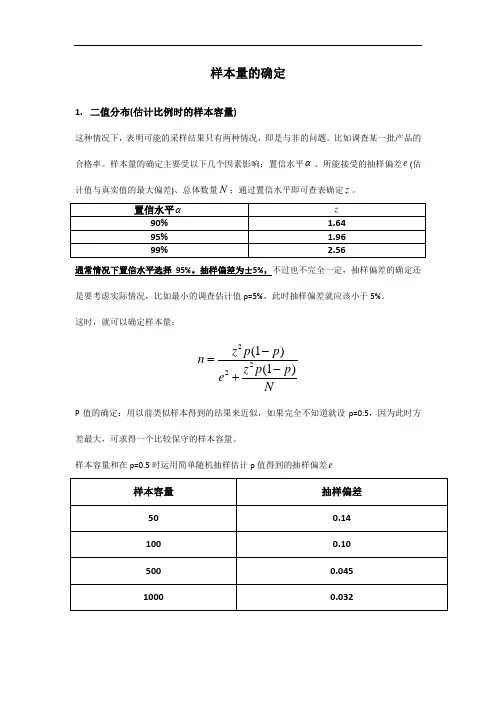
这种情况下，表明可能的采样结果只有两种情况，即是与非的问题。比如调查某一批产品的合格率。样本量的确定主要受以下几个因素影响：置信水平α、所能接受的抽样偏差e (估计值与真实值的最大偏差)、总体数量N ；通过置信水平即可查表确定z 。
通常情况下置信水平选择95%。抽样偏差为±5%，不过也不完全一定，抽样偏差的确定还是要考虑实际情况，比如最小的调查估计值p=5%，此时抽样偏差就应该小于5%。 这时，就可以确定样本量：
22
2(1)(1)z p p n z p p e N
-=-+
P 值的确定：用以前类似样本得到的结果来近似，如果完全不知道就设p=0.5，因为此时方差最大，可求得一个比较保守的样本容量。
样本容量和在p=0.5时运用简单随机抽样估计p 值得到的抽样偏差e
如果总体容量N 非常大，可近似为无穷，那么上面这个公式可简化成：
22
(1)z p p n e -=
事实上当总体容量很小时，不会采用抽样调查，而是普查了。
2. 正态分布(估计均值时的样本容量)
在这种情况下，表明采样的结果是具有多样性的，并不局限在0、1上。比如对某一城市老年人的患病年龄进行统计。这个时候，样本量同样受如下几个因素影响：置信水平α、所能接受的抽样偏差e (估计值与真实值的最大偏差)、总体数量N 。 样本量为：
22
222
z S n z S e N
=
+
S 表明的是总体标准差，这个可以用以前类似样本得到的S 或是实验调查样本的S 来近似。 同样，如果总体容量N 非常大，可近似为无穷，那么上面这个公式可简化成：
22
2
z S n e
=
理论基础：
根据数理统计知识，样本均值对总体均值可构造如下统计量：
x
X u
σ-，他满足标准正态分
布，查表即可得到某一显著性水平下这个统计量的值，这里面的x σ表示总体均值估计量的标准误差。
在无放回简单随机抽样情况下，总体均值估计量的标准误差表达式：
x σ=
如果误差界限设为e，那么：
(1)
n S
e z
N N
=-
解得：
22
22
2
z S
n
z S
e
N
=
+
对于二值分布，p的总体方差为：
2(1)
S p p
=-
此时：
2
2
2
(1)
(1)
z p p
n
z p p
e
N
-
=
-
+
当然，这里只考虑了简单随机抽样，对于分层抽样和整群抽样，需要再乘以一个设计效应，分层抽样效率高于简单随机抽样，效应因子小于1，整群抽样效率低于简单随机抽样，效应因子大于1.
总体大小对于样本量也是有影响的，当总体个数越小时，影响越明显。
二者之间并不是线性关系，因此样本量并不是越大越好。《会变的线条》
教学设计
胶南市第三实验小学王静
【教材分析】
《会变的线条》选自义务教育课程标准实验教科书《美术》（人美版）第三册。这一课目的是引导学生认识不同种线条带给人的美感，让学生熟悉并掌握线条的运用，创作出优秀的线描作品，培养学生的造型能力。
【教学目标】
（1）初步感受不同种线条带给人的美感。培养学生的造型能力。
（2）能用不同种线条组织一幅画面，表现出一定的美感。
（3）通过对作品的观察、比较、培养学生的观察、分析能力。
【教学重点】初步感受、体验艺术作品中线的美感。
【教学难点】如何运用不同线表现美感。
【教学过程】
一、组织教学，检查学具
用你的坐姿告诉老师你喜欢上美术课。
二、导入新课
师在黑板上画“~~~~~`”，问：看今天的美术课堂，老师给大家带来了什么？
（板书：线条）
别小看这条线，它很神奇，还是一个小小的魔术师呢，不信你看。
师课件演示（线条魔术）
师：刚才我们看到这根直线像一个魔术师一样“变化多端”（板书），今天，我们就来了解会变的线条。
师板书课题：会变的线条
三、讲授新课：
（一）认识线
认识自然和生活中的线：