高斯滤波的C语言实现

C语言生成高斯曲线详解及示例
高斯曲线是一种常见的概率分布曲线，它在许多领域都有广泛的应用，如统计学、信号处理、图像处理等。

在C语言中，我们可以使用数学库函数来生成高斯曲线。

一、高斯曲线的数学表达式
高斯曲线的数学表达式为：
f(x) = a * exp(-(x-b)^2 / (2 * c^2))
其中，a是峰值，b是期望值，c是标准差。

二、C语言生成高斯曲线的示例代码
下面是一个使用C语言生成高斯曲线的示例代码：
在上面的代码中，我们使用rand()函数生成0到1之间的随机数，然后将其作为参数传递给log()函数计算自然对数的值。

接着，我们使用sqrt()函数计算高斯曲线的横坐标。

最后，我们使用exp()函数计算高斯曲线的纵坐标，并将其输出到控制台。

三、注意事项
在使用C语言生成高斯曲线时，需要注意以下几点：
1.高斯曲线的参数需要根据具体的应用场景进行调整。

2.在生成随机数时，需要使用rand()函数和RAND_MAX常量来保证随机数的范
围和精度。

3.在计算高斯曲线的横坐标时，需要使用sqrt()函数来计算平方根。

卡尔曼滤波代码c卡尔曼滤波是一种常用的估计和预测算法，广泛应用于信号处理、控制系统、机器学习等领域。

本文将介绍卡尔曼滤波的原理，并提供一个简单的C语言实现示例。

卡尔曼滤波是一种基于线性高斯模型的递推滤波算法。

它通过将系统的状态分为观测变量和内部状态变量，并建立观测模型和状态转移模型来估计系统的内部状态。

卡尔曼滤波的基本思想是，通过对观测数据进行动态修正和整合，提高对内部状态的估计精度。

以下是一个简单的C语言实现示例，用于演示一维卡尔曼滤波的过程：```c#include <stdio.h>#define Q 0.01 // 系统噪声协方差#define R 0.1 // 观测噪声协方差float kalman_filter(float z){static float x_hat = 0; // 状态估计static float P = 1; // 状态估计协方差static float K = 0; // 卡尔曼增益// 预测float x_hat_minus = x_hat; // 先验估计float P_minus = P + Q; // 先验估计协方差// 更新K = P_minus / (P_minus + R); // 计算卡尔曼增益x_hat = x_hat_minus + K * (z - x_hat_minus); // 更新状态估计P = (1 - K) * P_minus; // 更新状态估计协方差return x_hat;}int main() {float measurements[] = {1.1, 1.2, 1.3, 1.4, 1.5}; // 观测数据int num_measurements = sizeof(measurements) / sizeof(measurements[0]);for (int i = 0; i < num_measurements; ++i) {float estimate = kalman_filter(measurements[i]);printf("Measurement: %.1f, Estimate: %.3f\n", measurements[i], estimate);}return 0;}```在上述示例代码中，我们定义了卡尔曼滤波的噪声协方差Q和R，分别表示系统和观测的噪声。

C语言是一种广泛应用于计算机科学和工程领域的编程语言。

它的灵活性和效率使其成为开发各种类型软件的理想选择。

C语言也被用于处理和分析数据，包括在信号处理和曲线拟合中。

Savitzky-Golay滤波则是一种常用的信号处理方法，被广泛用于去噪和平滑数据，同时也能被用来拟合曲线。

在C语言中实现Savitzky-Golay滤波拟合曲线需要一定的技术和步骤。

一、了解Savitzky-Golay滤波1. Savitzky-Golay滤波是一种基于最小二乘法的平滑技术，它在信号处理中广泛应用于去除噪声和平滑曲线。

它的基本原理是利用多项式拟合来估计出每个数据点的值，从而实现平滑效果。

2. 与其他滤波技术相比，Savitzky-Golay滤波具有较好的抗噪声能力，可以保留原始信号的特征，同时也能有效地去除高频噪声。

3. 在实际应用中，Savitzky-Golay滤波通常需要指定滤波的窗口大小和拟合的多项式阶数，以及对于边界点的处理方法等参数。

二、C语言中实现Savitzky-Golay滤波拟合曲线的步骤1. 数据的导入和准备：首先需要在C语言中导入需要处理的数据，可以是一维数组或者二维数组，这取决于数据的维度。

数据在应用Savitzky-Golay滤波前，需要进行一定的预处理，如去除异常值或者空值等。

2. 编写Savitzky-Golay滤波函数：在C语言中，可以编写Savitzky-Golay滤波的函数，该函数接受输入数据以及滤波窗口大小、多项式阶数等参数，然后对数据进行滤波处理，并返回滤波后的结果。

3. 数据拟合和曲线绘制：经过Savitzky-Golay滤波处理后的数据可以进行拟合和曲线绘制，这可以通过调用C语言中的数学库函数来实现，也可以自行编写拟合和绘制曲线的函数。

4. 参数优化和性能评估：在实际应用中，为了得到最佳的滤波效果，需要对滤波窗口大小、多项式阶数等参数进行优化，这可以通过实验和性能评估来完成，以确保滤波后的数据能够符合预期的要求。

高斯滤波函数高斯滤波函数是一种常用的图像处理方法，它可以用来平滑图像并去除噪声。

该函数基于高斯分布的特性，将图像中每个像素的值与周围像素的值进行加权平均，从而达到平滑的效果。

高斯滤波函数的数学表达式为：$$G(x,y) = \frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}$$其中，$x$和$y$表示像素的坐标，$\sigma$表示高斯分布的标准差。

在实际应用中，通常会选择不同的标准差来达到不同的平滑效果。

高斯滤波函数的实现可以通过卷积运算来完成。

具体来说，对于图像中的每个像素，我们可以将其周围的像素按照高斯分布的权重进行加权平均，从而得到该像素的新值。

这个过程可以用下面的公式来表示：$$I'(x,y) = \frac{1}{\sum_{i=-k}^k\sum_{j=-k}^k G(i,j)}\sum_{i=-k}^k\sum_{j=-k}^k G(i,j)I(x+i,y+j)$$其中，$I(x,y)$表示原始图像中的像素值，$I'(x,y)$表示经过高斯滤波后的像素值，$k$表示卷积核的大小，$G(i,j)$表示卷积核中第$(i,j)$个元素的权重。

在实际应用中，高斯滤波函数通常会被用来去除图像中的噪声。

由于噪声通常是随机的，因此可以通过多次应用高斯滤波函数来进一步平滑图像。

不过需要注意的是，过度平滑可能会导致图像失去细节，因此需要根据具体情况来选择合适的平滑程度。

总之，高斯滤波函数是一种常用的图像处理方法，它可以用来平滑图像并去除噪声。

通过卷积运算，我们可以将每个像素的值与周围像素的值进行加权平均，从而达到平滑的效果。

在实际应用中，需要根据具体情况来选择合适的标准差和卷积核大小，以达到最佳的平滑效果。

图像滤波之⾼斯滤波介绍1 ⾼斯滤波简介 了解⾼斯滤波之前，我们⾸先熟悉⼀下⾼斯噪声。

⾼斯噪声是指它的服从（即）的⼀类噪声。

如果⼀个噪声，它的幅度分布服从⾼斯分布，⽽它的⼜是均匀分布的，则称它为⾼斯⽩噪声。

⾼斯⽩噪声的⼆阶矩不相关，⼀阶矩为，是指先后信号在时间上的相关性，包括和。

⾼斯滤波器是⼀类根据⾼斯函数的形状来选择权值的线性平滑滤波器。

⾼斯平滑滤波器对于抑制服从正态分布的噪声⾮常有效。

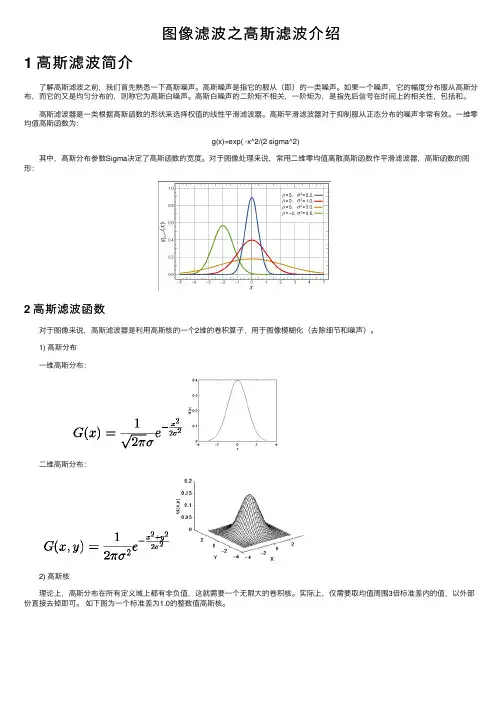
⼀维零均值⾼斯函数为： g(x)=exp( -x^2/(2 sigma^2) 其中，⾼斯分布参数Sigma决定了⾼斯函数的宽度。

对于图像处理来说，常⽤⼆维零均值离散⾼斯函数作平滑滤波器，⾼斯函数的图形：2 ⾼斯滤波函数 对于图像来说，⾼斯滤波器是利⽤⾼斯核的⼀个2维的卷积算⼦，⽤于图像模糊化（去除细节和噪声）。

1) ⾼斯分布 ⼀维⾼斯分布： ⼆维⾼斯分布： 2) ⾼斯核 理论上，⾼斯分布在所有定义域上都有⾮负值，这就需要⼀个⽆限⼤的卷积核。

实际上，仅需要取均值周围3倍标准差内的值，以外部份直接去掉即可。

如下图为⼀个标准差为1.0的整数值⾼斯核。

3 ⾼斯滤波性质 ⾼斯函数具有五个重要的性质，这些性质使得它在早期图像处理中特别有⽤．这些性质表明，⾼斯平滑滤波器⽆论在空间域还是在频率域都是⼗分有效的低通滤波器，且在实际图像处理中得到了⼯程⼈员的有效使⽤．⾼斯函数具有五个⼗分重要的性质，它们是： （1）⼆维⾼斯函数具有旋转对称性，即滤波器在各个⽅向上的平滑程度是相同的．⼀般来说，⼀幅图像的边缘⽅向是事先不知道的，因此，在滤波前是⽆法确定⼀个⽅向上⽐另⼀⽅向上需要更多的平滑．旋转对称性意味着⾼斯平滑滤波器在后续边缘检测中不会偏向任⼀⽅向． （2）⾼斯函数是单值函数．这表明，⾼斯滤波器⽤像素邻域的加权均值来代替该点的像素值，⽽每⼀邻域像素点权值是随该点与中⼼点的距离单调增减的．这⼀性质是很重要的，因为边缘是⼀种图像局部特征，如果平滑运算对离算⼦中⼼很远的像素点仍然有很⼤作⽤，则平滑运算会使图像失真． （3）⾼斯函数的傅⽴叶变换频谱是单瓣的．正如下⾯所⽰，这⼀性质是⾼斯函数付⽴叶变换等于⾼斯函数本⾝这⼀事实的直接推论．图像常被不希望的⾼频信号所污染(噪声和细纹理)．⽽所希望的图像特征（如边缘），既含有低频分量，⼜含有⾼频分量．⾼斯函数付⽴叶变换的单瓣意味着平滑图像不会被不需要的⾼频信号所污染，同时保留了⼤部分所需信号． （4）⾼斯滤波器宽度(决定着平滑程度)是由参数σ表征的，⽽且σ和平滑程度的关系是⾮常简单的．σ越⼤，⾼斯滤波器的频带就越宽，平滑程度就越好．通过调节平滑程度参数σ，可在图像特征过分模糊(过平滑)与平滑图像中由于噪声和细纹理所引起的过多的不希望突变量(⽋平滑)之间取得折衷． （5）由于⾼斯函数的可分离性，较⼤尺⼨的⾼斯滤波器可以得以有效地实现．⼆维⾼斯函数卷积可以分两步来进⾏，⾸先将图像与⼀维⾼斯函数进⾏卷积，然后将卷积结果与⽅向垂直的相同⼀维⾼斯函数卷积．因此，⼆维⾼斯滤波的计算量随滤波模板宽度成线性增长⽽不是成平⽅增长．4 ⾼斯滤波应⽤ ⾼斯滤波后图像被平滑的程度取决于标准差。

c语言滤波程序C语言滤波程序滤波是信号处理中常用的技术，它可以通过去除噪声或者平滑信号来提取出我们所关心的信息。

在C语言中，我们可以通过编写滤波程序来实现这一目的。

一、滤波的基本原理滤波的基本原理是通过对输入信号进行加权平均或者卷积运算，从而得到滤波后的输出信号。

常见的滤波方法有移动平均滤波、中值滤波和低通滤波等。

1. 移动平均滤波移动平均滤波是一种简单有效的滤波方法，它通过计算一定窗口大小内的信号均值来平滑信号。

具体步骤如下：（1）定义一个窗口大小N；（2）从输入信号的第一个样本开始，计算窗口内信号的均值；（3）将计算得到的均值作为输出信号，并将窗口向后移动一个样本；（4）重复上述步骤，直到处理完所有样本。

2. 中值滤波中值滤波是一种非线性滤波方法，它通过计算窗口内信号的中值来平滑信号。

具体步骤如下：（1）定义一个窗口大小N；（2）从输入信号的第一个样本开始，将窗口内的信号排序，取中间值作为输出信号；（3）将窗口向后移动一个样本；（4）重复上述步骤，直到处理完所有样本。

3. 低通滤波低通滤波是一种常用的滤波方法，它可以去除高频噪声，保留低频信号。

具体步骤如下：（1）定义一个截止频率fc；（2）将输入信号进行傅里叶变换，得到频域表示；（3）将高于截止频率的部分置零，得到滤波后的频域表示；（4）将滤波后的频域表示进行傅里叶反变换，得到滤波后的时域信号。

二、C语言实现滤波程序在C语言中，我们可以使用数组来表示信号，并通过循环和条件判断语句来实现滤波算法。

下面以移动平均滤波为例，给出一个简单的滤波程序：```c#include <stdio.h>#define WINDOW_SIZE 5float movingAverageFilter(float signal[], int size){float filteredSignal[size];int i, j;float sum;for (i = 0; i < size; i++){sum = 0;for (j = i - WINDOW_SIZE / 2; j <= i + WINDOW_SIZE / 2; j++){if (j >= 0 && j < size){sum += signal[j];}}filteredSignal[i] = sum / WINDOW_SIZE;}return filteredSignal;}int main(){float signal[] = {1.2, 2.5, 3.1, 4.6, 5.2, 6.3, 7.4, 8.9, 9.7, 10.3}; int size = sizeof(signal) / sizeof(float);float filteredSignal[size];filteredSignal = movingAverageFilter(signal, size);for (int i = 0; i < size; i++){printf("%.2f ", filteredSignal[i]);}printf("\n");return 0;}```在这个程序中，我们首先定义了一个窗口大小WINDOW_SIZE，然后定义了一个移动平均滤波函数movingAverageFilter。

opencv中的高斯滤波计算过程高斯滤波是图像处理中常用的一种平滑滤波方法，通过对图像中的像素进行加权平均来降低噪声的影响。

本文将详细介绍高斯滤波的计算过程。

1. 高斯滤波的基本原理高斯滤波是一种线性平滑滤波方法，它利用高斯函数对图像进行卷积操作。

高斯函数是一种钟形曲线，其形状由方差决定。

在图像处理中，高斯滤波可以有效地降低图像中的噪声，并且保持图像的边缘信息。

2. 高斯滤波的计算过程高斯滤波的计算过程可以分为以下几个步骤：步骤1：确定滤波器大小在进行高斯滤波之前，我们首先需要确定滤波器的大小。

滤波器的大小通常是一个奇数，例如3x3、5x5或7x7等。

较大的滤波器可以提供更强的平滑效果，但会导致图像的细节丢失。

步骤2：生成高斯滤波器模板高斯滤波器模板是一个二维矩阵，用于对图像进行卷积操作。

模板的大小与滤波器的大小相同。

模板中的每个元素表示在该位置处的像素与中心像素的距离。

步骤3：计算高斯滤波器权重在生成高斯滤波器模板后，我们需要计算每个位置上的权重。

权重是通过高斯函数计算得到的，与距离中心像素的距离有关。

距离越远，权重越小。

步骤4：对图像进行卷积操作卷积操作是将滤波器模板与图像进行逐像素的计算。

对于每个像素，将滤波器模板中的元素与对应位置的像素相乘，再将所有乘积相加，得到最终的输出像素值。

这个过程需要在图像的每个像素位置上进行。

3. 高斯滤波的应用场景高斯滤波常用于图像处理中的平滑和去噪操作。

由于高斯滤波可以有效地抑制噪声，因此在图像处理中被广泛应用。

常见的应用场景包括人脸识别、图像增强、图像分割等。

4. 高斯滤波的优缺点高斯滤波具有以下优点：- 高斯滤波可以有效地降低图像中的噪声，提高图像质量。

- 高斯滤波可以保留图像的边缘信息，不会造成图像模糊。

然而，高斯滤波也存在一些缺点：- 高斯滤波无法完全去除图像中的噪声，对于一些较大的噪声还需要采用其他方法进行处理。

- 高斯滤波会导致图像的细节丢失，对于一些需要保留细节信息的应用场景可能不适用。

c++ 高斯模糊算法《C语言高斯模糊算法》一、简介高斯模糊是一种常见的图像处理算法，用于对图像进行平滑处理，消除图像中的噪声和细节，使图像更加平滑。

本篇文章将介绍高斯模糊算法的基本原理和C语言实现方法。

二、基本原理高斯模糊算法的核心思想是通过在图像上应用高斯函数来模糊图像。

高斯函数是一种具有对称性的曲线，具有平滑过渡的特点。

在图像处理中，高斯模糊算法会对图像中的每个像素应用高斯函数，并将相邻像素的值进行加权平均，从而得到模糊后的像素值。

为了实现高斯模糊，需要计算每个像素周围像素值的加权平均值。

为了使算法更加高效，可以使用二维高斯函数来计算加权平均值。

具体来说，可以将图像划分为多个像素块，对每个像素块应用高斯函数，并计算模糊后的像素值。

三、C语言实现以下是一个简单的C语言实现高斯模糊的示例代码：```c#include<stdio.h>#include<stdlib.h>#include<math.h>#defineIMAGE_WIDTH640//图像宽度#defineIMAGE_HEIGHT480//图像高度#defineWINDOW_WIDTH32//窗口宽度#defineWINDOW_HEIGHT32//窗口高度#defineSIGMA2.0//高斯函数标准差voidgaussian_blur(unsignedchar*image,intwidth,intheight){ inti,j;unsignedchar*window=(unsignedchar*)malloc(WINDOW_WIDTH*WI NDOW_HEIGHT*sizeof(unsignedchar));for(i=0;i<height;i++){for(j=0;j<width;j++){intsum=0;for(intk=-WINDOW_HEIGHT/2;k<=WINDOW_HEIGHT/2;k++){intx=j+k*WINDOW_WIDTH;if(x>=0&&x<width){sum+=image[i*width+x]*exp(-(k*k)/(2*SIGMA*SIGMA));}}image[i*width+j]=sum/(WINDOW_HEIGHT*WINDOW_WIDTH);}}free(window);}```该代码实现了一个简单的双层高斯模糊算法。

高效滤波器 c语言
在C语言中，实现高效滤波器可以采用多种方法。

首先，滤波器可以是数字滤波器，用于对数字信号进行滤波处理。

常见的数字滤波器包括FIR（有限脉冲响应）滤波器和IIR（无限脉冲响应）滤波器。

在C语言中，可以通过实现这些滤波器的算法来实现高效的滤波器。

对于FIR滤波器，可以使用C语言编写滤波器的差分方程，并利用循环来实现滤波器的计算。

FIR滤波器的特点是易于设计和稳定，因此在C语言中实现起来比较高效。

对于IIR滤波器，可以使用C语言编写递归形式的差分方程来实现滤波器。

IIR滤波器相对于FIR滤波器来说，可以实现更高阶的滤波器，并且具有更窄的过渡带和更快的计算速度。

除了直接实现滤波器算法外，还可以利用C语言中的优化技巧来提高滤波器的计算效率。

比如，可以使用SIMD指令集来进行并行计算，或者利用多线程来加速滤波器的计算过程。

另外，C语言中也有一些开源的数字信号处理库，比如FFT库
和滤波器库，可以直接调用这些库来实现高效的滤波器。

这些库通常经过优化，能够提供高效的数字信号处理功能。

总之，实现高效滤波器的关键在于选择合适的滤波器算法，并结合C语言的优化技巧来提高计算效率。

通过合理的算法设计和代码优化，可以在C语言中实现高效的滤波器。

/*给定一个【0,1】区间均匀随机数，个顶产生泊松分布的随机数原理方法，程序，代码解题思路：1.输入【0,1】区间的概率值P和常数r2.求解K的阶乘，r的K次方,e的-R次方。

利用泊松分布的函数（将其从0到K累加）计算此时的概率su3.比较su和输入P的值，知道su值大于P,输出这时的K值即可。

*/#include<stdio.h>#include<math.h>int fun(int k) //求K的阶乘{if(k==0)return 1;elsereturn (k*fun(k-1));}double power(double n,int k) //求r的K次方{int i;if(k==0)return 1;else{for(i=0;i<k;i++)n*=n;return n;}}void main(){double su=0.0,p,r; //r为λ的值int k=0;printf("please input r：\n");scanf("%lf",&r);printf("please input P-([0,1])：\n");scanf("%lf",&p);while(su<p){su+=(power(r,k)/fun(k))*exp(-r);su*=100;su+=0.5;su=(int)(su);su/=100.0;k++;}printf("随机数k的值为：\n");printf("k=%d\n",k-1);printf("~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\n"); }/*给出产生高斯分布的随机数原理，方法，程序代码*/#include<stdio.h>#include<math.h>#define N 10000#define PI 3.1415926void main(){double m,f=0.0 ,y,x,x1,x2,n,r; //n为μ，r为δprintf("please input n(μ) and r(δ)：");scanf("%lf,%lf",&n,&r);printf("please input y[0-1]：");scanf("%lf",&y);x1=n-10*r;x2=n+10*r;x=x1;m=(x2-x1)/N;do{f+=m*(1/(sqrt(2*PI)*r)*exp(-((x-n)*(x-n))/2));x+=m;}while(f<y);printf("%lf\n",x-m);}。

高斯滤波（高斯平滑）是数字图像处理和计算机视觉里面最常见的操作。

平时，我们都是用Matlab或者OpenCV的函数调用：imfilter或者cvSmooth，并不关心底层的实现。

然而当开发者要自己实现高斯滤波的时候，往往就会很迷惘，经常会被下面几个问题所困扰：1、给定sigma，即标准偏差，怎么确定离散化后的滤波器窗口大小？2、给定窗口大小，怎么计算高斯核的sigma，即标准偏差？3、怎么实现可分离滤波器？在网上搜了一下，还真没几个人把实现的细节讲清楚了。

这里，我尝试结合三份源码，做个小小的总结。

三份源码分别是：1、OpenCV中的cvfilter.cpp2、autopano-sift-c中的GaussianConvolution.c3、GIMP中的blur-gauss.c和unsharp-mask.c在图像处理中，高斯滤波一般有两种实现方式，一种是用离散化的滑动窗口进行卷积运算，另一种则是通过傅里叶变换来实现。

最常见的就是第一种卷积核实现，只有当离散化的窗口非常大，计算非常耗时（这时可使用可分离滤波器）的情况下，可能会考虑基于傅里叶变换的实现方法。

这里我们只讨论第一种方法。

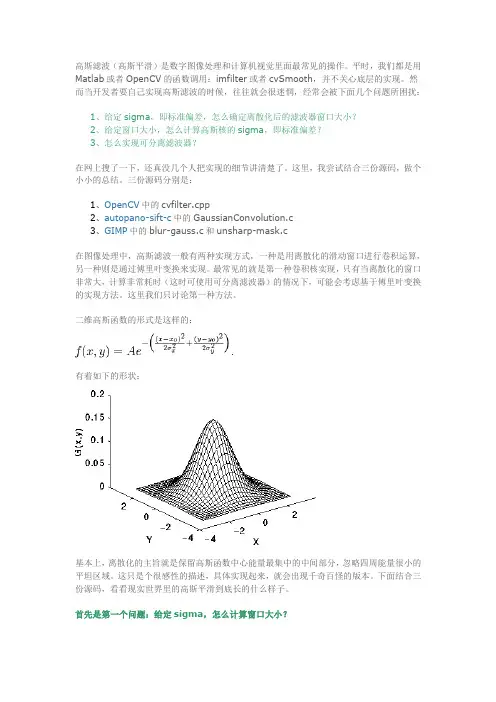
二维高斯函数的形式是这样的：有着如下的形状：基本上，离散化的主旨就是保留高斯函数中心能量最集中的中间部分，忽略四周能量很小的平坦区域。

这只是个很感性的描述，具体实现起来，就会出现千奇百怪的版本。

下面结合三份源码，看看现实世界里的高斯平滑到底长的什么样子。

首先是第一个问题：给定sigma，怎么计算窗口大小？直接上OpenCV的源码，在cvFilter函数中：param1 = cvRound(sigma1*(depth == CV_8U ? 3 : 4)*2 + 1)|1;OpenCV认为半径为3*sigma的窗口就是高斯函数的能量最集中的区域。

（在图像位深度不是8的时候，使用4*sigma半径的窗口？）autopan0-sift-c是图像拼接软件hugin里面的sift实现，在实现DoG的时候需要做不同尺度的高斯平滑，在GaussianConvolution_new1函数中实现如下：dim = 1 + 2 * ((int) (3.0 * sigma));可见autopano也是实现的3*sigma半径的窗口。

图像处理－线性滤波－3⾼斯滤波器对于图像来说，⾼斯滤波器是利⽤⾼斯核的⼀个2维的卷积算⼦，⽤于图像模糊化（去除细节和噪声）。

1. ⾼斯分布⼀维⾼斯分布，⼆维⾼斯分布2.⾼斯核理论上，⾼斯分布在所有定义域上都有⾮负值，这就需要⼀个⽆限⼤的卷积核。

实际上，仅需要取均值周围3倍标准差内的值，以外部份直接去掉即可。

如下图为⼀个标准差为1.0的整数值⾼斯核。

3. ⾼斯滤波（平滑）完成了⾼斯核的构造后，⾼斯滤波就是⽤此核来执⾏标准的卷积。

4.应⽤⾼斯滤波后图像被平滑的程度取决于标准差。

它的输出是领域像素的加权平均，同时离中⼼越近的像素权重越⾼。

因此，相对于均值滤波（mean filter）它的平滑效果更柔和，⽽且边缘保留的也更好。

⾼斯滤波被⽤作为平滑滤波器的本质原因是因为它是⼀个低通滤波器，见下图。

⽽且，⼤部份基于卷积平滑滤波器都是低通滤波器。

图.⾼斯滤波器（标准差=3像素）的频率响应。

The spatial frequency axis is marked in cycles per pixel,and hence no value above 0.5 has a real meaning。

Matlab函数：h = fspecial('gaussian', hsize, sigma) returns a rotationally symmetric Gaussian lowpass filter of size hsize with standard deviation sigma (positive). hsize can be a vector specifying the number of rows and columns in h, or it can be a scalar, in which case h is a square matrix.The default value for hsize is [3 3]; the default value for sigma is 0.5.5 资源：。

【1】基于C语言的高斯曲线拟合原理及实现在统计学和数据分析中，高斯曲线是一个常见的概率密度函数，常用于描述连续型随机变量的分布。

高斯曲线拟合是通过拟合高斯函数来近似描述一个数据集的分布。

在本文中，我们将讨论基于C语言的高斯曲线拟合原理及实现。

【2】高斯曲线的概念高斯曲线又称正态分布曲线，是由高斯函数绘制的一种光滑曲线，通常呈钟形。

它的数学表达式为：\[f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]其中，μ是均值，σ是标准差，e是自然对数的底。

【3】高斯曲线拟合原理高斯曲线拟合即是通过寻找最佳的μ和σ值，使得高斯函数能够最好地拟合数据集的分布。

一般来说，拟合的好坏可以通过计算残差平方和来评估，残差平方和越小，拟合效果越好。

【4】基于C语言的高斯曲线拟合实现我们需要准备一个包含数据集的数组，然后利用最小二乘法来拟合高斯函数。

最小二乘法是一种通过最小化数据的实际观测值与拟合值之间的残差平方和来确定参数估计值的方法。

接下来，我们可以利用C语言中的数值计算库，比如GNU Scientific Library（GSL）来实现高斯曲线拟合的算法。

GSL是一个功能强大的数值计算库，提供了许多常用的数学函数和数值算法，包括最小二乘拟合算法。

我们可以使用GSL库中的函数来进行高斯曲线拟合，比如gsl_multifit_fdfsolver，可以进行高斯模型的非线性最小二乘拟合。

【5】个人观点和理解在实际的数据分析应用中，高斯曲线拟合可以帮助我们更好地理解数据的分布规律，从而进行更准确的预测和决策。

而利用C语言来实现高斯曲线拟合，不仅可以充分发挥C语言在科学计算和数据处理方面的优势，还可以让我们更深入地理解最小二乘拟合算法的原理和实现方法。

【6】总结通过本文的讨论，我们了解了高斯曲线的概念、拟合原理以及在C语言中的实现方法。

高斯曲线拟合不仅可以帮助我们更好地描述数据分布，还可以为我们提供更多的数据分析工具和方法。

opencv源码解析之（4）：GaussianBlur（）这⼀节来真正进⼊opencv的源码分析中，本次分析的函数是GaussianBlur()，即⾼斯滤波函数。

在前前⾯博⽂《opencv源码解析之滤波前⾔2》：中已经阐述了这个函数的⽤法，即：其函数声明为：void GaussianBlur(InputArray src, OutputArray dst, Size ksize, double sigmaX, double sigmaY=0, int borderType=BORDER_DEFAULT ) ;功能：对输⼊的图像src进⾏⾼斯滤波后⽤dst输出。

参数：src和dst当然分别是输⼊图像和输出图像。

Ksize为⾼斯滤波器模板⼤⼩，sigmaX和sigmaY分别为⾼斯滤波在横线和竖向的滤波系数。

borderType为边缘扩展点插值类型。

接下来的⼯作就是进⼊GaussianBlur函数内部，跟踪其函数代码，经过分析，在该函数内部调⽤了很多其他的函数，其调⽤的函数层次结构如下图所⽰：这⾥我们分析源代码不需要深⼊到最底层，我们只需分析到函数createSeparableLinearFilter和getGaussianKernel这⼀层。

那就开始我们的源码分析⼯作吧！从函数调⽤层次结构图可以看出，要分析函数GaussianBlur，必须先分析其调⽤过的内部函数。

因此⾸先分析函数getGaussianKernel。

功能：返回⼀个ksize*1的数组，数组元素满⾜⾼斯公式：其中只有系数alpha和参数sigma未知，sigma的求法为：如果输⼊sigma为⾮正，则计算公式为：sigma = 0.3*((ksize-1)*0.5 - 1) + 0.8 .如果输⼊sigma为正，则就⽤该输⼊参数sigma。

最后alpha为归⼀化系数，即计算出的ksize个数之和必须为1，所以后⾯只需求ksize个数，计算其和并求倒即可。

基于c语言的高斯曲线拟合原理以及实现高斯曲线拟合是一种常见的曲线拟合方法，用于拟合具有高斯形状的数据。

其原理是将待拟合的数据拟合成高斯函数的形式，即使用高斯函数来描述数据的分布。

高斯函数的一般形式为：f(x) = A * exp(-((x - μ)^2) / (2 * σ^2))其中，A是高斯函数的幅度，μ是高斯函数的均值，σ是高斯函数的标准差。

实现高斯曲线拟合的步骤如下：1. 初始化拟合参数：根据待拟合数据的特点，初始化高斯函数的参数A、μ和σ的初值。

2. 计算拟合函数值：根据当前的参数值，计算高斯函数在每个点上的值。

3. 计算误差函数：将计算得到的拟合函数值与待拟合数据进行比较，计算两者之间的误差，例如可以使用均方误差（MSE）作为误差函数。

4. 优化参数：使用优化算法（如最小二乘法、梯度下降法等）来调整参数的值，使得误差函数最小化。

5. 更新参数：根据优化算法得到的新参数值，更新高斯函数的参数。

6. 重复步骤2-5，直到误差函数达到满意的程度或达到最大迭代次数。

7. 输出最终拟合函数：根据最终的参数值，得到最优的高斯函数拟合曲线。

下面是一个简单的使用C语言实现高斯曲线拟合的例子：```c#include <stdio.h>#include <math.h>// 待拟合数据的x和y坐标float x[] = {1.0, 2.0, 3.0, 4.0, 5.0};float y[] = {0.2, 0.8, 1.6, 3.0, 4.6};// 高斯函数的参数float A = 1.0;float mu = 3.0;float sigma = 1.0;// 计算高斯函数的值float gaussian(float x, float A, float mu, float sigma) {return A * exp(-pow((x - mu), 2) / (2 * pow(sigma, 2)));}// 计算误差函数（均方误差）float error() {float err = 0.0;int i;for (i = 0; i < 5; i++) {float y_fit = gaussian(x[i], A, mu, sigma);err += pow((y[i] - y_fit), 2);}return err;}// 优化参数void optimize() {float step_size = 0.01;int max_iter = 1000;int iter = 0;float err;do {float grad_A = 0.0, grad_mu = 0.0, grad_sigma = 0.0;// 计算梯度int i;for (i = 0; i < 5; i++) {float y_fit = gaussian(x[i], A, mu, sigma);grad_A += -2 * (y[i] - y_fit) * y_fit / A;grad_mu += -2 * (y[i] - y_fit) * y_fit * (x[i] - mu) /pow(sigma, 2);grad_sigma += -2 * (y[i] - y_fit) * y_fit * pow((x[i] - mu), 2) / pow(sigma, 3);}// 更新参数A -= step_size * grad_A;mu -= step_size * grad_mu;sigma -= step_size * grad_sigma;// 计算误差err = error();iter++;} while (iter < max_iter && err > 1e-6);printf("A = %f\nmu = %f\nsigma = %f\n", A, mu, sigma);}int main() {optimize();return 0;}```该例子中假设待拟合的数据为一组已知的x和y坐标，通过不断优化高斯函数的参数A、μ和σ，最终得到最优的拟合结果。

. . 邻域滤波（卷积）

邻域算子值利用给定像素周围像素的值决定此像素的最终输出。如图左边图像与中间图像卷积禅城右边图像。目标图像中绿色的像素由原图像中蓝色标记的像素计算得到。

通用线性邻域滤波是一种常用的邻域算子，输入像素加权得到输出像素： 其中权重核 为“滤波系数”。上面的式子可以简记为： 【方框滤波】 最简单的线性滤波是移动平均或方框滤波，用 窗口中的像素值平均后输出，核函数为：

其实等价于图像与全部元素值为1的核函数进行卷积再进行尺度缩放。 代码 OpenCV中的 blur函数是进行标准方框滤波： . . [cpp] view plain copy 1. void cv::blur( InputArray src, OutputArray dst, 2. Size ksize, Point anchor, int borderType ) 3. { 4. boxFilter( src, dst, -1, ksize, anchor, true, borderType ); 5. }

而boxFilter函数源码如下： [cpp] view plain copy 1. cv::Ptr cv::createBoxFilter( int srcType, int dstType, Size ksize, 2. Point anchor, bool normalize, int borderType ) 3. { 4. int sdepth = CV_MAT_DEPTH(srcType); 5. int cn = CV_MAT_CN(srcType), sumType = CV_64F; 6. if( sdepth <= CV_32S && (!normalize || 7. ksize.width*ksize.height <= (sdepth == CV_8U ? (1<<23) : 8. sdepth == CV_16U ? (1 << 15) : (1 << 16))) ) 9. sumType = CV_32S; 10. sumType = CV_MAKETYPE( sumType, cn ); 11. 12. Ptr rowFilter = getRowSumFilter(srcType, sumType, ksize.width, anchor.x );

维纳滤波算法c语言维纳滤波算法是一种经典的信号处理算法，常用于降噪和信号增强。

本文将介绍维纳滤波算法的原理及其在C语言中的实现。

维纳滤波算法是由诺伯特·维纳在20世纪40年代提出的，用于处理受噪声干扰的信号。

该算法基于最小均方误差准则，通过对信号和噪声的统计特性进行建模，实现对噪声的抑制和信号的恢复。

在维纳滤波算法中，我们首先需要对信号和噪声的统计特性进行建模。

通常情况下，我们假设信号和噪声都是高斯分布的，并且它们是相互独立的。

这个假设在很多实际应用中是成立的。

接下来，我们需要对信号和噪声的功率谱密度进行估计。

功率谱密度是信号在频域上的表示，它描述了信号在不同频率上的能量分布。

通过估计信号和噪声的功率谱密度，我们可以得到它们在频域上的特性。

在维纳滤波算法中，最重要的一步是对信号进行滤波。

我们可以使用频域滤波的方法来实现。

具体而言，我们将信号和噪声的功率谱密度分别进行傅里叶变换，然后将信号的频谱进行加权，最后再进行反傅里叶变换，得到滤波后的信号。

在C语言中，我们可以使用FFT（快速傅里叶变换）库来实现傅里叶变换和反傅里叶变换。

常用的FFT库有FFTW和KISSFFT等。

这些库提供了方便易用的接口，可以快速计算傅里叶变换和反傅里叶变换。

在进行频域滤波时，我们需要对信号的频谱进行加权。

通常情况下，我们可以使用信噪比（SNR）来进行加权。

信噪比描述了信号与噪声之间的相对强度关系。

通过调整信噪比，我们可以控制滤波后的信号的增强程度。

在C语言中，我们可以通过对信号和噪声的频谱进行逐点相除来实现加权。

具体而言，我们可以先计算信号和噪声的功率谱密度的比值，然后将信号的频谱与该比值进行逐点相乘，最后再进行反傅里叶变换，得到滤波后的信号。

维纳滤波算法在降噪和信号增强方面具有广泛的应用。

例如，在语音信号处理中，维纳滤波算法可以用于降低噪声对语音信号的影响，提高语音的清晰度和可懂度。

在图像处理中，维纳滤波算法可以用于去除图像中的噪声，提高图像的质量和细节。