行列式的计算开题报告总结.doc

存档编号赣南师学院学士学位论文行列式的若干计算技巧与方法目录摘要 (1)关键字 (1)Abstract (1)Key words (1)引言 (2)1.行列式的概念及性质 (2)1.1 n阶行列式的定义 (2)1.2 行列式的性质 (3)2.行列式计算的几种常见技巧和方法 (5)2.1 定义法 (5)2.2 利用行列式的性质 (6)2.3 降阶法 (9)2.4 升阶法（加边法） (11)2.5 数学归纳法 (12)2.6 递推法 (14)3. 行列式计算的几种特殊技巧和方法 (16)3.1 拆行（列）法 (16)3.2 构造法 (17)3.3 特征值法 (19)4. 几类特殊行列式的计算技巧和方法 (19)4.1 三角形行列式 (19)4.2 “爪”字型行列式 (20)4.3 “么”字型行列式 (21)4.4 “两线”型行列式 (23)4.5 “三对角”型行列式 (24)4.6 德蒙德行列式 (25)5.行列式的计算方法的综合运用 (27)5.1 降阶法和递推法 (28)5.2 逐行相加减和套用德蒙德行列式 (28)5.3 构造法和套用德蒙德行列式 (29)小结 (30)参考文献 (31)行列式的若干计算技巧与方法摘要：行列式是高等代数的一个基本概念，求解行列式是在高等代数的学习中遇到的基本问题，每一种复杂的高阶行列式都有其独特的求解方法．本文主要介绍了求行列式值的一些常用方法和一些特殊的行列式的求值方法．如：化三角形法、降阶法和数学归纳法等多种计算方法以及Vandermonde行列式、“两线型”行列式和“爪”字型行列式等多种特殊行列式．并对相应例题进行了分析和归纳，总结了与每种方法相适应的行列式的特征．关键词：行列式行列式的计算方法 Vandermonde行列式The Calculation of Determinant Abstract: The determinant is a basic concept of higher mathematics. The solution of determinant is the basic question, and each kind of complex higher order determinant has its special solution method. This paper mainly introduces the methods for calculation of determinant. For example, the triangle method, order reduction method，mathematical induction method and Vandermonde determinant, two linear determinant，claw type determinant and so on. The paper also analyzes the corresponding examples, and summarizes the characteristic of determinants corresponding to each method.Key words: Determinant The calculation of determinant Vandermonde determinant引言：行列式的计算是高等代数的重要容之一，也是学习过程的一个难点．对于低阶行列式，我们可以利用行列式的定义和性质计算．但对于高阶行列式，如果直接利用定义和性质计算，则计算量大，很难得到结果．因此，研究行列式的计算方法和技巧就显得十分必要．本文主要介绍了几种计算方法和技巧，还有一些特殊行列式的计算方法．1．行列式的概念及性质1.1 n 阶行列式的定义我们知道，二、三阶行列式的定义如下：22211211a a a a =21122211a a a a -，=333231232221131211a a a a a a a a a .312213332112322311322113312312332211a a a a a a a a a a a a a a a a a a ---++从二、三阶行列式的在规律引出n 阶行列式的定义． 设有2n 个数，排成n 行n 列的数表nnn n nn a a a a a a a a a212222111211，即n 阶行列式．这个行列式等于所有取自不同行不同列的n 个元素的乘积n 21nj j 2j 1a a a ⑴的代数和，这里n 21j j j 是n 21，，， 的一个排列,每一项⑴都按下列规则带有符号：当n 21j j j 是偶排列时, ⑴带正号；当n 21j j j 是奇排列时, ⑴带负号． 即nnn n nn a a a a a a a a a212222111211=()()n21n21n 21nj j 2j 1j j j j j j 1a a a τ∑-，这里∑n21j j j 表示对所有n 级排列求和.1.2 行列式的性质性质1 行列互换，行列式不变．即nna a a a a a a a a a a a a a a a a a n2n1n22212n12111nnn2n12n 22211n 1211= .性质2 一个数乘行列式的一行（或列），等于用这个数乘此行列式．即=nnn2n1in i2i1n 11211k k k a a a a a a a a ak nna a a a a a a a an2n1in i2i1n 11211. 性质3 如果行列式的某一行（或列）是两组数的和，那么该行列式就等于两个行列式的和，且这两个行列式除去该行（或列）以外的各行（或列）全与原来行列式的对应的行（或列）一样．即11121111211112111221212121212.n n n n n n n n n nnn n nnn n nna a a a a a a a abc b c b c b b b c c c a a a a a a a a a +++=+ 性质4 如果行列式中有两行（或列）对应元素相同或成比例，那么行列式为零．即k a a a ka ka ka a a a a a a nn n n in i i in i i n=21212111211nnn n in i i in i i na a a a a a a a a a a a 21212111211=0. 性质5 把一行的倍数加到另一行，行列式不变．即=+++nn n n kn k k kn in k i k i na a a a a a ca a ca a ca a a a a2121221111211nnn n kn k k in i i n a a a a a a a a a a a a 21212111211. 性质6 对换行列式中两行的位置，行列式反号.即nn n n kn k k ini i n a a a a a a a a a a a a 21212111211=-nnn n in i i kn k k n a a a a a a a a a a a a21212111211.性质7 行列式一行（或列）元素全为零，则行列式为零．即00000nn1-n n,n2n1n 11-n ,11211=a a a a a a a a.2、行列式的几种常见计算技巧和方法2.1 定义法适用于任何类型行列式的计算，但当阶数较多、数字较大时，计算量大，有一定的局限性．例1 计算行列式0004003002001000.解析：这是一个四级行列式，在展开式中应该有244=！项，但由于出现很多的零，所以不等于零的项数就大大减少．具体的说，展开式中的项的一般形式是43214321j j j j a a a a ．显然，如果41≠j ，那么011=j a ，从而这个项就等于零．因此只须考虑41=j 的项，同理只须考虑1,2,3432===j j j 的这些项，这就是说，行列式中不为零的项只有41322314a a a a ，而()64321=τ，所以此项取正号．故004003002001000=()()241413223144321=-a a a a τ.2.2 利用行列式的性质即把已知行列式通过行列式的性质化为上三角形或下三角形.该方法适用于低阶行列式． 2.2.1 化三角形法上、下三角形行列式的形式及其值分别如下：nn n nn a a a a a a a a a a a a a2211nn333223221131211000000=，nn nnn n n a a a a a a a a a a a a a 2211321333231222111000000=. 例2 计算行列式nn n n b a a a a a b a a a a ++=+21211211n 111D .解析：观察行列式的特点，主对角线下方的元素与第一行元素对应相同，故用第一行的()1-倍加到下面各行便可使主对角线下方的元素全部变为零．即：化为上三角形．解：将该行列式第一行的()1-倍分别加到第2,3…（1n +）行上去，可得121n 11210000D 0n n na a ab b b b b +==.2.2.2 连加法这类行列式的特征是行列式某行（或列）加上其余各行（或列）后，使该行（或列）元素均相等或出现较多零，从而简化行列式的计算．这类计算行列式的方法称为连加法．例3 计算行列式mx x x x m x x x x mx D n n n n ---=212121.解： mx x mxx m x m xx x mxn ni in ni in ni i-----=∑∑∑===212121n Dmx x x m x x x m x n n nn i i --⎪⎭⎫ ⎝⎛-=∑=2221111mm x x m x nn i i --⎪⎭⎫ ⎝⎛-=∑=0000121()⎪⎭⎫ ⎝⎛--=∑=-m x m ni i n 11.2.2.3 滚动消去法当行列式每两行的值比较接近时，可采用让邻行中的某一行减或者加上另一行的若干倍，这种方法叫滚动消去法．例4 计算行列式()2122123123122121321D n ≥-------=n n n n n n n n nn.解：从最后一行开始每行减去上一行，有1111111111111111321D n ---------=n n 1111120022200021321----=n n 0111100011000011132122+-=-n n n ()()21211-++-=n n n .2.2.4 逐行相加减对于有些行列式，虽然前n 行的和全相同，但却为零．用连加法明显不行，这是我们可以尝试用逐行相加减的方法．例5 计算行列式111110000000000000D 32211n na a a a a a a ----=. 解：将第一列加到第二列，新的第二列加到第三列，以此类推，得：1321000000000000000D 321+----=n na a a a n()()()()()n n n a a a n a a a n 21n 21n 2211111+-=+--=+.2.3 降阶法将高阶行列式化为低阶行列式再求解． 2.3.1 按某一行（或列）展开例6 解行列式1221n 1000000000100001D a a a a a xx x x n n n-----=.解：按最后一行展开，得n n n n n a x a x a x a D ++++=---12211 .2.3.2 按拉普拉斯公式展开拉普拉斯定理如下：设在行列式D 中任意选定了()1-n k 1k ≤≤个行.由这k 行元素所组成的一切k 级子式与它们的代数余子式的乘积的和等于行列式D.即n n 2211A M A M A M D +++= ，其中i A 是子式i M 对应的代数余子式．即nn nn nnnn nnB A BC A •=0， nn nn nnnnnn B A B C A •=0. 例7 解行列式γβββββγββββγλbbbaa a a n =D .解：从第三行开始，每行都减去上一行；再从第三列开始，每列都加到第二列，得βγβγγββββγλ---=0000D n b aa a a()()βγβγββββγλ---+-=0000021n b aa aa n()()βγβγβγλ--•-+-=000021n ba n ()()[]()21n 2-----+=n ab n βγβλλγ.2.4 升阶法就是把n 阶行列式增加一行一列变成n+1阶行列式，再通过性质化简算出结果，这种计算行列式的方法叫做升阶法或加边法．升阶法的最大特点就是要找每行或每列相同的因子,那么升阶之后，就可以利用行列式的性质把绝大多数元素化为0，这样就达到简化计算的效果．其中，添加行与列的方式一般有五种：首行首列，首行末列，末行首列，末行末列以及一般行列的位置．例8 解行列式D=111110111110111110111110 .解：使行列式D 变成1+n 阶行列式，即111010110110101110011111D =.再将第一行的()1-倍加到其他各行，得：D=1101001001010001111111--------. 从第二列开始，每列乘以()1-加到第一列，得：100100000100000101111)1n D ------=（ ()()1n 11n --=+.2.5数学归纳法有些行列式，可通过计算低阶行列式的值发现其规律，然后提出假设，再利用数学归纳法去证明．对于高阶行列式的证明问题，数学归纳法是常用的方法．例9 计算行列式βββββcos 211cos 200000cos 210001cos 210001cos=n D .解:用数学归纳法证明. 当1=n 时，βcos 1=D .当2=n 时，ββββ2cos 1cos 2cos 211cos 22=-==D .猜想，βn D n cos =.由上可知，当1=n ，2=n 时，结论成立．假设当k n =时，结论成立．即：βk D k cos =.现证当1+=k n 时，结论也成立．当1+=k n 时，βββββcos 211cos 200000cos 210001cos 210001cos 1=+k D .将1+k D 按最后一行展开，得()βββββcos 20000cos 21001cos 21001cos cos 21D 111k •-=++++k k()10cos 21001cos 2101cos 11 βββkk ++-+ 1cos 2--=k k D D β.因为βk D k cos =，()()βββββββsin sin cos cos cos 1cos 1k k k k D k +=-=-=-，所以1+k D 1cos 2--=k k D D βββββββsin sin cos cos cos cos 2k k k --= ββββsin sin cos cos k k -= ()β1cos +=k .这就证明了当1+=k n 时也成立，从而由数学归纳法可知，对一切的自然数，结论都成立． 即：βn D n cos =.2.6 递推法技巧分析：若n 阶行列式D 满足关系式021=++--n n n cD bD aD .则作特征方程02=++c bx ax .① 若0≠∆，则特征方程有两个不等根，则1211--+=n n n Bx Ax D ．② 若0=∆，则特征方程有重根21x x =，则()11-+=n n x nB A D ． 在①②中， A ，B 均为待定系数，可令2,1==n n 求出．例10 计算行列式94000005940000000594000005940000059D n =.解：按第一列展开，得21209---=n n n D D D .即020921=+---n n n D D D ．作特征方程02092=+-x x .解得5,421==x x .则1154--•+•=n n n B A D .当1=n 时，B A +=9； 当2=n 时，B A 5461+=. 解得25,16=-=B A ，所以1145++-=n n n D .3、行列式的几种特殊计算技巧和方法3.1 拆行（列）法3.1.1 概念及计算方法拆行（列）法（或称分裂行列式法），就是将所给的行列式拆成两个或若干个行列式之和，然后再求行列式的值．拆行（列）法有两种情况，一是行列式中有某行（列）是两项之和，可直接利用性质拆项；二是所给行列式中行（列）没有两项之和，这时需保持行列式之值不变，使其化为两项和． 3.1.2 例题解析例11 计算行列式nn n n a a a a a a a a --------=-1110000011000110001D 133221.解：把第一列的元素看成两项的和进行拆列，得nn n n a a a a a a a a --+-+--+-+--=-1100010000001100001010001D 133221.110100001100010000110001000001100011000113322113322nn n nn n a a a a a a a a a a a a a a a -------+-------=--上面第一个行列式的值为1，所以nn n n a a a a a a a ------=-1101000010011D 13321111--=n D a .这个式子在对于任何()2≥n n 都成立，因此有111--=n n D a D()()n n n a a a a a a D a a 2112112211111---+++-==--=()∏∑==-+=ij j ii a 1n111.3.2 构造法3.2.1 概念及计算方法有些行列式通过直接求解比较麻烦，这时可同时构造一个容易求解的行列式，从而求出原行列式的值． 3.2.2 例题解析例12 求行列式n nn nn nn n nnn x x x x x x x x x x x x D21222212222121111---=.解：虽然n D 不是德蒙德行列式，但可以考虑构造1+n 阶的德蒙德行列式来间接求出n D 的值． 构造1+n 阶的德蒙德行列式，得()nnnn nn n nn n n n nn n n nx x x x x x x x x x x x x x x x x x x x x f21111211222221222221211111--------=. 将()x f 按第1+n 列展开，得()n n n n n n n n x A x A x A A x f 1,111,1,21,1++-+++++++= ，其中，1-n x的系数为()()n n n n n n D D A -=-=+++11,1.又根据德蒙德行列式的结果知()()()()()∏≤<≤----=ni j j in x xx x x x x x x f 121 .由上式可求得1-n x 的系数为()()∏≤<≤-+-ni j j in x xx x x 121 .故有()()∏≤<≤-+++=ni j j in n x xx x x D 121 .3.3 特征值法3.3.1 概念及计算方法设n λλλ ，，21是n 级矩阵A 的全部特征值，则有公式 n A λλλ 21=.故只要能求出矩阵A 的全部特征值，那么就可以计算出A 的行列式．3.3.2 例题解析例13 若n λλλ ，，21是n 级矩阵A 的全部特征值，证明：A 可逆当且仅当它的特征值全不为零． 证明：因为n A λλλ 21=，则A 可逆()n i i n 2,1000A 21=≠⇔≠⇔≠⇔λλλλ. 即A 可逆当且仅当它的特征值全不为零．4、几类特殊的行列式的巧妙计算技巧和方法4.1 三角形行列式4.1.1 概念形如nn n n n a a a a a a a a a a 333223221131211，nnn n n a a a a a a a a a a321333231222111这样的行列式，形状像个三角形，故称为“三角形”行列式． 4.1.2 计算方法 由行列式的定义可知，nn nnn nn a a a a a a a a a a a a a2211333223221131211000000=,nn nnn n n a a a a a a a a a a a a a 2211321333231222111000000=. 4.2 “爪”字型行列式4.2.1 概念形如nnna c a c a cb b b a2211210，nnn c a c a c a a b b b2211012，nnn b b b a a c a c a c 211122，121122a b b b c a c a c a nn n这样的行列式，形状像个“爪”字，故称它们为“爪”字型行列式． 4.2.2 计算方法利用对角线消去行列式中的“横线”或“竖线”，均可把行列式化成“三角形”行列式．此方法可归纳为：“爪”字对角消竖横． 4.2.3 例题解析例14 计算行列式na a a a 111111321，其中.,2,1,0n i a i =≠分析：这是一个典型的“爪”字型行列式，计算时可将行列式的第.),3,2(n i i =列元素乘以ia 1-后都加到第一列上，原行列式可化为三角形行列式．解:na a a a 111111321nni ia a a a a 00011113221∑=-=⎪⎪⎭⎫⎝⎛-=∑=ni i n aa a a a 21321. 4.3 “么”字型行列式4.3.1 概念形如n n n b b b a a c a c a c 211122，nn na b c a b c a b c a2221110，n n nc a c a c a a b b b 2211012，0111222a cb ac b a c b a nn n ，121122c a c a b a b c a b nnn，n n n a c a c a c b b b a2211210，0121122a b b b c a c a c a nnn，nnn b a b c b a b a c a c 12211201这样的行列式，形状像个“么”字，因此常称它们为“么”字型行列式． 4.3.2 计算方法利用“么”字的一个撇消去另一个撇，就可以把行列式化为三角形行列式．此方法可以归纳为：“么”字两撇相互消．注意：消第一撇的方向是沿着“么”的方向，从后向前，利用n a 消去n c ，然后再用1-n a 消去1-n c ，依次类推． 4.3.3 例题解析例15 计算1+n 阶行列式nn n b b b D 1111111111----=-+ .解：从最后一行开始后一行加到前一行（即消去第一撇），得nnn ni ini in b b b bb D 11111111-+--+-=-==+∑∑()()()⎪⎭⎫ ⎝⎛+--•-=∑=+ni i nn n b 121111()()⎪⎭⎫ ⎝⎛+--=∑=+ni i n n b 12311.4.4 “两线”型行列式4.4.1 概念形如nnn a b b b a b a0000000012211-这样的行列式叫做“两线型”行列式． 4.4.2 计算方法对于这样的行列式，可通过直接展开法求解．4.4.3 例题解析例16 求行列式nn n n a b b b a b a00000000D 12211-=. 解：按第一列展开，得()1221112211000010000-+-+-+=n n n nn n b b a b b a b b a a D()n n n b b b a a a 211211+-+=.4.5 “三对角”型行列式4.5.1 概念形如ba ab ba ab b a abb a ab b a +++++10000000000100000100000这样的行列式，叫做“三对角型”行列式． 4.5.2 计算方法对于这样的行列式，可直接展开得到两项递推关系式，然后变形进行两次递推或利用数学归纳法证明． 4.5.3 例题解析例17 求行列式ba ab ba ab b a abb a ab b a n +++++=10000000000000100000100000D.解：按第一列展开，得()ba ab ba b a ab b a abb a ab D b a n n +++++-+=-100000010000100000D 1()21---+=n n abD D b a .变形，得()211D ----=-n n n n aD D b aD .由于2221,b ab a D b a D ++=+=， 从而利用上述递推公式得()211D ----=-n n n n aD D b aD ()()n n n n b aD D b aD D b =-==-=---122322 .故()nn n n n n n n n n b ab b a D a b b aD a b aD D ++++==++=+=------12211121 n n n n b ab b a a ++++=--11 .4.6 Vandermonde 行列式4.6.1 概念形如113121122322213211111----n nn n n nna a a a a a a a a a a a这样的行列式，成为n 级的德蒙德行列式．4.6.2 计算方法通过数学归纳法证明，可得()∏≤<≤-----=11113121122322213211111i j j i n nn n n nna a a a a a a a a a a a a a. 4.6.3 例题解析例18 求行列式n nn nn nn n nnn x x x x x x x x x x x x D21222212222121111---=.解：虽然n D 不是德蒙德行列式，但可以考虑构造1+n 阶的德蒙德行列式来间接求出n D 的值． 构造1+n 阶的德蒙德行列式，得()nnnn nn n nn n n n nn n n nx x x x x x x x x x x x x x x x x x x x x f21111211222221222221211111--------=. 将()x f 按第1+n 列展开，得()n n n n n n n n x A x A x A A x f 1,111,1,21,1++-+++++++= ， 其中，1-n x 的系数为()()n n n n n n D D A -=-=+++11,1.又根据德蒙德行列式的结果知()()()()()∏≤<≤----=ni j j in x xx x x x x x x f 121 .由上式可求得1-n x 的系数为()()∏≤<≤-+-ni j j in x xx x x 121 ,故有()()∏≤<≤-+++=ni j j in n x xx x x D 121 .5、行列式的计算方法的综合运用有些行列式如果只使用一种计算方法不易计算，这时就需要结合多种计算方法，使计算简便易行．下面就列举几种行列式计算方法的综合应用．5.1 降阶法和递推法例19 计算行列式2100012000002100012100012D=n .分析：乍一看该行列式，并没有什么规律．但仔细观察便会发现，按第一行展开便可得到1-n 阶的形式．解：将行列式按第一行展开，得212D ---=n n n D D . 即211D ----=-n n n n D D D .∴12312211=-=-==-=----D D D D D D n n n n . ∴()()111111---++++==+=n n n n D D D()121+=+-=n n .5.2 逐行相加减和套用德蒙德行列式例20 计算行列式43423332232213124243232221214321sin sin sin sin sin sin sin sin sin sin sin sin sin sin sin sin sin 1sin 1sin 1sin 11111D ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ++++++++++++=解：从第一行开始，依次用上一行的()1-倍加到下一行，进行逐行相加，得43332313423222124321sin sin sin sin sin sin sin sin sin sin sin sin 1111ϕϕϕϕϕϕϕϕϕϕϕϕ=D . 再由德蒙德行列式，得()∏≤<≤-==4143332313423222124321sin sin sin sin sin sin sin sin sin sin sin sin sin sin 1111i j j i D ϕϕϕϕϕϕϕϕϕϕϕϕϕϕ. 5.3 构造法和套用德蒙德行列式例21 求行列式n nn nn nn n nnn x x x x x x x x x x x x D21222212222121111---=.解：虽然n D 不是德蒙德行列式，但可以考虑构造1+n 阶的德蒙德行列式来间接求出n D 的值． 构造1+n 阶的德蒙德行列式，得()nnnn nn n nn n n n nn n n nx x x x x x x x x x x x x x x x x x x x x f21111211222221222221211111--------=.将()x f 按第1+n 列展开，得()n n n n n n n n x A x A x A A x f 1,111,1,21,1++-+++++++= ，其中，1-n x 的系数为()()n n n n n n D D A -=-=+++11,1.又根据德蒙德行列式的结果知()()()()()∏≤<≤----=ni j j in x xx x x x x x x f 121 .由上式可求得1-n x 的系数为()()∏≤<≤-+-ni j j in x xx x x 121 .故有()()∏≤<≤-+++=ni j j in n x xx x x D 121 .小结本文主要介绍了行列式计算的一些技巧和方法，还有一些特殊行列式的计算技巧，通过归纳和总结这些技巧和方法，让读者在计算行列式时游刃有余．然而在这么多方法面前，我们需要多观察、多思考，这样便于我们更加轻松地解决有关行列式的问题，也让我们更加灵活的运用这些方法和技巧来解决实际问题．参考文献:[1]北大数学系代数小组. 高等代数（第三版）[M].：高等教育，2003：50～104.[2]钱. 高等代数题解精粹[M].：中央民族大学，2002：24～58[3]家保，中华，陆一南.若干类型行列式计算方法.科学技术学院学报（自然科学版），2012年3月，30(2).[4]鹏辉.行列式的计算技巧.学院报，2011年4月，33（4）.[5]丁冰.三线型行列式的计算.科技通报,2012年2月,28(2).[6]龚德仁.高阶行列式计算的若干技巧.课外阅读（中下）.2012年03期.[7]新功.行列式的计算方法探讨.师大学学报（自然科学版），2011年7月,28(4).[8]王爱霞.关于n阶行列式的计算方法与技巧的探讨.教育学院学报.2012年第1期.[9] 樊正华，徐新萍.浅谈行列式的计算方法.教育学院学报（自然科学），2011年2月，27(1).[10]卢潮辉.三对角行列式的计算. 职业技术学院学报,2010年3月,9(2).[11] 林.求n阶行列式的几种方法和技巧. 科技信息报，2007年第8期.[12]“爪”字型和“么”字型行列式的计算.理科教学研究(短文集锦),2006年第4期.。

行列式的计算方法总结行列式是数学中一类特殊的数值，它可以用于解决各种数学问题，如线性方程组的解、二次行列式的特征根以及三角形的面积等。

它的计算方法也颇为多样，各种行列式的计算方法可以归纳总结如下：第一种是规则式子求行列式的方法，即规则式子求行列式的值。

这种方法包括常见的拆分积式法，它可以用来计算简单行列式，其解算步骤如下：把行列式的第一行和其他所有行有序的放在一起，按列乘以每列的分量，然后把乘积相加，即可求出行列式的值。

另一种常用的计算行列式的方法是运用行列式的转置法则，这也是一种简单的计算行列式的方法，它的解算步骤如下：先把行列式的行和列都交换一下，然后把交换后的新行列式进行上面第一种规则式子求行列式的求值，便可求出行列式的值。

此外，还有多元函数求行列式的方法，以及行列式求导、求偏导数的方法。

多元函数求行列式的方法就是将行列式用多元函数的形式表示出来，然后用函数定义求和解决之。

行列式求导、求偏导数的方法就是将行列式的变量替换为一个新的变量，然后进行积分，并求出偏导数，最终得到行列式的值。

最后一种常用的计算行列式的方法是拆解行列式的方法，这是一种比较复杂的行列式计算方法。

它的解算步骤如下：先把行列式拆解成几个子行列式，然后逐步把子行列式拆解为更小的子行列式，最终得到一个最小子行列式，将其值替换到初始行列式中计算，即可求出该行列式的值。

以上是行列式的计算方法总结，由于行列式的类型众多，其计算方法也多如牛毛，仅有上述几种计算方法是不够的，若想解决复杂的行列式计算，还需要运用其他更加复杂的计算方法，如克莱姆法、罗宾逊法、孟加拉法等。

此外，计算行列式还需要掌握矩阵运算的基础知识，运用高等数学知识，才能解决复杂的行列式计算问题。

总之，行列式的计算是一件非常有技巧性的事情，找到合适的计算方法，解决行列式计算的难题，有助于提高数学的解题能力。

行列式计算方法总结行列式是线性代数中的一个重要概念，它在数学和物理等领域都有着广泛的应用。

在实际运用中，我们常常需要对行列式进行计算，因此掌握行列式的计算方法是非常重要的。

本文将对行列式的计算方法进行总结，希望能够帮助大家更好地理解和掌握行列式的相关知识。

1. 二阶行列式的计算方法。

对于二阶行列式，计算方法非常简单。

设。

\[D=\begin{vmatrix} a & b \\ c & d \end{vmatrix}\]则行列式D的计算公式为。

\[D=ad-bc\]2. 三阶行列式的计算方法。

对于三阶行列式，计算稍显复杂，但我们可以利用代数余子式的方法来进行计算。

设。

\[D=\begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix}\]则行列式D的计算公式为。

\[D=aei+bfg+cdh-ceg-bdi-afh\]3. n阶行列式的计算方法。

对于n阶行列式，我们可以利用拉普拉斯展开等方法进行计算。

拉普拉斯展开是一种递归的方法，通过不断地将n阶行列式化为n-1阶行列式的形式来进行计算。

在实际运用中，我们可以根据具体情况选择合适的方法来进行计算，以提高计算的效率。

4. 行列式的性质。

行列式具有许多重要的性质，例如行列式与它的转置行列式相等、行列式中某一行（列）乘以一个数k，等于这个数与该行列式的乘积等等。

这些性质在行列式的计算过程中起着重要的作用，可以帮助我们简化计算，提高计算的效率。

5. 行列式的应用。

行列式在数学和物理等领域有着广泛的应用，例如在线性方程组的求解、矩阵的求逆、向量的叉乘等方面都有着重要的作用。

掌握行列式的计算方法不仅可以帮助我们更好地理解线性代数的相关知识，还可以为我们在实际问题中的求解提供有力的工具。

总结。

行列式是线性代数中的重要内容，掌握行列式的计算方法对于我们更好地理解和运用线性代数知识具有重要意义。

行列式的几种常见计算技巧和方法2.1 定义法适用于任何类型行列式的计算，但当阶数较多、数字较大时，计算量大，有一定的局限性．例1 计算行列式0004003002001000.解析：这是一个四级行列式，在展开式中应该有244=！项，但由于出现很多的零，所以不等于零的项数就大大减少．具体的说，展开式中的项的一般形式是43214321j j j j a a a a ．显然，如果41≠j ，那么011=j a ，从而这个项就等于零．因此只须考虑41=j 的项，同理只须考虑1,2,3432===j j j 的这些项，这就是说，行列式中不为零的项只有41322314a a a a ，而()64321=τ，所以此项取正号．故004003002001000=()()241413223144321=-a a a a τ.2.2 利用行列式的性质即把已知行列式通过行列式的性质化为上三角形或下三角形.该方法适用于低阶行列式． 2.2.1 化三角形法上、下三角形行列式的形式及其值分别如下：nn n nn a a a a a a a a a a a a a K ΛM O M M M K K K 2211nn333223221131211000000=，nn nnn n n a a a a a a a a a a a a a K ΛM O M M M K K K 2211321333231222111000000=. 例2 计算行列式nn nnb a a a a a b a a a a ++=+KM O M M M K K 21211211n 111D . 解析：观察行列式的特点，主对角线下方的元素与第一行元素对应相同，故用第一行的()1-倍加到下面各行便可使主对角线下方的元素全部变为零．即：化为上三角形．解：将该行列式第一行的()1-倍分别加到第2,3…（1n +）行上去，可得121n 11210000D 000n n na a ab b b b b +==KK M M M O M K.2.2.2 连加法这类行列式的特征是行列式某行（或列）加上其余各行（或列）后，使该行（或列）元素均相等或出现较多零，从而简化行列式的计算．这类计算行列式的方法称为连加法．例3 计算行列式mx x x x m x x x x mx D n nn n ---=ΛM O M M ΛΛ212121. 解： mx x mxx m x m xx x mxn ni in ni in ni i-----=∑∑∑===ΛM O M MΛΛ212121n Dmx x x m x x x m x n n n n i i --⎪⎭⎫ ⎝⎛-=∑=ΛM O M M ΛΛ2221111mm x x m x n n i i --⎪⎭⎫ ⎝⎛-=∑=ΛM OM M ΛΛ0000121()⎪⎭⎫ ⎝⎛--=∑=-m x m n i i n 11. 2.2.3 滚动消去法当行列式每两行的值比较接近时，可采用让邻行中的某一行减或者加上另一行的若干倍，这种方法叫滚动消去法．例4 计算行列式()2122123123122121321D n ≥-------=n n n n n n n n nn ΛM M O M M M ΛΛΛ. 解：从最后一行开始每行减去上一行，有1111111111*********D n ---------=ΛM M O M M M ΛΛΛn n 1111120022200021321----=ΛM M O M M M ΛΛΛn n 0111100011000011132122ΛM M O M M M ΛΛΛ+-=-n n n ()()21211-++-=n n n .2.2.4 逐行相加减对于有些行列式，虽然前n 行的和全相同，但却为零．用连加法明显不行，这是我们可以尝试用逐行相加减的方法．例5 计算行列式111110000000000000D 32211ΛΛM M O M M MΛMΛn n a a a a a a a ----=. 解：将第一列加到第二列，新的第二列加到第三列，以此类推，得：13210000000000000000D 321+----=n na a a a n ΛΛM M O M M M ΛΛΛ ()()()()()n n n a a a n a a a n ΛΛ21n 21n 2211111+-=+--=+.2.3 降阶法将高阶行列式化为低阶行列式再求解．2.3.1 按某一行（或列）展开例6 解行列式1221n 1000000000100001D a a a a a x x x x n n nKKM M O M M M O K K -----=.解：按最后一行展开，得n n n n n a x a x a x a D ++++=---12211K .2.3.2 按拉普拉斯公式展开拉普拉斯定理如下：设在行列式D 中任意选定了()1-n k 1k ≤≤个行.由这k 行元素所组成的一切k 级子式与它们的代数余子式的乘积的和等于行列式D.即n n 2211A M A M A M D +++=Λ，其中i A 是子式i M 对应的代数余子式．即nn nn nnnn nnB A BC A •=0， nn nn nnnnnn B A B C A •=0. 例7 解行列式γβββββγββββγλΛMO M M M M ΛΛΛb bbaa a a n =D .解：从第三行开始，每行都减去上一行；再从第三列开始，每列都加到第二列，得βγβγγββββγλ---=ΛM O M M M M ΛΛΛ00000D n b aa a a()()βγβγββββγλ---+-=ΛM O M M M M ΛΛΛ00000021n b a a aa n ()()βγβγβγλ--•-+-=ΛMO M M Λ000021n ba n ()()[]()21n 2-----+=n ab n βγβλλγ.2.4 升阶法就是把n 阶行列式增加一行一列变成n+1阶行列式，再通过性质化简算出结果，这种计算行列式的方法叫做升阶法或加边法．升阶法的最大特点就是要找每行或每列相同的因子,那么升阶之后，就可以利用行列式的性质把绝大多数元素化为0，这样就达到简化计算的效果．其中，添加行与列的方式一般有五种：首行首列，首行末列，末行首列，末行末列以及一般行列的位置．例8 解行列式D=111110111110111110111110ΛΛM M O M M M ΛΛΛ. 解：使行列式D 变成1+n 阶行列式，即111010110110101110011111D ΛΛM M OM M M ΛΛΛ=. 再将第一行的()1-倍加到其他各行，得：D=1101001001010001111111--------ΛΛM M O M M M ΛΛΛ. 从第二列开始，每列乘以()1-加到第一列，得：10010000010000011111)1n D ------=ΛΛM M O M M M ΛΛΛ（ ()()1n 11n --=+.2.5数学归纳法有些行列式，可通过计算低阶行列式的值发现其规律，然后提出假设，再利用数学归纳法去证明．对于高阶行列式的证明问题，数学归纳法是常用的方法．例9 计算行列式βββββcos 211cos 200000cos 210001cos 210001cos ΛΛM M O M M M ΛΛΛ=n D . 解:用数学归纳法证明. 当1=n 时，βcos 1=D . 当2=n 时，ββββ2cos 1cos 2cos 211cos 22=-==D .猜想，βn D n cos =.由上可知，当1=n ，2=n 时，结论成立．假设当k n =时，结论成立．即：βk D k cos =.现证当1+=k n 时，结论也成立．当1+=k n 时，βββββcos 211cos 200000cos 210001cos 210001cos 1ΛΛM M O M M M ΛΛΛ=+k D .将1+k D 按最后一行展开，得()βββββcos 20000cos 21001cos 21001cos cos 21D 111k ΛM O M M M ΛΛΛ•-=++++k k()10cos 21001cos 21001cos 11ΛM O M M M ΛΛΛβββkk ++-+ 1cos 2--=k k D D β.因为βk D k cos =，()()βββββββsin sin cos cos cos 1cos 1k k k k D k +=-=-=-，所以1+k D 1cos 2--=k k D D βββββββsin sin cos cos cos cos 2k k k --= ββββsin sin cos cos k k -= ()β1cos +=k .这就证明了当1+=k n 时也成立，从而由数学归纳法可知，对一切的自然数，结论都成立． 即：βn D n cos =.2.6 递推法技巧分析：若n 阶行列式D 满足关系式021=++--n n n cD bD aD .则作特征方程02=++c bx ax .① 若0≠∆，则特征方程有两个不等根，则1211--+=n n n Bx Ax D ．② 若0=∆，则特征方程有重根21x x =，则()11-+=n n x nB A D ． 在①②中， A ，B 均为待定系数，可令2,1==n n 求出．例10 计算行列式94000005940000000594000005940000059D n ΛΛM M M O M M M M ΛΛΛ=.解：按第一列展开，得21209---=n n n D D D .即020921=+---n n n D D D ．作特征方程02092=+-x x .解得5,421==x x .则1154--•+•=n n n B A D .当1=n 时，B A +=9；当2=n 时，B A 5461+=. 解得25,16=-=B A ，所以1145++-=n n n D .3、行列式的几种特殊计算技巧和方法3.1 拆行（列）法3.1.1 概念及计算方法拆行（列）法（或称分裂行列式法），就是将所给的行列式拆成两个或若干个行列式之和，然后再求行列式的值．拆行（列）法有两种情况，一是行列式中有某行（列）是两项之和，可直接利用性质拆项；二是所给行列式中行（列）没有两项之和，这时需保持行列式之值不变，使其化为两项和． 3.1.2 例题解析例11 计算行列式nn n n a a a a a a a a --------=-1110000011000110001D 133221ΛΛM M O M M M ΛΛΛ.解：把第一列的元素看成两项的和进行拆列，得nn n n a a a a a a a a --+-+--+-+--=-110010000001100001010001D 133221ΛΛM M O M M M ΛΛΛ .1101000001100010000110001000001100011000113322113322nnn nn n a a a a a a a a a a a a a a a -------+-------=--ΛΛM MO M M M ΛΛΛΛΛM M O M M M ΛΛΛ上面第一个行列式的值为1，所以nnn n a a a a a a a ------=-11001000010011D 13321ΛΛM M O M MΛΛ 111--=n D a .这个式子在对于任何()2≥n n 都成立，因此有111--=n n D a D()()n n n a a a a a a D a a ΛΛΛ2112112211111---+++-==--=()∏∑==-+=ij j ii a 1n111.3.2 构造法3.2.1 概念及计算方法有些行列式通过直接求解比较麻烦，这时可同时构造一个容易求解的行列式，从而求出原行列式的值． 3.2.2 例题解析例12 求行列式n nn nn n n n nnn x x x x x x x x x x x x D ΛΛMM MM ΛΛΛ21222212222121111---=.解：虽然n D 不是范德蒙德行列式，但可以考虑构造1+n 阶的范德蒙德行列式来间接求出n D 的值． 构造1+n 阶的范德蒙德行列式，得()nn nn nn n n n n n n n n n n n x x x x x x x x x x x x x x x x x x x x x f ΛΛΛM M O M MΛΛΛ21111211222221222221211111--------=. 将()x f 按第1+n 列展开，得()n n n n n n n n x A x A x A A x f 1,111,1,21,1++-+++++++=Λ，其中，1-n x的系数为()()n n n n n n D D A -=-=+++11,1.又根据范德蒙德行列式的结果知()()()()()∏≤<≤----=ni j j in x xx x x x x x x f 121Λ.由上式可求得1-n x 的系数为()()∏≤<≤-+-ni j j in x xx x x 121Λ.故有()()∏≤<≤-+++=ni j j in n x xx x x D 121Λ.3.3 特征值法3.3.1 概念及计算方法设n λλλΛ，，21是n 级矩阵A 的全部特征值，则有公式 n A λλλΛ21=.故只要能求出矩阵A 的全部特征值，那么就可以计算出A 的行列式．3.3.2 例题解析例13 若n λλλΛ，，21是n 级矩阵A 的全部特征值，证明：A 可逆当且仅当它的特征值全不为零． 证明：因为n A λλλΛ21=，则A 可逆()n i i n ΛΛ2,1000A 21=≠⇔≠⇔≠⇔λλλλ.即A 可逆当且仅当它的特征值全不为零．4、几类特殊的行列式的巧妙计算技巧和方法4.1 三角形行列式4.1.1 概念形如nn n nn a a a a a a a a a a M OKK K 333223221131211，nnn n n a a a a a a a a a a ΛO M M M 321333231222111这样的行列式，形状像个三角形，故称为“三角形”行列式． 4.1.2 计算方法 由行列式的定义可知，nn nnn nn a a a a a a a a a a a a a K ΛM O M M M K K K 2211333223221131211000000=,nn nnn n n a a a a a a a a a a a a a K ΛM O M M M K K K 2211321333231222111000000=. 4.2 “爪”字型行列式4.2.1 概念形如nn na c a c a cb b b a OM Λ2211210，nnnc a c a c a a b b b M N Λ2211012，nnn b b b a a c a c a c ΛNM 2101122，121122a b b b c a c a c a nn nΛMO这样的行列式，形状像个“爪”字，故称它们为“爪”字型行列式． 4.2.2 计算方法利用对角线消去行列式中的“横线”或“竖线”，均可把行列式化成“三角形”行列式．此方法可归纳为：“爪”字对角消竖横． 4.2.3 例题解析例14 计算行列式na a a a 111111321OM Λ，其中.,2,1,0n i a i Λ=≠分析：这是一个典型的“爪”字型行列式，计算时可将行列式的第.),3,2(n i i Λ=列元素乘以ia 1-后都加到第一列上，原行列式可化为三角形行列式．解:na a a a 111111321OM Λ nni ia a a a a 00011113221OM Λ∑=-=⎪⎪⎭⎫⎝⎛-=∑=ni i n aa a a a 21321Λ. 4.3 “么”字型行列式4.3.1 概念形如n nn b b b a a c a c a c ΛNN 2101122，nn n a b c a b c a b c a OO2221110，n n nc a c a c a a b b b N N Λ2211012，0111222a c b a c b a c b a n n n OM O ，1021122c a c a b a b c a b nn n NN M ，n nna c a c a cb b b a O OΛ2211210，0121122a b b b c a c a c a nn nΛO O，nnn b a b c b a b a c a c 12211201NN 这样的行列式，形状像个“么”字，因此常称它们为“么”字型行列式． 4.3.2 计算方法利用“么”字的一个撇消去另一个撇，就可以把行列式化为三角形行列式．此方法可以归纳为：“么”字两撇相互消．注意：消第一撇的方向是沿着“么”的方向，从后向前，利用n a 消去n c ，然后再用1-n a 消去1-n c ，依次类推． 4.3.3 例题解析例15 计算1+n 阶行列式nn n b b b D 1111111111----=-+M NN M NN .解：从最后一行开始后一行加到前一行（即消去第一撇），得nnn ni ini in b b b bb D 11111111-+--+-=-==+∑∑MN MN()()()⎪⎭⎫ ⎝⎛+--•-=∑=+ni i nn n b 121111()()⎪⎭⎫ ⎝⎛+--=∑=+ni i n n b 12311.4.4 “两线”型行列式4.4.1 概念形如nnn a b b b a b a ΛΛM M M M MΛΛ00000000012211-这样的行列式叫做“两线型”行列式． 4.4.2 计算方法对于这样的行列式，可通过直接展开法求解． 4.4.3 例题解析例16 求行列式nn n n a b b b a b a ΛΛM M M M MΛΛ000000000D 12211-=. 解：按第一列展开，得()122111221100010000-+-+-+=n n n nn n b b a b b a b b a a D ΛM O M M ΛΛΛΛM O M M Λ()n n n b b b a a a ΛΛ211211+-+=.4.5 “三对角”型行列式4.5.1 概念形如ba ab b a ab b a abb a ab b a +++++10000000000100000100000ΛΛM M O M M M M M ΛΛΛ 这样的行列式，叫做“三对角型”行列式．4.5.2 计算方法对于这样的行列式，可直接展开得到两项递推关系式，然后变形进行两次递推或利用数学归纳法证明． 4.5.3 例题解析例17 求行列式ba ab b a ab b a abb a ab b a n +++++=10000000000000100000100000D ΛΛM M O M M M M M ΛΛΛ. 解：按第一列展开，得()ba ab b a b a ab b a abb a ab D b a n n +++++-+=-10000010000100000D 1ΛΛM M O M M M ΛΛΛ ()21---+=n n abD D b a .变形，得()211D ----=-n n n n aD D b aD .由于2221,b ab a D b a D ++=+=， 从而利用上述递推公式得()211D ----=-n n n n aD D b aD ()()n n n n b aD D b aD D b =-==-=---122322Λ.故()nn n n n n n n n n b ab b a D a b b aD a b aD D ++++==++=+=------12211121ΛΛn n n n b ab b a a ++++=--11Λ.4.6 Vandermonde 行列式4.6.1 概念形如113121122322213211111----n nn n n n n a a a a a a a a a a a a ΛM O M M M ΛΛΛ这样的行列式，成为n 级的范德蒙德行列式．4.6.2 计算方法通过数学归纳法证明，可得()∏≤<≤-----=11113121122322213211111i j j i n nn n n nn a a a a a a a a a a a a a a ΛM O M M M ΛΛΛ. 4.6.3 例题解析例18 求行列式n nn nn n n n nnn x x x x x x x x x x x x D ΛΛMM MM ΛΛΛ21222212222121111---=.解：虽然n D 不是范德蒙德行列式，但可以考虑构造1+n 阶的范德蒙德行列式来间接求出n D 的值． 构造1+n 阶的范德蒙德行列式，得()nn nn nn n n n n n n n n n n n x x x x x x x x x x x x x x x x x x x x x f ΛΛΛM M O M MΛΛΛ21111211222221222221211111--------=. 将()x f 按第1+n 列展开，得()n n n n n n n n x A x A x A A x f 1,111,1,21,1++-+++++++=Λ， 其中，1-n x 的系数为()()n n n n n n D D A -=-=+++11,1.又根据范德蒙德行列式的结果知()()()()()∏≤<≤----=ni j j in x xx x x x x x x f 121Λ.由上式可求得1-n x 的系数为()()∏≤<≤-+-ni j j in x xx x x 121Λ,故有()()∏≤<≤-+++=ni j j in n x xx x x D 121Λ.5、行列式的计算方法的综合运用有些行列式如果只使用一种计算方法不易计算，这时就需要结合多种计算方法，使计算简便易行．下面就列举几种行列式计算方法的综合应用．5.1 降阶法和递推法例19 计算行列式2100012000002100012100012D ΛΛM M O M M M ΛΛΛ=n . 分析：乍一看该行列式，并没有什么规律．但仔细观察便会发现，按第一行展开便可得到1-n 阶的形式．解：将行列式按第一行展开，得212D ---=n n n D D . 即211D ----=-n n n n D D D .∴12312211=-=-==-=----D D D D D D n n n n Λ. ∴()()111111---++++==+=n n n n D D D ΛΛ()121+=+-=n n .5.2 逐行相加减和套用范德蒙德行列式例20 计算行列式43423332232213124243232221214321sin sin sin sin sin sin sin sin sin sin sin sin sin sin sin sin sin 1sin 1sin 1sin 11111D ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ++++++++++++=解：从第一行开始，依次用上一行的()1-倍加到下一行，进行逐行相加，得43332313423222124321sin sin sin sin sin sin sin sin sin sin sin sin 1111ϕϕϕϕϕϕϕϕϕϕϕϕ=D .再由范德蒙德行列式，得()∏≤<≤-==4143332313423222124321sin sin sin sin sin sin sin sin sin sin sin sin sin sin 1111i j j i D ϕϕϕϕϕϕϕϕϕϕϕϕϕϕ.5.3 构造法和套用范德蒙德行列式例21 求行列式n nn nn n n n nnn x x x x x x x x x x x x D ΛΛMM MM ΛΛΛ21222212222121111---=.解：虽然n D 不是范德蒙德行列式，但可以考虑构造1+n 阶的范德蒙德行列式来间接求出n D 的值． 构造1+n 阶的范德蒙德行列式，得()nn nn nn n n n n n n n n n n n x x x x x x x x x x x x x x x x x x x x x f ΛΛΛM M O M MΛΛΛ21111211222221222221211111--------=.将()x f 按第1+n 列展开，得()n n n n n n n n x A x A x A A x f 1,111,1,21,1++-+++++++=Λ，其中，1-n x 的系数为()()n n n n n n D D A -=-=+++11,1.又根据范德蒙德行列式的结果知()()()()()∏≤<≤----=ni j j in x xx x x x x x x f 121Λ.由上式可求得1-n x 的系数为()()∏≤<≤-+-ni j j in x xx x x 121Λ.故有()()∏≤<≤-+++=ni j j in n x xx x x D 121Λ.。

1 行列式的概念及性质1.1 行列式的概念n 级行列式nnn n nn a a a a a a a a a212222111211等于所有取自不同行不同列的个元素的乘积n nj j j a a a 2121的代数和，这里的n j j j 21是1，2，…，n 的一个排列，每一项都按下列规则带有符号：当n j j j 21是偶排列时，带有正号；当n j j j 21是奇排列时，带有负号。

这一定义可写成，这里∑nj j j 21表示对所有n 级排列的求和。

1.2 行列式的性质[1]性质1 行列互换，行列式值不变，即=nn n n n na a a a a a a a a212222111211nnn n n n a a a a a a a a a 212221212111性质2 行列式中某一行（列）元素有公因子k ，则k 可以提到行列式记号之外，即=nnn n in i i na a a ka ka ka a a a212111211nnn n in i i na a a a a a a a a k 212111211 这就是说，一行的公因子可以提出去，或者说以一数乘以行列式的一行就相当于用这个nn nnj j j j j j r j j j nnn n nn a a a a a a a a a a a a 21212121)(212222111211)1(∑-=数乘以此行列式。

事实上，nnn n in i i n a a a ka ka ka a a a212111211=11i i A ka +22i i A ka +in in A ka + =21(i i A a k +22i i A a +)in in A a +nnn n in i i n a a a a a a a a a k212111211= ， 令k =0，如果行列式中任一行为零，那么行列式值为零。

性质3 如果行列式中某列（或行）中各元素均为两项之和，即),,2,1(n i c b a ij ij ij =+=，则这个行列式等于另两个行列式之和。

数学与统计学学院中期报告学院:专业:年级:题目:学生姓名: 学号:指导教师姓名职称:年月日目录1 引言 (1)2行列式性质 (2)3行列式计算方法 (6)3.1定义法 (6)3.2递推法 (9)3.3化三角法 (9)3.4拆元法 (11)3 .4加边法 (12)3.6数学归结法 (13)3.7降价法 (15)3.8利用普拉斯定理 (16)3.9利用范德蒙行列式参考文献....................................................................................................... 错误！未定义书签。

8行列式的概念及应用摘要：本文先列举行列式计算相关性质，然后归纳总结出行列式的方法，包括：定义法，化三角法，递推法，拆元法，加边法，数学归结法，降价法，利用拉普拉斯定理，利用范德蒙行列式。

关键词：行列式；线性方程组；范德蒙行列式The concept and application of determinant Summary:This article lists calculated properties of determinants, and then sum up the determinant method, including: Definition, triangulation, recursive method, remove method, bordered by, mathematical resolution method, cut method, using Laplace theorem, using the vandermonde determinant.Keywords: determinant;Linear equations;;Vandermonde determinant1 引言行列式的概念最初是伴随着方程组的求解而发展起来的。

行列式展开与应用例题和知识点总结一、行列式的定义对于一个\（n\）阶方阵\（A ＝（a_{ij}）＼），其行列式\（｜A|＼）定义为：＼｜A| ＝＼sum_{＼sigma\in S_n}（－1)＾｛＼tau(＼sigma)｝a_{1\sigma(1)｝a_{2\sigma(2)｝＼cdots a_{n\sigma(n)｝＼其中\（S_n\）是\（n\）个元素的全排列集合，＼（＼tau(＼sigma)＼）是排列\（＼sigma\）的逆序数。

对于二阶行列式，有\（＼begin{vmatrix}a_{11} ＆ a_{12} ＼＼a_{21} ＆ a_{22}＼end{vmatrix} ＝ a_{11}a_{22} a_{12}a_{21}＼）对于三阶行列式，有\（＼begin{vmatrix}a_{11} ＆ a_{12} ＆ a_{13} ＼＼ a_{21} ＆ a_{22} ＆ a_{23} ＼＼ a_{31} ＆ a_{32} ＆ a_{33}＼end{vmatrix} ＝ a_{11}a_{22}a_{33} ＋ a_{12}a_{23}a_{31} ＋a_{13}a_{21}a_{32} a_{13}a_{22}a_{31} a_{12}a_{21}a_{33}a_{11}a_{23}a_{32}＼）二、行列式的性质1、行列式与它的转置行列式相等。

2、对换行列式的两行（列），行列式变号。

3、行列式中某行（列）的公因子可以提到行列式外面。

4、若行列式中有两行（列）元素成比例，则行列式为零。

5、若行列式的某行（列）的元素都是两个数之和，则行列式可以拆分成两个行列式之和。

6、把行列式的某行（列）的倍数加到另一行（列），行列式不变。

三、行列式的展开1、按行展开设\（A ＝（a_{ij}）＼）是\（n\）阶方阵，＼（A_{ij}＼）是\（a_{ij}＼）的代数余子式，则\（｜A| ＝ a_{i1}A_{i1} ＋ a_{i2}A_{i2} ＋＼cdots ＋ a_{in}A_{in}＼）（＼（i\）为任意行）2、按列展开类似地，＼（｜A| ＝ a_{1j}A_{1j} ＋ a_{2j}A_{2j} ＋＼cdots ＋a_{nj}A_{nj}＼）（＼（j\）为任意列）四、应用例题例 1：计算行列式\（＼begin{vmatrix}2 ＆－1 ＆ 3 ＼＼ 1 ＆ 2 ＆ 0＼＼ 4 ＆ 1 ＆ 5\end{vmatrix}＼）解：按照三阶行列式的展开公式计算：＼＼begin{align}＆＼begin{vmatrix}2 ＆－1 ＆ 3 ＼＼ 1 ＆ 2 ＆ 0 ＼＼ 4 ＆ 1 ＆5\end{vmatrix}＼＼＝＆2\times\begin{vmatrix}2 ＆ 0 ＼＼ 1 ＆ 5\end{vmatrix} （－1)＼times\begin{vmatrix}1 ＆ 0 ＼＼ 4 ＆ 5\end{vmatrix} ＋3\times\begin{vmatrix}1 ＆ 2 ＼＼ 4 ＆ 1\end{vmatrix}＼＼＝＆2\times(2\times5 0\times1) ＋ 1\times(1\times5 0\times4) ＋3\times(1\times1 2\times4)＼＼＝＆2\times10 ＋ 5 ＋ 3\times(－7)＼＼＝＆20 ＋ 5 21\＼＝＆4＼end{align}＼例 2：已知\（＼begin{vmatrix}1 ＆ 2 ＆ 3 ＼＼ 2 ＆ 3 ＆ x ＼＼ 3 ＆x ＆ 1\end{vmatrix} ＝ 0\），求\（x\）的值。

计算行列式的方法总结计算行列式的方法总结行列式涉及的方面很多，例如判断矩阵可逆与否要计算行列式的值、解线性方程组、特征值等都与求行列式密不可分，所以各种类型解行列式的方法一定要掌握好，才能写好行列式，下面是计算行列式的方法总结，一起来看看吧！计算行列式的方法总结(一)首先，行列式的性质要熟练掌握性质1行列互换，行列式的值不变。

性质2交换行列式的两行(列)，行列式的值变号。

推论若行列式中有两行(列)的对应元素相同，则此行列式的值为零。

性质3若行列式的某一行(列)各元素都有公因子k，则k可提到行列式外。

推论1数k乘行列式，等于用数k乘该行列式的某一行(列)。

推论2若行列式有两行(列)元素对应成比例，则该行列式的值为零。

性质4若行列式中某行(列)的每一个元素均为两数之和，则这个行列式等于两个行列式的和，这两个行列式分别以这两组数作为该行(列)的元素，其余各行(列)与原行列式相同。

性质5将行列式某行(列)的k倍加到另一行(列)上，行列式的值不变。

行列式展开法：行列式按某行(列)展开也是解行列式常用的方法。

行列式展开定理：定理1：n阶行列式D等于它的任一行(列)的各元素与各自的代数余子式乘积之和。

定理2：行列式D的某一行(列)各元素与另一行(列)对应元素的代数余子式乘积之和必为零。

(二)几种特殊行列式的值有关行列式的若干个重要公式：为便于考生综合复习及掌握概念间的联系，现将以后各章所涉及的有关行列式的几个重要公式罗列于下：2017考研数学：行列式的计算行列式是线性代数的一部分，题目比较灵活，下面小编为同学们简单讲一下行列式的几种计算方法，希望同学们可以有所启发，弄清楚这种类型题。

对于数值型行列式来说，我们先看低阶行列式的计算，对于二阶或者三阶行列式其是有自己的计算公式的，我们可以直接计算。

三阶以上的行列式，一般可以运用行列式按行或者按列展开定理展开为低阶行列式再进行计算，对于较复杂的三阶行列式也可以考虑先进行展开。

2、用降价法计算行列式（常用） 直接应用按行(列)展开法则计算行列式, 运算量较大, 尤其是高阶行列式. 因此, 计算 行列式时，一般可先用行列式的性质将行列式中某一行(列)化为仅含有一个非零元素, 再按 此行(列)展开,化为低一阶的行列式, 如此继续下去直到化为三阶或二阶行列式. 3、拉普拉斯定理（一般少用）
2 1 0 2 0 1
1 （3） 1
5
10 1 0 0 （第一、二两行相等） 27
2 1 1 （4） 4 2 2 0 （第二、三列相等）
7 3 3
1 例 4（1） 0
2
1 1 2
2 5 0 因为第三行是第一行的 2 倍. 22
1 4 10
2 8 35
（2）
0 因为第一列与第二列成比例,即第二列是第一列的 4
2
.
1 2 3 0 1 3 2 0
注: 一般来说下式是不成立的
a11 b11 a21 b21
a12 b12 a11 a22 b22 a21
a12 b11 a22 b21
b12 . b22
1 3 1 1 3 1
例 9（1） 1 4 1r2 r1 0 1 0 ,上式表示第一行乘以-1 后加第二行上去, 其值
建议收藏下3 载6 1本2 1文2 ，4 以便随时学习！
2 3 0 32 3 0 ,
51 2 512
再计算
124 12 4
124 122 102
D 3 2 3 0 3 0 7 8 27 0 7 8 54 0 7 4 54 0 3 4 54 3 162.
5 1 2 0 9 18 0 1 2 0 1 1 0 0 1
称 Aij 为元素 aij 的代数余子式.
引理（常用） 一个 n 阶行列式 D , 若其中第 i 行所有元素除 aij 外都为零，则该行列式

a11
a12 a1n c2 cn .
b1 c1 b2 c2 bn cn b1 an1
性质 4
bn c1 an1
an 2

ann
an1
an 2 ann
an 2 ann
如果行列式中有两行（或列）对应元素相同或成比例，那
ai 2 ain a k1 =ak 2 akn a i1 an 2 ann a n1
a11 0 a n1 a12 a1,n -1 0 0 a n2 a n,n -1
a k 2 a kn a in a nn
于出现很多的零，所以不等于零的项数就大大减少．具体的说，展开 式中的项的一般形式是 a1 j1 a 2 j2 a 3 j3 a 4 j4 ． 显然， 如果 j1 4 ， 那么 a1 j1 0 ，
4
从而这个项就等于零．因此只须考虑 j1 4 的项，同理只须考虑
j 2 3, j 3 2, j 4 1 的这些项，这就是说，行列式中不为零的项只有 a14 a 23 a 32 a 41 ，而 4321 6 ，所以此项取正号．故 0 0 0 4 0 0 3 0 0 2 0 0 1 0 4321 a14 a 23 a32 a 41 24 . = 1 0 0
x1 m x2 x1 x2 m 例 3 计算行列式 Dn x1 x2
xn xn . xn m
x
解： D n
n
x
i 1 n
i 1 n
i
m
x2

xn xn
i
m x2 m m x2

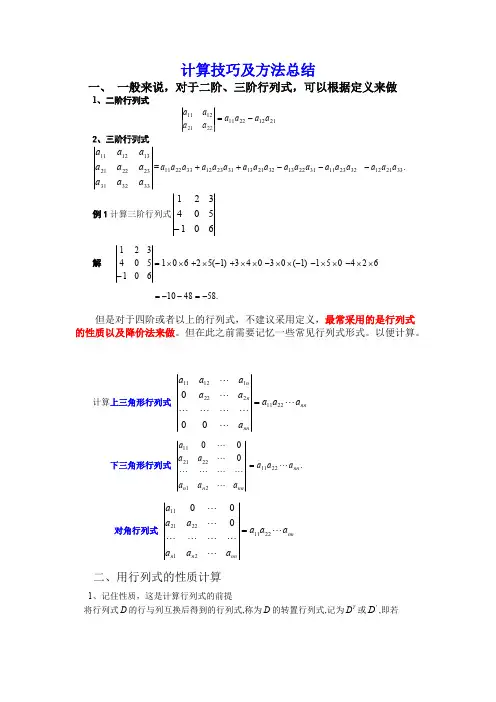
行列式的计算技巧与方法总结行列式是线性代数中的重要概念，广泛应用于各个领域，如线性方程组的求解、线性变换的判断等。

在实际应用中，计算行列式是一个必不可少的环节。

本文将对行列式的计算技巧和方法进行总结，以便读者能够更加轻松地解决行列式相关问题。

一、行列式的定义行列式是一个数。

行列式的定义通常有多种不同的形式，其中最常见的是按照矩阵的形式定义的。

对于一个n阶方阵A=(a_ij)，其行列式记作det(A)，可以通过以下方式计算：det(A) = a_11 * C_11 + a_12 * C_12 + ... + (-1)^(n+1) * a_1n * C_1n其中，C_ij是指元素a_ij的代数余子式。

二、行列式的计算方法1.二阶行列式的计算对于2阶方阵A=(a_11,a_12;a_21,a_22)，其行列式可以直接通过以下公式计算：det(A) = a_11 * a_22 - a_12 * a_212.三阶行列式的计算对于3阶方阵A=(a_11,a_12,a_13;a_21,a_22,a_23;a_31,a_32,a_33)，可以通过Sarrus法则来计算行列式：det(A) = a_11*a_22*a_33 + a_12*a_23*a_31 + a_13*a_21*a_32 -a_13*a_22*a_31 - a_12*a_21*a_33 - a_11*a_23*a_323.高阶行列式的计算对于n(n>3)阶方阵A，一般采用高斯消元法将矩阵转化为上三角矩阵，然后再计算行列式的值。

具体操作如下：a)对第一列进行第二行、第三行、..、第n行的倍加，使得第一列除了第一个元素外的其他元素都为0。

b)接着在第二列中对第三行、第四行、..、第n行的倍加，使得第二列除了第二个元素外的其他元素都为0。

c)重复以上步骤，直到将矩阵转化为上三角矩阵。

d)上三角矩阵的行列式等于主对角线上的元素相乘。

4.行列式的性质行列式具有以下性质，可以在计算中灵活运用：a)行互换或列互换，行列式的值不变，其符号变为相反数。

行列式的计算方法总结行列式是矩阵的一个重要的数值性质，它将一个矩阵映射为一个数。

行列式的计算方法有多种，包括按定义展开、按行（列）展开、按特定行（列）展开、按相似行变化展开、按行列变换展开等等。

下面将总结行列式的计算方法。

1. 按定义展开法：行列式的定义是通过求和的形式给出的，具体计算步骤如下：a. 对于1×1的矩阵，直接返回矩阵元素的值。

b. 对于n×n的矩阵A，选择第一行或第一列，如第一行，则有det(A) = a_{11} * det(A_{11}) - a_{12} * det(A_{12}) + ... + (-1)^(1+n) * a_{1n} * det(A_{1n})，其中A_{ij}表示删去第i行第j列后的（n-1）×（n-1）的矩阵。

c. 迭代调用行列式计算函数，直到矩阵规模变为1×1，然后返回最终的计算结果。

2. 按行（列）展开法：选择任意一行（列），对于这一行（列）的每个元素aij，计算aij*（-1）^(i+j)*Det(Aij)，其中Det(Aij)表示矩阵A删去第i行第j列后的（n-1）×（n-1）的矩阵的行列式。

将所有结果相加即可获得行列式的值。

3. 按特定行（列）展开法：对于任意一行（列）i，选择元素a_{ik}，其中k≤n。

根据特定行（列）展开的性质，行列式的值可以表示为det(A) =a_{ik} * C_{ik}，其中C_{ik}表示A中删去第i行第k列后的（n-1）×（n-1）的矩阵的行列式。

简而言之，即选取矩阵中的某个元素，用这个元素乘以它的代数余子式（或称余子式）再相加。

4. 按相似行变化展开法：相似行是指行向量的倍数，对于具有相似行的矩阵A，其行列式的值为零。

因此，可以选择特定的行对矩阵进行行变换，使得相似行变成0，从而简化计算。

这需要根据具体的矩阵进行分析，选择合适的行变换方式。

5. 按行列变换展开法：行列变换可以通过交换两行（列）或某行（列）乘以一个非零数加到另外一行（列）上进行。

关于矩阵行列式的不等式的开题报告矩阵行列式是线性代数中一个非常重要的概念，它可以用来判断矩阵是否可逆、计算矩阵的逆、确定矩阵的特征值等等。

矩阵行列式的性质不但在理论上有很多深刻的结论，而且在实际中也有着广泛的应用。

其中，对于行列式的不等式研究，一直以来都是线性代数研究的热点。

本文将探讨矩阵行列式的不等式问题，主要分为以下几个方面：一、矩阵行列式的定义及性质在矩阵行列式的定义中，我们需要了解行列式的概念、计算方法以及推导过程。

同时，在矩阵行列式的性质中，我们还将涉及到行列式和矩阵的关系、行列式的运算性质、行列式的性质等方面的内容。

这部分内容是后续内容的基础。

二、行列式的不等式行列式的不等式问题包括有以下几种类型：1、Sylvester不等式。

Sylvester不等式是矩阵行列式不等式研究的基础，它是矩阵行列式的下界。

在研究Sylvester不等式时，需要包括矩阵的元素是实数、矩阵的元素是非负实数、矩阵的元素是正实数等不同情况的讨论。

2、矩阵行列式的上界。

在矩阵行列式上界的研究中，我们需要讨论矩阵的元素是实数、矩阵的元素是非负实数和矩阵的元素是正实数等不同情况。

在计算矩阵行列式上界时，我们可以使用行列式的性质，或者采用各种类型的变换来实现。

3、绝对值不等式。

在绝对值不等式的研究中，我们需要探讨矩阵元素的绝对值是否影响行列式上限的大小。

本部分将讨论使用绝对值不等式求矩阵行列式上界的具体方法。

4、其他不等式问题。

本部分将包括多元不等式问题、矩阵估计问题等其他不等式问题的研究。

三、行列式不等式的应用在行列式不等式的应用研究中，我们将探讨矩阵行列式在其他数学领域和实际问题中的具体应用。

例如，矩阵行列式在微积分中的应用、在概率统计中的应用、在物理中的应用等等。

同时，我们也将讨论矩阵行列式在生活和工作中的应用实例。

总的来说，在矩阵行列式不等式的研究中，我们将会去发掘不同情况下的规律和方法，并且对不同情况下的矩阵行列式进行实际应用，希望从中发现更多的矩阵行列式不等式的性质和应用。

线性代数行列式的计算与性质行列式在数学中，是一个函数，其定义域为的矩阵，取值为一个标量，写作或。

行列式可以看做是有向面积或体积的概念在一般的欧几里得空间中的推广。

或者说，在维欧几里得空间中，行列式描述的是一个线性变换对“体积”所造成的影响。

无论是在线性代数、多项式理论，还是在微积分学中（比如说换元积分法中），行列式作为基本的数学工具，都有着重要的应用。

行列式概念最早出现在解线性方程组的过程中。

十七世纪晚期，关孝和与莱布尼茨的著作中已经使用行列式来确定线性方程组解的个数以及形式。

十八世纪开始，行列式开始作为独立的数学概念被研究。

十九世纪以后，行列式理论进一步得到发展和完善.矩阵概念的引入使得更多有关行列式的性质被发现,行列式在许多领域都逐渐显现出重要的意义和作用,出现了线性自同态和矢量组的行列式的定义。

行列式的特性可以被概括为一个多次交替线性形式，这个本质使得行列式在欧几里德空间中可以成为描述“体积”的函数.矩阵A 的行列式有时也记作｜A|。

绝对值和矩阵范数也使用这个记法,有可能和行列式的记法混淆。

不过矩阵范数通常以双垂直线来表示(如：)，且可以使用下标。

此外，矩阵的绝对值是没有定义的。

因此，行列式经常使用垂直线记法（例如：克莱姆法则和子式).例如，一个矩阵:A=⎪⎪⎪⎭⎫⎝⎛ihgfedcba，行列式也写作，或明确的写作：A=ihgfedcba，即把矩阵的方括号以细长的垂直线取代行列式的概念最初是伴随着方程组的求解而发展起来的。

行列式的提出可以追溯到十七世纪，最初的雏形由日本数学家关孝和与德国数学家戈特弗里德·莱布尼茨各自独立得出，时间大致相同.一、行列式的定义与计算一个n 阶方块矩阵 A 的行列式可直观地定义如下：其中，是集合{ 1, 2, 。

.，n ｝上置换的全体，即集合｛ 1, 2， ...，n }到自身上的一一映射（双射）的全体;表示对全部元素的求和,即对于每个，在加法算式中出现一次;对于每一对满足的数对，是矩阵 A 的第i 行第j 列的元素。

行列式的若干计算技巧与方法目　录，()()βββββββsin sin cos cos cos 1cos 1k k k k D k +=-=-=-所以1+k D 1cos 2--=k k D D βββββββsin sin cos cos cos cos 2k k k --=ββββsin sin cos cos k k -=.()β1cos +=k 这就证明了当时也成立，从而由数学归纳法可知，1+=k n 对一切的自然数，结论都成立．即：.βn D n cos =2.6 递推法技巧分析：若阶行列式满足关系式n D .021=++--n n n cD bD aD 则作特征方程.02=++c bx ax ①若，则特征方程有两个不等根，则0≠∆．1211--+=n n n Bx Ax D ②若，则特征方程有重根，则0=∆21x x =解得，25,16=-=B A 所以.1145++-=n n n D 3、行列式的几种特殊计算技巧和方法3.1 拆行（列）法3.1.1 概念及计算方法拆行（列）法（或称分裂行列式法），就是将所给的行列式拆成两个或若干个行列式之和，然后再求行列式的值．拆行（列）法有两种情况，一是行列式中有某行（列）是两项之和，可直接利用性质拆项；二是所给行列式中行（列）没有两项之和，这时需保持行列式之值不变，使其化为两项和．3.1.2 例题解析例11 计算行列式小结本文主要介绍了行列式计算的一些技巧和方法，还有一些特殊行列式的计算技巧，通过归纳和总结这些技巧和方法，让读者在计算行列式时游刃有余．然而在这么多方法面前，我们需要多观察、多思考，这样便于我们更加轻松地解决有关行列式的问题，也让我们更加灵活的运用这些方法和技巧来解决实际问题．参考文献:[1]北大数学系代数小组. 高等代数（第三版）[M].北京：高等教育出版社，2003：50～104.[2]钱吉林. 高等代数题解精粹[M].北京：中央民族大学出版社，2002：24～58[3]刘家保，陈中华，陆一南.若干类型行列式计算方法.佛山科学技术学院学报（自然科学版），2012年3月，30(2).[4]杨鹏辉.行列式的计算技巧.宜春学院报，2011年4月，33（4）.[5]丁冰.三线型行列式的计算.科技通报,2012年2月,28(2).[6]龚德仁.高阶行列式计算的若干技巧.课外阅读（中下）.2012年03期.[7]张新功.行列式的计算方法探讨.重庆师范大学学报（自然科学版），2011年7月,28(4).[8]王爱霞.关于n阶行列式的计算方法与技巧的探讨.佳木斯教育学院学报.2012年第1期.[9] 樊正华，徐新萍.浅谈行列式的计算方法.江苏教育学院学报（自然科学），2011年2月，27(1).[10]卢潮辉.三对角行列式的计算. 漯河职业技术学院学报,2010年3月,9(2).[11] 陈林.求n阶行列式的几种方法和技巧. 科技信息报，2007年第8期.[12]“爪”字型和“么”字型行列式的计算.河北理科教学研究(短文集锦),2006年第4期.学习体会与建议：计算行列式的最重要的一点就是化繁就简。

在计算对角行列式时，需要注意保持运算 的正确性，避免因元素位置错位导致计算 错误。
计算公式
对角行列式的计算公式为 $Delta = prod_{i=1}^{n} a_{ii}$，其中 $a_{ii}$ 表 示第 $i$ 行第 $i$ 列的元素。
04
行列式计算在矩阵中的应 用
行列式与矩阵的逆
总结词
上三角行列式的计算公式为 $Delta = sum_{i=1}^{n} (1)^{i+j} a_{ij} prod_{k=1}^{i1} a_{ik}$，其中 $a_{ij}$ 表示 第 $i$ 行第 $j$ 列的元素。
在计算上三角行列式时，需要 注意保持运算的正确性，避免 因元素位置错位导致计算错误 。
矩阵的秩是其行或列向量中线性无关向量的个数，而零行列式的矩阵必然有零秩 。因此，通过计算行列式值，可以确定矩阵秩的性质。
行列式与线性方程组
总结词
行列式在解线性方程组中起到关键作 用，通过行列式的性质可以简化方程 组的求解过程。
详细描述
对于线性方程组，如果系数矩阵的行 列式不为零，则该方程组有唯一解。 此外，行列式的性质如代数余子式等 在方程组的求解过程中也具有重要应 用。
代数余子式是由去掉一个元素后得到的$(n-1)$阶行列 式乘以一个系数$(n-1)$得到的。这种方法在实际应用 中较为常用，特别是在行列式中有很多零元素的情况。
展开法Βιβλιοθήκη 展开法是一种基于行列式展开定理的计算行列式值的方 法。具体来说，对于一个$n$阶行列式$|begin{matrix} a_{11} & a_{12} & cdots & a_{1n} a_{21} & a_{22} & cdots & a_{2n} vdots & vdots & ddots & vdots a_{n1} & a_{n2} & cdots & a_{nn} end{matrix}|$，其 值等于按照某一行或某一列展开后的代数和。

行列式的计算方法总结行列式的计算方法有哪些呢?可能大部分同学并不知道。

为了普及知识。

下面是由小编为大家整理的“行列式的计算方法总结”，仅供参考，欢迎大家阅读。

行列式的计算方法总结第一、行列式的计算利用的是行列式的性质，而行列式的本质是一个数字，所以行列式的变化都是建立在已有性质的基础上的等量变化，改变的是行列式的“外观”。

第二、行列式的计算的一个基本思路就是通过行列式的性质把一个普通的行列式变化成为一个我们可以口算的行列式(比如，上三角，下三角，对角型，反对角，两行成比例等)第三、行列式的计算最重要的两个性质：(1)对换行列式中两行(列)位置，行列式反号(2)把行列式的某一行(列)的倍数加到另一行(列)，行列式不变对于(1)主要注意：每一次交换都会出一个负号;换行(列)的主要目的就是调整0的位置，例如下题，只要调整一下第一行的位置，就能变成下三角。

拓展阅读：行列式的性质有哪些?行列式与它的转置行列式相等;互换行列式的两行(列)，行列式变号;行列式的某一行(列)的所有的元素都乘以同一数k，等于用数k乘此行列式;行列式如果有两行(列)元素成比例，则此行列式等于零;若行列式的某一列(行)的元素都是两数之和，则这个行列式是对应两个行列式的和;把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去，行列式不变。

n阶行列式实质上是一个n^2元的函数，当把n^2个元素都代上常数时，自然得到一个数。

当我们写的时候，写成一个表是为了方便的反映函数的物性。

当然，决不是指任何n^2元函数都是行列式，具体的行列式函数定义你找书一看看。

为了让你自己觉得好理解一些，你可以试着照行列式的定义把行列式写成多项式和的常见形式，当然那个形式比较复杂，但本质上与行列式是一样的，只是写成行列式易于直观的做各种运算处理。