数

名词解释数的形成数的形成是人类文明发展过程中的一个重要标志。

数的形成源于人们对于事物数量的认知和表达的需求。

在人类社会的起初阶段，人们面对的是简单的实际事物，如动物的数量、土地的面积等，他们通过有限的观察和经验总结出一些用来表示数量的符号。

随着时间的推移和文明的进步，随之而来的是对更复杂事物数量的认知和表示需求的加深，从而推动了数的形成过程。

数的形成是基于人类的感知和认知能力。

人类天生具有数的观念，它体现了人类对世界的一种基本了解和秩序感。

通过数的形成，人类可以更加准确地描述和表达事物的数量。

例如，在狩猎社会时代，人类会使用手指、竹签等来表示动物的数量；而在农耕社会时代，人们则开始使用计算工具如算筹、算盘等来进行更复杂的计算。

数的形成也受到语言、文化和社会环境等因素的影响。

不同语言和文化对于数的表达方式可能存在差异。

数的形成不仅仅是简单的数量表示，还包含了文化、习俗、信仰等因素的渗透。

例如，在中国文化中，数字七常被视为吉利的数字，代表着好运；而在西方文化中，数字13则被视为不吉利的数字，常被视为不祥之兆。

数的形成是一项长期而演进的过程。

在人类社会发展的过程中，数的形成不断被改进和发展。

从最早的简单记号到后来的数字符号系统、算术运算法则，人们通过对数的研究和应用不断提高了对数的认知和运用能力。

数的形成也推动了其他领域的发展，如物理学、经济学等。

数的形成对人类社会的进步和发展起到了重要的推动作用。

数的形成不仅仅是对数量的表达，更是对世界的认知和理解。

通过数的形成，人们可以更好地把握事物的本质和规律，从而更加高效地利用和管理资源，推动社会的发展与进步。

总之，数的形成是人类文明进程中的一个重要组成部分。

它源于人们对于数量的认知和表达需求，基于人类的感知和认知能力，在语言、文化和社会环境等因素的影响下不断演进发展。

数的形成不仅仅是对数量的表达，更是对世界的认知和理解。

通过数的形成，人类可以更好地描述和把握事物的本质和规律，推动社会的进步和发展。

算一个数的技巧和方法
算一个数的技巧和方法有很多种，下面列举一些常用的方法：
1.分解质因数法：将一个数分解成几个质数的乘积，可以帮助我们快速计算一个数的因数和约数。

2.近似估算法：使用近似值或者舍入法来快速估算一个数的大小，可以用于大数的计算或者解决实际问题中的快速估算。

3.位运算：对于二进制数，可以使用位运算（如按位与、按位或、按位异或）来对数字进行快速计算，适用于计算机领域。

4.凑整法：对于带有小数的数，可以利用凑整法将小数部分舍入或者进位，快速得到一个近似的整数结果。

5.倍数法：对于某些特殊规律的数字，可以使用倍数法来找到特定的倍数或者判断是否为某数的倍数。

6.平均分配法：对于一些需要平均分配的问题，可以使用平均分配法来计算每个部分的数量或者大小。

以上只是一些常见的方法和技巧，具体选择哪种方法取决于具体的情况和需要解
决的问题。

在实际问题中，还可以根据问题的特点和要求，结合不同的方法和技巧来解决。

数与数量的关系在我们日常生活中，数和数量是密不可分的。

数是用来表示事物的个数或大小的抽象概念，而数量则是指具体的事物个数或大小。

数与数量之间的关系既有相互依存，又有相互制约。

首先，数是数量的基础。

数是人类为了对事物进行计数而发明的一种抽象概念。

通过数的概念，我们可以对事物的个数进行精确描述和记录。

例如，我们可以说一个篮球队有12名队员，一本书有200页等等。

这些数的概念帮助我们理解和把握事物的数量，从而更好地进行分析和决策。

然而，数量也反过来影响着数的概念。

在现实世界中，事物的数量是有限的，而数的概念则是无限的。

这就意味着，数的概念可以帮助我们超越现实世界的限制，进行更广阔的思考。

例如，我们可以想象一个无限大的数列，或者思考无限小的数值。

这种抽象思维的能力，使得我们能够进行更深入的数学研究和探索。

另外，数和数量之间还存在着相互制约的关系。

数的概念是抽象的，而数量则是具体的。

当我们用数来描述和记录事物的数量时，我们必须考虑到数的概念是否能够准确地反映事物的实际情况。

例如，当我们说一只猫有四条腿时，我们假设猫的数量是一个整数，并且每只猫都有四条腿。

然而，在现实世界中，可能存在着一些特殊情况，比如有些猫只有三条腿或者五条腿。

这就是数与数量之间的差异，数的概念往往只是对数量的一种近似描述。

此外，数和数量之间还存在着一种相互转化的关系。

数可以通过计算和运算的方式来转化为数量，而数量也可以通过测量和统计的方式来转化为数。

例如，我们可以通过计算一个篮球队的总得分来得到一个具体的数值，或者通过测量一本书的厚度来得到一个具体的数值。

这种数与数量之间的转化，使得我们能够更准确地理解和描述事物的特征和变化。

综上所述，数与数量之间存在着密切的关系。

数是数量的基础，通过数的概念我们可以对事物的个数进行精确描述和记录。

同时，数量也反过来影响着数的概念，使得我们能够进行更广阔的思考和探索。

数和数量之间还存在着相互制约和相互转化的关系，使得我们能够更准确地理解和描述事物的特征和变化。

数组词_数的组词_数字组词数组词_数的组词“数”字在开头的词语数黄道黑数贫嘴数九天数喇数点数墨数课数九数叨数落数不着数得着数数数得上数算数罟数往知来数码港数码数目可观数秒数念数礼忘文数日恶数次数黄道白数奇不遇数量积数蚂蚁数番数相数駡数伤数欠数息数粒数武数策数奇数罪数命数词数列数表数额数位数目数珠数量数棊数米量柴数杂数码相机数术数米而炊数责数学期望数学数字通信数字信号数字相机数字电视数字化数目字数字数四数码囚禁数字模型数理模型数字系统数组数纪数量级数学混沌数摞数控数据数米而饮数据容量数番家数家数来宝数骂数驳数器数奇命蹇数据成员数度数据库管理系统数据库数控刨床数罪并罚数砖头数墨寻行数道数理逻辑数迹数巡数蓍数字菠菜数黄瓜，道茄子数学课数说数字电话数量词数白论黄数黑论黄数短论长数黑论白数论数让数计数参数十载数值数据修改数位汇流数伏数字传播数理化数以百计数以千计数据冗余数内数阵数量优先数字音频光盘数字视频光盘数字控制数制数码印刷数据缩减数祖忘典数典忘祖数典数世同堂数东瓜，道茄子数学作业数奇不偶数见不鲜数不胜数数不上数不清数以万计数一数二数九寒天数九天寒数九隆冬数据中心数中“数”字在结尾的词语齿数数数上岁数频数项数补数罪数多不胜数无理数气数最小公倍数膨胀系数金谷酒数十进对数三角函数常用对数舾装数衔窭数已知数有理数顷数重数极数推数查数月数星数訾数枚数言数情数目数够数徽数衍数等数加数夏数易数页数睇数篇数至数民数率数窭数景数淹数絓数凡数意数擢数谲数朔数畡数幻数本数年数盐数票数满数奸数慧数画数确数足数默数暗数荐数积数恩数朒数趸数策数辩数智数繁数道数期数百数诵数趣数盾数量数抛数面数支数趋数生数顺数盈数器数象数起数金数方数蹇数酌数抄数僻数禄数称数审数书数理数豫数禅数悉数额数真数着数余数算数正数心数素数系数整数成数奇数定数顶数零数有数路数虚数实数总数凑数小数答数解数礼数次数教数收数概数械数拉梅系数样数校数条数权数机数未知数算术平均数术数木数见数烦数灾数火数料数殊数死数辈数轨数车量斗数照数自然数点数比转数比数赢数质数责数负数字数理查孙数复数备数离数恤数恒数弹性系数恩格尔系数少数多数质因数因数回数自由基数基数垫片系数放坡系数在数地数缪数缕数编数给数组数线数细数经数约数等差级数等比级数音级数级数以数结尾的组词较多，已为您省略部分组词“数”字在中间的词语倒数方程一目数行高数脸乘数效应皮数杆有效数字少数民族小数点多言数穷少数派系数法地理数据接收数据指数期寥寥数笔寥寥数几如数家珍罗马数字啜茗数碗命舛数奇负数演员吹毛数睫后缀数组正数集合口数粥气数已尽廖廖数笔地理数据库石庆数马寥寥数年飞将数奇悉数奉还如数奉还天文数字寻行数墨循行数墨变数器寻宫数调读数语句寥寥数语杂数诗可数名词论黄数黑论黄数白讳树数马电子数字计算机程序计数器烛照数计计数器计数管参数规划分数值辄作数日恶代数学基本定理代数方程代数和代数学代数式参数优化余数定理个人数字助理救数人函数指针函数论劫数难逃身兼数职内部数组阿拉伯数字五格数理出数儿色数儿辈数儿水数制大数法则等差数列等比数列凿龟数筴凿龟数策分数线象数理占卜数只偶卜数师少数决具体数值象数义理简丝数米射幸数跌，不如审发为数不多江山如此多娇引无数英雄尽折腰江山如此多娇引无数英雄竞折腰无穷递缩等比数列无用数据泣数行下一日纵敌，数世之患称薪而爨，数粒乃炊。

数的读法和写法数的读法和写法是数学中最基础的知识点之一，对于中小学生来说，掌握数的读法和写法对于日后的数学学习具有重要的意义。

一、数的读法1.阿拉伯数字的读法：0读作“零”，1读作“一”，2读作“二”，3读作“三”，4读作“四”，5读作“五”，6读作“六”，7读作“七”，8读作“八”，9读作“九”。

2.多位数的读法：从高位到低位，一级一级地读，每一级末尾的0不读出来，其他数位连续几个0都只读一个零。

3.小数的读法：整数部分按照整数的读法来读，小数点读作“点”，小数部分顺次读出每一个数位上的数字。

二、数的写法1.阿拉伯数字的写法：按照数的读法，从高位到低位，一级一级地写，哪一个数位上一个单位也没有，就在那个数位上写0。

2.多位数的写法：每一位上的数字根据数的读法来写，哪一个数位上一个单位也没有，就在那个数位上写0。

3.小数的写法：整数部分按照整数的写法来写，小数点写在个位的右下角，小数部分顺次写出每一个数位上的数字。

4.零的读法和写法：零读作“零”，写作0。

5.负数的读法和写法：负数读作“负几”，写作-几，例如-3读作“负三”，写作-3。

6.分数的读法和写法：分数的读法是“分子分母”，分子读作“几”，分母读作“分之几”，例如2/3读作“二分之三”；分数的写法是先写分数线，再写分母，最后写分子，例如2/3写作“二分之三”。

以上就是数的读法和写法的相关知识点，希望对你有所帮助。

习题及方法：1.读法习题：请读出以下数字的正确读法。

答案：一千零二十三的读法是“一千零二十三”。

解题思路：从高位到低位读，每一级末尾的0不读出来，其他数位连续几个0都只读一个零。

2.写法习题：请写出以下数字的正确写法。

答案：三千零六的写法是“3006”。

解题思路：每一位上的数字根据数的读法来写，哪一个数位上一个单位也没有，就在那个数位上写0。

3.小数的读法习题：请读出以下小数的正确读法。

答案：12.34的读法是“十二点三四”。

解题思路：整数部分按照整数的读法来读，小数点读作“点”，小数部分顺次读出每一个数位上的数字。

数组词导读：组词大全数组词发音：数1、[shù] 2、[shǔ]如数家珍、屈指可数、数罪并罚、不可胜数、术数、擢发难数、浑身解数、数学、心中有数、滥竽充数、数一数二、异数、计数、素数、共轭复数、天数、代数、虚数、数落、人数、中数、复种指数、权数、数值、奇数、参数、等差数列、级数、倍数、数数、因数、整数、度数、基数、悉数、分数、质数、易数、除数、指数、算数、膨胀系数、余数定理、约数、数不胜数【组词解释与造句】数学[shù xué]：研究现实世界的空间形式和数量关系的科学。

包括算术、代数、几何、三角、微积分等。

【造句】数学像无穷能量的恒星，像美丽难忘的星河，像浩瀚无边的宇宙，陪我津津有味地翱翔在知识的世界里……倍数[bèi shù]：一数能被另一数整除时，此数即为另一数的倍数。

【造句】小明考试得分是我考试得分的倍数。

浑身解数[hún shēn xiè shù]：浑身：全身，指所有的；解数：那套数，指武艺。

所有的本领，全部的权术手腕。

【造句】只要你使出了浑身解数就算是输了哪也无所谓。

心中有数[xīn zhōng yǒu shù]：对情况和问题有基本的了解，处理事情有一定把握。

【造句】做什么事情都要先做到心中有数，不能鲁莽行事。

滥竽充数[làn yú chōng shù]：滥：失实的，假的。

不会吹竽的人混在吹竽的队伍里充数。

比喻无本领的冒充有本领，次货冒充好货。

【造句】知之为知之，不知为不知，你可千万不要不懂装懂、滥竽充数啊。

数落[shǔ luò]：列举过失加以指责。

泛指责备，和批评的意思相近。

【造句】老师老是数落我，我感到很自卑。

数一数二[shǔ yī shǔèr]：不算第一也算第二。

形容突出。

【造句】他的学习成绩在班里是数一数二的。

数不胜数[shǔ bù shèng shǔ]：数：计算。

数与数量小学数学基础概念解析数学是一门研究数量、结构、变化以及空间等概念的科学。

在学习数学的过程中，我们要先从最基础的数与数量开始探索。

本文将对小学数学中数与数量的概念进行解析，帮助读者加深对这些重要概念的理解。

一、数与数量的区别在日常生活中，我们经常会用到“数”和“数量”这两个词，它们似乎有些相似，但实际上在数学中有着不同的含义。

首先，数是数学的基础，它是用来表示事物的概念，如1、2、3等，表示了事物的个数。

数可以进行计算、运算，可以比较大小，如3大于2，这些是数的特性。

而数量则是指事物的多少，数和数量有着密切的关系。

数量是用数来表示的，它依赖于数的概念，它描述的是事物的多少，如有3个苹果。

总的来说，数是用来表示个别的事物的个数，而数量则是用数来表示大体上的事物的多少。

二、数与数量的关系数与数量是紧密相关的概念。

数是用来表示事物的个数的，而事物的个数就是数量。

在数学中，我们可以利用数来计算、比较和描述事物的数量。

比如，小明有2个苹果，小红有3个苹果，那么总的苹果数量就是2个加上3个，即5个苹果。

另外，数还可以用来表示无穷大和无穷小的概念，如数轴上的正负无穷。

总的来说，数是用来表示个数的，而数量则是用数来表示的。

三、数与数量的应用数与数量的应用非常广泛，在日常生活和学习中都能见到它们的身影。

首先，数与数量在计数和计量方面有着重要作用。

例如，在购物时我们要计算物品的价格和数量，使用数的概念可以帮助我们进行计算。

其次，数与数量也在比较和排序方面有着应用。

我们可以通过比较数的大小来判断事物的多少和大小关系。

此外，数与数量在数学问题的解决中也发挥着重要的作用。

在解决实际问题时，我们需要用到数与数量的概念，例如计算面积、体积等。

总之，数与数量是数学的基础，也是应用广泛的概念，在日常生活和学习中都起着重要的作用。

四、小学数学学习中的数与数量在小学数学学习中，数与数量是最基础的概念之一，学生们需要通过掌握这些概念来建立数学思维和解决数学问题的能力。

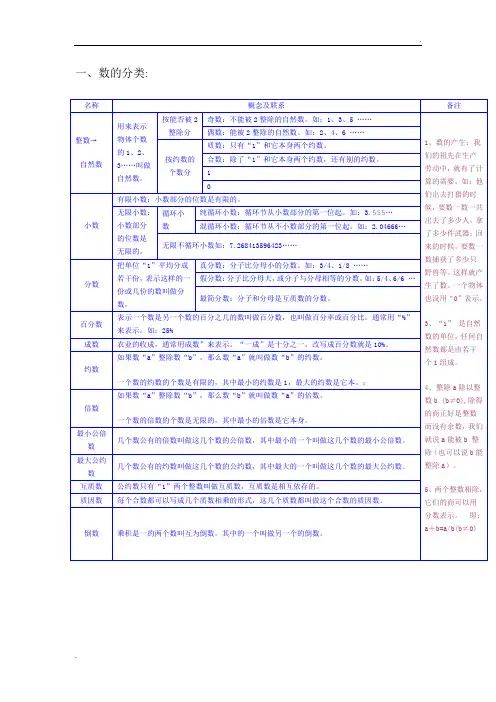
一、数的分类:2、整数和小数数位顺序表3、数的读写4、数的改写1、整数改写成用"万"或"亿"作单位的数：把一个较大的多位数，改写成用"万"（或"亿"）作单位的数，只要在"万"位或（"亿"位）的右下角点上小数点，再在这个数的末尾添上"万"字（或"亿"字）。

2、小数改写成分数：先改写成分母是10，100，1000的分数，再约分。

如：0.25 = 25/100 = 1/43、小数改写成百分数：先把小数点向右移动两位，添上"%"。

如：0.725 = 72.5%4、数改写成小数：如果是带分数要先化成假分数，再用分数的分子去除以分母。

如：3 4/5 = 19/5 = 19÷5 = 3.8 27/8 = 27÷8 = 3.6255、分数改成百分数：先改写成小数，再改写。

6、百分数改写成小数：先去掉"%"号，再把小数点向左移两位。

7、百分数改写成小数：先改写成小数，再改写。

8、省略一个数某一位后面的尾数，写成近似数。

（1）用"四舍五入"法：看要保留的这一位后一位的数是否满5，如果满5就向前一位进一；否则，则舍去尾数。

如：4.62975≈ 4。

63（保留两位小数） 4．62975≈ 4。

6（保留一位小数）（2）进位法：一般用于在材料需求上，只要保留的数位后面还有别的数，就向前一位进1。

5、数大小的比较1、比较两个整数的大小：1）如果位数不同，那么位数多的数就大；2）如果位数相同，左起第一位上的数大的那个数就大；3）如果左起第一位上的数相同，就比较左起第二位上的数……2、比较两个小数的大小：1）先看它们的整数部分，整数部分大那个数就大，2）整数部分相同的，十分位上的数大的那个数就大；3）十分位上的数也相同的，百分位上的数大的那个数就大。

“数”的读音分别是【shù】、【shǔ】和【shuò】。

组词：【shù】:数学、少数、次数、负数、基数。

【shǔ】：数落、数伏、数说、历数、计数。

【shuò】:数数、频数、数次、多言数穷、数见不鲜。

•【shù】：⒈数学【shùxué】①释义：研究现实世界的空间形式和数量关系的科学。

包括算术、代数、几何、三角、微积分等②造句：我们要善于运用归纳法解决数学难题。

⒉少数【shǎo shù】①释义：较少的数量。

对“多数”而言。

②造句：少数人趁世贸大厦倒塌之际浑水摸鱼。

⒊次数【cìshù】①释义：同一个动作或事件重复出现的回数②造句：他参赛次数最多，是游泳队里资格最老的成员。

⒋负数【fùshù】①释义：小于零的数。

负数在数前加负号来表示，如－3，－5。

②造句：别人从零起步，而我从负数起步。

⒌基数【jīshù】①释义：用于表示事物个数的数。

如一、二、三……一百、三千等普通整数，区别于第一、第二、第三……第一百、第三千等序数。

②造句：地籍簿在获得税收基数方面得到重复利用。

•【shǔ】:⒈数落【shǔluo】①释义：.列举过失进行指责，也泛指指责②造句：小明被同学们数落得有点恼火了。

⒉数伏【shǔfú】①释义：夏至后第三个庚日开始的三伏天;也指进入伏天②造句：该团队正在开发的帮浦仅需要数伏特电力，手表用的电池就可以提供了。

⒊数说【shǔshuō】①释义：责骂;数落②造句：大多数说地老天荒，却极少到人老珠黄。

⒋历数【lìshù】①释义：指推算岁时节气的次序。

②造句：历数古今中外一切有大建树者，无一不惜时如金。

⒌计数【jìshǔ】①释义：数数或计算。

②造句：朕为始皇帝。

后世以计数，二世三世至于万世，传之无穷！•【shuò】:⒈数数【shuòshuò】①释义：犹汲汲。

名词解释数的组成数的组成是一个数学概念，它指的是将数字通过不同的方式组合在一起形成新的数字。

在数学中，数的组成涉及到各种不同的基本运算和操作，包括加法、减法、乘法、除法等。

通过了解数的组成，我们可以更好地理解数学运算和数字之间的关系。

首先，数的组成涉及到基本的加法和减法运算。

在数学中，我们可以将两个或多个数字相加或相减，得到一个新的数字。

例如，将3和5相加，我们得到了8这个新的数字。

而将8减去3，我们得到了5这个结果。

这种通过加法和减法运算得到的新的数字，就是数的组成的一种方式。

数的组成还包括乘法和除法运算。

乘法是一种将两个或多个数字相乘的运算。

例如，将2乘以3，我们得到了6这个新的数字。

除法是一种将一个数字分割成若干份的运算。

例如，将8分成两份，我们得到了4这个结果。

通过乘法和除法运算，我们可以得到不同的数字组合，从而形成数的组成的另一种方式。

另外，数的组成还可以涉及到分数和小数。

分数是一种用分子和分母表示的数，它表示了整体中的一部分。

通过将一个数字作为分子，另一个数字作为分母，我们可以得到一个分数。

例如，将1作为分子，3作为分母，我们得到了一个分数1/3。

小数是一种用十进制表示的数，它包括整数部分和小数部分。

通过将一个数字的小数部分写出来，我们可以得到一个小数。

例如，将1.5的小数部分写出来，我们得到了一个小数0.5。

分数和小数是数的组成的另一种方式，它们使我们能够更准确地表示和比较数字。

数的组成还可以通过数的位数进行解释。

每个数字都有一定的位数，从个位到十位、百位、千位等。

通过将不同位上的数字组合在一起，我们可以得到一个新的数字。

例如，将6和7组合在一起，我们得到了67这个新的数字。

通过理解数字的位数，我们可以更好地理解和运用数的组成的概念。

总之，数的组成是将数字通过不同的方式组合在一起形成新的数字的概念。

通过加法、减法、乘法、除法、分数、小数和位数等运算和概念，我们可以更好地理解数的组成，并应用于数学中的各种问题和计算中。

各种数一．简单的：自然数用以计量事物的件数或表示事物次序的数。

即用数码0，1，2，3，4，……所表示的数。

表示物体个数的数叫自然数，自然数由0开始(包括0)，一个接一个，组成一个无穷的集体。

自然数包括0。

自然数包括全体非负整数（小数不算）。

整数整数（Integer）：像-2，-1，0，1，2这样的数称为整数。

（整数是表示物体个数的数，0表示有0个物体）整数是人类能够掌握的最基本的数学工具。

整数的全体构成整数集，整数集合是一个数环。

在整数系中，自然数为0和正整数的统称，称0为零，称-1、-2、-3、…、-n、… (n为整数)为负整数。

正整数、零与负整数构成整数系。

一个给定的整数n可以是负（n∈Z-）非负数（n∈Z*），零（n=0）或正数（n∈Z+）．负数负数是数学术语，指小于0的实数，如−3。

负数是同绝对值正数的相反数。

任何正数前加上负号都等于负数。

在数轴线上，负数都在0的左侧，所有的负数都比自然数小。

负数用负号（Minus Sign，即相当于减号）“－”标记，如−2，−45，−0.6等。

分数把单位“1”平均分成若干份，表示这样的一份或几份的数叫分数。

表示这样的一份的数叫分数单位。

分数也有“成绩”的意思，如考试分数（我心中的痛）。

单位分数分子是1，分母是等于或大于2的自然数的分数叫做单位分数，记为1/n.单位分数又叫分数单位或“单分子分数”，它还有一个名称“埃及分数”。

1页二进分数（有些复杂）二进分数，也称为二进有理数，是一种分母是2的乘方的分数。

可以表示成a/2^n，其中，a 是一个整数，n 是一个自然数。

例如：1/2，3/8，而1/3就不是。

(英制单位中广泛采用二进分数，例如3/4英寸，1/16英寸，1/2磅。

)所有二进分数组成的集合在实数轴上是稠密的：任何实数x都可以用形为的二进分数无限逼近。

与实数轴上的其它稠密集，例如有理数相比，二进分数是相对“小”的稠密集，这就是为什么它们有时出现在证明中（例如乌雷松引理）。

数与数量关系数与数量关系是数学中的一个重要概念，它涉及到数的运算、比较和表示等方面。

在我们日常生活中，数与数量关系也是无处不在的。

本文将从数与数量关系的定义、数的分类、数的运算和比较等方面展开讨论。

一、数与数量关系的定义数是用来表示事物的数量的概念，它可以是一个确切的数字，也可以是一个范围或区间。

数量则是指具体事物的个数或大小。

数与数量之间的关系可以通过数的运算和比较来体现。

二、数的分类根据数的性质和特点，我们可以将数分为整数、分数、小数和无理数等几类。

1. 整数：整数是没有小数部分和分数部分的数，包括正整数、负整数和零。

整数可以用来表示具体的数量，比如班级的人数、书店的图书数量等。

2. 分数：分数是指一个整体被分成若干等份后的一份或几份，它由分子和分母两部分组成，分子表示被分出的部分，分母表示整体被分成的份数。

分数可以用来表示部分的数量，比如一杯水喝掉了三分之一，还剩下两分之一。

3. 小数：小数是指一个数被分成若干等份后的一份或几份，并且每份都可以用十进制表示。

小数可以用来表示精确的数量，比如货币的金额、温度的度数等。

4. 无理数：无理数是指不能表示为两个整数之比的数，它包括无限不循环小数和根号数等。

无理数可以用来表示无限或无法精确表示的数量，比如圆周率π、自然对数的底数e等。

三、数的运算数的运算是指对数进行加、减、乘、除等操作，以得到新的数或确定数的关系。

数的运算可以通过各种运算法则和公式来进行。

1. 加法：加法是将两个数相加，得到它们的和。

加法可以用来计算多个数量的总和，比如购物时计算商品的总价。

2. 减法：减法是将一个数从另一个数中减去，得到它们的差。

减法可以用来计算数量的减少或相对差异，比如两次测量的温度差、两个日期之间的天数等。

3. 乘法：乘法是将两个数相乘，得到它们的积。

乘法可以用来计算数量的倍数或扩大比例，比如购买多个相同商品的总价、放大或缩小的比例等。

4. 除法：除法是将一个数除以另一个数，得到它们的商。

数学中的各种数
1.质数与合数
质数,又名素数,是指只能被1和自身整除的数.如2.3. 5. 7. 11……
合数,是指除了1与自身之外还有其他的约数,如4.除了1与4
之外,它还能被2整除.
2、公因数、最大公约数和最小公倍数
公因数,又称公约数,在两个或两个以上的自然数中,如果它们有相同的因数,那么这些因数就叫做它们的公因数.任何两个自然数都
有公因数1.(除零以外)而这些公因数中最大的那个称为这些正整数的最大公因数.
求几个整数的最大公因数,只要把它们的所有共有的素因数连乘,所得的积就是它们的最大公因数.
3、实数与虚数
负数开平方,在实数范围内无解.
数学家们就把这种运算的结果叫做虚数,因为这样的运算在实数范围内无法解释,所以叫虚数.
实数和虚数组成的一对数在复数范围内看成一个数,起名为复数.
于是,实数成为特殊的复数(缺序数部分),虚数也成为特殊的复数(缺实数部分).
虚数单位为i, i即根号负1.。

数的分类
根据数的不同性质，可将数分为很多种类，奇数和偶数。

整数中能被2整除的数是偶数，不能被2整除的数是奇数，质数，⼜称素数，有⽆限个。

定义为在⼤于1的⾃然数中，除了1和它本⾝以外，不再有其他因数，合数，合数指⾃然数中除了能被1和本⾝整除外还能被其他数，0除外整除的⾃然数。

扩展资料
我们把0 1 2 3 4等全体⾮负整数组成的称为⾃然数，有理数和⽆理数。

除法运算，为了使数集合对加减乘除四则运算都是封闭的就必须增加新的`数如7/11 11/7 为两个整数之⽐，称为可⽐数分数，现在称为有理数，⽽⽆理数的发现，对以整数为基础的毕⽒哲学是⼀次致命的打击，数学史上把这件事，称为第⼀次数学危机，圆周率π，就是其中最重要的⼀个，实数，有理数和⽆理数的总称。

数的口诀与数的顺序数学是一门普及度很高的学科，我们在学习和使用数学的过程中，经常遇到数的口诀和数的顺序的问题。

数的口诀是指用来快速记忆和计算数学口诀的一种方法，数的顺序则是指数的排列顺序及其规律。

本文将探讨数的口诀与数的顺序，帮助读者更好地掌握这些概念。

一、数的口诀数的口诀在数学教育中起着至关重要的作用。

通过掌握数的口诀，我们可以更快速、准确地进行计算。

下面我们来介绍一些常见的数的口诀。

1. 乘法口诀：乘法口诀是指用来快速记忆乘法表的方法。

乘法口诀的基本规则是，排在第一行和第一列的数称为被乘数和乘数，两者相乘的结果称为积。

根据乘法口诀，我们可以很容易地计算任何两个整数的乘积。

2. 加法口诀：加法口诀是指用来快速记忆加法表的方法。

加法口诀的基本规则是，将两个数的各位数相加，如果大于10，则进位到高位。

通过加法口诀，我们可以很方便地计算任意两个整数的和。

3. 减法口诀：减法口诀是指用来快速计算减法的方法。

减法口诀的基本规则是，先计算个位数，如果被减数小于减数，则向高位借位。

通过减法口诀，我们可以很轻松地计算任意两个整数的差。

二、数的顺序数的顺序是在数学中常见的概念之一。

它指的是数的排列顺序及其规律。

数的顺序主要包括递增顺序和递减顺序两种。

1. 递增顺序：递增顺序指的是数从小到大排列的顺序。

当我们将一组数按照递增顺序排列时，可以更方便地进行比较和计算。

递增顺序在数学中得到广泛应用，如在解方程、排序等问题中都有重要的作用。

2. 递减顺序：递减顺序指的是数从大到小排列的顺序。

递减顺序与递增顺序相反，但同样在数学中具有重要的应用价值。

递减顺序在求最大值、排序等问题中经常被使用。

三、数的口诀与数的顺序的联系数的口诀和数的顺序在数学学习中有紧密的联系。

通过掌握数的口诀，我们能够更方便地进行数的顺序的计算和比较。

例如，当我们学习乘法的口诀时，可以发现乘法口诀的结果可以按照递增顺序排列。

这可以帮助我们在使用乘法口诀时更好地理解和应用乘法的基本概念。