2019届江西省上饶市高三第二次联考数学(理)试卷

2019届江西省上饶二中高三上学期月考数学试卷（理科）考试时间：120分钟 总分：150分第I 卷 （选择题 共60分）一、选择题（本大题12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合{}2|1log A x N x k =∈<<，若集合A 中至少有3个元素，则k 的取值范围为（ ） A ．()8,+∞ B ．[)8,+∞ C ．()16,+∞ D ．[)16,+∞2．在ABC ∆中，a b c ，，分别为角A B C ，，所对的边，若2cos sin 0cos sin A A B B +-=+，则a bc+的值是（ ）A ．1BCD ．2 3．已知()()sin 02f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭，的最小正周期为π，若其图像向左平移3π个单位长度后关于y 轴对称，则（ ）A ．23πωϕ==， B ．26πωϕ==， C ．46πωϕ==， D ．26πωϕ==-，4．已知1OA =，3OB =，0OA OB ⋅=，点C 在AOB ∠内，且OC 与OA 的夹角为30︒，设()OC mOA nOB m n R =+∈，，则mn的值为（ ） A ．2 B ．52C ．3D ．4 5．等差数列{}n a 中，n S 是其前n 项和，19a =-，97297S S-=，则10S 等于（ ）A ．0B ．-9C ．10D ．-10 6．等差数列{}n a 的前n 项和为n S ，若1122S =，则378a a a ++=（ ） A ．18 B ．12 C ．9 D ．67．等比数列{}n a 的各项均为正数，且564718a a a a +=，则3132310l og l o gl o g a a a+++等于（ ）A ．5B ．9C ．3log 45D ．108．已知实数x y ，满足约束条件04340x x y y >⎧⎪+≤⎨⎪≥⎩，则1y z x +=的最小值为（ ）A ．-2B ．2C ．-1D ．1 9．设x y R ∈，，11a b >>，，若3x y a b ==，a b +=11x y+的最大值为（ ） A ．2 B ．32 C ．1 D ．1210．在矩形ABCD 中，AB =4，BC =3，沿AC 将△ABC 折起，使面ABC ⊥面ACD ，则四面体ABCD 的外接球的体积为（ ）A ．12512π B ．1259π C ．1256π D ．1253π11．若直线()00ax y a -=≠与函数()22cos 12ln2x f x x x+=+-的图像交于不同的两点A B ，，且点()60C ，，若()D m n ，满足DA DB CD +=，则m n +=（ ）A ．1B ．2C ．3D ．412．已知函数()()()202x f x f f x e x x e '=+-，若存在实数m 使得不等式()22f m n n ≤-成立，则实数n 的取值范围为（ ）A ．[)1,1,2⎛⎤-∞-+∞ ⎥⎝⎦B ．(]1,1,2⎡⎫-∞-+∞⎪⎢⎣⎭C ．(]1,0,2⎡⎫-∞+∞⎪⎢⎣⎭ D ．[)1,0,2⎛⎤-∞-+∞ ⎥⎝⎦第II 卷 （非选择题 共90分）二、填空题（每小题5分，共20分） 13．已知复数211i z i=+-，则220151z z z ++++的值为 ．14．已知向量()21a =-，，()6b x =，，且//a b ，则a b -= ． 15．在ABC ∆中，内角A B C ，，的对边分别为a b c ，，，已知222sin sin sin sin sin A CB AC +=+，若ABC ∆的面积为4，则当a c +最小时，ABC ∆的周长为 ．16．已知正方体ABCD —A 1B 1C 1D 1的体积为1，点M 在线段BC 上（点M 异于点B 、C ），点N 为线段CC 1的中点，若平面AMN 截正方体ABCD —A 1B 1C 1D 1所得截面为四边形，则线段BM 长的取值范围为 ．三、解答题（解答应写出必要计算过程，推理步骤和文字说明，共70分） 17．（本小题满分10分）已知数列{}n a 的前n 项和为n S ，且满足()112n n S a n N +=-∈． （1）求n S ；（2）若()3112231111log 1=n n n n n b S T b b b b b b ++=--+++，，求n T ．18．（本小题满分12分）如图，在平面四边形ABCD 中，34ABC π∠=，AB AD ⊥，1AB =． （1）若AC ，求ABC ∆的面积； （2）若6ADC π∠=，4CD =，求sin CAD ∠．19．（本小题满分12分）如图，在平面四边形ABCD 中，32BA BC ⋅=．（1）若BA 与BC 的夹角为30︒，求ABC ∆的面积ABC S ∆； （2）若4AC =，O 为AC 的中点，G 为ABC ∆的重心，且OG 与OD 互为相反向量，求AD CD ⋅的值．20．（本小题满分12分）已知函数()()21cos cos 02f x x x x ωωωω=-+>，与()f x 图像的对称轴3x π=相邻的()f x 的零点为12x π=．（1）讨论函数()f x 在区间5,1212ππ⎡⎤-⎢⎥⎣⎦上的单调性； （2）设ABC ∆的内角A B C ，，的对应边分别为a bc ，，且c =()1f C =，若向量()1,sin m A =，与向量()2,sin n B =共线，求a b ，的值．21．（本小题满分12分）如图，在四棱锥P -ABCD 中，PD ⊥面ABCD ，底面ABCD 为正方形，BC =PD =2，E 为PC 中点，CB =3CG ． （1）求证：PC ⊥BC ；（2）在AD 边上是否存在一点M ，使P A //面MEG ？若存在，求出AM 的长，若不存在，请说明理由．22．（本小题满分12分）已知函数()()2ln f x ax x x x a R =+-∈．（1）若函数()f x 在()0,+∞上单调递增，求实数a 的取值范围； （2）若函数()f x 有两个极值点()1212x x x x ≠，，证明212x x e >．数学参考答案（理科）一、选择题（本大题12小题，每小题5分，共60分。

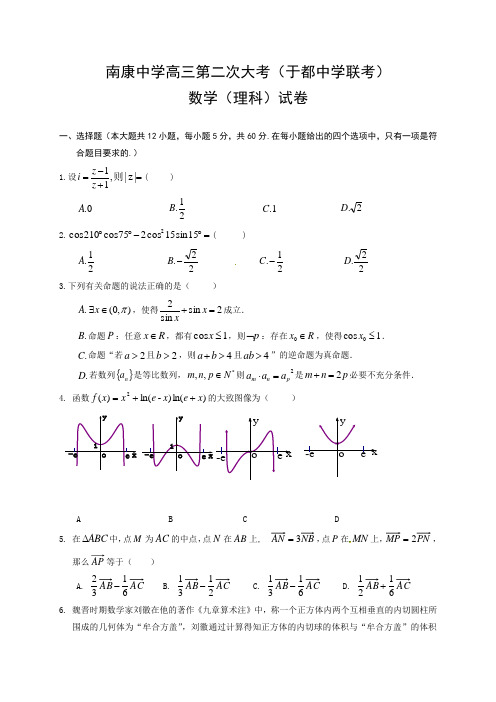
南康中学高三第二次大考（于都中学联考）数学（理科）试卷一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.） 1.设=+-=|z |,11则z z i ( ) 0.A 21.B 1.C 2.D2.=︒-︒︒15sin 15cos 275cos 210cos 2( )21.A 22.-B 21.-C 22.D3.下列有关命题的说法正确的是（ ）.A ),0(π∈∃x ，使得2sin sin 2=+x x成立． .B 命题P ：任意R x ∈，都有1cos ≤x ，则p ⌝：存在R x ∈0，使得1cos 0≤x ．.C 命题“若2>a 且2>b ，则4>+b a 且4>ab ”的逆命题为真命题．.D 若数列{}n a 是等比数列，*,,N p n m ∈则2p n m a a a =⋅是p n m 2=+必要不充分条件．4. 函数)ln()-ln()(2x e x e x x f ++=的大致图像为（ ）A B C D 5. 在ABC ∆中，点M 为AC 的中点，点N 在AB 上,3=，点P 在MN 上，2=，那么等于（ ）A.6132- B. 2131-C. 6131-D. 6121+ 6. 魏晋时期数学家刘徽在他的著作《九章算术注》中，称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖”，刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比应为π：4．若正方体的棱长为2，则“牟合方盖”的体积为（ ） A ．16B ．16C ．D ．7. 若等差数列{}n a 的前n 项和为n S ，且84=S ，48=S ，则=16S （ ）A ．25 B ．25- C ．40 D ．40- 8.已知函数()()sin 0,02f x x πωϕωϕ⎛⎫=+><< ⎪⎝⎭，()11f x =，()20f x =，若12min12x x -=，且1122f ⎛⎫=⎪⎝⎭，则()f x 的单调递增区间为（ ） A ．152,2,66k k k Z ⎡⎤-++∈⎢⎥⎣⎦B ．512,2,66k k k Z ⎡⎤-++∈⎢⎥⎣⎦．C ．512,2,66k k k Z ππ⎡⎤-++∈⎢⎥⎣⎦D ．172,2,66k k k Z ⎡⎤++∈⎢⎥⎣⎦9. 若(),log 43log 24ab b a =+则b a +的最小值是（ ）A ．326+ B. 327+ C. 346+ D. 347+10. 椭圆:G )0(12222>>=+b a by a x 的两个焦点)0,(1c -F ，)0,(2c F ，M 是椭圆上的一点，且满足.021=⋅F F 则椭圆离心率e 的取值范围为（ ）A ．]22,0( B ．)22,0( C ．)1,22(D ．)1,22[11. 已知B A ,是球O 的球面上两点，且球的半径为3，︒=∠90AOB ，C 为该球面上的动点．当三棱锥ABC O -的体积取得最大值时，则过C B A ,,三点的截面的面积为（ ） A ．π6B ．π12C ．π18D ．π3612. 已知函数21-2)(,1ln )(x e x g x x f =+=，若)(=)(n g m f 成立，则n m -的最小值是（ ） A.2ln +21B.2-eC. 21-2ln D. 21-e 二、填空题（本大题共4小题，每题5分，共20分.请将正确答案填在答题卷相应位置．．．．．．．．．．．．．．．.） 13. 若函数)121()(3a x x f x+-=为偶函数，则a 的值为14. 已知实数y x ,满足⎪⎩⎪⎨⎧≥≤-+≥--20123401y y x y x ，则123++-=x y x z 的最大值为 ．15. 点P 是椭圆221122111(0)x y a b a b +=>>和双曲线222222221(0,0)x y a b a b -=>>的一个交点，12,F F 是椭圆和双曲线的公共焦点,123F PF π∠=，则12b b 的值是 16. 已知定义在)2,2(ππ-上的函数)(x f 满足1)6(),()(=-=-πf x f x f ，对任意)2,0(π∈x ，不等式()tan ()f x x f x '>恒成立，其中)('x f 是的)(x f 导数，则不等式x x f sin 2)(<的解集为________．三、解答题（本大题共6小题，共70分,解答应写出必要的文字说明、证明过程及演算步骤） 17.（本题满分10分）已知函数R a a x x x f ∈---=,21)(. (1)当3=a 时，解不等式2)(-<x f ；(2)当)1,(-∞∈x 时，0)(<x f 恒成立，求a 的取值范围.18.（本题满分12分）在数列{}n a 中，已知)(log 32,41,41*4111N n a b a a a n n n n ∈=+==+. （1）求证：数列{}n b 是等差数列；（2）设数列{}n c 满足n n n b a c ⋅=，{}n c 的前n 项和n S .求证32<n s19.（本题满分12分）已知,,a b c 分别为ABC ∆三个内角,,A B C 的对边，且cos aC sin 0C b c --=．（1）求A ；（2）若AD 为BC 边上的中线，1cos 7B =，AD =，求ABC ∆的面积．20．（本题满分12分）如图，在四棱锥P ABCD -中，ABCD 为矩形，APB ∆是以P ∠为直角的等腰直角三角形，平面PAB ⊥平面ABCD ．（1）证明：平面PAD ⊥平面PBC ；（2）M 为直线PC 的中点，且2AP AD ==，求二面角A MD B --的正弦值．21. （本题满分12分）设抛物线()240y mx m =>的准线与x 轴交于1F ,抛物线的焦点为2F ，以12F F 、为焦点，离心率12e =的椭圆与抛物线的一个交点为23E ⎛ ⎝⎭；自1F 引直线交抛物线于P Q 、两个不同的点，设.11Q F P F λ=.（1）求抛物线的方程和椭圆的方程； （2）若1,12λ⎡⎫∈⎪⎢⎣⎭，求PQ 的取值范围.22.（本题满分12分）函数a ax x x x f (12ln )(2+-+=为常数） (1)讨论函数)(x f 的单凋性；(2)若存在]1,0(∈0x 使得对任意的]0,2(-∈a 不等式4+2+>)(+)1+(220a a x f a me a（其中e 为自然对数的底数）都成立，求实数m 的取值范围．南康中学2019届高三寒假数学（理科）测试参考答案一、选择题：1-12：CBDA DCDB DDAA 二、填空题13.21 14. 4915.3 16. )6,0()6,2(πππ -三、解答题17. 【详解】（1）当3=a 时，2)(-<x f ，有2321)(-<---=x x x f所以⎩⎨⎧-<-+-<23211x x x 或⎪⎩⎪⎨⎧-<-+-≤≤2321231x x x 或⎪⎩⎪⎨⎧-<+-->232123x x x ， 所以0<x 或φ∈x 或4>x ， 综上，不等式解集为{}40|><x x x 或 （2）当)1,(-∞∈x 时，0)(<x f 恒成立，有0|2|1<---a x x 。

上饶市重点中学2019届高三六校第二次联考（上饶市一中、上饶市二中、上饶县中、玉山一中、余干中学、天佑中学）文科数学注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔在答题卡上填写自己的准考证号、姓名、试室号和座位号。

用2B 型铅笔把答题卡上试室号、座位号对应的信息点涂黑。

2．选择题每小题选出答案后，用2B 型铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卡整洁。

考试结束后，将试卷和答题卡一并交回。

一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知[)+∞=,A 1，[]130-=a ,B ，若∅≠B A ，则实数a 的取值范围是（ ） A ．[)∞+，1B ．⎥⎦⎤⎢⎣⎡121， C ．⎪⎭⎫⎢⎣⎡∞+，32 D ．()∞+，12．已知复数21z ,z 在复平面内对应的点关于虚轴对称，若i z 211-=，则=21z z （ ） A ．i 5453- B ．i 5453+-C ．i 5453--D ．i 5453+ 3．某班有40位同学，座位号记为01，02，…，40，用下面的随机数表选取5组数作为参加青年志愿者活动的5位同学的座位号.4954 4454 8217 3793 2378 8735 2096 4384 2634 9164 5724 5506 8877 0474 4767 2176 3350 2583 9212 0767 5086选取方法是从随机数表第一行的第11列和第12列数字开始，由左到右依次选取两个数字，则选出来的第5个志愿者的座位号是（ ）A ．09B ．20C ．37D ．384．执行如图所示的程序框图，若输出的S 为4，则输入的x 应为（ ） A ．2- B ．16 C ．82或- D ．162或- 5．若双曲线122=-my x 的实轴长是虚轴长的两倍，则=m （ ）A ．41 B ．21C ．4D ．2 6．已知角α的终边经过点A ()1，a ，若点A 在抛物线x y 342=的准线上，则αcos =（ ） A ．23 B ．23- C ．21 D ．21-7．已知命题54x x ,R x :p <∈∀；命题2-=+∈∃x cos x sin ,R x :q ，则下列形式的命题中为真命题的是（ ） A ．q p ∧ B ．()q p ∧⌝ C ．()q p ⌝∧D ．()()q p ⌝∧⌝8．如图所示是某几何体的三视图，则它的表面积是（ ）A ．π7B ．π8C ．()π27+D ．()π26+9．函数是（ ） A ．最小正周期为2π的偶函数 B ．最小正周期为π的奇函数 C ．最小正周期为2π的奇函数D ．最小正周期为π的偶函数10．有一种“三角形”能够像圆一样当作轮子用. 这种神奇的三角形，就是以19世纪德国工程师勒洛的名字命名的勒洛三角形.这种三角形常出现在制造业中（例如扫地机器人）.三个等半径的圆两两互相经过圆心，三个圆相交的部分就是勒洛三角形，如图所示.现从图中的勒洛三角形内部随机取一点，则此点取自阴影部分的概率为（ ） A ．324332--ππ B ．3332-πC ．3223-πD ．322332--ππ11．已知函数()⎪⎩⎪⎨⎧<⎪⎭⎫ ⎝⎛->=010x ,x lg x ,x lg x f ，若()()m f m f ->，则实数m 的取值范围是（ ）A ．()()+∞-,,101B ．()()+∞-∞-,,11C ．()()1001,, -D ． ()()101,, -∞-12．已知()0,2-A ,()0,2B ，若x 轴上方的点P 满足对任意R ∈λ2≥-成立，则P 点纵坐标的最小值为（ ） A ．41 B ．21C ．1D ．2二、填空题（本大题共4小题，每小题5分，共20分） 13．曲线()x xx f e3-=在点()30,处的切线方程为 ． 14．若y ,x 满足约束条件⎪⎩⎪⎨⎧≤≥+-≤--,y ,y x ,y x 001022则51+-=x y z 的最小值为 ．15．在ABC ∆中，角C ,B ,A 的对边分别为c ,b ,a .若b a >，且A sin b a 23=，则=B ．16．已知椭圆C 的方程为13922=+y x ，B ,A 为椭圆C 的左右顶点，P 为椭圆C上不同于B ,A 的动点，直线6=x 与直线PB ,PA 分别交于N ,M 两点，若()09,D ，则过N ,M ,D 三点的圆必过x 轴上不同于点D 的定点，其坐标为 ．三、解答题（解答应写出必要计算过程，推理步骤和文字说明，共70分） （一）必考题:共60分 17．（本小题满分12分）已知等比数列{}n a 的各项均为正数，且18221=+a a，622316a a a =（1）求数列{}n a 的通项公式；（2）设n na logb 2-=，求数列⎭⎬⎫⎩⎨⎧+11n n bb 的前n 项和n T ． 18．（本小题满分12分）如图，在ABC ∆中，AC BC ⊥，E ,D 分别为AC ,AB 的中点，将ADE ∆沿DE 折起到PDE ∆的位置． （1）证明：PEC BC 平面⊥； （2）若CD BC PC ,BP ===，37，求四棱锥BCEDP -的体积．19．（本小题满分12分）十九大提出：坚决打赢脱贫攻坚战，做到精准扶贫，我省某帮扶单位为帮助定点扶贫村真正脱贫，坚持扶贫同扶智相结合，帮助贫困村种植脐橙，并利用互联网电商进行销售，为了更好销售，现从该村的脐橙树上随机摘下100个脐橙进行测重，其质量分布在区间[]500200,（单位：克），统计质量的数据作出其频率分布直方图如图所示： （1）按分层抽样的方法从质量落在[)[)450400400350,,，的脐橙中随机抽取5个，再从这5个脐橙中随机抽2个，求这2个脐橙质量至少有一个不小于400克的概率；（2）以各组数据的中间数值代表这组数据的平均水平，以频率代表概率，已知该村的脐橙种植地上大约还有100000个脐橙待出售，某电商提出两种收购方案： A ．所有脐橙均以7元/千克收购；B ．低于350克的脐橙以2元/个收购，其余的以3元/个收购 请你通过计算为该村选择收益较好的方案． （参考数据：（225×0.05+275×0.16+325×0.24+375×0.3+425×0.2+475×0.05＝354.5）20．（本小题满分12分）设抛物线()022>=p px y 的焦点为F，抛物线上的点H到y轴的距离等于1-HF ．（1）求p 的值； （2）如图，过点()()00>m ,m E 作互相垂直的两条直线交抛物线于D ,C ,B ,A ，且N,M 分别是CD ,AB 的中点，求EMN ∆面积的最小值．21．（本小题满分12分）已知函数()()()R a x ln x a x g ,xe x f x ∈+==，2．（1）求()f x 单调区间；（2）若()()x g x f ≥在[)∞+，1上恒成立，求a 的取值范围．（二）选考题:共10分。

学霸养成.2020高考数学热点难点必杀技系列—导数近几年高考试卷及各地模拟试卷中常出现在函数背景下处理含有两个变量的等式与不等式问题,这类问题由于变量多,不少同学不知如何下手,其实如能以函数思想为指导,把双变量问题转化为一个或两个一元函数问题,再利用导数就可有效地加以解决.1.【2018全国卷Ⅰ】已知函数1()ln f x x a x x=-+． (1)讨论()f x 的单调性；(2)若()f x 存在两个极值点12,x x ,证明：1212()()2-<--f x f x a x x ．一、与函数单调性有关的双变量问题此类问题一般是给出含有()()1212,,,x x f x f x 的不等式,若能通过变形,把不等式两边转化为同源函数,可利用函数单调性定义构造单调函数,再利用导数求解.【例1】【湖南省师范大学附属中学2019届高三下学期模拟】 已知函数,,当时,不等式恒成立,则实数的取值范围为A ．B ．C ．D ．【对点训练】【安徽省淮南市2019届高三第一次模拟】已知函数()ln 1f x x ax =-+,其中a 为实常数. （1）若当0a >时,()f x 在区间[1,]e 上的最大值为1-,求a 的值；（2）对任意不同两点()()11,A x f x ,()()22,B x f x ,设直线AB 的斜率为k ,若120x x k ++>恒成立,求a 的取值范围.二、与极值点有关的双变量问题与极值点12,x x 有关的双变量问题,一般是根据12,x x 是方程()0f x '=的两个根,确定12,x x 的关系,再通过消元转化为只含有1x 或2x 的关系式,再构造函数解题,有时也可以把所给条件转化为12,x x 的齐次式,然后转化为关于21x x 的函数. 【例2】【山东省潍坊市2019届高三5月三模】已知函数2()ln 2()f x x a x x a R =+-∈. （1）求()f x 的单调递增区间；（2）若函数()f x 有两个极值点1212,()x x x x <且12()0f x mx -≥恒成立,求实数m 的取值范围.【对点训练】【辽宁省沈阳市东北育才学校2019届高三第八次模拟】已知函数2()2ln ()f x x ax x a R =-+∈两个极值()1212,x x x x <点.（1）当5a =时,求()()21f x f x -； （2）当a ≥,求()()21f x f x -的最大值. 三、与零点有关的双变量问题与函数零点12,x x 有关的双变量问题,一般是根据12,x x 是方程()0f x =的两个根,确定12,x x 的关系,再通过消元转化为只含有1x 或2x 的关系式,再构造函数解题,有时也可以把所给条件转化为12,x x 的齐次式,然后转化为关于21x x 的函数,有时也可转化为关于12x x -的函数,若函数中含有参数,可考虑把参数消去,或转化为以参数为自变量的函数.【例3】【黑龙江省哈尔滨市2019届高三二模】已知函数()ln()xf x e x m =-+,其中1m ≥. （1）设0x =是函数()f x 的极值点,讨论函数()f x 的单调性； （2）若()y f x =有两个不同的零点1x 和2x ,且120x x <<, （i ）求参数m 的取值范围； （ii ）求证：2121ln(1)1x x ex x e ---+>-.【对点训练】【云南省玉溪市第一中学2019届高三上学期第二次调研】设R a ∈,函数()ln f x x ax =-, （1）讨论()f x 的单调性；（2）若()f x 有两个相异零点12,x x ,求证12ln ln 2x x +>.四、独立双变量,各自构造一元函数此类问题一般是给出两个独立变量,通过变形,构造两个函数,再利用导数知识求解. 【例4】【江西省上饶市2019届高三第二次模拟】已知实数x ,y 满足()2ln 436326x y x y e x y +-+--≥+-,则x y +的值为（ ） A ．2B ．1C ．0D ．1-【对点训练】【四川省绵阳市2018届高三第三次诊断】对于任意的实数[]1,x e ∈,总存在三个不同的实数[]1,4y ∈-,使得21ln 0y y xe ax x ---=成立,则实数a 的取值范围是（ ）A ．3163,e e ⎡⎤⎢⎥⎣⎦ B ．3160,e ⎛⎤ ⎥⎝⎦ C ．23163,e e e ⎡⎫-⎪⎢⎣⎭ D ．23161,e e e ⎡⎫-⎪⎢⎣⎭ 五、独立双变量,换元构造一元函数【例5】【河南省名校鹤壁高中2019届高三压轴第二次考试】若存在正实数,使得关于的方程有两个不等的实根（其中是自然对数的底数）,则实数的取值范围是（ ） A ．B ．C ．D ．1.【2019年山西省太原市高三模拟】已知2a >,函数()1e ln exf x x ax =+-. （1）证明：()f x 有两个极值点；（2）若()1212,x x x x <是函数()f x 的两个极值点,证明：()()212ln f x f x a -<. 2．【天津市实验中学2019届高三第六次阶段考】已知函数211()ln 2f x x a x x a ⎛⎫=-++ ⎪⎝⎭,其中0a >. （1）当2a =时,求曲线()y f x =在点()()1,1f 处切线的方程； （2）当1a ≠时,求函数()f x 的单调区间；（3）若10,2a ⎛⎫∈ ⎪⎝⎭,证明对任意()12121,,12x x x x ⎡⎤∈≠⎢⎥⎣⎦,()()12221212f x f x x x -<-恒成立.3．【内蒙古2019届高三高考一模】已知函数21()()2ln f x ax bx x a R =+--∈． (1)当0b =时,讨论函数()f x 的单调区间；(2)当1x y e >>-时,求证：ln(1)ln(1)x y e y e x +>+． 4．设函数()ln (1)x f x x a x e =--,其中a R ∈. （1）若0a ≤,讨论()f x 的单调性； （2）若10a e<<, （i ）证明()f x 恰有两个零点（ii ）设0x 为()f x 的极值点,1x 为()f x 的零点,且10x x >,证明0132x x ->. 5．【安徽省1号卷A10联盟2019届高考最后一卷】已知函数,()()1ln 1,f x m x m R x=+-∈ （1）若函数()f x 有2个零点,求m 的取值范围；（2）若()()21g x f x x x=++有两个极值点12,x x ,且12x x <,求证：()211ln 22g x x <- 6．【黑龙江省哈尔滨市第三中学2019届高三第二次模拟】已知函数()ln()xf x e x m =-+,其中1m ≥. （1）设0x =是函数()f x 的极值点,讨论函数()f x 的单调性； （2）若()y f x =有两个不同的零点1x 和2x ,且120x x <<, （i ）求参数m 的取值范围； （ii ）求证：2121ln(1)1x x ex x e ---+>-.7．【四川省绵阳市2019届高三下学期第三次诊断】已知函数()()21f x x axlnx ax 2a R 2=-++∈有两个不同的极值点x 1,x 2,且x 1＜x 2． （1）求实数a 的取值范围； （2）求证：x 1x 2＜a 2．8．【云南省师范大学附属中学2019届高三第八次月考】已知函数21()2ln 2f x x x a x =-+,其中0a >. （1）讨论()f x 的单调性；（2）若()f x 有两个极值点1x ,2x ,证明：123()()2f x f x -<+<-.。

2018—2019学年度上学期高三学年第二次调研考试数学（理）试卷考试说明：（1）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，满分150分.考试时间为120分钟；（2）第I 卷，第II 卷试题答案均答在答题卡上，交卷时只交答题卡.第I 卷（选择题，共60分）一、选择题：（本大题共 12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）A +4i 1•已知i 为虚数单位，则复数4i的虚部是2 —i11. 11.1111 A.i B. iC.—D.—5 3532.已知角:的终边经过点P(3, -4)，则 cos ：二4334A .B .C .—D .5 55 53.若sin 一仝，则—32 11 2 A .-B.-C.― D .3333x4.已知命题p :函数y =2的图象与函数y=log 2x 的图象关于直线 y =x 对称，命题q : 6.若函数f （x ）二sin x cos x 在［-m, m ］上是增函数，则 m 的最大值是3 二兀A . ■-B .C . 一D .-函数 3y =x 的图象与函数y - x 3的图象关于直线 y 二x 对称，则下列命题中为真命题的是A. p q B . (—p) (5)C .O qD.p (P5.函数f (x)二 cos 2 x 、、3 s 1 n in x ( x [0, 3])的最大值为A . 2B .3+ 1C .3 3 + — D .542 4414247.将函数f(x)—的图象向右平移-个单位长度，8. 9. 来的1，纵坐标不变，所得图象的函数解析式为2y 二si n(2x -23) y =sin(2x - J)1 兀y 二s in (2X-3)y = sin(2x —斗)33 f (x)满足：对任意的实数 x 都有 f(x ，2) =-f(x)，且 f (1) = 一1, f (2) =-2 函数 则 f (1) f (2) f (3) HI f (2019)的值为B . -1如下图所示的程序框图输出的结果是 '开始一2018 是.否i 是奇数S=0,i=1 是wD .C . 2D . -2A . 2018B . -1010 10.函数f(x) =ln x2 2 -e A 的图象大致是1009A . 11.已知定义在R 上的偶函数 f (x)在0,= 是单调递增的，若不等式 f (ax - 4) _ f (x 5)对任意X ，1,2 1恒成立，则实数 ；_ 3 111B .」C .亠0(D ._-—3 IL 2,22 _2 ,2a 的取值范围为 A .2 1112若存在x • ［e,e ］，使得关于x 的不等式^，4X a 成立，则实数3的取值范围是D . 1一丄「1 4e第口卷(非选择题，共90 分)二、填空题：(本大题共4小题，每小题5分，共20分.将答案填在答题卡相应的位置上 )13. 函数f(x) = log 1 (x 2 -5x 6)的单调递增区间为 _____________________ .22 m 2 4m 214. 已知幕函数f x 二m+1 x -丄在 0, •::上单调递减，则函数f (x)的解析式为 _______________ .5：：.15. 已知函数 f (x)二 cos(，x • J (「：•：： :■■ - 0,p : | )的最小正周期为 二，x 为 y =f (x)图2 12象的对称轴，则函数 f (x)在区间［0,二］上零点的个数为 _______________ .b16. 已知k 0 b 0且kx • b _ In x • 4 对任意的x • -4恒成立，则一的最小值k为 _______________ .三、解答题：(本大题共 6小题，共70分，解答应写出文字说明，证明过程或演算步骤.) 17. (本题10分)f 兀 )4 了兀兀)已知 sin x , x,- 16 丿5I 3 6丿1(1 )求5巾i 2x •—的值; I 6丿 (2)求tan x 的值.I 12丿B .18. (本题12分)已知函数 f(x) = x 3sin - cos- -cos 2 - 12 2 2 2 '(1) 求函数y = f(x)的单调递减区间；(2) 设y = g(x )图象与y = f (x)图象关于直线x 对称，求x [,0]时，y = g(x)的值域.4219.(本题12分)已知 f (x )=|x-1 + x-2 , g (x ) = ax (a ^R ). (1 )当a =1时，解不等式f x 广g x ；(2)若-x^O,壯辽时f x g x 恒成立，求实数 a 的取值范围.20. (本题12分)平面直角坐标系xOy 中，曲线G 过点P(1,1)，其参数方程为以原点O 为极点，x 轴非负半轴为极轴建立极坐标系，曲线 「C O S v 4 C 03- . 0(“求曲线G 的普通方程和曲线 C2的直角坐标方程;21. (本题12分)2 2已知椭圆C:^^ =1 a b 0过点2,0 , P 1,0为C 内一点，过点P 的直线l 交椭圆Ca b(1)求椭圆C 的方程;C 2极坐标方程(t 为参数)，(2)已知曲线G 和曲线C 2交于A, B 两点，求1|PA|—的值.|PB|B 两点,AP 王 PBO 为坐标原点，当 AB OP =0 时，AB 「3 .AP = 'PB ,(2)求实数■的取值范围.22. (本题12分)x 2设函数f (x)二e 3x -ax 3 a R .(1)当a =1时,求函数f (x)的单调区间；(2)-x ：= (0, • ：：), f (x) _ 0恒成立，求最大的正整数a的值；(3)- x, y (0,2)且x y = 2，证明:e x(x-1) e y(y-1) x(x-3)(x-1)2 y(y-3)(y-1)2_ 0.22. 8 ；2018— 2019学年度上学期高三学年第二次调研考试数学试卷答案（选择题，共60 分）一•选择题 CCBAA,DDDCA,AB 第口卷（非选择题,共90分）二.填空题 14. f(X )=X15. 2 16.317. 解答题7 25 ；(1)18. (1) 每一个19. (1) 1(2) - -[2宀2 二，2k 第宀5 二],(k Z)；3 3 1(2) a —2x :: 1 或 x 3 ；20. (2)21. (1)(2) 1,3】1 ⑵[]]2二 3(1) (2) (3)（0,二）单调递增; （-二,0）单调递减， 易求 e 6，所以a 的最大正整数值为 证明略.22.8 ；。

2019届高三年级第一学期月考数学试卷（理科）考试时间：120分钟 总分：150分第I 卷 （选择题 共60分）一、选择题（本大题12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合{}2|1log A x N x k =∈<<，若集合A 中至少有3个元素，则k 的取值范围为（ ）A ．()8,+∞B ．[)8,+∞C ．()16,+∞D ．[)16,+∞ 2．在ABC ∆中，a bc ，，分别为角A B C ，，所对的边，若2cos sin 0cos sin A A B B +-=+，则a bc+的值是（ ）A ．1BCD ．23．已知()()sin 02f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭，的最小正周期为π，若其图像向左平移3π个单位长度后关于y 轴对称，则（ ）A ．23πωϕ==， B ．26πωϕ==， C ．46πωϕ==， D ．26πωϕ==-，4．已知1OA =，3OB =，0OA OB ⋅=，点C 在AOB ∠内，且OC 与OA 的夹角为30︒，设()OC mOA nOB m n R =+∈，，则mn的值为（ ） A ．2 B ．52C ．3D ．4 5．等差数列{}n a 中，n S 是其前n 项和，19a =-，97297S S-=，则10S 等于（ ）A ．0B ．-9C ．10D ．-10 6．等差数列{}n a 的前n 项和为n S ，若1122S =，则378a a a ++=（ ） A ．18 B ．12 C ．9 D ．67．等比数列{}n a 的各项均为正数，且564718a a a a +=，则3132310l og l o g l o g a a a+++等于（ ）A ．5B ．9C ．3log 45D ．108．已知实数x y ，满足约束条件04340x x y y >⎧⎪+≤⎨⎪≥⎩，则1y z x +=的最小值为（ ）A ．-2B ．2C ．-1D ．1 9．设x y R ∈，，11a b >>，，若3x y a b ==，a b +=则11x y+的最大值为（ ） A ．2 B ．32 C ．1 D ．1210．在矩形ABCD 中，AB =4，BC =3，沿AC 将△ABC 折起，使面ABC ⊥面ACD ，则四面体ABCD 的外接球的体积为（ ）A ．12512π B ．1259π C ．1256π D ．1253π11．若直线()00ax y a -=≠与函数()22cos 12ln2x f x x x+=+-的图像交于不同的两点A B ，，且点()60C ，，若()D m n ，满足DA DB CD +=，则m n +=（ ）A ．1B ．2C ．3D ．4 12．已知函数()()()202x f x f f x e x x e '=+-，若存在实数m 使得不等式()22f m n n ≤-成立，则实数n 的取值范围为（ ）A ．[)1,1,2⎛⎤-∞-+∞ ⎥⎝⎦B ．(]1,1,2⎡⎫-∞-+∞⎪⎢⎣⎭C ．(]1,0,2⎡⎫-∞+∞⎪⎢⎣⎭ D ．[)1,0,2⎛⎤-∞-+∞ ⎥⎝⎦第II 卷 （非选择题 共90分）二、填空题（每小题5分，共20分） 13．已知复数211i z i=+-，则220151z z z ++++的值为 ．14．已知向量()21a =-，，()6b x =，，且//a b ，则a b -= ．15．在ABC ∆中，内角A B C ，，的对边分别为a b c ，，，已知222sin sin sin sin sin A C B A C +=+，若ABC ∆，则当a c +最小时，ABC ∆的周长为 ．16．已知正方体ABCD —A 1B 1C 1D 1的体积为1，点M 在线段BC 上（点M 异于点B 、C ），点N 为线段CC 1的中点，若平面AMN 截正方体ABCD —A 1B 1C 1D 1所得截面为四边形，则线段BM 长的取值范围为 ．三、解答题（解答应写出必要计算过程，推理步骤和文字说明，共70分） 17．（本小题满分10分）已知数列{}n a 的前n 项和为n S ，且满足()112n n S a n N +=-∈． （1）求n S ；（2）若()3112231111log 1=n n n n n b S T b b b b b b ++=--+++，，求n T ．18．（本小题满分12分）如图，在平面四边形ABCD 中，34ABC π∠=，AB AD ⊥，1AB =． （1）若AC =ABC ∆的面积； （2）若6ADC π∠=，4CD =，求sin CAD ∠．19．（本小题满分12分）如图，在平面四边形ABCD 中，32BA BC ⋅=． （1）若BA 与BC 的夹角为30︒，求ABC ∆的面积ABC S ∆；（2）若4AC =，O 为AC 的中点，G 为ABC∆的重心，且OG 与OD 互为相反向量，求AD CD ⋅的值．20．（本小题满分12分） 已知函数()()21cos cos 02f x x x x ωωωω=-+>，与()f x 图像的对称轴3x π=相邻的()f x 的零点为12x π=．（1）讨论函数()f x 在区间5,1212ππ⎡⎤-⎢⎥⎣⎦上的单调性；（2）设ABC ∆的内角A B C ，，的对应边分别为a b c ，，且c =()1f C =，若向量()1,sin m A =，与向量()2,sin n B =共线，求a b ，的值．21．（本小题满分12分）如图，在四棱锥P -ABCD 中，PD ⊥面ABCD ，底面ABCD 为正方形，BC =PD =2，E 为PC 中点，CB =3CG ．（1）求证：PC ⊥BC ；（2）在AD 边上是否存在一点M ，使PA //面MEG ？若存在，求出AM 的长，若不存在，请说明理由．22．（本小题满分12分）已知函数()()2ln f x ax x x x a R =+-∈．（1）若函数()f x 在()0,+∞上单调递增，求实数a 的取值范围；（2）若函数()f x 有两个极值点()1212x x x x ≠，，证明212x x e >．数学参考答案（理科）一、选择题（本大题12小题，每小题5分，共60分。

江西上高二中、临川二中2019高三联考试题--数学（理）【一】选择题：(本大题共10小题，每题5分，共50分、在每题给出的四个选项中，只有一项为哪一项符合题目要求的)、 1、假设复数12z =-，那么z 2=〔 〕A、12- B、12- C12i D12i2、向量()21=，a ，()2x =-，b ，假设a ∥b ，那么a +b 等于〔 〕A 、()2,1-- B 、()2,1C 、()3,1- D 、()3,1-3. 在空间直角坐标系中，一定点到三个坐标轴的距离基本上2，那么该定点到原点的距离是〔 〕B.4. 在直线6x π=-，曲线cos y x =及x 轴y 轴所围成的封闭图形的面积是〔 〕A. 2πD. 125、假设正四棱锥的左视图如右图所示. 那么该正四棱锥体积是〔〕A 、324 B 、334 C 、322 D 、3326.球O 的球面上有四点S 、A 、B 、C,其中O 、A 、B 、C 四点共面，△ABC 是边长为2的正三角形，平面SAB ⊥平面ABC,那么棱锥S-ABC 的体积的最大值为〔 〕B. 137.定义在R 上的函数)(x f y =满足)()5(x f x f -=+，5()()2x f x '-0>，21x x <,那么是521<+x x 的〔 〕条件、A 、充分不必要B 、必要不充分C 、充分必要D 、既不充分也不必要8.数列{}n a 的首项为3，{}n b 为等差数列且1n n n b a a +=-，假设32b =-，212b =，那么8a =〔 〕A 、0B 、109-C 、78-D 、11 9. 在△ABC 中，AC ＝6，BC ＝7，cos A ＝15，O 是△ABC 的内心，假设OP xOA yOB =+，其中01,01x y ≤≤≤≤,动点P 的轨迹所覆盖的面积为〔 〕103 D. 20310.假设集合A 具有以下性质：①0A ∈，1A ∈；②假设,x y A ∈，那么x y A -∈，且0x ≠时，1Ax∈ 、那么称集合A 是“好集”、〔1〕集合{}1,0,1B =-是好集；〔2〕有理数集Q 是“好集”；〔3〕设集合A 是“好集”，假设,x y A ∈，那么x y A +∈；(4)设集合A 是“好集”，假设,x y A ∈，那么必有xy A ∈；〔5〕对任意的一个“好集A ，假设,x y A ∈，且0x ≠，那么必有yAx∈.A 、2个B 、3个C 、4个D 、5个【二】填空题：〔本大题共5小题，每题5分，共25分〕. 11、()πϕϕπ<<=+0,23)2sin(，那么ϕtan =________、12.过双曲线22221(0,0)x y a b a b-=>>的右顶点A 作斜率为1-的直线，该直线与双曲线的两条渐进线的交点分别为B 、C .假设12AB BC=，那么双曲线的离心率是________、 13.把正数排列成如图甲的三角形数阵，然后擦去偶数行中的奇数和奇数行中的偶数，得到如图乙的三角形数阵，现把图乙中的数按从小到大的顺序排成一列，得到一个数列{na }，假设na ＝2018，那么n ＝.1 1234 24 56789 579 10111213141516 10121416 甲乙 14.函数111,0,22()12,,22x x x f x x -⎧⎡⎫+∈⎪⎪⎢⎪⎣⎭=⎨⎡⎫⎪∈⎪⎢⎪⎣⎭⎩，假设存在1x ，2x ，当1202x x ≤<<时，()()12f x f x =，那么()12x f x 的取值范围是________、15.选做题〔以下两题选做一题，假设两题都做，那么以第〔1〕题计分〕 〔1〕点C 极坐标为(2,)3π，那么以C 为圆心，半径r=2的圆的极坐标方程是________.〔2〕函数()|21||23|f x x x =++-、假设关于x 的不等式|1|)(-<a x f 的解集非空，那么实数a 的取值范围是________、 【三】解答题；本大题共6小题，共75分 16.〔本小题总分值12分〕在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，且满足c -〕BA BC ∙=c CB CA ∙ 〔1〕求角B 的大小; 〔2〕假设6BA BC -=求△ABC 面积的最大值.17.〔本小题总分值12分〕某游乐场有A 、B 两种闯关游戏，甲、乙、丙、丁四人参加，其中甲乙两人各自独立进行游戏A ，丙丁两人各自独立进行游戏B 、甲、乙两人各自闯关成功的概率均为13，丙、丁两人各自闯关成功的概率均为12、〔1〕求游戏A 被闯关成功的人数多于游戏B 被闯关成功的人数的概率； 〔2〕记游戏A 、B 被闯关总人数为ξ，求ξ的分布列和期望. 18.〔本小题总分值12分〕如图，四棱锥P ABCD -中，侧面PDC 是边长为2的正三角形，且与底面垂直，底面ABCD 是60ADC ∠=的菱形，M 为PB 的中点. (I)求证：PA ⊥平面CDM ；(Ⅱ)求二面角D MC B --的余弦值.19.〔本小题总分值12分〕 数列{n a }的前n 项和为2nS =-2(1)na n+(1)n ≥〔1〕求证：数列n a n ⎧⎫⎨⎬⎩⎭是等比数列；〔2〕设数列{2n n a }的前n 项和为n T .n A ＝1231111nT T T T ++++. 试比较nA 与2nna 的大小. 20、〔本小题总分值13分〕i ，j 是x ，y 轴正方向的单位向量，设()1a xi y j =+-，()1b xi y j =++，且满足22a b +=.〔1〕求点(,)P x y 的轨迹C 的方程；〔2〕设点(0,1)F ，点A 、B 、C 、D 在曲线C 上，假设AF 与FB 共线，CF 与FD 共线，且0AF CF ∙=，求四边形ACBD 的面积的最小值和最大值. 21、〔本小题总分值14分〕函数()ln f x x x =，2()2g x x ax =-+-、 〔1〕求函数()f x 在[],2t t +(0t >)上的最小值；〔2〕假设函数()y f x =与()y g x =的图象恰有一个公共点，求实数a 的值； 〔3〕假设函数()()y f x g x =+有两个不同的极值点1x ，2x 12()x x <，且21ln 2x x ->，求实数a 的取值范围、联考题数学〔理科〕答案17.(I)21211137233233436p ⎛⎫=⨯⨯⨯+⨯⨯=⎪⎝⎭〔Ⅱ〕ξ可取0，1，2，3，43E ξ=18〔I 〕取AP 的中点N ，连接MN ，易知，在菱形ABCD 中，由于60ADC ∠=， 那么AO CD ⊥，又PO CD ⊥，那么CD APO ⊥平面，即CD PA ⊥， 又在PAB ∆中，中位线//MN 12AB ，1//2CO AB ，那么//MN CO ， 那么四边形OCMN 为，因此//MC ON ，在APO ∆中，AO PO =，那么ON AP ⊥，故AP MC ⊥而MC CD C =，那么PA MCD ⊥平面〔Ⅱ〕由〔I 〕知MC PAB ⊥平面，那么NMB ∠为二面角D MC B --的平面角，在RtPAB ∆中，易得PA =PB ===，cosAB PBA PB ∠===，cos cos()NMB PBA π∠=-∠=故，所求二面角的余弦值为19解：〔1〕证明：11123a s a ==-得112a =当m ≥2时，由22(1)n n s a n =-+得1122(1)1n n s a n --=-+-， 1因此1122(1)(1)1n n n n na s s a a n n --=-=+-+-， 整理得12nan =×11n a n --〔n ≥2〕， 因此数列{na n}是首项及公比均为12的等比数列。

江西省红色七校2019届高三第二次联考理科数学试题一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合2{|log (2)2}A x R x =∈-<，{1,0,1,2,3}B =-，则A B ⋂真子集的个数（ ） A ．8 B ．7 C ．4 D ．162．若复数(2)()z ai a i =+-在复平面内对应的点在第三象限,其中a R ∈，i 为虚数单位，则实数a 取值范围为（ ）A ．(B ．(C ．D ．[3.已知0.21.1a =，0.2log 1.1b =， 1.10.2c =，则（ ） A ．a b c >>B ．b c a >>C ．a c b >>D ．c a b >>4.下图为国家统计局发布的2018年上半年全国居民消费价格指数（CPI ）数据折线图，（注：同比是今年第n 个月与去年第n 个月之比，环比是现在的统计周期和上一个统计周期之比）下列说法错误的是（ ）A 2018年6月CPI 环比下降0.1%，同比上涨1.9%B 2018年3月CPI 环比下降1.1%，同比上涨2.1%C 2018年2月CPI 环比上涨0.6%，同比上涨1.4%D 2018年6月CPI 同比涨幅比上月略微扩大0.1个百分点5．261(1)(1)x x+-的展开式中，常数项为( )A ．－15B ．16C ．15D ．－166.如图，网格纸上小正方形的边长为1，粗线画出的是某几 何体的三视图，则该几何体的体积为 （ ） A 362π- B 364π- C 482π- D 484π-7．函数()sin()(0,0,)2f x A x A πωϕωϕ=+>><的部分图像如图所示，则1cos2sin 2ϕϕ-=（ ）A ．12 BC 8.有一程序框图如图所示，要求运行后输出的值为大于1000的最小数值，则在空白的判断框内可以填入的是A ．5i ≥B ．6i ≥C ．7i ≥D ．8i ≥9．已知点F 双曲线2222:1(0,0)x y C a b a b-=>>右焦点，直线2y b =与双曲C 交于,A B 两点，且90AFB ∠=o ，则该双曲线的离心率为 （ ）10．杨辉三角，又称帕斯卡三角，是二项式系数在三角形中的 一种几何排列.在我国南宋数学家杨辉所著的《详解九章算 法》（1261年）一书中用如图所示的三角形解释二项式乘方展 开式的系数规律.现把杨辉三角中的数从上到下，从左到右依次排列，得数列：1,1,1,1,2,1,1,3,3,1,1,4,6,4,1…….记作数列{}n a ，若数列{}n a 的前n 项和为n S ，则80S =（ ）A. 2059B. 4108C. 2048D. 4095 11.如图，单位正方体1111ABCD A B C D -的对角面11BB D D 上存在一 动点P ，过点P 作垂直于平面11BB D D 的直线，与正方体表面相交 于M N 、两点.则BMN V 的面积最大值为 （ ）B. 1212.已知()1,1(01),,1xx a x f x a a a a x ⎧-+>⎪=>≠⎨+≤⎪⎩且若()f x 有最小值，则实数a 的取值范围是 （ ） A 2(,1)3 B (1,)+∞ C 2(0,(1,)3⎤⋃+∞⎥⎦ D 2(,1)(1,)3⋃+∞二、填空题：本大题共4小题，每小题5分，共20分．13．已知向量,a b 满足||||2==a b ,且2=g a b ,则向量a 与b 的夹角为 .14.已知实数x ，y 满足02601x y x y x -≤⎧⎪+-≤⎨⎪≥-⎩，则13y x --的取值范围为_____． 15.某外商计划在4个候选城市中投资3个不同的项目，且在同一个城市投资的项目不超过2个，则该外商不同的投资方案有________种．16.在ABC ∆中，角,,A B C 所对的边分别是,,a b c ，若4cos a bC b a+=，且2c =，则ABC ∆的周长取值范围为__________________。