【名师点睛】高中数学必修一 指数及指数函数 知识点+例题+课堂练习+课后练习题(含答案)

高中数学必修1知识点总结—指数及指数函数1、 根式na （一般的，如果n x a =，那么x 叫做a 的n 次方根，其中*1,n n N >∈且.）35325325n n n ⎧=⎪⎨-=-⎪⎩正数的次方根是正数如当是奇数时，负数的次方根是负数如20,n a n an ⎧>±⎪⎨⎪⎩正数的次方根有个，且互为相反数如：则次方根为当是偶数时，负数没有偶次方根0的任何次方根都是0，记作0n2、nna的讨论 n nn a a =当是奇数时，；,0,0n n a a n a a a a ≥⎧==⎨-≤⎩当是偶数时， （2）分数指数幂的概念）分数指数幂的概念①正数的正分数指数幂的意义是：(0,,,mnmna a a m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是：11()()(0,,,m mmnnnaa m n N a a-+==>∈且1)n >．0的负分数指数幂没有意义．义． 注意口诀：底数取倒数，指数取相反数．底数取倒数，指数取相反数． （3）分数指数幂的运算性质）分数指数幂的运算性质①(0,,)rsr saa aa r s R +⋅=>∈ ②()(0,,)r s rsa a a r s R =>∈③()(0,0,)rr rab a b a b r R =>>∈一、 指数计算公式：()Q s r a ∈>,,0_____=⋅s r a a ________=sraa _____)(=s r a ______)(=r ab )1,,0_______(>∈>=*n N n m a anm，________=n na 练习 计算下列各式的值：计算下列各式的值：（1）)4()3)((636131212132b a b a b a ÷- （2）()322175.003129721687064.0+⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛---（3）421033)21(25.0)21()4(--⨯+-- （4）33)3(625π-+-2．已知31=+-x x ，则=+-22x x 已知23=a,513=b，则=-ba 23＝____________. 3. 若21025x x =，则10x x-等于_________________【2.1.2】指数函数及其性质（4）指数函数）指数函数函数名称函数名称指数函数指数函数定义定义函数(0x y a a =>且1)a ≠叫做指数函数叫做指数函数图象图象1a >01a <<定义域定义域 R 值域值域(0,)+∞过定点过定点 图象过定点(0,1)，即当0x=时，1y =．奇偶性奇偶性 非奇非偶非奇非偶单调性单调性在R 上是增函数上是增函数在R 上是减函数上是减函数函数值的函数值的 变化情况变化情况1(0)1(0)1(0)x x x a x a x a x >>==<< 1(0)1(0)1(0)x x x a x a x a x <>==>< a 变化对变化对 图象的影响图象的影响 在第一象限内，a 越大图象越高；在第二象限内，a 越大图象越低．越大图象越低．题型1、求函数经过的点 1、2)(f 1-=+x a x )10(≠>a a 且过定点______________2、函数y=4+a x -1的图象恒过定点P 的坐标是________________3.已知指数函数图像经过点)3,1(-p ，则=)3(f题型2、 图像问题1.下列说法中：下列说法中：①任取x ∈R 都有3x >2x ； ②当a >1时，任取x ∈R 都有a x >a －x ；③函数y =(3)－x 是增函数；④函数y =2|x |的最小值为1 ；⑤在同一坐标系中，y =2x 与y =2－x 的图象对称于y 轴。

第四章指数函数与对数函数指数课后篇巩固提升合格考达标练1.(2021天津滨海新区高一期中)下列运算正确的是( )A.a 2·a 3=a 6 B .(3a )3=9a 3 C .√a 88=a D .(-2a 2)3=-8a 62·a 3=a 5,故A 错误;(3a )3=27a 3,故B 错误;√a 88=|a|={a ,a ≥0,-a ,a <0,故C 错误;(-2a 2)3=-8a 6,故D 正确.故选D .2.(2021湖北武汉高一期中)若a<0,则化简a √-1a 得 ( )A.-√-aB.√-aC.-√aD.√aa<0,∴a √-1a =-√a 2×√-1a =-√a 2(-1a)=-√-a .故选A .3.(2021福建福州三中高一期中)已知x 2+x -2=3,则x+x -1的值为( ) A.√5 B .1 C .±√5 D .±1(x+x -1)2=x 2+x -2+2=5,可得x+x -1=±√5.故选C .4.(112)0-(1-0.5-2)÷(278)23的值为()A.-13 B.13C.43D.73=1-(1-22)÷(32)2=1-(-3)×49=73.故选D . 5.若√4a 2-4a +1=1-2a ,则a 的取值范围是 .-∞,12]√4a 2-4a +1=√(2a -1)2=|2a-1|=1-2a ,∴2a-1≤0,即a ≤12.6.若α,β是方程5x 2+10x+1=0的两个根,则2α·2β= ,(2α)β= .215,得α+β=-2,αβ=15,则2α·2β=2α+β=2-2=14,(2α)β=2αβ=215. 7.化简求值:(1)(94)12-(9.6)0-(278)-23+(23)2; (2)(a 12·√b 23)-3÷√b -4·√a -2(a>0,b>0).原式=[(32)2]12-1-[(23)3]23+(23)2=32-1-49+49=12;(2)原式=a -32·b -2÷b -2·a -12=a -1·b 0=1a .等级考提升练8.(2021河北张家口张垣联盟高一联考)将根式√a √a √aa化简为指数式是( ) A.a-18B.a 18C.a-78D.a-34=a 12+14+18-1=a-18,故选A .9.(2021河南开封高一期中)已知正数x 满足x 12+x -12=√5,则x 2+x -2=( ) A.6 B .7 C .8 D .9x 满足x 12+x -12=√5,所以(x 12+x -12)2=5,即x+x -1+2=5,则x+x -1=3,所以(x +x -1)2=9,即x 2+x -2+2=9,因此x 2+x -2=7.故选B .10.(多选题)(2021河北唐山一中高一期中)下列计算正确的是( )A.√(-3)412=√-33B .(a 23b 12)(-3a 12b 13)÷13a 16b 56=-9a (a>0,b>0)C .√√93=√33D .√-2√23=-213√(-3)4=√3412=√33,故A 错误;(a 23b 12)(-3a 12b 13)÷13a 16b 56=-9a 23+12-16b 12+13-56=-9a ,故B 正确;√√93=916=(32)16=313=√33,故C 正确;√-2√23=(-2√2)13=(-2×212)13=(-232)13=-212,故D 错误.故选BC .11.已知x 2+x -2=2√2,且x>1,则x 2-x -2的值为 ( )A.2或-2B.-2C.√6D.2方法一)∵x>1,∴x 2>1.由x -2+x 2=2√2,可得x 2=√2+1, ∴x 2-x -2=√2+1-√2+1=√2+1-(√2-1)=2.(方法二)令x 2-x -2=t , ① ∵x -2+x 2=2√2,②∴由①2-②2,得t 2=4.∵x>1,∴x 2>x -2, ∴t>0,于是t=2,即x 2-x -2=2,故选D .12.(多选题)(2021江苏扬州邗江高一期中)下列根式与分数指数幂的互化正确的是( ) A.-√x =(-x )12 B.√y 26=y 12(y<0) C.x -13=√x3(x ≠0)D .[√(-x )23]34=x 12(x>0)A,因为-√x =-x 12(x ≥0),而(-x )12=√-x (x ≤0),所以A 错误; 对于选项B,因为√y 26=-y 13(y<0),所以B 错误;对于选项C,x -13=√x3(x ≠0),所以C 正确;对于选项D,[√(-x )23]34=x 2×13×34=x 12(x>0),所以D 正确.13.若a>0,b>0,则化简√b 3a √a2b6的结果为 .√b3a√a 2b6=√b 3a(a 2b6)12=√b 3a ab3=1.14.化简:(2-a )[(a-2)-2(-a )12]12=.-a )14a ≤0,则(a-2)-2=(2-a )-2,所以原式=(2-a )[(2-a )-2·(-a )12]12 =(2-a )(2-a )-1(-a )14=(-a )14.15.化简求值: (1)0.125-13−(98)0+[(-2)2]32+(√2×√33)6;(2)(5116)0.5+√(-10)2-2√3×√276-4π0÷(34)-1.根据指数幂与根式的运算,化简可得0.125-13−(98)0+[(-2)2]32+(√2×√33)6=[(2)-3]-13−(98)0+(22)32+(212×313)6=2-1+8+(212)6(313)6=2-1+8+8×9=81.(2)由分数指数幂及根式的运算,化简可得(5116)0.5+√(-10)2-2√3×√276-4π0÷(34)-1=[(32)4]0.5+10-2√3×(33)16-4×34=94+10-2√3×√3-3 =94+10-6-3=134. 16.已知a 2x =√2+1,求a 3x +a -3xa x +a -x 的值.a2x=√2+1,∴a-2x=√2+1=√2-1,即a2x+a-2x=2√2,∴a3x+a-3xa x+a-x=(a x+a-x)(a2x+a-2x-1)a x+a-x=a2x+a-2x-1=2√2-1.新情境创新练17.(2021黑龙江大庆实验中学高一期末)已知实数x满足3×16x+2×81x=5×36x,则x的值为.或123×16x+2×81x=5×36x,所以3×24x+2×34x=5×(2×3)2x,则3×24x+2×34x=5×22x×32x,所以3×24x+2×34x-5×22x×32x=0,即(3×22x-2×32x)(22x-32x)=0,所以3×22x-2×32x=0,或22x-32x=0,解得x=12或x=0.。

(名师选题)部编版高中数学必修一第四章指数函数与对数函数带答案知识点总结(超全)单选题1、已知函数f (x )=log a (x −b )（a >0且a ≠1，a ，b 为常数）的图象如图，则下列结论正确的是（ ）A ．a >0，b <−1B ．a >0，−1<b <0C ．0<a <1，b <−1D ．0<a <1，−1<b <02、下列计算中结果正确的是（ ）A ．log 102+log 105=1B ．log 46log 43=log 42=12 C ．(log 515)3=3log 515=−3D ．13log 28=√log 283=√33 3、若32是函数f (x )=2x 2−ax +3的一个零点，则f (x )的另一个零点为（ ） A ．1B ．2C ．（1，0）D ．（2，0）4、Logistic 模型是常用数学模型之一，可应用于流行病学领域．有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I (t )(t 的单位：天)的Logistic 模型：I(t)=K1+e −0.23(t−53)，其中K 为最大确诊病例数．当I (t ∗)=0.95K 时，标志着已初步遏制疫情，则t ∗约为（ ）（ln19≈3）A ．60B ．63C ．66D ．695、果农采摘水果，采摘下来的水果会慢慢失去新鲜度．已知某种水果失去新鲜度h 与其采摘后时间t （天）满足的函数关系式为ℎ=m ⋅a t ．若采摘后10天，这种水果失去的新鲜度为10%，采摘后20天，这种水果失去的新鲜度为20%．那么采摘下来的这种水果多长时间后失去40%新鲜度（ ）A ．25天B ．30天C ．35天D ．40天6、下列各组函数中，表示同一个函数的是（ ）A ．y =1与y =x 0B ．y =x 与y =(√x)2C ．y =2log 2x 与y =log 2x 2D ．y =ln 1+x 1−x 与y =ln (1+x )−ln (1−x )7、设f(x)=log 2(1x+a +1)是奇函数，若函数g(x)图象与函数f(x)图象关于直线y =x 对称，则g(x)的值域为（ ）A ．(−∞,−12)∪(12,+∞)B ．(−12,12)C ．(−∞,−2)∪(2,+∞)D ．(−2,2)8、已知0<a <1,b <−1，则函数y =a x +b 的图像必定不经过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限多选题9、若函数y =a x −(b +1)（a >0且a ≠1）的图像过第一、三、四象限，则必有（ ）．A ．0<a <1B ．a >1C ．b >0D ．b <010、（多选题）下列计算正确的是（ ）A ．√(−3)412=√−33B ．(a 23b 12)(−3a 12b 13)÷(13a 16b 56)=−9a a >0,b >0 C ．√√93=√33D ．已知x 2+x −2=2，则x +x −1=211、已知a ，b 均为正实数，若log a b +log b a =52，a b =b a ，则ab =（ ）A ．12B ．√22C ．√2D ．2填空题12、对数型函数f (x )的值域为[0,+∞)，且在(0,+∞)上单调递增，则满足题意的一个函数解析式为______．部编版高中数学必修一第四章指数函数与对数函数带答案(十三)参考答案1、答案：D分析：根据函数图象及对数函数的性质可求解.因为函数f (x )=log a (x −b )为减函数，所以0<a <1又因为函数图象与x 轴的交点在正半轴，所以x =1+b >0，即b >−1又因为函数图象与y 轴有交点，所以b <0，所以−1<b <0，故选：D2、答案：A分析：直接根据对数的运算性质及换底公式计算可得；解：对于A ：log 102+log 105=log 10(2×5)=log 1010=1，故A 正确；对于B ：log 46log 43=log 36，故B 错误； 对于C ：(log 515)3=(log 55−1)3=(−log 55)3=−1，故C 错误； 对于D ：13log 28=13log 223=13×3log 22=1，故D 错误； 故选：A3、答案：A分析：由32是函数f (x )=2x 2−ax +3的一个零点，可得a 值，再利用韦达定理列方程解出f (x )的另一个零点． 因为32是函数f (x )=2x 2−ax +3的一个零点，所以f (32)=2×(32)2−a ×32+3=0，解得a =5．设另一个零点为x 0，则x 0+32=52，解得x 0=1，所以f (x )的另一个零点为1．故选：A ．4、答案：C分析：将t =t ∗代入函数I (t )=K 1+e −0.23(t−53)结合I (t ∗)=0.95K 求得t ∗即可得解.∵I (t )=K 1+e −0.23(t−53)，所以I (t ∗)=K 1+e −0.23(t ∗−53)=0.95K ，则e 0.23(t∗−53)=19，所以，0.23(t ∗−53)=ln19≈3，解得t ∗≈30.23+53≈66.故选：C.小提示：本题考查对数的运算，考查指数与对数的互化，考查计算能力，属于中等题.5、答案：B分析：根据给定条件求出m 及a 10的值，再利用给定公式计算失去40%新鲜度对应的时间作答.依题意，{10%=m ⋅a 1020%=m ⋅a 20，解得m =120,a 10=2，当ℎ=40%时，40%=120⋅a t ， 即40%=120⋅a 10⋅a t−10，解得a t−10=4=(a 10)2=a 20，于是得t −10=20，解得t =30，所以采摘下来的这种水果30天后失去40%新鲜度.故选：B6、答案：D分析：分别计算每个选项中两个函数的定义域和对应关系，定义域和对应关系都相同的是同一个函数，即可得正确选项.对于A ：y =1定义域为R ，y =x 0定义域为{x|x ≠0}，定义域不同不是同一个函数，故选项A 不正确； 对于B ：y =x 定义域为R ，y =(√x)2的定义域为{x|x ≥0}，定义域不同不是同一个函数，故选项B 不正确； 对于C ：y =2log 2x 的定义域为{x|x >0}，y =log 2x 2定义域为{x|x ≠0}，定义域不同不是同一个函数，故选项C 不正确；对于D ：由1+x 1−x >0可得(x +1)(x −1)<0，解得：−1<x <1，所以y =ln 1+x 1−x 的定义域为{x|−1<x <1}，由{1+x >01−x >0可得−1<x <1，所以函数y =ln (1+x )−ln (1−x )的定义域为{x|−1<x <1}且y =ln (1+x )−ln (1−x )=ln 1+x 1−x ，所以两个函数定义域相同对应关系也相同是同一个函数，故选项D 正确， 故选：D.7、答案：A分析：先求出f(x)的定义域，然后利用奇函数的性质求出a 的值，从而得到f(x)的定义域，然后利用反函数的定义，即可求出g(x)的值域．因为f(x)=log 2(1x+a +1)，所以1x+a +1=1+x+a x+a >0可得x <−a −1或x >−a ，所以f(x)的定义域为{x|x <−a −1或x >−a}，因为f(x)是奇函数，定义域关于原点对称，所以−a −1=a ，解得a =−12， 所以f(x)的定义域为(−∞,−12)∪(12,+∞)， 因为函数g(x)图象与函数f(x)图象关于直线y =x 对称，所以g(x)与f(x)互为反函数，故g(x)的值域即为f(x)的定义域(−∞,−12)∪(12,+∞).故选：A .8、答案：A解析：根据指数函数的图象结合图象的平移可得正确的选项.因为0<a <1，故y =a x 的图象经过第一象限和第二象限，且当x 越来越大时，图象与x 轴无限接近.因为b <−1，故y =a x 的图象向下平移超过一个单位，故y =a x +b 的图象不过第一象限.故选：A ．9、答案：BC分析：对底数a 分情况讨论即可得答案.解：若0<a <1，则y =a x −(b +1)的图像必过第二象限，而函数y =a x −(b +1)（a >0且a ≠1）的图像过第一、三、四象限，所以a >1．当a >1时，要使y =a x −(b +1)的图像过第一、三、四象限，则b +1>1，即b >0．故选：BC小提示：此题考查了指数函数的图像和性质，属于基础题.10、答案：BC解析：根据根式运算和指数幂的运算法则求解判断.A. √(−3)412=√3412=√33，故错误；B. (a 23b 12)(−3a 12b 13)÷(13a 16b 56)=−9a23+12−16b 12+13−56=−9a ，故正确； C. √√93=916=(32)16=313=√33，故正确；D. 因为x 2+x −2=(x +x −1)2−2=2，所以(x +x −1)2=4，则x +x −1=±2，故错误； 故选：BC11、答案：AD分析：令t =log a b ，代入可求出t ，可得a 与b 的关系式，再代入a b =b a 即可求出a ，b 的值. 令t =log a b ，则t +1t =52， 所以2t 2−5t +2=0，即(2t −1)(t −2)=0，解得t =12或t =2，即log a b =12或log a b =2，所以a =b 2或a 2=b ，因为a b =b a ，代入得2b =a =b 2或b =2a =a 2，所以a =4，b =2或a =2，b =4，所以a b =2或a b =12.故选：AD.小提示：本题主要考查了对数的运算及性质，属于中档题.12、答案：f (x )=|log 2(x +1)|（答案不唯一，满足f (x )=|log a (x +b )|，a >1，b ≥1即可） 分析：根据题意可利用对数函数的性质和图像的翻折进行构造函数.∵函数f (x )的值域为[0,+∞)，且在(0,+∞)上单调递增，∴满足题意的一个函数是f (x )=|log 2(x +1)|．所以答案是：f (x )=|log 2(x +1)|（答案不唯一）。

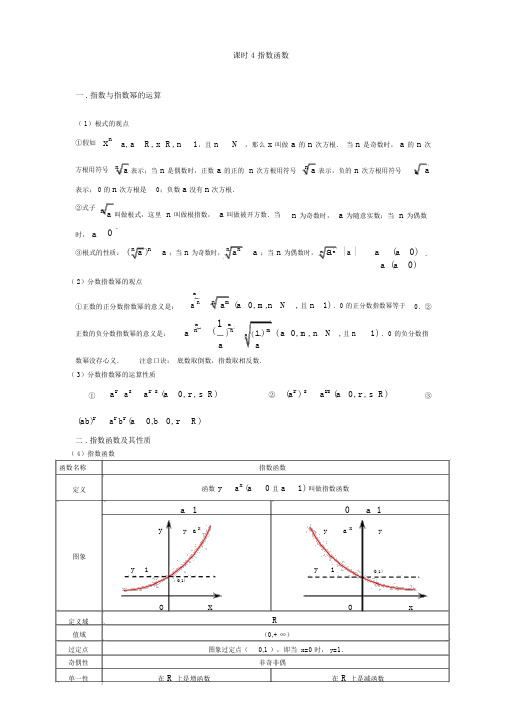
课时 4 指数函数一 . 指数与指数幂的运算（ 1）根式的观点①假如xna, a R, x R, n 1，且 nN ，那么 x 叫做 a 的 n 次方根． 当 n 是奇数时， a 的 n 次方根用符号 na 表示；当 n 是偶数时，正数 a 的正的 n 次方根用符号na 表示，负的 n 次方根用符号na表示； 0 的 n 次方根是 0；负数 a 没有 n 次方根．②式子 n a 叫做根式，这里 n 叫做根指数， a 叫做被开方数．当n 为奇数时， a 为随意实数；当 n 为偶数时， a．③根式的性质： (na )n a ；当 n 为奇数时， n a n a ；当 n 为偶数时， n a n | a |a (a 0) ．a (a 0)（ 2）分数指数幂的观点mna m (a①正数的正分数指数幂的意义是：a n 0, m,n N , 且 n 1) ．0 的正分数指数幂等于0．②m(1m1 ) m( a正数的负分数指数幂的意义是：a n)n n (0, m, n N , 且 n1) ．0 的负分数指aa数幂没存心义． 注意口诀： 底数取倒数，指数取相反数．（ 3）分数指数幂的运算性质①a r a s a r s (a 0, r , s R)② (ar) sa rs (a 0, r , s R)③(ab)ra rb r (a0,b 0, rR)二 . 指数函数及其性质（ 4）指数函数函数名称指数函数定义函数 ya x (a 0 且 a1) 叫做指数函数a 1a 1yy a xya xy图象y1y1(0,1)(0,1)OxOx定义域 R值域（0,+ ∞）过定点 图象过定点（0,1 ），即当 x=0 时， y=1．奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y ＞ 1(x ＞ 0), y=1(x=0), 0＜ y ＜ 1(x ＜ 0)y ＞ 1(x ＜ 0), y=1(x=0), 0＜ y ＜ 1(x ＞ 0)变化状况a 变化对在第一象限内， a 越大图象越高，越凑近 y 轴； 在第一象限内， a 越小图象越高，越凑近 y 轴； 图象影响在第二象限内，a 越大图象越低，越凑近x 轴．在第二象限内，a 越小图象越低，越凑近x 轴．三 .例题剖析1.设 a 、 b 知足 0<a<b<1,以下不等式中正确的选项是 ( C)A.a a <a bB.b a <b bC.a a <b aD.b b <a b 分析： A 、B 不切合底数在 (0,1) 之间的单一性 ; C 、 D 指数同样 , 底小值小 . 应选 C. 2.若 0<a<1,则函数 y=a x 与 y=(a-1)x 2 的图象可能是 (D )分析： 当 0<a<1 时 ,y=a x 为减函数 ,a-1<0, 因此 y=(a-1)x2张口向下 , 应选 D.3.设指数函数 f(x)=a x (a>0 且 a ≠ 1),则以下等式中不正确的选项是 ( D )A.f(x+y)=f(x)f(y)f (x)B.f(x-y)=f ( y)C.f(nx)= ［ f(x) ］ nD.f ［ (xy) n ］ =［ f(x) ］ n ［ f(y) ］ n (n ∈ N * )分析： 易知 A 、 B 、 C 都正确 .对于 D,f ［(xy)n］ =a (xy)n , 而［ f(x) ］ n ·［f(y) ］ n =(a x ) n ·(a y ) n =a nx+ny , 一般状况下 D 不建立 .11 34.设 a= ( 3) 3,b= ( 4)4,c= ( 3) 4,则 a 、b 、 c 的大小关系是 ( B )43 2A.c<a<b3分析： a= ( )B.c<b<aC.b<a<cD.b<c<a1 111(8133( 4)3 ( 4) 4=b, b=(4) 4)4(3) 4 =c.∴ a>b>c.3 332725.设 f(x)=4 x -2x+1,则 f -1 (0)=______1____________. 分析： 令 f -1 (0)=a, 则 f(a)=0 即有 4a -2 · 2a =0.2a · (2 a -2)=0, 而 2a >0,∴ 2a =2 得 a=1.6.函数 y=a x-3 +4(a>0 且 a ≠ 1)的反函数的图象恒过定点 ______(5,3)____________.分析： 因 y=a x 的图象恒过定点 (0,1), 向右平移 3 个单位 , 向上平移 4 个单位获得 y=a x-3 +4 的图象 , 易知恒过定点 (3,5).故其反函数过定点 (5,3).10 x 10 x.证明 f(x) 在 R 上是增函数 .7.已知函数 f(x)=x10 x10x1010x102x1,设 x 1<x 2∈ R,则f(x 1)-f(x2)=10x 1 1010x 1 10x 110x 210 x 2102 x 11 102 x 21 2(102 x 1102 x2).x 110x2 10x2 102 x1 1102 x21(102 x11)(102 x 2 1)∵ y=10 x是增函数 ,∴ 10 2x 1 10 2x 2 <0.而 10 2x 1 +1>0, 102 x 2 +1>0,故当 x <x 时 ,f(x)-f(x )<0,1212即 f(x 1)<f(x 2). 因此 f(x) 是增函数 .8.若定义运算 a b=b, ab,则函数 f(x)=3 x3-x 的值域为 ( A )a, a b,A.(0,1]B. ［ 1,+∞ )C.(0,+ ∞ )D.(- ∞ ,+∞ )分析： 当 3x ≥3-x , 即 x ≥ 0 时 ,f(x)=3-x∈(0,1 ］ ;x-x, 即 x<0 时 ,f(x)=3x∈ (0,1).3 x , x 0, 当 3<3∴ f(x)=x值域为 (0,1).3x ,0,9.函数 y=a x 与 y=-a -x (a>0,a ≠1) 的图象 ( C )A. 对于 x 轴对称B.对于 y 轴对称C.对于原点对称D.对于直线 y=-x 对称分析： 可利用函数图象的对称性来判断两图象的关系.10.当 x ∈［ -1,1］时 ,函数 f(x)=3 x-2 的值域为 _______［ -5,1 ］ ___________.3分析： f(x) 在［ -1,1 ］上单一递加 .11.设有两个命题 :(1)对于 x 的不等式 x 2+2ax+4>0对全部 x ∈ R 恒建立 ;(2) 函数 f(x)=-(5-2a) x是减函数 .若命题 (1)和 (2)中有且仅有一个是真命题 ,则实数 a 的取值范围是 _______(- ∞ ,-2)__________.分析： (1) 为真命题=(2a) 2-16<0-2<a<2. (2)为真命题 5-2a>1 a<2.若 (1) 假 (2) 真 , 则 a ∈ (- ∞ ,-2]. 若 (1) 真 (2) 假, 则 a ∈ (-2,2)∩［ 2,+ ∞］=.故 a 的取值范围为 (- ∞ ,-2).12.求函数 y=4 -x -2-x +1,x ∈［ -3,2］的最大值和最小值 .解： 设 2-x=t, 由 x ∈［ -3,2 ］得 t ∈［ 1,8 ］ , 于是 y=t 2-t+1=(t-1)2+3. 当 t= 1时 ,y3 .424有最小值 这时 x=1.当 t=8 时 ,y 有最大值57.这时 x=-3.2413.已知对于 x 的方程 2a2x-2-7a x-1 +3=0 有一个根是 2,求 a 的值和方程其他的根 . 解： ∵ 2 是方程 2a2x-2-9a x-1+4=0 的根 , 将 x=2 代入方程解得 a= 1或 a=4.2(1) 当 a= 1时 , 原方程化为 2· ( 1)2x-2-9(1) x-1 +4=0.①222x-1 2令 y=( 1) , 方程①变成 2y -9y+4=0,2解得 y 1=4,y 2= 1.∴ ( 1) x-1 =42x=-1,2( 1 ) x-1 = 1x=2.22(2) 当 a=4 时 , 原方程化为 2· 42x-2 -9 · 4x-1 +4=0. ②令 t=4 x-1 , 则方程②变成 2t 2-9t+4=0. 解得 t 1=4,t 2= 1.x-12=4x=2,∴44x-1 = 1x=- 1 .22故方程此外两根是当 a= 1时 ,x=-1;1 .2当 a=4 时 ,x=-214.函数 y= (1) 3 4xx 2的单一递加区间是 ( D )3A. ［ 1,2］B.［ 2,3］C.(-∞ ,2]D.［ 2,+∞ )分析： 由于 y=3x2-4x+3 , 又 y=3t 单一递加 ,t=x 2-4x+3 在 x ∈［ 2,+ ∞ ) 上递加 , 故所求的递加区间为［ 2,+ ∞ ).15.已知 f(x)=3 x-b (2≤ x ≤ 4,b 为常数 ) 的图象经过点 (2,1), 则 F(x)=f 2(x)-2f(x) 的值域为 ( B )A. ［ -1,+∞ )B. ［ -1,63)C.［ 0,+∞ )D.(0,63 ］分析： 由 f(2)=1, 得 32-b =1,b=2,f(x)=3 x-2.∴ F (x)= ［ f(x)-1 ］2-1=(3 x-2 -1) 2-1. 令 t=3 x-2 ,2 ≤x ≤4.2∴g(t)=(t-1) - 1,t ∈［ 1,9 ］.2.1 指数函数练习1．以下各式中建立的一项A ． ( n)71n 7 m 7B ．12 ( 3)433m3C ． 4 x 3y 3( x y) 4D ．393321111 1 52．化简 (a 3 b 2 )( 3a 2 b 3 ) ( a 6 b 6 ) 的结果3D ． 9a 2 A ． 6aB ． aC ． 9a3．设指数函数 f ( x)a x ( a 0, a1) ，则以下等式中不正确的选项是f (x) A ． f(x+y)=f(x) ·f(y)B ． f （ x y ）f ( y)C ． f (nx)[ f ( x)]n (nQ )D ． f ( xy) n [ f ( x)] n ·[f ( y)] n1 4．函数 y (x5) 0 ( x 2)2A ． { x | x 5, x 2}B ． { x | x 2}C ． { x | x 5}D ． { x | 2 x 5或 x 5}（）（）（）(n N )（ ）5．若指数函数 y a x 在 [－ 1,1]上的最大值与最小值的差是1，则底数 a 等于 （）A ．15 B ．1 5 C ．15D ．5 122 226．当 a0 时，函数 y axb 和 yb ax 的图象只可能是（）7．函数 f ( x)2 |x| 的值域是（）A ． (0,1]B ． (0,1)C ． (0, )D ． R8．函数 f ( x)2 x 1, x 0，知足 f ( x)1的 x 的取值范围1x 2 , x（）A ． ( 1,1)B ． ( 1, )C ． { x | x 0或 x2}D ． { x | x 1或 x1}9．函数 y(1) x 2x2得单一递加区间是2（）A ．[ 1,1]B ． ( , 1]C ．[2,)D ．[ 1,2]2exe x210．已知 f ( x)（）2 ，则以下正确的选项是A ．奇函数，在 R 上为增函数B ．偶函数，在 R 上为增函数C ．奇函数，在 R 上为减函数D ．偶函数，在 R 上为减函数11．已知函数 f (x)的定义域是（1， 2），则函数 f (2 x ) 的定义域是.12．当 a ＞0 且 a ≠1 时，函数 f (x)=a x －2－ 3 必过定点.三、解答题：13．求函数 y1的定义域 .x5 x 1114．若 a ＞0， b ＞ 0，且 a+b=c ，求证： (1) 当r ＞1时， a r +b r ＜ c r ； (2) 当r ＜ 1时， a r +b r ＞ c r .a x 1 15．已知函数 f ( x)(a ＞1) .a x1（ 1）判断函数 f (x) 的奇偶性；（ 2）证明 f (x)在 (－∞， +∞ )上是增函数 .xa16．函数 f(x) ＝ a (a>0 ，且 a ≠1) 在区间 [1,2] 上的最大值比最小值大2，求 a 的值．参照答案一、 DCDDD AADDA二、 11． (0,1)；12． (2，－ 2) ；三、 13． 解：要使函数存心义一定：x 1 0x 1x0 x 0x 1∴ 定义域为 ： x xR 且 x0, x 1a rrrb r此中a1,0b114． 解：ba，c rcccc.r ＞1 ，a rb ra b 1，r r r当因此+b＜ c ；时c c c crrrrr当 r ＜ 1 时， aba b1， 因此 a +b ＞c .ccc c15． 解 ：(1)是奇函数 .(2) 设x ＜x ，则 f (x 1 )ax11 ax21 。

(名师选题)部编版高中数学必修一第四章指数函数与对数函数带答案基础知识点归纳总结单选题1、已知函数f(x)={log 12x,x >0,a ⋅(13)x,x ≤0,若关于x 的方程f[f(x)]=0有且只有一个实数根，则实数a 的取值范围是（ ）A ．(−∞,0)∪(0,1)B ．(−∞,0)∪(1,+∞)C ．(−∞,0)D ．(0,1)∪(1,+∞) 2、设f(x)=log 2(1x+a+1)是奇函数，若函数g(x)图象与函数f(x)图象关于直线y =x 对称，则g(x)的值域为（ ）A ．(−∞,−12)∪(12,+∞)B ．(−12,12) C ．(−∞,−2)∪(2,+∞)D ．(−2,2)3、已知0<a <1,b <−1，则函数y =a x +b 的图像必定不经过（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限4、果农采摘水果，采摘下来的水果会慢慢失去新鲜度．已知某种水果失去新鲜度h 与其采摘后时间t （天）满足的函数关系式为ℎ=m ⋅a t ．若采摘后10天，这种水果失去的新鲜度为10%，采摘后20天，这种水果失去的新鲜度为20%．那么采摘下来的这种水果在多长时间后失去50%新鲜度（已知lg2≈0.3，结果取整数）（ ）A ．23天B ．33天C ．43天D ．50天 5、已知函数f(x)=9+x 2x，g(x)=log 2x +a ，若存在x 1∈[3,4]，对任意x 2∈[4,8]，使得f(x 1)≥g(x 2)，则实数a 的取值范围是（ ）A ．(−∞,134]B ．(134,+∞)C ．(0,134)D ．（1，4）6、计算：2lg √5−lg 4−12=（ ） A ．10B ．1C ．2D ．lg 57、设函数f （x ）＝ln |2x +1|﹣ln |2x ﹣1|，则f （x ）（ ）A ．是偶函数，且在 (12，+∞)单调递增 B ．是奇函数，且在 (−12，12)单调递增 C ．是偶函数，且在(−∞，−12)单调递增 D ．是奇函数，且在 (−∞，−12)单调递增8、已知y 1=(13)x，y 2=3x ，y 3=10−x ，y 4=10x ，则在同一平面直角坐标系内，它们的图象大致为（ ）A ．B ．C ．D ．多选题9、已知函数f (x )=lnx +ln (2−x )，则（ ） A ．f (x )在(0,2)单调递增B ．f (x )在(0,1)单调递增，在(1,2)单调递减C ．y =f (x )的图象关于直线x =1对称D ．y =f (x )的图象关于点(1,0)对称10、已知函数f (x )={|lnx |,x >0−x 2+1,x ≤0，若存在a <b <c ，使得f (a )=f (b )=f (c )成立，则（ ）A ．bc =1B ．b +c =1C．a+b+c>1D．abc<−111、(多选)某食品的保鲜时间t(单位：小时)与储藏温度x(单位：℃)满足函数关系t＝{64,x≤0,2kx+6,x>0,且该食品在4 ℃的保鲜时间是16小时．已知甲在某日上午10时购买了该食品，并将其遗放在室外，且此日的室外温度随时刻的变化如图所示，则下列结论中正确的是（）A．该食品在6 ℃的保鲜时间是8小时B．当x∈[－6，6]时，该食品的保鲜时间t随着x的增大而逐渐减少C．到了此日13时，甲所购买的食品还在保鲜时间内D．到了此日14时，甲所购买的食品已然过了保鲜时间填空题12、若指数函数的图像经过点(2,14)，则指数函数的解析式为___．部编版高中数学必修一第四章指数函数与对数函数带答案(六)参考答案1、答案：B分析：利用换元法设t =f (x )，则等价为f (t )=0有且只有一个实数根，分a <0,a =0,a >0 三种情况进行讨论，结合函数的图象，求出a 的取值范围. 令f(x)=t ，则方程f[f(x)]=0等价于f(t)=0，当a =0时，此时当x ≤0时，f (x )=a ⋅(13)x=0，此时函数有无数个零点，不符合题意；当a ≠0，则f(x)=a ⋅(13)x≠0，所以由f(t)=log 12t =0，得t =1，则关于x 的方程f[f(x)]=0有且只有一个实数根等价于关于x 的方程f(x)=1有且只有一个实数根，作出f(x)的图象如图：当a <0时，由图象可知直线y =1与y =f(x)的图象只有一个交点，恒满足条件； 当a >0时，要使直线y =1与y =f(x)的图象只有一个交点， 则只需要当x ≤0时，直线y =1与f(x)=a ⋅(13)x的图象没有交点，因为x ≤0 时，f (x )=a ⋅(13)x∈[a,+∞)，此时f (x ) 最小值为a ，所以a >1，综上所述，实数a 的取值范围是(−∞,0)∪(1,+∞)， 故选：B. 2、答案：A分析：先求出f(x)的定义域，然后利用奇函数的性质求出a 的值，从而得到f(x)的定义域，然后利用反函数的定义，即可求出g(x)的值域． 因为f(x)=log 2(1x+a+1)，所以1x+a +1=1+x+a x+a>0可得x <−a −1或x >−a ，所以f(x)的定义域为{x|x <−a −1或x >−a}，因为f(x)是奇函数，定义域关于原点对称，所以−a −1=a ，解得a =−12，所以f(x)的定义域为(−∞,−12)∪(12,+∞)，因为函数g(x)图象与函数f(x)图象关于直线y =x 对称， 所以g(x)与f(x)互为反函数，故g(x)的值域即为f(x)的定义域(−∞,−12)∪(12,+∞).故选：A . 3、答案：A解析：根据指数函数的图象结合图象的平移可得正确的选项. 因为0<a <1，故y =a x 的图象经过第一象限和第二象限， 且当x 越来越大时，图象与x 轴无限接近.因为b <−1，故y =a x 的图象向下平移超过一个单位，故y =a x +b 的图象不过第一象限. 故选：A ． 4、答案：B分析：根据题设条件先求出m 、a ，从而得到ℎ=120⋅2110t ，据此可求失去50%新鲜度对应的时间.{10%=m ⋅a 1020%=m ⋅a 20⇒{a 10=2,m =120 ，故a =2110，故ℎ=120⋅2110t ， 令ℎ=12，∴2t10=10,∴t 10lg2=1，故t =100.3≈33， 故选：B. 5、答案：A分析：将问题化为在对应定义域内f(x 1)max ≥g(x 2)max ，结合对勾函数和对数函数性质求它们的最值，即可求参数范围.由题意知：f(x)在[3,4]上的最大值大于或等于g(x)在[4,8]上的最大值即可． 当x ∈[3,4]时，f(x)=9x +x ，由对勾函数的性质得：f(x)在[3,4]上单调递增，故f(x)max =f(4)=94+4=254．当x ∈[4,8]时，g(x)=log 2x +a 单调递增，则g(x)max =g(8)=log 28+a =3+a ， 所以254≥3+a ，可得a ≤134．故选：A 6、答案：B分析：应用对数的运算性质求值即可. 2lg √5−lg 4−12=lg(√5)2+lg √4=lg5+lg2=lg10=1.故选：B 7、答案：B分析：先求出f (x )的定义域结合奇偶函数的定义判断f (x )的奇偶性，设t ＝|2x+12x−1|，则y ＝ln t ，由复合函数的单调性判断f (x )的单调性，即可求出答案.解：由{2x +1≠02x −1≠0，得x ≠±12．又f （﹣x ）＝ln |﹣2x +1|﹣ln |﹣2x ﹣1|＝﹣（ln |2x +1|﹣ln |2x ﹣1|）＝﹣f （x ）， ∴f （x ）为奇函数，由f （x ）＝ln |2x +1|﹣ln |2x ﹣1|＝ln |2x+12x−1|， ∵2x+12x−1=1+22x−1=1+1x−12．可得内层函数t ＝|2x+12x−1|的图象如图，在（﹣∞，−12），（12，+∞）上单调递减，在（−12，12）上单调递增， 又对数式y ＝lnt 是定义域内的增函数，由复合函数的单调性可得，f （x ）在（−12，12）上单调递增，在（﹣∞，−12），（12，+∞）上单调递减．故选：B ．8、答案：A分析：根据指数函数的单调性及图像特征进行比较，即可判断.y 2=3x 与y 4=10x 是增函数，y 1=(13)x与y 3=10−x =(110)x是减函数，在第一象限内作直线x =1，该直线与四条曲线交点的纵坐标的大小对应各底数的大小，易知：选A ． 故选：A 9、答案：BC分析：由题可得函数的定义域，化简函数f (x )=lnx (2−x )=ln (−x 2+2x )，分析函数的单调性和对称性，从而判断选项.函数的定义域满足{x >02−x >0，即0<x <2，即函数的定义域是{x |0<x <2 }， ∵f (x )=lnx (2−x )=ln (−x 2+2x )，设t =−x 2+2x =−(x −1)2+1，则函数在(0,1)单调递增，在(1,2)单调递减， 又函数y =lnt 单调递增，由复合函数单调性可知函数f (x )在(0,1)单调递增，在(1,2)单调递减，故A 错误，B 正确； 因为f (1+x )=ln (1+x )+ln (1−x ),f (1−x )=ln (1−x )+ln (1+x ),所以f (1−x )=f (1+x )，即函数y =f (x )图象关于直线x =1对称，故C 正确； 又f (12)=ln 12+ln (2−12)=ln 34，f (32)=ln 32+ln (2−32)=ln 34，所以f (12)=f (32)=ln 34，所以D 错误． 故选：BC ． 10、答案：AC分析：采用数形结合可知−1<a ≤0，1e ≤b <1，1<c ≤e ，然后简单计算可知b +c >1，bc =1，a +b +c >1，故可知结果. 如图：可知−1<a ≤0，1e ≤b <1，1<c ≤e ，则b +c >c >1， 且−lnb =lnc ，所以lnb +lnc =lnbc =0，即bc =1.因为bc =1，所以abc =a ∈(−1,0]，a +b +c =a +1c +c >a +2>1. 故选:AC.11、答案：AD分析：由题设可得k=−1即可写出解析式，再结合各选项的描述及函数图象判断正误即可.2，由题设，可得24k+6=16，解得k=−12∴t={64,x≤0，26−x2,x>0∴x=6，则t=23=8，A正确；x∈[−6,0]时，保鲜时间恒为64小时，x∈(0,6]时，保鲜时间t随x增大而减小，B错误；此日11时，温度超过11度，其保鲜时间不超过2小时，故到13时甲所购食品不在保鲜时间内，C错误；由上分析知：此日14时，甲所购食品已过保鲜时间，D正确.故选：AD.)x12、答案：f(x)=(12分析：设指数函数的解析式为f（x）=a x（a＞0且a≠1）,代入(2,1)计算即可得解.4解：设指数函数的解析式为f（x）=a x（a＞0且a≠1），∴a2=1，4，解得a=12∴f(x)=(1)x.2)x.所以答案是：f(x)=(12。

【名师点睛】高中数学必修一指数及指数函数知识点+例题+课堂练习+课后练习题(含答案)指数与指数函数1.指数及其相关概念:n, (1)n次方根:如果存在实数x，使得x=a(a?R,n>1,n?N)，那么x叫做a的n 次方根.(2)求a的n次方根，叫做a开n次方，称作开方运算;当n是奇数时，正数的n次方根是一个正数，负数的n次方根是一个负数.表示为: ;当n是偶数时，正数的n次方根有个，表示为 ; 2.分数指数:mn 正分数指数幂:a= ;(a>0,m,n?N*,且n>1)m,n 负分数指数幂:a= = ;(a>0,m,n?N*,且n>1) 3.指数幂的运算性质:nnnnnn = ;= (当n为奇数时);= = (当n为偶数时); aa(a)rs (1)a?a= ;(a>0,r,s?Q)sr (2)(a)= = ;(a>0,b>0,r,s?Q)3)(ab)r= ;(a>0,b>0,r,s?Q) (4.指数函数:x(1)一般地，函数y=a(a>0且a?1,x?R)叫做指数函数.(2)图象性质:0<a<1 a>1图象定义域值域过定点单调性在R上 ; 在R上 ;x (3)结合函数图象总结出a、x、a三者之间的一种大小关系:x 当x>0时，若a>1，则a 1;若0<a<1，则 ;x 当x<0时，若a>1，则 ;若0<a<1，则a 1.第 1 页共 1 页2233【例1】(1)填空:?= ;?= ;?= (x<1); x,2x，1(,5)(,3)213,,164334324 ?= ;?= ;?= ;7= . 825()(3,,),(3,,)811y32【例2】(1)已知，则的值为 . x3x,2,(4,6x),(x，y,1)623 (2)若，则实数a的取值范围是( ) 4a,4a，1,1,2aA.a?RB.a=0.5C.a>0.5D.a?0.52,3 (3)若x,2，则x= .x【例3】(1)函数f(x)=a与g(x)=ax-a的图象大致是( )xxxx (2)曲线C，C，C，C分别是指数函数y=a，y=b，y=c，y=d的图象，判断a，b，c，d， 12341234. 1的大小关系是x (3)用min{a,b,c}表示a,b,c三个数中的最小值，设f(x)=min{2,x+2,10-x}(x?0),则f(x)的最大值为( )A.4B.5C.6D.7函数图象过定点问题x【例4】(1)指数函数y=a(a>0,且a?1)的图象恒过定点 .x+2 (2)函数f(x)=a+2(a>0,且a?1)的图象恒过定点 . 【例5】(1)比较下来各题中两个值的大小:2.53-0.1-0.20.33.1-0.3-3.1 ?1.7,1.7; ?0.8,0.8; ?1.7,0.9; ?1.7,0.9..232322555()()() (2)设a=，b=，c=，则a、b、c的大小关系是( ) 555A.a>c>bB.a>b>cC.c>a>bD.b>c>a【例6】求下列函数的定义域、值域:12,x1，2x,xx,1 (1)y,2; (2); (3). y,3y,2第 2 页共 2 页.21x,2x【例7】(1)函数f(x)=的单调增区间为，值域为 . f(x),()3xx，1(2)已知. f(x),4,2，3?当f(x)的定义域为(-?,0]时，函数的值域为 ;?当f(x)的值域为[2,11]时，x的取值范围是 .课堂练习: x1.如果函数f(x)=(1-2a)在实数集R上是减函数,那么实数a的取值范围是( )A.(0,0.5)B.(0.5,，?)C.(-?,0.5)D.(-0.5,0.5)112a，13,2a2.若()<()，则实数a的取值范围是( ) 4411()1，，?A.(,+?) B. C.(,?，1) D.(-?,) 2210.90.48,1.53.设y=4，y=8，y=()，则( ) 1232A.y>y>yB.y>y>yC.y>y>yD.y>y>y 312213 123132x-14..若函数y=3?2的反函数的图像经过P点，则P点坐标是( )A.(2，5)B.(1，3)C.(5，2)D.(3，1) x5.设函数f(x)定义在实数集上，它的图象关于直线x=1对称，且当x?1时，f(x)=3,1，则有( )xyx-y6.若10=3,10=4,则10= .22,3x7.函数y=3的单调递减区间是 .8.下列空格中填“>、<或,”(2.53.2,1.2,1.5(1)1.5______1.5，(2)0.5______0.5.9.填空:x (1)已知函数f(x)=2,?当x?1时，函数值域为 ;?当x>0时，函数值域为 ;x(2)已知函数g(x)=(0.5),1当x?0时，函数值域为 ;2当x<1时，函数值域为 .11,2x10.根据下列条件确定实数x的取值范围:( a,()(a,0且a,1)a第 3 页共 3 页222x,3x，1x，2x,511.设0<a<1,解关于x的不等式a>a.212.已知a>0且a?1，讨论f(x)=a-x，3x，2的单调性(x,x13.已知函数 f(x),3，3.(1)判断函数的奇偶性;(2)求函数的单调增区间，并证明(11xxf(x),(),()，114.求函数(x?[-3,2])的单调区间及其值域. 42 第 4 页共 4 页x,x10,1015.已知. (),fxx,x10，10(1)判断函数f(x)的奇偶性;(2)证明:f(x)是定义域内的增函数;(3)求f(x)的值域.课后练习题第 5 页共 5 页参考答案例1.例2.例3.例4.例5.第 6 页共 6 页例6.例7.课堂练习参考答案 1.A.2.A.第 7 页共 7 页3.D.4.B.x5.B.因为f(x)的图象关于直线x=1对称，所以f(1/3)=f(5/3)，f(2/3)=f(4/3)，因为函数f(x)=3,1在[1，，?)上是增函数，所以f(5/3)>f(3/2)>f(4/3)，即f(2/3)<f(3/2)<f(1/3)(故选B.6.答案为:0.75;7.答案为:(0,+?);2.53.2,1.2,1.58.答案为:(1)1.5<1.5.(2)0.5<0.5.9.答案为:(1)(0,2];(1，+?);(2)(0,1],(0.5,+?). 2x,10.5x10.解:原不等式可以化为a>a，因为函数y=a(a>0且a?1)当底数a大于1时在R上是增函数;当底数a大于0小于1时在R上是减函数，所以当a>1时，由2x,1>0.5，解得x>0.75;当0<a<1时，由2x,1<0.5，解得x<0.75.综上可知:当a>1时，x>0.75;当0<a<1时，x<0.75.x11.解:?0<a<2,? y=a在(-，+)上为减函数， ,,22222x,3x，1x，2x,5? a>a, ?2x-3x+1<x+2x-5,解得2<x<3,22=-x，3x，2=-(x-1.5)，4.25， 12.解:设u则当x?1.5时，u是减函数，当x?1.5时，u是增函数(uu又当a>1时，y=a是增函数，当0<a<1时，y=a是减函数，2所以当a>1时，原函数f(x)=a-x，3x，2在[1.5,+?)上是减函数，在(-?,1.5]上是增函数(2当0<a<1时，原函数f(x)=a-x，3x，2在[1.5,+?)是增函数，在(-?,1.5]上是减函数(,x,(,x),xxx,x13.解:(1)f(-x)=3，3=3，3=f(x)且x?R，?函数f(x)=3，3是偶函数((2)由(1)知，函数的单调区间为(-?，0]及[0，，?)，且[0，，?)是单调增区间(现证明如下:x1-x1x2-x2设0?x<x，则f(x)-f(x)=3，3-3-3 1212,3x，x113x1,3x2112=3x-3x，-=3x,3x，=(3x,3x)?. 1212213x3x3x3x3x，x121212?0?x<x，?3x>3x，3x，x>1，?f(x),f(x)<0，即f(x)<f(x)， 1221121212?函数在[0，，?)上单调递增，即函数的单调增区间为[0，，?)( 14.第 8 页共 8 页15.第 9 页共 9 页课后练习参考答案 1.2.B3.第 10 页共 10 页4.5.第 11 页共 11 页。

§3 指数函数课后训练巩固提升1.如果指数函数y=f(x)的图象经过点(-2,14),那么f(4)·f(2)等于( ).A.8B.16C.32D.64f(x)=a x (a>0,且a≠1),由条件知f(-2)=14,故a -2=14,所以a=2,因此f(x)=2x ,所以f(4)·f(2)=24×22=64.2.不论a 取何正实数,函数f(x)=a x+1-2的图象恒过点( ).A.(-1,-1)B.(-1,0)C.(0,-1)D.(-1,-3)x+1=0,则x=-1,f(-1)=1-2=-1,所以f(x)的图象恒过点(-1,-1).3.函数y=a |x|(0<a<1)的大致图象是( ).|x|(0<a<1)是偶函数,先画出当x≥0时的图象,再画出关于y 轴对称的图象.又0<a<1,故选C.4.(多选题)已知函数f(x)=πx ,g(x)=(1π)x,则下列说法正确的有( ). A.f (15)>g (16) B.f(x)与g(x)的图象关于x 轴对称C.f(x)与g(x)的图象关于y 轴对称D.f(x)与g(x)的图象可能有两个公共点(15)=π15>1,g (16)=(1π)16<1, 所以f (15)>g (16).故A 正确. 设点(x,y)为函数f(x)=πx 的图象上任意一点,则点(-x,y)为函数g(x)=π-x =(1π)x的图象上的点.因为点(x,y)与点(-x,y)关于y 轴对称,所以函数f(x)=πx 与g(x)=(1π)x的图象关于y 轴对称.故C 正确,B 错误. f(x)与g(x)的图象只有一个公共点(0,1).故D 错误.5.若指数函数f(x)=a x (a>0,且a≠1)的图象过点(2,14),则满足a x 2>a 2-x 的x 的取值范围是( ).A.{x |-1<x <12}B.{x|-2<x<1}C.{x|x<-2,或x>1}D.{x |x <-1,或x >12},f(2)=14,即a 2=14, 所以a=12, 所以a x 2>a 2-x ,即(12)x 2>(12)2-x ,所以x 2<2-x,即x 2+x-2<0,解得-2<x<1.6.若-1<x<0,a=2-x ,b=2x ,c=0.2x ,则a,b,c 的大小关系是 .(用“<”连接)-1<x<0,所以由指数函数的图象和性质,可得b=2x <1,a=2-x >1,c=0.2x >1.又因为2-x =0.5x <0.2x ,所以b<a<c.7.已知定义在R 上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=a x -a -x +2(a>0,且a≠1).若g(2)=a,则f(2)= ,函数f(x)的图象与x 轴的交点坐标为 .f(x)是奇函数,g(x)是偶函数,∴由f(x)+g(x)=a x -a -x +2,①得f(-x)+g(-x)=-f(x)+g(x)=a-x-a x+2,②①+②,得2g(x)=4,即g(x)=2;①-②,得2f(x)=2a x-2a-x,即f(x)=a x-a-x.又g(2)=a,∴a=2,∴f(x)=2x-2-x,.∴f(2)=22-2-2=154令f(x)=0,得2x-2-x=0,解得x=0.故所求交点坐标为(0,0).(0,0)8.已知函数y=9x-2·3x+2,x∈[1,2],求函数的值域.x-2·3x+2=(3x)2-2·3x+2.设t=3x.∵x∈[1,2],∴t∈[3,9],则函数化为y=f(t)=t2-2t+2,t∈[3,9]. ∴f(t)在区间[3,9]上单调递增,∴f(3)≤f(t)≤f(9),即5≤f(t)≤65.故所求值域为[5,65].9.已知定义在R上的函数f(x)=2x-1.2|x|(1)若f(的取值范围.当x<0时,f(x)=0,没有符合要求的x;当x≥0时,f(x)=2x-12x,由2x-12x =32,得2·22x-3·2x-2=0,将上式看成关于2x的一元二次方程,解得2x=2或2x=-12.∵2x>0,∴2x=2,∴x=1.综上所述,所求f(t)≥0恒成立,即2t(22t-122t )+m(2t-12t)≥0恒成立,即m(22t-1)≥-(24t-1)恒成立.∵22t-1>0,∴m≥-(22t+1)恒成立.∵t∈[1,2],∴-(22t+1)∈[-17,-5], 故实数m的取值范围是[-5,+∞).。

4.3.2 对数的运算课后训练巩固提升1.(多选题)若a>0,且a≠1,x∈R,y∈R,且xy>0,则下列各式不恒成立的是( )A.log a x2=2log a xB.log a x2=2log a|x|C.log a(xy)=log a x+log a yD.log a(xy)=log a|x|+log a|y|xy>0,所以x>0,y>0或x<0,y<0.若x<0,则A不成立;若x<0,y<0,则C也不成立,故选AC.2.已知a=log32,则log38-2log36=( )A.a-2B.5a-2C.3a-(1+a)2D.3a-a2-16=3log32-2(log32+log33)=3a-2(a+1)=a-2.38-2log3×log36×log6x=2,则x等于( )3.若log513A.9B.19C.25D.125由对数换底公式得-lg3lg5×lg6lg3×lgx lg6=2,即lgx=-2lg5,解得x=5-2=125.4.若lg a,lg b 是方程2x 2-4x+1=0的两根,则(lg a b)2=( )A.14B.12C.1D.2lga+lgb=2,lga·lgb=12.所以(lg a b )2=(lga-lgb)2=(lga+lgb)2-4lga·lgb=22-4×12=2.5.已知4a =5b =10,则1a+2b = .4a =5b =10,∴a=log 410,1a=lg4,b=log 510,1b=lg5,∴1a+2b=lg4+2lg5=lg4+lg25=lg100=2.6.计算:(1)(log 3312)2+log 0.2514+9log 5√5-lo g √31;(2)2lg2+lg31+12lg0.36+13lg8.(log 3312)2+log 0.2514+9log 5√5-lo g √31=(12)2+1+9×12-0=14+1+92=234.(2)2lg2+lg31+12lg0.36+13lg8=2lg2+lg31+12lg0.62+13lg23=2lg2+lg31+lg0.6+lg2=2lg2+lg31+lg6-lg10+lg2=2lg2+lg3lg6+lg2=2lg2+lg3lg2+lg3+lg2=2lg2+lg32lg2+lg3=1.1.计算(log 32+log 23)2-log 32log 23−log 23log 32的值是( )A.log 26B.log 36C.2D.1=(log 32)2+2log 32·log 23+(log 23)2-(log 32)2-(log 23)2=2.2.若lg x-lg y=t,则lg (x 2)3-lg (y 2)3=( )A.3tB.32tC.tD.t2(x 2)3-lg (y 2)3=3lg x2-3lg y2=3lg xy =3(lgx-lgy)=3t.3.若实数a,b,c 满足16a =505b =2 020c =2 022,则下列式子正确的是( ) A.1a +2b =2cB.2a +2b =1cC.1a+1b=2cD.2a+1b=2c,得42a =505b =c =,所以2a=log 4,b=log 505,c=log, 所以12a=log4,1b=log505,1c=log,而4×505=,所以12a+1b=1c,即1a+2b=2c,故选A.4.方程log 2x+1log (x+1)2=1的解是x= .log 2x+log 2(x+1)=1,即log 2[x(x+1)]=1,即x(x+1)=2,解得x=1或x=-2.又{x >0,x +1>0,即x >0,x +1≠1,所以x=1.5.已知>0,且log=40,log (的值为 .log=40,∴log m y=140.又log m (z=112,∴log m z=112-log m x-log m y=112−124−140=160.∴log z m=60. 6.已知使log 23×log 34×log 45×…×log (k+1)(k+2)(k ∈N *)为整数的k 称为“企盼数”,则在区间[1,1 000]上“企盼数”共有个. log 23×log 34×log 45×…×log (k+1)(k+2)=lg3lg2×lg4lg3×…×lg (k+2)lg (k+1)=log 2(k+2)为整数,可知k+2=2n (n ∈Z).又k ∈[1,1000],所以k+2=22,23,…,29,故k ∈{2,6,14,30,62,126,254,510},所以在区间[1,1000]上共有8个“企盼数”. 7.已知4a =8,2m =9n =36,且1m +12n=b,试比较1.5a 与0.8b 的大小.4a=8,∴22a=23,∴2a=3,即a=32. ∵2m=9n=36,∴m=log236,n=log936.又1m +12n=b,∴b=1log236+12log936=log362+12log369=log362+log363=log366=12.∵y=1.5x在R上单调递增,y=0.8x在R上单调递减,∴1.5a=1.532>1.50=1,0.8b=0.812<0.80=1,∴1.5a>0.8b.。

课时4指数函数一. 指数与指数幂的运算（1）根式的概念 ①如果,,,1nxa a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n表示；当n 是偶数时，正数a 的正的nn次方根用符号0的n 次方根是0；负数a 没有n 次方根．n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥．③根式的性质：n a =；当na =；当n(0)|| (0)a a a a a ≥⎧==⎨-<⎩．（2）分数指数幂的概念①正数的正分数指数幂的意义是：0,,,m naa m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是： 1()0,,,m m nn aa m n N a -+==>∈且1)n >．0的负分数指数幂没有意义．注意口诀：底数取倒数，指数取相反数． （3）分数指数幂的运算性质①(0,,)rs r s aa a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r r ab a b a b r R =>>∈二.指数函数及其性质（4）指数函数a 变化对图象影响在第一象限内，a 越大图象越高，越靠近y 轴； 在第二象限内，a 越大图象越低，越靠近x 轴． 在第一象限内，a 越小图象越高，越靠近y 轴； 在第二象限内，a 越小图象越低，越靠近x 轴．三.例题分析1.设a 、b 满足0<a<b<1,下列不等式中正确的是(C) A.a a <a b B.b a <b b C.a a <b a D.b b <a b解析：A 、B 不符合底数在(0,1)之间的单调性;C 、D 指数相同,底小值小.故选C. 2.若0<a<1,则函数y=a x 与y=(a-1)x 2的图象可能是(D)解析：当0<a<1时,y=a x为减函数,a-1<0,所以y=(a-1)x 2开口向下,故选D.3.设指数函数f(x)=a x (a>0且a ≠1),则下列等式中不正确的是(D) A.f(x+y)=f(x)f(y)B.f(x-y)=)()(y f x f C.f(nx)=［f(x)］n D.f ［(xy)n ］=［f(x)］n ［f(y)］n (n ∈N *) 解析：易知A 、B 、C 都正确. 对于D,f ［(xy)n］=a(xy)n,而［f(x)］n·［f(y)］n=(a x )n·(a y)n=anx+ny,一般情况下D 不成立.4.设a=31)43(-,b=41)34(-,c=43)23(-,则a 、b 、c 的大小关系是(B)A.c<a<bB.c<b<aC.b<a<cD.b<c<a解析：a=413131)34()34()43(>=-=b,b=434141)23()278()34(-=>=c.∴a>b>c.5.设f(x)=4x -2x+1,则f -1(0)=______1____________. 解析：令f -1(0)=a,则f(a)=0即有4a-2·2a=0.2a·(2a-2)=0,而2a>0,∴2a=2得a=1.6.函数y=a x-3+4(a>0且a ≠1)的反函数的图象恒过定点______(5,3)____________.解析：因y=a x的图象恒过定点(0,1),向右平移3个单位,向上平移4个单位得到y=a x-3+4的图象,易知恒过定点(3,5).故其反函数过定点(5,3).7.已知函数f(x)=xx xx --+-10101010.证明f(x)在R 上是增函数.证明：∵f(x)=1101101010101022+-=+---x x xx x x , 设x 1<x 2∈R ,则f(x 1)-f(x 2)=)110)(110()1010(21101101101101010101010101010212122112222111122222222++-=+--+-=+--+-----x x x x x x x x x x x x x x x x . ∵y=10x 是增函数, ∴21221010x x -<0. 而1210x +1>0,2210x +1>0, 故当x 1<x 2时,f(x 1)-f(x 2)<0, 即f(x 1)<f(x 2). 所以f(x)是增函数.8.若定义运算a ⊗b=⎩⎨⎧<≥,,,,b a a b a b 则函数f(x)=3x ⊗3-x 的值域为(A)A.(0,1]B.［1,+∞)C.(0,+∞)D.(-∞,+∞)解析：当3x ≥3-x ,即x ≥0时,f(x)=3-x ∈(0,1］;当3x<3-x,即x<0时,f(x)=3x∈(0,1).∴f(x)=⎩⎨⎧<≥-,0,3,0,3x x x x 值域为(0,1).9.函数y=a x 与y=-a -x (a>0,a ≠1)的图象(C) A.关于x 轴对称B.关于y 轴对称 C.关于原点对称D.关于直线y=-x 对称解析：可利用函数图象的对称性来判断两图象的关系.10.当x ∈［-1,1］时,函数f(x)=3x -2的值域为_______［-35,1］___________. 解析：f(x)在［-1,1］上单调递增.11.设有两个命题:(1)关于x 的不等式x 2+2ax+4>0对一切x ∈R 恒成立;(2)函数f(x)=-(5-2a)x 是减函数.若命题(1)和(2)中有且仅有一个是真命题,则实数a 的取值范围是_______(-∞,-2)__________.解析：(1)为真命题⇔Δ=(2a)2-16<0⇔-2<a<2.(2)为真命题⇔5-2a>1⇔a<2.若(1)假(2)真,则a ∈(-∞,-2].若(1)真(2)假,则a ∈(-2,2)∩［2,+∞］=∅. 故a 的取值范围为(-∞,-2).12.求函数y=4-x -2-x +1,x ∈［-3,2］的最大值和最小值. 解：设2-x =t,由x ∈［-3,2］得t ∈［41,8］,于是y=t 2-t+1=(t-21)2+43.当t=21时,y 有最小值43.这时x=1.当t=8时,y 有最大值57.这时x=-3. 13.已知关于x 的方程2a 2x-2-7a x-1+3=0有一个根是2,求a 的值和方程其余的根. 解：∵2是方程2a 2x-2-9a x-1+4=0的根,将x=2代入方程解得a=21或a=4. (1)当a=21时,原方程化为2·(21)2x-2-9(21)x-1+4=0.① 令y=(21)x-1,方程①变为2y 2-9y+4=0, 解得y 1=4,y 2=21.∴(21)x-1=4⇒x=-1,(21)x-1=21⇒x=2. (2)当a=4时,原方程化为2·42x-2-9·4x-1+4=0.② 令t=4x-1,则方程②变为2t 2-9t+4=0.解得t 1=4,t 2=21. ∴4x-1=4⇒x=2, 4x-1=21⇒x=-21. 故方程另外两根是当a=21时,x=-1; 当a=4时,x=-21. 14.函数y=243)31(x x -+-的单调递增区间是(D) A.［1,2］B.［2,3］C.(-∞,2]D.［2,+∞)解析：因为y=3x2-4x+3,又y=3t 单调递增,t=x 2-4x+3在x∈［2,+∞)上递增,故所求的递增区间为［2,+∞).15.已知f(x)=3x-b (2≤x ≤4,b 为常数)的图象经过点(2,1),则F(x)=f 2(x)-2f(x)的值域为(B) A.［-1,+∞)B.［-1,63) C.［0,+∞)D.(0,63］解析：由f(2)=1,得32-b =1,b=2,f(x)=3x-2. ∴F(x)=［f(x)-1］2-1=(3x-2-1)2-1. 令t=3x-2,2≤x≤4.∴g(t)=(t -1)2-1,t∈［1,9］. ∴所求值域为［-1,63］.2.1指数函数练习1．下列各式中成立的一项（）A ．7177)(m n mn= B ．31243)3(-=-C ．43433)(y x y x +=+D ．3339=2．化简)31()3)((656131212132b a b a b a ÷-的结果（）A ．a 6B ．a -C ．a 9-D ．29a3．设指数函数)1,0()(≠>=a a a x f x ，则下列等式中不正确的是（） A ．f (x +y )=f(x )·f (y ) B ．)()(y f x f y x f =-）（ C ．)()]([)(Q n x f nx f n∈=D ．)()]([·)]([)(+∈=N n y f x f xy f n n n4．函数21)2()5(--+-=x x y（）A ．}2,5|{≠≠x x xB ．}2|{>x xC ．}5|{>x xD ．}552|{><<x x x 或5．若指数函数x a y =在[－1,1]上的最大值与最小值的差是1，则底数a 等于 （）A ．251+B ．251+- C ．251± D ．215± 6．当a ≠0时，函数y ax b =+和y b ax =的图象只可能是 （）7．函数||2)(x x f -=的值域是（）A ．]1,0(B ．)1,0(C ．),0(+∞D ．R8．函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ，满足1)(>x f 的x 的取值范围 （）A ．)1,1(-B ．),1(+∞-C ．}20|{-<>x x x 或D ．}11|{-<>x x x 或9．函数22)21(++-=x x y 得单调递增区间是 （）A ．]21,1[-B ．]1,(--∞C ．),2[+∞D ．]2,21[10．已知2)(xx e e x f --=，则下列正确的是 （）A ．奇函数，在R 上为增函数B ．偶函数，在R 上为增函数C ．奇函数，在R 上为减函数D ．偶函数，在R 上为减函数 11．已知函数f (x )的定义域是（1，2），则函数)2(x f 的定义域是. 12．当a ＞0且a ≠1时，函数f (x )=a x －2－3必过定点. 三、解答题：13．求函数y x x =--1511的定义域.14．若a ＞0，b ＞0，且a +b =c ，求证：(1)当r ＞1时，a r +b r ＜c r ；(2)当r ＜1时，a r +b r ＞c r .15．已知函数11)(+-=x x a a x f (a ＞1).（1）判断函数f (x )的奇偶性；（2）证明f (x )在(－∞，+∞)上是增函数.16．函数f(x)＝a x(a>0，且a ≠1)在区间[1,2]上的最大值比最小值大，求a 的值．参考答案一、DCDDDAADDA二、11．(0,1)；12．(2，－2)； 三、13．解：要使函数有意义必须：∴定义域为：{}x x R x x ∈≠≠且01,14．解：rrrrr c b c a c b a ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+，其中10,10<<<<cbc a . 当r ＞1时，1=+<⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr，所以a r +b r ＜c r； 当r ＜1时，1=+>⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr ，所以a r +b r ＞c r . 15．解：(1)是奇函数.(2)设x 1＜x 2，则1111)()(221121+--+-=-x x x x a a a a x f x f 。