驻波解析

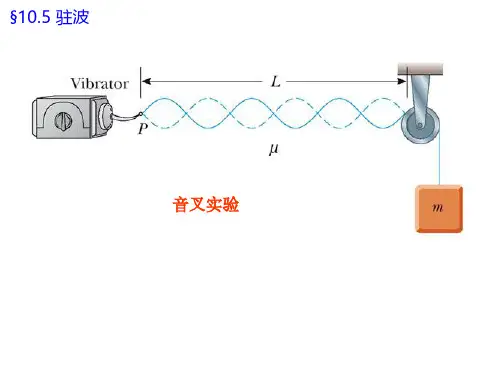
驻波实验原理驻波是指在一定条件下，波的幅度在空间中形成固定的分布规律。

驻波实验是物理学实验中的经典实验之一，通过实验可以直观地观察驻波的形成和性质，深入理解波动现象的规律。

下面我们将介绍驻波实验的原理及其相关知识。

首先，让我们来了解一下驻波的形成条件。

驻波是由两组波在同一介质中叠加形成的，其中一组波称为入射波，另一组波称为反射波。

当这两组波的频率相同、波长相同且振幅相同的情况下，它们之间会发生干涉现象，从而形成驻波。

在一维情况下，驻波的节点和腹部分别对应波的振幅为零和波的振幅最大的位置。

其次，我们来探讨一下驻波实验的基本原理。

驻波实验通常使用弦波实验装置进行，实验装置包括固定端和可调节的振动源。

首先，将弦固定在两端并使其保持水平，然后通过振动源产生一定频率的波，波在弦上传播并反射，最终形成驻波。

通过调节振动源的频率和弦的张力，可以观察到不同频率下的驻波形态，从而验证驻波的形成条件和驻波节点、腹的位置。

在实验过程中，我们可以利用驻波的节点和腹的位置来测定波长，并通过测量不同频率下的节点间距离来验证波长与频率的关系。

此外，还可以通过测量不同频率下驻波的振幅来研究驻波的能量分布规律。

通过这些实验数据，我们可以得到驻波的频率、波长和振幅等性质，进一步认识驻波的特点和规律。

最后，让我们总结一下驻波实验的意义。

驻波实验不仅可以帮助我们直观地认识波动现象，还可以验证波动理论中的相关知识，如波的叠加原理、波的干涉现象等。

通过驻波实验，我们可以深入理解波动的基本规律，为进一步研究波动现象和应用波动理论打下基础。

综上所述，驻波实验是一项重要的物理实验，通过实验可以直观地观察驻波的形成和性质，深入理解波动现象的规律。

通过驻波实验，我们可以验证波动理论中的相关知识，认识驻波的特点和规律，为进一步研究波动现象和应用波动理论提供基础。

希望本文的介绍能够帮助大家更好地理解驻波实验的原理及意义。

驻波详细资料大全驻波（stationary wave）频率相同、传输方向相反的两种波（不一定是电波），沿传输线形成的一种分布状态。

其中的一个波一般是另一个波的反射波。

在两者电压（或电流）相加的点出现波腹，在两者电压（或电流）相减的点形成波节。

在波形上，波节和波腹的位置始终是不变的，给人“驻立不动的印象，但它的瞬时值是随时间而改变的。

如果这两种波的幅值相等，则波节的幅值为零。

基本介绍•中文名：驻波•外文名：stationary wave (standing wave)•套用学科：物理•特点：波面水平时，流速绝对值最大使用,特性,产生驻波的条件,特点,举例,套用,驻波比,使用由于节点静止不动，所以波形没有传播。

能量以动能和位能的形式交换储存，亦传播不出去。

驻波测量两相邻波节间的距离就可测定波长。

各种乐器，包括弦乐器、管乐器和打击乐器，都是由于产生驻波而发声。

为得到最强的驻波，弦或管内空气柱的长度L必须等于半波长的整数倍，即，k为整数，λ为波长。

因而弦或管中能存在的驻波波长为kλ/2，相应的振动频率为2*3.14u/λ，υ为波速。

k=1时，称为基频，除基频外，还存在频率为kn1的倍频。

特性入射波（推进波）与反射波相互干扰而形成的波形不再推进（仅波腹上、下振动，波节不移动）的波浪，称驻波。

驻波多发生在海岸陡壁或直立式水工建筑物前面。

紧靠陡壁附近的海水面随时间虽作周期性升降，海水呈往复流动，但并不向前传播，水面基本上是水平的，这就是由于受岸壁的限制使入射波与反射波相互干扰而形成的。

波面随时间作周期性的升降，每隔偶数个半个波长就有一个波面升降幅度为最大的断面，称为波腹；当波面升降的幅度为0时的断面，称为波节。

相邻两波节间的水平距离仍为半个波长，因此驻波的波面包含一系列的波腹和波节，腹节相间，波腹处的波面的高低虽有周期性变化，但此断面的水平位置是固定的，波节的位置也是固定的。

这与进行波的波峰、波谷沿水平方向移动的现象正好相反，驻波的形状不传播，故名驻波。

驻波与声波干涉现象驻波与声波干涉现象是物理学中常见的现象，它们在波动理论中具有重要的地位。

驻波是指在一定空间范围内，两个同频率、振幅相等、方向相反的波相遇而形成的波动现象。

声波是一种机械波，是由介质的微小振动传播而产生的波动现象。

本文将分别介绍驻波和声波干涉现象，探讨它们的特点、形成条件以及在实际生活中的应用。

驻波的特点及形成条件驻波是由两个同频率、振幅相等、方向相反的波在一定空间范围内相遇而形成的波动现象。

驻波的特点包括以下几点：1. 节点和腹点：在驻波中，波的振幅在空间中存在着明显的变化。

波的振幅为零的点称为节点，而振幅达到最大值的点称为腹点。

2. 波节和波腹间距：相邻的节点和腹点之间的距离称为波节和波腹间距，通常用λ/2来表示，其中λ为波长。

3. 能量不传输：在驻波中，能量不会传输，而是在波的振幅发生变化的区域内来回传播。

驻波的形成条件主要包括两个方面：一是波源必须是同频率、振幅相等、方向相反的波；二是波源之间的距离必须满足一定条件，使得波在空间中发生干涉而形成驻波。

声波干涉现象及应用声波是一种机械波，是由介质的微小振动传播而产生的波动现象。

声波在空气、水等介质中传播，具有一定的频率和振幅。

声波干涉是指两个或多个声波相遇而产生干涉现象的过程。

声波干涉的特点包括以下几点：1. 声强增强和减弱：当两个声波相遇时，如果它们的相位相同，则声波的声强会增强；如果它们的相位相反，则声波的声强会减弱。

2. 声音的清晰度：声波干涉可以使声音的清晰度得到提高，这在音响系统和录音设备中有着重要的应用。

3. 声音的定位：声波干涉还可以用来实现声音的定位，例如在音响系统中通过调节扬声器的位置和角度来实现声音的定位效果。

声波干涉在实际生活中有着广泛的应用，例如在音响系统、录音设备、声纳系统等方面都有着重要的作用。

通过合理地利用声波干涉现象，可以改善声音的传播效果，提高声音的清晰度和定位准确度。

总结驻波与声波干涉现象是波动理论中重要的内容，它们在物理学和工程技术领域有着广泛的应用。

驻波驻波（standing wave）频率和振幅均相同、振动方向一致、传播方向相反的两列波叠加后形成的波。

波在介质中传播时其波形不断向前推进，故称行波；上述两列波叠加后波形并不向前推进，故称驻波。

例如，如图所示，一弦线的一端与音叉一臂相连，另一端经支点O并跨过滑轮后与一重物相连。

音叉振动后在弦线上产生一自左向右传播的行波，传到支点O 后发生反射，弦线中产生一自右向左传播的反射波，当弦长接近1／2波长的整数倍时。

两列波叠加后弦线上各点的位移为（设音叉振动规律为u＝Acosωt）u（x，t）＝2Asin（x）sin（ωt ）＝A（x）sin（ωt），弦线上每个固定的点均作简谐运动，但不同点的振幅不同，由x值决定。

振幅为零的点称为波节，振幅最大处称为波腹。

波节两侧的振动相位相反。

相邻两波节或波腹间的距离都是半个波长。

在行波中能量随波的传播而不断向前传递，其平均能流密度不为零；但驻波的平均能流密度等于零，能量只能在波节与波腹间来回运行。

测量两相邻波节间的距离就可测定波长。

各种乐器，包括弦乐器、管乐器和打击乐器，都是由于产生驻波而发声。

为得到最强的驻波，弦或管内空气柱的长度L必须等于半波长的整数倍，即，k为整数，λ为波长。

因而弦或管中能存在的驻波波长为，相应的振动频率为，υ为波速。

k＝1时，，称为基频，除基频外，还可存在频率为kn1的倍频。

入射波（推进波）与反射波相互干扰而形成的波形不再推进（仅波腹上、下振动，波节不移动）的波浪，称驻波。

驻波多发生在海岸陡壁或直立式水工建筑物前面。

紧靠陡壁附近的海水面随时间虽作周期性升降，海水呈往复流动，但并不向前传播，水面基本上是水平的，这就是由于受岸壁的限制使入射波与反射波相互干扰而形成的。

波面随时间作周期性的升降，每隔半个波长就有一个波面升降幅度为最大的断面，称为波腹；当波面升降的幅度为0时的断面，称为波节。

相邻两波节间的水平距离仍为半个波长，因此驻波的波面包含一系列的波腹和波节，腹节相间，波腹处的波面的高低虽有周期性变化，但此断面的水平位置是固定的，波节的位置也是固定的。

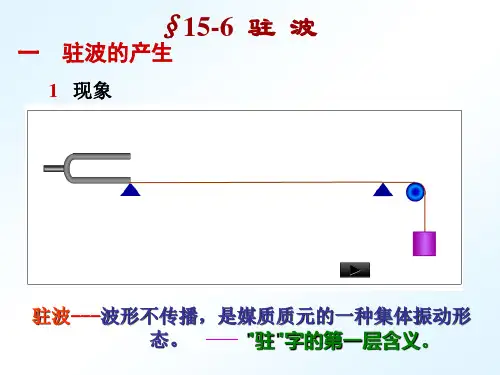
10.7 驻波教学目的1．知道驻波现象及什么是波节、波腹，驻波是一种特殊的干涉现象．2．理解驻波的形成过程，理解驻波与行波的区别，理解空气柱共鸣的条件．引入新课一列波在向前传播的途中遇到障碍物或者两种介质的分界面时，会发生反射，如果反射波和原来向前传播的波相互叠加，会发生什么现象呢？一、驻波1、驻波的演示:如课本图10－31所示，把弦线的一端A固定在电磁打点计时器的振针上，另一端跨过定滑轮拴一个砝码盘，盘上放砝码，将弦线拉平．在靠近定滑轮的B处，用一个尖劈把弦线支起来．接通电磁打点计时器的电源，振针振动时，有一列波向定滑轮的一侧传播，并在B处发生反射．改变尖劈的位置，来调节AB的长度，当尖劈调到某适当位置时，可以看到，弦线会分段振动起来．2、几个概念：①波节——弦线上有些点始终是静止不动的，这些点叫做波节．波腹——在波节和波节之间的那段弦线上，各质点以相同的频率、相同的步调振动，但振幅不同，振幅最大的那些点叫做波腹．在相邻的两段弦线上，质点的振动方向是相反的．相邻的两个波节(或波腹)之间的距离等于半个波长，即等于λ/2．②驻波——波形虽然随时间而改变，但是不向任何方向移动，这种现象叫做驻波．波形不传播，是媒质质元的一种集体振动形态。

"驻"字的第一层含义。

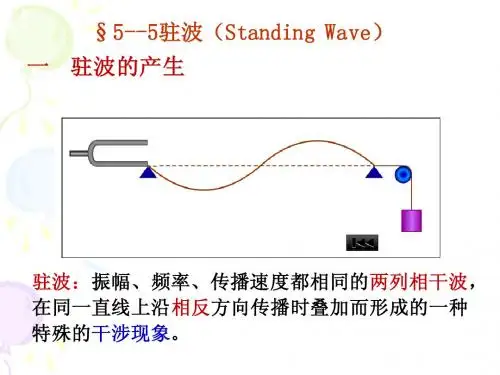
行波——驻波跟前面讲过的波形向前传播的那种波显然是不同的，相对于驻波来说波形向前传播的那种波叫行波．③驻波与行波的区别A物理意义不同：驻波是两列波的特殊干涉现象，行波是一列波在介质中的传播．B质点振动不同：相邻波节间质点运动方向一致．波节两侧质点振动方向总相反．C波形不同：波形向前传播的是行波，波形不向任何方向传播的是驻波．3、驻波的形成两列振幅相同的相干波在同一直线上沿相反方向传播时形成的叠加波。

①两列沿相反方向传播的振幅相同、频率相同的波叠加，形成驻波．②振幅相同、频率相同波的叠加．三、驻波的特点课本10－33中用虚线表示两列沿相反方向传播的振幅相同、频率相同波的叠加，用实线表示这两列波叠加后形成的合成波．图中画出了每隔T/8周期波形的变化情况．由图可以看出，合成波在波节的位置(图中的“·”表示)，位移始终为零．在两波节之间，各质点以相同的步调在振动，两波节之间的中点振幅最大，就是波腹(图中用“＋”表示)．驻波不是振动状态的传播，也没有能量的传播。

驻波计算公式（原创版）目录1.驻波的定义和特点2.驻波计算公式的推导3.驻波计算公式的应用4.驻波计算公式的局限性正文1.驻波的定义和特点驻波是一种特殊的波动现象，指的是两个相同频率、相同振幅、沿相反方向传播的波在空间某一点叠加而形成的波。

驻波的特性是振幅不变、能量不衰减，且在驻波节点处，两个相反方向传播的波的振幅都为零。

这种独特的波动现象在物理、声学、光学等领域有着广泛的应用。

2.驻波计算公式的推导驻波计算公式的推导过程较为复杂，涉及到波动方程的求解。

在此，我们简要介绍一种基于波动方程的驻波计算方法。

假设有两个相同频率、相同振幅的正弦波，它们沿 x 轴传播，其中一个波沿 x 轴正方向传播，另一个波沿 x 轴负方向传播。

它们的波动方程分别为：y1 = A * sin(k1 * x - ωt)y2 = A * sin(k2 * x + ωt)其中，A 表示振幅，k1 和 k2 分别表示两个波的波数，ω表示角频率，t 表示时间。

当两个波在某一点叠加时，驻波的振幅为：y = sqrt(y1^2 + y2^2)驻波的波数为：k = (k1 + k2) / 2驻波的角频率为：ω = (ω1 + ω2) / 23.驻波计算公式的应用驻波计算公式在许多领域都有广泛的应用，例如在声学中，它可以用来分析声波在封闭空间中的传播特性；在光学中，它可以用来研究光的干涉现象等。

通过驻波计算公式，我们可以更好地理解驻波的形成机制，从而更好地利用和控制驻波现象。

4.驻波计算公式的局限性虽然驻波计算公式在许多领域有着广泛的应用，但它也有一定的局限性。

首先，驻波计算公式是基于波动方程推导而来的，因此它只能适用于线性波动系统。

驻波和模态的关系
驻波和模态在物理和工程领域中都是用来描述波动现象的术语，但它们有着不同的含义和用途。

驻波是一种特殊的波，由两个相同频率、振幅和方向的行波在一定介质中相互叠加所形成。

在驻波中，能量在介质中来回反复传递，而不是向前传播。

驻波的形成需要两个相等但相反的波来迎面相遇，并且它们之间有阻抗匹配，这样才能使得波反射回去产生持续的波幅叠加现象。

在声波和电磁波中，驻波可以在管道、谐振腔以及天线上形成。

模态则是指一个系统的振动形式或振动模式，是系统固有的振动特性。

在物理和工程领域中，模态分析是一种常用的方法，用于研究系统的振动特性、动态响应和稳定性等。

模态分析可以通过数学模型、实验手段或两者结合的方法进行。

在数学模型中，模态被表示为线性方程组的解，描述了系统在不同频率下的振动行为。

在实验模态分析中，通过测量系统的振动响应和激励信号来识别系统的模态参数，如模态频率、模态阻尼比和模态振型等。

总的来说，驻波和模态都是描述波动现象的术语，但驻波更侧重于波动形式的描述，而模态则更侧重于系统振动特性的描述。

在实际应用中，驻波和模态分析的方法可以相互借鉴和应用，例如在声学和振动控制领域中，驻波的概念可以用来分析和设计声学系统和振动控制系统的动态特性。

入射波和反射波合成的驻波方程驻波是波动现象中的一种特殊形式，它是由两个同频率、同振幅的波相互叠加而形成的。

这两个波分别是入射波和反射波。

入射波是由外部源产生、传播到介质中的波，而反射波则是由介质边界上的反射产生的波。

当入射波和反射波在介质中相遇时，它们会发生干涉现象，形成驻波。

驻波方程描述了驻波的形态，它是通过将入射波和反射波的振动方程相加而得到的。

驻波方程的形式可以表示为y(x, t) = 2Acos(kx)cos(ωt)，其中A表示振幅，k表示波数，x表示空间坐标，ω表示角频率，t表示时间。

这个方程说明了驻波的振幅是随着空间坐标和时间的变化而变化的。

驻波方程中的第一项2Acos(kx)表示了波的空间分布，它是由入射波和反射波的振动相长叠加形成的。

这一项的振幅是2A，表示振幅的加倍效应。

而cos(kx)则表示了波的空间分布，它随着空间坐标的变化而变化，在介质中形成驻波的节点和腹部。

驻波方程中的第二项cos(ωt)表示了波的时间分布，它随着时间的变化而变化，在介质中形成驻波的稳定振动。

这一项的振幅是恒定的，不随时间的变化而变化。

驻波方程描述了驻波的空间和时间特征，它可以用来分析驻波的性质和行为。

通过解析驻波方程，可以得到驻波的振幅、波长、频率等参数。

驻波是一种重要的物理现象，在许多领域中都有应用。

例如，在声学中，驻波可以解释声波在管道、弦线等介质中的传播和共振现象。

在光学中，驻波可以解释光波在光纤、薄膜等介质中的传播和干涉现象。

在电磁学中，驻波可以解释电磁波在导线、天线等介质中的传播和驻波现象。

驻波方程描述了驻波的形态和特征，它通过入射波和反射波的叠加得到。

驻波方程在物理学中有着广泛的应用，可以用来解释和分析驻波现象。

通过研究驻波方程，可以深入理解驻波的本质，并在实际应用中发挥作用。