如何在Zemax下模拟单模光纤的光束耦合
- 格式:doc
- 大小:503.50 KB
- 文档页数:16

zemax单模光纤耦合设计Zemax是一种常用的光学设计软件,可以用于设计和优化光学系统。
在光纤通信中,光纤耦合是一个重要的问题,因为光纤耦合的效率直接影响到光信号传输的质量和距离。
本文将介绍如何使用Zemax 进行单模光纤耦合的设计。
单模光纤是一种能够传输单个模式光信号的光纤,具有较小的传输损耗和较高的带宽。
光纤耦合是将光信号从光源传输到光纤的过程,其目标是尽可能地将光信号聚焦在光纤的入口面上,使光信号能够有效地进入光纤。
在Zemax中进行光纤耦合设计,首先需要建立光学系统模型。
光学系统模型包括光源、透镜、光纤等元件。
其中,光源可以是LED、激光器等发光源,透镜用于调节光束的形状和聚焦效果,光纤是光信号传输的通道。
在建立光学系统模型后,需要定义光纤的入口面和出口面。
光纤的入口面是光纤与外界的接口,光信号需要从这里进入光纤。
出口面是光纤与接收器的接口,光信号需要从光纤传输到接收器上。
接下来,需要选择合适的透镜和光纤参数。
透镜的选择主要考虑透镜的焦距和孔径,以及透镜与光纤的距离。
光纤的参数包括芯径、包层折射率和长度等。
这些参数的选择将直接影响到光纤耦合的效率和质量。
在Zemax中,可以使用光线追迹和优化算法来模拟和优化光纤耦合。
光线追迹可以模拟光线在系统中的传播路径和光强分布,从而评估光纤耦合的效果。
优化算法可以根据设定的目标函数来优化系统的参数,以最大化光纤耦合的效率。
在进行光纤耦合设计时,需要注意以下几点。
首先,光纤的入口面和出口面应当对准光源和接收器。
其次,透镜和光纤的位置和参数应当合理选择,以使光线能够有效地聚焦在光纤的入口面上。
此外,还应当考虑光纤的对准误差和传输损耗等因素。
Zemax是一种强大的光学设计软件,可以用于单模光纤耦合的设计和优化。
通过合理选择透镜和光纤的参数,并使用光线追迹和优化算法,可以实现高效的光纤耦合。
光纤耦合的设计是光纤通信中的重要环节,对于提高光信号传输的质量和距离具有重要意义。

zemax光纤耦合效率摘要:1.Zemax 光纤耦合效率简介2.Zemax 光纤耦合效率的计算方法3.Zemax 光纤耦合效率的影响因素4.Zemax 光纤耦合效率的提高方法5.总结正文:【1.Zemax 光纤耦合效率简介】Zemax 光纤耦合效率是指在光学系统中,光纤与光源之间的能量传递效率。
在光纤通信、光纤传感和光纤激光等领域中,光纤耦合效率对于系统的性能具有重要意义。
Zemax 作为一款光学设计软件,可以方便地计算和优化光纤耦合效率,从而提高整个光学系统的性能。
【2.Zemax 光纤耦合效率的计算方法】Zemax 中,光纤耦合效率的计算采用耦合系数法。
具体步骤如下:1) 在Zemax 中创建一个光学系统,将光源、光纤和接收器等元件添加到系统中;2) 在光源和光纤之间设置一个耦合器,并设置适当的耦合系数;3) 运行光学仿真,得到光源输出光强的分布;4) 计算光纤中的光强分布;5) 根据光纤中的光强分布,计算光纤耦合效率。
【3.Zemax 光纤耦合效率的影响因素】Zemax 光纤耦合效率受多种因素影响,主要包括:1) 光源的类型和特性;2) 光纤的类型和特性;3) 耦合器的类型和特性;4) 光源与光纤之间的距离;5) 耦合系数的大小。
【4.Zemax 光纤耦合效率的提高方法】为了提高Zemax 光纤耦合效率,可以采取以下措施:1) 选择合适的光源和光纤类型,以提高它们的匹配度;2) 选择合适的耦合器类型,并设置适当的耦合系数;3) 优化光源与光纤之间的距离,以提高能量传递效率;4) 对光学系统进行优化,以降低系统中的损耗。
【5.总结】Zemax 光纤耦合效率是光学系统性能的关键指标之一。
通过合理的设计、优化和计算,可以有效提高光纤耦合效率,从而提升整个光学系统的性能。

绿光半导体激光器单管合束及光纤耦合技术研究摘要:近年来,随着我国经济的高速发展和科技的进步,光电器件与材料相关领域的研发不断取得新进展,性能得到明显强化,在各大领域得到广泛应用。
为进一步提高半导体激光功率,可以采用激光器单管合束及光纤耦合技术。
基于此,分析研究绿光半导体激光器单管合束及光纤耦合技术,对提高仪器总功率以及将其应用于更多领域有重要的现实意义。
关键词:绿光半导体激光器;单管合束;光纤耦合前言:利用合束技术可以使多个半导体激光器在光纤中进行耦合,由此形成半导体激光器的光学器件,保证激光的输出功率,提高激光束的质量。
目前,国内外已广泛使用多种红外波段的半导体激光器,广泛用于彩色显示、激光印刷、高密度光盘存储等领域,但目前对于可见光波段激光耦合模块尤其是绿光波段的研究还很少,因此,对绿光高功率半导体激光器光纤耦合模块进行深入研究,是当前光电器件与材料相关领域研发重点之一。
1半导体激光器光纤耦合模块研究半导体激光器技术已经相对成熟,由于其具有光束不均匀性、单元功率低等特点,在一定程度上限制其应用领域。
为保证半导体激光器的功率输出,需要对激光器进行多层叠加,这会一定程度上限制光束质量。
随着半导体耦合技术的不断发展和进步,通过使用半导体激光器进行合束,可以有效提升光束的质量,实现激光远距离柔性传输。
最早的光纤是20世纪50年代研制出来的,后来被人们逐渐推广使用。
在20世纪70年代,就有国外公司利用化学气相沉积法得到了损耗较低的光纤,随着半导体激光器的迅速发展和光纤耦合技术的发展,人们对不同类型的半导体激光器进行了大量的研究,并取得了大量的成果。
2半导体激光器非相干合束技术目前,半导体激光器的合束技术方法有两种:相干合束和非相干合束。
半导体激光器利用光束准直技术和聚焦耦合技术,使多个光束单元的耦合成为可能。
在相干合束技术的应用中,采用了相位控制方法,使激光阵列各发光元件产生同一波长的光束,从而达到相干合束。
?
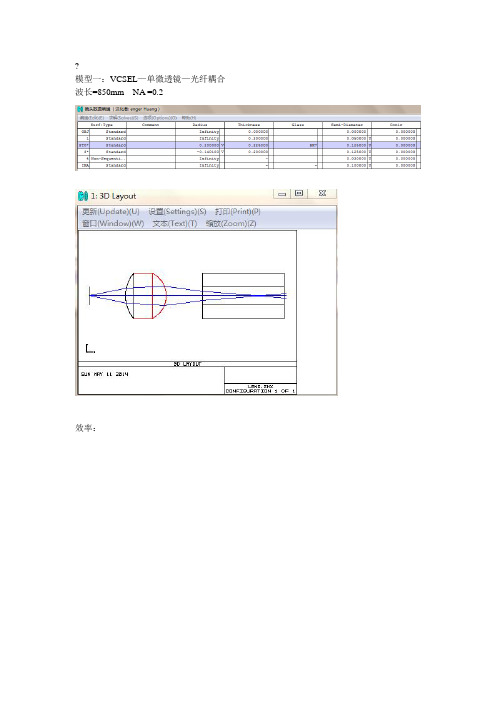
模型一:VCSEL—单微透镜—光纤耦合波长=850mm NA =0.2
效率:
结构简单,单效率不高,光路不稳定,不符合研究要求。
模型二:VCSEL—双微透镜—光纤耦合
波长=850mm NA =0.14
效率:
效率虽高,但不符合研究的背景要求,舍弃。
模型三:VCSEL—双透镜—光纤耦合(MMF=50/125)波长=850mm NA =0.2
效率:
根据参考文献:长春理工大学光电工程学院吉林长春130021;2中国科学院半导体研究所北京100083的研究
这个模型也就能达到30%左右的效率,舍弃。
模型四:VCSEL—双微透镜—MMF(62.5/125)
波长=850mm NA=0.2
效率:
根据参考文献,吧光纤和透镜接在一起,调整参数(往研究背景靠近),在第二个透镜出口处的光澜腰束小于光纤内径,光纤在光纤中光路无反射最好,直接照到光纤末端45°面上。
根据华中科技大学,物理电子学,对于光电互联板的耦合效率的研究,得知这样的效率能达到80%左右。
模型五:光纤末端45°角反射与光波导耦合
效率:。
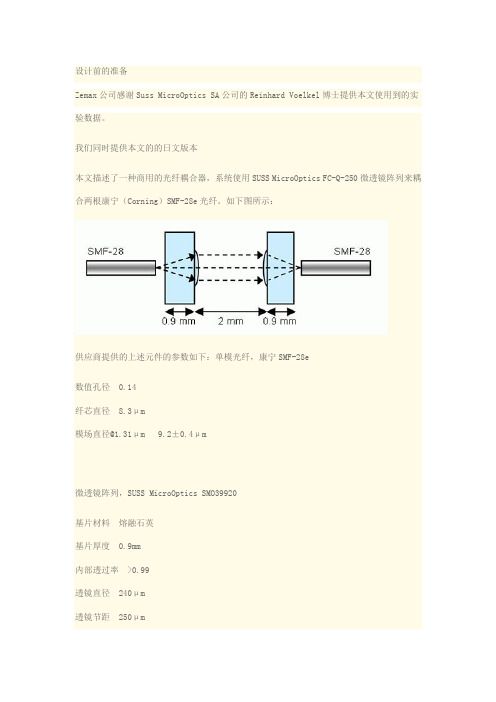
设计前的准备Zemax公司感谢Suss MicroOptics SA公司的Reinhard Voelkel博士提供本文使用到的实验数据。
我们同时提供本文的的日文版本本文描述了一种商用的光纤耦合器,系统使用SUSS MicroOptics FC-Q-250微透镜阵列来耦合两根康宁(Corning)SMF-28e光纤。
如下图所示:供应商提供的上述元件的参数如下:单模光纤,康宁SMF-28e数值孔径0.14纤芯直径8.3μm模场直径@1.31μm 9.2±0.4μm微透镜阵列,SUSS MicroOptics SMO39920基片材料熔融石英基片厚度0.9mm内部透过率>0.99透镜直径240μm透镜节距250μm曲率半径330μm圆锥常数(Conic constant)0数值孔径0.17附件中的文件single mode coupler.zmx是整个系统的Zemax文件。
请注意一下几点:物面到透镜的距离和透镜到像面的距离设定为0.1mm,是因为这比较接近实际情况。
后面经过优化过程时候,这个尺寸还会发生变化;透镜到像面的距离使用了Pick-up solve,以确保和前面的物面到透镜的距离之间相等。
既然两组透镜和光纤之间是完全一致的(在制造公差之内),因而整个系统也就应该是空间反演对称和轴对称的(either way round);两个透镜之间的距离设定为2mm,因为这个是实验中使用的数据。
同样地,这个距离后面也将会被严格的优化;系统孔径光阑设定为根据光阑尺寸浮动(float by stop size),而光阑设定在第一个透镜的后表面。
这就意味着系统的孔径光阑由透镜的实际孔径决定。
因而光纤的模式在这个系统中传输的过程中,就有可能受限于透镜的实际孔径。
在这个例子中,光纤的模式要比透镜的实际孔径小很多。
当心“数值孔径”的多种不同定义。
它有可能指的是边缘光束倾角的正弦值,有可能是光强降低到 1/e2时的光束倾角的正弦值(我们将会看到Zemax会在不同的场合使用这两种定义),也有可能定义为光强降到1%峰值强度时光束倾角的正弦值,康宁便使用这种定义。

LD耦合模拟演示 2019.6.12目录第一章绪论 (3)第二章半导体激光与光纤耦合的理论 (4)2.1 半导体激光器输出光束特性 (4)2.2 光纤的基本理论 (5)2.3 光纤耦合条件 (6)第三章 10WLD耦合模拟 (7)3.1 光路结构及器件参数 (7)3.2 耦合模拟 (7)3.3 光路优化 (9)第四章大功率LD耦合模拟 (10)4.1 光路结构 (10)4.2 耦合模拟 (11)第五章结论 (16)第一章绪论本文利用Zemax对10W与30W两种LD耦合方式进行了模拟,除对现有10WLD 耦合工作进行验证之外,也为30WLD的光纤耦合工作提供了设计指导。
第二章半导体激光与光纤耦合的理论2.1 半导体激光器输出光束特性温度对半导体输出功率的影响很大,温度越高,LD的输出功率越低。
这就使得LD的有源层非常薄,厚度大约只有1μm,宽度一般在几十到几百μm。
由于有源层非常狭窄,激光在传输的过程中就会发生衍射,光束会变得发散,如图1所示。
图表 1 半导体激光器出射光斑示意图半导体激光器的桶中功率(PIB)定义为:光强下降到最大光强的1/2处所对应的角度,即半亮全宽时的全角发散角。
垂直发散角用θ⊥表示,水平发散角用θ∥表示。
对于激光与光纤的耦合,发散角越小,调整的容忍度越大,越有利于高效率的耦合。
我们选择的LD芯片为Oclaro的SES12-915-02,其输出的中心波长为910nm,输出功率12W,θ⊥为58°,θ∥为10.5°。
2.2 光纤的基本理论图表 2 光纤的结构光纤的一般结构如图2所示,纤芯与包层为其结构主体。
最外的涂覆层用于保护光纤,纤芯的折射率为n1,包层折射率为n2,n1>n2,因此光束在纤芯与包层的交界面可以发生全反射而实现低损传播。
为了满足全反射的实现条件,对照射到光纤端面的角度有要求,通过推算不难得到以下的公式:(1.1)其中NA为光纤的数值孔径,n0为空气折射率,简单计算可以取1,φ0为入射光束与水平方向的夹角,大于此数值的光束由于不能发生全反射而无法耦合入光纤。
如何在Zemax下模拟单模光纤的光束耦合设计前的准备Zemax公司感谢Suss MicroOptics SA公司的Reinhard Voelkel博士提供本文使用到的实验数据。
我们同时提供本文的的日文版本本文描述了一种商用的光纤耦合器,系统使用SUSS MicroOptics FC-Q-250微透镜阵列来耦合两根康宁(Corning)SMF-28e光纤。
如下图所示:供应商提供的上述元件的参数如下:单模光纤,康宁SMF-28e数值孔径0.14纤芯直径8.3μm模场直径@1.31μm 9.2±0.4μm微透镜阵列,SUSS MicroOptics SMO39920基片材料熔融石英基片厚度0.9mm内部透过率>0.99透镜直径240μm透镜节距250μm曲率半径330μm圆锥常数(Conic constant)0数值孔径0.17附件中的文件single mode coupler.zmx是整个系统的Zemax文件。
请注意一下几点:物面到透镜的距离和透镜到像面的距离设定为0.1mm,是因为这比较接近实际情况。
后面经过优化过程时候,这个尺寸还会发生变化;透镜到像面的距离使用了Pick-up solve,以确保和前面的物面到透镜的距离之间相等。
既然两组透镜和光纤之间是完全一致的(在制造公差之内),因而整个系统也就应该是空间反演对称和轴对称的(either way round);两个透镜之间的距离设定为2mm,因为这个是实验中使用的数据。
同样地,这个距离后面也将会被严格的优化;系统孔径光阑设定为根据光阑尺寸浮动(float by stop size),而光阑设定在第一个透镜的后表面。
这就意味着系统的孔径光阑由透镜的实际孔径决定。
因而光纤的模式在这个系统中传输的过程中,就有可能受限于透镜的实际孔径。
在这个例子中,光纤的模式要比透镜的实际孔径小很多。
当心“数值孔径”的多种不同定义。
它有可能指的是边缘光束倾角的正弦值,有可能是光强降低到1/e2时的光束倾角的正弦值(我们将会看到Zemax会在不同的场合使用这两种定义),也有可能定义为光强降到1%峰值强度时光束倾角的正弦值,康宁便使用这种定义。
ZEMAX光学设计:模拟单模光纤耦合设计指标:单模光纤的规格为纤芯直径为8.3um,数值孔径0.14,模场直径9.2±************;透镜的规格为:熔融石英(Silica),厚度0.9mm,直径0.24mm,曲率半径0.33mm,数值孔径0.17。
出射单模光纤到第一个透镜的初始距离为0.1mm,第二个透镜到耦合光纤的初始距离也是0.1mm;两个透镜之间的初始距离为2mm。
(该设计来自ZEMAX自带实例)设计仿真:(1)单模光纤耦合在系统通用对话框中设置孔径。
在孔径类型中选择“Float By Stop Size”,Apodization Type选择“Gaussian”,Apodization Factor为3.0,这样设置可以产生高斯分布的光束。
在视场设定对话框中设置1个视场,Field Type为“angle”,如下图:在波长设定对话框中,选择1.310um一个波长,如下图:LDE初始结构,如下图:此时,2D Layout,如下图:查看点列图:光纤在波长1.31um的模场直径为9.2±0.4um,因此可以按照下图所示来设置近轴高斯光束。
将Waist Size设置为0.0046,Surf 1 to Waist设置为-0.1,这样,此时的束腰位置就位于在输入光纤的位置。
查看Paraxial Gaussian Beam Data:上图中,像面(IMA)上的Size约为5.56um,而物面(OBJ)上的Size为4.6um,考虑到希望该系统的输入和输出是互易的,那么,我们可以通过优化光纤与透镜之间的距离来优化像面上的Size 到4.6um。
打开MFE,添加GBPS操作数,设置如下:GBPS操作数,在Wave定义的波长上,指定面后的光学空间中近轴高斯光束的尺寸。
将LDE中物面的厚度设置为变量,此时,第5面的厚度也会相应变化。
同时,将第2面的曲率半径也设置为变量,那第4面的曲率半径也会相应变化。
设计前的准备Zemax公司感谢Suss MicroOptics SA公司的Reinhard Voelkel博士提供本文使用到的实验数据。
我们同时提供本文的的日文版本本文描述了一种商用的光纤耦合器,系统使用SUSS MicroOptics FC-Q-250微透镜阵列来耦合两根康宁(Corning)SMF-28e光纤。
如下图所示:供应商提供的上述元件的参数如下:单模光纤,康宁SMF-28e数值孔径 0.14纤芯直径8.3μm模场直径@1.31μm 9.2±0.4μm微透镜阵列,SUSS MicroOptics SMO39920基片材料熔融石英基片厚度 0.9mm内部透过率 >0.99透镜直径240μm透镜节距250μm曲率半径330μm圆锥常数(Conic constant) 0数值孔径 0.17附件中的文件single mode coupler.zmx 是整个系统的Zemax文件。
请注意一下几点:物面到透镜的距离和透镜到像面的距离设定为0.1mm,是因为这比较接近实际情况。
后面经过优化过程时候,这个尺寸还会发生变化;透镜到像面的距离使用了Pick-up solve,以确保和前面的物面到透镜的距离之间相等。
既然两组透镜和光纤之间是完全一致的(在制造公差之内),因而整个系统也就应该是空间反演对称和轴对称的(either way round);两个透镜之间的距离设定为2mm,因为这个是实验中使用的数据。
同样地,这个距离后面也将会被严格的优化;系统孔径光阑设定为根据光阑尺寸浮动(float by stop size),而光阑设定在第一个透镜的后表面。
这就意味着系统的孔径光阑由透镜的实际孔径决定。
因而光纤的模式在这个系统中传输的过程中,就有可能受限于透镜的实际孔径。
在这个例子中,光纤的模式要比透镜的实际孔径小很多。
当心“数值孔径”的多种不同定义。
它有可能指的是边缘光束倾角的正弦值,有可能是光强降低到1/e2时的光束倾角的正弦值(我们将会看到Zemax会在不同的场合使用这两种定义),也有可能定义为光强降到1%峰值强度时光束倾角的正弦值,康宁便使用这种定义。
如何在Zemax下模拟单模光纤的光束耦合设计前的准备Zemax公司感谢Suss MicroOptics SA公司的Reinhard Voelkel博士提供本文使用到的实验数据。
我们同时提供本文的的日文版本本文描述了一种商用的光纤耦合器,系统使用SUSS MicroOptics FC-Q-250微透镜阵列来耦合两根康宁(Corning)SMF-28e光纤。
如下图所示:供应商提供的上述元件的参数如下:单模光纤,康宁SMF-28e数值孔径0.14纤芯直径8.3μm模场直径@1.31μm 9.2±0.4μm微透镜阵列,SUSS MicroOptics SMO39920基片材料熔融石英基片厚度0.9mm内部透过率>0.99透镜直径240μm透镜节距250μm曲率半径330μm圆锥常数(Conic constant)0数值孔径0.17附件中的文件single mode coupler.zmx是整个系统的Zemax文件。
请注意一下几点:物面到透镜的距离和透镜到像面的距离设定为0.1mm,是因为这比较接近实际情况。
后面经过优化过程时候,这个尺寸还会发生变化;透镜到像面的距离使用了Pick-up solve,以确保和前面的物面到透镜的距离之间相等。
既然两组透镜和光纤之间是完全一致的(在制造公差之内),因而整个系统也就应该是空间反演对称和轴对称的(either way round);两个透镜之间的距离设定为2mm,因为这个是实验中使用的数据。
同样地,这个距离后面也将会被严格的优化;系统孔径光阑设定为根据光阑尺寸浮动(float by stop size),而光阑设定在第一个透镜的后表面。
这就意味着系统的孔径光阑由透镜的实际孔径决定。
因而光纤的模式在这个系统中传输的过程中,就有可能受限于透镜的实际孔径。
在这个例子中,光纤的模式要比透镜的实际孔径小很多。
当心“数值孔径”的多种不同定义。
它有可能指的是边缘光束倾角的正弦值,有可能是光强降低到1/e2时的光束倾角的正弦值(我们将会看到Zemax会在不同的场合使用这两种定义),也有可能定义为光强降到1%峰值强度时光束倾角的正弦值,康宁便使用这种定义。
这些非常重要!孔径上定义了高斯切趾(Gaussian apodization),用来产生光束的高斯分布。
当前这只是一种近似,后面将会做进一步的精确的计算。
透镜孔径的大部分区域是衍射受限的光学质量的,并且被光纤模式照射到的区域是衍射受限的。
使用旁轴高斯光束计算旁轴高斯光束算法是最简单可以用来分析光纤耦合的分析方法。
不过,这种方法只能获得对系统性能初步的了解。
根据康宁的产品参数表,光纤在1.31μm波长下的模场直径为9.2±0.4μm。
因此,我们按照下图所示的情形设置旁轴高斯光束计算(Analysis>Physical Optics>Paraxial Gaussian Beam):图中光束的束腰直径Waist总是相对于表面1来计算的,在本例中它和物面出于同一个位置。
因此,高斯光束的束腰直径4.6μm就位于源光纤的位置。
光束然后传输经过光学系统。
从上图我们可以看出表面3上的1/e2光束直径是65μm,而表面4是70μm。
这些表面的实际的物理半口径为120μm。
也就是说大约两个光束直径以外的光将会被阻隔掉。
另外需要注意的是像面并非位于光束最佳聚焦聚焦点处:像面处光斑的大小为5.3μm,而其实根据系统的对称性的假定,高斯束腰直径应该是4.6μm。
我们将会优化表面1的厚度(同时也会通过Pick-up solve来控制表面5的厚度)来改进这些。
请注意表面5的厚度是通过Pick-up solve来控制的,因为我们希望系统倒过来使用时也能得到同样的耦合效果:我们使用了完全相同的两组光纤和透镜(在制造公差范围内),因而我们期望最好的系统是输入输出互易的。
Zemax中有一项优化操作数(operand)GBPS,指的是旁轴高斯光束尺寸,可以用来优化光纤和耦合镜头之间的距离。
根据系统的上述对称性,我们知道,高斯光束束腰的最佳尺寸是4.6μm,因此,优化函数就只有简单的一行,如下图:优化后给出的光纤到透镜之间的距离为0.117mm,下面是相应的旁轴高斯光束的数据:上述便是旁轴高斯光束计算所能给我们提供的信息。
相关的Zemax文件为optimization.zmx。
返回目录使用单模光纤耦合计算单模光纤耦合计算方法(位于Analysis>Calculations>Fiber Coupling Efficiency)提供了更加有力的用来分析具有高斯分布的光纤模式的能力。
它会执行两种计算:能量传输计算(energytransport calculation)和模式匹配计算(modematching calculation)。
系统效率(system efficiency:S)是用通过入瞳(entrance pupil)的所有光能量,并且考虑了渐晕(vignetting)和偏振光传输情况下,经过系统之后的能量的总和除以从光纤辐射的所有能量得到的:这里Fs(x,y)指的是源光纤的振幅函数,分子是仅在光学系统的入瞳处的积分,而t(x,y)是光学系统的振幅传输函数。
传输过程受到体吸收和光学镀膜(打开偏振传输的情况下)的影响。
光学系统中的像差所引起的位相差也会影响光纤的耦合效率。
当向接收光纤传输的汇聚波前的各个点上的模式完全和光纤的模式(包括振幅和位相)想匹配的时候,耦合效率达到最大。
它的数学描述是通过光纤和波前振幅之间的重叠积分(overlap integral)来定义的:这里Fr(x,y)用来描述接收光纤复振幅函数,W(x,y)是光学系统出瞳处的波前的复振幅函数,而符号' 代表了复数共轭操作。
注意这些函数都是复数形式的,因而这个表达式是相干重叠积分。
T的最大值为1.0,并且随着光纤的振幅和位相和波前振幅位相之间的失配的增加而降低。
Zemax会计算上述的S和T的值。
总的功率耦合效率也是从这些数据得来的。
Zemax也会计算理论上的最大耦合效率,这个计算是在胡略了像差但是考虑模式的渐晕、传输和其他振幅失配因素之后得来的。
在计算中,源光纤模式和接收光纤模式是通过高斯光束的数值孔径NA(定义为物方或者像方的介质折射率和光束上功率降到1/e2处的半张角的正弦的乘积)这个角度可以通过下面两种方法计算获得:通过高斯光束计算得来的发散角,使用模场直径来定义光束束腰直径(参见本文前面的计算);根据康宁产品参数表中提供的1%功率处的NA计算得到1/e2处的数值孔径。
通常,NA大约为0.09,因此耦合效率的计算设置如下图所示:得到的计算结果如下:我们也可以一行优化函数来优化系统的耦合效率,该操作数为FICL:经过几个优化循环之后,光纤到透镜的距离变成了0.11mm(而在旁轴高斯光束计算中为0.117),详细的结果如下:注意一下几点:系统耦合效率(system efficiency)并未显著改变,因为这主要是由表面的孔径和模式尺寸决定的,而轻微的离焦对其的影响并不大;接收端耦合效率(Receiver efficiency)得到了提升,因为重新聚焦使得源光纤模式在经过系统传输之后更好地和接收光纤的模式匹配;最大耦合效率(maximum efficiency)可以通过下述方法得到提升:增加非球面,增加额外的表面等等。
本例中,这个耦合效率基本达到了极限。
本节使用的zemax源文件为after FICL optimization.zmx返回目录使用物理光学计算(Using the phsical optics calculation)在单模光纤耦合计算的基础上运用物理光学传输算法可以极大的扩展这个方法的应用。
类似地,我们需要计算基于物理光学传输的重叠积分,这样做有一下几点好处:可以定义任何复杂模式,而不仅限于高斯模式;当接收光纤位置的时候,光纤耦合重叠积分可以在任何一个表面上计算,这包括当不仅限于代表光纤的表面;外部程序,比如光束传输(Beam Propagation和时域有限差分方法(Finite-Difference-Time Domain)代码,可以使用成.zbf文件格式或者生成DLL接口,用来计算光纤(或者任何集成光学元件)的模式结构,并且可以将其表达成和室的复杂振幅分布函数的形式。
关于这一点,可以参看这篇文章;由于传输受光阑限制或者远距离传输产生的衍射效应也可以得到准确的模拟。
POP计算可以通过以下窗口设置,点击Analysis>Physical Optics>Phusical Optics Propagation打开设置窗口:以上设置了表面1上的束腰半口径为4.6μm的高斯模式,并且经过系统传输至像面,在像面上我们使用完全相同的模式来计算重叠积分。
在光束的参数设置表中,我们词啊用了256×256的采样率,然后需要点击Auto按钮来设定合适的起始矩阵;物理光学窗口中关于光纤耦合的报告,可以参看下图中红色框选区域。
优化函数编辑器中的POPD操作数可以给出所有的物理光学数据,这通常是更有用一些。
具体的关于POPD操作数的叙述可以参考用户手册中的优化那一章。
POPD操作数直接调用先前保存的POP Analysis窗口中的设置,因此,在优化之前先要去设置一下这些参数。
POPD数据(通过优化函数得到)描述Description 数值Value0 Total Fiber Coupling 0.9941 System Efficiency 0.9982 Receiver Efficiency 0.99610 Pilot Beam Waist 4.57μm23 Effective Beam Width 4.84μm26 M2 1.082位相是你需要关注的最有用的信息,因为Irradiance Profile几乎是理想的高斯形(M2为1.082)。
接收端的模式实际上在每个地方都几乎为零,因此位相也直接告诉我们模式失配的程度。
要显示位相信息,打开POP设置窗口的显示(Display)那一栏,按照下图所示的方式设置:注意位相图的抛物线和四次曲线的形状,这等价于聚焦和球差。
另外也要注意透镜边缘对位相曲线产生的影响。
根据系统的效率(System efficiency),我们知道由于透镜外相尺寸的限制,系统约有小于1%的能量损耗。
如果我们进一步对光纤耦合效率进行优化(记住光纤和透镜的距离是唯一的变量),我们可以得到少量的提升:光纤耦合效率并未得到显著提升,这是因为位相差产生的位置对应的能量非常低:{上图可以通过下述方法得到:从POP窗口中输出cross-section形式的irradiance图,然后克隆它(windows>clone),然后将克隆后的窗口设置成显示位相,而非光强,介质在windows菜单中选择overlay...将这两个曲线重叠成上图的样子。