途径:利用单位圆中正弦、余弦线来解决。
描图:用光滑曲线
y
B
1
将这些正弦线的 终点连结起来
A
O1
O
2
4
5
2
x
3
3
3
3
-1
y=sinx
终边相同角的三角函数值相等 即: sin(x+2k)=sinx, kZ
x[0,2]
f(x2k)f(x)利用图象平移
y=sinx xR
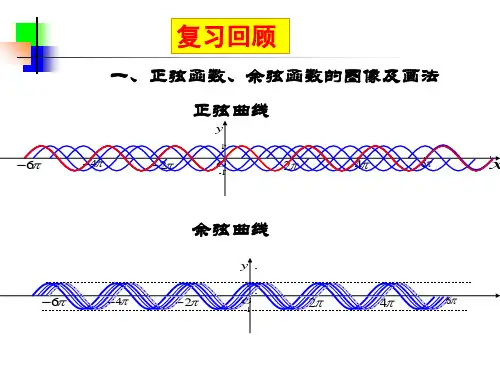
正弦、余弦函数的图象
y 1
o
2
2
-1
y=sinx x[0,2]
y
y=sinx xR
1
-4 -3
-2
- o
-1
3
2
x
2
正弦曲 线
2
3
4
5 6 x
正弦、余弦函数的图象
如何作出正弦函数的图象(在精确度要求不太高时)?
y
五点画图法
1
(2
,1)
( 2 ,1)
( ,0)
( 2 ,0)
五点法——
2
(
(0,0)o
(0,0)
2
(0,0)
-1
(0,0)
汇报人:XXX 汇报日期:20XX年10月10日
2 ,0) x
2 ,0)
( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0)
正弦、余弦函数的图象
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
正弦函数的图象 y=cosx=sin(x+ ), xR
2