九年级综合题

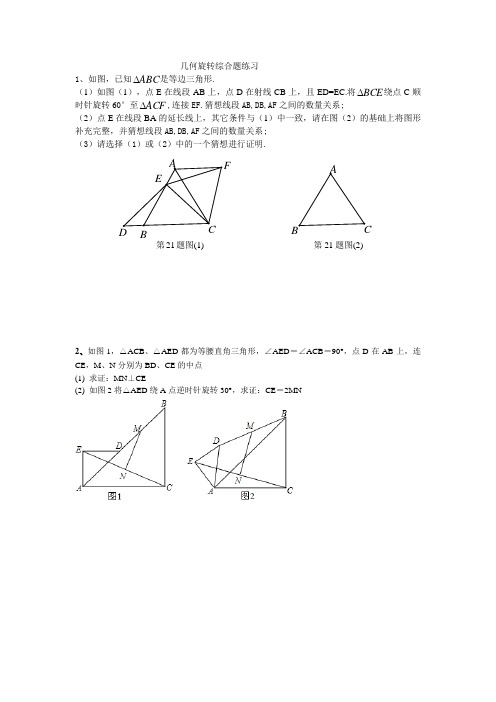
几何旋转综合题练习1、如图，已知ABC ∆是等边三角形.（1）如图（1），点E 在线段AB 上，点D 在射线CB 上，且ED=EC.将BCE ∆绕点C 顺时针旋转60°至ACF ∆,连接EF.猜想线段AB,DB,AF 之间的数量关系;（2）点E 在线段BA 的延长线上，其它条件与（1）中一致，请在图（2）的基础上将图形补充完整，并猜想线段AB,DB,AF 之间的数量关系; （3）请选择（1）或（2）中的一个猜想进行证明.2、如图1，△ACB 、△AED 都为等腰直角三角形，∠AED ＝∠ACB ＝90°，点D 在AB 上，连CE ，M 、N 分别为BD 、CE 的中点(1) 求证：MN ⊥CE(2) 如图2将△AED 绕A 点逆时针旋转30°，求证：CE ＝2MNA B C A C D E 第21题图(1) 第21题图(2)3、在等腰Rt △ABC 和等腰Rt △A 1B 1C 1中,斜边B 1C 1中点O 也是BC 的中点。

(1)如图1，则AA 1与CC 1的数量关系是 ；位置关系是 。

(2)如图2，将△A 1B 1C 1绕点O 顺时针旋转一定角度，上述结论是否仍然成立，请证明你的结论。

(3)如图3，在（2）的基础上，直线AA 1、CC 1交于点P ，设AB=4，则PB 长的最小值是 。

4、已知，正方形ABCD 的边长为4，点E 是对角线BD 延长线上一点，AE ＝BD ．将△ABE 绕点A 顺时针旋转α度（0°＜α＜360°）得到△AB ′E ′，点B 、E 的对应点分别为B ′、E ′ (1) 如图1，当α＝30°时，求证：B ′C ＝DE(2) 连接B ′E 、DE ′，当B ′E ＝DE ′时，请用图2求α的值(3) 如图3，点P 为AB 的中点，点Q 为线段B ′E ′上任意一点，试探究，在此旋转过程中，线段PQ 长度的取值范围为_______________A 1C 1O B C B 1A 1C 1O B C B 1PA 1C 1OB CB 1图1 图2 图3P E DA B C F P E D A B C F E DA CB F 5、如图P 为等边△ABC 外一点，AH 垂直平分PC 于点H ，∠BAP 的平分线交PC 于点D (1) 求证：DP ＝DB (2) 求证：DA ＋DB ＝DC(3) 若等边△ABC 边长为14，连接BH ，当△BDH 为等边三角形时，请直接写出CP 的长度为_________6、如图，四边形ABCD 为正方形，△BEF 为等腰直角三角形（∠BFE=900，点B 、E 、F ，按逆时针排列），点P 为DE 的中点，连PC ，PF(1)如图①，点E 在BC 上，则线段PC 、PF 有何数量关系和位置关系？请写出你的结论，并证明．(2)如图②，将△BEF 绕点B 顺时针旋转a(O<a<450)，则线段PC ，PF 有何数量关系和位置关系？请写出你的结论，并证明．(3)如图③，若AB=1，△AEF 为等腰直角三角形，且∠A EF=90°，△AEF 绕点A 逆时针旋转过程中，能使点F 落在BC 上，且AB 平分EF ，直接写出AE 的值是________．图① 图② 图③7、已知等腰Rt △ABC 和等腰Rt △EDF ，其中D 、G 分别为斜边AB 、EF 的中点，连CE ，又M 为BC 中点，N 为CE 的中点，连MN 、MG(1) 如图1，当DE 恰好过M 点时，求证：∠NMG ＝45°，且MG ＝2MN(2) 如图2，当等腰Rt △EDF 绕D 点旋转一定的度数时，第(1)问中的结论是否仍成立，并证明 (3) 如图3，连BF ，已知P 为BF 的中点，连CF 与PN ，直接写出CFPN＝______8、已知：如图，在Rt △ABC 中，AC=BC ，CD ⊥AB 于D ，AB=10，将CD 绕着D 点顺时针旋转a （0°<a<90°）到DP 的位置，作PQ ⊥CD 于Q ，点I 是△PQD 角平分线的交点，连IP ，IC ，（1）如图1，在PD 旋转的过程中，线段IC 与IP 之间是否存在某种确定不变的关系？请证明你的猜想。

（第4题）九年级数学上册期末复习综合测试题（含答案）一、选择题（本大题共6小题，每小题2分，共12分．） 1．一元二次方程 x 2＝x 的根是（ ）A ．x 1＝0，x 2＝1B ．x 1＝0，x 2＝－1C ．x 1＝x 2＝0D ．x 1＝x 2＝12．一个不透明布袋中有2个红球，3个白球，这些球除颜色外无其他差别，摇匀后从中随机摸出一个小球，该小球是红色的概率为（ ）A ．12B ．23C ．15D ．253．若一组数据 2，3，4，5，x 的方差比另一组数据 5，6，7，8，9 的方差大，则 x 的值可能是（ ） A ．1B ．4C ．6D ．84．如图，OA 、OB 是⊙O 的半径，C 是⊙O 上一点．若∠OAC ＝16°，∠OBC ＝54°，则 ∠AOB 的度数是（ ）A ．70°B ．72°C ．74°D ．76°5．若关于x 的一元二次方程ax 2＋k ＝0的一个根为2，则二次函数y ＝a (x ＋1)2＋k 与x 轴的交点坐标为（ ） A ．(－3，0)、(1，0) B ．(－2，0)、(2，0) C ．(－1，0)、(1，0)D ．(－1，0)、(3，0)6．如图，在Rt △ABC ，∠ACB ＝90°，AC ＝4，BC ＝3，点D ，E 分别在AB ，AC 上，连接DE ，将△ADE 沿DE 翻折，使点A 的对应点F 落在BC 的延长线上，若FD 平分∠EFB ，则AD 的长为（ ） A ． 157B ．207C ．258D ．259二、填空题（本大题共10小题，每小题2分，共20分．） 7（第12题）l 1 l 2l 3A BCEFD （第11题）8．若a b ＝43，则a －b b＝ ．9．设x 1、x 2是方程x 2＋mx －m ＋3＝0的两个根，则x 1＋x 2－x 1x 2＝ ．10．把抛物线y ＝－x 2向左平移2个单位，然后向上平移3个单位，则平移后该抛物线相应的函数表达式为 ．11．如图，l 1∥l 2∥l 3，若AD ＝1，BE ＝3，CF ＝6，则ABBC的值为 ．12．如图，点A 、B 、C 在⊙O 上，⊙O 的半径为3，∠AOC ＝的长为 ． 13．已知关于x 的函数y ＝x 2＋2mx ＋1，若x ＞1时，y 随x 的增大而增大，则m 的取值范围是 ．14．如图，弦AB 是⊙O 的内接正六边形的一边，弦AC 是⊙O 的内接正方形的一边，若 BC ＝2＋23，则⊙O 的半径为 ．15．如图，正方形ABCD 的边长是4，点E 在DC 上，点F 在AC 上，∠BFE ＝90°，若 CE ＝116．如图，在矩形ABCD 中，AB ＝2，AD ＝4，点E 、F 分别为AD 、CD 边上的点，且EF 的长为2，点G 为EF 的中点，点P 为BC 上一动点，则P A ＋PG 的最小值为 ． 三、解答题（本大题共11小题，共88分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤）17．（8分）解方程：（1）x 2－4x －5＝0； （2）x 2－4＝2x (x －2)．18．（8分）甲乙两人在相同条件下完成了5次射击训练，两人的成绩（单位：环）如下（1）甲射击成绩的中位数为 环，乙射击成绩的众数为 环；（2）计算两人射击成绩的方差；（3）根据训练成绩，你认为选派哪一名队员参赛更好，为什么？19．（8分）某校开展秋季运动会，需运动员代表进行发言，从甲、乙、丙、丁四名运动员中随机抽取．（1）若随机抽取1名，甲被抽中的概率为 ； （2）若随机抽取2名，求甲在其中的概率．20．（7分）如图，在△ABC 中，点D 、E 分别在AB 、AC 上，且∠BCE ＋∠BDE ＝180°． （1）求证：△ADE ∽△ACB ；（2）连接BE 、CD ，求证：△AEB ∽△ADC ．21．（8分）如图是二次函数y ＝－x 2＋bx ＋c 的图像． （1）求该二次函数的关系式及顶点坐标； （2）当y ＞0时 x 的取值范围是 ；（3）当m ＜x ＜m ＋4时，－5＜y ≤4，则m 的值为 ．22．（7分）在Rt △ABC ，∠BAC ＝90°，AB ＝AC ，D 、E、F 分别为BC 、AB 、AC 边上的点，且∠EDF ＝45°．（1）求证：△EBD ∽△DCF ；（2）当D 是BC 的中点时，连接EF ，若CF ＝5，DF ＝4，则EF 的长为 ．23．（8分）某超市销售一种商品，成本为每千克50元．当每千克售价60元时，每天的销售量为60千克，经市场调查，当每千克售价增加1元，每天的销售量减少2千克． （1）为保证某天获得750元的销售利润，则该天的销售单价应定为多少？ （2）当销售单价定为多少时，才能使当天的销售利润最大？最大利润是多少？24．（8分）如图，AB 为⊙O 的直径，弦CD ⊥AB 于点P ，连接BC ，过点D 作DE ⊥CD ，交⊙O 于点E ，连接AE ，F 是DE 延长线上一点，且∠BCD ＝∠F AE ． （1）求证：AF 是⊙O 的切线；（2）若AF ＝2，EF ＝1，求⊙O 的半径．25．（8分）已知二次函数y ＝(x －2)(x －m )（m 为常数）． （1）求证：不论m 为何值，该函数的图像与x 轴总有公共点；（2）若M （－1，0）， N （3，0），该函数图像与线段MN 只有1个公共点，直接写出 m 的取值范围；（3）若点A （－1，a ），B （1，b ），C （3，c ）在该函数的图像上，当abc ＜0时，结合函数图像，直接写出m 的取值范围.26．（8分）如图，四边形ABCD 内接于⊙O ，AB ＝AC ，BD ⊥AC ，垂足为E ． （1）求证：∠BAC ＝2∠DAC ； （2）若AB ＝10，CD ＝5，求BC 的长．27．（10分）定义：圆心在三角形的一边上，与另一边相切，且经过三角形一个顶点（非切点）的圆，称为这个三角形圆心所在边上的“伴随圆”．（1） 如图①，在△ABC 中，∠C ＝90°，AB ＝5，AC ＝3，则BC 边上的伴随圆的半径为 ． （2）如图②，△ABC 中，AB ＝AC ＝5，BC ＝6，直接写出它的所有伴随圆的半径． （3）如图③，△ABC 中，∠ACB ＝90°，点E 在边AB 上，AE ＝2BE ，D 为AC 的中点，且∠CED ＝90°．①求证：△CED 的外接圆是△ABC 的AC 边上的伴随圆； ②DE的值为 ．参考答案说明：本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参照本评分标准的精神给分．一、选择题（本大题共6小题，每小题2分，共12分）二、填空题（本大题共10小题，每小题2分，共20分）7．9 8．13 9．－3 10．y ＝－(x ＋2)2＋3 11．2312．2π 13．m ≥－1 14． 2 2 15．322 16．4 2 －1三、解答题（本大题共11小题，共88分） 17．（8分）（1）解：x 2－4x －5＝0 x 2－4x ＋4＝5＋4(x －2)2＝9 ········································································································ 1分x －2＝±3 ········································································································ 2分 ∴ x 1＝5，x 2＝－1． ··························································································· 4分 （2）解：x 2－4＝2x (x －2) x 2－4＝2x 2－4xx 2－4x ＋4＝0 ··································································································· 5分 (x －2)2＝0 ········································································································ 6分 ∴ x 1＝x 2＝2． ··································································································· 8分 18．（8分）（1）7；8 ········································································································ 2分 （2）s 2甲＝(7－8)2＋(7－8) 2＋(10－8)2＋(9－8)2＋(7－8)25＝1.6环2． ······························ 4分s 2乙＝(8－8)2＋(8－8) 2＋ (7－8)2＋(8－8)2＋(9－8)25＝0.4环2． ······································ 6分（3）选择乙．因为甲乙两人平均数相同均为8，说明两人实力相当，但s 2乙＜s 2甲，乙的成绩更加稳定，所以选乙． ······················································································· 8分19．（8分）（1）14． ·········································································································· 2分（2）解：随机抽取两名运动员，共有6种等可能性结果：（甲，乙）、（甲，丙）、（甲，丁）、（乙，丙）、（乙，丁）、（丙，丁）．其中满足“有甲运动员”(记为事件A )的结果只有3种，所以P (A )＝12． ·································································································· 8分20．（7分）（1）证明：∵ ∠BCE ＋∠BDE ＝180°， ∠EDA ＋∠BDE ＝180°，∴ ∠EDA ＝∠BCE ． ·························································································· 1分 又 ∠A ＝∠A ， ································································································· 2分 ∴ △ADE ∽△ACB ． ·························································································· 3分 （2）∵ △ADE ∽△ACB ， ∴ AD AC ＝AE AB， ·········································· 4分 ∴AD AE ＝ACAB， ······································· 5分 又 ∠A ＝∠A ， ········································ 6分 ∴ △AEB ∽△ADC ． ································· 7分21．（8分）（1）将(0，3)、 (3，0)代入，得⎩⎨⎧3＝c ，0＝－9＋3b ＋c································································································· 1分解得⎩⎨⎧c ＝3，b ＝2····································································································· 2分∴ y ＝－x 2＋2x ＋3 ····························································································· 3分 ∴ 顶点坐标为(1，4) ························································································ 4分 （2）－1＜x ＜3. ······························································································ 6分 （3）－2或0 ···································································································· 8分 22．（7分）（1）解：∵∠BAC ＝90°，AB ＝AC ，∴ ∠B ＝∠C ＝45°． ··························································································· 1分 ∴ 在△BDE 中，∠BED ＋∠BDE ＝180°－∠B ＝135°， ∵ ∠EDF ＝45°，∴ ∠BDE ＋∠CDF ＝135°，∴ ∠BED ＝∠CDF ． ·························································································· 3分 ∵ ∠B ＝∠C ，∴ △EBD ∽△DCF ． ·························································································· 5分 （2 ········································································································ 7分23．（8分）（1）解：设每千克的销售价增加x 元，根据题意，得(60＋x －50) (60－2x )＝750 ··················································································· 2分 ∴ x 1＝5，x 2＝15． ····························································································· 3分 60＋5＝65或60＋15＝75 ···················································································· 4分 答：销售单价为65或75元时获得利润750元． （2）解：每千克的销售价增加x 元，利润为w 元．w ＝(60＋x －50) (60－2x ) ···················································································· 6分 ＝－2(x －10)2＋800 ···························································································· 7分 ∵ a ＝－2＜0，∴ 当x ＝10时，w 有最大值800． ········································································ 8分 60＋10＝70答：当销售单价为70元时获得最大利润，为800元． 24．（8分） （1）连接BD ．∵ AB 为⊙O 的直径，CD ⊥AB ，∴ ⌒BC ＝ ⌒BD ， ························································· 1分 ∴ ∠BDC ＝∠BCD ．∵ 四边形ABDE 为⊙O 的内接四边形，∴ ∠BDE ＋∠BAE ＝180°，即∠BDC ＋∠CDF ＋∠BAE ····· 2分∵ DE ⊥CD ， ∴ ∠CDF ＝90°， ∴ ∠BDC ＋∠BAE ＝90°．∵ ∠BCD ＝∠F AE ， ·························································································· 3分 ∴ ∠BAE ＋∠F AE ＝90°，即∠F AB ＝90°， ∴ AF ⊥AB ． 又 点A 在⊙O 上，∴ AF 与⊙O 相切． ·························································································· 4分 （2）过点O 作OG ⊥DF 垂足为G ． ∵ ∠F AB ＝∠D ＝∠APD ＝90°， ∴ 四边形APDF 是矩形， ∴ ∠F ＝90°．∵ ∠F AB ＝∠F ＝∠OGF ＝90°， ∴ 四边形AOGF 是矩形，∴ AF ＝OG ，AO ＝GF ． ···················································· 5分 设OE ＝OA ＝r ，则GE ＝r －1．在Rt △OGE 中，由勾股定理得OG 2＋GE 2＝OE 2， ···················································· 6分 即4＋(r －1)2＝r 2， ···························································································· 7分 解得r ＝5 2 ． ····································································································· 8分25．（8分）（1）令y ＝0，即(x －2)(x －m )＝0 ········································································· 1分 ∴ x 1＝2，x 2＝m ． ····························································································· 2分 当m ＝2时，x 1＝x 2，方程有两个相等的实数根； 当m ≠2时，x 1≠x 2，方程有两个不等的实数根． ∴ 不论m 为何值，方程总有实数根；∴ 不论m 为何值，该函数的图像与x 轴总有公共点． ·············································· 3分 （2）m ＝2或m ＞3或m ＜－1． ··········································································· 6分 （3）－1＜m ＜1或m ＞3． ·················································································· 8分 26．（8分）。

综合测试题时间：90分钟满分：100分一、选择题(每小题3分，共36分)1．(滨州中考)下列说法不正确的是( C )A．炒菜时，满屋飘香，表明分子在不停地做无规则运动B．用水作为汽车发动机的冷却剂，主要是因为水的比热容较大C．煤的热值比干木柴的大，煤燃烧时放出的热量比干木柴燃烧时放出的热量多D．四冲程汽油机的做功冲程中，内能转化为机械能2．(岳阳中考)把毛皮摩擦过的橡胶棒靠近轻质小球，小球被吸引，则这个小球( D ) A．一定不带电 B．一定带负电 C．一定带正电 D．可能不带电3．(南宁中考)某种电脑键盘清洁器有两个开关，开关S1只控制照明用的小灯泡L，开关S2只控制吸尘用的电动机M。

如图所示的四个电路中，符合上述要求的是( D )4．(聊城中考)在家庭电路中，插座、螺口节能灯和开关的连接正确的是( B )5．(北京中考)下列选项中符合安全用电要求的是( B )A．用湿手按已接电的插座上的开关B．及时更换家庭电路中绝缘皮老化、破损的导线C．在未断开电开关的情况下，用湿布擦拭电视机D．把用电器的三脚插头改为两脚插头接在两孔插座上使用6．(绵阳中考)电视机、微波炉等家用电器给我们的生活带了许多方便，微波炉使用的电磁波波长很短，但比电视机遥控器所用的波长要长些。

下列电磁波成分中波长比电视机遥控器所用波长长的是( D )A．γ射线 B．可见光 C．红外线 D．无线电波7．(黄石中考)下列关于能与可持续发展及信息的传递的叙述中正确的是( D )A．太阳内部每时每刻都在发生着核裂变释放巨大的核能B．石油是可再生能C．激光在光导纤维中始终沿直线传播D．黄石交通广播电台的频率是103.3 MH，广播电台发射的电磁波是靠迅速变化的电流实现的8．(衡阳中考)在探究“通电螺线管外部磁场分布”的实验中，开关断开时小磁针甲、乙的指向如图所示，当开关闭合时，通电螺线管有磁性，则下列说法正确的是( B ) A．小磁针甲偏转，小磁针乙不偏转B．小磁针乙偏转，小磁针甲不偏转C．小磁针甲、乙均偏转D．滑动变阻器滑片P从右向左滑动时，通电螺线管的磁性逐渐增强9．(苏州中考)在“探究影响电流热效应的因素”实验中，可通过观察玻璃管中煤油柱的高度变化比较电阻丝产生热量的多少(如图)。

人教版九年级数学期末考试综合复习测试题（含答案）一．选择题（共10小题，每小题3分，共30分）1．计算，3(2)a -结果正确的是( )A ．32a -B ．36a -C ．38a -D ．38a2．据教育部统计，2022年高校毕业生约1076万人，用科学记数法表示1076万为( )A ．4107610⨯B ．61.07610⨯C ．71.07610⨯D ．80.107610⨯3．下列汽车标志中，是中心对称图形的是( ) A ． B ． C ． D ．4．如图所示，直线//EF GH ，射线AC 分别交直线EF 、GH 于点B 和点C ，AD EF ⊥于点D ，如果20A ∠=︒，则(ACH ∠= )A ．160︒B ．110︒C ．100︒D ．70︒5．如图，已知ABC ADE ∆≅∆，若70E ∠=︒，30D ∠=︒，则BAC ∠的度数是( )A ．70︒B ．80︒C ．40︒D ．30︒6．方程2210x x --=实数根的情况为( )A ．有两个不相等的实数根B ．有两个相等的实数根C ．没有实数根D ．不能确定7．在平面直角坐标系中，若点(1,)A a b -+与点(,3)B a b -关于原点对称，则点(,)C a b 在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限8．如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与ABC ∆相似的是( )A ．B ．C ．D ．9．已知正比例函数11(0)y k x k =≠的图象与反比例函数22(0)k y k x =≠的图象交于A ，B 两点，其中点A 在第二象限，横坐标为2-，另一交点B 的纵坐标为1-，则12(k k ⋅= )A ．4B ．4-C ．1-D ．110．已知(3,2)A --，(1,2)B -，抛物线2(0)y ax bx c a =++>顶点在线段AB 上运动，形状保持不变，与x 轴交于C ，D 两点(C 在D 的右侧），下列结论：①2c -；②当0x >时，一定有y 随x 的增大而增大；③若点D 横坐标的最小值为5-，则点C 横坐标的最大值为3；④当四边形ABCD 为平行四边形时，12a =． 其中正确的是( )A ．①③B ．②③C ．①④D ．①③④二．填空题（共5小题，每小题3分，共15分）11．因式分解：22416x y -= ． 12．若2|2|(3)0x y -++=，则2()x y += ．13．已知m ，()n m n ≠是一元二次方程220230x x +-=的两个实数根，则代数式22m m n ++的值为 ．14．如图，A ，B ，C ，D 是O 上的四点，且点B 是AC 的中点，BD 交OC 于点E ，60OED ∠=︒，35OCD ∠=︒，那么AOC ∠的度数是 ．15．如图，E 为正方形ABCD 内一点，5AD =，4AE =，将ADE ∆绕点A 顺时针旋转90︒到ABE ∆'，则边DE 所扫过的区域（图中阴影部分）的面积为 ．题14图 题15图三．解答题（一）（共3小题，每小题8分，共24分）16．（1）计算：0111(2021)()2cos45221π--++-︒+； （2）先化简，再求值：23210(1)19x x x x --⋅---，其中x 是1、2、3中的一个合适的数．17．如图，DE AB ⊥于E ，DF AC ⊥于F ，若BD CD =，BE CF =．求证：（1）AD 平分BAC ∠；（2）2AC AB BE =+．18．今年，我市某学校举办了为贫困生捐赠书包活动．该学校用2000元在某商店购进一批学生书包，随后发现书包数量不够，于是又购进第二批同样的书包，所购数量是第一批的3倍，每个书包比第一批购买时贵了4元，结果第二批用了6300元．（1）该学校第一批购进的学生书包每个多少元？（2）如果该商店第一批、第二批学生书包每个的进价分别是68元、70元，售给该学校的这些学生书包，该商店盈利多少元？四．解答题（二）（共3小题，每小题9分，共27分）19．某银行柜台在储户人数较多时常开放1、2、3、4号窗口办理日常业务，一般是先到取号机拿号，按顾客“先到达，先服务“的方式服务（1）求某储户在3号窗口办业务的概率是（2）储户乙取号时发现储户甲已办理完业务准备离开（储户甲、乙先后到达银行取号办理业务），请用树状图或列表法求储户甲、乙两人在同一柜台办理业务的概率．20．如图，在平行四边形ABCD 中，BD AB ⊥，延长AB 至点E ，使BE AB =，连接EC ．（1）求证：四边形BECD 是矩形．（2）连接AC ，若3AD =，2CD =，求AC 的长．21．Rt ABO ∆的顶点A 是双曲线k y x =与直线(1)y x k =--+在第二象限的交点，AB 垂直x 轴于点B 且32ABO S ∆=． （1）求这两个函数解析式；（2）求AOC ∆的面积；（3）根据图象直接写出不等式(1)k x k x >-+的解集．五．解答题（三）（共2小题，每小题12分，共24分）22．如图，AB 是⊙O 的直径，C 、D 是⊙O 上两点，连接CD ，C 是的中点，过点C 作AD 的垂线，垂足是E ．连接AC 交BD 于点F ．（1）求证：CE 是⊙O 的切线；（2）求证：△CDF ∽△CAD ；（3）若DF ＝2，CD ＝，求AC 值．23．如图，在平面直角坐标系中，抛物线21y ax bx =++交y 轴于点A ，交x 轴正半轴于点(4,0)B ，交直线AD 于点5(3,)2D ，过点D 作DC x ⊥轴于点C ． （1）求抛物线的解析式；（2）点P 为x 轴正半轴上一动点，过点P 作PN x ⊥轴交直线AD 于点M ，交抛物线于点N ；若点P 在线段OC 上（不与O 、C 重合），连接CM ，求PCM ∆面积的最大值。

九年级数学第一学期期末考试综合复习测试题（含答案）一．选择题（共10小题，每小题3分，共30分） 1．2022的相反数是( )A ．2022B ．2022-C ．12022D ．2022± 2．若代数式3125m x y -与822m nx y +-是同类项，则( )A ．73m =，83n =-B ．3m =，4n =C ．73m =，4n =- D ．3m =，4n =-3．下列四组线段中，能组成直角三角形的是( ) A ．1a =，3b =，3c = B ．2a =，3b =，4c = C ．2a =，4b =，5c =D ．3a =，4b =，5c = 4．如图所示，直线//a b ，231∠=︒，28A ∠=︒，则1(∠= )A ．61︒B ．60︒C ．59︒D ．58︒5．下列关于事件发生可能性的表述，正确的是( )A ．“在地面向上抛石子后落在地上”是随机事件B ．掷两枚硬币，朝上面是一正面一反面的概率为13C ．在同批次10000件产品中抽取100件发现有5件次品，则这批产品中大约有500件左右的次品D ．彩票的中奖率为10%，则买100张彩票必有10张中奖6．某校10名学生参加课外实践活动的时间分别为：3，3，6，4，3，7，5，7，4，9（单位：小时），这组数据的众数和中位数分别为( ) A ．9和7 B ．3和3 C ．3和4.5 D ．3和5 7．一个正多边形的每一个内角都是150︒，则它的边数为( ) A ．6 B ．9 C ．12 D ．158．若不等式组841x x x m +<-⎧⎨>⎩的解集是3x >，则m 的取值范围是( )A ．3m <B ．3mC ．3m >D ．3m9．已知关于x 的一元二次方程22(21)0x m x m --+=有实数根，则m 的取值范围是( ) A ．14m 且0m ≠ B ．14m C ．14m < D ．14m >10．如图1，一个扇形纸片的圆心角为90︒，半径为6．如图2，将这张扇形纸片折叠，使点A 与点O 恰好重合，折痕为CD ，图中阴影为重合部分，则阴影部分的面积为( )A ．9632π-B ．693π-C ．91232π-D ．94π二．填空题（共5小题，每小题3分，共15分） 11．将数据2022万用科学记数法表示为 ．12．已知当3x =时，代数式35ax bx +-的值为20，则当3x =-时，代数式35ax bx +-的值是 ．13．将抛物线229y x x =-+-向左平移2个单位，再向上平移1个单位后，得到的抛物线的解析式为 ．14．已知ABC ∆中，点O 是ABC ∆的外心，140BOC ∠=︒，那么BAC ∠的度数为 ．15．如图，在正方形ABCD 中，顶点(5,0)A -，(5,10)C ，点F 是BC 的中点，CD 与y 轴交于点E ，AF 与BE 交于点G ，将正方形ABCD 绕点O 顺时针旋转，每次旋转90︒，则第2023次旋转结束时，点G 的坐标为 ．三．解答题（一）（共3小题，每小题8分，共24分） 16．计算（1）2()(2)x y x y x +--；（2）2219(1)244a a a a --÷--+．17．如图，90ACB ∠=︒，AC AD =．（1）过点D 作AB 的垂线DE 交BC 与点E ，连接AE ．（尺规作图，并保留作图痕迹） （2）如果8BD =，10BE =，求BC 的长．18．如图，在四边形ABCD 中，AC 与BD 交于点O ，BE AC ⊥，DF AC ⊥，垂足分别为点E ，F ，且BE DF =，ABD BDC ∠=∠．求证：四边形ABCD 是平行四边形．四．解答题（二）（共3小题，每小题9分，共27分） 19．阳光中学为了丰富学生的课余生活，计划购买围棋和中国象棋供棋类兴趣小组活动使用，若购买3副围棋和5副中国象棋需要98元；若购买1副围棋和2副中国象棋需要36元．（1）求每副围棋和每副中国象棋各多少元；（2）阳光中学决定购买围棋和中国象棋共40副，总费用不超过538元，且围棋的副数不低于象棋的副数，问阳光中学有几种购买方案；（3）请求出最省钱的方案需要多少钱？20．我市某中学举行“中国梦⋅我的梦”的演讲比赛，赛后整理参赛学生的成绩，将学生的成绩分为A，B，C，D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整，请你根据统计图解答下列问题．（1）参加比赛的学生人数共有名，在扇形统计图中，表示“D等级”的扇形的圆心角为度，图中m的值为；（2）补全条形统计图；（3）组委会决定从本次比赛中获得A等级的学生中，选出两名去参加市中学生演讲比赛，已知A等级中男生只有1名，请用画树状图或列表的方法求出所选学生恰是一男一女的概率．21．22．某网店专售一款新型钢笔，其成本为20元/支，销售中发现，该商品每天的销售量y与销售单价x（元/支）之间存在如下关系：10400y x=-+，自武汉爆发了“新型冠状病毒”疫情该网店店主决定从每天获得的利润中抽出200元捐赠给武汉，同时又让顾客得到实惠，当销售单价定位多少元时，捐款后每天剩余利润为550元？五．解答题（三）（共2小题，每小题12分，共24分）22．如图，以点O为圆心，AB长为直径作圆，在O上取一点C，延长AB至点D，连接DC，过点A作O的切线交DC的延长线于点E，且DCB DAC∠=∠．（1）求证：CD是O的切线；（2）若6AD=，2:3BC CA=，求AE的长．23．如图，在平面直角坐标系中，直线33y x =--与x 轴交于点A ，与y 轴交于点C ．抛物线2y x bx c =++经过A 、C 两点，且与x 轴交于另一点B （点B 在点A 右侧）． （1）求抛物线的解析式；（2）若点M 是线段BC 上一动点，过点M 的直线ED 平行y 轴交x 轴于点D ，交抛物线于点E ，求ME 长的最大值及此时点M 的坐标； （3）在（2）的条件下：当ME 取得最大值时，在x 轴上是否存在这样的点P ，使得以点M 、点B 、点P 为顶点的三角形是等腰三角形？若存在，请直接写出所有点P 的坐标；若不存在，请说明理由．答案一．选择题1． B ．2． D ．3． D ．4． C ．5． C ．6． C ．7． C ．8． B ．9． B ．10． C ． 二．填空题11． 72.02210⨯．12． 30-．13． 228y x x =---．14． 70︒或110︒．15． (4,3)-． 三．解答题16．解：（1）2()(2)x y x y x +--22222x xy y xy x =++-- 2y =；（2）2219(1)244a a a a --÷--+ 23(3)(3)2(2)a a a a a ---+=÷-- 23(2)2(3)(3)a a a a a --=⋅---+ 23a a -=--． 17．解：（1）如图所示即为所求作的图形． （2）ED 垂直AB ， 90ADE EDB ∴∠=∠=︒，在Rt BDE ∆中，22221086DE BE BD =-=-=， 在Rt ADE ∆和Rt ACE ∆中， AC ADAE AE =⎧⎨=⎩， Rt ADE Rt ACE(HL)∴∆≅∆， 6EC ED ∴==， 16BC BE EC ∴=+=．18．证明：ABD BDC ∠=∠， //AB CD ∴．BAE DCF ∴∠=∠．在ABE ∆与CDF ∆中， 90BAE DCF AEB CFD BE DF ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩． ()ABE CDF AAS ∴∆≅∆． AB CD ∴=．∴四边形ABCD 是平行四边形．19．解：（1）设每副围棋x 元，每副中国象棋y 元，根据题意得：3598236x y x y +=⎧⎨+=⎩，∴1610x y =⎧⎨=⎩，∴每副围棋16元，每副中国象棋10元；（2）设购买围棋z 副，则购买象棋(40)z -副， 根据题意得：1610(40)538m m +-，40m z -，2023m ∴，m 可以取20、21、22、23则有：方案一：购买围棋20副，购买中国象棋20副方案二：购买围棋21副，购买中国象棋19副方案：购买围棋22副，购买中国象棋18副方案四：购买围棋23副，购买中国象棋17副由4种方案；（3）由上一问可知共有四种方案：方案一：购买围棋20副，购买中国象棋20副；方案二：购买围棋21副，购买中国象棋19副；方案三：购买围棋22副，购买中国象棋18副；方案四：购买围棋23副，购买中国象棋17副；方案一需要20162010520x x +=； 方案二需要21161910526x x +=； 方案三需要22161810532x x +=； 方案四需要23161710538x x +=； 所以最省钱是方案一，需要520元．20．（1）解：根据题意得：总人数为：315%20÷=（人)， 表示“D 等级”的扇形的圆心角为43607220⨯︒=︒；C等级所占的百分比为8100%40% 20⨯=，所以40m=，故答案为：20，72，40．（2）解：等级B的人数为20(384)5-++=（人)，补全统计图，如图所示：（3）解：根据题意，列出表格，如下：男女1女2男女1、男女2、男女1男、女1女2、女1女2男、女2女1、女2共有6种等可能结果，其中恰是一男一女的有4种，所以恰是一男一女的概率为42 63 =．21．解：由题意可得(20)(10400)200550x x--+-=解得125x=，235x=因为要让顾客得到实惠，所以25x=答：当销售单价定为25元时，捐款后每天剩余利润为550元．22．（1）证明：连接OC，OE，如图，AB为直径，90ACB∴∠=︒，即190BCO∠+∠=︒，又DCB CAD∠=∠，1CAD∠=∠，1DCB∴∠=∠，90DCB BCO ∴∠+∠=︒，即90DCO ∠=︒， CD ∴是O 的切线；（2）解：EC ，EA 为O 的切线， EC EA ∴=，AE AD ⊥， OC OA =， OE AC ∴⊥，90BAC EAC ∴∠+∠=︒，90AEO EAC ∠+∠=︒， BAC AEO ∴∠=∠， tan tan BAC AEO ∴∠=∠，∴23BC AO AC AE ==， Rt DCO Rt DAE ∆∆∽，∴23CD OC OA DA AE AE ===， 2643CD ∴=⨯=， 在Rt DAE ∆中，设AE x =，222(4)6x x ∴+=+， 解得52x =． 即AE 的长为52．23．解：（1）直线33y x =--与x 轴、y 轴分别交于点A 、C ， (1,0)A ∴-，(0,3)C -抛物线2y x bx c =++经过点(1,0)A -，(0,3)C -， ∴103b c c -+=⎧⎨=-⎩，解得23b c =-⎧⎨=-⎩，∴抛物线的解析式为223y x x =--．（2）设(E x ，223)(03)x x x --<<，则(,3)M x x -， 222393(23)3()24ME x x x x x x ∴=----=-+=--+，∴当32x =时，94ME =最大，此时3(2M ，3)2-． （3）存在．如图3，由（2）得，当ME 最大时，则3(2D ，0)，3(2M ，3)2-，32DO DB DM ∴===； 90BDM ∠=︒，223332()()222OM BM ∴==+=． 点1P 、2P 、3P 、4P 在x 轴上， 当点1P 与原点O 重合时，则1322PM BM ==，1(0,0)P ； 当2322BP BM ==时，则232632322OP -=-=， 2632(2P -∴，0)； 当点3P 与点D 重合时，则3332P M P B ==，33(2P ，0)； 当4322BP BM ==时，则432632322OP +=+=， 4632(2P +∴，0)． 综上所述，1(0,0)P ，2632(2P -，0)，33(2P ，0)，4632(2P +，0)．。

九年级英语综合练习题30题答案解析1.There is a book on the table.（）book is mine.A.TheB.AC.AnD./答案解析：A。

本题考查定冠词the 的用法。

这里特指桌子上的那本书，所以用定冠词the。

选项B“a”表示泛指一本，但此处不是泛指。

选项C“an”用在元音音素开头的单词前，此处不合适。

选项 D 不填冠词不符合语法要求。

2.She is（）kind girl.A.aB.anC.theD./答案解析：A。

本题考查不定冠词的用法。

“kind”是以辅音音素开头的单词，所以用不定冠词a。

选项B“an”用于元音音素开头的单词前。

选项C“the”是定冠词，此处不是特指。

选项 D 不填冠词不符合语法要求。

3.I（）to school every day.A.goB.goesC.goingD.to go答案解析：A。

本题考查一般现在时中动词的用法。

主语是I，第一人称，谓语动词用原形go。

选项B“goes”是第三人称单数形式。

选项C“going”是现在分词形式。

选项D“to go”是动词不定式形式。

4.He（）playing football.A.likeB.likesC.likingD.to like答案解析：B。

本题考查一般现在时中第三人称单数的用法。

主语是he，第三人称单数，谓语动词用likes。

选项A“like”是原形，主语不是第一、二人称或复数时不能用。

选项C“liking”是现在分词形式。

选项D“to like”是动词不定式形式。

5.The dog is（）under the tree.A.sleepB.sleepsC.sleepingD.to sleep答案解析：C。

本题考查现在进行时的用法。

现在进行时的构成是be+动词的现在分词，所以用sleeping。

选项A“sleep”是原形。

选项B“sleeps”是第三人称单数形式。

选项D“to sleep”是动词不定式形式。

九年级中考数学综合训练题（4）一．选择题（共12小题，满分36分，每小题3分）1．（3分）＝（）A．B．C．D．2．（3分）如图所示的几何体的主视图是（）A．B．C．D．3．（3分）如图，P A、PB是⊙O的切线，切点分别为A、B，点C在⊙O上，如果∠P＝50°，那么∠ACB等于（）A．40°B．50°C．65°D．130°4．（3分）为了比较某校同学汉字听写谁更优秀，语文老师随机抽取了10次听写情况，发现甲乙两人平均成绩一样，甲、乙的方差分别为2.7和3.2，则下列说法正确的是（）A．甲的发挥更稳定B．乙的发挥更稳定C．甲、乙同学一样稳定D．无法确定甲、乙谁更稳定5．（3分）如图所示，三角形ABC中，∠BAC＝90°，过点A画AD⊥BC，则下列说法不正确的是（）A．线段AD是点A与直线BC上各点连接的所有线段中最短的B．线段AB是点B到直线AD的垂线段C．点A到直线BC的距离是线段AD的长D．点C到直线AB的距离是线段AC的长6．（3分）某校数学课外活动探究小组，在老师的引导下进一步研究了完全平方公式．结合实数的性质发现以下规律：对于任意正数a、b，都有a+b≥2成立．某同学在做一个面积为3 600cm2，对角线相互垂直的四边形风筝时，运用上述规律，求得用来作对角线用的竹条至少需要准备xcm．则x的值是（）A．120B．60C．120D．607．（3分）如图，梯形ABCD中，AD∥BC，DC⊥BC，将梯形沿对角线BD折叠，点A恰好落在边DC中点E处，若BC＝2，则线段AB的长为（）A．2B．C．2D．8．（3分）在函数中，自变量x的取值范围是（）A．x＜B．x≠﹣C．x≠D．x＞9．（3分）如图，矩形ABCD中，F是DC上一点，BF⊥AC，垂足为E，AB＝2AD＝4，则CF长度是（）A．B．C．D．110．（3分）如图，反比例函数（k＞0）与一次函数的图象相交于两点A（x1，y1），B（x2，y2），线段AB交y轴与C，当|x1﹣x2|＝2且AC＝2BC时，k、b的值分别为（）A．k＝，b＝2B．k＝，b＝1C．k＝，b＝D．k＝，b＝11．（3分）如图，直线y＝kx+b（k＜0）交y轴于点A，交x轴于点B，且（AB+OA）（AB ﹣OA）＝，则不等式kx+b＞0的解集为（）A．x＞B．x＞3C．x＜D．x＜312．（3分），，，＝﹣…从计算结果中找出规律，并用这一规律计算：（+++…+）（+1）结果为（）A．2005B．2006C．2007D．2008二．填空题（共6小题，满分18分，每小题3分）13．（3分）如图，海平面上灯塔O方圆100千米范围内有暗礁．一艘轮船自西向东方向航行，在点A处测量得灯塔O在北偏东60°方向，继续航行100千米后，在点B处测量得灯塔O在北偏东37°方向．请你作出判断，为了避免触礁，这艘轮船是否要改变航向？．（填“是”或“否”，参考数据：sin37°≈0.6018，cos37°≈0.7986，tan37°≈0.7536，cot37°≈1.327，≈1.732）．14．（3分）不等式组的整数解的积为．15．（3分）+（b+2）2+|c﹣2022|＝0，则（a+b）c的值为．16．（3分）定义新运算“*”．规则：a*b＝a（a≥b）或者a*b＝b（a＜b）如1*2＝2，（﹣3）*2＝2．若x2+x﹣1＝0的根为x1、x2，则x1*x2的值为：．17．（3分）如图，已知矩形DEFG内接于Rt△ABC，D在AB上，E、F在BC上，G在AC 上，∠BAC＝90°，AB＝6cm，AC＝8cm，，则矩形的边长DG＝．18．（3分）已知在平面直角坐标系中，点O为坐标原点，过O的直线OM经过点A（6，6），过A作正方形ABCD，在直线OA上有一点E，过E作正方形EFGH，已知直线OC经过点G，且正方形ABCD的边长为2，正方形EFGH的边长为3，则点F的坐标为．三．解答题（共7小题，满分66分）19．（6分）化简求值：（﹣）÷，其中a＝+1，b＝﹣1．20．（8分）阅读下面材料，再回答问题：有一些几何图形可以被某条直线分成面积相等的两部分，我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”，如：圆的直径所在的直线是圆的“二分线”，正方形的对角线所在的直线是正方形的“二分线”．解决下列问题：（1）菱形的“二分线”可以是．（2）三角形的“二分线”可以是．（3）在图中，试用两种不同的方法分别画出等腰梯形ABCD的“二分线”，并说明你的画法．21．（10分）掷①②两枚正六面体骰子，它们的点数和可能有哪些值？请在下表中列出来，并用表中的信息求：（1）“点数和为7点”的概率P1；（2）“两颗骰子点数相同”的概率P2；（3）“两颗骰子点数都是相同偶数”的概率P3．22．（10分）已知关于x的方程（a+c）x2+bx﹣（a+2c）＝0的两根之和为1，两根的倒数和为﹣2．（1）求这个方程的两根之积；（2）求a：b：c．23．（10分）采购员用一张1万元支票去购物．购单价为590元的A种物品若干件，又购单价为670元的B种物品若干件，其中B种件数多于A种件数，找回了几张100元和几张10元的（10元的不超过9张）．如把购A种物品和B种物品的件数互换，找回的100元和10元的钞票张数也恰好相反，则原来购B种物品多少件？24．（10分）如图，已知AC、AB是⊙O的弦，AB＞AC．（1）在图（a）中，能否在AB上确定一点E，使得AC2＝AE•AB，为什么？（2）在图（b）中，在条件（1）的结论下延长EC到P，连接PB，如果PB＝PE，试判断PB和⊙O的位置关系，并说明理由．25．（12分）如图，一次函数y＝﹣x+3的图象交x轴于点A，交y轴于点Q，抛物线y＝ax2+bx+c （a≠0）的顶点为C，其图象过A、Q两点，并与x轴交于另一个点B（B点在A点左侧），△ABC三内角∠OAC、∠ABC、∠ACB的对边为a1，b1，c1．若关于x的方程a1（1﹣x2）+2b1x+c1（1+x2）＝0有两个相等实数根，且a1＝b1；（1）试判定△ABC的形状；（2）当时求此抛物线的解析式；（3）在（2）的条件下，抛物线上是否存在点P，使S△ABP＝S四边形ACBQ？若存在，求出P点坐标；若不存在，请说明理由．。

人教版九年级语文期末综合试题（含答案解析）一（30分）1．下列加点字的注音全都正确的一项是（3分）A．伫．立(zhù) 嗔．怪(chēn)锲．而不舍(qiè)B．腆．着(diǎn)聒．噪(guō)面面厮觑．(qù)C．纤．细(xiān) 狡黠．(xiá)拈．弓搭箭(zhān)D．拮．据(jié)肖．像(xiào) 恪．尽职守(gè)2．下列词语中没有别字的一项是（3分）A．汲取繁衍金璧辉煌吹毛求疵B．取谛绰刀断章取义怒不可遏C．麾军藉贯恃才放旷恼羞成怒D．诘难喑哑黎民百姓豁然贯通3．依次填入下列横线处的词语，最恰当的一项是（3分）①从4月1号起，浙江省开始新的最低工资标准，每月从1100元调整到1310元，超过了一直高居榜首的上海，成为目前全国最低工资标准最高的省份。

②夜幕降临，钱塘江在点点灯光的下，显得格外宁静美丽。

③数年的，唐老师已能娴熟地将新课改精神融入课堂教学，带给学生和评委耳目一新之感，并最终赢得了这次优质课评比的一等奖。

A．履行映衬苦口婆心B．执行映照苦心孤诣C．履行映照苦心孤诣D．执行映衬苦口婆心4．下列句子中标点符号使用都正确的一项是（3分）A．这位普普通通的山区教师，以持之以恒，慷慨无私的助学善举感动了中国。

B．富春山水之美在于精致而大气，她宛如江南女子尽显柔美情怀，又像热血男儿袒露宽阔胸怀。

C．“知屋漏者在宇下，知政失者在草野”。

温总理引用这句名言意在说明：要想了解政策的缺失，就必须深入民间调查。

D．依我之见，少年写作文，就应该多写一点“有意思”的事。

何必那么深刻，何必那么深沉？故作高深，一本正经，老气横秋，少了童年的童趣和稚气，倒没有什么可爱之处。

5．下列关于文学常识的说法，有错误的一项是（3分）A．《陈涉世家》节选自西汉著名史学家司马迁写的我国第一部纪传体通史《史记》。

B．《故乡》描写了我回故乡的所见所闻所感，着力描写了中年闰土和杨二嫂这两个人物形象。

XX学年第二学期海珠区九年级综合练习（一）物理试卷一、单选题（每小题3 分，共36 分）1．甲电磁波的频率是1300kHz，乙电磁波的频率是1000MHz．比较两电磁波A．甲电磁波频率较大B．乙电磁波频率较大C．甲电磁波在真空中传播的速度较大D．乙电磁波在真空中传播的速度较大2．关于太阳能凉帽（如图所示），下列说法正确的是电扇太阳能电池板A．太阳能电池板把太阳能转化为化学能B．电扇工作时获得的机械能由电能转化而来C．电能是可再生能源D．太阳能是不可再生能源3．在加热材料M 的一段时间内，M 的体积增大，温度一直低于其熔点．此过程A．M 处于固态B．M 的质量变大C．M 处于液态D．M 的密度变大4．天芯在拉大提琴时，相比粗钢丝弦，细钢丝弦发出的声音频率较高．则A．细钢丝弦发出的是超声波B．细钢丝弦振动的幅度比较大C．细钢丝弦振动1 次所用的时间较长D．1s 内细钢丝弦振动的次数较多5．蜡烛、透镜（焦距f=10cm）、光屏在光具座上的位置如图所示时，光屏上恰好成像．下列说法正确的是光具座A．此时光屏上成倒立缩小的像B．此时光屏上成正立放大的像C．透镜位置不变，将蜡烛向右移动后，调整光屏位置，光屏上一定能成像D．透镜位置不变，将蜡烛向左移动后，调整光屏位置，光屏上一定能成像①小球 细绳O② vM③④气态制冷剂 乙 甲6．被细绳拴着的小球在水．平．桌．面．绕 O 点以大小为 v 的速度做圆周运动，轨迹如图中虚线① 所示．每一时刻小球的速度方向与细绳垂直，不计阻力，某时刻小球在图示 M 位置时细 绳断．则小球A ．沿原来圆形轨迹①以速度 v 运动B ．沿轨迹②以速度 v 做匀速直线运动C ．沿轨迹③以速度 v 做匀速直线运动D ．沿轨迹④竖直向下运动7．右图是冰箱制冷剂循环路线示意图．制冷剂在 冷冻室的管子里发生的物态变化是 A ．液化 B ．升华 C ．汽化 D ．凝固冷冻室的管子液态制冷剂气态制冷剂8．把榴莲和煮熟的咸鱼都放在冰箱里同一层，到了第二天，老王吃榴莲时闻到有一股咸鱼 味．以下判断正确的是A ．打开冰箱时，榴莲的温度肯定比咸鱼的低B ．榴莲肯定吸收了咸鱼的热量C ．咸鱼不停地做机械运动D ．吃咸鱼时也会闻到有榴莲味9．甲、乙两人同时从同一起跑线出发，同向做匀速直线运动，某时刻他们的位置如下图所 示．四个坐标图象中，能正确反映上述特征的图象是起跑线甲s甲 s乙 v 甲v乙甲乙乙A tBtCtDt10．下列说法正确的是 A ．太阳光通过三棱镜分解出红、绿、蓝共三种色光，这是光的色散 B ．三原色光按一定的比例混合，可以产生白光 C ．烤炉用红外线加热食品，主要是利用红外线传递信息D ．紫外线照射百元钞能看到 “100”的萤光标记，因为人眼看到了纸币反射的紫外线11．下图所示电路盒内有电源和导线，面板上有两个灯泡L1、L2，两个开关S1、S2．要探究盒内的电路连接，小明做了多次实验并将结果填入下表．以下四个电路，符合上述发光情况的是A B C D12．小明连好甲实验的电路（电路各部分接触良好）．开关闭合前，在导线下方的小磁针指向固定不变．开关试触，小磁针没有发生偏转．当只把电源正、负极对调，进行乙实验，开关试触，发现小磁针的指向作了180º偏转．以下观点正确的是甲实验乙实验试触时A．开关没闭合时，小磁针的N 极指向地磁的北极B．甲实验开关闭合时，小磁针没有偏转，说明此时导线周围不存在磁场C．乙实验试触时，导线对小磁针有力的作用，小磁针对导线没有力的作用D．本组实验说明，电流的磁场方向与电流方向有关S2L1L2S1S2L1S1L2S2L2L1S1S2L2L1S1只闭合开关S1S2S1、S2L1 发光情况亮不亮亮L2 发光情况亮不亮不亮L1 S1L2S2电 阻散失的能量 共 1400J燃料完全燃烧释放 的能量有用机械能 600J30º水面图 1井的底部第二部分（非选择题 共 64 分）二、填空 作图题（共 27 分）13．图 1 所示，用一块平面镜使一束光竖．直．射入水井． （1）画出光经过空气和水，射到井底的光路． （2）通过作图标出平面镜（用“”表示）的位置．要求：保留作图痕迹．（3）光经过平面镜发生反射，在图中标出反射角的度数．火线零线 地线图 214．插线板上：指示灯在开关断开时不亮，插孔不能提供工作电压；而在开关闭合时指示灯 发光，插孔可以提供工作电压；若指示灯损坏，开关闭合时插孔也能提供工作电压．根据 上述特点，在图 2 中画出开关、指示灯和插孔的连接方式，并把接线板与电源线接通．15．图 3 是小轿车汽油机工作时的能量转化示意图．已知： 汽油热值 q =4.6×107J/kg ，比热容 c =2.2×103J/（kg •℃） （1）该热机的效率是．（2）若该车完全燃烧 2kg 汽油，释放的能量为J ．图 316．如图 4 所示，在粗糙轨道的 A 处，小球具有 10J 的重力势能．它被静止释放后，运动 到轨道 C 处．图 4B MNC图 5B（1）小球在 MN 段的速度大小会不会发生改变？请说明原因． 答：．原因是：．（2）若把后半段的水平直轨道改为弯曲轨道，如图 5 所示．小球仍在 A 点静止释放，到达 最高点 D 时，它的动能为J ．小球在 A 点时的机械能在 D 点的机械能．（选填：“＜”、“＞”或“＝”）AhDh ′ Aha IN bS17．如图 6 所示，把两个发光二极管极性相反地并联起来，组成二极管组．把它的 a 、 b 端 分别接在手摇发电机和干电池组上时，将观察到的现象记录在下表中．甲 乙a（1）表格中漏写的现象是．b（2）该发电机工作时的能量转化是：能转化为能；（3）图 7 是研究交流发电机的原理图． 图 6 当线圈在磁体中顺时针转动时，ab 中电流方向如图 7 所示； 当线圈在另外一个磁体中逆时针转动时，在图 8 中用箭头标出 ab 中电流方向．图 7图 818．车轮与地面的接触面积，与汽车轮胎气压、轮胎对地压力有关．现测得某．个．轮．胎．数据在 下表（其它因素已控制相同）实验1 2 3 4 轮胎气压 /×105Pa 4.6 4.6 8.1 8.1 轮胎对地压力 /×104NF 1 F 2 F 3 F 4 车轮与地面的接触面积 /×10-2m 23.64.03.03.6（1）若实验 1 中的 F 1=1.8×104 N ，则该轮胎对地面压强的大小为 Pa ．（2）表格中的两个力：F 1F 2．（选填：“＝”或“≠”）判断的依据是：．19．如图 9 所示，可绕 O 点转动的杠杆（质量忽略不计），在 C 点挂一个质量为 10kg 的物 体 M ．依次在 A 、B 两点沿与圆 O 相切的方向用力拉，都使杠杆在水平位置平衡．已知： CO=OD=DA=AB （g 取 10N/kg ） （1）作出 F A 的动力臂 l A ；F A =N ．（2）比较两个力的大小：F AF B ．推导分析过程是：．（3）若在 E 点施加最小的动力，也能使杠杆水平平衡．在图 9 中画出该力 F E 的示意图．CODAEBF B F AM图 9aSbN手摇发电机 干电池组 现 象甲、乙交替发光甲一直发光； 乙1 23A0 1 2 3V0.6 33 15定值电阻P三、解析题（第 20 题 7 分，第 21 题 9 分，共 16 分）20．一个西瓜慢慢放入装满水的桶中时，排出 40N 的水，最后漂浮如图 10 所示． （g 取 10N/kg ；ρ 水=1.0×103kg/m 3） （1）求西瓜的重力．（2）从水中缓慢托起西瓜，直到它离开水面的过程中，小明感到：竖直向上用的力越来越大． 请用学过的知识解释这种现象．（3）如图 11 所示，小明抱着西瓜，从一楼匀速走到二楼． 小明对西瓜做了多少功？图 1021．为比较两种液体的比热容大小，小明用图 12 所示两相同的装置盛质量相同的甲、乙两 种液体进行实验．其中两电热器规格均为“220V ，880W ”，实验时均正常工作，实验数 据记录如下表．忽略热量损失，求：（1）电热器正常工作电流是多大？其阻值是多大？ （2）乙液体中的电热器，消耗的电能是多少？ （3）哪种液体的比热容较大？写出分析的过程．电热器 图 12物质 初始温度/℃加热时间/s最后温度/℃甲液体 20 200 50 乙液体2010050四、实验 探究题（共 21 分）22．在验证“通过导体的电流与导体两端电压的关系”的实验中（1）用笔画线代替导线，将图 13 中的电路连接完整．并在方框内画出对应的电路图．图 13图 11（2）下表是通过实验得到的几组数据．实验次数 1 2 3 4 5 6电压/V 0.4 0.8 1.2 2.2 2.4电流/A 0.08 0.16 0.24 0.4 0.48①第4 次实验时的电压表、电流表如图14 所示．U/V2.42.01.61.20.8图14 0.40 0.16 0.32 0.48图15I/A 由图可知，仪器测得：U ＝V；I ＝A．②在表中数据在图15 的坐标系中描点．小芳分析其中一组数据可能是读数时出错，需要剔除，这是第次实验的数据．并完成连线．（3）换用另一个定值电阻再次进行验证实验．当开关闭合时，小明发现电流表指针偏转，而电压表指针没有偏转（电压表经检测，能正常使用）．则电路可能发生的故障是．23．小明猜想：滑动摩擦力大小与以下三个因素有关①接触面所受的压力大小；②接触面的粗糙程度；③接触面面积大小（1）如图16 所示，两材质相同的正方体木块，N 木块长度为cm．图16 NM（2）为了探究“滑动摩擦力大小与接触面面积大小”的关系，小明利用以上两木块、书桌 的水平面和弹簧测力计进行实验探究． ①第 1次实验时示意图如下，存在的错误是．②重新准确做出第 1 次实验后，再做了第 2 次实验．在方框内画出第 2 次实验时的示意图．第 1 次实验 第 2 次实验③上述两次实验操作均正确，以“ ”表示被拉物体，在方框内画出物体在水平方向的受力 示意图．图 17④其中第 1 次测力计的示数如图 17 所示，f 1= N ；第 2 次实验，测得物体所受的摩擦力为 f 2． 通过比较，小明发现：f 1= f 2 ．由此可以初步认为．24．如图 18 所示，水平台上有一个量程足够大的天平，小明只用这个器材（含砝码）设计实验，测量自带学生奶（如图 19 所示，可自行处理）的密度．图 18（1）调节天平水平平衡．具体的操作是：．（2）实验步骤（测量的物理量要用符号表示）图 19（3）牛奶密度表达式：ρ 奶＝．游码平衡螺母 M N测力计净含量 200mlXX 学年下学期海珠区九年级综合测试（一）物理参考答案一、选择题（每小题 3 分，共 36 分）每小题给出的四个选项中，只有一项最符合题意． 1．B 2．B 3．A4．D5．D6．B7．C8．D9．D10．B11．B 12．D二．填空 作图题（共 27 分） 13．14．15．（1）30%；（2）9.2×107J16．（1）会；水平方向受到摩擦力，物体受力不平衡（或：由于存在摩擦，部分动能转化为 内能）（2）0；＞17．（1）不发光；（2）机械；电；（3）18．（1）5×105 Pa ；（2）≠； 因为轮胎气压相等，而车与地面的接触面积不相等，所以压力不等。

2023年人教版九年级物理(下册)期末综合试题及答案(时间：60分钟分数：100分)班级：姓名：分数：一、选择题（每题2分，共30分）1、为了检验人躺着和站立时身体长度是否有差异，选用下列哪种尺最合适（）A．量程3m，分度值1mm B．量程10m，分度值1dmC．量程30cm，分度值1mm D．量程15cm，分度值0.5mm2、太阳光通过树叶间的空隙，在地上形成许多圆形的光斑，这些圆形光斑是（）A．树叶的虚像B．树叶的实像C．太阳的虚像D．太阳的实像3、如图所示，底面积相同的甲、乙两容器，装有高度、质量均相同的不同液体，则它们对容器底部压强的大小关系正确的是（）A．p甲＞p乙B．p甲＜p乙C．p甲=p乙D．条件不足，无法判断4、如图所示电路，闭合开关S1、S2，下列对电路的分析正确的是（）A．L1与L2串联B．电流表A1测L1的电流C．当开关S2断开时,通过L1的电流变小D．当开关S2断开时，电流表A2的示数变小5、小明用调好的天平称物体的质量时，在天平的右盘加了几个砝码后，指针还是稍微偏左．再放入质量最小的砝码，指针又稍微偏右，接下来操作正确的是（）A．将横梁上的平衡螺母向左调B．将处在零刻度位置的游码向右移C．取出最小的砝码，将横梁上的平衡螺母向右调D．取出最小的砝码，将处在零刻度位置的游码向右移6、下列物体重力约为1N的是（）A．一枚大头针 B．两个鸡蛋 C．一头奶牛D．一个篮球7、小明为养鸡场设计报警电路．养鸡场的前、后门分别装有开关S1、S2，动物闯入时开关会自动闭合．要求：只要动物闯入任意一个门，电铃都能响起报警．如图中符合设计要求的是（）A． B． C． D．8、物理上常通过声波的波形图来反映声波的特点．如图所示，根据甲、乙两个音叉振动时发出声音的波形图，下列判断正确的是（）A．甲音叉比乙音叉振动得快B．甲音叉比乙音叉发声的音调低C．甲、乙两音叉发声的频率相同D．甲音叉发声的响度比乙音叉发声的响度大9、如图所示的电路中，小灯泡L1、L2规格相同，闭合开关S后，发现L1不亮，L2发光．此电路的故障可能是（）A．灯 L1短路B．灯 L2短路C．灯 L1断路D．开关 S 接触不良10、下列估测最接近于实际的是（）A．一支全新2B铅笔的长度约为20cm B．人步行的速度约为5m/s C．一个普通中学生的重力约为50N D．人感到舒适的气温约为39°C 11、某汽车在平直公路上行驶，其s-t图象如图所示，下列描述正确的是（）A．0～t1做加速直线运动B．t1～t2做匀速直线运动C．0～t1比t2～t3运动的路程长D．0～t1比t2～t3运动的速度大12、甲、乙两物体，同时从同一地点沿直线向同一方向运动，它们的s−t图象如图所示．下列说法正确的是（）A．2~4s内乙做匀速直线运动 B．4s时甲、乙两物体的速度相等C．0~4s内乙的平均速度为2m/s D．3s时甲在乙的前方13、在商场内乘坐电梯上升时，乘客说自己是静止的，该乘客所选的参照物是（）A．上升的电梯 B．地面 C．商场内的收银员 D．货架上的商品14、将地面上的一本物理课本捡起来放到课桌上，对物理课本所做的功最接近（）A．0.02J B．0.2J C．2J D．20J15、如图所示，灯L1、L2完全相同，闭合开关S，只有一盏灯发光且只有一个电表有示数，其故障可能是（）A．L1短路B．L2短路C．L1断路D．L2断路二、填空题（每题2分，共10分）1、100g热水和50g冷水混合后（不考虑热量损失），则热水降低的温度_______冷水升高的温度（填“大于”、“等于”或“小于”），热水放出的热量_______冷水吸收的热量．（填“大于”、“等于”或“小于”）2、在春季运动会上，班级的男同学吹气球时发现：用手轻轻一压，气球就变扁了，说明力可以改变_____；用手轻轻一推，气球就向一侧飞走了，说明力可以改变_____．3、我们班文艺委员的歌声很像某位歌星，这是指他们的____（选填“音调”“音色”“响度”）相近，但是她有时也在自习课上唱歌，此时她“美妙”的歌声属于____（选填“乐音”“噪音”）．4、水平桌面上的甲、乙两圆柱形容器，装有质量相同的水，如图所示．水对甲、乙两容器底的压力和压强的大小关系分别是：F甲_____F乙；p甲_____p 乙．（都选填“＞”、“＜”或“＝”）5、日常生活中声音的“高”与“低”，其物理意义是不同的，有时指音调，有时指响度，例如：一名男低音歌手正在放声高歌，这是的“低”指的是________；“高”指的是________．成语“震耳欲聋”，从声音的特性分析，描述的是________的大小．三、作图题（每题5分，共10分）1、如图所示，利用羊角锤撬起钉子，请你在羊角锤A点处画出所能施加最小动力F1，并画出阻力F2的阻力臂l2。