最新北师大版初中七年级数学上册4.2 比较线段的长短学案
- 格式:doc
- 大小:99.50 KB
- 文档页数:4

4.2 比较线段的长短1.了解“两点之间,线段最短”.2.能借助尺、规等工具比较两条线段的大小,能用圆规作一条线段等于已知线段.3.了解线段的中点及线段的和、差、倍、分的意义,并能根据条件求出线段的长.一、情境导入爱护花草树木是我们每个人都应具备的优秀品质.从教学楼到图书馆,总有少数同学不走人行道而横穿草坪(如图),同学们,你觉得这样做对吗?为了解释这种现象,学习了下面的知识,你就会知道.二、合作探究探究点一:线段长度的计算【类型一】 根据线段的中点求线段的长如图,若线段AB =20cm ,点C 是线段AB 上一点,M 、N 分别是线段AC 、BC 的中点.(1)求线段MN 的长;(2)根据(1)中的计算过程和结果,设AB =a ,其它条件不变,你能猜出MN 的长度吗?请用简洁的话表达你发现的规律.解析:(1)先根据M 、N 分别是线段AC 、BC 的中点得出MC =12AC ,CN =12BC ,再由线段AB =20cm 即可求出结果;(2)根据(1)中的条件可得出结论.解:(1)∵M 、N 分别是线段AC 、BC 的中点,∴MC =12AC ,CN =12BC ,∵线段AB =20cm , ∴MN =MC +CN =12(AC +BC )=12AB =10cm ; (2)由(1)得,MN =MC +CN =12(AC +BC )=12AB =12a .即MN 始终等于AB 的一半.方法总结:根据线段的中点表示出线段的长,再根据线段的和、差求未知线段的长度.【类型二】 已知线段的比求线段的长如图,B 、C 两点把线段AD 分成2∶3∶4的三部分,点E 是线段AD 的中点,EC=2cm ,求:(1)AD 的长;(2)AB ∶BE .解析:(1)根据线段的比,可设出未知数,根据线段的和差,可列方程,根据解方程,可得x 的值,根据x 的值,可得AD 的长度;(2)根据线段的和差,可得线段BE 的长,根据比的意义,可得出答案.解:(1)设AB =2x ,则BC =3x ,CD =4x ,由线段的和差,得AD =AB +BC +CD =9x .由E 为AD 的中点,得ED =12AD =92x . 由线段的和差得,CE =DE -CD =92x -4x =x 2=2. 解得x =4.∴AD =9x =36(cm ).(2)AB =2x =8,BC =3x =12.由线段的和差,得BE =BC -CE =12-2=10(cm ).∴AB ∶BE =8∶10=4∶5.方法总结:在遇到线段之间比的问题时,往往设出未知数,列方程解答.【类型三】 当图不确定时求线段的长如果线段AB =6,点C 在直线AB 上,BC =4,D 是AC 的中点,那么A 、D 两点间的距离是( )A.5B.2.5C.5或2.5D.5或1解析:本题有两种情形:(1)当点C 在线段AB 上时,如图:AC =AB -BC ,又∵AB =6,BC =4,∴AC =6-4=2,∵D 是AC 的中点,∴AD =1;(2)当点C 在线段AB 的延长线上时,如图:AC =AB +BC ,又∵AB =6,BC =4,∴AC =6+4=10,∵D 是AC 的中点,∴AD =5.故选D.方法总结:解答本题关键是正确画图,本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解.探究点二:线段性质的应用如图,把弯曲的河道改直,能够缩短航程,这样做的根据是( )A.两点之间,直线最短B.两点确定一条线段C.两点确定一条直线D.两点之间,线段最短解析:把弯曲的河道改直缩短航程的根据是:两点之间,线段最短.故选D.方法总结:本题考查了线段的性质,熟记两点之间线段最短是解题的关键.三、板书设计教学过程中,强调学生通过想象、合作交流等数学探究过程,了解线段大小的比较方法,学习使用几何工具的操作方法,发展几何图形意识和探究意识,激发学生解决问题的积极性和主动性.。
4.2比较线段的长短学习目标:1.理解线段的性质;2.能借助直尺、圆规等工具比较两条线段的长短,并会作一条线段等于已知线段;3.学会简单的线段之间的和差计算。
学习方法:自主研究——合作沟通——总结应用学习互动:一、研究线段的性质:1.右图是我市交通地图的一部分,请你画出从“环岛” 到“茂华”的路线草图(画出 4 条即可 ),2.你喜爱从哪条路线抵达学校?为何?3.从中能够得出什么结论?____________________________________活学活用:(1)如图,已知从 A 地到 B 地共有五条路,小红应选择第 _______条路近来,用数学知识解说是由于 ______________________________ 。
(2)如下图,三角形 ABC 的三边可表示成线段 AB 、AC 、 BC ,在下边的横线上填入“ >”、“ <”、“=”。
①AB+AC______BC ;② AB+BC______AC ;③你还可获取的式子是: ______________________ 。
二、比较两条线段的长短1.试比较右图中线段a、b 的大小:a_______ b与伙伴沟通你的结论。
感悟:从比较两个同学的身高你能获取比较线段长短的方法吗?概括:比较两条线段长短的方法有:_________________________________________ 。
2.如何画一条线段等于已知线段?已知线段a,画线段AB= a并谈谈你的画法。
概括: ____________________________________________.活学活用:(1) 依据线段的长短, 能够进行线段之间的和差计算。
如右图:点 C 、D 在线段 AB 上,填空:① AD=______ + _______ ;② CD=B C - ______;③ BD=A B -_____=_____- CD※方法总结:确立线段的和差的方法是:察看点各点在同向来线上的相对地点。

《4.2比拟线段的长短》教学设计教学重点与难点教学重点:1、线段长短的两种比拟方法;2、线段中点的概念及表示方法。
教学难点:1、掌握线段比拟的正确方法;2、线段中点的应用。
学情分析认知根底:学生在阶段对线段已经有了一定的认识,对于线段的长短也有了感性的认识,在比拟线段长短的问题上都有了自己一定的方法,这些为本章的深入学习奠定了根底。
活动经验根底:在中,教材为学生提供了大量生动有趣的现实情境,通过观察、测量、画图、模型操作、拼摆、图案设计等活动,使学生在活动中自觉体会线段长短的概念及相互比拟的方法,同时在活动中也培养了学生良好的情感态度,顺利实现了由到的学习过渡,以积极的态度投入数学的学习,具备了一定的主动参与、合作意识和初步的观察、分析、抽象概括的能力。
在对线段的长度有了一定的了解后,比照比拟线段也有了自己的方法,初步地实现了由感性认识到理性认识的过渡,在这一根底之上使学生进一步对线段的和差进行探究,理解线段中点及等分点的特性,从而将图形与数量关系结合在一起。
教学目标1、使学生在理解线段概念的根底上,了解线段的长度可以用正数来表示,因而线段可以度量、比拟大小以及进行一些运算,使学生对几何图形与数之间的联系有一定的认识,从而初步了解数形结合的思想。
2、掌握比拟线段长短的两种方法。
3、会用直尺和圆规画一条线段等于线段;理解线段和、差的概念及画法。
4、理解两点间距离的概念和线段中点的概念及表示方法;学会线段中点的简单应用。
教学方法通过创设情境,以问题为载体给学生提供探索的空间,引导学生积极探索。
教学环节的设计与展开,都以问题的解决为中心,构建了“以问题研究和学生活动〞为中心的课堂学习环境,使教学过程成为在教师指导下学生的一种自主探索的学习活动过程,在探索中形成自己的观点。
教学过程一、创设情境,引入新课设计说明:从简单的生活现象出发,开门见山,引出课题。
问题:A处有一只蚂蚁,想取位于B处的食物。
你估计蚂蚁会走怎样的路线?线段的根本性质:综上所述,根据生活经验,容易发现:两点之间的所有连线中,线段最短这一事实可以简述为:两点之间线段最短。

新北师大版七年级数学上册学案:4.2比较线段的长短学习内容:比较线段的长短教学设计 (收获)二、小组学习 [来源:学&科&网]已知线段AB=10cm,在直线AB 上有一点C ,BC=4cm,点M 是线段AC 的中点,试计算线段AM 的长。
三、展示反馈:(展示你的风采) [来源:Z §xx §]1)已知线段a.b 求作一条线段c,使c=a+b2)在直线l 上顺次取A.B.C 三点,使得AB=6cm,BC=2cm,如果O 是线段AC 的中点,求线段AO,BO,CO.的长。
( 画出图形)上题中AO+BO= cm=线段 的长,AO+OC= cm=线段 的长。
AB-OA= cm- cm= cm =线段 的长。
BC=线段 —线段 。
[来源学科网]3)在直线l 上有A.B.C 三点顺次排列,已知AB=3cm,BC=8cm,M.N 分别为AB.BC 的中点,画出图形,并求出MN 的长。
学习目标:能借助于尺、规等工具比较两条线段的大小并作一条线段等于已 知线段重点 :比较两条线段的大小并作一条线段等于已知线段 难点: 作一条线段等于已知线段自主学习:(相信你一定行﹗)一、认真阅读课本P 110页议一议上面的内容,解决下列问题:1、观察此页的第一个图,从A 地到C 地有 ______条道路,______条道路最近,可得结论简称为 ___________________________。
2、若已知线段AC 的长度为5cm ,则点A 与点C 之间的距离为____cm 。
二、认真阅读课本P 110页议一议下方的内容,解决下列问题:1、如下图所示,线段AB 与线段CD 的长短关系为_______________,若要比较线段AB 与线段CD 的长短,你有哪些方法?2、模仿例题:已知线段a,用尺规作一条线段AB ,使线段AB = a (写出作法) a教学反思 (疑惑)baA BC D3、如右图所示,点C、D在线段AB上,则AB = AC + ____, CD = AD - ____;若C是线段AD的中点,则AC = _____ = ______。

2 比较线段的长短●情景导入 同学们请看大屏幕,认识他们吗?我们目测一下他们的身高,发现姚明高一些.那要是让潘长江老师站到二楼上,姚明站在地面上呢? 如果我们用线段来表示人的身高,又如何比较线段的长短呢?从而引入课题.【教学与建议】教学:把现实生活中的比高矮问题抽象成线段比较长短问题,激发学生解决问题的热情.建议:重点让学生明白两条线段长短的比较方法.●置疑导入 师:如图,从A 村到B 村有四条道路可供选择,你愿意选第几条道路?说出你的理由. 生:走第②条路.因为这条路是直路,感觉它最近.师:虽说条条大路通罗马,但我们都希望走条近路.那么怎样找出最近的路呢?你是怎样得出结论的? 【教学与建议】教学:利用生活中熟悉的情境,极大地激发学生的学习热情.建议:在学生操作时,教师要引导学生进行思考、分析.*命题角度1 利用两点之间线段最短解决问题根据两点之间的所有连线中,线段最短,解决实际问题.【例1】在春季运动会上,七年级的同学想举行一次拔河比赛,他们想从两条大绳中挑出一条最长的绳子,请你为他们选择一种合适的方法是(A)A .把两条大绳的一端对齐,然后拉直两条大绳,另一端在外面的即为长绳B .把两条绳子重合,观察另一端的情况C .把两条绳子接在一起D .没有办法挑选【例2】为抄近路践踏草坪是一种不文明现象,如图是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是(C)A.经过两点有一条直线,并且只有一条直线B .两条直线相交只有一个交点C .两点之间的所有连线中,线段最短D .两点之间线段的长度,叫做这两点之间的距离【例3】把一条弯曲的河道改直,可以缩短航程,这样做的根据是__两点之间线段最短__. *命题角度2 比较线段的长短比较线段长度常用的方法有两种:(1)度量法;(2)叠合法. 【例4】用度量法可得下列线段中最长的是(B)A BC D *命题角度3 线段中点的概念辨析中点具备两个特点:①点在线段上;②把线段分成相等的两条线段,这两者缺一不可. 【例5】如图,B 是线段AD 的中点,C 是BD 上一点,则下列结论中错误的是(C)A .BC =AB -CD B .BC =AC -BDC .BC =12 (AD -CD ) D .BC =12AD -CD【例6】已知线段AB 和点P ,如果P A +PB =AB ,且P A =PB ,则(A) A .点P 为AB 中点 B .点P 在线段AB 的延长线上C .点P 在线段AB 外D .无法确定 *命题角度4 求线段的长度求线段长度,通常借助线段中点的性质和线段的比进行线段长度的变换进行求解.【例7】如图,长度为12 cm 的线段AB 的中点为M ,C 为线段MB 上一点,且MC ∶CB =1∶2,则线段AC 的长度为(A)A .8 cmB .6 cmC .4 cmD .2 cm【例8】如图,B ,C 两点把线段AD 分成长度比为2∶3∶4的三部分,点E 是线段AD 的中点,EC =2 cm ,求:(1)AD 的长; (2)AB ∶BE .解:(1)因为AB ∶BC ∶CD =2∶3∶4,点E 是线段AD 的中点,所以CD =49 AD ,ED =12AD ,所以EC =ED-CD =12 AD -49 AD =2,解得AD =36 cm ;(2)由(1)知,AD =36 cm ,易得AB =36×29 =8(cm),BC =36×39=12(cm),BE =BC -EC =12-2=10(cm).所以AB ∶BE =8∶10=4∶5.高效课堂 教学设计1.借助情境了解“两点之间线段最短”的性质. 2.能借助尺、规等工具比较两条线段的大小. 3.能用圆规作一条线段等于已知线段.线段长短的两种比较方法:线段中点的概念及表示方法;线段的和、差、倍、分关系.叠合法比较两条线段大小;会画一条线段等于已知线段.活动一:创设情境 导入新课(课件:公园曲桥、河道改直的图片)把弯曲的河道改直就可以缩短航程.在公园的河面上修建曲折的桥,就能增加观光的路程,你知道这其中的道理吗?怎样比较两个同学的高矮?你有哪些方法?活动二:实践探究 交流新知 【探究1】 线段公理问题:(多媒体投影P 110图4-6)学生通过观察,实际操作,容易得出线段AC 最短.【归纳】两点之间的所有连线中,线段最短.这一事实可以简述为:两点之间线段最短.我们把两点之间线段的长度,叫做这两点之间的距离.【探究2】 线段的比较多媒体展示P 110“议一议”【归纳】如果直接观察难以判断,我们可以有两种方法进行比较:一种方法是用刻度尺量出它们的长度,再进行比较,即度量法;另一种方法是把其中的一条线段移到另一条线段上去,将其中的一个端点重合在一起加以比较,即叠合法.活动三:开放训练 应用举例【例1】(教材P 111例题)如图,已知线段AB ,用尺规作一条线段等于已知线段AB . 【方法指导】学生通过操作,掌握作一条线段等于已知线段的方法.解:作图步骤如下:(1)作射线A ′C ′(如图所示);(2)用圆规在射线A ′C ′上截取A ′B ′=AB . 线段A ′B ′就是所求作的线段.【例2】(1)如图,点M 把线段AB 分成相等的两条线段AM 与BM ,点M 叫做线段AB 的中点.这时AM =BM =12 AB (或AB =2AM =2BM ).(2)在直线l 上顺次取A ,B ,C 三点,使得AB =4 cm ,BC =3 cm.如果点O 是线段AC 的中点,那么线段OB 的长度是多少?【方法指导】学生画图加以分析,与同伴进行交流,进一步掌握线段中点的性质. 解:如图所示:OB =4-4+32=0.5(cm).活动四:随堂练习1.如图,在我国“西气东输”的过程中,从A 城市往B 城市架设管道,有三条路可供选择,在不考虑其他因素的情况下,架设管道的最短路线是__①__,依据是__两点之间线段最短__.2.已知线段AB =6 cm ,在直线AB 上取点C ,使BC =3 cm ,则线段AC 的长是__9或3__cm. 3.教材第112页上方的“随堂练习”第1题. 解:可用刻度尺量出折线AB 各段线段的长度,再量出线段A ′B ′的长度.将折线AB 各段线段的长度和与A ′B ′的长度作比较,也可用尺规作图法将AB 的每段长度移到线段A ′B ′上,再做判断.4.教材第112页上方的“随堂练习”第2题.解:5.已知线段AB =6,点C 在直线AB 上,BC =4,D 是AC 的中点,那么A ,D 两点间的距离是多少? 解:5或1.活动五:课堂小结与作业学生活动:通过这节课的学习,你掌握了哪些新知识?还有哪些疑问?教学说明:教师引导学生回顾线段的公理,线段的比较,线段的中点等知识,让学生大胆发言,积极与同伴交流,进行知识的提炼和归纳.作业:课本P 112习题4.2中的T 2、T 3、T 4本节课的内容是比较线段的长短,这涉及线段的度量和比较,是几何中的一个基本问题.在教学过程中,把身边的数学材料引入课堂,从而使原来枯燥无味的讲解转变为生动活泼的学习活动,调动了学生学习的积极性,加深了学生对几何知识的理解,从而达到了很好的教学效果,同时也培养了学生分析问题、解决问题、应用数学知识的能力.。

4.2比较线段的长短导学案学习目标:能借助直尺、圆规等工具,比较两条线段的长短。
能用圆规作一条线段等于已知线段。
重点:了解线段性质及比较方法,两点之间的距离的概念和线段中点的概念。
难点:比较线段长短的方法,线段中点的表示方法和应用。
学习过程:课前热身:辨别直线、射线、线段,并能用不同的方法表示它们.自主学习:阅读课本110-111页内容,完成下列问题,1.在地面上有两点A 和C ,C 处放有一块骨头,三只不同颜色的小狗从A 点跑到C 点吃骨头,所经过的路线不同,请同学们辨别,哪只狗更聪明.结论:____________________________________________________2.探究:比较线段的长短怎样比较两根筷子的长短.方法:___________________3.探究:作一条线段等于已知线段方法:___________________4.探究:线段的中点线段的中点的定义:____________________________因为点M 在线段AB 上,M 是AB 的中点所以 AM=_____=________或AB=________=________.反馈检测:判断:1.两点之间的线段叫做这两点间的距离 ( )2.如果点C 是线段AB 的中点,那么AC CB = ( )3.如果AC CB =,那么点C 是AB 的中点 ( )选择:1.两点之间线段的长度是( )A .线段的中点B .线段最短C .这两点间的距离D .线段的三等分点2.在跳绳比赛中,要在两条长度相近的绳中挑选一条最长的绳子参加比赛,最简单的选择方法是( )A .把两根绳子接在一起B .把两条绳子一端对齐,然后拉直两条绳子,另一端在外面的即为长绳 AB MC.用尺量绳长D.没有办法挑选实践应用1.有一弯曲的灌渠流经一片农田,为了缩短流程,以减少分水的过分流失,现要将该灌渠改直,请问这应用的是什么结论?2.如图,点C是线段AB上的一点,点M是线段AB的中点,点N是线段BC的中点.(1)如果10cmAB=,3cmAM=,求NC的长.(2)如果6cmMN=,求AB的长.布置作业:4.2知识技能1, 2 , 3 学习反思:A BM C。
课时课题:第四章 第2节 比较线段的长短教学目标:1.借助具体情境,了解“两点之间线段最短”的性质.2.能借助直尺、圆规等工具比较两条线段的长短.3.能用圆规作一条线段等于已知线段.4.理解两点间距离的概念和线段中点的概念及表示方法.教学重点与难点:重点:掌握线段比较的正确方法,线段中点的概念及表示方法.难点:线段中点的概念及表示方法.教法及学法指导:教法:启发式教学法.学法:自主探索、合作交流.课前准备:多媒体课件.教学过程:一.巧设情境 引入新知师:上节课我们认识了直线、线段、射线,你能画出这些线并用字母表示出来吗?生:动手画出(1)直线AB ; (2)射线OM ; (3)线段CD.师:如图1 从A 地到C 地有四条道路,你站在A 处,C 处有一小弟弟摔倒了,你会选择走哪条路去帮助他?图1生:学生发言,易于得出线段AC 最短.师:如图2,从教室A 地到图书馆B ,总有少数同学不走人行道而横穿草坪,这是为什么呢? FEDC B A图2生:因为走的路程最短.师:两种情景你能得到什么结论?生:结论:两点之间的所有连线中,线段最短.简述为:两点之间线段最短.师:两点之间线段的长度,叫做这两点之间的距离.设计意图:利用生活中可以感知的的情境,极大激发学习兴趣,使学生感受生活中所蕴含的数学道理.二.小组合作共同探索图1 图2 图3 师:怎样比较两棵树的高矮?怎样比较两根铅笔的长短?怎样比较窗框相邻两边的长?生:讨论交流,得出答案:图1直接观察就可以比较;图2观察难以判断,可以测量或将一端重合;图3 可以用绳子或刻度尺测量.师:把两棵树的高度、两根铅笔的长、窗框相邻两边的长看成两条线段,怎么比较它们大小?类比于线段怎么比较两条线段的长短?生:通过小组讨论交流得出如果两条线段长短相差很大,直接观察就可以比较.如果直接观察难以判断,我们可以有两种比较方法:第一种方法是:度量法. 即用刻度尺量出两条线段的长度,再进行比较第二种方法是:叠合法. 方法:先把两条线段的一端重合,另一端落在同侧,根据另一端落下的位置,来比较. 注意:起点对齐,看终点.这时我们可以借助圆规来完成.师:画出两条线段,讨论比较方法.生:同位之间互考,一生上黑板演示两种比较方法.线段AB 与线段CD 相等, 线段AB 大于线段CD , 线段AB 与小于线段CD ,记作AB=CD 记作AB>CD 记作AB<CD练习:176页知识技能第1题设计意图:在具体问题中设问,在解答问题中形成认知冲突,激发学生的解决问题的热情.让学生感受从实际问题中抽象出所要比较的线段大小的的过程.三. 动手操作,探索新知:师:你能用圆规画出一条线段等于已知线段吗?(黑板上画出已知线段,同时要求学生在纸上画出已知线段,并尝试.)小组合作交流画法:生:上黑板演示并说明作图过程.师生归纳出三步骤:1、作射线A ’C ’;2、用圆规在射线A ’C ’上截取A ’B ’=AB ;线段AB 就是所求作的线段.动手试试:随堂练习176页2题. 设计意图:让学生自己在动手操作中去真正的感受用尺、规作图,并用语言口头表述做法,并开始有作图痕迹意识.用尺规作一条线段等于已知线段,其实就是“叠合法”的具体运用。
4.1比较线段的长短导学目标1、线段的性质:两点之间,线段最2、掌握比较线段长短的两种方法3、会用直尺和圆规画一条线段等于已知线段4、理解线段和、差的概念及画法。
5、理解两点间距离的概念和线段中点的概念及表示方法,学会线段中点的简单应用导学重点:线段长短的两种比较方法导学难点: 对线段与数之间的认识,掌握线段比较的正确方法 温故:线段的定义链接:两只长短不同的筷子如何比较它们的长短?比较长短的关键是什么? 新知一、线段的性质及两点之间的距离的教学1、 阅读课本139页,思考小猫与小狗为何走课本所示的路线,这说明了什么问题?2、 什么叫做两点之间的距离?二、如何比较线段长短的教学 画出AB 、CD 两条线段。
(长短不一) 1.“议一议” 怎样比较两条线段的长短?叠合法:把线段AB 、CD 放在同一直线上比较,步骤有三: ① 将线段AB 的端点A 与线段CD 的端点C 重合 ② 将线段AB 沿着线段CD 的方向落下③ 若端点B 与端点D 重合,则得到线段AB 等于线段CD ,可记做:AB=CD (几何语言)若端点B 落在D 内,则得到线段AB 小于线段CD ,可记做:AB <CD若端点B 落在D 外,则得到线段AB 大于线段CD ,可记做:AB >CD 如图12度量法:用刻度尺分别量出线段AB 和线段CD 的长度,再将长度进行比较。
三、如何用圆规做一条线段等于已知线段及线段的和差A CD1、已知线段a (如图),用直尺和圆规画一条线段,使它等于已知线段a 。
a2、已知线段a 、b ,画一条线段c ,使它的长度等于已知线段的长度的和。
3画一条线段d ,使它的长度等于已知线段的长度的差四、线段中点的教学阅读课本140页明确线段中点的定义 定义:用几何语言表示:∵点C 是线段AB 的中点∴ AC=BC=12 AB (或AB=2AC=2BC )对应练习:(1)填空:如图D已知点C 是线段AB 的中点,点D 是线段AC 的中点,①AB= BC ②BC= AD ③BD=_____AD(2)P C D例题:如上图,点P 是线段的中点,点C 、D 把线段AB 三等分。
4.2 比较线段的长短
学习目标:
1.理解线段的性质;
2.能借助直尺、圆规等工具比较两条线段的长短,并会作一条线段等于已知线段;
3.学会简单的线段之间的和差计算。
学习方法:自主探究——合作交流——总结应用
学习互动:
一、探究线段的性质:
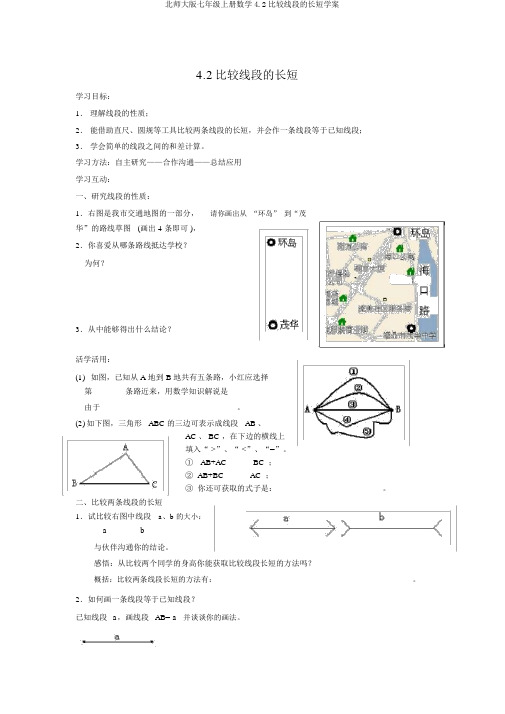
1.右图是我市交通地图的一部分,请你画出从“环岛”
到“茂华”的路线草图(画出4条即
可),
2.你喜欢从哪条路线到达学校?
为什么?
3.从中可以得出什么结论?
____________________________________
活学活用:
(1)如图,已知从A地到B地共有五条路,小红应
选择
第_______条路最近,用数学知识解释是
因为______________________________。
(2)如图所示,三角形ABC的三边可表示成线段AB、
AC、BC,在下面的横线上
填入“>”、“<”、“=”。
① AB+AC______BC ;
② AB+BC______AC ;
③ 你还可得到的式子是:______________________。
二、比较两条线段的长短
1.试比较右图中线段a 、b 的
大小:
a_______ b
与同伴交流你的结论。
感悟:从比较两个同学的身高你能获得比较线段长短的方法吗?
归纳:比较两条线段长短的方法有:_________________________________________。
2.如何画一条线段等于已知线段?
已知线段a ,画线段AB= a 并说说你的画法。
归纳:____________________________________________.
活学活用:
(1)根据线段的长短,可以进行线段之间的和
差计算。
如右图:点C 、D 在线段AB 上,填空:
① AD=______ + _______;
② CD=BC -______;③ BD=AB -_____=_____-CD
※方法总结:确定线段的和差的方法是:观察点各点在同一直线上的相对位置。
(2) 已知线段a 、b ,画线段
AB= a +2b.
※方法总结:作一线段等于已知线段,①需在一条射线上截取作出;②按“+”接,“-”反的原则截取;③指明图中哪条线段就是所求作的线段。
三、线段的和差计算:
1.画线段AB=6㎝,在AB 上画出中点C ,则可得
AC=______ = ________ =
__________.
2.如图,AB=8㎝,CB=5㎝,D 是AC 的中点,求DC 的长。
解:∵ AB=8㎝,CB=5㎝
∴ AC=______—_______ (表示出线段
和差)
=__________
∵ D 是AC 的中点
∴ DC=_______=_______
3.在直线l 上顺次..
取A 、B 、C 三点,使得AB=4㎝,BC=3㎝.如果O 是线段AC 的中点,求线段OB 的长度。
※ 变式:如果将第3题中的“顺次”去掉,又会是怎样的结果呢?请思考。
当堂检测
1.把一段弯曲的公路改为直路,可以缩短路程,其理由是( )
A .两点可以确定一条直线
B .线段有两个端点
C .两点之间,线段最短
D .线段可以比较大小
2.若线段AB=4㎝,在线段AB 上截取BC=1㎝,则AC=____________。
3.如图,C 是AB 的中点,D 是BC 的中点,下面
等式不正确的是( )
A .CD=AC —D
B B .CD=AD —BC
C .CD=12AB —B
D D .CD=15
AB 4.以下条件能确定点C 是线段AB 的中点的条件是( ) A .AC=BC B .AC=
12AB C .AB=2CB D .AB=2AC=2CB 5.如图,已知线段 a 、b ,画一条线段AB ,使AB=2a —
b.
﹡6.已知线段AB=14㎝,C点在AB上,BC=3
4
AC,求BC的长。