煤炭储量计算方法之等高线法

煤层储量的计算方法小结- [笔记]目前我实现过三种方法：1，根据等值线数据，用每条等值线的“走势”区分其所在柱体的体积的正负。

所谓趋势是指柱体位于“谷”还是“峰”上。

这种方法不能处理煤体中有空洞的情况，比如同一标高有数条等值线，有的勾勒的是煤体轮廓，有的勾勒的是煤体内部的岩体的轮廓。

2，根据等值线数据，用等值线面积的正负剔除每一梯级的无效面积。

对每一梯级按台体模型计算体积。

等值线的面积正负由其被包围圈数决定：偶数为正，奇数为负。

这种方法能处理空洞，但目前的实现的效率不高，判断两个等值线的包含关系很费时，一条等值线很容易有近千个顶点。

利用等值线数据计算体积的一个致命缺点是：没法处理边界上的未闭合等值线。

看过国外一个人的做法是人为在原始数据点周围增加一圈伪数据点。

3，根据三角网数据，把上表面为三角网、下表面为水平面的实体分解为一系列三角柱体（顶部一般是斜的）。

这种方法既快又好。

以上方法都受限于数据源：离散点坐标->三角网->等值线。

4，商业软件Surfer是先把数据点网格化，在网格数据的基础上进行包括体积在内各种统计。

网格数据有很多好处：1，可以生成相对平滑的等值线。

从三角网得用等值线是大尺度的折线，要拟合成平滑的曲线并不是件容易的事。

从网格数据得到的等值线最然也是折线，但尺度要小得多。

2，可以计算上下两个表面都是曲面的实体的体积。

如果用三角网，不易处理上下两个表面相交的情况。

3，生成剖面很容易。

§2 矿藏储量计算1.Бауман方法假定有一张矿藏的等高线图，高程差是h，地图上所表示的一圈，实际上便是一定高程的矿体的截面积.我们来估计两张这样的平面之间的矿藏的体积.这两张平面之间的距离便是高程差h.我们以A，B各表示下、上两个等高线圈所包围的截面(见图1，它们的面积亦记为A，B).Бауман建议用来估算这两个高程间的一片的体积υ，此处T(A，B)是用以下方法所画出的图形的面积，称它为Бауман改正数.如图2中，从制高点O出发，作放射线OP，这放射线在地图上A，B之间的长度是l.另作图3，取一点O′，与OP同方向取O′P′=l.当P 延着A的周界走一圈时，P′也得一图形，这图形的面积就称为Бауман改正数.因为它依赖于两截面A与B，所以我们用T(A，B)来表示它.把算出来的矿体体积一片一片地加起来，就得到矿藏的体积V.换言之，设矿体的等高线图的n+1条等高线所围成的面积依次为S0，S1，…，S n，则矿体的体积V由下式来近似计算：此处h为高程差(图4).定理①(Бауман)已知物体的下底A与上底B 其面积亦记为A，B)均为平面，且A平行于B，h为它们之间的高，O为B上一点，若用任意通过O而垂直于B的平面来截物体，所得的截面都是四边形，则物体的体积υ恰如(1)式所示.证以O为中心，引进极坐标(见图5).命高度为z的等高线的极坐标方程为ρ=ρ(z，θ)(O≤θ≤2π)，其中，ρ(z，O)=ρ(z，2π).今后我们常假定ρ(z，θ)(O≤θ≤2π，O≤z≤h)是连续的，我们不妨假定A，B的高程各为O及h.并且记ρ1(θ)=ρ(O，θ)，ρ2(θ)=ρ(h，θ).由假定可知因此物体的体积为，．定理证完.2.Бауман公式，截锥公式与梯形公式的关系假定物体的下底A与上底B均为平面，且A平行于B，h为它们之间的高，O为B上一点，除Бауман公式外，常用下面两公式来近似计算物体的体积：式(4).定理1 不等式υ≤υ1≤υ2(5)恒成立，当且仅当物体为截锥，且此锥体的顶点至底面A的垂线通过点O时，υ=υ1，当且仅当A=B时，υ1=υ2.证如Бауман定理中的假定.由Бауман公式及Буняков-cкий-Schwarz不等式可知当且仅当ρ1(θ)=cρ2(θ)(0≤θ≤2π，c为常数)时，即当这物体为一截头锥体，而此锥体的顶点至底面A的垂线通过点O时，才会取等号(图6).又由于所以，υ1≤υ2当且仅当A=B时取等值，定理证完.关于这三个公式的比较问题，我们认为主要应该从量纲来看，面的量纲为2.所以把面的量纲考虑为1所得出的公式，局限性往往是比较大的.梯形公式是把中间截面看成上底与下底的算术平均而得到的，所以把面的量纲当作1.Бауман公式则是将中间截面作为量纲2来考虑的.详言之它假定了ρ(z，θ)，为ρ(0，θ)，与ρ(h，θ)关于z的线性_到的(见1).截锥公式亦是将中间截面的量纲考虑为2.但比Бауман公式还多假定了ρ(0，θ)=cρ(h，θ)(0≤θ≤2π)，此处c为一常数.因此我们认为Бауман公式更具有普遍性，所以用它来近似计算物体的体积，一般说来，应该比较精确，但这并不排斥对于某些个别物体，用其他两个公式更恰当些的可能性.例如有一梯形，其上底与下底的宽度相等(如图7所示).用梯形公式反而能获得它的真正体积，而用Бауман公式与截锥公式来计算，结果就偏低了.不过，我们注意此时这梯形的截面的量纲为1(由于沿y轴未变).相对于Бауман公式，我们还可以估计用梯形公式与截锥公的相对偏差.对于Бауман公式算出的结果的相对偏差为_因为T(A，B)≤A-B 即此不等式显然成立)，所以3.建议一个计算矿藏储量的公式Бауман公式是假定ρ(z，θ)为ρ(0，θ)与ρ(h，θ)关于z的线性关系而得到的.如果我们将两相邻分层放在一起估计，即已知相邻三等高线ρ(0，θ)，ρ(h，θ)与ρ(2h，θ).我们用通过ρ(0，θ)，ρ(h，θ)与ρ(2h，θ)的抛物线所形成的曲面ρ=ρ(z，θ)来逼近矿体这两分层的表面，因此我们建议用如下的计算方法.命A，B，C分别表示连续三等高线所围成的截面(面积亦记为A，B，C)，A与B及B与C之间的距离都是h，则这两片在一起的体积可用以下公式来近似计算+2T(B，C)-T(A，C)).(6)如果不计(6)式中的第二项，就是熟知的(Соболевский公式.把二片二片的体积总加起来，就得到矿藏的总体积V的近似公式.换言之，设矿藏的等高线图的2n+1条等高线所围成的面积依次为S0，S1，…，S2n，而高程差为h，则矿藏的体积V由下式来近似计算注意：如果等高线图含有偶数条等高线，则最上面一片可以单独估计，其余的用公式(7).定理2 已知物体的上底C与下底A均为平面，B为中间截面(面积亦分别记为C，A，B)，且A，C都与B平行，A与B之间及B与C间的距离都是h，O为C上一点(图8).若用任意通过O而垂直于C的平面截物体，所得的截面的周界均由两条直线及两条抛物线所构成，则物体的体积υ3恰如(6)式所示.证以O为中心，引进极坐标，命高度为z的等高线的极坐标方程为ρ=ρ(z，θ)(O≤θ≤2π，ρ(z，O)=ρ(z，2π)).不妨假定A，B，C的高程分别为0，h，2h，并且记ρ1(θ)=ρ(O，θ)，ρ2(θ)=ρ(h，θ)，ρ3(θ)=ρ(2h，θ)由假定可知因此物体的体积υ3为定理证完.。

煤层储量计算图的编制方法摘要:通过储量图的编制,掌握底板等高线的制作方法,储量块段的圈定方法,可采边界的划分,储量级别的确定,为煤矿的生产和设计奠定一定的技术基础。

关键词:储量计算等高线可采边界储量级别生产矿井的煤层储量计算图是以煤层等高线图或煤层立面投影图（附有采掘工程）为基础,注记各种煤层储量计算数据,圈定各级储量计算块段即成储量计算图。

一、比例尺和内容储量计算图的比例尺为1:500——1:5000。

图面内容主要包括以下几方面:地理坐标方格网、指北线,以及图名、图签、图例和比例尺等。

1.煤层上方地面主要建筑、铁路、公路及地表水体（河流、湖泊、水库等）2.通过该煤层的所有井巷工程、钻孔、探槽、探井、探巷、生产小窑和老窑,以及它们的名称和编号;勘探线及编号。

3.各勘探工程及井巷工程的见煤点位置或煤层厚度测量点位置、每层厚度及底板标高。

4.煤层底板等高线及标高值;断煤交线及断层名称或编号;煤层尖灭界线、岩浆侵入体界线、陷落柱界线、煤层冲蚀界线等。

5.井田边界、煤层露头线、采空区边界线、老窑积水范围界线、煤层风氧化带边界线等。

6.还应绘出储量计算边界、不同储量类别和级别的界线、各种煤柱界线、储量计算块段界线（每一块段均标注出编号、储量级别、平均煤厚、平均倾角和储量值等）;各勘探工程及井巷工程的见煤点或煤层厚度测量点,要绘出煤层小柱状（比例尺1:200或1:100）,注示主要煤质指标（灰分）。

二、编制方法和步骤储量计算图的编制,首先要绘制煤层等高线图,然后在煤层等高线图的基础之上划分块段、圈定储量和进行储量计算,最后进行检查、校对和整理。

（一）绘制煤层等高线图1.准备底图。

依据编图范围和比例尺确定图幅;绘制地理坐标方格网,注明每一经、纬线的坐标值,标出指北线。

2.根据地形地质图或地形图,转绘地面建筑、铁路、公路及地表水体等。

3.依据分层采掘工程平面图,将通过该煤层的所有井巷工程转绘下来,依据坐标值,将穿过该煤层的各个勘探工程、生产小窑及老窑等投绘到图上;注明上述每一工程的名称或编号。

煤炭储量计算方法之储量计算的根本参数煤炭储量计算方法二、储量计算的根本参数(一)计算面积确实定根据储量计算一般要求与通用公式，计算储量时所使用的面积有如下几种：(1)当煤层倾角小于15。

时，可以直接采用在煤层底板等高线图上测定的水平面积;(2)当煤层倾角在15。

~60。

时，就需要将煤层底板等高线图上所测定的水平面积换算成真面积，换算公式为S = S’/cosa式中，S为真面积;S’为在煤层底板等高线图上测定的水平面积;a为煤层倾角。

(3)当煤层倾角大于60。

时就需要将煤层立面图(即立面投影图)上量得的立面面积换算成真面积，换算公式为：S = S〞 / sina式中，S为真面积;S〞为在煤层立面投影图上测定的立面面积;a为煤层倾角。

(4)急倾斜煤层，其产状沿走向、倾向变化很大，直立倒转频繁，这就需要编制煤层立面展开图，在其上测定的面积，可直接用于储量计算。

以上种种方法均需要从图纸上测定面积，如何测定，以下介绍几种常用的方法。

(1)求积仪法。

利用求积仪测定面积是煤炭储量计算中最常用的一种方法。

过去经常使用的求积仪一种是带有可变臂杆的定极求积仪，一种是固定臂杆的定极求积仪。

而现在又有了精度更高，使用更为方便的求积仪。

每一种求积仪都带有详细的说明书，对其原理和使用说明不再赘述。

(2)透明纸格法。

先将绘有间隔1cm平行线的透明纸蒙在待测的平面图形上，如图2-8-5，整个欲测图形的面积即等于假如干小梯形面积之和，每一条被欲测图形所截的横线长度，为梯形的横中线，其高为1。

整个欲测图形面积实际等于被截的每一横线长度之和。

被截的每一横线的长度，可用尺子直接量得，也可用曲线仪测得。

这样求得的面积，再根据平面图的比例尺换算成实际面积。

图2-8-5用曲线仪和透明方格纸测量面积使用本方法要注意两个问题：其一，在用透明格纸蒙欲测图形时，必须注意使图形两端的条带宽度接近或等于0.5cm;其二，为了检查测定结果，可变换透明格纸的位置，再测定一次，两次测定值的误差不超过2%时，取两次测定结果的平均值。

复杂条件下煤层底板等高线生成算法研究摘要:详细介绍了一个利用ARX 进行的AutoCAD 二次开发的实例，利用ARX 、MFC 、数据库等来生成煤层底板等高线。

本算法较原来的算法有极大的改进，在运算速度和生成的等高线的效果上都很理想，和目前煤炭行业比较流行的龙软RIS 相比，本算法在处理含断层的复杂地质条件下等高线的生成上有明显优势。

关键词:ARX ；煤层底板等高线；二次开发中图分类号:TD80文献标识码:A 文章编号:1008-8725（2010）07-0052-03Research of a Algorithm to Generate the Coal-basedBottom Contour Under Complicated ConditionsTANG Wan-jun,JIANG Xin-yu,LIU Shan-zhong（College of Resource and Environment Engineering,Liaoning Technical University,Fuxin 123000,China ）Abstract:This paper introduces an instance of AutoCAD second development carried out by ARX,using ARX,MFC,databases,etc.to generate the coal seam floor contour lines.This algo －rithm is better than the original algorithm in the computing speed and the resulting effect on the contour paring with one of the most popular soft,longruan RIS,our algorithm has an obvious advantage in dealing with the generation of contour lines under complicated conditions which has the geological faults.Key words:ARX;coal seam floor contour;redevelopment收稿日期:2009-11-20;修订日期:2010-04-20作者简介:汤万钧（1988-），男，河南焦作人，现为辽宁工程技术大学资源与环境学院学生。

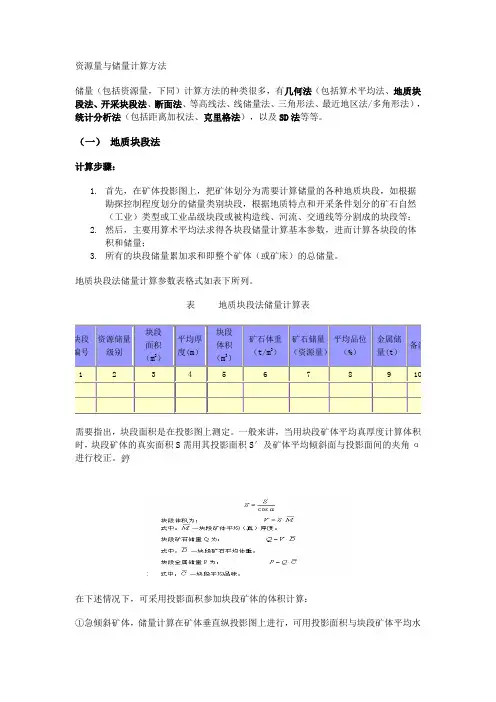
资源量与储量计算方法储量（包括资源量，下同）计算方法的种类很多，有几何法（包括算术平均法、地质块段法、开采块段法、断面法、等高线法、线储量法、三角形法、最近地区法/多角形法），统计分析法（包括距离加权法、克里格法），以及SD 法等等。

（一） 地质块段法计算步骤：1. 首先，在矿体投影图上，把矿体划分为需要计算储量的各种地质块段，如根据勘探控制程度划分的储量类别块段，根据地质特点和开采条件划分的矿石自然（工业）类型或工业品级块段或被构造线、河流、交通线等分割成的块段等； 2. 然后，主要用算术平均法求得各块段储量计算基本参数，进而计算各块段的体积和储量；3. 所有的块段储量累加求和即整个矿体（或矿床）的总储量。

地质块段法储量计算参数表格式如表下所列。

表 地质块段法储量计算表块段 编号 资源储量级别 块段 面积 （m 2）平均厚度(m ） 块段 体积 （m 3）矿石体重（t/m 3） 矿石储量（资源量） 平均品位（%） 金属储量(t ） 备注123 45678910需要指出，块段面积是在投影图上测定。

一般来讲，当用块段矿体平均真厚度计算体积时，块段矿体的真实面积S 需用其投影面积S′及矿体平均倾斜面与投影面间的夹角α进行校正。

在下述情况下，可采用投影面积参加块段矿体的体积计算：①急倾斜矿体，储量计算在矿体垂直纵投影图上进行，可用投影面积与块段矿体平均水平（假）厚度的乘积求得块段矿体体积。

图在矿体垂直投影图上划分开采块段(a)、(b)—垂直平面纵投影图； (c)、(d)—立体图1—矿体块段投影； 2—矿体断面及取样位置②水平或缓倾斜矿体，在水平投影图上测定块段矿体的投影面积后，可用其与块段矿体的平均铅垂（假）厚度的乘积求得块段矿体体积。

优点：适用性强。

地质块段法适用于任何产状、形态的矿体，它具有不需另作复杂图件、计算方法简单的优点，并能根据需要划分块段，所以广泛使用。

当勘探工程分布不规则，或用断面法不能正确反映剖面间矿体的体积变化时，或厚度、品位变化不大的层状或脉状矿体，一般均可用地质块段法计算资源量和储量。

储量级别、储量分类及计算一、储量级别1、地质可靠程度地质可靠程度反映了矿产勘查阶段工作成果的不同精度，分为预测的、推断的、控制的和探明的四种。

（1）预测的：是指对具有矿化潜力较大的地区经过预查得出的结果。

在有足够的数据并能与地质特征相似的已知矿床类比时，才能估算出预测的资源量。

（2）推断的：是指对普查区按照普查的精度大致查明矿产的地质特征以及矿体（矿点）的展布特征、品位、质量，也包括那些地质可靠程度较高的基础储量或资源量外推的部分。

由于信息有限，不确定因素多，矿体（点）的连续性是推断的，矿产资源数量的估算所依据的数据有限，可信程度较低。

（3）控制的：是指对矿区的一定范围依照详查的精度基本查明了矿床的主要地质特征、矿体的形态、产状、规模、矿石质量、品位及开采技术条件，矿体的连续性基本确定，矿产资源数量估算所依据的数据较多，可信度较高。

（4）探明的：是指在矿区的勘探范围依照勘探的精度详细查明了矿床的地质特征、矿体的形态、产状、规模、矿石质量、品位及开采技术条件，矿体的连续性已经确定，矿产资源数量估算所依据的数据详尽，可信度高。

2、可行性评价阶段可行性评价分为概略研究、预可行性研究、可行性研究三个阶段。

（1）概略研究：是指对矿床开发经济意义的概略评价。

所采用的矿石品位、矿体厚度、埋藏深度等指标通常是我国矿山几十年来的经验数据，采矿成本是根据同类矿山生产估计的。

其目的是为了由此确定投资机会。

由于概略研究一般缺乏准确参数和评价所必需的详细资料，所估算的资源量只具内蕴经济意义。

（2）预可行性研究：是指对矿床开发经济意义的初步评价。

其结果可以为该矿床是否进行勘探或为可行性研究提供决策依据。

进行着类研究，通常应有详查或勘探后采用参考工业指标求得的矿产资源/储量数，实验室规模的加工选冶试验资料，以及通过价目表或类似矿山开采对比所获数据估算的成本。

预可行性研究内容与可行性研究相同，但详细程度次之。

当投资者为选择拟建项目而进行预可行性研究时，应选择适合当时市场价格的指标及个项参数，且论证项目尽可能齐全。

储量计算其它方法
[导读]储量计算其它方法有最近地区法、三角形法、等高线法及等值线法等。

各方法的具体作法和计算如下文详述。

除上述储量计算方法之外，还有最近地区法、三角形法、等高线法及等值线法等。

最近地区法又称多角形法。

它的实质是将形状不规则的矿体，人为地简化为许多便于计算体积的多角形柱状体。

即在储量计算平面图所圈定的矿体范围内，以每个勘探工程为中心。

按其与各相邻工程的二分之一距离，将矿体分为一系列紧密连接的多角形地区，再依据每个多角形地区中心的工程资料分别计算其矿产储量。

此法不能反映矿体真实特点，而且计算繁琐，故很少应用。

三角形法的实质是把形状不规则的矿体，人为地简化为许多便于计算体积的三棱柱体。

即在储量计算平面图所圈定的矿体范围内，以直线连接各相邻勘探工程，把矿体分为一系列紧密连接的三角形块段。

再依据三角形块段顶点的勘探工程资料，分别计算各块段的矿产储量。

此法在实际工程中亦很少应用。

等高线法是层状沉积矿床中常用的一种储量计算法。

它以矿层顶板或底板等高线图为基础，把矿层分为若干倾角相近的部分，然后用一定的公式分别计算其体积和储量。

它的特点是可以直接反映矿层的产状和埋藏特点，适用于产状和厚度都比较稳定，倾角中等，并有足够勘探工程控制的矿床。

等值线法是利用矿体等厚线图或厚度－品位等值线图，把形状复杂的矿体变为一个体积相同、底面平坦而顶面高低起伏的几何体，然后用一定的公式分别计算各等值线间块段的体积和储量。

其优点是可以借助上述图件，表示出矿体形态、有用组份的分布及变化特点，但缺点是制图复杂，所以在实际工作中应用不广。

估算矿产资源/储量的方法
一、几何图形法
1、断面法：
（1）平行断面法
①梯形公式 V=L/2(S1+S2)
②截锥公式
③锥体公式 V=SL/3
④楔形公式 V=SL/2
⑤似柱体公式 V=L/6（2a1b1+b1a2）
（2）不平行断面法
2、算术平均法
3、地质断面法
4、开采块段法
5、等高线法
二、SD法
以最佳结构地质变量为基础，以断面构形替代空间构形为核心，以 spline函数及分维几何学为工具的估算方法，立足于传统的断面法。

它适用于不同矿床类型、矿体规模、产状、不同矿产勘查阶段，还可对估算的成果作精度预测。

三、地质统计学法
是以区域化变量理论作为基础，以变异函数作为主要工具，对既具有随机性、又具有结构性的变量进行统计学研究，估算时能充分考虑品位的空间变异性和矿化强度在空间的分布特征，使估算结果更加符合地质规律，置信度高，但需有较多的样本个体为基础。

勘查过程中，针对矿床的地质特征，运用这种方法，还能制定或检验合理的勘探工程间距。

有距离加权法、相关分析法、克里格法。

内蕴经济资源量是矿产资源勘查工作自普查至勘探，地质可靠程度达到了推断的至探明的，但可行性评价工作只进行了概略研究，由于技术经济参数取值于经验数据，未与市场挂钩，区分不出其真实的经济意义，统归为内蕴经济资源量。

可细分为3个类型：
探明的内蕴经济资源量(331)
控制的内蕴经济资源量(332)
推断的内蕴经济资源量(333)。

煤炭储量计算方法之储量计算的基本参数煤炭储量计算方法二、储量计算的基本参数(一)计算面积的确定根据储量计算一般要求及通用公式，计算储量时所使用的面积有如下几种：(1)当煤层倾角小于15。

时，可以直接采用在煤层底板等高线图上测定的水平面积；⑵当煤层倾角在15。

~60。

时，就需要将煤层底板等高线图上所测定的水平面积换算成真面积，换算公式为S = S ' /cosa式中，S为真面积;S '为在煤层底板等高线图上测定的水平面积;a为煤层倾角。

(3)当煤层倾角大于60。

时就需要将煤层立面图(即立面投影图)上量得的立面面积换算成真面积，换算公式为：S = S ” / sina式中，S为真面积;S”为在煤层立面投影图上测定的立面面积;a为煤层倾角。

(4)急倾斜煤层，其产状沿走向、倾向变化很大，直立倒转频繁，这就需要编制煤层立面展开图，在其上测定的面积，可直接用于储量计算。

以上种种方法均需要从图纸上测定面积，如何测定，以下介绍几种常用的方法。

(1)求积仪法利用求积仪测定面积是煤炭储量计算中最常用的一种方法。

过去经常使用的求积仪一种是带有可变臂杆的定极求积仪，一种是固定臂杆的定极求积仪。

而现在又有了精度更高，使用更为方便的求积仪。

每一种求积仪都带有详细的说明书，对其原理和使用说明不再赘述。

⑵透明纸格法。

先将绘有间隔1cm平行线的透明纸蒙在待测的平面图形上，如图2-8-5，整个欲测图形的面积即等于若干小梯形面积之和，每一条被欲测图形所截的横线长度，为梯形的横中线，其高为1。

整个欲测图形面积实际等于被截的每一横线长度之和。

被截的每一横线的长度，可用尺子直接量得，也可用曲线仪测得。

这样求得的面积，再根据平面图的比例尺换算成实际面积。

图2-8-5用曲线仪和透明方格纸测量面积图2-8-5 用曲线仪和透明方格纸测量面积使用本方法要注意两个问题：其一，在用透明格纸蒙欲测图形时，必须注意使图形两端的条带宽度接近或等于0.5cm;其二，为了检查测定结果，可变换透明格纸的位置，再测定一次，两次测定值的误差不超过2%寸，取两次测定结果的平均值。

第二章采区储量计算第一节采区边界采区上部边界为采区回风大巷，下部边界为采区运输大巷，采区西部为二J 九采区，采区东部边界为二五采区。

走向长度600 米，斜长400 米，平均倾角15°，面积240000 平方米。

第二节采区储量按照等高线法求采区储量：所谓等高线法就是在煤层底板等高线图上，按煤层厚度或倾角大致稳定的范围内沿煤层底板等高线分为若干块段，分别计算各块段的储量，煤层总储量即为单个块段储量之和，本设计采用此储量计算方法。

式中Q—煤炭工业储量，万t；Si—块段水平投影面积,㎞2；α —煤层倾角，采用块段内的平均倾角，15º；Mi—块段煤层的平均厚度，m；Yi—块段内煤层的容重，t/m3。

根据地质报告资料及煤层底板等高线可知：S=248466.3m2，α =15°, Mi=2.71m2 Yi=1.5t/m3 代入上式得：Q=248466.3×2.6×1.5 cos15° =93.6 万t 所以，本采区的工业储量为93.6 万t。

矿井的可采储量公式为：Z=(Zc-P)×C 式中Z—矿井可采储量，万t；Zc—矿井工业储量，万t；P—各种永久煤柱储量损失之和，万t；C—采区回采率，薄煤层不低于0.85；中厚煤层不低于0.80；厚煤层不低于0.75，本矿井取0.80。

Z=(93.6-13.26)×0.8 =64.3 万t采区储量表地质储量（万吨）煤层可利用地永久煤质储量二2 80.34可采储量（万吨）64.3柱13.26合计93.6备注第三节采区生产能力采区设计年工作日300 天，每天三班作业，三班生产。

采区生产设计一个采煤队。

回采工作面生产能力的确定a、回采工作面日生产能力A1=L×h×b×r×K1×K2 =120×2.6×1.2×1.5×0.95×0.8 =426.8(t) 式中A——日生产能力，吨L——工作面长度，m b——工作面推进度，m h——工作面平均采高，m r——煤的容重，取1.5t/m3 K1——工作面回采率，取95% K2——正规循环率，取80% b、掘进出煤量掘进出煤量一般为采面出煤量的5%，故掘进出煤量为A2=426.8×5% =21.2（吨）故采区日出煤量为：426.8+21.2=448（吨）c、生产能力确定采区设计年生产能力为A=(A1+A2) ×D =448×300 =134400(t) 式中A——采区生产能力，吨D——年生产日数，取300 天根据以上计算采区生产能力为14 万吨。

常用储量计算方法及其应用条件1）断面法：将矿体用若干个剖面截成若干个块段，分别计算每个块段的储量，然后将各块段的储量和起来既得到矿体的储量。

这种用断面划分块段求储量的方法叫断面法。

如果是用一系列垂直剖面划分块段而计算储量者，叫做垂直断面法；用以犀利水平断面划分块段计算储量者，叫水平断面法。

在垂直断面法中，如果断面与断面之间平行，称为平行断面法；若不平行则为不平行断面法。

平行断面法的优点在于断面图保持了矿体断面的真实形状，直观的反映了地质构造特征；储量计算时，可根据出量级别、矿石类型、工业品级等的要求任意划分块段，具有相当的灵活性。

任意形状的矿床都可用断面法。

因其优点较多，称为目前最常用的储量计算方法。

2)算术平均法：这种方法的基本特点是将整个矿体的各种参数都用简单算术平均法求得其平均值，从而计算矿体的储量。

他一般是利用水平投影图或垂直纵投影图来进行的，有时也在平行矿体倾斜面的投影图上进行。

算术平均法是所有储量计算方法中最简单的方法，也无须做复杂的图件。

因此，在矿点检查、矿区评价阶段常用这种方法计算。

当探矿工程数量较少，分布又不均匀，矿体各项指标值变化较大时，此法仅能得出粗略的计算结果。

此法没有按矿石类型、工业品级、储量级别等划分块段分别计算。

因此在勘探阶段很少用这种方法。

3）地质块断法：在计算方法上，地质块断法和算术平均法基本一样，所不同者仅在于它不是将整个矿体一起计算，而是按需要将矿体划分成若干块断，每个块断都用算术平均法计算出块断的储量。

有时根据指标值的变化特点，也用加权平均法计算。

所有块断储量之和即为全矿体的储量。

地质块断法具有算术平均法的所有优点，同时还弥补了算术平均法不能按需要划分块断的缺点。

它可以是用在任何大小、形状和产状的矿体上，特别是层状、似层状、透镜状矿体，而且勘查方法对它也没有影响。

因此，地质块断法成为目前勘探阶段储量计算的主要方法之一。

4）开采块断法：当矿体被坑道切割成许多开采块断时，常用此法计算储量。

第二十五讲煤层底板等高线图一．概述1．概念及原理将各煤层底板等高线，用标高投影的方法，投形到同一水平面上，按一定比例和规定的线条、符号绘制而成的图纸称为煤层底板等高线图。

2．主要反映内容煤层产状、地质构造3．用途（1）采区规划（2）储量计算（3）构造预测4．比例1：2000二．煤层产状三要素：走向、倾向、倾角1．煤层走向煤层底板等高线的方向，即为煤层的走向用方位角表示。

2．煤层倾向在水平面内，垂直煤层底板等高线由高到底的方向，即为煤层倾向，用方位角表示，并与走向相差90°。

3．煤层倾角煤层倾斜线与倾斜线之间的夹角即为煤层倾角。

规定：为确保走向的单一性，煤层的走向比煤层的倾向小90°。

三．煤层构造形状1．单斜构造在一定范围内，大致向一个方向倾斜的煤层，称为单斜构造。

2．穹窿构造，盆地构造3．曲构造煤层核部、冀部、轴面、轴线、枢纽4．断层构造（1）断层概念概念：煤层受力后发生断裂并发生明显的相对位移形成的构造形态，标为断层。

（2）断层要素断面、断盘、断面交线、断距。

（3）断层的性质正断层逆断层（4）断层煤层底板等高线的特征正断层煤层底板等高线的特征：煤层底板等高线遇断面交线中断，断面交线之间，等高线缺失。

逆断层煤层底板等高线的特征：煤层底板等高线遇断面交线中断，断面交线之间，等高线重叠。

（5）断距地层断距、水平断距、落差。

落差：断层上下盘同一煤层地板对应点之间的垂直距离，即为落差。

（6）断层产状走向：断面交线上高程相等点的连线方向，即为断层的走向。

倾向：在水平面上，垂直断层走向由高到底的方向，称为断层的倾向。

倾角：断层面与水平面的夹角（最大锐角）。

四、煤层底板等高线图的识读1．单线追索法由图一侧选择一根等高线，观测其变化情况，若等高线弯曲表示有褶曲，若等高线断开表示有断层。

2．划分块段以断面交线为界将煤层分为若干个块段，对每一块段煤层的产状进行分析、判断。

3．整体分析最后再把各个块段联系起来，综合分析，分析有几条断层，每条断层的性质及其与其他构造的相互联系等。