下载文档原格式
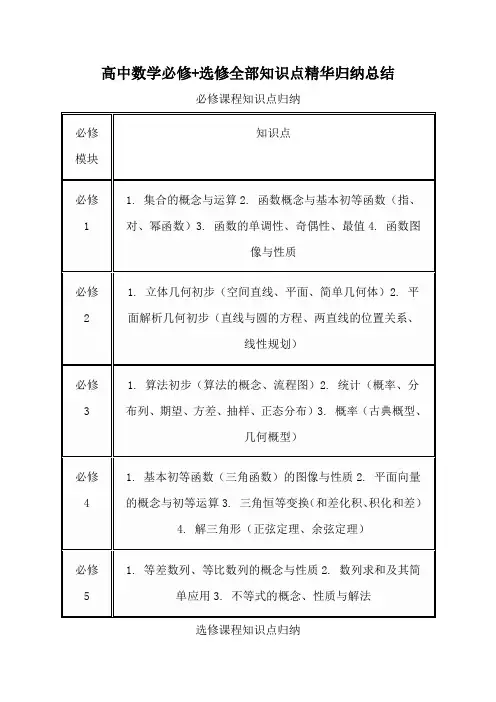
高中数学必修+选修知识点精华讲义高中数学必修+选修知识点精华讲义(新课标)高中数学必修+选修知识点精华讲义新课标引言1.课程内容:必修课程由5个模块组成:必修1:集合、函数概念与基本初等函数(指、对、幂函数):算法初步、统计、概率。
必修4: 必修2:立体几何初步、平面解析几何初步。
必修3基本初等函数(三角函数)、平面向量、三角恒等变换。
必修5:解三角形、数列、不等式。
以上是每一个高中学生所必须学习的。
上述内容覆盖了高中阶段传统的数学基础知识和基本技能的主要部分，其中包括集合、函数、数列、不等式、解三角形、立体几何初步、平面解析几何初步等。
不同的是在保证打好基础的同时，进一步强调了这些知识的发生、发展过程和实际应用，而不在技巧与难度上做过高的要求。
此外，基础内容还增加了向量、算法、概率、统计等内容。
选修课程有4个系列: 系列1:由2个模块组成。
选修1—1:常用逻辑用语、圆锥曲线与方程、导数及其应用。
选修1—2:统计案例、推理与证明、数系的扩充与复数、框图系列2:由3个模块组成。
选修2—1:常用逻辑用语、圆锥曲线与方程、空间向量与立体几何。
选修2—2:导数及其应用，推理与证明、数系的扩充与复数选修2—3:计数原理、随机变量及其分布列，统计案例。
- 1 -系列3:由6个专题组成。
选修3—1:数学史选讲。
选修3—2:信息安全与密码。
选修3—3:球面上的几何。
选修3—4:对称与群。
选修3—5:欧拉公式与闭曲面分类。
选修3—6:三等分角与数域扩充。
系列4:由10个专题组成。
选修4—1:几何证明选讲。
选修4—2:矩阵与变换。
选修4—3:数列与差分。
选修4—4:坐标系与参数方程。
选修4—5:不等式选讲。
选修4—6:初等数论初步。
选修4—7:优选法与试验设计初步。
选修4—8:统筹法与图论初步。
选修4—9:风险与决策。
选修4—10:开关电路与布尔代数。
2(重难点及考点:重点:函数，数列，三角函数，平面向量，圆锥曲线，立体几何，导数难点:函数、圆锥曲线高考相关考点:?集合与简易逻辑:集合的概念与运算、简易逻辑、充要条件?函数:映射与函数、函数解析式与定义域、值域与最值、反函数、三大性质、函数图象、指数与指数函数、对数与对数函数、函数的应用?数列:数列的有关概念、等差数列、等比数列、数列求和、数列的应用?三角函数:有关概念、同角关系与诱导公式、和、差、倍、半公式、求值、化简、证明、三角函数的图象与性质、三角函数的应用?平面向量:有关概念与初等运算、坐标运算、数量积及其应用?不等式:概念与性质、均值不等式、不等式的证明、不等式的解法、绝对值不等式、不等式的应用?直线和圆的方程:直线的方程、两直线的位置关系、线性规划、圆、直线与圆的位置关系?圆锥曲线方程:椭圆、双曲线、抛物线、直线与圆锥曲线的位置关系、轨迹问题、圆锥曲线的应用?直线、平面、简单几何体:空间直线、直线与平面、平面与平面、棱柱、棱锥、球、空间向量?排列、组合和概率:排列、组合应用题、二项式定理及其应用?概率与统计:概率、分布列、期望、方差、抽样、正态分布?导数:导数的概念、求导、导数的应用 ?复数:复数的概念与运算1、一般地，由所有属于集合A或集合B的元素组成的集合，称为集合A与B的并集.记作:A B. 2、一般地，由属于集合A且属于集合B的所有元素组成的集合，称为A与B的交集.记作:A B. 3、全集、补集,CUA {x|x U,且x U} ?1.2.1、函数的概念1、设A、B是非空的数集，如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有惟一确定的数f,x,和它对应，那么就称f:A B为集合A到集合B的一个函数，记作:y f,x,,x A.2、一个函数的构成要素为:定义域、对应关系、值域.如果两个函数的定义域相同，并且对应关系完全一致，则称这两个函数相等. ?1.2.2、函数的表示法1、函数的三种表示方法:解析法、图象法、列表法. ?1.3.1、单调性与最大(小)值 1、注意函数单调性的证明方法:(1)定义法:设x1、x2 [a,b],x1 x2那么第一章:集合与函数概念 ?1.1.1、集合1、把研究的对象统称为元素，把一些元素组成的总体叫做集合。
高中数学全部知识点提纲整理高中数学全部知识点提纲整理一、集合与简易逻辑1.集合的元素具有确定性、无序性和互异性.2.对集合，时，必须注意到“极端”情况：或;求集合的子集时是否注意到是任何集合的子集、是任何非空集合的真子集.3.判断命题的真假关键是“抓住关联字词”;注意：“不‘或’即‘且’，不‘且’即‘或’”.4.“或命题”的真假特点是“一真即真，要假全假”;“且命题”的真假特点是“一假即假，要真全真”;“非命题”的真假特点是“一真一假”.5.四种命题中“‘逆’者‘交换’也”、“‘否’者‘否定’也”.原命题等价于逆否命题，但原命题与逆命题、否命题都不等价.反证法分为三步：假设、推矛、得果.8.充要条件二、函数1.指数式、对数式，2.(1)映射是“‘全部射出’加‘一箭一雕’”;映射中第一个集合中的元素必有像，但第二个集合中的元素不一定有原像( 中元素的像有且仅有下一个，但中元素的原像可能没有，也可任意个);函数是“非空数集上的映射”，其中“值域是映射中像集的子集”.(2)函数图像与轴垂线至多一个公共点，但与轴垂线的公共点可能没有，也可任意个.(3)函数图像一定是坐标系中的曲线，但坐标系中的曲线不一定能成为函数图像.3.单调性和奇偶性(1)奇函数在关于原点对称的区间上若有单调性，则其单调性完全相同.偶函数在关于原点对称的区间上若有单调性，则其单调性恰恰相反.(2)复合函数的单调性特点是：“同性得增，增必同性;异性得减，减必异性”.复合函数的奇偶性特点是：“内偶则偶，内奇同外”.复合函数要考虑定义域的变化。
(即复合有意义)4.对称性与周期性(以下结论要消化吸收，不可强记)(1)函数与函数的图像关于直线(轴)对称.推广一：如果函数对于一切，都有成立，那么的图像关于直线(由“和的一半确定”)对称.推广二：函数，的图像关于直线对称.(2)函数与函数的图像关于直线(轴)对称.(3)函数与函数的图像关于坐标原点中心对称.三、数列1.数列的通项、数列项的项数，递推公式与递推数列，数列的通项与数列的前项和公式的关系2.等差数列中(1)等差数列公差的取值与等差数列的单调性.(2)也成等差数列.(3)两等差数列对应项和(差)组成的新数列仍成等差数列.(4) 仍成等差数列.(5)“首正”的递等差数列中，前项和的最大值是所有非负项之和;“首负”的递增等差数列中，前项和的最小值是所有非正项之和;(6)有限等差数列中，奇数项和与偶数项和的存在必然联系，由数列的总项数是偶数还是奇数决定.若总项数为偶数，则“偶数项和“奇数项和=总项数的一半与其公差的积;若总项数为奇数，则“奇数项和-偶数项和”=此数列的中项.(7)两数的等差中项惟一存在.在遇到三数或四数成等差数列时，常考虑选用“中项关系”转化求解.(8)判定数列是否是等差数列的主要方法有：定义法、中项法、通项法、和式法、图像法(也就是说数列是等差数列的充要条件主要有这五种形式).3.等比数列中：(1)等比数列的符号特征(全正或全负或一正一负)，等比数列的首项、公比与等比数列的单调性.(2)两等比数列对应项积(商)组成的新数列仍成等比数列.(3)“首大于1”的正值递减等比数列中，前项积的最大值是所有大于或等于1的项的积;“首小于1”的正值递增等比数列中，前项积的最小值是所有小于或等于1的项的积;(4)有限等比数列中，奇数项和与偶数项和的存在必然联系，由数列的总项数是偶数还是奇数决定.若总项数为偶数，则“偶数项和”=“奇数项和”与“公比”的积;若总项数为奇数，则“奇数项和“首项”加上“公比”与“偶数项和”积的和.(5)并非任何两数总有等比中项.仅当实数同号时，实数存在等比中项.对同号两实数的等比中项不仅存在，而且有一对.也就是说，两实数要么没有等比中项(非同号时)，如果有，必有一对(同号时).在遇到三数或四数成等差数列时，常优先考虑选用“中项关系”转化求解.(6)判定数列是否是等比数列的方法主要有：定义法、中项法、通项法、和式法(也就是说数列是等比数列的充要条件主要有这四种形式).4.等差数列与等比数列的联系(1)如果数列成等差数列，那么数列( 总有意义)必成等比数列.(2)如果数列成等比数列，那么数列必成等差数列.(3)如果数列既成等差数列又成等比数列，那么数列是非零常数数列;但数列是常数数列仅是数列既成等差数列又成等比数列的必要非充分条件.(4)如果两等差数列有公共项，那么由他们的公共项顺次组成的新数列也是等差数列，且新等差数列的公差是原两等差数列公差的最小公倍数.如果一个等差数列与一个等比数列有公共项顺次组成新数列，那么常选用“由特殊到一般的方法”进行研讨，且以其等比数列的项为主，探求等比数列中那些项是他们的公共项，并构成新的数列.5.数列求和的常用方法：(1)公式法：①等差数列求和公式(三种形式)，②等比数列求和公式(三种形式)，(2)分组求和法：在直接运用公式法求和有困难时，常将“和式”中“同类项”先合并在一起，再运用公式法求和.(3)倒序相加法：在数列求和中，若和式中到首尾距离相等的两项和有其共性或数列的通项与组合数相关联，则常可考虑选用倒序相加法，发挥其共性的作用求和(这也是等差数列前和公式的推导方法).(4)错位相减法：如果数列的通项是由一个等差数列的通项与一个等比数列的通项相乘构成，那么常选用错位相减法，将其和转化为“一个新的的等比数列的和”求解(注意：一般错位相减后，其中“新等比数列的项数是原数列的项数减一的差”!)(这也是等比数列前和公式的推导方法之一).(5)裂项相消法：如果数列的通项可“分裂成两项差”的形式，且相邻项分裂后相关联，那么常选用裂项相消法求和(6)通项转换法。
高二数学知识点提纲第一章第一节：二次函数1. 二次函数的定义2. 二次函数的图像及性质a. 平移b. 翻折c. 对称性d. 极值点3. 二次函数的解析式4. 二次函数在实际问题中的应用第二节：数列与数列的求和1. 数列的定义与表示方法2. 等差数列a. 等差数列的通项公式b. 等差数列的前n项和公式c. 等差数列的性质与应用3. 等比数列a. 等比数列的通项公式b. 等比数列的前n项和公式c. 等比数列的性质与应用4. 数列求和公式的推导5. 数列在数学问题中的应用第三节：立体几何与三角函数1. 空间几何基本概念2. 空间几何中的平行关系3. 空间几何中的垂直关系4. 空间几何中的距离计算5. 空间几何中的三角函数a. 正弦、余弦、正切的定义与性质b. 三角函数的图像与周期性6. 三角函数在实际问题中的应用第四节：概率与统计1. 概率的基本定义与性质2. 事件的组合与计算a. 互斥事件与对立事件b. 事件的加法原理3. 条件概率与独立事件a. 条件概率的定义b. 独立事件的概念与判定4. 统计学基本概念a. 数据的收集与整理b. 数据的分析与解读5. 正态分布与标准正态分布a. 正态分布的性质与应用b. 标准正态分布的概念与应用第五节：解析几何1. 平面解析几何基本概念2. 直线的方程与性质a. 一般式与截距式b. 直线的斜率与倾斜角c. 直线的平行与垂直关系判定3. 圆的方程与性质a. 标准式与一般式b. 圆的半径、直径与弧长的计算c. 圆与直线的位置关系判定以上为高二数学知识点提纲第一章的内容概述。
通过学习这些内容，同学们将对二次函数、数列与数列的求和、立体几何与三角函数、概率与统计以及解析几何等数学知识点有着全面的了解和掌握。
希望同学们能够在学习中勤思考、多实践，提升自己的数学能力。
加油！。
1.3.从“物不知数”到“中国剩余定理”-苏教版选修3-1 数学史选讲教案1. 前言苏教版选修3-1 数学史选讲教案是高中数学课程中的一篇重要文献，对于理解数学史上的经典数学成果、欣赏数学思想的美妙、认识数学在人类文化发展史上的地位等方面都有很大的帮助。
本篇文档将以该教案中的“从‘物不知数’到‘中国剩余定理’”为主题，进行详细阐述。
2. 从“物不知数”到“中国剩余定理”2.1 “物不知数”“物不知数”是公元前5世纪中国战国时期的墓葬铭文上出现的一个术语, 指代一种无限大的概念。
自然数、有理数、无理数、实数、复数的概念在古代都被称为“数”，但是人们逐渐认识到自然数、有理数等有限数量的数无法涵盖所有“量”的概念，因此自然而然地出现了“物不知数”这个概念。
公元7世纪，印度的天文学家、数学家布拉玛叶在发明数字0的基础上，创立了零和负数的概念，并把负数的运算规则用棒图表示出来。
在此基础上，人们对于“物不知数”的理解也有了新的发展。
公元9世纪的波斯数学家阿尔芒努菲发明了一种叫做“代数”的数学分支，并成功地运用它解决了经济、工程等实际问题。
但是当时人们对于“物不知数”的概念仍存在一定的争议。
直到16世纪，意大利数学家卡塔兰引入了现在我们所熟悉的符号x作为未知数的代表，才彻底解决了“物不知数”的概念问题。
2.2 中国剩余定理中国剩余定理是中国古代代数学的一个重要成果，被称为“中国古最代表性的数学成就之一”。
它的主要思想是：如果我们知道了一个方程组的多个模数之间的互质关系，那么我们就能通过对它们取模运算得到同余的方程组，通过合并这些方程组的解，得到原方程组的解。
公元3世纪左右，中国数学家孙子定深刻认识到了数学中“恰当用数”的重要性，并在《孙子算经》中阐述了“合数不知一”、“十倍于九”等数学原理。
中国剩余定理在此基础上得以发展。
公元13世纪的中国数学家李冶在其所著的《详解九章算术》中，阐述了中国剩余定理的基本思想，并提出了它的具体计算方法。
必修一第一章信使与函数概念1．1 集合1．1．1 集合的含义与表示1．1．2集合间的基本关系1．1．3集合的基本运算1．2函数及其表示1．2．1 函数的概念1．2．2函数的表示法1．3 函数的基本性质1．3．1 单调性与最大(小)值1．3．2奇偶性第二章基本初等函数2．1指数函数2．1．1 指数与指数幂的运算2．1．2指数函数及其性质2．2对数函数2．2．1对数与对数运算2．2．2对数函数及其性质2．3幂函数第三章函数的应用3．1 函数与方程3．2 函数模型及其应用3．2．1 几类不同增长的函数模型3．2．2 函数模型的应用实例必修二第一章空间几何体1.1 空间几何体的结构1.2 空间几何体的三视图和直观图1.3空间几何体的表面积与体积1.3.1 柱体、锥体、台体的表面积与体积1.3.2球的体积和表面积第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.1 平面2.1.2 空间中直线与直线之间的位置关系2.1.3 空间中直线与平面之间的位置关系2.1.4 平面与平面之间的位置关系2.2 直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定2.2.2 平面与平面平行的判定2.2.3 直线与平面平行的性质2.2.4 平面与平面平行的性质2.3 直线、平面垂直的判定及其性质.2.3.1 直线与平面垂直的判定2.3.2 平面与平面垂直的判定2.3.3 直线与平面垂直的性质2.3.4 平面与平面垂直的性质第三章直线与方程3.1 直线的倾斜角与斜率3.1.1 倾斜角与斜率3.1.2 两条直线平行与垂直的判定3.2直线的方程3.2.1 直线的点斜式方程3.2.2 直线的两点式方程3.2.3 直线的一般式方程3.3直线的交点坐标与距离公式3.3.1 两条直线的交点坐标3.3.2 两点间的距离3.3.3 点到直线的距离3.3.4 两条平行直线间的距离第四章圆与方程4.1 圆的方程4.1.1 圆的标准方程4.1.2 圆的一般方程4.2直线、圆的位置关系4.2.1 直线与圆的位置关系4.2.2 圆与圆的位置关系4.2.3 直线与圆的方程的应用4.3 空间直角坐标系必修三第一章算法初步1.1 算法与程序框图1.1.1 算法的概念1.1.2程序框图与算法的基本逻辑结构1.2基本算法语句1.2.1 输入语句、输出语句和赋值语句1.2.2 条件语句1.2.3循环语句1.3算法案例第二章统计2.1 随机抽样2.1.1 简单随机抽样2.1.2 系统抽样2.1.3 分层抽样2.2用样本估计总体2.2.1 用样本的频率分布估计总体分布2.2.2 用样本的数字特征估计总体的数字特征2.3变量间的相关关系第三章概率3.1 随机事件的概率3.1.1 随机事件的概率3.1.2概率的意义3.1.3概率的基本性质3.2 古典概型3.3 几何概型必修四第一章三角函数1.1 任意角和弧度制1.2 任意角的三角函数1.3 三角函数的诱导公式1.4 三角函数的图象与性质1.5 函数y=Asin的图象1.5 三角函数模型的简单应用第二章平面向量2.1 平面向量的实际背景及基本概念2.2 平面向量的线性运算2.3 平面向量的基本定理及坐标表示2.4 平面向量的数量积2.5 平面向量应用举例第三章三角恒等变换3.1 两角和与差的正弦、余弦和正切公式3.2 简单的三角恒等变换必修五第一章解三角形3／1.1 正弦定理和余弦定理3／1.1.1 正弦定理15／课后习题全解17／1.1.2 余弦定理28／课后习题全解32／1.2 应用举例43／课后习题全解50／1.3 实习作业54／章末总结提高60／章末习题全解第二章数列68／2.1 数列的概念与简单表示法80／课后习题全解85／2.2 等差数列97／课后习题全解101／2.3 等差数列的前z项和117／课后习题全解124／2.4 等比数列144／课后习题全解150／2.5 等比数列的前月项和166／课后习题全解172／章末总结提高187／章末习题全解第三章不等式197／3.1 不等关系与不等式210／课后习题全解213／3.2 一元二次不等式及其解法228／课后习题全解234／3.3 二元一次不等式(组)与简单的线性规划问题248／课后习题全解256／3.4 基本不等式272／课后习题全解278／章末总结提高286／章末习题全解。
高中数学知识点提要高中数学是一门重要的学科，涵盖了众多的知识点。
这些知识点相互关联，构成了一个完整的知识体系。
下面为大家梳理一下高中数学的主要知识点。
一、集合与函数1、集合集合是数学中最基本的概念之一。
集合由一些确定的、不同的对象组成。
集合的表示方法有列举法、描述法和图示法。
集合的运算包括交集、并集和补集。
2、函数函数是高中数学的重点。
函数定义为两个非空数集之间的一种对应关系。
函数的三要素是定义域、值域和对应法则。
常见的函数类型有一次函数、二次函数、反比例函数、指数函数、对数函数和幂函数等。
函数的性质包括单调性、奇偶性、周期性和对称性。
二、三角函数1、任意角和弧度制了解任意角的概念，掌握弧度制与角度制的换算。
2、三角函数的定义通过角的终边上的点的坐标来定义三角函数。
3、诱导公式用于将不同角度的三角函数值进行转化。
4、三角函数的图象和性质包括正弦函数、余弦函数、正切函数的图象、周期、定义域、值域、单调性等。
5、三角恒等变换掌握两角和与差的正弦、余弦、正切公式，二倍角公式等，能进行三角函数的化简、求值和证明。
三、数列1、数列的概念数列是按照一定顺序排列的一列数。
2、等差数列通项公式、前 n 项和公式，以及等差数列的性质。
3、等比数列通项公式、前 n 项和公式，以及等比数列的性质。
4、数列求和掌握等差数列和等比数列的求和方法，以及错位相减法、裂项相消法等常见的数列求和技巧。
四、不等式1、不等式的性质包括传递性、加法和乘法法则等。
2、一元二次不等式求解一元二次不等式的步骤和方法。
3、基本不等式重要的不等式，如均值不等式，用于求最值和证明不等式。
五、立体几何1、空间几何体认识柱体、锥体、台体和球体的结构特征，掌握它们的表面积和体积公式。
2、点、直线、平面的位置关系理解线线、线面、面面的平行和垂直关系，能够进行证明和计算。
六、平面解析几何1、直线方程掌握直线的点斜式、斜截式、两点式、一般式方程。
2、圆的方程圆的标准方程和一般方程，以及直线与圆的位置关系。
高三数学知识点总结全提纲第一章代数与方程1.1 一元一次方程及其应用1.1.1 一元一次方程的定义与性质1.1.2 解一元一次方程的基本方法1.1.3 一元一次方程的应用1.2 一元二次方程及其应用1.2.1 一元二次方程的定义与性质1.2.2 解一元二次方程的基本方法1.2.3 一元二次方程的应用1.3 不等式1.3.1 一元一次不等式的定义与解法1.3.2 一元二次不等式的定义与解法1.3.3 不等式组的解法与应用第二章几何与三角形2.1 点、线、面及其关系2.1.1 点、线、面的基本概念2.1.2 平行与垂直关系2.1.3 点、线、面之间的位置关系2.2 三角形与相关概念2.2.1 三角形的定义与性质2.2.2 直角三角形的性质与应用2.2.3 等腰三角形的性质与应用2.2.4 等边三角形的性质与应用2.3 三角形的三心与圆2.3.1 三角形的外心与外接圆2.3.2 三角形的内心与内切圆2.3.3 三角形的重心与重心连线第三章空间与向量3.1 空间几何与立体图形3.1.1 空间几何的基本概念与公理3.1.2 空间几何中的平行关系3.1.3 空间几何中的垂直关系3.2 空间向量与向量运算3.2.1 空间向量的定义与性质3.2.2 空间向量的加法与减法3.2.3 空间向量的数量积与向量积3.3 空间几何中的位置关系3.3.1 点与直线的位置关系3.3.2 点与平面的位置关系3.3.3 直线与平面的位置关系第四章概率与统计4.1 随机事件与概率4.1.1 随机事件的定义与性质4.1.2 概率的基本概念与性质4.1.3 概率计算与应用4.2 统计与统计量4.2.1 数据的收集与整理4.2.2 统计量的计算与应用4.2.3 抽样调查与样本估计4.3 概率与统计的应用4.3.1 随机变量与概率分布4.3.2 统计推断与假设检验4.3.3 概率与统计的实际应用第五章排列组合与数列5.1 排列与组合5.1.1 排列与组合的基本概念与性质5.1.2 排列与组合的计算与应用5.1.3 Pn原理与鸽巢原理5.2 等差数列与等比数列5.2.1 等差数列的概念与性质5.2.2 等差数列的通项与求和公式5.2.3 等比数列的概念与性质5.2.4 等比数列的通项与求和公式5.3 递推数列与特殊数列5.3.1 递推数列的定义与性质5.3.2 斐波那契数列与裴波那契数列5.3.3 序数与序列的应用总结：以上是高三数学知识点的全提纲，涵盖了高中数学课程的所有重要内容。
高中数学知识点提纲推荐文章人教版高中数学知识点提纲热度：高中数学全部知识点提纲整理热度：高中物理知识点提纲热度：人教版高中生物知识点总结提纲热度：高中语文知识点提纲热度：学数学要对整个数学知识点的脉络有清晰的掌握，就是心中要有一个发展的数学框架。
把每单元前的单元介绍看看，注意后几行，一般都是重点。
以下是小编给大家整理的高中数学知识点提纲，希望对大家有所帮助，欢迎阅读!高中数学知识点提纲1一、集合、简易逻辑(14课时,8个)1.集合;2.子集;3.补集;4.交集;5.并集;6.逻辑连结词;7.四种命题;8.充要条件.二、函数(30课时,12个)1.映射;2.函数;3.函数的单调性;4.反函数;5.互为反函数的函数图象间的关系;6.指数概念的扩充;7.有理指数幂的运算;8.指数函数;9.对数;10.对数的运算性质;11.对数函数.12.函数的应用举例.三、数列(12课时,5个)1.数列;2.等差数列及其通项公式;3.等差数列前n项和公式;4.等比数列及其通顶公式;5.等比数列前n项和公式.四、三角函数(46课时17个)1.角的概念的推广;2.弧度制;3.任意角的三角函数;4,单位圆中的三角函数线;5.同角三角函数的基本关系式;6.正弦、余弦的诱导公式’7.两角和与差的正弦、余弦、正切;8.二倍角的正弦、余弦、正切;9.正弦函数、余弦函数的图象和性质;10.周期函数;11.函数的奇偶性;12.函数的图象;13.正切函数的图象和性质;14.已知三角函数值求角;15.正弦定理;16余弦定理;17斜三角形解法举例.五、平面向量(12课时,8个)1.向量2.向量的加法与减法3.实数与向量的积;4.平面向量的坐标表示;5.线段的定比分点;6.平面向量的数量积;7.平面两点间的距离;8.平移.六、不等式(22课时,5个)1.不等式;2.不等式的基本性质;3.不等式的证明;4.不等式的解法;5.含绝对值的不等式.七、直线和圆的方程(22课时,12个)1.直线的倾斜角和斜率;2.直线方程的点斜式和两点式;3.直线方程的一般式;4.两条直线平行与垂直的条件;5.两条直线的交角;6.点到直线的距离;7.用二元一次不等式表示平面区域;8.简单线性规划问题.9.曲线与方程的概念;10.由已知条件列出曲线方程;11.圆的标准方程和一般方程;12.圆的参数方程.八、圆锥曲线(18课时,7个)1椭圆及其标准方程;2.椭圆的简单几何性质;3.椭圆的参数方程;4.双曲线及其标准方程;5.双曲线的简单几何性质;6.抛物线及其标准方程;7.抛物线的简单几何性质.九、(B)直线、平面、简单何体(36课时,28个)1.平面及基本性质;2.平面图形直观图的画法;3.平面直线;4.直线和平面平行的判定与性质;5,直线和平面垂直的判与性质;6.三垂线定理及其逆定理;7.两个平面的位置关系;8.空间向量及其加法、减法与数乘;9.空间向量的坐标表示;10.空间向量的数量积;11.直线的方向向量;12.异面直线所成的角;13.异面直线的公垂线;14异面直线的距离;15.直线和平面垂直的性质;16.平面的法向量;17.点到平面的距离;18.直线和平面所成的角;19.向量在平面内的射影;20.平面与平面平行的性质;21.平行平面间的距离;22.二面角及其平面角;23.两个平面垂直的判定和性质;24.多面体;25.棱柱;26.棱锥;27.正多面体;28.球.十、排列、组合、二项式定理(18课时,8个)1.分类计数原理与分步计数原理.2.排列;3.排列数公式’4.组合;5.组合数公式;6.组合数的两个性质;7.二项式定理;8.二项展开式的性质.十一、概率(12课时,5个)1.随机事件的概率;2.等可能事件的概率;3.互斥事件有一个发生的概率;4.相互独立事件同时发生的概率;5.独立重复试验.选修Ⅱ(24个)十二、概率与统计(14课时,6个)1.离散型随机变量的分布列;2.离散型随机变量的期望值和方差;3.抽样方法;4.总体分布的估计;5.正态分布;6.线性回归.十三、极限(12课时,6个)1.数学归纳法;2.数学归纳法应用举例;3.数列的极限;4.函数的极限;5.极限的四则运算;6.函数的连续性.十四、导数(18课时,8个)1.导数的概念;2.导数的几何意义;3.几种常见函数的导数;4.两个函数的和、差、积、商的导数;5.复合函数的导数;6.基本导数公式;7.利用导数研究函数的单调性和极值;8函数的值和最小值.十五、复数(4课时,4个)1.复数的概念;2.复数的加法和减法;3.复数的乘法和除法答案补充高中数学有130个知识点，从前一份试卷要考查90个知识点，覆盖率达70%左右，而且把这一项作为衡量试卷成功与否的标准之一.这一传统近年被打破，取而代之的是关注思维，突出能力，重视思想方法和思维能力的考查.现在的我们学数学比前人幸福啊!!相信对你的学习会有帮助的，祝你成功!答案补充一试全国高中数x 的一试竞赛大纲，完全按照全日制中学《数学教学大纲》中所规定的教学要求和内容，即高考所规定的知识范围和方法，在方法的要求上略有提高，其中概率和微积分初步不考。
