基于Matlab弧面分度凸轮的建模
- 格式：pdf
- 大小：692.19 KB
- 文档页数：5
下载文档原格式
合集下载
基于MATLAB的凸轮轮廓线设计与运动仿真毕业设计
(此文档为word格式，下载后您可任意编辑修改！)第1章绪论1.1 机构学的现状与发展1.1.1 机构学的概况机构学是以运动几何学和力学为主要理论基础，以数学分析为主要手段，对各类机构进行运动和动力分析与综合的学科。
机构学为创造新的机器和进行机械发明与改革提供正确有效的理论和方法，以设计出更经济合理、更先进的机械设备，来满足生产发展和人们生活的需求。
机构学的发展将直接影响到机械工业各类产品的工作性能以及许多行业生产设备的机械化和自动化程度。
机构学作为机械工程技术科学中的一门主要基础学科，近年来由于机电一体化高技术科学特别是工业机器人与特种机器人的发展对机构学理论和技术上的要求，使机构学学科达到了一个崭新的阶段。
在国际学术讨论会上，各国科学家一致认为它有如旭日东升，正显出其无比强大的生命力。
机构学一方面由简单的运动分析与综合向复杂的运动分析与综合方面发展，另一方面也由机构运动学向机构动力分析与综合方向发展，研究机构系统的合理组成的方法及其判据，分析研究机器在传递运动、力和做功过程中出现的各种问题。
机构精度问题也相应地由静态分析走向动态分析。
机构联结件的间隙在高速运转时有不容忽视的影响，因而需要研究机构间间隙、摩擦、润滑与冲击引起的机构变形、稳态与非稳态下的动态响应和过渡过程问题。
在惯性力作用下，由于机构上刚度薄弱环节的弹性变形，由此研究以振动理论多自由度模态化、线性与非线性、随机的功率谱与载荷谱等为分析手段和方法而形成的运动弹性动力学问题，以及视整个机构系统为柔性的多柔体系统动力学和逆动力学分析、综合及控制问题。
它是把整个机构看成是由多刚体组成的多刚体动力学、结构动力学及自动控制等学科发展的交叉边缘学科。
由多种、多个构件组成的机构称为组合机构。
组合机构与机构系统组成理论的发展使机构学已成为重型、精密及各种复合机械和智能机械、仿生机械、机器人等高技术科学的设计基础理论学科。
1.1.2机构学的现状（1）平面与空间连杆机构的结构理论研究研究机构的结构单元及机构拓扑结构特征，如主动副存在准则、活动度类型及其判定、拓扑结构的同构判定、消极子运动链判定等。
基于MATLAB的凸轮轮廓曲线设计
tulun=@(x) (200*((x./pi)-1/(2*pi)*sin(2*x))).*(x>=0&x<= pi)+(-200/pi*x+400).*(x>=pi&x<=2*pi); i=1; （下转第174页）
《科技传播》 2011•8（上） 176
应用技术 Applied Technology
4 结论
在隧道施工的整个工程中 ， 一旦发生灾害性事故 ， 不仅延误 工期、大幅度提高工程费用 ， 同时如处理不当 ， 还会遗留工程质 量后患 ， 甚至出现人生伤害 ， 但由于隧道施工地质条件的不断变 化， 当一些不能预计到的突发现象发生时 ， 应采取各种应变措施 ， 按照安全、优质、高效、投资节约的总原则对事故进行处理 ， 这 就是动态施工管理的本质含义。 在软弱围岩中的隧道施工 ， 导致塌方的原因虽然是多种多样 的， 但如果在施工管理和技术上加以认真地改善 ， 遵循“先预探、 管超前、预注浆、短进尺、弱爆破、强支护、早封闭、勤量测、 图 23.1.3 差动变压器结构示意图 图 3 差动变压器原理图 锚杆 快反馈、紧衬砌”的施工原则 ， 加强超前地质预报和监控量测信 当铁芯由中心向上端移动时， L1 和 L2 的电感耦合增加， e2 增大， 而 L1 和 L3 的电感耦合减小， 锚杆是隧道施工过程中维护围岩稳定 ， 保证施工安全的重要 息反馈 ， 及时调整设计参数 ， 就会使塌方事故得到有效控制 ， 因 e3 变小，故两个次级绕组便产生电压差△e（△e=e2—e3） ，此输出电压△e 与铁芯的位移在一定范 支护手段之一 ， 施工完成后 ， 在一定程度上还可以作为永久支护 此要更多地从施工方面去分析塌方的原因 ， 如由于抢工期心切而 围内成线性关系，因此差动变压器就将铁芯的位移量转换成电量。当铁芯由中心向下移动时，L1 结构的一部分发挥作用。对于软弱围岩中的隧道施工 ， 锚杆能有 忽略地质因素 ； 片面追求进尺而不及时封闭断面或不及时跟进衬 与 L3 的电感耦合增大， e3 增大，而 L1 与 L2 的耦合减小，e2 变小，故次级输出电压△ e =e3—e2 ， 此输出电压在相位上改变了 180º。在图（四）中，铁芯由中心零点向任一端移动时，次级输出电压 效限制约束围岩变形 ， 制止围岩强度的恶化 ， 其加固作用 ， 可使 砌； 在出现塌方迹象时不采取或被动采取辅助措施 ； 破碎岩层中 △e 均为交流，若△ e 直接使用电压表测量，只能反映位移的大小，不能反映方向，为了达到消除 围岩中松动区的节理裂隙及破裂面等得以联结 ， 使锚固区围岩形 不设超前支护或支护不到位等 ， 都是造成塌方或是塌方扩大的原 零点残余电压及辨别方向的目的，必须经过放大和相位调节，才能得到正、负极性的输出电压，从 成整体加固带 ， 大幅提高围岩强度 ， 同时锚杆群可有效提高层状 因。 而判断出铁芯的正、负方向。 围岩的层间结合力 ， 以提高隧道的整体稳定性。 若忽略涡流损耗、铁损等因素，差动变压器的输出由下式确定： 参考文献 锚杆施工中 ， 要合理确定锚杆参数 ， 充分发挥群锚作用 ， 避 若铁芯处于中间平衡位置 [1]关宝树，杨其新.地下工程概论[M].成都：西南交通大学 免不配置垫板、布置不合理、砂浆充填不密实及长锚短打等现象 △e = 0 出版社，2001. 若铁芯上升时 发生。 [2]铁道部.铁路隧道工程施工技术指南（TZ 204-2008）[S]. ui 3.2 塌方处理效果 △e = 2ω△M 北京：中国铁道出版社，2008. 2 2 R p + ( ωL p ) 本次塌方处理从 7 月 24 日开始 ， 至 9 月底处理完毕 ， 整个处 [3]铁道部.铁路隧道喷锚构筑法技术规范[S].北京：中国铁 理过程历时 2 个多月 ， 实际注浆量 224.0m3。注浆完毕后 ， 开挖情 道出版社，2002. 若铁芯下降时 况显示 ， 坍体泥岩破碎体及土石松散体相当于凝结成一个低标号 [4]铁路工程施工技术手册——隧道（上、下册）[M].北京： ui ，经量测资料分析 ， 的混凝土整体 ， 隧道拱部也具备了自稳能力 中国铁道出版社，2003. △e = -2ω△M
基于MATLAB的凸轮设计
基于MATLAB的凸轮设计凸轮是一种用于转动机件的机械元件，常用于驱动一些运动部件做往复运动或者周期性运动。
在机械设计中，通过凸轮的设计可以实现复杂的运动路径，以及具有特定速度和加速度要求的运动。
MATLAB是一种强大的数学计算和编程环境，可以用于进行科学计算、数据分析和算法开发。
在凸轮设计中，MATLAB可以用于凸轮曲线的生成、设计和优化。
本文将介绍如何基于MATLAB进行凸轮设计。
在凸轮设计中，最重要的是凸轮曲线的生成。
凸轮曲线是一个由数据点组成的模板，通过插值或者数值逼近的方法可以生成一个光滑的凸轮曲线。
在 MATLAB 中，可以使用插值函数 interp1 或者曲线拟合函数polyfit 进行凸轮曲线的生成。
具体步骤如下：1.定义凸轮的设计参数，例如凸轮的半径、凸轮转动的角度范围等；2.根据凸轮的设计参数，生成一些数据点，这些数据点可以通过数学计算或者几何建模等方式得到；3. 使用插值函数 interp1 或者曲线拟合函数 polyfit 对这些数据点进行插值或者拟合，得到一个平滑的曲线；4.根据凸轮转动的角度范围，生成一系列角度的数据点；5. 使用插值函数 interp1 或者曲线拟合函数 polyval 对这些角度的数据点进行插值或者拟合，得到一系列对应的曲线坐标点；6.将这些坐标点绘制成凸轮曲线，并进行可视化。
除了凸轮曲线的生成，MATLAB 还可以用于凸轮的设计和优化。
凸轮设计包括凸轮的尺寸设计、运动路径设计等。
在 MATLAB 中，可以使用优化函数 fmincon 或者遗传算法函数 ga 进行凸轮设计的优化，以获得符合设计要求的凸轮参数。
具体步骤如下：1.定义凸轮的设计变量和目标函数。
设计变量可以是凸轮的尺寸参数，例如凸轮半径、凸轮高度等；目标函数可以是凸轮的运动路径误差、速度误差等。
2.定义凸轮的约束条件。
约束条件可以是凸轮的尺寸范围、速度和加速度的限制等。
3. 使用优化函数 fmincon 或者遗传算法函数 ga 对凸轮的设计变量进行优化，以使目标函数最小化或者最大化。
基于MATLAB和SolidWorks的平行分度凸轮设计
基于MATLAB和SolidWorks的平行分度凸轮设计
蔡玉强;赵长庆
【期刊名称】《机械工程与自动化》
【年(卷),期】2018(000)002
【摘要】根据反转法得到平行分度凸轮的廓线方程,避免了繁琐的计算.分析了平行分度凸轮的设计参数,并利用MATLAB语言编程,绘制出凸轮轮廓曲线,将得到的数据文件通过.txt的方式导入SolidWorks进行参数化实体建模.这种方法能够很快地得到凸轮廓型,为平行分度凸轮的设计提供了一种新的思路.
【总页数】3页(P70-72)
【作者】蔡玉强;赵长庆
【作者单位】华北理工大学机械工程学院,河北唐山 063210;华北理工大学机械工程学院,河北唐山 063210
【正文语种】中文
【中图分类】TH132.47;TP391.7
【相关文献】
1.基于MATLAB和SolidWorks软件的共轭凸轮设计及运动仿真 [J], 李艳莉;张海燕;李茂斌
2.基于MATLAB和Solidworks的弧面凸轮设计及3D建模 [J], 袁伟
3.基于MATLAB和Creo的平行分度凸轮机构的设计 [J], 蔡玉强;姚佳
4.基于MATLAB和Creo的三片式平行分度凸轮的设计 [J], 李建功;冯敦敦
5.基于MATLAB和SolidWorks的弧面分度凸轮三维实体建模 [J], 王建林;张丹丹
因版权原因，仅展示原文概要，查看原文内容请购买。
matlab凸轮轮廓设计及仿真说明书
1.2
滚子半径
=40
1
第一章：工作意义
1.1本次课程设计意义1.2已知条件
第二章：工作设计过程5
2.1:设计思路5
2.2:滚子从动件各个阶段相关方程6
2.பைடு நூலகம்：盘型凸轮理论与实际轮廓方程7
工工“..A作……'A程过A程
3.1:滚子从动件各各阶段MATLAB程序编制…*8
3.2:凸轮的理论实际运动仿真程序编制
12
第四章…？： •……
运行结果
17
4.1：滚子运动的位移图17
4.2：滚子运动的速度图17
4.3：滚子运动的加速度图，局部加速度图……18—
44滚子运动的仿真图19
4.5：滚子运动的理论与实际轮廓图20
6.1：参考文献
22
第一章：工作意义
1.1 本次课程设计意义凸轮是一个具有曲线轮廓或凹槽的构件， 一般为主动件， 作等速回转运动或往复直线运动。与凸轮轮廓接触，并传递 动力和实 现预定的运动规律的构件， 一般做往复直线运动或 摆动，称为从动件。凸轮机构在应用中的基本特点在于能使
程和回程。凸轮轮廓曲线决定于位移曲线的
形状。在某些机械中，位移曲线由工艺过程决定，但一般
情况下只有行程和对应的凸轮转角根据工作需要决定，而
曲线的形状则由设计者选定，可以有多种运动规律。传统的凸轮运动
规律有等速、等加速-等减速、余弦加速度和正弦 加速度等。等速运 动规律因有速度突变，会产生强烈的刚性 冲击，只适用于低速。等加 速-等减速和余弦加速度也有加速度突变，会引起柔性冲击，只适用
思路口。因此，基于MATLAB件进行凸轮机构的解析法设计，可以解
决设计工作量大的问题。
本此课程设计基于MATLAB软件进行凸轮轮廓曲线的 解析法 设计，并 对的运动规律凸轮进行仿真，其具体方法为首先精确地 计算出轮 廓线
滚子半径
=40
1
第一章：工作意义
1.1本次课程设计意义1.2已知条件
第二章：工作设计过程5
2.1:设计思路5
2.2:滚子从动件各个阶段相关方程6
2.பைடு நூலகம்：盘型凸轮理论与实际轮廓方程7
工工“..A作……'A程过A程
3.1:滚子从动件各各阶段MATLAB程序编制…*8
3.2:凸轮的理论实际运动仿真程序编制
12
第四章…？： •……
运行结果
17
4.1：滚子运动的位移图17
4.2：滚子运动的速度图17
4.3：滚子运动的加速度图，局部加速度图……18—
44滚子运动的仿真图19
4.5：滚子运动的理论与实际轮廓图20
6.1：参考文献
22
第一章：工作意义
1.1 本次课程设计意义凸轮是一个具有曲线轮廓或凹槽的构件， 一般为主动件， 作等速回转运动或往复直线运动。与凸轮轮廓接触，并传递 动力和实 现预定的运动规律的构件， 一般做往复直线运动或 摆动，称为从动件。凸轮机构在应用中的基本特点在于能使
程和回程。凸轮轮廓曲线决定于位移曲线的
形状。在某些机械中，位移曲线由工艺过程决定，但一般
情况下只有行程和对应的凸轮转角根据工作需要决定，而
曲线的形状则由设计者选定，可以有多种运动规律。传统的凸轮运动
规律有等速、等加速-等减速、余弦加速度和正弦 加速度等。等速运 动规律因有速度突变，会产生强烈的刚性 冲击，只适用于低速。等加 速-等减速和余弦加速度也有加速度突变，会引起柔性冲击，只适用
思路口。因此，基于MATLAB件进行凸轮机构的解析法设计，可以解
决设计工作量大的问题。
本此课程设计基于MATLAB软件进行凸轮轮廓曲线的 解析法 设计，并 对的运动规律凸轮进行仿真，其具体方法为首先精确地 计算出轮 廓线
基于MATLAB软件的凸轮轮廓曲线设计_
基于ＭＡＴＬＡＢ软件的凸轮轮廓曲线设计摘要：以偏置移动从动件盘形凸轮为例，基于ＭＡＴＬＡＢ软件对凸轮轮廓曲线进展了解析法设计．绘制出轮廓曲线。
运行结果说明：在从动件运动规律确定的情况下，利用ＭＡＴＬＡＢ软件以很方便、快捷地得到凸轮的轮廓曲线。
关键词：凸轮机构；凸轮轮廓曲线；ＭＡＴＬＡＢ；解析法前言凸轮轮廓曲线的设计，一般可分为图解法和解析法．利用图解法能比拟方便地绘制出各种平面凸轮的轮廓曲线．但这种方法仅适用于比拟简单的构造，用它对复杂构造进展设计那么比拟困难，而且利用图解法进展构造设计，作图误差较大，对一些精度要求高的构造不能满足设计要求。
解析法可以根据设计要求，通过推导机构中各局部之间的几何关系，建立相应的方程，准确地计算出轮廓线上各点的坐标，然后把凸轮的轮廓曲线准确地绘制出来．但是，当从动件运动规律比拟复杂时，利用解析法获得凸轮的轮廓曲线的工作量比拟大．而ＭＡＴＬＡＢ软件提供了强大的矩阵处理和绘图功能，具有核心函数和工具箱．其编程代码接近数学推导公式，简洁直观，操作简易，人机交互性能好，且可以方便迅速地用三维图形、图像、声音、动画等表达计算结果、拓展思路［１］。
因此，基于ＭＡＴＬＡＢ软件进展凸轮机构的解析法设计，可以解决设计工作量大的问题。
本文基于ＭＡＴＬＡＢ软件进展凸轮轮廓曲线的解析法设计，利用?机械原理?课程的计算机辅助教学，及常用机构的计算机辅助设计．其具体方法为首先准确地计算出轮廓线上各点的坐标，然后运用ＭＡＴＬＡＢ绘制比拟准确的凸轮轮廓曲线。
1 设计的意义与条件1.1意义凸轮机构是由具有曲线轮廓或凹槽的构件，通过高副接触带动从动件实现预期运动规律的一种高副机构，它广泛地应用于各种机械，特别是自动机械、自动控制装置和装配生产线中，是工程实际中用于实现机械化和自动化的一种常用机构。
所以，在凸轮的加工中，准确确实定凸轮的轮廓，这对于保证凸轮所带动从动件的运动规律是尤为重要的。
1.2条件偏置移动从动件盘形凸轮设计条件〔图1〕:凸轮作逆时针方向转动,从动件偏置在凸轮轴心的右边从动件在推程作等加速/等减速运动,在回程作余弦加速度运动基圆半径rb = 40 mm，滚子半径rt = 10mm，推杆偏距e = 15 mm，推程升程h = 50 mm，推程运动角ft = 100度，远休止角fs = 60度回程运动角fh = 90度，推程许用压力角alp = 35度。
弧面分度凸轮的三维建模
建立数学模型 由凸轮和转盘的相对位置和啮合关系建 立如图 ’ 所示的四套右手坐标系 ( + ) 。
" , # 面对 !’ 箭头看， 滚子在 " 处垂直于 !’ 轴的截面 " - # 面对 #! 箭头看， 通过凸轮中心 $! 并垂直于 #! 半径为 "%! 的凸轮截面 ! 来稿日期： ’..> 8 !. 8 ’.
角速度比 & "% ’ "# ( )! （ ,$" # # ./0,!! ） #" 1 + （ !! 023,!! ） *（ ! + ,） ! , , ) ! ! + , !! ） ,$" 4 ! + , !! ） ［ （ # - )（ ./0 ］* （ #" 1 + ［ % - !! 023（ ! + ,） ) ! , , ) #!$"; ! ;#%!" )! （ ,$" # # ./0,!! ） #" 1 + （ , + !! 023,!! ） *（ ! + ,） ! , ,
凸轮转角 ! !"; !;#$" #$ "; !;#!$"
转盘相应的角位移 # "
图 ) 模型构造流程图
各个滚子的起始位置角如表 % ： #! 为滚子的起始位置角， 表 % 滚子的起始位置角
滚子代号 #! 5/6 # !’* 5/6 % ! ’ -* 5/6 ) - )! ’ *
构造过程如下： 由 A;BC;D 程 序 得 到 如图 % 所 #N、 %O、 %N、 )O（ 示） 四组曲面的点云坐标， 将 这 些 数 据 导 入 9:;<=P >;?=，得到如图 , 所示的 结果。
" , # 面对 !’ 箭头看， 滚子在 " 处垂直于 !’ 轴的截面 " - # 面对 #! 箭头看， 通过凸轮中心 $! 并垂直于 #! 半径为 "%! 的凸轮截面 ! 来稿日期： ’..> 8 !. 8 ’.
角速度比 & "% ’ "# ( )! （ ,$" # # ./0,!! ） #" 1 + （ !! 023,!! ） *（ ! + ,） ! , , ) ! ! + , !! ） ,$" 4 ! + , !! ） ［ （ # - )（ ./0 ］* （ #" 1 + ［ % - !! 023（ ! + ,） ) ! , , ) #!$"; ! ;#%!" )! （ ,$" # # ./0,!! ） #" 1 + （ , + !! 023,!! ） *（ ! + ,） ! , ,
凸轮转角 ! !"; !;#$" #$ "; !;#!$"
转盘相应的角位移 # "
图 ) 模型构造流程图
各个滚子的起始位置角如表 % ： #! 为滚子的起始位置角， 表 % 滚子的起始位置角
滚子代号 #! 5/6 # !’* 5/6 % ! ’ -* 5/6 ) - )! ’ *
构造过程如下： 由 A;BC;D 程 序 得 到 如图 % 所 #N、 %O、 %N、 )O（ 示） 四组曲面的点云坐标， 将 这 些 数 据 导 入 9:;<=P >;?=，得到如图 , 所示的 结果。
凸轮的matlab绘制
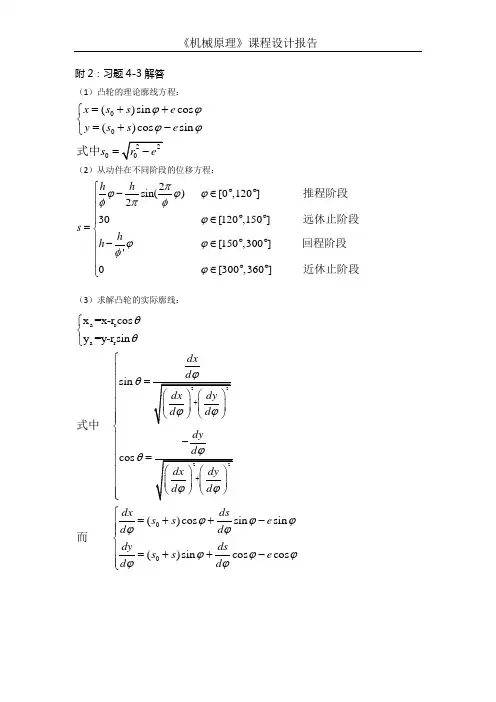
附2：习题4-3解答（1）凸轮的理论廓线方程：000()sin cos ()cos sin x s s e y s s e s ϕϕϕϕ=++⎧⎨=+-⎩=式中 （2）从动件在不同阶段的位移方程：2sin()[0,120]230[120,150][150,300]'0[300,360]h h s h h πϕϕϕφπφϕϕϕφϕ⎧-∈︒︒⎪⎪∈︒︒⎪=⎨⎪-∈︒︒⎪⎪∈︒︒⎩推程阶段远休止阶段回程阶段近休止阶段（3）求解凸轮的实际廓线：a r a r 00x =x-r cos y =y-r sin sin cos ()cos sin sin ()sin cos cos dx dy dxds s s e d d dy ds s s e d d θθθθϕϕϕϕϕϕϕϕϕϕ⎧⎨⎩⎧⎪=⎪⎪⎪⎪⎪⎨⎪-⎪=⎪⎪⎪⎪⎩⎧=++-⎪⎪⎨⎪=++-⎪⎩式中而同样，由于位移s 与从动件所处的运动阶段有关，所以有：2cos()[0,120]0[120,150]s [150,300]'0[300,360]h hd hd πϕϕφφφϕϕϕφϕ⎧-∈︒︒⎪⎪∈︒︒⎪=⎨⎪∈︒︒⎪⎪∈︒︒⎩推程阶段远休止阶段回程阶段近休止阶段（4）代入已知条件，并用Matlab 语言编程求解，编程代码如下： disp ' ******** 偏置直动滚子从动件盘形凸轮设计 ********' disp '已知条件:'disp ' 凸轮作逆时针方向转动,从动件偏置在凸轮轴心的右边'disp ' 从动件在推程作摆线运动规律运动,在回程作等速运动规律运动' ro = 50;rr = 10;e = 12;h = 30;ft = 120;fs = 30;fh = 150;fprintf (1,' 基圆半径 ro = %3.4f mm \n',ro) fprintf (1,' 滚子半径 rr = %3.4f mm \n',rr) fprintf (1,' 推杆偏距 e = %3.4f mm \n',e) fprintf (1,' 推程行程 h = %3.4f mm \n',h) fprintf (1,' 推程运动角 ft = %3.4f 度 \n',ft) fprintf (1,' 远休止角 fs = %3.4f 度 \n',fs) fprintf (1,' 回程运动角 fh = %3.4f 度 \n',fh) hd = pi / 180;du = 180 / pi; so = sqrt( ro^2 - e^2 ); d1 = ft + fs;d2 = ft + fs + fh; disp ' 'disp '计算过程和输出结果:'disp ' 1-1 推程(摆线运动规律运动)' s = zeros(ft);ds = zeros(ft);d2s = zeros(ft); for f = 1 : fts(f) = h * f / ft - h * sin(2 * pi * f / ft) / (2 * pi);s = s(f);ds(f) = h / (ft * hd) - h / (ft * hd) * cos(2 * pi * f / ft);ds = ds(f); d2s(f) = 2 * pi * h / (ft * hd) ^ 2 * sin(2 * pi * f / ft);d2s = d2s(f); enddisp ' 1-2 回程(等速运动规律运动)' s = zeros(fh);ds = zeros(fh);d2s = zeros(fh); for f = d1 : d2s(f) = h - h * (f-150) / fh; s = s(f); ds(f) = - h / (fh * hd);ds = ds(f); d2s(f) = 0;d2s = d2s(f); enddisp ' 2- 计算凸轮理论廓线与实际廓线的直角坐标'n = 360;s = zeros(n);ds = zeros(n);r = zeros(n);rp = zeros(n);x = zeros(n);y = zeros(n);dx = zeros(n);dy = zeros(n);xx = zeros(n);yy = zeros(n);xa = zeros(n);ya = zeros(n);xxa = zeros(n);yya = zeros(n);for f = 1 : nif f <= fts(f) = h * f / ft - h * sin(2 * pi * f / ft) / (2 * pi);s = s(f);ds(f) = h /(ft * hd) - h / (ft * hd) * cos(2 * pi * f / ft); ds = ds(f);elseif f > ft & f <= d1s = h;ds = 0;elseif f > d1 & f <= d2s(f) = h - h * (f-150) / fh; s = s(f);ds(f) = - h / (fh * hd);ds = ds(f);elseif f > d2 & f <= ns = 0;ds = 0;endxx(f) = (so + s) * sin(f * hd) + e * cos(f * hd); x = xx(f);yy(f) = (so + s) * cos(f * hd) - e * sin(f * hd); y = yy(f);dx(f) = (ds - e) * sin(f * hd) + (so + s) * cos(f * hd); dx = dx(f);dy(f) = (ds - e) * cos(f * hd) - (so + s) * sin(f * hd); dy = dy(f);xxa(f) = x + rr * dy / sqrt(dx ^ 2 + dy ^ 2);xa = xxa(f);yya(f) = y - rr * dx / sqrt(dx ^ 2 + dy ^ 2);ya = yya(f);r(f) = sqrt (x ^2 + y ^2 );rp(f) = sqrt (xa ^2 + ya ^2 );enddisp ' 2-1 推程(摆线运动规律运动)'disp ' 凸轮转角理论x 理论y 实际x 实际y' for f = 10 : 10 :ftnu = [f xx(f) yy(f) xxa(f) yya(f)];disp(nu)enddisp ' 2-2 回程(等速运动规律运动)'disp ' 凸轮转角理论x 理论y 实际x 实际y' for f = d1 : 10 : d2nu = [f xx(f) yy(f) xxa(f) yya(f)];disp(nu)enddisp ' 2-3 凸轮轮廓向径'disp ' 凸轮转角理论r 实际r'for f = 10 : 10 : nnu = [f r(f) rp(f)];disp(nu)enddisp '绘制凸轮的理论轮廓和实际轮廓:'plot(xx,yy,'r-.') % 理论轮廓(红色,点划线)axis ([-(ro+h-10) (ro+h+10) -(ro+h+10) (ro+rr+10)]) % 横轴和纵轴的下限和上限axis equal % 横轴和纵轴的尺度比例相同text(ro+h+3,0,'X') % 标注横轴text(0,ro+rr+3,'Y') % 标注纵轴text(-5,5,'O') % 标注直角坐标系原点title('偏置直动滚子从动件盘形凸轮设计') % 标注图形标题hold on; % 保持图形plot([-(ro+h) (ro+h)],[0 0],'k') % 横轴(黑色)plot([0 0],[-(ro+h) (ro+rr)],'k') % 纵轴(黑色)plot([e e],[0 (ro+rr)],'k--') % 初始偏置位置(黑色,虚线) ct = linspace(0,2*pi); % 画圆的极角变化范围plot(ro*cos(ct),ro*sin(ct),'g') % 基圆(绿色)plot(e*cos(ct),e*sin(ct),'c--') % 偏距圆(蓝绿色,虚线)plot(e + rr*cos(ct),so + rr*sin(ct),'y') % 滚子圆(黄色)plot(xxa,yya,'b') % 实际轮廓(蓝色)（5）求解凸轮理论廓线和实际廓线坐标值如下：******** 偏置直动滚子从动件盘形凸轮设计********已知条件:凸轮作逆时针方向转动,从动件偏置在凸轮轴心的右边从动件在推程作摆线运动规律运动,在回程作等速运动规律运动基圆半径ro = 50.0000 mm滚子半径rr = 10.0000 mm推杆偏距 e = 12.0000 mm推程行程h = 30.0000 mm推程运动角ft = 120.0000 度远休止角fs = 30.0000 度回程运动角fh = 150.0000 度计算过程和输出结果:1-1 推程(摆线运动规律运动)1-2 回程(等速运动规律运动)计算凸轮理论廓线与实际廓线的直角坐标2-1 推程(摆线运动规律运动)凸轮转角理论x 理论y 实际x 实际y10.0000 20.2659 45.8284 16.5674 36.537520.0000 28.1734 42.3200 23.8536 33.301230.0000 36.0243 38.3959 31.4216 29.518140.0000 44.1625 33.9622 39.1460 25.311550.0000 52.6430 28.5078 46.7788 20.407760.0000 61.0261 21.3770 53.9159 14.345370.0000 68.4036 12.1267 59.9368 6.8057 80.0000 73.6533 0.8019 64.1128 -2.1946 90.0000 75.8133 -12.0000 65.8180 -12.3064 100.0000 74.4098 -25.3056 64.6887 -22.9602 110.0000 69.5921 -38.0996 60.7079 -33.5092 120.0000 62.0165 -49.6616 54.2107 -43.41102-2 回程(等速运动规律运动)凸轮转角理论x 理论y 实际x 实际y 150.0000 28.8770 -74.0165 25.2424 -64.7004 160.0000 14.9014 -76.0270 14.3851 -66.0404 170.0000 1.1258 -75.4900 2.4259 -65.5749 180.0000 -12.0000 -72.5386 -8.9229 -63.0238 190.0000 -24.0666 -67.3832 -19.3110 -58.5864 200.0000 -34.7179 -60.3010 -28.4390 -52.5180 210.0000 -43.6616 -51.6242 -36.0665 -45.1192 220.0000 -50.6772 -41.7260 -42.0190 -36.7223 230.0000 -55.6208 -31.0065 -46.1908 -27.6786 240.0000 -58.4280 -19.8770 -48.5462 -18.3440 250.0000 -59.1126 -8.7451 -49.1177 -9.0659 260.0000 -57.7635 1.9999 -48.0018 -0.1704 270.0000 -54.5386 12.0000 -45.3524 8.0487 280.0000 -49.6567 20.9409 -41.3723 15.3401 290.0000 -43.3865 28.5615 -36.3031 21.5028 300.0000 -36.0357 34.6616 -30.4141 26.39132-3 凸轮轮廓向径凸轮转角理论r 实际r10.0000 50.1094 40.118220.0000 50.8402 40.962930.0000 52.6498 43.111940.0000 55.7114 46.616350.0000 59.8663 51.036660.0000 64.6619 55.791770.0000 69.4702 60.322080.0000 73.6577 64.150490.0000 76.7571 66.9586100.0000 78.5951 68.6426110.0000 79.3387 69.3420120.0000 79.4501 69.4501130.0000 79.4501 69.4501140.0000 79.4501 69.4501150.0000 79.4501 69.4501160.0000 77.4736 67.5889170.0000 75.4984 65.6197180.0000 73.5245 63.6524190.0000 71.5521 61.6869200.0000 69.5812 59.7237210.0000 67.6121 57.7628220.0000 65.6448 55.8044230.0000 63.6795 53.8489240.0000 61.7165 51.8964250.0000 59.7559 49.9474260.0000 57.7981 48.0021270.0000 55.8432 46.0611280.0000 53.8916 44.1247290.0000 51.9438 42.1935300.0000 50.0000 40.2681310.0000 50.0000 40.0000320 50 40330.0000 50.0000 40.0000340 50 40350.0000 50.0000 40.0000360.0000 50.0000 40.0000（6）由Matlab绘制的实际图轮廓线和理论图轮廓线如下：图例：绿色——基圆；红色点划线——理论廓线；蓝色——实际廓线；黄色——滚子圆；蓝绿色，虚线——偏距圆；黑色，虚线——初始偏置位置；。
基于虚拟技术的弧面分度凸轮机构研究
限元 软件 ＭＡ ＲＣ对分 度盘 与 凸轮 啮合 处进 行 了应 力 分析 ， 到 所设 计 的弧 面分度 凸轮机 构的 全 得
面分析 结果 ， 为机 构优 化和 制造提 供 了重要 依 据 。
关键 词 ： 面分度 凸轮 ； 弧 虚拟 技 术 ； 力 学分析 ； 限元 分析 动 有
中图分 类号 ： Ｈｌ ２ Ｔ ｌ 文 献标识 码 ： Ａ 文 章编 号 ：６ ２ ６ ６ ２ ０ ）３—０ ２ —０ １ ７ —１ １ （０ ７ １ ０４ ４
高校 和企 业 在 弧 面 分 度 凸轮 机 构 的理 论 研 究 ＿ 、 １ Ｊ
结 构设 计制 造 与检 测 等 方 面 都做 了大 量 的研 究 工 作， 经过 ２ 年 的努 力 ， ０多 目前 已在 设计 、 测 、 检 制造 等方 面取得 了丰硕 的成 果 。 目前 研 究 主要 针 对该 机构 的数学 建模 和三 维
面分 度机 构 中各 坐标 系 ， 对 坐标 系为 Ｏ１ Ｙ ｚ 绝 ｚｌ１ ｌ 与 机 架 固 连 为 固 定 性 坐 标 ， 相 对 坐 标 系
Ｏ ｚ Ｙ 、 ３ ３３ ３Ｏ ２ ２２ ２Ｏ ｚ Ｙ 、 ｚ ｚ
一一分别对应弧面凸 ｚ
基金项目： 浙江工业大学机械制造及 自动化省部共建教育部重点实验室 资助 作者 简介： 王 莉 （９ １ ， ， １８ 一）女 陕西咸阳人 ， 浙江工业大学硕 士研究 生， 主要研究方 向为计算机辅助设计与工程结 构分析 。
（ 图 ４所示 ） 如 。
接着 通 过坐标 变换 矩 阵 ， 得第 ｉ 求 个滚 子 的坐标 系 Ｏｒ ｒ 与弧 面 凸轮 固连 的坐 标 系 ０２． ２ ２ ｉｉ ｚ ＸＹ ａ ｚ 之 Ｔ ２
间 的关 系为 ：
机构 ， 与棘轮机构 、 槽轮机构等传统 的间歇分度机 构相 比 ， 有分 度精 度高 、 力学 特性好 、 具 动 承载能 力 大等优 点 。该机 构 已广 泛 应 用 于各 种 轻 工 自动化
面分析 结果 ， 为机 构优 化和 制造提 供 了重要 依 据 。
关键 词 ： 面分度 凸轮 ； 弧 虚拟 技 术 ； 力 学分析 ； 限元 分析 动 有
中图分 类号 ： Ｈｌ ２ Ｔ ｌ 文 献标识 码 ： Ａ 文 章编 号 ：６ ２ ６ ６ ２ ０ ）３—０ ２ —０ １ ７ —１ １ （０ ７ １ ０４ ４
高校 和企 业 在 弧 面 分 度 凸轮 机 构 的理 论 研 究 ＿ 、 １ Ｊ
结 构设 计制 造 与检 测 等 方 面 都做 了大 量 的研 究 工 作， 经过 ２ 年 的努 力 ， ０多 目前 已在 设计 、 测 、 检 制造 等方 面取得 了丰硕 的成 果 。 目前 研 究 主要 针 对该 机构 的数学 建模 和三 维
面分 度机 构 中各 坐标 系 ， 对 坐标 系为 Ｏ１ Ｙ ｚ 绝 ｚｌ１ ｌ 与 机 架 固 连 为 固 定 性 坐 标 ， 相 对 坐 标 系
Ｏ ｚ Ｙ 、 ３ ３３ ３Ｏ ２ ２２ ２Ｏ ｚ Ｙ 、 ｚ ｚ
一一分别对应弧面凸 ｚ
基金项目： 浙江工业大学机械制造及 自动化省部共建教育部重点实验室 资助 作者 简介： 王 莉 （９ １ ， ， １８ 一）女 陕西咸阳人 ， 浙江工业大学硕 士研究 生， 主要研究方 向为计算机辅助设计与工程结 构分析 。
（ 图 ４所示 ） 如 。
接着 通 过坐标 变换 矩 阵 ， 得第 ｉ 求 个滚 子 的坐标 系 Ｏｒ ｒ 与弧 面 凸轮 固连 的坐 标 系 ０２． ２ ２ ｉｉ ｚ ＸＹ ａ ｚ 之 Ｔ ２
间 的关 系为 ：
机构 ， 与棘轮机构 、 槽轮机构等传统 的间歇分度机 构相 比 ， 有分 度精 度高 、 力学 特性好 、 具 动 承载能 力 大等优 点 。该机 构 已广 泛 应 用 于各 种 轻 工 自动化
弧面分度凸轮三维模型建立
弧面分度凸轮三维模型建立作者：韩先征来源：《数字技术与应用》2012年第01期摘要：从分度凸轮工作侧面的成型机理，探讨了应用三维软件精确成型的方法，详细给出了创建步骤。
系统分析了工作侧面的成型原理，给出了建立关键的空间三维曲线方程计算公式。
关键词：凸轮弧面分度凸轮机构轨迹曲面实体中图分类号：TH132.47 文献标识码：A 文章编号：1007-9416(2012)01-0117-02凸轮在机械机构中的应用非常广泛，如包装设备、医疗设备、内燃机、机械手、数控机床、生产线上比较常见，按照其廓面曲线的形状可以分为平面凸轮和空间凸轮。
弧面分度凸轮（也称为是FERGUSON凸轮）属于空间分度凸轮的一种，空间分度凸轮具有结构紧凑、传动载荷大、定位准确、够够自锁、噪音小、运转可靠等诸多优点。
过去对空间凸轮的研究主要放在工作面形状的设计计算与测量误差分析上，由于空间凸轮工作面形状的复杂性，其设计公式繁杂，计算结果数据量大，限制了在实际加工中的应用。
随着通用三维机械设计软件的普及，利用三维软件设计凸轮并计算加工刀路路径就显得容易和准确。
本文具体介绍了建立弧面分度凸轮模型的方法。
1、目前对空间槽轮凸轮的研究现状弧面分度凸轮机构是一种精密传动机构，因其具有分度数大、分度精度高、定位可靠等优点，被广泛应用于各类自动机械中。
相对于美国、日本等发达国家，我国研究弧面分度凸轮的时间相对较短，而凸轮机构工作廓面的复杂性，使得其设计理论和制造技术相对比较复杂，从而制约了弧面分度凸轮机构的普及。
弧面分度凸轮的结构参数计算的主要是放在对其工作面的形状描述上。
由于该工作面和从动滚子（一般为圆柱面或者圆锥面）是啮合线接触，从严格的理论上讲弧面分度凸轮的工作面是包络面。
该面的形状在工作的分度期间其形状复杂、成型机理抽象、加工困难。
目前对该类凸轮的研究很多，大致分为以下几种类型，(1)对该类凸轮工作廓面的几何描述。
使用到的工具主要是曲面的共扼理论和坐标变换。
基于MATLAB和SolidWorks的弧面分度凸轮三维实体建模
基于MATLAB和SolidWorks的弧面分度凸轮三维实体建
模
王建林;张丹丹
【期刊名称】《包头职业技术学院学报》
【年(卷),期】2012(013)001
【摘要】针对弧面凸轮式自动换刀装置(ATC)用弧面分度凸轮工作廓面的特殊性,以孤面分度凸轮工作轮廓面为基础,提出了一种新的建模方法,应用MATLAB与SolidWorks软件相结合实现ATC用复杂弧面分度凸轮的三维实体建模,同时运用SolidWoks中的COSMOSMotion插件实现运动仿真,验证了设计的正确性.【总页数】3页(P4-6)
【作者】王建林;张丹丹
【作者单位】包头职业技术学院数控技术系,内蒙古包头014030
【正文语种】中文
【相关文献】
1.基于UG NX6.0的弧面分度凸轮三维实体建模与仿真加工 [J], 曹巨江;李龙刚;吕凯归;黎忠炎
2.弧面分度凸轮机构的廓面研究及基于SolidWorks的实体造型 [J], 郑武;熊绮华;尹明富;褚金奎
3.基于SolidWorks滚珠型弧面分度凸轮三维建模及运动仿真研究 [J], 郑锐;罗天鑫;焦禹萃
4.基于SolidWorks弧面分度凸轮的参数化三维实体造型方法 [J], 刘海涛;王好臣;
刘伟洪
5.基于MATLAB和Pro/E的弧面分度凸轮三维实体建模 [J], 李龙刚;曹巨江;李士玉;白银科
因版权原因，仅展示原文概要，查看原文内容请购买。
基于MATLAB和SolidWorks的平行分度凸轮设计
图 １ 几 种 常 用 外 接 平 行 分 度 凸 轮 示 意 图
在间歇运 动 循 环 中，凸 轮 以 角 速 度 ω 匀 速 转 动，
其 中 与 之 啮 合 的 分 度 盘 转 过 的 角 度θ 和 凸 轮 的 自 转 角
度β（β＝ω狋，狋为 时 间 ）存 在 着 如 下 函 数 关 系 ：
θ＝犳（ω狋）．
（华北理工大学 机械工程学院，河北 唐山 ０６３２１０）
摘要：根据反转法得到平行分度凸轮的廓线方程，避免了繁琐的计算。分析了平行分度凸轮的设计参数，并 利用 ＭＡＴＬＡＢ 语言编程，绘制出凸轮轮廓曲 线， 将 得 到 的 数 据 文 件 通 过．ｔｘｔ的 方 式 导 入 ＳｏｌｉｄＷｏｒｋｓ进 行 参数化实体建模。这种方法能够很快地得到凸轮廓型，为平行分度凸轮的设计提供了一种新的思路。 关 键 词 ： 平 行 分 度 凸 轮 ； 轮 廓 曲 线 ； ＭＡＴＬＡＢ；ＳｏｌｉｄＷｏｒｋｓ 中 图 分 类 号 ：ＴＨ１３２．４７∶ＴＰ３９１．７ 文 献 标 识 码 ：Ａ
在这样关系：（γ２犘ｍａｘ＋狉狉２）１ ２ ≤γ犜ｍａｘ，将其代入式（９）得：
ε≥２犿πｃｏｓ－１犪２＋狉犱２２－犪γ狉犱２犘ｍａｘ－狉狉２ ．
（１０）
为保证连续传动令ε＞ １，经过等式变换可得凸轮
实 际 廓 线 最 大 外 径γ犘ｍａｘ应 满 足 ：
γ犘ｍａｘ≥（犪２＋狉犱２－２犪狉犱ｃｏｓ（２π／犿）－狉狉２）１ ２ ．（１１）
犓狉犪 都 对 压 力 角 有 一 定 影 响 。
３ 凸 轮 轮 廓 曲 线 的 绘 制
以三片式平行分 度 凸 轮 为 例，满 足 设 计 要 求 参 数
如下：中心距犪＝１６０ ｍｍ；滚 子 半 径狉狉＝２１ ｍｍ；滚 子
在间歇运 动 循 环 中，凸 轮 以 角 速 度 ω 匀 速 转 动，
其 中 与 之 啮 合 的 分 度 盘 转 过 的 角 度θ 和 凸 轮 的 自 转 角
度β（β＝ω狋，狋为 时 间 ）存 在 着 如 下 函 数 关 系 ：
θ＝犳（ω狋）．
（华北理工大学 机械工程学院，河北 唐山 ０６３２１０）
摘要：根据反转法得到平行分度凸轮的廓线方程，避免了繁琐的计算。分析了平行分度凸轮的设计参数，并 利用 ＭＡＴＬＡＢ 语言编程，绘制出凸轮轮廓曲 线， 将 得 到 的 数 据 文 件 通 过．ｔｘｔ的 方 式 导 入 ＳｏｌｉｄＷｏｒｋｓ进 行 参数化实体建模。这种方法能够很快地得到凸轮廓型，为平行分度凸轮的设计提供了一种新的思路。 关 键 词 ： 平 行 分 度 凸 轮 ； 轮 廓 曲 线 ； ＭＡＴＬＡＢ；ＳｏｌｉｄＷｏｒｋｓ 中 图 分 类 号 ：ＴＨ１３２．４７∶ＴＰ３９１．７ 文 献 标 识 码 ：Ａ
在这样关系：（γ２犘ｍａｘ＋狉狉２）１ ２ ≤γ犜ｍａｘ，将其代入式（９）得：
ε≥２犿πｃｏｓ－１犪２＋狉犱２２－犪γ狉犱２犘ｍａｘ－狉狉２ ．
（１０）
为保证连续传动令ε＞ １，经过等式变换可得凸轮
实 际 廓 线 最 大 外 径γ犘ｍａｘ应 满 足 ：
γ犘ｍａｘ≥（犪２＋狉犱２－２犪狉犱ｃｏｓ（２π／犿）－狉狉２）１ ２ ．（１１）
犓狉犪 都 对 压 力 角 有 一 定 影 响 。
３ 凸 轮 轮 廓 曲 线 的 绘 制
以三片式平行分 度 凸 轮 为 例，满 足 设 计 要 求 参 数
如下：中心距犪＝１６０ ｍｍ；滚 子 半 径狉狉＝２１ ｍｍ；滚 子
基于MATLAB的凸轮机构设计及仿真软件的开发
基于MATLAB的凸轮机构设计及仿真软件的开发
田绿竹;霍平
【期刊名称】《机电一体化》
【年(卷),期】2009()4
【摘要】为提高凸轮机构的设计精度和效率，利用MATLAB语言开发了凸轮机构CAD系统。
该系统界面友好，功能强大，控制方便，能快速、准确地完成各种凸轮轮廓曲线生成、刀具中心轨迹坐标输出等的计算机辅助设计。
【总页数】3页(P95-96)
【关键词】凸轮机构;CAD;计算机仿真
【作者】田绿竹;霍平
【作者单位】河北理工大学机械工程学院
【正文语种】中文
【中图分类】TH112.2;TP273
【相关文献】
1.基于SolidWorks与Matlab的凸轮机构设计与仿真运动分析 [J], 李雅昔;王宏斌;李晓莉
2.基于MATLAB软件的铰链四杆机构运动分析仿真软件开发 [J], 覃虹桥;魏承辉;罗佑新
3.基于VRML和MATLAB的凸轮机构运动仿真设计 [J], 江北大;孔凡宝;王宁
4.基于MATLAB凸轮机构CAD软件系统的开发 [J], 田绿竹;霍平;程秀芳
5.基于MATLAB的行走机构设计及仿真软件的开发 [J], 程秀芳;高瑞香
因版权原因，仅展示原文概要，查看原文内容请购买。
单头弧面分度凸轮实体建模新方法及运动仿真
Ａｂ ｓ ｔ ｒ ａ ｃ ｔ ：Ｂｅ ｃ ａ ｕ ｓ ｅ ｔ ｈ ｅ ｄ ｅ ｓ ｉ ｇ ｎ ｏ ｆ ｇ ｌ ｏ ｂ ｏ ｉ ｄ ｉ ｎ ｄ ｅ ｘ ｉ ｎ ｇ ｃ ａ ｍ ｓ ｏ ｌ ｉ ｄ ｉ ｓ ｃ ｏ ｍｐ ｌ ｉ ｃ ａ ｔ ｅ ｄ， ｉ ｔ ｃ ａ ｎ ｂ ｅ ｍｏ ｄ ｅ ｌ ｅ ｄ ｂ ｙ ｍａ ｎｙ ｍｅ ｈｏ ｔ ｄ ｓ ． Ａｆ ｔｅ ｒ ｃ ｏ ｍｍ ｏ ｎ ｍｏ ｄ ｅ ｌ ｉ ｎ ｇ ｍｅ ｈｏ ｔ ｄｓ ｎａ ａ ｌ ｙ ｚ ｅ ｄ，ａ ｎ ｅ ｗ ｍｏ ｄ ｅ ｌ ｉ ｎ ｇ ｍｅ ｔ ｈ ｏ ｄ ｉ ｓ ｇ ｉ ｖ ｅ ｎ．Ｔｈ ｅ ｃ ａ ｍ ｃ ｕ ｒ ｖ ｅ ｓ ｓ ｅ — ｌ ｅ ｃ ｔ ｅ ｄ ａ ｒ ｅ ｃ ｏ ｍｐ ｕ ｔ ｅ ｄ ｎｄ ａ ｎａ ａ ｌｙ ｚ ｅ ｄ ｂ ｙ Ｍａ ｔ ｌ ａ ｂ ｓ ｏ ｔｗ ａ ｆ ｒｅ，ａ ｎ ｄ ｈｅ ｔ ｄ ａ ｔ ａ ｏ ｆ ｍｏ ｄ ｅ ｌ ｉ ｎ ｇ ｒｅ ａ ｉ ｍｐ ｏ ｒ ｔ ｅ ｄ ａ ｎ ｄ ｄ ｏ ｎ ｅ ｍｏ ｄ — ｅ ｌ ｉ ｎ ｇ ａ ｎ ｄ ｋ ｉ ｎ ｅ ｍａ ｔ ｉ ｃ ｓ ｓ ｉ ｍｕ ｌ ａ ｉｏ ｔ ｎ ｎａ ａ ｌ ｙ ｓ ｉ ｓ ｉ ｎ Ｓ ｏ ｌ ｉ ｄ ｗｏ ｒ ｋｓ ｓ ｏ ｆ ｔ ｗａ ｒｅ ． Ｔｈ ｅ ｒ ｅ ｓ ｕ ｌ ｔ ｓ ｓ ｈ ｏ ｗ ｈａ ｔ ｔ ｔ ｈ ｅ ｎ ｅ ｗ ｍｅ ｈｏ ｔ ｄ ｏ ｆ ｍｏ ｌ ｄ ｉ ｎ ｇ ｇ ｌ ｏ ｂ ｏ ｉ ｄ ｉ ｎ ｄ ｅ ｘ ｉ ｎ ｇ ｃ ａ ｍ ｉ ｓ ｓ ｉ ｍｐ ｌ ｅ，ｐ ｒ ｅ ｃ ｉ ｓ ｅ ａ ｎ ｄ ｆ ｅ ａ ｓ ｉ ｂ ｌ ｅ ． Ｋｅ ｙ ｗｏ ｒ ｄ ｓ：ｉ ｎ ｄ ｅ ｘ ｉ ｎ ｇ Ｃ ａ ｌ Ｔ Ｉ ； ｃ ａ ｍ ｃ ｕ ｒ ｖ ｅ； ｓ ｏ ｌ ｉ ｄ ｍｅ ｌ ｄｉ ｎ ｇ； ｍｏ ｉｏ ｔ ｎ ｓ ｉ ｍｕ ｌ ａ ｔ ｉ ｏ ｎ
基于MATLAB的凸轮机构优化设计
基于MATLAB的凸轮机构优化设计范佳琦【摘要】现今广泛应用的凸轮柱塞式湿喷浆机在实际使用的过程中存在些许问题,如运行时振动较大、出料不均匀、堵管等,经分析知,凸轮机构对其影响较大.文中运用凸轮的理论设计依据,建立相关的数学模型,通过MATLAB编写程序,从而对喷浆机的凸轮进行优化设计与计算,给出了喷浆机凸轮的设计流程和MATLAB的M文件的编写流程,以达到理论与软件结合,从而使其设计计算更加快捷准确,对混凝土喷浆机凸轮的设计缺陷进行优化改进,使之更加可靠实用.【期刊名称】《机械工程师》【年(卷),期】2016(000)001【总页数】3页(P128-130)【关键词】喷浆机;数学模型;MATLAB;凸轮设计【作者】范佳琦【作者单位】北京理工大学机械与车辆学院,北京 100081【正文语种】中文【中图分类】TP391.7;TH12凸轮机构广泛应用于混凝土喷浆机中。
混凝土喷浆机凸轮机构的关键要求，是在满足使用要求的基础上，能够保证结构紧凑、良好的运动和传力性能。
结构参数是结构正常运行的理论保证，故为保证其要求，控制和优化其相关参数，是混凝土喷浆机设计的重点，在此，运用MATLAB的强大数据计算能力和数据可视化功能，可简洁、准确地进行喷浆机凸轮机构的设计［1-3］。
1.1 喷浆机凸轮机构设计的基本流程（见图1）1.2 建立数学模型为使计算公式统一，引入凸轮转向系数λ和从动件偏置方向系数p，并做出表1规定。
1）根据反转法原理，可以得出喷浆机凸轮理论轮廓的直角坐标方程式：式中：为凸轮转角；s为从动件位移；s0为结构常数，s0=2）喷浆机凸轮实际轮廓直角坐标系方程式：3）喷浆机凸轮轮廓线理论压力角：4）喷浆机轮廓上理论曲率半径：5）喷浆机凸轮轮廓直角坐标的一阶和二阶导函数为：编写MATLAB的M文件的流程如图2所示。
3.1 已知条件凸轮作逆时针方向转动，从动件偏置在凸轮轴心的右边，即：λ=-1；p=1，从动件在推程作等加速、等减速运动，在回程作余弦加速度运动，其相关参数见表2［5-6］。
基于MATLAB的凸轮机构运动分析
基于MATLAB的凸轮机构运动分析徐勇;佟军民【摘要】介绍了利用MATLAB语言来求解凸轮机构的运动规律,并且使其结果可视化.从而使机构的运动分析直观、简单和精确,大大提高凸轮机构的设计精度和效率.【期刊名称】《机械研究与应用》【年(卷),期】2003(016)004【总页数】2页(P51-51,55)【关键词】凸轮;运动;MATLAB【作者】徐勇;佟军民【作者单位】兰州理工大学,机电学院,甘肃,兰州,730050;许昌机电职业技术学院,河南,许昌【正文语种】中文【中图分类】工业技术第 16 卷第 4 期2003年 12 月机械研究与应用 MECHANICAL RESEARCH&APPLICATION Vol16N042003-12基于 MATLAB的凸轮机构运动分析徐勇 1 ，佟军民 2 (1 ．兰州理工大学机电学院，甘肃兰州 730050 ；2．许昌机电职业技术学院，河南许昌)摘要：介绍了利用 MATLAB 语言来求解凸轮机构的运动规律，并且使其结果可视化。
从而使机构的运动分析直观、简单和精确，大大提高凸轮机构的设计精度和效率。
关麓词：凸轮；运动；MATLAB 中图分类号：TP391.72 文献标识码：A文章编号：1007-4414(2003)04-0051-01 l 前言MATLAB 是Mathworks 公司于 1982 年推出的一套功能强大的工程计算软件‘ 1]，广泛应用于自动控制、机械设计、流体力学和数理统计等工程领域，被誉为巨人肩上的工具。
它集数值分析、矩阵运算、信号处理和图形显示于一体，构成了一个方便的、界面友好的用户环境。
工程人员通过使用MATLAB提供的工具箱，可以高效求勰复杂的工程问题，并可以对系统进行动态仿真，用强大的图形功能对数值计算结果进行显示。
在机械传动系统中，机构的运动分析是机械系统分析的基础。
设计者可以根据原动件的运动规律，来求出机构上其它构件和该构件上特定点的位移、速度和加速度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
基于Matlab GUI的弧面分度凸轮轮廓曲面计算平台的设计
作者：曹顺辉
摘要：介绍了利用Matlab 7.0的图形用户界面（Graphical User Interface,GUI）设计弧面分度凸轮工作廓面坐标计算平台的方法和步骤。
使用户不必去了解复杂的Matlab代码及程序，直接通过该平台就可以很便捷的进行凸轮工作廓面的计算工作。
并利用最终输出的坐标文件结合三维造型软件SolidWorks完成弧面分度凸轮工作廓面的三维建模。
关键字：GUI 弧面分度凸轮 三维实体建模 图形用户界面 Matlab
1 引言
弧面分度凸轮机构(图1)用于两垂直交错轴间的间歇分度步进传动，这种机构不需要其他附属装置即可完成较精确的分度定位[1]。
和其他几种常见的间歇分度机构相比，可以在高速、重载的情况下使用，而且运行比较平稳，无较大冲击，定位精度高。
但是由于弧面分度凸轮的工作廓面为空间不可展曲面，很难用常规的机械方法绘制[1]。
通过Matlab编程语言，首先建立凸轮工作廓面坐标的数学模型，然后再结合Matlab的图形用户界面（GUI）设计功能，为用户提供一个图形界面。
通过这个界面用户可以很便捷地进行一些复杂的数据处理和运算工作，而不必去了解界面背后代码和程序的运行过程，因此具有更加广泛的应用意义。
图1
2 Matlab 图形用户界面（GUI）简介
图形用户界面（GUI）是一个整合了诸如窗口、图标、按钮、菜单和文本等图形对象的接口，用户选中或者激活这些对象通常都会导致某个动作或者变化的发生[2]。
是用户和计算机程序之间进行信息交互的一种方法，用户通过键盘、鼠标、麦克风或者绘图板等设备向计算机输入相关信息，计算机可以通过屏幕上显示图形和文本、利用喇叭发出声音来向用户提供相关信息。
因此对于一个操作系统或者应用程序来说，用户接口是一个十分关键的因素，它定义了这些系统或应用程序提供给用户的视觉感受和使用感觉，因此一个友好而高效的用户接口对于应用程序或者计算机的使用者具有极强的吸引力[2]。
Matlab7.0中的图形用户接口开发环境（Graphical User Interface Development Environment,GUIDE）提供了一系列工具用于建立GUI对象，这些工具在很大程度上简化了设计和建立GUI的过程[3]。
设计者通过运用GUIDE可以完成GUI图形界面的布局设计以及GUI编程工作，而这些也正是开发图形用户界面（GUI）的基本流程。
2 弧面分度凸轮轮廓曲面计算平台的GUI设计流程
在开始进行GUI设计前，首先需要对所面临的问题进行精确描述，即我们遇到的到底是什么问题。
然后定义输入和输出量，即我们的目的和现有的条件。
最后针对问题，设计算法，逐层分解，逐步求精，再把算法转换为Matlab语言。
在本文中我们要解决的问题是：在用户给定所需要的参数以后，经过数据处理和计算，最后输出记录有凸轮工作轮廓曲面坐标的文本文件。
这个问题的输入量为计算凸轮工作轮廓曲面坐标所需的相关参数，输出量为凸轮工作轮廓曲面的坐标。
在搞清楚上面这些问题以后，就可以开始GUI的设计工作。
3.1 图形用户界面的布局设计
3.1.1 在进行GUI设计时，根据预先定义的输入量和输出量来确定界面中所需要的控件的类型和数量。
在稿纸上对将要设计的图形用户界面的布局进行初步的构思，否则盲目性太大不利于后期的编程工作。
在表1中列出了在计算弧面分度凸轮轮廓曲面坐标时需要的相关参数。
表1 弧面分度凸轮轮廓曲面计算参数表
项目 计算公式与说明 结果
凸轮分度期转角 常用的为120°~240° =120°
转盘分度数I I表示转盘转一周中的停歇次数 I=8
中心距C 凸轮和分度盘的中心距离 C=180mm
滚子半径 =22mm
间隙e e=(0.2~0.3)b e=6mm
滚子宽度b b=(1~1.4) b=24mm
凸轮分度廓线头数H 单头H=1,双头H=2 1
旋向系数p 左旋p=+1,右旋p=-1 1
分度盘运动规律 选择需要的运动规律 改进正弦加速度
廓面选择 选择要计算的轮廓曲面 1L,2L,2R,3R
3.1.2 在构思好将要设计的界面布后，就可以开始具体的设计工作。
打开Matlab软件，在命令窗口（Command Window）中输入guide,确认后打开GUIDE快速启动窗口，选择新建一个空白样板（Black GUI）,如图2所示。
图2
如上图示，GUI编辑界面主要包括GUI对象选择区、GUI工具栏、GUI布局区3个部分[3]。
在空白的GUI样板的编辑区不会有任何figure子对象存在，必须由用户按照预先的设计进
行添加。
根据表1中罗列的参数和GUI界面布局的初步构思，确定该界面需要的控件为触控按钮（Push Button）3个，静态文本标签（Static Text）12个，可编辑文本（Edit Text）8个，弹出式菜单（Pop-up Menu）2件。
在GUI编辑界面左边的GUI对象选择区选择需要的控件在GUI布局区中，按照图3所示进行布局，并对控件的属性进行设置，完成图形用户界面的布局设计工作，最后保存文件。
图3
3.2 编写回调函数（Callback）代码
在保存GUI程序时，Matlab会自动生成.fig和.m文件，其中的.m文件包含了界面上所有组件的回调函数（Call Back）。
所谓回调，是指当与某一特定的的属性相关联的用户动作发生时，需要执行的代码。
在大多数情况下，回调都是函数调用，通常通用的就是定义回调的那个函数。
用户可以对回调进行设置，以便让Matlab执行特定的任务。
[2]这也是GUI 编程的核心工作。
而在弧面分度凸轮轮廓曲面坐标计算程序的GUI中，回调函数的代码编写工作主要包含两部分内容：
3.2.1 对于界面上的可编辑文本（Edit Text）控件，在用户输入相应的参数值时，要求只能输入数字类字符，否则予以弹窗提示。
可以在对应控件的回调函数内增加下面的代码实现这个功能。
str=get(handles.edit1,’string’);%读取输入的字符串
if isempty(str2num(str)) %判断字符串是否为纯数字
msgbox(‘Input error’,’Error’);%如果不是纯数字，弹窗提示
return;
end
3.2.2编写触控按钮“计算”和“退出”的回调函数代码。
界面中“计算”的回调函数是曲面坐标计算程序算法的具体体现，“计算”按钮的回调函数部分代码如下：
str1=get(handles.popupmenu2,’string’);%读取下拉菜单的取值，即运动规律的选择值
str2=get(handles.popupmenu3,’string’);%读取下拉菜单的取值，即曲面的选择值
if (str2num(str1)==2& str2num(str2)==1) %如果选择改进正弦加速度且选择要计算的曲面为1L面
… … %1L曲面坐标计算程序
else if (str2num(str1)==2&str2num(str2)==2) %如果选择改进正弦加速度且选择要计算的曲面为2L面
… … %2L曲面坐标计算程序
else … …
… …
end
4 实例计算
完成编写回调函数代码的工作，确保代码可以顺利运行。
弧面分度凸轮轮廓曲面计算平台的构建已经基本完成，在界面里输入相应的参数的数值（参照表1），如图4所示，计算后得出记录有曲面（3L）坐标的文件（图5）。
图4 图5
同理，计算出曲面1L、2L、2R以及定位环面的坐标并保存为txt文本格式。
完成曲面坐标的计算后，将坐标值导入SolidWorks中（图6），完成弧面分度凸轮的三维造型（图7）。
图6 图7
5总结
运用Matlab结合三维软件进行弧面分度凸轮工作廓面实体造型的流程一般是首先编写计算凸轮工作廓面坐标的M文件（脚本），然后再将计算结果导入三维软件中进行实体建模。
如果当要计算的凸轮的参数发生改变时，就需要对M文件中相应的参数进行更改，然后才能运行程序，计算坐标。
在此文中介绍的应用Matlab GUI开发设计的弧面分度凸轮工作廓面坐标计算平台，用户不用直接面对程序代码，使用更加便捷，具有更加广泛的应用意义。
参考文献：
[1]机械设计手册（第五版）：单行本.机构/成大先主编.-北京：化学工业出版社，2010.1
[2]精通Matlab7/(美)亨塞尔曼（Hanselman.D.）,(美)利特菲尔德（Littlefield,B.）著：朱仁峰译.-北京：清华大学出版社，2006.5
[3]MATLAB GUI设计学习手册/罗华飞编著.—2版.-北京：北京航空航天大学出版社，2011.2。