m序列扩频码的生成.

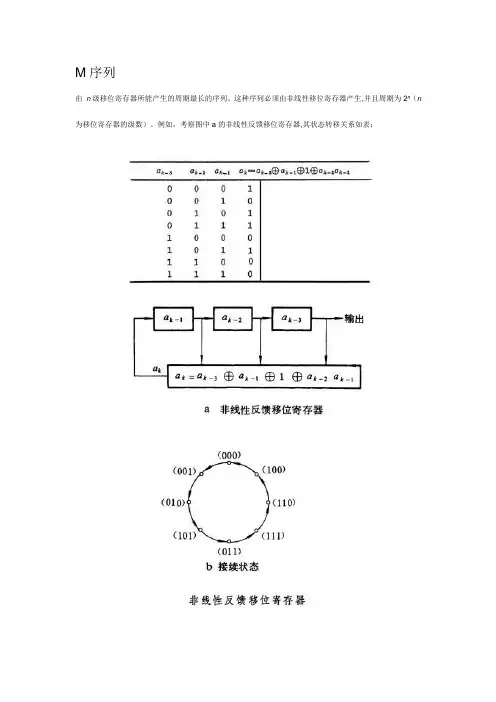
M序列由n级移位寄存器所能产生的周期最长的序列。

这种序列必须由非线性移位寄存器产生,并且周期为2n（n 为移位寄存器的级数）。

例如，考察图中a的非线性反馈移位寄存器,其状态转移关系如表：状态(a k-3，a k-2，a k-1)的接续状态是(a k-2,a k-1，a k)，其中a k＝a k-3嘰a k-1嘰1嘰a k-2a k-1是一种非线性逻辑。

从任一状态出发，例如从(000)出发,其接续状态恰好构成一个完全循环(图b)，由此产生一个周期为23＝8的3级序列。

M序列最早是用抽象的数学方法构造的。

它出现于组合数学的一些数学游戏中，例如L.欧拉关于哥尼斯堡的七桥问题等。

后来发现这种序列具有某些良好的伪随机特性。

例如,M序列在一个周期中，0与1的个数各占一半。

同时,同样长度的0游程与1游程也各占一半。

所有这些性质在数据通信、自动控制、光学技术和密码学诸领域中均有重要应用。

隐蔽通信内容的通信方式。

为了使非法的截收者不能理解通信内容的含义，信息在传输前必须先进行各种形式的变化，成为加密信息，在收信端进行相应的逆变化以恢复原信息。

电报通信、电话通信、图像通信和数据通信,都有相应的保密技术问题。

另一方面,为了从保密通信中获得军事、政治、经济、技术等机密信息，破译技术也在发展。

保密技术和破译技术是在相互对立中发展起来的。

1881年世界上出现了第一个电话保密专利。

电话保密开始是采用模拟保密或置乱的方法，即把话音的频谱或时间分段打乱。

置乱后的信号仍保持连续变化的性质。

在第二次世界大战期间，频域和时域的置乱器在技术上已基本成熟。

70年代以来，由于采用集成电路，电话保密通信得到进一步完善。

但置乱器仍是有线载波和短波单边带电话保密通信的主要手段。

模拟保密还可以采用加噪声掩盖、人工混响或逆向混响等方法，但因恢复后话音的质量大幅度下降或保密效果差，这些方法没有得到推广应用。

数字保密是由文字密码发展起来的。

数字信号（包括由模拟信号转换成的数字信号），由相同速率的密码序列加密，成为数字保密信号；保密信号传输到收信端后由同一密码序列去密，恢复原数字信号。

1、生成m序列及m序列性质实验产生7位m序列，频率100Hz，模拟线性反馈移位寄存器序列，原理图如下：clear all;clc;X1=0;X2=0;X3=1;m=350; %重复50遍的7位单极性m序列for i=1:mY3=X3; Y2=X2; Y1=X1;X3=Y2; X2=Y1;X1=xor(Y3,Y1);L(i)=Y1;endfor i=1:mM(i)=1-2*L(i); %将单极性m序列变为双极性m序列endk=1:1:m;figure(1)subplot(3,1,1) %做m序列图stem(k-1,M);axis([0,7,-1,1]);xlabel('k');ylabel('M序列');title('移位寄存器产生的双极性7位M序列') ;subplot(3,1,2)ym=fft(M,4096);magm=abs(ym); %求双极性m序列频谱fm=(1:2048)*200/2048;plot(fm,magm(1:2048)*2/4096);if x_rand(i)>=0.5 %大于等于0.5的取1，小于0.5的取0x(i)=1;a=a+1;else x(i)=0;endendt=0:N-1;figure(2) %做信息码图subplot(2,1,1)stem(t,x);title('扩频前待发送二进制信息序列');tt=0:349;subplot(2,1,2)l=1:7*N;y(l)=0;for i=1:Nk=7*i-6;y(k)=x(i);k=k+1;y(k)=x(i);k=k+1;y(k)=x(i);k=k+1;y(k)=x(i);k=k+1;y(k)=x(i);k =k+1;y(k)=x(i);k=k+1;y(k)=x(i);ends(l)=0;for i=1:350 %扩频后，码率变为100/7*7=100Hzs(i)=xor(L(i),y(i));endtt=0:7*N-1;stem(tt,s);axis([0,350,0,1]);title('扩频后的待发送序列码');N=400000;ybb=fft(s_bpskb,N); %无扩频信号BPSK调制频谱magb=abs(ybb);fbb=(1:N/2)*100000/N;subplot(2,1,1)plot(fbb,magb(1:N/2)*2/N);axis([1700,2300,0,0.8]);title('扩频前调制信号频谱');xlabel('Hz');subplot(2,1,2)yb=fft(s_bpsk,N); %扩频信号BPSK调制频谱mag=abs(yb);fb=(1:N/2)*100000/N;plot(fb,mag(1:N/2)*2/N);axis([1700,2300,0,0.8]);title('扩频后调制信号频谱');xlabel('Hz');title('扩频后经加噪过信道后的信号与原信号时域波形对比'); xlabel('t');axis([0.0675,0.0725,-1.2,1.2]);subplot(2,2,2)ybba=fft(s_bpskba,N); %无扩频调制信号经信道后频谱分析magba=abs(ybba);plot(fbb,magba(1:N/2)*2/N);title('扩频前经信道调制信号频谱');axis([1700,2300,0,0.8]);xlabel('Hz');subplot(2,2,4)yba=fft(s_bpska,N); %扩频调制信号经信道后频谱分析maga=abs(yba);fb=(1:N/2)*100000/N;plot(fb,maga(1:N/2)*2/N);axis([1700,2300,0,0.8]);xlabel('Hz');title('扩频后经信道调制信号频谱');幅，符合高斯白噪声的原理。

一、扩频码序列
在扩频系统中，信号频谱的扩展是通过扩频码实现的。

扩频系统的性能和扩频码的性能有很大关系，对扩频码通常有下列要求：易于产生；具有随机性；扩频码应该具有尽肯能长的周期，使干扰者难以从扩频码的一小段中重建整个码序列；扩频码具有良好的自相关和互相关特性，以利于接收时的捕获和跟踪，以及多用户检测等。

从理论上说，用纯随机序列去扩展频谱是最理想的。

例如，高斯白噪声，但在接收机中为解扩的需要，应当有一个同发送端扩频码同步的副本，因此，实际上只能用伪随机或防噪声序列作为扩频码。

伪随机序列具有类似噪声的性质，但它又是周期性有规律的，易于产生和处理。

扩频码中应用最多的是m序列，又称最大长度序列，还有Gold序列、Walsh码序列等。

二、m序列
三、仿真实现
本程序实现的功能：生成n=3的m序列，其中第一个寄存器与第三个寄存器与反馈加法器相连，寄存器的初始值都为1。

程序源代码请参考m_sequence.m。

（注：使用时需要修改m_sequence.txt文件后缀格式，修改为m_sequence.m，然后用MATLAB打开运行。

其他程序也是如此。

）
其中产生m序列的功能通过调用函数mseq来实现，mseq函数代码请参考mseq.m，函数中第28行的shift函数是完成序列的循环移位，它的代码请参考shift.m。

完成相关的设定（寄存器连接方式，初始值）后，直接调用mseq函数即可生成对应的m序列。

程序运行结果为
mout =
1 1 1 0 1 0 0。

m序列原理m序列是一种特殊的伪随机序列，具有良好的随机性质和周期性，广泛应用于通信、密码学、雷达、遥感等领域。

m序列的原理是基于线性反馈移位寄存器（LFSR）的工作原理，通过适当的初值和反馈多项式，可以生成具有良好随机性质的序列。

m序列的生成原理是基于LFSR的工作原理。

LFSR是一种线性反馈移位寄存器，它由若干个存储单元和适当的反馈电路组成。

在LFSR中，存储单元中的数据按照时钟信号不断移位，同时根据反馈电路的控制，将某些位上的数据进行异或运算，得到新的输入数据，从而实现序列的生成。

通过适当选择LFSR的初值和反馈多项式，可以得到不同长度的m序列。

m序列具有良好的随机性质和周期性。

由于m序列的生成原理是基于LFSR的移位和异或运算，使得序列中的数据呈现出随机分布的特性。

同时，由于LFSR的结构和反馈多项式的选择，m序列具有很长的周期，甚至可以达到最大周期2^n-1，其中n为LFSR的位数。

这使得m序列在伪随机序列中具有较好的性能。

m序列在通信、密码学、雷达、遥感等领域有着广泛的应用。

在通信系统中，m序列可以作为扩频序列，用于码分多址（CDMA）通信系统中的信道编码和解码，提高通信系统的抗干扰能力和安全性。

在密码学中，m序列可以作为密钥序列，用于数据加密和解密，保障通信的安全性。

在雷达和遥感领域，m序列可以作为调制序列，用于信号的调制和解调，提高信号的分辨率和抗干扰能力。

总之，m序列作为一种特殊的伪随机序列，具有良好的随机性质和周期性，在通信、密码学、雷达、遥感等领域有着广泛的应用前景。

通过深入理解m序列的生成原理和特性，可以更好地应用于实际系统中，提高系统的性能和安全性。

m序列的原理及应用1. 什么是m序列？m序列，全名为最大长度线性反馈移位寄存器序列（Maximum Length Sequence），是一种特殊的二进制序列。

m序列的特点是具有最长的周期，并且波形均匀随机分布。

m序列可以通过一个线性反馈移位寄存器（LFSR）来生成。

2. m序列的生成原理m序列的生成原理基于线性反馈移位寄存器（LFSR）的运算。

LFSR是一种用于产生伪随机序列的硬件电路。

LFSR由寄存器和反馈函数组成。

寄存器是一组存储数据的单元，通常是一组触发器，每个触发器存储一个二进制位。

反馈函数根据寄存器的当前状态产生下一个状态。

反馈函数一般采用异或操作。

m序列的生成就是通过不断移位和反馈计算，使得LFSR的状态变化遍历所有可能的状态，从而生成了m序列。

3. m序列的应用m序列由于其随机性和均匀性，被广泛应用于通信、加密、导航等领域。

3.1 通信领域在通信领域中，m序列被用作伪随机序列发生器。

伪随机序列在信号传输、数据调制等方面起到关键作用。

m序列具有具有良好的互相关性和自相关性性质，能够提供伪随机的编码和解码功能。

3.2 加密领域m序列在加密领域中作为密钥序列广泛使用。

由于m序列的随机性和不可预测性，能有效地保护数据的安全性。

一种常见的应用是m序列与明文进行异或运算，生成密文，从而实现加密功能。

3.3 导航领域在导航领域中，m序列被用于全球卫星导航系统（GNSS）中的扩频码。

扩频码是通过将原始导航信号与m序列进行乘法运算而生成的。

m序列的均匀随机性使得扩频码具有良好的抗多径和抗干扰性能。

4. m序列的特点4.1 最长周期m序列具有最长的周期，周期长度为2^N-1，其中N为LFSR的位数。

这意味着m序列可以生成非常长的伪随机序列。

4.2 均匀随机性m序列的波形均匀分布，具有良好的随机性。

这个特性使得m序列在各个应用领域都能发挥重要作用。

4.3 线性可预测性m序列是由线性反馈移位寄存器生成的，其生成过程可以被完全预测。

目录前言 (1)第一章设计任务 (2)1.2设计内容 (2)1.2设计要求 (2)1.3系统框图 (2)第二章m序列的分析 (4)2.1m序列的含义 (4)2.2m序列产生的原理 (5)2.2m序列的性质 (6)2.3自相关特性 (7)第三章m序列的设计 (8)3.1特征多项式确定 (8)3.2本原多项式的确定 (9)3.3m序列的发生 (10)第四章程序调试及结果分析 (11)4.1m序列的仿真结果及分析 (12)4.2该设计的序列相关性仿真结果及分析 (13)结论 (14)参考文献 (15)附录：程序代码 (16)前言扩频通信因其具有抗干扰、抗多径衰落、抗侦察等优点在通信领域中得到广泛应用。

扩频序列的设计和选择是扩频通信的关键技术，扩频序列性能的优劣在很大程度上决定了通信系统的多址干扰和符号间干扰的大小，从而直接影响到系统的性能。

因此，深入研究扩频序列的性质，构造设计具有良好相关性的扩频序列，来满足扩频系统的要求，是直接序列扩频系统的核心课题。

白噪声是一种随机过程，它有极其优良的相关特性。

但至今无法实现白噪声的放大、调制、检测、同步及控制等，而只能用类似于白噪声统计特性的伪随机序列来逼近它，并作为扩频系统的扩频码。

常见的伪随机序列有m 序列、GOLD 序列、M 序列、Walsh 序列等。

m 序列是目前研究最为彻底的伪随机序列，m 序列容易产生，有优良的自相关和互相关特性。

序列是伪随机序列的一种情况。

他可以在很多领域中都有重要应用。

由n级移位寄存器所能产生的周期最长的序列。

这种序列必须由非线性移位寄存器产生,并且周期为2n（n为移位寄存器的级数）。

通过对伪随机码中常用的m序列的结构和性质进行了分析，本文给出了基于MATLAB平台的m序列生成算法及代码伪随机序列分析。

第一章 设计任务1.2 设计内容掌握PN 序列的相关知识，掌握m 序列的产生原理及其在matlab 中的产生方法，对特定长度的m 序列，分析其性质，及其用来构造其它序列的方法；研究伪随机序列在跳频通信中的应用方法。

5G M序列简介在5G通信技术中，M序列（M-sequence）是一种用于生成伪随机码（Pseudo Random Code）的序列。

M序列具有良好的随机性和周期性，并且在5G系统中具有广泛的应用。

本文将对5G M序列进行详细介绍，包括其定义、特性、生成方法以及应用场景等。

定义M序列是一种由二进制数字（0和1）组成的序列，具有良好的随机性和周期性。

M序列的长度通常为2的幂次方减1，例如15、31、63等。

M序列的生成是通过反馈移位寄存器（Feedback Shift Register，FSR）实现的，其中寄存器中的位通过特定的异或运算进行更新，从而生成下一个位的值。

特性1.随机性：M序列具有良好的随机性，其序列中的0和1的分布接近均匀分布，能够提供高度的随机性，从而增强数据的安全性和抗干扰能力。

2.周期性：M序列的周期性非常好，其周期长度为2的幂次方减1。

例如，一个15位的M序列的周期长度为2^15-1=32767，能够满足5G系统对长周期序列的需求。

3.自相关性：M序列的自相关性非常低，即序列与其自身进行互相关运算后，得到的结果接近于0。

这种特性使得M序列在通信系统中能够提供良好的互相干扰抑制能力。

生成方法M序列的生成方法基于反馈移位寄存器（FSR），其具体步骤如下：1.初始化寄存器：将FSR中的所有位初始化为非零的值，通常选择全1或全0。

2.生成序列：通过不断进行异或运算来更新FSR中的位，从而生成M序列。

具体更新方法根据FSR的结构和反馈多项式来确定。

3.输出序列：根据需要，可以选择输出M序列的全部或部分位。

如果只需要部分位，则可以通过截取序列的方式来实现。

应用场景M序列在5G系统中有许多重要的应用场景，包括：1.扩频技术：M序列被广泛用于扩频技术中，通过将原始数据序列与M序列进行异或运算，可以将信号的频带扩展，从而提高系统的抗干扰能力和容量。

2.导频序列：在5G系统中，M序列被用作导频序列，用于信道估计、频率同步等关键环节。

实验九 m 序列产生及其特性实验一、实验目的通过本实验掌握m 序列的特性、产生方法及应用。

二、实验内容1、观察m 序列，识别其特征。

2、观察m 序列的自相关特性。

三、基本原理m 序列是有n 级线性移位寄存器产生的周期为21n -的码序列，是最长线性移位寄存器序列的简称。

码分多址系统主要采用两种长度的m 序列：一种是周期为1521-的m 序列，又称短PN 序列；另一种是周期为4221-的m 序列，又称为长PN 码序列。

m 序列主要有两个功能：①扩展调制信号的带宽到更大的传输带宽，即所谓的扩展频谱；②区分通过多址接入方式使用同一传输频带的不同用户的信号。

1、产生原理图9-1示出的是由n 级移位寄存器构成的码序列发生器。

寄存器的状态决定于时钟控制下输入的信息（“0”或“1”），例如第I 级移位寄存器状态决定于前一时钟脉冲后的第i －1级移位寄存器的状态。

图中C 0，C 1，…，C n 均为反馈线，其中C 0＝C n ＝1，表示反馈连接。

因为m 序列是由循环序列发生器产生的，因此C 0和C n 肯定为1，即参与反馈。

而反馈系数C 1，C 2，…，C n－1若为1，参与反馈；若为0，则表示断开反馈线，即开路，无反馈连线。

图9-1 n 级循环序列发生器的模型一个线性反馈移动寄存器能否产生m 序列，决定于它的反馈系数(0,1,2,,)i c i n =，下表中列出了部分m 序列的反馈系数i c ，按照下表中的系数来构造移位寄存器，就能产生相应的m 序列。

表9-1 部分m 序列的反馈系数表根据表9-1中的八进制的反馈系数，可以确定m 序列发生器的结构。

以7级m 序列反馈系数8(211)i C =为例，首先将八进制的系数转化为二进制的系数即2(010001001)i C =，由此我们可以得到各级反馈系数分别为：01C =、10C =、30C =、41C =、50C =、60C =、71C =，由此就很容易地构造出相应的m 序列发生器。