结构动力学原理与地震易损性分析(朱健编著)思维导图
- 格式:xmin
- 大小:5.45 KB
- 文档页数:1





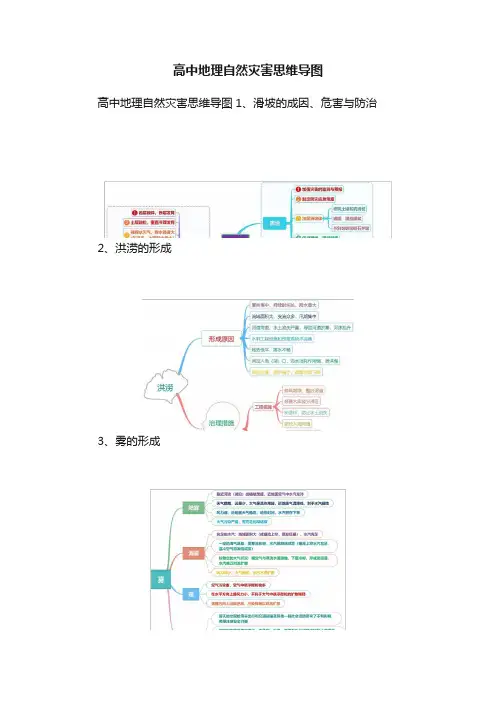
高中地理自然灾害思维导图
高中地理自然灾害思维导图1、滑坡的成因、危害与防治
2、洪涝的形成
3、雾的形成
1.自然灾害分布的一般描述
(1)空间分布:集中分布在……地区,由……向……减少(或增加)。
(2)时间分布:主要发生在……季,……季多发,……季较少。
2.自然灾害成因的分析思路
主要从自然原因(气候、地形、河流、植被、土壤)和人为原因两方面综合分析。
气象灾害侧重气候、河流等方面;地震、火山侧重地壳运动等内力作用方面;滑坡、泥石流需要结合内、外力作用综合分析。
3.防灾措施
(1)工程措施:修建各种减灾、防灾工程,如在河流沿岸建防洪大堤、防护林、实施护坡工程等。
(2)非工程措施:加强灾害的宣传教育,树立减灾、防灾意识;建立、健全法规体系;加强对灾害的监测和预报;建立灾害应急机制,增强应急救援能力等。
