异面直线的距离求法

例说异面直线间距离的求法求异面直线间的距离是立体几何中的一个重点，也是一个难点，它涉及概念多，覆盖知识面广，综合性强。

因教材对这类问题的解法介绍得不多，加之学生受解平几问题的影响，故在求解此类问题时常常思维受阻。

这里举一例说明异面直线间距离的一些常用求法，供解题参考。

问题：在棱长为a 的正方体AC 1中，求直线BD 与B 1C 的距离。

分析：求异面直线的距离可以根据定义直接作出异面直线的公垂线段并求出其长度，但通常作异面直线公垂线都比较困难。

这时可以转化为直线与平面间距离，或转化为两平行平面间距离或用函数法进行求解，还可以利用空间向量求解。

解法1：（构造）函数法[转化为求函数的最值] 在B 1C 上任取一点P ，作PE ⊥BC 于E ，过E 作EO ⊥BD 与O ，连PO ，如图1，易知PO 为直线BD 与B 1C 的公垂线段，应使其最小， 设PE x =则CE x =，BE a x =-，)EO a x =-，PO == 所以a PO 33min =，即直线BD 与B 1C 的距离为a 33。

评注：直接作二异面直线的公垂线段困难，可考虑看能否把几何问题代数化，即把求异面直线的距离转化为求一元函数的最值，从而可避免因找异面直线的公垂线段而作大量的辅助线、辅助面，同时减少利用线线、线面垂线定理的次数。

解法2：转化法——面面距离法[线线距离⇒面面距离]因为1B C ⊂面11B D C ，BD ⊂面1BDA ，且面11B D C ∥面1BDA ， 所以面11B D C 与面1BDA 间的距离和直线BD 与B 1C 的距离相等， 连1AC ，设1AC 面1BDA M =，1AC 面11B D C N =，如图2，易证1AC ⊥面1BDA ，1AC ⊥面11B D C ，则线段MN 的长即为所求， 又设ACBD O =，11111AC B D O =，连1OA 、1O C ，显然1OA ⊂面1BDA ，1O C ⊂面11B D C ， 故11OA AC M =，11O C AC N =，从而易得1113AM MN NC AC ===， 所以MN a =，故直线BD 与B 1C 的距离为a 33。

向量法求异面直线所成的距离
异面直线是指不在同一平面上的两条直线。

求解这两条异面直线所成的距离，可以使用向量法。

向量法可以通过向量的数量积和向量的模长求得两条直线之间的距离。

下面我们通过实例来详细说明向量法如何求解两条异面直线之间的距离。

假设有两条异面直线，它们的方程分别为：
直线1:
$x = 3 + 2t$
$y = 1 - t$
$z = -2 + 3t$
首先我们需要确定两条直线上的任意两个点，然后用这两个点之间的连线构成的向量来表示两条直线之间的直线向量。

所以我们任意选择直线1上的两个点 $A(3,1,-2)$ 和$B(5,-1,4)$ ，计算它们之间的向量：
$\vec{AB} = \overrightarrow{AB} = \begin{pmatrix} 5 - 3 \\ -1 - 1 \\ 4 - (-2) \end{pmatrix} = \begin{pmatrix} 2 \\ -2 \\ 6 \end{pmatrix}$
同样，我们任意选择直线2上的两个点 $C(1,2,5)$ 和 $D(5,6,15)$，计算它们之间的向量：
然后，我们需要求解两条直线之间的最短距离，也就是求解这两个向量的数量积：
$\vec{AB} \cdot \vec{CD} = 2 \times 4 + (-2) \times 4 + 6 \times 10 = 52$
接下来，我们需要计算两个向量的模长：
因此，两条直线之间的距离为：
因此，两条异面直线所成的距离为 $\frac{13}{19}$。

空间向量求异面直线的距离方法1. 直接法！嘿，你看，就像你要直接找到两个异面直线之间最短的那条线一样，非常直白地去求啊。

比如正方体里的两条异面棱，你就直观地去找到它们之间最短距离的那个线段。

2. 转化法呀！哎呀，这就像你走不通一条路，那咱就换条路走嘛。

把异面直线的距离转化成别的容易求的距离呀。

比如在三棱锥里，把异面直线的距离转化成求某个面到另一条线的距离。

3. 向量法呗！哇塞，这可厉害啦。

利用向量来搞定异面直线的距离。

就像有了个神奇的工具！比如在一个复杂的几何体中，用向量来算算异面直线的距离，超酷的好不好！4. 定义法呢！这不就跟你找东西按照规定的方法去找一样嘛。

按照异面直线距离的定义去求解呀。

就像找一个特定的宝藏，按照线索去找。

比如在一个棱柱里，根据定义慢慢找异面直线的距离。

5. 等体积法呀！嘿呀，这就好像不同的方法可以解决同一个问题一样。

通过等体积来求出异面直线的距离哟。

比如在一个四面体中，通过等体积的巧妙变换来求出需要的距离。

6. 最值法啦！想想看呀，就跟我们追求最好的结果一样。

找到某个关联量的最值来得到异面直线的距离。

像在一个特殊的图形中，通过巧妙地找最值来求出异面直线的距离。

7. 射影法哟！哇，这就像影子一样，通过它来找到距离呢。

比如在一个有特点的几何体中，利用射影的原理来求异面直线的距离。

8. 公式法咯！简单直接啊，用专门的公式来算。

就好像有个现成的答案等你用一样。

比如在某些典型的模型中，用适用的公式快速求出异面直线的距离。

9. 拼凑法呀！哈哈，就像是把零碎的东西拼凑起来一样。

通过巧妙地拼凑来找到异面直线的距离呢。

比如在一个不规则的几何体中，一点点拼凑出求解异面直线距离的条件。

我的观点结论是：这些方法各有特点，我们要根据具体情况灵活运用，总能找到异面直线的距离呀！。

异面直线间的间隔之青柳念文创作求异面直线之间的间隔是平面几何重、难点之一.常有操纵图形性质，直接找出该公垂线，然后求解；或者通过空间图形性质，将异面直线间隔转化为直线与其平行平面间的间隔，或转化为分别过两异面直线的平行平面间的间隔，或转为求一元二次函数的最值问题，或用等体积变换的方法来解.常常使用方法有：1、定义法2、垂直平面法（转化为线面距）3、转化为面面距4、代数求极值法5、公式法6、射影法7、向量法8、等积法1 定义法就是先作出这两条异面直线的公垂线，然后求出公垂线的长，即异面直线之间的间隔.例1 已知：边长a为的两个正方形面直线CD与AE间的间隔.思路分析：由四边形ABCD和CDEF是正方形，得CD⊥AD，CD⊥DE，即CD⊥平面ADE，过D作DH⊥AE于H，可得DH⊥AE，DH⊥CD，所以DH是异面直线AE、CD的公垂线.在⊿ADE中，∠ADE=1200，AD=DE=a，即异面直线CD与AE2 垂直平面法：转化为线面间隔，若a、b是两条异面直线，过b上一点A作a的平行线a/，记a/与b确定的平面α.从而，异面直线a、b间的间隔等于线面a、α间的间隔.例1 如图，BF、AE两条异面直线分别在直二面角P-AB-Q的两个面内，和棱分别成α、β角，又它们和棱的交点间的间隔为d，求两条异面直线BF、AE间的间隔.思路分析：BF、AE两条异面直线分别在直二面角P-AB-Q 的两个面内，∠EAB=α，∠FAB=β，AB=d，在平面Q内，过B作BH‖AE，将异面直线BF、AE间的间隔转化为AE与平面BCD间的间隔，即为A到平面BCD间的间隔，又因二面角P-AB-Q是直二面角，过A作AC⊥AB交BF于C，即AC⊥平面ABD，过A作AD⊥BD交于D，保持CD.设A到平面BCD的间隔为h.由体积法V A-BCD=V C-ABD，得3转化为面面间隔若a、b是两条异面直线，则存在两个平行平面α、β，且a∈α、b∈β.求a、b两条异面直线的间隔转化为平行平面α、β间的间隔.例3已知：三棱锥S-ABC中，SA=BC=13，SB=AC=14，SC=AB=15，求异面直线AS与BC的间隔.思路分析：这是一不容易直接求解的几何题，把它补成一个易求解的几何体的典型例子，常常有时还常把残破形体补成完整形体；不规则形体补成规则形体；不熟悉形体补成熟悉形体等.所以，把三棱锥的四个面联想到长方体割去四个直三棱锥所得，因此，将三棱锥补形转化为长方体，设长方形的长、宽、高分别为x、y、z，解得x=3，y=2，z=1.由于平面SA‖平面BC，平面SA、平面BC间的间隔是2，所以异面直线AS与BC的间隔是2.4 代数求极值法根据异面直线间间隔是分别在两条异面直线上的两点间间隔的最小值，可用求函数最小值的方法来求异面直线间的间隔.例4 已知正方体ABCD-A1B1C1D1的棱长1 AC为a ，求A 1B 与D 1B 1的间隔.思路分析：在A 1B 上任取一点M ，作MP ⊥A 1B 1，PN ⊥B 1D 1，则MN ⊥B 1D 1，只要求出MN 的最小值即可.设A 1M=x ，则，A 1所以PB 1=a，PN=（a）sin450–x ），当MN min5公式法异面直线间间隔公式：隔.例 5 已知圆柱的底面半径为3，高为4，A 、B 两点分别在两底面圆周上，而且AB=5，求异面直线AB 与轴OO /之间的间隔.思路分析：在圆柱底面上AO ⊥OO /，BO /⊥OO /，又OO /是圆柱的高，AB=5，所以即异面直线AB 与轴OO /之间的6 射影法将两条异面直线射影到同一平面内，射影分别是点和直线或两条平行线，那末点和直线或两条平行线间的间隔就是两条异面直线射影间间隔.例 6 在正方体ABCD-A 1B 1C 1D 1中，AB=1，M 、N 分别是棱AB 、CC 1的中点，E 是BD 的中点.求异面直线D 1M 、EN 间的间隔.思路分析：两条异面直线比较难转化为线面、面面间隔时，可采取射影到同一平面内，把异面直线D 1M 、EN 射影到同一平面BC 1内，转化为BC 1、QN 的间隔，显然，易知BC 1、QN 的间隔为所以异面直线D 1M 、EN7.向量法：先求两异面直线的公共法向量，再求两异面直线上两点的保持线段在 公共法向量上的射影长.例7 已知：正方体ABCD-A 1B 1C 1D 1的棱长为求异面直线DA 1与AC 的间隔.看做是.此题教员引导，学生口述，教员在课件上演示解题过程，总结解题步调.1NC解：如图所示建立空间直角坐标系D-xyz∴D(0,0,0)A1(1,0,1) A(1,0,0) C(0,1,0)异面直线DA1与AC∴异面直线DA1与AC的间隔为步调小结：求异面直线间的间隔:⑴建立空间直角坐标系；⑵写出点的坐标，求出向量坐标；隔公式.例8 已知：SA⊥平面ABCD,∠DAB=∠SA=AB=BC=a,AD=2a，求A到平面SCD的间隔.解：如图所示建立空间直角坐标系A—xyz∴A（0,0,0）C(a,a,0) D(0,2a,0) S(0,0,a) ∴设面SCD∴点A到面SCD A到面SCD的间隔为36a八等积法把异面直线间的间隔转化为求某个特殊几何体的的高，操纵体积相等求出该高的长度.例：正四棱锥S-ABCD中，底面边长为a，侧棱长为b(b＞a)．求：底面临角线AC与侧棱SB间的间隔．设BC与平面SAD间的间隔为d，则以B为顶点，△SAD为底面的三棱锥的体积为而以S为顶点，△ABD为底面的三棱锥的体积为。

异面直线之间距离公式异面直线之间的距离公式是一个重要的几何定理，在几何学和物理学中有广泛的应用。

它可以用来计算两条不相交的直线之间的最短距离，而不需要求解两条直线的交点。

本文将简要介绍异面直线之间距离公式的概念和推导方法，并通过实际例子展示其应用。

异面直线指的是不在同一个平面上的直线。

在三维空间中，我们可以用参数方程或者点向式方程来表示一条直线。

假设我们有两条异面直线，分别用参数方程表示为：L1: x = x1 + a1t, y = y1 + b1t, z = z1 + c1tL2: x = x2 + a2s, y = y2 + b2s, z = z2 + c2s其中(x1, y1, z1)和(x2, y2, z2)是两条直线上的已知点，(a1, b1, c1)和(a2, b2, c2)是两条直线的方向向量，t和s是参数。

异面直线之间的距离可以通过求解它们的最近点来得到。

最近点是指两条直线上的点，它们的距离最短。

假设最近点分别为P和Q，它们分别在L1和L2上。

那么向量PQ就是两条直线之间的最短距离的方向向量。

我们可以通过以下步骤来推导异面直线之间距离的公式。

1. 首先，我们可以得到向量PQ的方向向量为：d = PQ = (x2 - x1, y2 - y1, z2 - z1)2. 由于向量d是与两条直线的方向向量正交的向量，即与(a1, b1,c1)和(a2, b2, c2)垂直。

因此，我们可以得到以下两个方程：(a1, b1, c1) · d = 0(a2, b2, c2) · d = 0其中·表示向量的点乘运算。

3. 将d的分量代入以上两个方程，我们可以得到一个关于t和s的线性方程组：(a1(x2 - x1) + b1(y2 - y1) + c1(z2 - z1))t = -a1(x1 - x2) - b1(y1 - y2) - c1(z1 - z2)(a2(x2 - x1) + b2(y2 - y1) + c2(z2 - z1))s = -a2(x1 - x2) - b2(y1 - y2) - c2(z1 - z2)4. 解这个线性方程组，我们可以得到t和s的值。

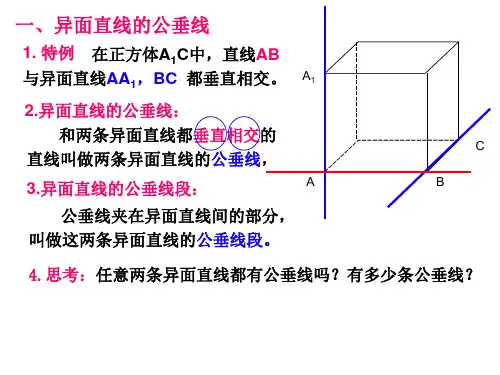
异面直线的距离求法咱们聊聊异面直线的那点事儿，特别是它们之间距离的那些小秘密。

在数学的浩瀚宇宙里，异面直线就像是两条永远不会交汇的银河，各自闪耀在各自的天际。

虽然它们看起来遥不可及，但咱们数学界的朋友们，总爱琢磨这些看似不可能的事儿，比如怎么计算它们之间的距离。

想象一下，你手里有两根笔直的铅笔，它们不在同一个平面上，就像是夜空中最亮的两颗星，遥遥相望。

这时候，你可能就纳闷了：这俩家伙到底隔了多远呢？别急，咱们有妙招。

首先，咱们得找个“桥梁”，让这两条直线能间接地“握手言和”。

这个桥梁，就是咱们常说的“公垂线段”。

你可以把它想象成一座连接两个星球的隐形桥梁，它垂直于这两条直线所在的平面，就像一根定海神针，稳稳地立在那儿。

要找这个公垂线段，咱们得先用点技巧。

假设这两条直线分别是A和B，咱们可以在A上随便找个点P，然后向B所在的方向投射一条光线，就像手电筒照亮夜空一样。

这条光线会与B有一个交点Q，但Q不一定是咱们要找的公垂线段的端点。

不过别急，咱们可以沿着这条光线，找到一个与B平行且与A垂直的平面。

在这个平面上，A会有一个“影子”，咱们称它为A'。

现在，A'和B就在同一个平面上了，它们之间的距离，就是咱们要找的异面直线的距离。

而A'到B的最短距离，就是咱们之前说的公垂线段的长度。

这个长度，就像是你和心仪的人之间的距离，虽然不能直接到达，但可以通过一些巧妙的方法，测量出那份微妙而确切的“远”。

计算这个距离的时候，咱们得用到一些三角函数和几何知识，就像是解谜游戏一样，一步步揭开谜底。

不过别担心，只要你跟着步骤走，就像跟着导航找路一样，总能找到那个答案。

说到这里，你是不是觉得异面直线的距离求法也没那么神秘了呢？其实，数学就像是一座宝藏岛，里面藏着无数的秘密和惊喜。

只要咱们用心去挖掘，总能发现那些隐藏在数字和公式背后的美丽和奥秘。

所以，下次当你再看到那些看似复杂的数学问题时，不妨换个角度，用一颗好奇和探索的心去面对它们。