河南省2018年中考数学总复习第一部分教材考点全解第七章图形与变换第24讲尺规作图、视图与投影课件
- 格式:ppt
- 大小:5.11 MB
- 文档页数:60

第七章图形与变换第二十四讲平移、旋转与对称【基础知识回顾】一、轴对称与轴对称图形:1、轴对称:把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形那么就说这两个图形成轴对称,这条直线叫2、轴对称图形:如果把一个图形沿着某条直线对折,直线两旁的部分能够互相那么这个图形叫做轴对称图形3、轴对称性质:⑴关于某条直线对称的两个图形⑵对应点连接被对称轴【名师提醒:1、轴对称是指个图形的位置关系,而轴对称图形是指个具有特殊形状的图形;2、对称轴是而不是线段,轴对称图形的对称轴不一定只有一条】二、图形的平移与旋转:1、平移:⑴定义:在平面内,把某个图形沿着某个移动一定的这样的图形运动称为平移⑵性质:Ⅰ、平移不改变图形的与,即平移前后的图形Ⅱ、平移前后的图形对应点所连的线段平行且【名师提醒:平移作图的关键是确定平移的和】2、旋转:⑴定义:在平面内,将一个图形绕一个定点沿某个方向旋转一个,这样的图形运动称为旋转,这个点称为转动的称为旋转角⑵旋转的性质:Ⅰ、旋转前后的图形Ⅱ、旋转前后的两个圆形中,对应点到旋转中心的距离都,每对对应点与旋转中心的连线所成的角度都是旋转角都【名师提醒:1、旋转作用的关键是确定、和,2、一个图形旋转一定角度后如果能与自身重合,那么这个图形就是旋转对称图形】三、中心对称与中心对称图形:1、中心对称:在平面内,一个图形绕某一点旋转1800能与另一个图形就说这两个图形关于这个点成中心对称,这个点叫做2、中心对称图形:一个图形绕着某点旋转后能与自身重合,这种图形叫中心对称图形,这个点叫做3、性质:在中心对称的两个图形中,对称点的连线都经过且被平分【名师提醒:1、中心对称是指个图形的位置关系,而中心对称图形是指个具有特殊形状的图形2、常见的轴对称图形有、、、、、等,常见的中心对称图形有、、、、、等3、所有的正n边形都是对称图形,且有条对称轴,边数为偶数的正多边形,又是对称图形,4、注意圆形的各种变换在平面直角坐标系中的运用】【典型例题解析】1.已知点P(3,-1)关于y轴的对称点Q的坐标是(a+b,1-b),则a b的值为.2.点P(2,-1)关于x轴对称的点P′的坐标是.3.在图示的方格纸中(1)作出△ABC关于MN对称的图形△A1B1C1;(2)说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?4.已知点P(3,2),则点P关于y轴的对称点P1的坐标是,点P关于原点O的对称点P2的坐标是5.下列图形中既是中心对称图形又是轴对称图形的是()A.B.C.D.6.点(3,2)关于x轴的对称点为()A.(3,-2)B.(-3,2)C.(-3,-2)D.(2,-3)7.在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度后,那么平移后对应的点A′的坐标是()A.(-2,-3)B.(-2,6)C.(1,3)D.(-2,1)8.如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于()A.55°B.70°C.125°D.145°9.P是∠AOB内一点,分别作点P关于直线OA、OB的对称点P1、P2,连接OP1、OP2,则下列结论正确的是()A.OP1⊥OP B.OP1=OP2C.OP1⊥OP2且OP1=OP2D.OP1≠OP2 10.已知点M(3,-2),将它先向左平移4个单位,再向上平移3个单位后得到点N,则点N的坐标是.11.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘周长为280m,且桥宽忽略不计,则小桥总长为m.12.如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB= °.13.如图,正方形ABCD的边长为4,点P在DC边上且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为.14.如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为.15.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.第二十五讲相似图形(一):【知识梳理】1.比例基本性质及运用(1)线段比的含义:如果选用同一长度单位得两条线段a、b的长度分别为m、n,那么就说这两条线段的比是a:b=m:n,或写成a m=b n,和数的一样,两条线段的比a、b中,a叫做比的前项 b叫做比的后项.注意:①针对两条线段;②两条线段的长度单位相同,但与所采用的单位无关;③其比值为一个不带单位的正数.(2)线段成比例及有关概念的意义:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段,已知四条线段a、b、c、d,如果a c=b d或a:b=c:d,那么a、b、c、d叫做成比例的项,线段a、d叫做比例外项,线段b、d叫做比例内项,线段d叫做a、b、c的第四比例项,当比例内项相同时,即a bb c=或a:b=b:c,那么线段b叫做线段a和c的比例中项.(3)比例的性质,①基本性质:如果a:b=c:d,那么ad=bc;反之亦成立。

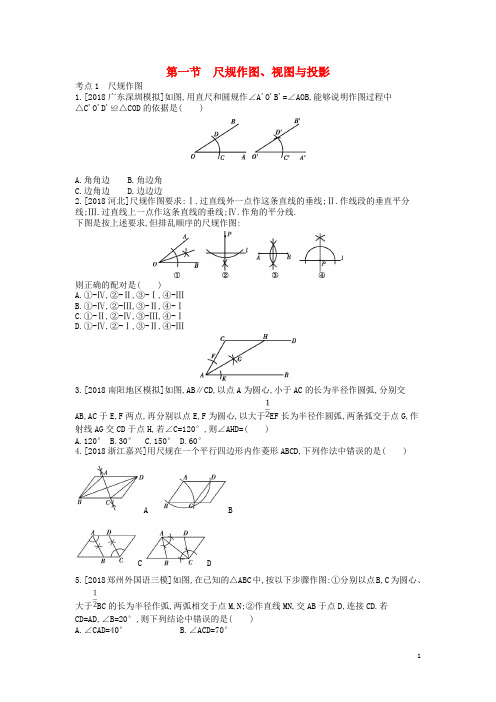
第一节尺规作图、视图与投影考点1 尺规作图1.[2018广东深圳模拟]如图,用直尺和圆规作∠A'O'B'=∠AOB,能够说明作图过程中△C'O'D'≌△COD的依据是( )A.角角边B.角边角C.边角边D.边边边2.[2018河北]尺规作图要求:Ⅰ.过直线外一点作这条直线的垂线;Ⅱ.作线段的垂直平分线;Ⅲ.过直线上一点作这条直线的垂线;Ⅳ.作角的平分线.下图是按上述要求,但排乱顺序的尺规作图:则正确的配对是( )A.①-Ⅳ,②-Ⅱ,③-Ⅰ,④-ⅢB.①-Ⅳ,②-Ⅲ,③-Ⅱ,④-ⅠC.①-Ⅱ,②-Ⅳ,③-Ⅲ,④-ⅠD.①-Ⅳ,②-Ⅰ,③-Ⅱ,④-Ⅲ3.[2018南阳地区模拟]如图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以点E,F为圆心,以大于EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=()A.120°B.30°C.150°D.60°4.[2018浙江嘉兴]用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )A BC D5.[2018郑州外国语三模]如图,在已知的△ABC中,按以下步骤作图:①分别以点B,C为圆心、大于BC的长为半径作弧,两弧相交于点M,N;②作直线MN,交AB于点D,连接CD.若CD=AD,∠B=20°,则下列结论中错误的是( )A.∠CAD=40°B.∠ACD=70°C.点D为△ABC的外心D.∠ACB=90°(第5题) (第6题)6.[2018开封二模]如图,在△ABC中,AD平分∠BAC,按如下步骤作图.第一步:分别以点A,D为圆心,大于AD的长为半径画弧,交于M,N两点;第二步:作直线MN分别交AB,AD,AC于点E,O,F;第三步:连接DE,DF.若BD=6,AF=4,CD=3,则BE的长是( )A.2B.4C.6D.8考点2 三视图的判断7.[2018山东潍坊]如图所示的几何体的左视图是( )A B C D8.[2017安徽]如图,一个放置在水平实验台上的锥形瓶,它的俯视图为( )A B C D9.[2018湖南常德]把图(1)中的正方体的一角切下后摆在图(2)所示的位置,则图(2)中的几何体的主视图为( )图(1) 图(2)A B C D10.[2018商丘地区模拟]如图是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的左视图为( )A B C D11.[2018海南]下列四个几何体中,主视图为圆的是( )A B C D12.[2018河南省实验三模]下列选项中,不是如图所示几何体的主视图、左视图、俯视图之一的是( )A B C D13.[2019原创]用若干个相同的小正方体搭成一个几何体模型,其主视图与左视图如图所示,则该几何体的俯视图不可能是( )A B C D考点3 根据三视图还原几何体14.[2018浙江金华]一个几何体的三视图如图所示,则该几何体是( )A.直三棱柱B.长方体C.圆锥D.立方体(第14题) (第15题) (第16题) 15.[2018青海]由一些相同的小立方块搭成的几何体的三视图如图所示,则搭成该几何体的小立方块有( )A.3个B.4个C.6个D.9个16.[2018南阳一模]如图是由几个相同的小正方体搭成的几何体的主视图与左视图,则搭成这个几何体的小正方体的个数最多是( )A.6B.7C.8D.917.[2018山东临沂]如图是一个几何体的三视图(图中尺寸单位:cm).根据图中所示数据求得这个几何体的侧面积是( )A.12 cm2B.(12+π)cm2C.6π cm2D.8π cm2考点4 立体图形的展开与折叠18.[2017河南B卷]下列不是正三棱柱的表面展开图的是( )A B C D19.[2018江苏常州]下列图形中,是圆锥的侧面展开图的是( )A B C D20.[2018郑州二模]小敏计划在暑假参加海外游学,她打算制作一个正方体礼盒送给外国朋友.如图是她设计的礼盒的平面展开图,请你判断,正方体礼盒上与“孝”字相对的面上的字是( )A.义B.仁C.智D.信21.[2018平顶山三模]图(1)和图(2)中所有的正方形都全等,将图(1)所示的正方形放在图(2)中的①②③④某一位置,所组成的图形不能..围成正方体的位置是( )图(1) 图(2)A.①B.②C.③D.④22.[2018驻马店地区模拟]若过正方体中有公共顶点的三条棱的中点切出一个角,形成如图所示的几何体,其正确展开图为( )23.[2016湖北恩施州]在广场的电子屏幕上有一个旋转的正方体,正方体的六个面上分别标有“恩施六城同创”六个字,如图是小明在三个不同时刻所观察到的图形,请你帮小明确定与“创”相对的面上的字是( )A.恩B.施C.城D.同第二节图形的对称、平移与旋转考点1 图形的轴对称1.[2018四川邵阳]下列图形中,是轴对称图形的是( )A B C D2.[2018河北]由“○”和“□”组成的轴对称图形如图所示,则该图形的对称轴是直线( )A.l1B.l2C.l3D.l43.[2018浙江嘉兴]将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )A B C D4.[2018广西梧州]如图,在△ABC中,AB=AC,∠C=70°,△AB'C'与△ABC关于直线EF对称,∠CAF=10°,连接BB',则∠ABB'的度数是( )A.30°B.35°C.40°D.45°(第4题) (第5题)5.[2018新疆]如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC 边上的中点,则MP+PN的最小值是( )A. B.1 C. D.26.[2017贵州贵阳]如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,则A'C的长的最小值是.考点2 图形的平移7.[2018四川南充]直线y=2x向下平移2个单位长度得到的直线是( )A.y=2(x+2)B.y=2(x-2)C.y=2x-2D.y=2x+28.[2018浙江温州]如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0,).现将该三角板向右平移使点A与点O重合,得到△OCB',则点B的对应点B'的坐标是( )A.(1,0)B.(,)C.(1,)D.(-1,)(第8题) (第9题)9.[2018江西]小军同学在网格纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形的顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有( )A.3种B.4种C.5种D.无数种10.[2018四川宜宾]如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC 的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )A.2B.3C. D.考点3 图形的旋转11.[2018黑龙江哈尔滨]下列图形中既是轴对称图形又是中心对称图形的是( )A B C D12.[2018四川绵阳]在平面直角坐标系中,以原点为旋转中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为( )A.(4,-3)B.(-4,3)C.(-3,4)D.(-3,-4)13.[2018海南]如图,在△ABC中,AB=8,AC=6,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC1,则BC1的长为( )A.6B.8C.10D.12(第13题) (第14题)14.[2017吉林长春]如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为.15.(8分)[2018广西北部湾经济区]如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).(1)将△ABC向下平移5个单位长度后得到△A1B1C1,请画出△A1B1C1;(点A,B,C的对应点分别为点A1,B1,C1)(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;(点A,B,C的对应点分别为点A2,B2,C2)(3)判断以O,A1,B为顶点的三角形的形状.(无需说明理由)16.(10分)[2018四川自贡中考改编]已知∠AOB=60°,在∠AOB的平分线OM上有一点C,将一个120°角的顶点与点C重合,它的两条边分别与直线OA,OB相交于点D,E.(1)当∠DCE绕点C旋转到CD与OA垂直时,如图(1),请猜想OE+OD与OC的数量关系,并说明理由;(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图(2)的位置,(1)中的结论是否成立?并说明理由.图(1) 图(2)1.[2018南阳地区模拟]如图,点O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心角为直角的扇形纸板的圆心放在点O处,并将纸板绕点O旋转,则正方形ABCD被纸板覆盖部分的面积为( )A.a2B.a2C.a2D. a(第1题) (第2题)2.[2018南阳一模]如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM长度的最大值是( )A.1B.2C.3D.43.[2018山东济南市中区二模改编]如图,把矩形纸片OABC放入平面直角坐标系中,使OA,OC 分别落在x轴,y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在点A'处,若OA=1,AB=2,则点A'的坐标为( )A.(-,)B.(-,)C.(-,)D.(-,)(第3题) (第4题)4.[2018周口地区模拟]如图,在平面直角坐标系中,原点O是等边三角形ABC的外心,若点A 的坐标为(0,3),将△ABC绕着点O顺时针旋转,每秒旋转60°,则第2 018秒时,点A的坐标为( )A.(0,3)B.(-,)C.(,-)D.(-3,3)5.[2017郑州外国语三模]如图,大小两个正方形在同一水平线上,小正方形从图(1)的位置开始,匀速向右平移,到图(3)的位置停止运动.若运动时间为x,两个正方形重叠部分的面积为y,则下列图象中,能表示y与x函数关系的大致图象是( )6.[2018郑州八中三模]如图,在矩形ABCD中,AB=3,AD=5,点E为射线CD上一动点,沿BE所在直线折叠矩形,如果点C的对应点C'恰好落在射线DA上,那么此时线段DC'的长度为.7.(10分)[2018河南省实验四模]如图(1),△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.(1)将△ADE绕点A 旋转,当C,D,E三点共线时,如图(2),连接BD,BE,有下列结论:①BD=CE,②BD⊥CE,③∠ACE+∠DBC=45°,④BE2=2(AD2+AB2).其中正确的是.(2)若AB=4,AD=2,把△ADE绕点A旋转.①当∠EAC=90°时,求PB的长;②求旋转过程中线段PB长的最大值.图(1) 图(2)备用图(1) 备用图(2)参考答案第一节尺规作图、视图与投影1.D 由题意可知,OD=OC=O'D'=O'C',CD=C'D',∴△COD≌△C'O'D'(SSS),故选D.2.D 题图①中的过程是作角的平分线(Ⅳ),题图②中的过程是过直线外一点作这条直线的垂线(Ⅰ),题图③中的过程是作线段的垂直平分线(Ⅱ),题图④中的过程是过直线上一点作这条直线的垂线(Ⅲ).故选D.3.C 由作法得AH平分∠BAC.∵AB∥CD,∴∠BAC=180°-∠C=180°-120°=60°,∴∠CAH=∠BAC=30°,∴∠AHD=∠CAH+∠C=30°+120°=150°.故选C.4.C A项中,由作图可知,AC⊥BD,且AC平分BD,BD平分AC,即四边形ABCD的对角线互相垂直平分,故四边形ABCD是菱形;B项中,由作图可知,AB=BC,AD=AB,故四边形ABCD是菱形;C项中,只能得出四边形ABCD是平行四边形;D项中,由作图可知,对角线AC平分∠BAD和∠BCD,可以得出四边形ABCD是菱形.故选C.5.A 由题意可知直线MN是线段BC的垂直平分线,∴BD=CD,∠B=∠BCD.∵∠B=20°,∴∠BCD=20°,∴∠CDA=20°+20°=40°.∵CD=AD,∴∠ACD=∠CAD==70°,故选项A中的结论错误,选项B中的结论正确.∵CD=AD,BD=CD,∴CD=AD=BD,∴点D为△ABC的外心,故选项C中的结论正确.∵∠ACD=70°,∠BCD=20°,∴∠ACB=70°+20°=90°,故选项D中的结论正确.6.D 由尺规作图可知MN是AD的垂直平分线,∴AE=DE,AF=DF,∠AOE=∠AOF=90°.∵AD是∠BAC的平分线,∴∠EAO=∠FAO.又∵AO=AO,∴△AEO≌△AFO,∴AE=AF,∴AE=DE=DF=AF,∴四边形AEDF是菱形,∴DF∥AB,∴△DCF∽△BCA,∴=,即=,解得BE=8.7.D 左视图是指观察者从左面看几何体所得到的平面图形,且看不见的轮廓线要用虚线表示,故选D.8.B 从正上方观察该锥形瓶,瓶口和瓶底都是圆,故它的俯视图是圆环.9.D 由题意得,题图(2)中的几何体的主视图为等腰三角形,且OS投影为等腰三角形底边上的高,故选D.10.A 从左面看可得到从左到右分别是3,2个正方形.故选A.11.C 选项A,B,C,D中几何体的主视图分别是矩形、三角形、圆、正方形.故选C.12.A 选项B,C,D中的图形分别是该几何体的俯视图、左视图和主视图,故选A.13.D 根据主视图、左视图,可知A,B,C中的图形均有可能是几何体的俯视图,只有D中的图形不可能是几何体的俯视图.故选D.14.A 由三视图的定义可知,该几何体是直三棱柱,故选A.15.B 如图是该几何体的俯视图,其上数字是该位置上小正方体的个数,故该几何体有4个小正方体组成.故选B.16.B 由主视图和左视图可知,该几何体的俯视图最多可由两行三列的小正方形组成,如图所示,小正方形内的数字是该位置上小正方体个数的最大值,故搭成这个几何体的小正方体的个数最多是7,故选B.17.C 由三视图知该几何体是圆柱体,且底面直径是2 cm,高是3 cm,则其侧面积为2π×3=6π(cm2).18.D 观察四个选项,可以发现前三个选项中的图形都可以围成三棱柱,而选项D中的图形在围成立体图形时,两个正三角形重叠在了一个底面上,故选D.19.B 圆锥的侧面展开图是扇形.故选B.20.B 将该平面展开图折叠后,“信”与“智”相对,“孝”与“仁“相对,“礼”与“义”相对.故选B.21.A 如图,当正方形放在①的位置时,若⑦是正方形的下面,则⑥是左面,⑤是上面,⑧是前面,①和⑨都是右面,此时没有后面,不能围成正方体,故选A.22.B 将各选项中的展开图折叠起来,可知A,C,D均不符合题意,只有B符合题意.故选B.23.D 由题图可以看出“六”与“同”、“城”、“创”、“施”相邻,故“六”与“恩”相对;“创”与“六”、“城”、“施”相邻,故“创”与“同”相对.故选D.第二节图形的对称、平移与旋转真题分点练1.B 由轴对称图形的定义可得,B中的图形是轴对称图形.2.C 该图形沿直线l3对折后,直线l3两旁的部分能够完全重合,故直线l3是该图形的对称轴.3.A 根据图形的对称性还原可知应选A.4.C ∵AB=AC,∠C=70°,∴∠ABC=70°,∴∠BAC=180°-2×70°=40°.∵△AB'C'与△ABC 关于直线EF对称,∴△BAC≌△B'AC',∠C'AF=∠CAF=10°,∴AB=AB',∠B'AC'=∠BAC=40°,∴∠BAB'=40°+10°+10°+40°=100°,∴∠ABB'=∠AB'B=×(180°-100°)=40°.故选C.5.B 如图,作点M关于直线AC的对称点M',连接M'N交AC于点P,此时MP+NP有最小值,最小值为M'N的长.∵菱形ABCD的对称轴为直线AC,点M是AB的中点,∴点M'是AD的中点,又∵点N是BC边上的中点,∴AM'∥BN,AM'=BN,∴四边形ABNM'是平行四边形,∴M'N=AB=1,即MP+PN的最小值为1,故选B.6.-1 根据折叠的性质,可知A'E=AE=AB=1,故点A'位于以点E为圆心、AE为半径的圆上,连接CE,根据“两点之间,线段最短”,可知当点A'在EC上时,A'C最短.在Rt△BCE中,BE=AB=1,BC=3,∠B=90°,∴CE==,∴A'C的长的最小值为CE-A'E=-1.7.C 把直线y=2x向下平移2个单位长度,得到的直线所对应的函数解析式为y=2x-2.故选C.8.C 由点A,B的坐标可知OA=1,OB=.由平移的性质可知OC=OA=1,CB'=OB=,∵点B'位于第一象限,∴点B'的坐标为(1,).9.C 因平移后的正方形的顶点也在格点上,且平移前后的两个正方形组成轴对称图形,故平移的方向有下面几种:①向上平移;②向下平移;③向右平移;④向右上方平移;⑤向右下方平移.故有5种平移方向.10.A 如图,∵S△ABC=9,S△A'EF=4,AD为BC边上的中线,∴S△A'DE=S△A'EF=2,S△ABD=S△ABC=.∵将△ABC沿BC边上的中线AD平移得到△A'B'C',∴A'E∥AB,∴∠DA'E=∠DAB,∠DEA'=∠DBA,∴△DA'E∽△DAB,∴()2=,即()2=,解得A'D=2或A'D=-(不合题意,舍去).故选A.11.C 选项A中的图形既不是轴对称图形,也不是中心对称图形;选项B中的图形是中心对称图形,不是轴对称图形;选项C中的图形既是轴对称图形,又是中心对称图形;选项D中的图形是轴对称图形,不是中心对称图形.故选C.12.B 如图,可得点B的坐标为(-4,3).13.C 由旋转可得∠CAC1=60°,∴∠BAC1=∠BAC+∠CAC1=60°+30°=90°.在Rt△BAC1中,AB=8,AC1=6,∴BC1===10.故选C.14.(-2,-3) 如图,过点A作AD⊥BC于点D,由点B,C的坐标为(2,1),(6,1),得BC=4.由∠BAC=90°,AB=AC,得AB=2,∠ABD=45°,∴BD=AD=2,A(4,3).设直线AB的解析式为y=kx+b,将点A,B的坐标分别代入,得解得故直线AB的解析式为y=x-1,当y=0时,x=1,即P(1,0),∴x A'=2x P-x A=2-4=-2,y A'=2y P-y A=0-3=-3,A'(-2,-3).15.(1)△A1B1C1如图所示. (3分)(2)△A2B2C2如图所示.(6分)(3)△OA1B是以点O为直角顶点的等腰直角三角形. (8分) 16.(1)OE+OD=OC.理由:∵OM是∠AOB的平分线,∴∠AOC=∠BOC=∠AOB=30°.∵CD⊥OA,∴∠ODC=90°,∴∠OCD=60°,∴∠OCE=∠DCE-∠OCD=60°.在Rt△OCD中,OD=OCcos 30°=OC,同理可得OE=OC,∴OE+OD=OC.(5分)(2)(1)中结论仍然成立.理由:如图,过点C作CF⊥OA于点F,CG⊥OB于点G,则∠OFC=∠OGC=90°.∵∠AOB=60°,∴∠FCG=120°.同(1)的方法,得OF=OC,OG=OC,∴OF+OG=OC.∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG.∵∠DCE=120°,∠FCG=120°,∴∠DCF=∠ECG,∴△CFD≌△CGE,∴DF=EG,∴OF=OD+DF=OD+EG,OG=OE-EG,∴OF+OG=OD+EG+OE-EG=OD+OE,∴OE+OD=OC.(10分)模拟提升练1.B 由题易知,正方形ABCD被纸板覆盖部分的面积是一定的.设扇形的半径交AD于点E,交CD于点F,连接OD,OC,如图.∵四边形ABCD为正方形,∴OD=OC,∠COD=90°,∠ODA=∠OCD=45°.∵∠EOF=90°,即∠EOD+∠DOF=90°.∵∠DOF+∠COF=90°,∴∠EOD=∠FOC.在△ODE和△OCF中,∴△ODE≌△OCF,∴S△ODE=S△OCF,∴S阴影部分=S△DOC=S正方形ABCD=a2.故选B.2.C 连接CP,∵∠ACB=90°,∠BAC=30°,BC=2,∴A'B'=AB=4.∵点P是A'B'的中点,∴CP=A'B'=×4=2,又∵点M是BC的中点,∴CM=BC=×2=1,∴PC+CM=3.∵PC+CM≥PM,∴当点P在BC的延长线上时,PM长度最大,是3,故选C.3.C 设A'B与y轴交于点E.由折叠的性质,可得∠A'BO=∠ABO.由AB∥y轴,得∠COB=∠ABO,∴∠A'BO=∠COB,∴EO=EB.设EO=EB=x,则CE=2-x.根据勾股定理可得CE2+BC2=EB2,∴(2-x)2+12=x2,解得x=,则EO=.过点A'作A'F⊥x轴于点F,则∠FA'O=∠A'OE,∴cos∠A'OE=cos∠FA'O,∴=,∴=,解得A'F=,∴OF==,∴A'(-,).4.C ∵360°÷60°=6,2 018=6×336+2,∴第2 018秒时,点A旋转到点A'处,如图,连接OA',∠AOA'=120°,OA'=OA=3,过点A'作A'H⊥x轴于点H.∵∠A'OH=30°,∴A'H=OA'=,OH=A'H=,∴A'(,-).故选C.5.C 在小正方形运动的过程中,y与x的函数关系为分段函数.随着时间x的增大,重叠部分的面积y由0开始增大;当小正方形全部进入大正方形后,重叠部分的面积达到最大值,并能保持一段时间;当小正方形开始从大正方形的右侧出来时,重叠部分的面积开始减小;当小正方形完全离开大正方形后,重叠部分的面积变为0.综上可知,选项C中的图象符合题意.6.1或9 由折叠的性质可知△BCE≌△BC'E,∴BC'=BC=AD=5.在Rt△ABC'中,由勾股定理得,AC'===4.分两种情况:①当点E在线段CD上时,如图(1),DC'=AD-AC'=5-4=1.②当点E在线段CD的延长线上时,如图(2),DC'=AD+AC'=5+4=9.图(1) 图(2)7.(1)①②③(3分)(2)①分两种情况讨论.a.如图(1),当点E在AB上时,BE=AB-AE=2.∵∠EAC=90°,∴CE==2.易证△ADB≌△AEC,∴∠DBA=∠ECA.∵∠PEB=∠AEC,∴△PEB∽△AEC,∴=,∴=,∴PB=.图(1) 图(2)b.如图(2),当点E在BA的延长线上时,BE=6.同a.可得△PEB∽△AE C,∴=,∴=,∴PB=.综上,PB=或.(7分)②如图(3),以点A为圆心、AD为半径画圆,当点B,E在☉A的异侧,且CE与☉A相切时,PB 的值最大.图(3)∵AE⊥EC,∴EC==2.由(1)可知,△ABD≌△ACE,∴∠ADB=∠AEC=90°,BD=CE=2,∴∠ADP=∠DAE=∠AEP=90°,∴四边形AEPD是矩形,∴PD=AE=2,∴PB=BD+PD=2+2.综上,PB长的最大值是2+2.(10分)。


