S面板数据模型操作命令

STATA面板数据模型操作命令讲解编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（STATA面板数据模型操作命令讲解）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为STATA面板数据模型操作命令讲解的全部内容。

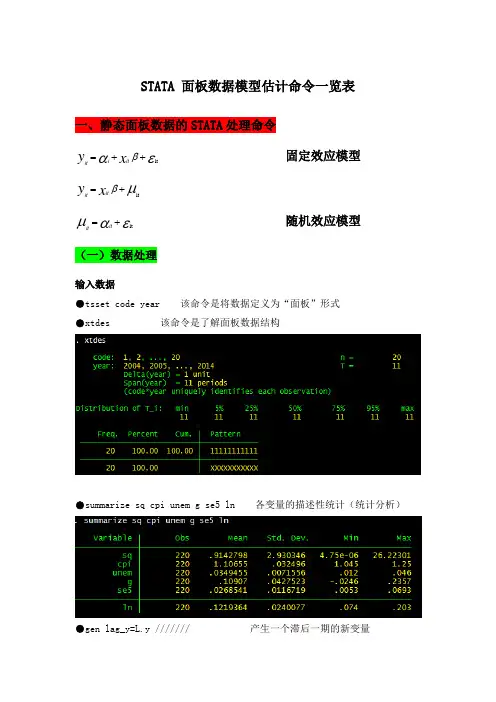
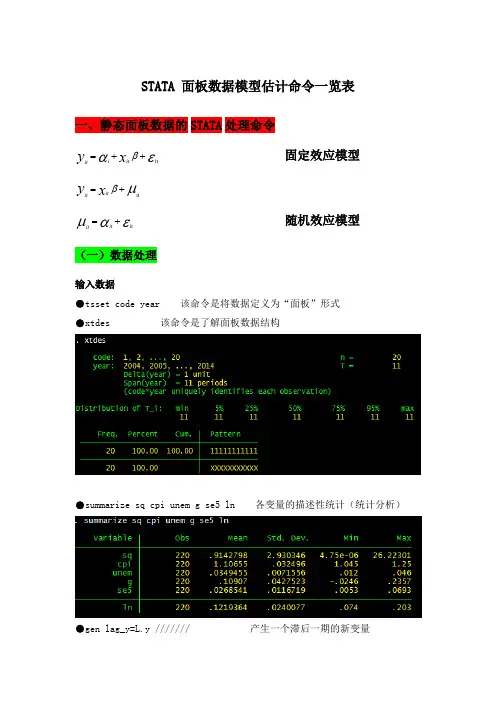
STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令固定效应模型 随机效应模型 (一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量εαβit++=x y it i it μβit+=x y it it εαμit+=ititgen F_y=F。

y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2。

y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应)（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln，fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0。

0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量）(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln，re （加上“qui"之后第一幅图将不会呈现）xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

STATA面板数据模型操作命令讲解编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（STATA面板数据模型操作命令讲解）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为STATA面板数据模型操作命令讲解的全部内容。

STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令 固定效应模型εαβit ++=x y it i it μβit +=x y it it随机效应模型εαμit +=it it (一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F 。

y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2。

y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应)（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln，fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0。

0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量）(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln，re （加上“qui"之后第一幅图将不会呈现）xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

STATA 面板数据模型估计命令一览表 一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型（一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

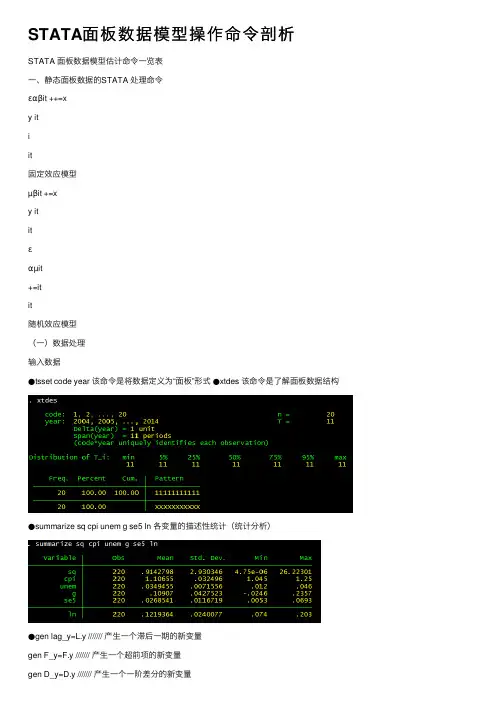
STATA⾯板数据模型操作命令剖析STATA ⾯板数据模型估计命令⼀览表⼀、静态⾯板数据的STATA 处理命令εαβit ++=xy itiit固定效应模型µβit +=xy ititεαµit+=itit随机效应模型（⼀）数据处理输⼊数据●tsset code year 该命令是将数据定义为“⾯板”形式●xtdes 该命令是了解⾯板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产⽣⼀个滞后⼀期的新变量gen F_y=F.y /////// 产⽣⼀个超前项的新变量gen D_y=D.y /////// 产⽣⼀个⼀阶差分的新变量gen D2_y=D2.y /////// 产⽣⼀个⼆阶差分的新变量（⼆）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使⽤OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型⽽⾔，回归结果中最后⼀⾏汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例⼦中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验⽅法：LM统计量）（原假设：使⽤OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第⼀幅图将不会呈现) xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应⾮常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验⽅法：Hausman检验）原假设：使⽤随机效应模型（个体效应与解释变量⽆关）通过上⾯分析，可以发现当模型加⼊了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是⽆法明确区分FE or RE的优劣，这需要进⾏接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进⾏Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满⾜。

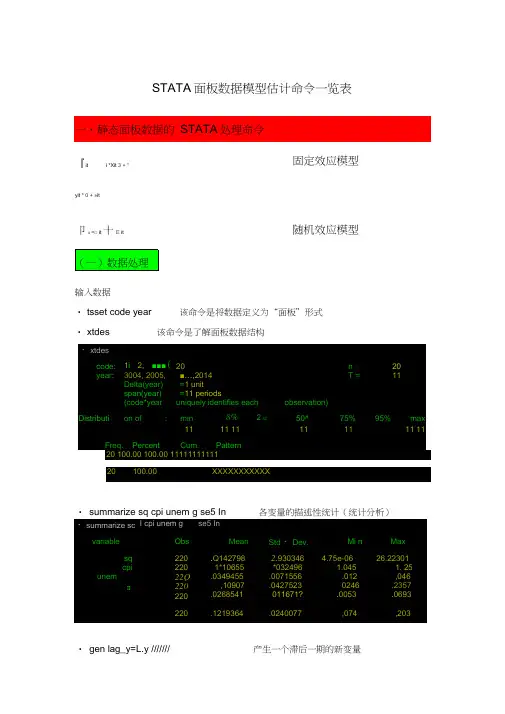
STATA面板数据模型估计命令一览表输入数据•tsset code year 该命令是将数据定义为“面板”形式•xtdes 该命令是了解面板数据结构• summarize sq cpi unem g se5 In 各变量的描述性统计（统计分析）• gen lag_y=L.y /////// 产生一个滞后一期的新变量to U 一 if对于固定效应模型而言，回归结果中最后一行汇报的F 统计量便在于检验所 有的个体效应整体上显著。

在我们这个例子中发现 F 统计量的概率为0.0000 , 检验结果表明固定效应模型优于混合 OLS 模型。

合效应还是随机效应） （检验方法：LM 统计量）（原假设：使用OLS 混合模型） • qui xtreg sq cpi unem g se5 ln,re（加上"qui ”之后第一幅图将不会呈现 ）xttest0xizretg s-<q cpifgen F_y=F.y /////// gen D_y=D.y /////// gen D2_y=D2.y ///////产生一个超前项的新变量 产生一个一阶差分的新变量 产生一个二阶差分的新变量（二）模型的筛选和检验• 1检验个体效应 （混合效应还是固定效应）（原假设：使用OLS 混合模型） • xtreg sq cpi unem g se5 ln,fe3C"t 『U<3 SCI C.IPm feor r Cu iO-23OZ O. O<7i67 O- 匕 Qm -Bk T -:<?■£ f 3 X dmts m 工■zd s d z mAm - -5 -1s u a 工一67 ■r.QB€BJL£3;4M 4Liny;工G-RO 丄 bo --A - « _ QprlsrlQ --mA6.2:sGctg scs0'.x丄z skJ>4y-- -S4S"0 Get 一一一GftlxJ2 IKqg4岭济34工Lu -^-3 ■■MB : od JL X QX 丄炮丄• 2、检验时间效应O- SZ £>&■ J d rn可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

STATA面板数据模型操作命令讲解STATA 面板数据模型估计命令一览表一、静态面板数据的STATA处理命令y it i xit it 固定效应模型yit x it itit it it 随机效应模型（一）数据处理输入数据●tsset code year该命令是将数据定义为“面板”形式●xtdes该命令是了解面板数据结构● summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）● gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS 混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F 统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F 统计量的概率为 0.0000 ，检验结果表明固定效应模型优于混合 OLS模型。

● 2、检验时间效应（混合效应还是随机效应）（检验方法：LM 统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5( 加上“ qui ”之后第一幅图将不会呈现) ln,re xttest0可以看出， LM检验得到的 P 值为 0.0000 ，表明随机效应非常显著。

可见，随机效应模型也优于混合 OLS模型。

● 3、检验固定效应模型or 随机效应模型（检验方法：Hausman 检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合 OLS模型。

但是无法明确区分 FE or RE 的优劣，这需要进行接下来的检验，如下：Step1 ：估计固定效应模型，存储估计结果Step2 ：估计随机效应模型，存储估计结果Step3 ：进行 Hausman检验●qui xtreg sq cpi unem g se5ln,fe est store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe ( 或者更优的是hausman fe,sigmamore/ sigmaless)可以看出， hausman检验的 P 值为 0.0000 ，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

STATA面板数据模型操作命令讲解STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令εαβit ++=xy itiit固定效应模型μβit +=xy ititεαμit+=itit随机效应模型〔一〕数据处理输入数据●tsset code year 该命令是将数据定义为“面板〞形式 ●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计〔统计分析〕●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量〔二〕模型的筛选和检验●1、检验个体效应〔混合效应还是固定效应〕〔原假设：使用OLS混合模型〕●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果说明固定效应模型优于混合OLS模型。

●2、检验时间效应〔混合效应还是随机效应〕〔检验方法：LM统计量〕〔原假设：使用OLS混合模型〕●qui xtreg sq cpi unem g se5 ln,re (加上“qui〞之后第一幅图将不会呈现)xttest0可以看出，LM检验得到的P值为0.0000，说明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型〔检验方法：Hausman检验〕原假设：使用随机效应模型〔个体效应与解释变量无关〕通过上面分析，可以发现当模型参加了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的根本假设得不到满足。

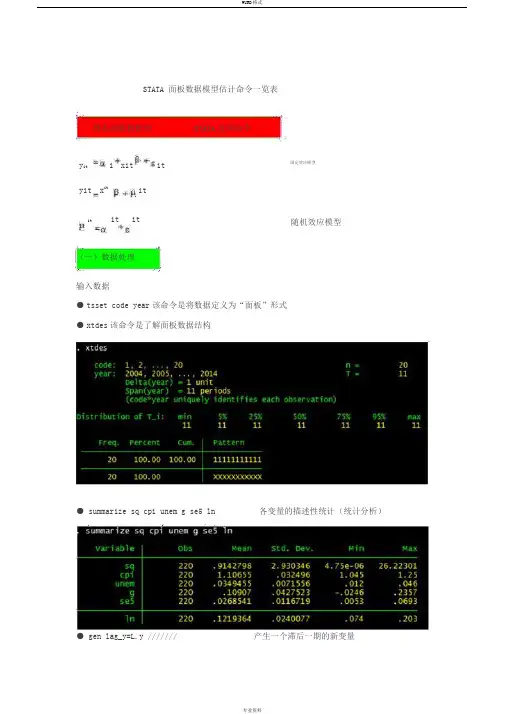
STATA 面板数据模型估计命令一览表一、静态面板数据的STATA处理命令y it i xit it 固定效应模型yit x it itit it it 随机效应模型（一）数据处理输入数据●tsset code year该命令是将数据定义为“面板”形式●xtdes该命令是了解面板数据结构● summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）● gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用 OLS 混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的 F 统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现 F 统计量的概率为 0.0000 ，检验结果表明固定效应模型优于混合 OLS模型。

● 2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5( 加上“ qui ”之后第一幅图将不会呈现) ln,re xttest0可以看出， LM检验得到的 P 值为 0.0000 ，表明随机效应非常显著。

可见，随机效应模型也优于混合 OLS模型。

● 3、检验固定效应模型or 随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合 OLS模型。

但是无法明确区分 FE or RE 的优劣，这需要进行接下来的检验，如下：Step1 ：估计固定效应模型，存储估计结果Step2 ：估计随机效应模型，存储估计结果Step3 ：进行 Hausman检验●qui xtreg sq cpi unem g se5ln,fe est store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe ( 或者更优的是 hausman fe,sigmamore/ sigmaless)可以看出， hausman检验的 P 值为 0.0000 ，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

02
下载EViews安装程序后，按照提示进行安装，选择 合适的安装路径和组件。
03
安装完成后，需要配置EViews的环境变量和启动选 项。
EViews软件界面与操作
EViews的界面包括菜单栏、工具栏、工作区、状态栏等部分，用户可以通 过菜单栏选择需要的命令和功能。
工作区是用户进行数据分析和模型估计的主要区域，可以显示数据表格、 图形、方程等。
固定效应模型
在固定效应模型中，个体固定效应被包括在内，这意 味着模型将考虑每个个体特有的不随时间变化的特征 对因变量的影响。在EViews中，可以通过在`xtreg`命 令后加上`fe`来指定固定效应模型。解读固定效应模型 的估计结果时，应注意观察固定效应的系数和显著性 水平，以了解不同个体的固定效应对因变量的影响程 度和显著性。
提高估计精度
相对于单一时间序列或横截面数据模型，面板数据模型能够利用更多的信息，提高估计 的精度。
面板数据模型在经济学研究中的挑战与展望
数据质量和可获得性
高质量的面板数据是进行面板数据分 析的前提，但获取高质量的面板数据 存在一定的难度。
动态面板数据分析
模型选择和设定
在应用面板数据模型时，需要合理选 择和设定模型，以避免模型误设导致 的估计偏误。
社会学研究 面板数据模型在社会学研究中用 于分析社会现象和趋势，如人口 变化、教育发展、犯罪率等。
医学研究 面板数据模型在医学研究中用于 分析疾病发病率、流行趋势、治 疗效果等，为医学研究和公共卫 生政策提供依据。
02
EViews软件介绍
EViews软件概述
EViews是一款专门用于计量经济学和时 间序列分析的软件，提供了一系列强大 的统计分析工具和图形化界面，方便用 户进行数据分析和模型估计。

STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令固定效应模型εαβit ++=x y it i it μβit +=x y it it随机效应模型εαμit +=it it （一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现)xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

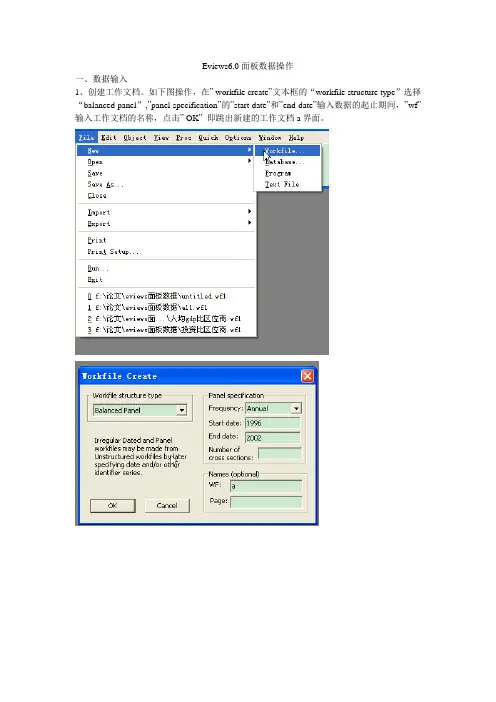
Eviews6.0面板数据操作一、数据输入1、创建工作文档。

如下图操作，在” workfile create”文本框的“workfile structure type”选择“balanced panel”,”panel specification”的”start date”和”end date”输入数据的起止期间，”wf”输入工作文档的名称，点击” OK”即跳出新建的工作文档a界面。

2、创建新对象。

操作如下图。

在”new object”文本框的”type of object”选择”pool”，”name for object ”输入新对象的名称。

创建成功后的界面如下面第3张图所示。

3、输入数据。

双击”workfile”界面的，跳出”pool”界面，输入个体。

一般输入方式为如下：若上海输入_sh，北京输入_bj,…。

个体输入完成后，点击该界面的键，在跳出的”series list”输入变量名称，注意变量后要加问号。

格式如下：y? x?。

点击”OK”后，跳出数据输入界面，如下面第4张图所示。

在这个界面上点击键，即可以输入或者从EXCEL处复制数据。

在输入数据后，记得保存数据。

保存操作如下：在跳出的“workfile save”文本框选择“ok”即可，则自动保存到我的文档。

然后在“workfile”界面如下会显示保存路径：d:\my documents\a.wf1。

若要保存到自己选择的路径下面，则在保存时选择“save as”,在跳出的文本框里选择自己要保存的路径以及命名文件名称。

4、单位根检验。

一般回归前要检验面板数据是否存在单位根，以检验数据的平稳性，避免伪回归，或虚假回归，确保估计的有效性。

单位根检验时要分变量检验。

（补充：网上对面板数据的单位根检验和协整检验存在不同意见，一般认为时间区间较小的面板数据无需进行这两个检验。

）（1）生成数据组。

如下图操作。

点击”make group”后在跳出的”series list”里输入要单位根检验的变量，完成后就会跳出如下图3所示的组数据。

一文读懂面板数据主要命令来源：网络，由计量经济学服务中心综合整理，转载请注明来源首先对面板数据进行声明：前面是截面单元，后面是时间标识：tsset company yeartsset industry year产生新的变量：gennewvar=human*lnrd产生滞后变量Genfiscal(2)=L2.fiscal产生差分变量Genfiscal(D)=D.fiscal一、描述性统计xtdes ：对Panel Data截面个数、时间跨度的整体描述Xtsum：分组内、组间和样本整体计算各个变量的基本统计量xttab 采用列表的方式显示某个变量的分布二、主要命令和方法Stata中用于估计面板模型的主要命令：xtregxtreg depvar [varlist] [if exp] , model_type [level(#) ] Model type 模型be Between-effects estimatorfe Fixed-effects estimatorre GLSRandom-effects estimatorpa GEEpopulation-averaged estimatormle Maximum-likelihood Random-effectsestimator主要估计方法：xtreg： Fixed-, between- and random-effects, and population-averaged linear modelsxtregar：Fixed- andrandom-effects linear models with an AR(1) disturbancextpcse ：OLS orPrais-Winsten models with panel-corrected standard errorsxtrchh ：Hildreth-Houckrandom coefficients modelsxtivreg ：Instrumentalvariables and two-stage least squares for panel-data modelsxtabond：Arellano-Bond linear, dynamic panel data estimatorxttobit ：Random-effectstobit modelsxtlogit ： Fixed-effects,random-effects, population-averaged logit modelsxtprobit ：Random-effects andpopulation-averaged probit modelsxtfrontier ：Stochastic frontiermodels for panel-dataxtrc gdp invest culture edu sci health social admin,beta三、xtreg命令的应用声明面板数据类型：tsset sheng t描述性统计：xtsum gdp investsci admin1.固定效应模型估计：xtreg gdp invest culture sci health admin techno,fe固定效应模型中个体效应和随机干扰项的方差估计值(分别为sigma u 和sigma e），二者之间的相关关系(rho)最后一行给出了检验固定效应是否显著的F 统计量和相应的P 值2.随机效应模型估计：xtreg gdp invest culture sci health admin techno,re检验随机效应模型是否优于混合OLS 模型：在进行随机效应回归之后，使用xttest0检验得到的P 值为0.0000，表明随机效应模型优于混合OLS 模型3. 最大似然估计Ml：xtreg gdp invest culture sci health admin techno,mleHausman检验Hausman检验究竟选择固定效应模型还是随机效应模型：第一步：估计固定效应模型，存储结果xtreg gdp invest culture sci health admin techno,feest store fe第二步：估计随机效应模型，存储结果xtreg gdp invest culture sci health admin techno,reest store re第三步：进行hausman检验hausman feHausman检验量为：H=(b-B)´[Var(b)-Var(B)]-1(b-B)～x2(k)Hausman统计量服从自由度为k的χ2分布。

STATA 面板数据模型估计命令一览表 一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型（一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

STATA面板数据模型估计命令一览表输入数据•tsset code year 该命令是将数据定义为“面板”形式•xtdes 该命令是了解面板数据结构• summarize sq cpi unem g se5 In 各变量的描述性统计（统计分析）• gen lag_y=L.y /////// 产生一个滞后一期的新变量to U 一 if对于固定效应模型而言，回归结果中最后一行汇报的F 统计量便在于检验所 有的个体效应整体上显著。

在我们这个例子中发现 F 统计量的概率为0.0000 , 检验结果表明固定效应模型优于混合 OLS 模型。

合效应还是随机效应） （检验方法：LM 统计量）（原假设：使用OLS 混合模型） • qui xtreg sq cpi unem g se5 ln,re（加上"qui ”之后第一幅图将不会呈现 ）xttest0xizretg s-<q cpifgen F_y=F.y /////// gen D_y=D.y /////// gen D2_y=D2.y ///////产生一个超前项的新变量 产生一个一阶差分的新变量 产生一个二阶差分的新变量（二）模型的筛选和检验• 1检验个体效应 （混合效应还是固定效应）（原假设：使用OLS 混合模型） • xtreg sq cpi unem g se5 ln,fe3C"t 『U<3 SCI C.IPm feor r Cu iO-23OZ O. O<7i67 O- 匕 Qm -Bk T -:<?■£ f 3 X dmts m 工■zd s d z mAm - -5 -1s u a 工一67 ■r.QB€BJL£3;4M 4Liny;工G-RO 丄 bo --A - « _ QprlsrlQ --mA6.2:sGctg scs0'.x丄z skJ>4y-- -S4S"0 Get 一一一GftlxJ2 IKqg4岭济34工Lu -^-3 ■■MB : od JL X QX 丄炮丄• 2、检验时间效应O- SZ £>&■ J d rn可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

STATA 面板数据模型估计命令一览表 一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型（一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。