高考数学复习-指数函数
- 格式:doc
- 大小:122.15 KB
- 文档页数:7




高考数学专题复习题:指数函数一、单项选择题(共8小题)1.若命题“,a b ∀∈R ,22b a a b -<-”为真命题,则a ,b 的大小关系为()A .a b <B .a b >C .a b≤D .a b ≥2.已知函数()2121x f x =-+,则对任意实数x ,有()A .()()0f x f x -+=B .()()0f x f x --=C .()()2f x f x -+=D .()()2f x f x --=3.已知()e e x x x f x a -=+是偶函数,则a =()A .2-B .1-C .1D .24.设函数2()21x f x =+,求得(5)(4)(0)(4)(5)f f f f f -+-+++++ 的值为()A .9B .11C .92D .1125.如果定义在R 上的函数()f x 满足()()0f x f x -+=,且当0x ≤时,()22x a f x =+,那么()1f =()A .2B .4C .2-D .4-6.函数2()2|e 1|x x f x =-的图象大致是()A .B .C .D .7.设函数()()12x x a f x -⎛⎫= ⎪⎝⎭在区间0,1单增,则a 的取值范围是()A .(],2∞--B .[)2,0-C .(]0,2D .[)2,+∞8.已知函数()20252025x x f x -=-,若0a >,0b >,且()()20f a f b -+=,则3111a b +++的最小值为()AB .1C .1D .二、多项选择题(共2小题)9.已知函数()312x f x x +=-,则下列结论正确的是()A .()f x 的值域是{}2y y ≠B .()f x 图象的对称中心为()2,3C .()()202620226f f +-=D .()2x f -的值域是14,2⎡⎫--⎪⎢⎣⎭10.已知函数e 1()e 1x x f x +=-,则下列结论正确的是()A .函数()f x 的定义域为RB .函数()f x 的值域为(,1)(1,)-∞-+∞C .()()0f x f x +-=D .函数()f x 为减函数三、填空题(共2小题)11.设函数()331x f x =+,则()()()()()54045f f f f f -+-+++++= ________.12.函数2x y m m =-+在(],2-∞上的最大值为4,则m 的取值范围是________.四、解答题(共2小题)13.已知函数2()12x xb f x a +=+⋅,若()f x 是定义域为R 的奇函数.(1)求出函数()f x 的解析式;(2)求不等式2(1)(35)0f x f x ++-<的解集.14.已知函数11()22x x f x a -=⋅+是定义域为R 的偶函数.(1)求实数a 的值;(2)若对任意x ∈R ,都有(2)()f x kf x ≥成立,求实数k 的取值范围.。

高中数学高考总复习指数与指数函数习题及详解一、选择题1.(2010·陕西文)下列四类函数中,具有性质“对任意的x >0,y >0,函数f (x )满足f (x +y )=f (x )f (y )”的是( )A .幂函数B .对数函数C .指数函数D .余弦函数[答案] C[解析] ∵(x +y )α≠x α·y α,log a (x +y )≠log a x +log a y ,a x +y =a x ·a y ,cos(x +y )=cos x cos y -sin x sin y ≠cos x cos y ,∴选C.2.(2010·南充市)若A ={x ∈Z |2≤22-x <8},B ={x ∈R ||x -1|>1},则A ∩(∁R B )的元素个数为( )A .0B .1C .2D .3[答案] C[解析] 由2≤22-x <8得,1≤2-x <3,∴-1<x ≤1,∵x ∈Z ,∴x =0或1,∴A ={0,1}; 由|x -1|>1得,x >2或x <0,∴B ={x |x >2或x <0},∴∁R B ={x |0≤x ≤2}, ∴A ∩∁U B ={0,1}.3.(文)(2010·北京崇文区)设a =⎝⎛⎭⎫120.5,b =0.30.5,c =log 0.30.2,则a 、b 、c 的大小关系是( )A .a >b >cB .a <b <cC .b <a <cD .a <c <b[答案] C[解析] y =x 0.5在(0,+∞)上是增函数,1>12>0.3,∴1>a >b ,又y =log 0.3x 在(0,+∞)上为减函数, ∴log 0.30.2>log 0.30.3=1,即c >1,∴b <a <c .(理)(2010·重庆诊断)设0<b <a <1,则下列不等式成立的是( ) A .ab <b 2<1 B.12<⎝⎛⎭⎫12a <⎝⎛⎭⎫12b C .a 2<ab <1D .log 12b <log 12a <0[答案] B[解析] 依题意得ab -b 2=b (a -b )>0,∴ab >b 2,因此A 不正确;同理可知C 不正确;由函数y =⎝⎛⎭⎫12x 在R 上是减函数得,当0<b <a <1时,有⎝⎛⎭⎫120>⎝⎛⎭⎫12b >⎝⎛⎭⎫12a >⎝⎛⎭⎫121,即12<⎝⎛⎭⎫12a <⎝⎛⎭⎫12b ,因此B 正确;同理可知D 不正确.综上所述,选B.[点评] 可利用a ,b 取值的任意性取特值检验,令b =14,a =12可得,14>18>116,∴a 2>ab >b 2,排除A 、C ;log 1214=2,log 1212=1,∴log 12b >log 12a ,排除D ,故选B.4.(文)(2010·泰安质检)某钢厂的年产量由1990年的40万吨增加到2000年的50万吨,如果按照这样的年增长率计算,则该钢厂2010年的年产量约为( )A .60万吨B .61万吨C .63万吨D .64万吨[答案] C[解析] 设年增长率为x ,则由题意知40(1+x )10=50,∴(1+x )10=54,∴2010年的年产量为40(1+x )20=40×⎝⎛⎭⎫542=2504≈63万吨.(理)(2010·安徽安庆联考)如图是一个算法的程序框图,当输入x 的值为3时,输出y 的结果恰好为13,则?处的关系式是( )A .y =log 9xB .y =3xC .y =3-xD .y =x 13[答案] B[解析] 输入x =3≤0不成立,故x =3-2=1,1≤0不成立,故x =1-2=-1,-1≤0成立,执行?后输出y =13,故选B.5.(2010·安徽理,6)设abc >0,二次函数f (x )=ax 2+bx +c 的图象可能是( )[答案] D[解析] 若a <0,则只能是 A 或B 选项,A 中-b2a <0,∴b <0,从而c >0与A 图不符;B 中-b2a >0,∴b >0,∴c <0与B 图也不符;若a >0,则抛物线开口向上,只能是C 或D 选项,则当b >0时,有c >0与C 、D 不符.当b <0时,有c <0,此时-b2a >0,且f (0)=c <0,故选D.6.(文)(2010·山东理,4)设f (x )为定义在R 上的奇函数,当x ≥0时,f (x )=2x +2x +b (b 为常数),则f (-1)=( )A .3B .1C .-1D .-3[答案] D[解析] ∵f (x )是奇函数,∴f (0)=0,即0=20+b ,∴b =-1,故f (1)=2+2-1=3,∴f (-1)=-f (1)=-3.(理)(2010·辽宁省实验中学)已知函数f (x )=2x -1,对于满足0<x 1<x 2<2的任意实数x 1,x 2,给出下列结论:(1)(x 2-x 1)[f (x 2)-f (x 1)]<0; (2)x 2f (x 1)<x 1f (x 2); (3)f (x 2)-f (x 1)>x 2-x 1; (4)f (x 1)+f (x 2)2>f⎝⎛⎭⎫x 1+x 22. 其中正确结论的序号是( ) A .(1)(2) B .(1)(3) C .(2)(4)D .(3)(4)[答案] C[解析] ∵f (x )为增函数,x 1<x 2,∴f (x 1)<f (x 2),∴(x 2-x 1)[f (x 2)-f (x 1)]>0,故(1)错; 排除A 、B ;A (x 1,f (x 1)),B (x 2,f (x 2))是f (x )=2x -1在(0,2)上任意两点,则k AB =f (x 2)-f (x 1)x 2-x 1不总大于1,故(3)错,排除D ,选C.7.(文)(2010·重庆南开中学)已知f (x )=a x ,g (x )=b x ,当f (x 1)=g (x 2)=3时,x 1>x 2,则a 与b 的大小关系不可能成立.....的是( ) A .b >a >1 B .a >1>b >0 C .0<a <b <1D .b >1>a >0[答案] D[解析] ∵f (x 1)=g (x 2)=3,∴ax 1=bx 2=3, ∴x 1=log a 3,x 2=log b 3,当b >1>a >0时,x 1<0,x 2>0不满足x 1>x 2.(理)(2010·辽宁文,10)设2a =5b =m ,且1a +1b =2,则m =( )A.10 B .10 C .20D .100[答案] A[解析] ∵2a =5b =m ∴a =log 2m b =log 5m ∴1a +1b =1log 2m +1log 5m =log m 2+log m 5=log m 10=2 ∴m =10 选A.8.(文)(2010·吉林市质检、上海松江市模拟)若函数f (x )=(k -1)a x -a -x (a >0且a ≠1)在R 上既是奇函数,又是减函数,则g (x )=log a (x +k )的图象是( )[答案] A[解析] ∵f (x )为奇函数,∴f (0)=0,∴k =2,f (x )=a x -a -x ,又f (x )为减函数,∴0<a <1, ∴g (x )=log a (x +2)的图象为A.(理)(2010·烟台中英文学校质检、海淀期中)在同一坐标系中画出函数y =log a x ,y =a x ,y =x +a 的图象,可能正确的是( )[答案] D[解析] 对于A ,y =x +a 中,0<a <1,故y =log a x 单减,与图象不符,排除A ;对于B 、C 由y =x +a 知,a >1,∴y =log a x 单调增,与图象不符,排除B 、C ,因此选D.9.(2010·深圳市调研)已知所有的点A n (n ,a n )(n ∈N *)都在函数y =a x (a >0,a ≠1)的图象上,则a 3+a 7与2a 5的大小关系是( )A .a 3+a 7>2a 5B .a 3+a 7<2a 5C .a 3+a 7=2a 5D .a 3+a 7与2a 5的大小关系与a 的值有关 [答案] A[解析] 因为所有的点A n (n ,a n )(n ∈N *)都在函数y =a x (a >0,a ≠1)的图象上,所以有a n=a n ,故a 3+a 7=a 3+a 7,由基本不等式得:a 3+a 7>2a 3·a 7=2a 10=2a 5,∴a 3+a 7>2a 5(因为a >0,a ≠1,从而基本不等式的等号不成立),故选A.10.(文)(2010·青岛市质检)过原点的直线与函数y =2x 的图象交于A ,B 两点,过B 作y 轴的垂线交函数y =4x 的图象于点C ,若直线AC 平行于y 轴,则点A 的坐标是( )A .(1,2)B .(2,4)C .(12,2)D .(0,1) [答案] A[解析] 设A (x 0,y 0),则y 0=2x 0,由条件知C (x 0,4x 0),∴y B =4x 0=22x 0,∴B (2x 0,22x 0),∵直线AB 过原点,∴k OA =k OB ,∴22x 02x 0=2x 0x 0,∴x 0=1,∴A (1,2).(理)(2010·湖南八校联考)已知函数f (x )=log 12(4x -2x +1+1)的值域是[0,+∞),则它的定义域可以是( )A .(0,1]B .(0,1)C .(-∞,1]D .(-∞,0] [答案] A[解析] 由题意知,log 12(4x -2x +1+1)≥0,则有0<4x -2x +1+1≤1,解得x ≤1且x ≠0,排除C 、D.经检验,当x ∈(0,1]时,f (x )的值域是[0,+∞).故选A.[点评] 由函数f (x )的值域为[0,+∞)知,令u =4x -2x +1+1,则log 12u ≥0,∴0<u ≤1,而u =(2x -1)2,∴x ≤1且x ≠0,而当x =1时,u =1,当x =0时,u =0,故0<x ≤1时,0<u ≤1,因此集合{x |x ≤1且x ≠0}的所有包含{x |0<x ≤1}的子集都可以取作该函数的定义域.二、填空题11.(文)已知函数f (x )=⎩⎪⎨⎪⎧⎝⎛⎭⎫13x x ∈[-1,0]3x x ∈(0,1],则f ⎝⎛⎭⎫log 312=________. [答案] 2[解析] ∵-1<log 312<0,∴f (log 312)=⎝⎛⎭⎫13log 312=(3log 312)-1=2. (理)(2010·北京东城区)定义在R 上的函数f (x )满足f (x )=⎩⎪⎨⎪⎧21-x x ≤0f (x -1)-f (x -2) x >0,则f (-1)=______,f (33)=________.[答案] 4,-2 [解析] f (-1)=21-(-1)=4,f (33)=f (32)-f (31)=f (31)-f (30)-f (31)=-f (30),同理f (30)=-f (27),∴f (33)=f (27),∴f (33)=f (3)=-f (0)=-2.12.(文)(2010·常德市检测)定义区间[x 1,x 2]的长度为x 2-x 1,已知函数f (x )=3|x |的定义域为[a ,b ],值域为[1,9],则区间[a ,b ]的长度的最大值为________,最小值为________.[答案] 4 2[解析] 由3|x |=1得x =0,由3|x |=9得x =±2,故f (x )=3|x |的值域为[1,9]时,其定义域可以为[0,2],[-2,0],[-2,2]及[-2,m ],0≤m ≤2或[n,2],-2≤n ≤0都可以,故区间[a ,b ]的最大长度为4,最小长度为2.(理)(2010·柳州市模考)已知⎝⎛⎭⎫2x -229的展开式的第7项为214,则x 的值为________.[答案] -13[解析] T 7=C 96(2x )3·⎝⎛⎭⎫-226=212×8x =214, ∴3x =-1,∴x =-13.13.已知函数f (x )=⎩⎪⎨⎪⎧⎝⎛⎭⎫12x x ≤1log 2(x -1) x >1,则f (x )≤12的解集为________.[答案] [1,2+1] [解析] 由f (x )≤12得,⎩⎪⎨⎪⎧⎝⎛⎭⎫12x ≤12x ≤1或⎩⎪⎨⎪⎧log 2(x -1)≤12x >1, ∴x =1或1<x ≤2+1,∴1≤x ≤2+1,故解集为[1,2+1].14.函数f (x )的定义由程序框图给出,程序运行时,输入h (x )=⎝⎛⎭⎫12x ,φ(x )=log 2x ,则f (12)+f (4)的值为________.[答案] -1516[解析] 由程序框图知f (x )=⎩⎪⎨⎪⎧φ(x ) h (x )>φ(x )h (x ) h (x )≤φ(x ),∵h ⎝⎛⎭⎫12=⎝⎛⎭⎫1212=22,φ⎝⎛⎭⎫12=-1,∴f ⎝⎛⎭⎫12=-1, ∵h (4)=116,φ(4)=2,∴f (4)=116,∴f ⎝⎛⎭⎫12+f (4)=-1+116=-1516. 三、解答题15.已知f (x )是定义在R 上的奇函数,且当x ∈(0,1)时,f (x )=2x 4x +1.(1)求f (x )在(-1,1)上的解析式; (2)证明:f (x )在(0,1)上是减函数.[解析] (1)∵f (x )是R 上的奇函数,∴f (0)=0, 又当x ∈(-1,0)时,-x ∈(0,1), ∴f (-x )=2-x4-x +1=2x1+4x,∵f (-x )=-f (x ),∴f (x )=-2x1+4x ,∴f (x )在(-1,1)上的解析式为f (x )=⎩⎨⎧2x4x +1x ∈(0,1)-2x 4x+1 x ∈(-1,0)0 x =0.(2)当x ∈(0,1)时,f (x )=2x4x +1.设0<x 1<x 2<1, 则f (x 1)-f (x 2)=2x 14x 1+1-2x 24x 2+1=(2x 2-2x 1)(2x 1+x 2-1)(4x 1+1)(4x 2+1),∵0<x 1<x 2<1,∴2x 2-2x 1>0,2x 1+x 2-1>0, ∴f (x 1)-f (x 2)>0,即f (x 1)>f (x 2), 故f (x )在(0,1)上是减函数.16.已知关于x 的方程9x -2×3x +(3k -1)=0有两个实数根,求实数k 的取值范围. [解析] 令3x =t ,则方程化为t 2-2t +(3t -1)=0,①要使原方程有两个实数根,方程①必须有两个正根 所以⎩⎪⎨⎪⎧Δ=(-2)2-4(3k -1)≥0t 1t 2=3k -1>0t 1+t 2=2>0解得13<k ≤23.[点评] ∵t =3x >0,∴原方程有两个实数根x 1、x 2,则对应的方程①应有两个正根t 1=3x 1,t 2=3x 2,而不是两个任意实数根.17.(文)(2010·辽宁省锦州市通考)已知函数f (x )=m ·2x +t 的图象经过点A (1,1),B (2,3)及C (n ,S n ),S n 为数列{a n }的前n 项和.(1)求a n 及S n ;(2)若数列{c n }满足c n =6na n -n ,求数列{c n }的前n 项和T n . [解析] (1)∵函数f (x )=m ·2x +t 的图象经过点A 、B ,∴⎩⎪⎨⎪⎧ 2m +t =14m +t =3,∴⎩⎪⎨⎪⎧m =1t =-1,∴f (x )=2x -1, ∴S n =2n -1,∴a n =2n -1.(2)c n =3n ·2n -n ,T n =c 1+c 2+…+c n =3×(1×2+2×22+3×23+…+n ·2n )-(1+2+…+n ),令P n =1×2+2×22+…+n ·2n ① 则2P n =1×22+2×23+…+n ·2n +1② ①-②得-P n =2+22+…+2n -n ·2n +1 =2×(2n -1)2-1-n ·2n +1=2n +1-2-n ·2n +1,∴P n =(n -1)2n +1+2, ∴T n =3(n -1)2n +1+6-n (n +1)2.(理)(2010·浙江台州模拟)定义在D 上的函数f (x ),如果满足:对任意x ∈D ,存在常数M >0,都有|f (x )|≤M 成立,则称f (x )是D 上的有界函数,其中M 称为函数f (x )的上界.已知函数f (x )=1+a ·⎝⎛⎭⎫12x +⎝⎛⎭⎫14x . (1)当a =1时,求函数f (x )在(-∞,0)上的值域,并判断函数f (x )在(-∞,0)上是否为有界函数,请说明理由;(2)若函数f (x )在[0,+∞)上是以3为上界的有界函数,求实数a 的取值范围. [解析] (1)当a =1时,f (x )=1+⎝⎛⎭⎫12x +⎝⎛⎭⎫14x . 因为f (x )在(-∞,0)上递减,所以f (x )>f (0)=3,即f (x )在(-∞,0)上的值域为(3,+∞).故不存在常数M >0,使|f (x )|≤M 成立. 所以函数f (x )在(-∞,0)上不是有界函数. (2)由题意知,|f (x )|≤3在[0,+∞)上恒成立. ∴-3≤f (x )≤3,即-4-⎝⎛⎭⎫14x≤a ·⎝⎛⎭⎫12x ≤2-⎝⎛⎭⎫14x , ∴-4·2x -⎝⎛⎭⎫12x≤a ≤2·2x-⎝⎛⎭⎫12x 在[0,+∞)上恒成立, 设2x =t ,h (t )=-4t -1t ,p (t )=2t -1t ,由x ∈[0,+∞)得t ≥1,设1≤t1<t2,h(t1)-h(t2)=(t2-t1)(4t1t2-1)t1t2>0p(t1)-p(t2)=(t1-t2)(2t1t2+1)t1t2<0所以h(t)在[1,+∞)上递减,p(t)在[1,+∞)上递增,h(t)在[1,+∞)上的最大值为h(1)=-5,p(t)在[1,+∞)上的最小值为p(1)=1,所以实数a的取值范围为[-5,1].。

指数函数判断下列结论是否正确(请在括号中打“√”或“×”) (1)n a n =(na )n =a .( )(2)分数指数幂m na 可以理解为mn个a 相乘.( )(3)(-1)24=(-1)12=-1.( ) (4)函数y =a -x 是R 上的增函数.( ) (5)函数21x y a +=(a >1)的值域是(0,+∞).( )(6)函数y =2x -1是指数函数.( )无题型一 指数幂的运算 例1 化简下列各式:(1)[(0.06415)-2.5]23-3338-π0; (2)a 43-8a 13b4b 23+23ab +a23÷(a23--23b a )×a ·3a 25a ·3a.化简(14)12-·(4ab -1)3(0.1)-1·(a 3·b -3)12=________. 题型二 指数函数的图象及应用例2 (1)已知实数a ,b 满足等式2 017a =2 018b ,下列五个关系式:①0<b <a ;②a <b <0;③0<a <b ;④b <a <0;⑤a =b .其中不可能成立的关系式有( )A.1个B.2个C.3个D.4个(2)已知函数f(x)=|2x-1|,a<b<c且f(a)>f(c)>f(b),则下列结论中,一定成立的是()A.a<0,b<0,c<0 B.a<0,b≥0,c>0C.2-a<2c D.2a+2c<2(1)已知函数f(x)=a x-b的图象如图所示,则函数g(x)=ax+b的图象可能是()(2)若曲线|y|=2x+1与直线y=b没有公共点,则b的取值范围是________.题型三指数函数的性质及应用命题点1指数函数单调性的应用例3(1)下列各式比较大小正确的是()A.1.72.5>1.73B.0.6-1>0.62C.0.8-0.1>1.250.2D.1.70.3<0.93.1(2)设函数f (x )=⎩⎪⎨⎪⎧(12)x -7,x <0,x ,x ≥0,若f (a )<1,则实数a 的取值范围是________.命题点2 复合函数的单调性例4 (1)已知函数f (x )=22x m-(m 为常数),若f (x )在区间[2,+∞)上是增函数,则m 的取值范围是________.(2)函数f (x )=⎝⎛⎭⎫12221x x -+-的单调减区间为_____________________________________. 引申探究函数f (x )=142x x +-的单调增区间是________.例5 (1)函数y =⎝⎛⎭⎫14x -⎝⎛⎭⎫12x +1在区间[-3,2]上的值域是________.(2)如果函数y =a 2x +2a x -1(a >0,且a ≠1)在区间[-1,1]上的最大值是14,则a 的值为________.(1)已知函数f (x )=⎩⎪⎨⎪⎧-(12)x ,a ≤x <0,-x 2+2x ,0≤x ≤4的值域是[-8,1],则实数a 的取值范围是( )A .(-∞,-3]B .[-3,0)C .[-3,-1]D .{-3}(2)已知函数f (x )=2x -12x ,函数g (x )=⎩⎪⎨⎪⎧f (x ),x ≥0,f (-x ),x <0,则函数g (x )的最小值是________.1.分数指数幂(1)我们规定正数的正分数指数幂的意义是m na =na m (a >0,m ,n ∈N *,且n >1).于是,在条件a >0,m ,n ∈N *,且n >1下,根式都可以写成分数指数幂的形式.正数的负分数指数幂的意义与负整数指数幂的意义相仿,我们规定m na-=1m na(a >0,m ,n ∈N *,且n >1).0的正分数指数幂等于0;0的负分数指数幂没有意义.(2)有理数指数幂的运算性质:a r a s =a r +s ,(a r )s =a rs ,(ab )r =a r b r ,其中a >0,b >0,r ,s ∈Q . 2.指数函数的图象与性质典例 已知函数y =b +22x xa+(a ,b 为常数,且a >0,a ≠1)在区间[-32,0]上有最大值3,最小值52,则a ,b 的值分别为________.1.已知函数f (x )=a x -2+2的图象恒过定点A ,则A 的坐标为( ) A .(0,1) B .(2,3) C .(3,2) D .(2,2)2.已知a =(35)13-,b =(35)14-,c =(32)34-,则a ,b ,c 的大小关系是( )A .c <a <b .a <b <c C .b <a <c.c <b <a3.计算:⎝⎛⎭⎫3213-×⎝⎛⎭⎫-760+814×42________. 4.函数y =8-23-x (x ≥0)的值域是________. 1.设2x =8y+1,9y =3x -9,则x +y 的值为( )A .18B .21C .24D .27 2.函数f (x )=2|x -1|的图象是( )3.已知a =40.2,b =0.40.2,c =0.40.8,则( ) A .a >b >c B .a >c >b C .c >a >bD .b >c >a4.已知f (x )=3x -b (2≤x ≤4,b 为常数)的图象经过点(2,1),则f (x )的值域为( ) A .[9,81] B .[3,9] C .[1,9]D .[1,+∞)5.若函数f (x )=2x +12x -a 是奇函数,则使f (x )>3成立的x 的取值范围为( )A .(-∞,-1)B .(-1,0)C .(0,1)D .(1,+∞)*6.已知g (x )=ax +1,f (x )=⎩⎪⎨⎪⎧2x -1,0≤x ≤2,-x 2,-2≤x <0,对任意x 1∈[-2,2],存在x 2∈[-2,2],使g (x 1)=f (x 2)成立,则a 的取值范围是( ) A .[-1,+∞) B .[-1,1] C .(0,1]D .(-∞,1]7.设函数f (x )=⎩⎪⎨⎪⎧e x -1,x <1,x 13,x ≥1,则使得f (x )≤2成立的x 的取值范围是________.8.若直线y =2a 与函数y =|a x -1|(a >0且a ≠1)的图象有两个公共点,则a 的取值范围是________. 9.已知y =f (x )是定义在R 上的奇函数且当x ≥0时,f (x )=-14x +12x ,则此函数的值域为________.10.当x ∈(-∞,-1]时,不等式(m 2-m )·4x -2x <0恒成立,则实数m 的取值范围是________. 11.已知函数f (x )=(23)|x |-a .(1)求f (x )的单调区间;(2)若f (x )的最大值等于94,求a 的值.12.已知函数f (x )=2431()3ax x -+.(1)若a =-1,求f (x )的单调区间; (2)若f (x )有最大值3,求a 的值.*13.已知函数f (x )=14x -λ2x -1+3(-1≤x ≤2).(1)若λ=32,求函数f (x )的值域;(2)若函数f (x )的最小值是1,求实数λ的值.指数函数判断下列结论是否正确(请在括号中打“√”或“×”)(1)nan=(na)n=a.(×)(2)分数指数幂可以理解为mn个a相乘.(×)(3)(-1) =(-1) =-1.(×)(4)函数y=a-x是R上的增函数.(×)(5)函数(a>1)的值域是(0,+∞).(×)(6)函数y=2x-1是指数函数.(×)无题型一指数幂的运算例1化简下列各式:(1)[(0.064 )-2.5] -3338-π0;(2)a -8a b4b +23ab+a ÷(a -23ba)×a•3a25a•3a.解(1)原式={[(641 000) ] } -(278) -1=[(410)3] -[(32)3] -1=52-32-1=0.(2)原式=a [ a 3-2b 3] a 2+a •2b +2b 2÷a -2b a×a•a a •a=a (a -2b )×aa -2b ×a a=a ×a×a =a2.思维升华(1)指数幂的运算首先将根式、分数指数幂统一为分数指数幂,以便利用法则计算,还应注意:①必须同底数幂相乘,指数才能相加;②运算的先后顺序.(2)当底数是负数时,先确定符号,再把底数化为正数.(3)运算结果不能同时含有根号和分数指数,也不能既有分母又含有负指数.化简(14) •4ab-130.1-1•a3•b-3=________.答案85解析原式=2×23•a •b 10•a •b =21+3×10-1=85.题型二指数函数的图象及应用例2(1)已知实数a,b满足等式2 017a=2 018b,下列五个关系式:①0<b<a;②a<b<0;③0<a<b;④b<a<0;⑤a=b.其中不可能成立的关系式有()A.1个B.2个C.3个D.4个(2)已知函数f(x)=|2x-1|,a<b<c且f(a)>f(c)>f(b),则下列结论中,一定成立的是()A.a<0,b<0,c<0 B.a<0,b≥0,c>0C.2-a<2c D.2a+2c<2答案(1)B(2)D解析(1)如图,观察易知,a,b的关系为a<b<0或0<b<a或a=b=0.(2)作出函数f(x)=|2x-1|的图象,如图,∵a<b<c且f(a)>f(c)>f(b),结合图象知,0<f(a)<1,a<0,c>0,∴0<2a<1.∴f(a)=|2a-1|=1-2a<1,∴f(c)<1,∴0<c<1.∴1<2c<2,∴f(c)=|2c-1|=2c-1,又∵f(a)>f(c),∴1-2a>2c-1,∴2a+2c<2,故选D.思维升华(1)已知函数解析式判断其图象一般是取特殊点,判断所给的图象是否过这些点,若不满足则排除.(2)对于有关指数型函数的图象问题,一般是从最基本的指数函数的图象入手,通过平移、伸缩、对称变换而得到.特别地,当底数a与1的大小关系不确定时应注意分类讨论.(3)有关指数方程、不等式问题的求解,往往利用相应的指数型函数图象,数形结合求解.(1)已知函数f(x)=ax-b的图象如图所示,则函数g(x)=ax+b的图象可能是()(2)若曲线|y|=2x+1与直线y=b没有公共点,则b的取值范围是________.答案(1)A(2)[-1,1]解析(1)由f(x)的单调性知0<a<1,又x=0时,a-b>1,x=1时,a1-b<1,∴0<b<1,对照图象知g(x)的图象可能是A.(2)曲线|y|=2x+1与直线y=b的图象如图所示,由图象可知:如果|y|=2x+1与直线y=b没有公共点,则b应满足的条件是b∈[-1,1].题型三指数函数的性质及应用命题点1指数函数单调性的应用例3(1)下列各式比较大小正确的是()A.1.72.5>1.73 B.0.6-1>0.62C.0.8-0.1>1.250.2 D.1.70.3<0.93.1(2)设函数f(x)=12x-7,x<0,x,x≥0,若f(a)<1,则实数a的取值范围是________.答案(1)B(2)(-3,1)解析(1)选项B中,∵y=0.6x是减函数,∴0.6-1>0.62.(2)当a<0时,不等式f(a)<1可化为(12)a-7<1,即(12)a<8,即(12)a<(12)-3,∴a>-3.又a<0,∴-3<a<0.当a≥0时,不等式f(a)<1可化为a<1.∴0≤a<1,综上,a的取值范围为(-3,1).命题点2复合函数的单调性例4(1)已知函数f(x)=2 (m为常数),若f(x)在区间[2,+∞)上是增函数,则m的取值范围是________.(2)函数f(x)=12 的单调减区间为_____________________________________.答案(1)(-∞,4](2)(-∞,1]解析(1)令t=|2x-m|,则t=|2x-m|在区间[m2,+∞)上单调递增,在区间(-∞,m2]上单调递减.而y=2t为R上的增函数,所以要使函数f(x)=2 在[2,+∞)上单调递增,则有m2≤2,即m≤4,所以m的取值范围是(-∞,4].(2)设u=-x2+2x+1,∵y=12u在R上为减函数,∴函数f(x)=的减区间即为函数u=-x2+2x+1的增区间.又u=-x2+2x+1的增区间为(-∞,1],∴f(x)的减区间为(-∞,1].引申探究函数f(x)=的单调增区间是________.答案[0,+∞)解析设t=2x,则y=t2-2t的单调增区间为[1,+∞),令2x≥1,得x≥0,∴函数f(x)=的单调增区间是[0,+∞).命题点3函数的值域(或最值)例5(1)函数y=14x-12x+1在区间[-3,2]上的值域是________.(2)如果函数y=a2x+2ax-1(a>0,且a≠1)在区间[-1,1]上的最大值是14,则a的值为________.答案(1)34,57(2)13或3解析(1)令t=12x,因为x∈[-3,2],所以t∈14,8,故y=t2-t+1=t-122+34.当t=12时,ymin=34;当t=8时,ymax=57.故所求函数的值域为34,57.(2)令ax=t,则y=a2x+2ax-1=t2+2t-1=(t+1)2-2.当a>1时,因为x∈[-1,1],所以t∈[1a,a],又函数y=(t+1)2-2在1a,a上单调递增,所以ymax=(a+1)2-2=14,解得a=3(负值舍去).当0<a<1时,因为x∈[-1,1],所以t∈[a,1a],又函数y=(t+1)2-2在[a,1a]上单调递增,则ymax=(1a+1)2-2=14,解得a=13(负值舍去).综上,a=3或a=13.思维升华(1)在利用指数函数性质解决相关综合问题时,要特别注意底数a的取值范围,并在必要时进行分类讨论.(2)与指数函数有关的指数型函数的定义域、值域(最值)、单调性、奇偶性的求解方法,要化归于指数函数来解.(1)已知函数f(x)=-12x,a≤x<0,-x2+2x,0≤x≤4的值域是[-8,1],则实数a的取值范围是()A.(-∞,-3] B.[-3,0)C.[-3,-1] D.{-3}(2)已知函数f(x)=2x-12x,函数g(x)=f x,x≥0,f-x,x<0,则函数g(x)的最小值是________.答案(1)B(2)0解析(1)当0≤x≤4时,f(x)∈[-8,1],当a≤x<0时,f(x)∈[-(12)a,-1),所以[-12a,-1)[-8,1],即-8≤-12a<-1,即-3≤a<0,所以实数a的取值范围是[-3,0).(2)当x≥0时,g(x)=f(x)=2x-12x为单调增函数,所以g(x)≥g(0)=0;当x<0时,g(x)=f(-x)=2-x-12-x为单调减函数,所以g(x)>g(0)=0,所以函数g(x)的最小值是0.1.分数指数幂(1)我们规定正数的正分数指数幂的意义是=nam(a>0,m,n∈N*,且n>1).于是,在条件a>0,m,n∈N*,且n>1下,根式都可以写成分数指数幂的形式.正数的负分数指数幂的意义与负整数指数幂的意义相仿,我们规定=1 (a>0,m,n∈N*,且n>1).0的正分数指数幂等于0;0的负分数指数幂没有意义.(2)有理数指数幂的运算性质:aras=ar+s,(ar)s=ars,(ab)r=arbr,其中a>0,b>0,r,s∈Q. 2.指数函数的图象与性质y=ax a>1 0<a<1图象定义域(1)R值域(2)(0,+∞)性质(3)过定点(0,1)(4)当x>0时,y>1;当x<0时,0<y<1 (5)当x>0时,0<y<1;当x<0时,y>1(6)在(-∞,+∞)上是增函数(7)在(-∞,+∞)上是减函数典例已知函数y=b+(a,b为常数,且a>0,a≠1)在区间[-32,0]上有最大值3,最小值52,则a,b的值分别为________.错解展示解析令t=x2+2x=(x+1)2-1,∵-32≤x≤0,∴-1≤t≤0.∵1a≤at≤1,∴b+1a≤b+at≤b+1,由b+1a=52,b+1=3,得a=2,b=2.答案2,2现场纠错解析令t=x2+2x=(x+1)2-1,∵x∈[-32,0],∴t∈[-1,0].①若a>1,函数f(x)=at在[-1,0]上为增函数,∴at∈[1a,1],b+∈[b+1a,b+1],依题意得b+1a=52,b+1=3,解得a=2,b=2.②若0<a<1,函数f(x)=at在[-1,0]上为减函数,∴at∈[1,1a],则b+∈[b+1,b+1a],依题意得b+1a=3,b+1=52,解得a=23,b=32.综上①②,所求a,b的值为a=2,b=2或a=23,b=32. 答案2,2或23,32纠错心得与指数函数、对数函数的单调性有关的问题,要对底数进行讨论. 1.已知函数f(x)=ax-2+2的图象恒过定点A,则A的坐标为() A.(0,1) B.(2,3) C.(3,2) D.(2,2)答案 B解析由a0=1知,当x-2=0,即x=2时,f(2)=3,即图象必过定点(2,3).2.已知a=(35) ,b=(35) ,c=(32) ,则a,b,c的大小关系是()A.c<a<b .a<b<cC.b<a<c .c<b<a答案 D解析∵y=(35)x是减函数,∴(35) >(35) >(35)0,即a>b>1,又c=(32) <(32)0=1,∴c<b<a.3.计算:32 ×-760+8 ×42-=________.答案 2解析原式=23 ×1+2 ×2 -23 =2.4.函数y=8-23-x(x≥0)的值域是________.答案[0,8)解析∵x≥0,∴-x≤0,∴3-x≤3,∴0<23-x≤23=8,∴0≤8-23-x<8,∴函数y=8-23-x的值域为[0,8).1.设2x=8y+1,9y=3x-9,则x+y的值为()A.18 B.21 C.24 D.27答案 D解析∵2x=8y+1=23(y+1),∴x=3y+3,∵9y=3x-9=32y,∴x-9=2y,解得x=21,y=6,∴x+y=27.2.函数f(x)=2|x-1|的图象是()答案 B解析∵|x-1|≥0,∴f(x)≥1,排除C、D.又x=1时,|f(x)|min=1,排除A.故选B.3.已知a=40.2,b=0.40.2,c=0.40.8,则()A.a>b>c B.a>c>bC.c>a>b D.b>c>a答案 A解析由0.2<0.8,底数0.4<1知,y=0.4x在R上为减函数,所以0.40.2>0.40.8,即b>c.又a=40.2>40=1,b=0.40.2<1,所以a>b.综上,a>b>c.4.已知f(x)=3x-b(2≤x≤4,b为常数)的图象经过点(2,1),则f(x)的值域为() A.[9,81] B.[3,9]C.[1,9] D.[1,+∞)答案 C解析由f(x)过定点(2,1)可知b=2,因为f(x)=3x-2在[2,4]上是增函数,所以f(x)min=f(2)=1,f(x)max=f(4)=9.故选C.5.若函数f(x)=2x+12x-a是奇函数,则使f(x)>3成立的x的取值范围为() A.(-∞,-1) B.(-1,0)C.(0,1) D.(1,+∞)答案 C解析∵f(x)为奇函数,∴f(-x)=-f(x),即2-x+12-x-a=-2x+12x-a,整理得(a-1)(2x+1)=0,∴a=1,∴f(x)>3即为2x+12x-1>3,当x>0时,2x-1>0,∴2x+1>3•2x-3,解得0<x<1;当x<0时,2x-1<0,∴2x+1<3•2x-3,无解.∴x的取值范围为(0,1).*6.已知g(x)=ax+1,f(x)=2x-1,0≤x≤2,-x2,-2≤x<0,对任意x1∈[-2,2],存在x2∈[-2,2],使g(x1)=f(x2)成立,则a的取值范围是()A.[-1,+∞) B.[-1,1]C.(0,1] D.(-∞,1]答案 B解析由题意可得g(x),x∈[-2,2]的值域为f(x),x∈[-2,2]的值域的子集.经分析知f(x),x∈[-2,2]的值域是[-4,3],当a=0时,g(x)=1,符合题意;当a>0时,g(x),x∈[-2,2]的值域是[-2a+1,2a+1],所以-2a+1≥-4,2a+1≤3,则0<a≤1;当a<0时,g(x),x∈[-2,2]的值域是[2a+1,-2a+1],所以2a+1≥-4,-2a+1≤3,则-1≤a<0.综上可得-1≤a≤1.7.设函数f(x)=ex-1,x<1,x ,x≥1,则使得f(x)≤2成立的x的取值范围是________.答案(-∞,8]解析当x<1时,由ex-1≤2,得x≤1+ln 2,∴x<1时恒成立;当x≥1时,由x ≤2,得x≤8,∴1≤x≤8.综上,符合题意的x的取值范围是(-∞,8].8.若直线y=2a与函数y=|ax-1|(a>0且a≠1)的图象有两个公共点,则a的取值范围是________.答案(0,12)解析(数形结合法)由图象可知0<2a<1,∴0<a<12.9.已知y=f(x)是定义在R上的奇函数且当x≥0时,f(x)=-14x+12x,则此函数的值域为________.答案[-14,14]解析设t=12x,当x≥0时,2x≥1,∴0<t≤1,f(t)=-t2+t=-(t-12)2+14.∴0≤f(t)≤14,故当x≥0时,f(x)∈[0,14].∵y=f(x)是定义在R上的奇函数,∴当x≤0时,f(x)∈[-14,0].故函数的值域为[-14,14].10.当x∈(-∞,-1]时,不等式(m2-m)•4x-2x<0恒成立,则实数m的取值范围是________.答案(-1,2)解析原不等式变形为m2-m<12x,因为函数y=12x在(-∞,-1]上是减函数,所以12x≥12-1=2,当x∈(-∞,-1]时,m2-m<12x恒成立等价于m2-m<2,解得-1<m<2.11.已知函数f(x)=(23)|x|-a.(1)求f(x)的单调区间;(2)若f(x)的最大值等于94,求a的值.解(1)令t=|x|-a,则f(x)=(23)t,不论a取何值,t在(-∞,0]上单调递减,在[0,+∞)上单调递增,又y=(23)t是单调递减的,因此f(x)的单调递增区间是(-∞,0],单调递减区间是[0,+∞).(2)由于f(x)的最大值是94,且94=(23)-2,所以g(x)=|x|-a应该有最小值-2,即g(0)=-2,从而a=2.12.已知函数f(x)=.(1)若a=-1,求f(x)的单调区间;(2)若f(x)有最大值3,求a的值.解(1)当a=-1时,f(x)=,令t=-x2-4x+3,由于t在(-∞,-2)上单调递增,在(-2,+∞)上单调递减,而y=13t在R上单调递减,所以f(x)在(-∞,-2)上单调递减,在(-2,+∞)上单调递增,即函数f(x)的单调递增区间是(-2,+∞),单调递减区间是(-∞,-2).(2)令g(x)=ax2-4x+3,则f(x)=13g(x),由于f(x)有最大值3,所以g(x)应有最小值-1,因此必有a>0,3a-4a=-1,解得a=1,即当f(x)有最大值3时,a的值为1.*13.已知函数f(x)=14x-λ2x-1+3(-1≤x≤2).(1)若λ=32,求函数f(x)的值域;(2)若函数f(x)的最小值是1,求实数λ的值.解(1)f(x)=14x-λ2x-1+3=(12)2x-2λ•(12)x+3(-1≤x≤2).设t=(12)x,得g(t)=t2-2λt+3(14≤t≤2).当λ=32时,g(t)=t2-3t+3=(t-32)2+34(14≤t≤2).所以g(t)max=g(14)=3716,g(t)min=g(32)=34.所以f(x)max=3716,f(x)min=34,故函数f(x)的值域为[34,3716].(2)由(1)得g(t)=t2-2λt+3=(t-λ)2+3-λ2(14≤t≤2).①当λ≤14时,g(t)min=g(14)=-λ2+4916,令-λ2+4916=1,得λ=338>14,不符合,舍去;②当14<λ≤2时,g(t)min=g(λ)=-λ2+3,令-λ2+3=1,得λ=2(λ=-2<14,不符合,舍去);③当λ>2时,g(t)min=g(2)=-4λ+7,令-4λ+7=1,得λ=32<2,不符合,舍去.综上所述,实数λ的值为2.。


指数函数高考知识点总结指数函数是高中数学中的重要内容,也是高考数学考试中经常涉及到的知识点之一。
指数函数是指以常数 e(自然对数的底数)为底数的函数,其形式可以写作 f(x) = a^x,其中 a 是一个大于 0 且不等于 1 的实数,x 是变量。
一、指数函数的定义和性质指数函数的定义是 f(x) = a^x,其中 a 是底数,x 是指数。
它的定义域是实数集,值域是正实数集。
指数函数的图像随着底数的不同而变化,底数 a 大于 1 时,图像呈现上升趋势;底数是 (0, 1) 之间的小数时,图像呈现下降趋势。
指数函数具有以下性质:1. 指数函数的导数等于其本身乘以常数 ln(a)(自然对数的底)。
2. 指数函数的导数在正实数上是严格递增的。
3. 当底数 a 大于 1 时,指数函数是增函数且过点 (0, 1);当底数 a 是 (0, 1) 之间的小数时,指数函数是减函数且过点 (0, 1)。
4. 指数函数是奇函数,即 f(-x) = 1 / a^x,其图像关于 y 轴对称。
5. 指数函数的图像在横轴上的渐近线为 y = 0,即当 x 趋近负无穷时,函数值趋近于 0。
二、指数函数的特殊情况1. 当底数 a 等于 e(自然对数的底数)时,指数函数称为自然指数函数,记作 f(x) = e^x。
自然指数函数具有特殊的性质,其导数和原函数等于它本身,即 f'(x) = e^x,∫ e^x dx = e^x + C。
2. 当指数 x 为 0 时,任何底数的指数函数的值都等于 1,即 a^0 = 1。
三、指数函数的应用指数函数广泛应用于各个领域,以下列举几个常见的应用:1. 经济增长模型:指数函数可以描述经济增长模型中的指数增长。
在经济学中,常用指数函数来预测人口增长、物价上涨以及国内生产总值的增长等。
2. 物质衰变模型:指数函数可以用来描述放射性物质的衰变过程。
放射性衰变的速率与剩余物质的量成正比,因此可以用指数函数来描述物质衰变的速度。

高考数学二轮复习 指数函数和对数函数一.知识整理: 基本概念及相关知识点:1、对数、对数的底数、真数:一般地,如果a (a >0,a ≠1)的b 次幂等于N ,就是a b=N ,那么数b 叫做以a 为底N 的对数,记为log a N =b .a 叫做对数的底数.N 叫做真数.负数和零没有对数.2、常用对数:通常将以10为底的对数叫做常用对数.3、自然对数:以e 为底的对数叫自然对数,N 的自然对数log a N 简记作ln N .4、对数的运算性质:如果a >0,a ≠1,M >0,N >0,那么(1)log a (MN )=log a M +log a N ; (2)NMa log =log a M -log a N ; (3)log a M n=n log a M (n ∈R ). 5、对数换底公式: bNN a a b log log log(a >0,a ≠1,b >0,b ≠1,N >0)6、指数函数:函数y =a x(a >0且a ≠1)叫做指数函数,其中x 是自变量,函数的定义域是R . 7、指数函数的图象与性质:a >1 0<a <1图 像(1)定义域:R (2)值域:(0+∞)(3)过点(0,1),即x =0时,y =1 (4)在R 上是增函数(4)在R 上是减函数8、对数函数:函数y = log a x (a >0,a ≠1)叫做对数函数,其中x 是自变量,函数的定义域是(0,+∞). 9、对数函数的图象与性质:a >1 0<a <1图 像性 质(1)定义域:(0,+∞) (2)值域:R(3)过点(1,0),即x =1时,y =0 (4)在(0,+∞)上是增函数(4)在(0,+∞)上是减函数10、指数方程与对数方程:在指数里含有未知数的方程叫做指数方程.在对数符号后面含有未知数的方程叫做对数方程.它们都属于超越方程,一般不可用初等方法求解. 11、最简单的指数方程:xa =b (a >0,a ≠1,b >0),它的解是x =a log b 12、最简单的对数方程:a log x =b (a >0,a ≠1),它的解是x =ba 概念辨析: 1.指数函数(1) 指数函数的定义:函数y =a x叫做指数函数,其中a 是一个大于零且不等于1的常量.函数的定义域是实数集R .在定义中,必须注意:①指数函数的形状,例如y =-2x,121+⎪⎭⎫ ⎝⎛=x y 都不能认为是指数函数,它们都是有关指数函数的复合函数;②指数函数的底在应用时的范围;③指数函数的定义域在求复合函数定义域的应用.(2) 在函数y =a x中规定底数a >0且a ≠1的理由:如果a =0,则当x >0时,a x恒等于0;当x ≤0时,a x无意义. 如果a <0,比如y =(-4)x ,这时对于41=x ,21=x ,等等,在实数范围内,函数值不存在. 如果a =1,y =1x=1是一个常量,对它就没有研究的必要.为了避免上述情况,所以规定底数a >0且a ≠1.(3) 指数函数y =a x在其底数a >1及0<a <1这两种情况下图象特征和性质如下:底数a >1 0<a <1图象xyOy=1y=a x (a>1)xyOy=1y=a x (0<a<1)性质①定义域 (-∞,+∞)②值域 (0,+∞).图象都位于x 轴上方且以x 轴为渐近线函数值的分布情况 ③当时x =0,y =1.图象都经过点(0,1) .④当x >0时,y >1当x <0时,0<y <1 ④当x >0时,0<y <1 当x<0时,y >1单调性⑤在(-∞,+∞)上是增函数⑤在(-∞,+∞)上是减函数注:① 注意根据图象记忆和应用性质:② 性质④可表述为:若(a -1)x >0,则a x>1;若(a -1)x <0,则0<a x<1. ③ 性质③实际上是性质④与性质②的推论. 2.对数(1) 对数的定义:如果a (a >0且a ≠1)的b 次幂等于N ,就是a b=N ,那么数b 就叫做以a 为底N 的对数,记作log a N =b ,其中a 叫做对数的底数,N 叫做真数,log a N 也叫做对数式.(2) 指数式与对数式的互化a b =N b =log a N (a >0且a ≠1,N >0)(3) 对数恒等式:N a Na =log (a >0,a ≠1,N >0)(4) 对数的性质:① 负数和零没有对数. ② 1的对数是零,即log a 1=0. ③ 底的对数等于1,即log a a =1. (5) 对数运算法则(a >0且a ≠1,M >0,N >0)① log a (MN )= log a M +log a N ② N M NMa a alog log log -=③ M n M a na log log =(n ∈R ) ④M nM a nalog 1log =(n ∈R ,n ≠0) (6) 对数换底公式:bNN a a b log log log =(a >0,a ≠1,b >0,b ≠1,N >0)推论:ab b a log 1log =b mnb a n a m log log =(7) 常用对数与自然对数.① 常用对数既是以10为底的对数,简记为lg N (N >0).② 自然对数即是以无理数e =2.71828…为底的对数,简记为ln N (N >0). (8)对可化为形如)(x f a=)(x g a(a >0,a ≠1)的指数方程,可转化为它的同解方程f (x )=g (x )求解;因为当且仅当幂指数相等时同底的幂相等.而对可化为形如a log f (x )= a log g (x )(a >0,a ≠1)的对数方程,在转化为方程f (x )=g (x )求解时,必须把所得的解代回原方程检验;因为从前者变为后者时,x 的取值范围可能扩大,有可能产生增根.某些指数方程与对数方程可以分别化为关于xa 与a log x 的可解方程,这时可用换元法先求出xa 与a log x 的值,再求x 的值;特别对形如x a2+b ·xa +c =0,可用换元法化为二次方程,先求出xa 或a log x ,再求x .但解对数方程时,始终要注意变形的同解性. 二.课堂练习:1.设a ,b ,c 都是正数,且3a=4b =6c ,那么 [ ]2.已知1<x <d , 令a=(x d log )2, b=2log x d , c=()x d d log log ,则[ ].A .a <b <cB .a <c <bC .c <b <aD .c <a <b3.已知y=loga(2-ax)在[0,1]上是x 的减函数,则a 的取值范围是 [ ].A .(0,1)B .(1,2)C .(0,2)D .(2,+∞)4 定义在(-∞,+∞)上的任意函数f (x )都可以表示成一个奇函数g (x )和一个偶函数h (x )之和,如果f (x )=lg(10x+1),其中x ∈(-∞,+∞),那么( )A g (x )=x , h (x )=lg(10x +10-x+2)B g (x )=21[lg(10x +1)+x ],h (x )= 21[lg(10x+1)-x ] C g (x )=2x ,h (x )=lg(10x +1)-2x D g (x )=-2x ,h (x )=lg(10x+1)+2x5 当a >1时,函数y =log a x 和y =(1-a )x 的图象只可能是( )A1oyx B1oyx C1oy x D1oyx6.若函数 a x f x+-=131)((a ≠0)是奇函数,则满足65)(=x f 的x 的取值集合为( ). (A) { log 32 } (B) { 1 } (C) {2 log 32 }(D) φ7.已知函数f ( x )的图象关于坐标原点成中心对称图形,且x < 0时,xx f ⎪⎭⎫⎝⎛=31)(,那么⎪⎭⎫⎝⎛21f 的值等于( ). (A)33(B) 3- (C) 3(D) 33-8.若2145-⎪⎭⎫⎝⎛=m ,3156-⎪⎭⎫ ⎝⎛=n , 2156-⎪⎭⎫⎝⎛=p ,则( ). (A) m < p < n (B) n < m < p (C) p < m < n(D) n < p < m9.函数y = log 2x 与)4(log 21x y =的图象( ).(A )关于直线x = 1对称 (B )关于直线y = x 对称 (C )关于直线y =-1对称 (D )关于直线y = 1对称10.函数5log log 2241++⎪⎪⎭⎫⎝⎛=x x y 在区间[2,4]上的最大值是( )(A) 4(B) 7(C)423 (D)4111.已知 -1≤x ≤2,则函数f(x)=3+2·3x+1-9x 的最大值为 最小值为 ; 12.方程 9-x-2·31-x= 27的解集为_____________________________.13.方程 log x (3x +4)=2的解集为__________________________.14.函数⎪⎭⎫⎝⎛-=12log 2x y 的反函数是________. 15.已知函数f (x )=log a (2-ax )在[0,1]上是x 的减函数,则实数a 的取值范围是____________. 16.方程log 2(9-2x)=3-x 的解集是__________. 17.已知函数()()0,1,022log <≠>-+=b a a bx bx x f a(1)求函数f(x)的定义域; (2)判断函数f(x)的奇偶性,并说明理由; (3)指出函数f(x)的单调区间; (4)求函数f(x)的反函数f-1(x).18.设10<<a ,函数()33log +-=x x x f a的定义域为[]n m ,,值域为[()1log -n a , ()1log -m a ]. (1)求证: m >3;(2)求a 的取值范围.19.已知函数f(x)=lg(ax-b x )(a >1>b >0).(1)求y=f(x)的定义域;(2)在函数y=f(x)的图象上是否存在不同的两点,使过这两点的直线平行于x 轴.20.函数f(x)=x a log 在区间[2,+∞)上总有|f(x)|>1成立,求实数a 的取值范围.21.已知函数f(x)=()12log 22++x ax . (1)若f(x)的定义域是R ,求实数a 的取值范围; (2)若f(x)的值域为R ,求实数a 的取值范围.22.已知函数()()()1,01log 2≠>--=a a x x x f a(1)求f(x)的定义域; (2)指出f(x)的单调性,并证明你的结论; (3)求满足f(x)<2的x 的取值范围.三.课后练习:1.设5x=1.5,(0.5)y =0.75,则x ,y 满足 [ ]. A .x >0,y >0 B .x <0,y <0 C .x >0,y <0 D .x <0,y >0 2.若loga2<logb2<0,则正确的大小关系是 [ ]. A .0<a <b <1 B .0<b <a <1 C .a >b >1 D .b >a >1 3.如果0<a <1,且x >y >1,则下列不等式中正确的是 [ ].A .a x <a yB .x a log >y a logC .x a ->y a -D .xa >y a4.函数()x f 的定义域是[]1,1-,那么函数⎪⎪⎭⎫ ⎝⎛x f 21log 的定义域是 [ ]A .⎥⎦⎤⎢⎣⎡2,21B .(0,2]C .[2,+∞)D .⎥⎦⎤⎝⎛21,05.若0<a <1, 则函数f(x)=loga(x+4)的图象一定不通过 [ ]. A .第一象限 B .第二象限 C .第三象限 D .第四象限6.使函数y=log2(x2-2|x|)的单调递增的区间是 [ ]. A .(-∞,-2) B .(0,1) C .(0,2) D .(2,+∞)7.已知logab=-2,那么 a+b 的最小值是 [ ].A .2233B .2323C .233D .3228.函数5log log 21241+-⎪⎪⎭⎫ ⎝⎛=x x y 在区间[]4,2上的最小值是 [ ].A .4B .8C .423 D .419.已知奇函数f(x)满足f(x-1)=f(x+2)对任意x ∈R 成立,并且当()1,0∈x 时,()13-=xx f ,那么⎪⎪⎭⎫ ⎝⎛36log 31f 的值为 [ ] A .31-B .31C .34D .34- 10.函数f(x)=loga(a-ax)(a >0,a ≠1)的定义域为_____;值域为_____.11.若函数()1211-⎪⎭⎫ ⎝⎛=+x x f 的反函数为()x g ,则()1+x g 的解析式为12.设12>>>a b a ,则a b abb a blog ,log ,log 从小到大的顺序是 13.已知0<a <1,那么x 的方程x a =|x a log |的实根的个数是______.14.已知函数()x x f 3log 2+=,x ∈[1,9],则()[]()22x f x f y +=的最大值是______.15.已知函数()()a ax x x f 3log 221+-=在区间[)+∞,2上是减函数,则实数a 的取值范围是______.17.已知实数p ,q 满足()()()1lg 2lg log lg 3++-=q q p ,试求实数p 的取值范围.18.已知函数f(x)=ax 在闭区间[-2,2]上的函数值总小于2,求实数a 的取值范围.19.设a ∈R ,试讨论关于x 的方程lg(x-1)+lg(3-x)=lg(a-x)的实数解的个数.20.已知函数()()()x p x x x x f -+-+-+=222log 1log 11log (1)求f(x)的定义域;(2)求f(x)的值域.21.设0<a <1,x 和y 满足3log log 3log =-+y a x x x a .如果y 有最大值42,求这时a 和x 的值.答案提示:课堂练习:1.B2.D3.B4 解析 由题意 g (x )+h (x )=lg(10x+1) ①又g (-x )+h (-x )=lg(10-x +1) 即-g (x )+h (x )=lg(10-x+1) ②由①②得 g (x )=2x ,h (x )=lg(10x+1)-2x 答案 C 5 解析 当a >1时,函数y =log a x 的图象只能在A 和C 中选,又a >1时,y =(1-a )x 为减函数 答案 B6. C .由 f ( x )是奇函数,故f (-1)=-f ( 1 ),即⎪⎭⎫⎝⎛+--=+--a a 1311311,解得 21=a .于是21131)(+-=x x f . 65)(=x f ,即6521131=+-x,化简得 3x= 4 .因此 x =2 log 32 . 7.B . f ( x )为奇函数. 331212121-=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛-f f .8.A .由函数 xy ⎪⎭⎫⎝⎛=56在R 上是增函数,可得 n > p ,从而否定(B )、(D ).又函数 21-=xy 在(0,+∞)上是减函数,可得m < p .9.C .在函数y = log 2x 图象上取一点P (1,0).可求得P 点关于直线x = 1的对称点为Q 1(1,0),P 点关于直线y = x 的对称点为Q 2(0,1),P 点关于直线y =-1的对称点为Q 3(1,-2),P 点关于直线y = 1的对称点为Q 4(1,2).经验证,其中只有Q 3点在函数)4(log 21x y =的图象上.10.D 11. 当t=3即x=1时,f(x)取最大值12,当t=9即 x=2时,f(x)取最小值-24. 12.{ -2 }.方程可化为 (3-x )2-6 (3-x)-27 = 0 .13.{ 4 } .解:x 2 = 3x + 4,并注意 x > 0,x ≠ 1. 14.y =2x +1+2 15.(1,2) 16.{0,3}.17. 所以f(x)的定义域为{x|x <2b 或x >-2b}.(2)对f(x)定义域内任意x ,有所以f(x)为奇函数.当a>1时在(0,+∞)上是增函数;当0<a<1时,在(0,+∞)上是减函数.它的单调性直观观察可得,如图2,于是有当a>1时,f(x)在(-∞,2b)上,在(-2b,+∞)上都是增函数,当0<a<1时,f(x)在(-∞,2b)上,在(-2b,+∞)上都是减函数.18.n>m,又由函数值域可知n>1,m>1,所以n>m>3,故m>3得证.y=logau为减函数,所以y=f(x)在[m,n]上为减函数,从而f(x)的值域为[f(n),ax2+(2a-1)x+3-3a=019.分析此题第(2)问是从几何角度探索函数图象的特征,但此函数图象并不会画,也不易画出,因此应转化为代数角度探索该函数相关的性质.(0,+∞).(2)先证f(x)在(0, +∞)上是增函数.任取0<x1<x2,由a>1>b>0,知ax1<ax2,bx1>bx2,所以0<ax1-bx1<ax2-bx2.因此 lg(ax1-bx1)<lg(ax2-bx2),即f(x1)<f(x2).所以f(x)在(0,+∞)上是增函数.假设函数y=f(x)的图象上存在不同的两点A(x1,y1),B(x2,y2),使直线AB平行于x轴,则x1≠x2,y1=y2.这与f(x)在(0,+∞)上是增函数(y1=y2则x1=x2)相矛盾.故在函数f(x)的图象上不存在不同的两点,使过这两点的直线平行于x轴.20.解依题意f(x)=logax在[2,+∞)上总有|f(x)|>1成立|logax|>1对任意x∈[2,+∞)都成立logax>1或logax<-1对任x∈[2,+∞)总成立y=logax在[2,+∞)上的最小值大于1或y=logax在[2,+∞)的最大值小于-1.而函数y=logax(x≥2)只有a>1有最小值loga2,只有当0<a<1时,有最大值loga2,于是有21.当a=0时,不等式化为2x+1>0,显然不合题意;综上可得,当a>1时,f(x) 的定义域是R.当a=0时,函数为u=2x+1,值域为R.符合题意;解得0<a≤1.综上所述当0≤a≤1时,f(x)的值域为R.课后作业:1.A 2.B 3.C 4.A 5.A 6.D 7.A 8.C 9.A10.a>1时(-∞,1),0<a<1时,(1,+∞);a>1时(-∞,1),0<a<1时,(1,+∞).11.()12log 2-+-x 12.b a aba b blog log log << 13.2 14.13 15.-4<a ≤420.(1)(1,p);(2)当p >3时,f(x)的值域为(-∞,2log2(p+1)-2];当1<p ≤3时,f(x)的值域为(-∞,1+log2(p-1))。

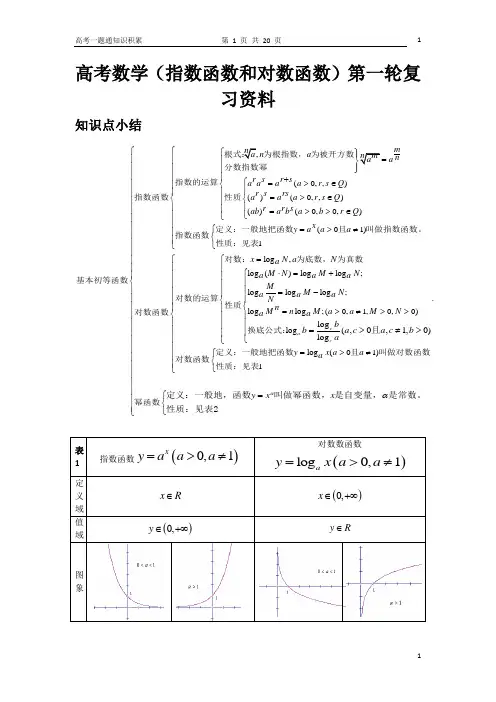
高考数学(指数函数和对数函数)第一轮复习资料知识点小结(0,,)()(0,,)()(0,0,)(01)1lo m n a n a r s r s a a a a r s Q r s rs a a a r s Q r r s ab a b a b r Q x y a a a x +=>∈=>∈=>>∈=>≠=⎧⎧⎪⎪⎪⎪⎪⎪⎧⎨⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎪⎩⎩⎪⎧⎪⎨⎪⎩⎩为根指数,为被开方数分数指数幂指数的运算指数函数性质定义:一般地把函数且叫做指数函数。
指数函数性质:见表对数:基本初等函数对数的运算对数函数g ,log ()log log ;log log log ;.log log ;(0,1,0,0)log log (01)1log (,0,1,0)log c a c N a N a M N M N a a a M M N a a a N n M n M a a M N a a y x a a a b b a c a c b a ⋅=+=-=>≠>>=>≠⎧⎧⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎨⎪⎪⎨⎪⎪⎪⎪⎪=>≠>⎪⎪⎩⎩⎧⎨⎩⎩为底数,为真数性质换底公式:定义:一般地把函数且叫做对数函数对数函数性质:见表且y x x αα⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧=⎪⎨⎪⎩⎩幂函数定义:一般地,函数叫做幂函数,是自变量,是常数。
性质:见表2试题选讲第一节对函数的进一步认识第一节 指数函数A 组1.(2010年黑龙江哈尔滨模拟)若a >1,b <0,且a b +a -b =22,则a b -a -b 的值等于________.解析:∵a >1,b <0,∴0<a b <1,a -b >1.又∵(a b +a -b )2=a 2b +a -2b +2=8,∴a 2b +a -2b =6,∴(a b -a -b )2=a 2b +a -2b -2=4,∴a b -a -b =-2.答案:-2 2.已知f (x )=a x +b 的图象如图所示,则f (3)=________.解析:由图象知f (0)=1+b =-2,∴b =-3.又f (2)=a 2-3=0,∴a =3,则f (3)=(3)3-3=33-3.答案:33-33.函数y =(12)2x -x 2的值域是________.解析:∵2x -x 2=-(x -1)2+1≤1, ∴(12)2x -x 2≥12.答案:[12,+∞) 4.(2009年高考山东卷)若函数f (x )=a x -x -a (a >0,且a ≠1)有两个零点,则实数a 的取值范围是________.解析:函数f (x )的零点的个数就是函数y =a x 与函数y =x +a 交点的个数,由函数的图象可知a >1时两函数图象有两个交点,0<a <1时两函数图象有惟一交点,故a >1. 答案:(1,+∞)5.(原创题)若函数f (x )=a x-1(a >0,a ≠1)的定义域和值域都是[0,2],则实数a 等于________.解析:由题意知⎩⎪⎨⎪⎧ 0<a <1a 2-1=0a 0-1=2无解或⎩⎪⎨⎪⎧a >1a 0-1=0a 2-1=2⇒a = 3.答案: 3 6.已知定义域为R 的函数f (x )=-2x +b2x +1+a是奇函数.(1)求a ,b 的值;(2)若对任意的t ∈R ,不等式f (t 2-2t )+f (2t 2-k )<0恒成立,求k 的取值范围.解:(1)因为f (x )是R 上的奇函数,所以f (0)=0,即-1+b2+a=0,解得b =1.从而有f (x )=-2x+12x +1+a .又由f (1)=-f (-1)知-2+14+a =--12+11+a,解得a =2.(2)法一:由(1)知f (x )=-2x +12x +1+2=-12+12x +1,由上式易知f (x )在R 上为减函数,又因f (x )是奇函数,从而不等式f (t 2-2t )+f (2t 2-k )<0⇔f (t 2-2t )<-f (2t 2-k )=f (-2t 2+k ).因f (x )是R 上的减函数,由上式推得t 2-2t >-2t 2+k .即对一切t ∈R 有3t 2-2t -k >0,从而Δ=4+12k <0,解得k <-13.法二:由(1)知f (x )=-2x +12x +1+2,又由题设条件得-2t 2-2t +12t 2-2t +1+2+-22t 2-k +122t 2-k +1+2<0即(22t2-k +1+2)(-2t2-2t+1)+(2t2-2t +1+2)(-22t2-k+1)<0整理得23t2-2t -k>1,因底数2>1,故3t 2-2t -k >0上式对一切t ∈R 均成立,从而判别式Δ=4+12k <0,解得k <-13.B 组1.如果函数f (x )=a x +b -1(a >0且a ≠1)的图象经过第一、二、四象限,不经过第三象限,那么一定有________.①0<a <1且b >0 ②0<a <1且0<b <1 ③a >1且b <0 ④a >1且b >0解析:当0<a <1时,把指数函数f (x )=a x 的图象向下平移,观察可知-1<b -1<0,即0<b <1.答案:②2.(2010年保定模拟)若f (x )=-x 2+2ax 与g (x )=(a +1)1-x 在区间[1,2]上都是减函数,则a 的取值范围是________.解析:f (x )=-x 2+2ax =-(x -a )2+a 2,所以f (x )在[a ,+∞)上为减函数,又f (x ),g (x )都在[1,2]上为减函数,所以需⎩⎪⎨⎪⎧a ≤1a +1>1⇒0<a ≤1.答案:(0,1]3.已知f (x ),g (x )都是定义在R 上的函数,且满足以下条件①f (x )=a x ·g (x )(a >0,a ≠1);②g (x )≠0;若f (1)g (1)+f (-1)g (-1)=52,则a 等于________.解析:由f (x )=a x ·g (x )得f (x )g (x )=a x ,所以f (1)g (1)+f (-1)g (-1)=52⇒a +a -1=52,解得a =2或12.答案:2或124.(2010年北京朝阳模拟)已知函数f (x )=a x (a >0且a ≠1),其反函数为f -1(x ).若f (2)=9,则f -1(13)+f (1)的值是________.解析:因为f (2)=a 2=9,且a >0,∴a =3,则f (x )=3x =13,∴x =-1,故f -1(13)=-1.又f (1)=3,所以f -1(13)+f (1)=2.答案:25.(2010年山东青岛质检)已知f (x )=(13)x ,若f (x )的图象关于直线x =1对称的图象对应的函数为g (x ),则g (x )的表达式为________.解析:设y =g (x )上任意一点P (x ,y ),P (x ,y )关于x =1的对称点P ′(2-x ,y )在f (x )=(13)x 上,∴y =(13)2-x =3x -2.答案:y =3x -2(x ∈R ) 6.(2009年高考山东卷改编)函数y =e x +e -xe x -e-x 的图象大致为________.解析:∵f (-x )=e -x+e x e -x -e x =-e x+e-xe x -e -x =-f (x ),∴f (x )为奇函数,排除④.又∵y =e x +e -x e x -e -x =e 2x +1e 2x -1=e 2x-1+2e 2x -1=1+2e 2x -1在(-∞,0)、(0,+∞)上都是减函数,排除②、③.答案:①7.(2009年高考辽宁卷改编)已知函数f (x )满足:当x ≥4时,f (x )=(12)x ;当x <4时,f (x )=f (x+1),则f (2+log 23)=________.解析:∵2<3<4=22,∴1<log 23<2.∴3<2+log 23<4,∴f (2+log 23)=f (3+log 23)=f (log 224)=(12)log 224=2-log 224=2log 2124=124.答案:1248.(2009年高考湖南卷改编)设函数y =f (x )在(-∞,+∞)内有定义,对于给定的正数K ,定义函数f K (x )=⎩⎪⎨⎪⎧f (x ),f (x )≤K ,K , f (x )>K .取函数f (x )=2-|x |,当K =12时,函数f K (x )的单调递增区间为________.解析:由f (x )=2-|x |≤12得x ≥1或x ≤-1,∴f K (x )=⎩⎪⎨⎪⎧2-|x |,x ≥1或x ≤-1,12,-1<x <1.则单调增区间为(-∞,-1].答案:(-∞,-1]9.函数y =2|x |的定义域为[a ,b ],值域为[1,16],当a 变动时,函数b =g (a )的图象可以是________.解析:函数y =2|x |的图象如图.当a =-4时,0≤b ≤4,当b =4时,-4≤a ≤0,答案:②10.(2010年宁夏银川模拟)已知函数f (x )=a 2x +2a x -1(a >0,且a ≠1)在区间[-1,1]上的最大值为14,求实数a 的值.解:f (x )=a 2x +2a x -1=(a x +1)2-2,∵x ∈[-1,1],(1)当0<a <1时,a ≤a x ≤1a ,∴当a x =1a 时,f (x )取得最大值.∴(1a +1)2-2=14,∴1a =3,∴a =13. (2)当a >1时,1a≤a x ≤a ,∴当a x =a 时,f (x )取得最大值.∴(a +1)2-2=14,∴a =3.综上可知,实数a 的值为13或3.11.已知函数f (x )=-22x -a +1.(1)求证:f (x )的图象关于点M (a ,-1)对称;(2)若f (x )≥-2x在x ≥a 上恒成立,求实数a 的取值范围.解:(1)证明:设f (x )的图象C 上任一点为P (x ,y ),则y =-22x -a +1,P (x ,y )关于点M (a ,-1)的对称点为P ′(2a -x ,-2-y ).∴-2-y =-2+22x -a +1=-2·2x -a 2x -a +1=-21+2-(x -a )=-22(2a -x )-a+1, 说明点P ′(2a -x ,-2-y )也在函数y =-22x -a +1的图象上,由点P 的任意性知,f (x )的图象关于点M (a ,-1)对称.(2)由f (x )≥-2x 得-22x -a +1≥-2x ,则22x -a +1≤2x ,化为2x -a ·2x +2x -2≥0,则有(2x )2+2a ·2x -2·2a ≥0在x ≥a 上恒成立.令g (t )=t 2+2a ·t -2·2a ,则有g (t )≥0在t ≥2a 上恒成立.∵g (t )的对称轴在t =0的左侧,∴g (t )在t ≥2a上为增函数. ∴g (2a )≥0.∴(2a )2+(2a )2-2·2a ≥0,∴2a (2a -1)≥0,则a ≥0.即实数a 的取值范围为a ≥0.12.(2008年高考江苏)若f 1(x )=3|x -p 1|,f 2(x )=2·3|x -p 2|,x ∈R ,p 1、p 2为常数,且f (x )=⎩⎪⎨⎪⎧f 1(x ),f 1(x )≤f 2(x ),f 2(x ),f 1(x )>f 2(x ).(1)求f (x )=f 1(x )对所有实数x 成立的充要条件(用p 1、p 2表示);(2)设a ,b 是两个实数,满足a <b ,且p 1、p 2∈(a ,b ).若f (a )=f (b ),求证:函数f (x )在区间[a ,b ]上的单调增区间的长度之和为b -a2(闭区间[m ,n ]的长度定义为n -m ).解:(1)f (x )=f 1(x )恒成立⇔f 1(x )≤f 2(x )⇔3|x -p 1|≤2·3|x -p 2|⇔3|x -p 1|-|x -p 2|≤2⇔|x -p 1|-|x -p 2|≤log 32.(*)若p 1=p 2,则(*)⇔0≤log 32,显然成立;若p 1≠p 2,记g (x )=|x -p 1|-|x -p 2|,当p 1>p 2时,g (x )=⎩⎪⎨⎪⎧p 1-p 2,x <p 2,-2x +p 1+p 2,p 2≤x ≤p 1,p 2-p 1,x >p 1.所以g (x )max =p 1-p 2,故只需p 1-p 2≤log 32. 当p 1<p 2时,g (x )=⎩⎪⎨⎪⎧p 1-p 2,x <p 1;2x -p 1-p 2,p 1≤x ≤p 2;p 2-p 1,x >p 2.所以g (x )max =p 2-p 1,故只需p 2-p 1≤log 32.综上所述,f (x )=f 1(x )对所有实数x 成立的充要条件是|p 1-p 2|≤log 32. (2)证明:分两种情形讨论. ①当|p 1-p 2|≤log 32时,由(1)知f (x )=f 1(x )(对所有实数x ∈[a ,b ]),则由f (a )=f (b )及a <p 1<b易知p 1=a +b2.再由f 1(x )=⎩⎪⎨⎪⎧3p 1-x ,x <p 1,3x -p 1,x ≥p 1,的单调性可知,f (x )在区间[a ,b ]上的单调增区间的长度为b -a +b 2=b -a2.②当|p 1-p 2|>log 32时,不妨设p 1<p 2,则p 2-p 1>log 32.于是,当x ≤p 1时,有f 1(x )=3p 1-x<3p 2-x <f 2(x ),从而f (x )=f 1(x ).当x ≥p 2时,f 1(x )=3x -p 1=3p 2-p 1·3x -p 2>3log 32·3x -p 2=f 2(x ),从而f (x )=f 2(x ).当p 1<x <p 2时,f 1(x )=3x -p 1及f 2(x )=2·3p 2-x ,由方程3x 0-p 1=2·3p 2-x 0,解得f 1(x )与f 2(x )图象交点的横坐标为x 0=p 1+p 22+12log 32.①显然p 1<x 0=p 2-12[(p 2-p 1)-log 32]<p 2,这表明x 0在p 1与p 2之间.由①易知f (x )=⎩⎪⎨⎪⎧f 1(x ),p 1≤x ≤x 0,f 2(x ),x 0<x ≤p 2.综上可知,在区间[a ,b ]上,f (x )=⎩⎪⎨⎪⎧f 1(x ),a ≤x ≤x 0,f 2(x ),x 0<x ≤b .故由函数f 1(x )与f 2(x )的单调性可知,f (x )在区间[a ,b ]上的单调增区间的长度之和为(x 0-p 1)+(b -p 2),由于f (a )=f (b ),即3p 1-a =2·3b -p 2,得p 1+p 2=a +b +log 32.②故由①②得(x 0-p 1)+(b -p 2)=b -12(p 1+p 2-log 32)=b -a 2.综合①、②可知,f (x )在区间[a ,b ]上单调增区间的长度之和为b -a2.第二节 对数函数A 组1.(2009年高考广东卷改编)若函数y =f (x )是函数y =a x (a >0,且a ≠1)的反函数,其图象经过点(a ,a ),则f (x )=________.解析:由题意f (x )=log a x ,∴a =log a a 12=12,∴f (x )=log 12x .答案:log 12x2.(2009年高考全国卷Ⅱ)设a =log 3π,b =log 23,c =log 32,则a 、b 、c 的大小关系是________.解析:a =log 3π>1,b =log 23=12log 23∈(12,1),c =log 32=12log 32∈(0,12),故有a >b >c .答案:a >b >c3.若函数f (x )=⎪⎩⎪⎨⎧∈-∈⎪⎭⎫ ⎝⎛]1,0[,4)0,1[,41x x xx,则f (log 43)=________.解析:0<log 43<1,∴f (log 43)=4log 43= 3.答案:3 4.如图所示,若函数f (x )=a x-1的图象经过点(4,2),则函数g (x )=log a 1x +1的图象是________.解析:由已知将点(4,2)代入y =a x -1,∴2=a4-1,即a =213>1.又1x +1是单调递减的,故g (x )递减且过(0,0)点,∴④正确.答案:④ 5.(原创题)已知函数f (x )=a log 2x +b log 3x +2,且f (12010)=4,则f (2010)的值为_.解析:设F (x )=f (x )-2,即F (x )=a log 2x +b log 3x ,则F (1x )=a log 21x +b log 31x=-(a log 2x+b log 3x )=-F (x ),∴F (2010)=-F (12010)=-[f (12010)-2]=-2,即f (2010)-2=-2,故f (2010)=0.答案:06.若f (x )=x 2-x +b ,且f (log 2a )=b ,log 2f (a )=2(a >0且a ≠1).(1)求f (log 2x )的最小值及相应x 的值;(2)若f (log 2x )>f (1)且log 2f (x )<f (1),求x 的取值范围.解:(1)∵f (x )=x 2-x +b ,∴f (log 2a )=(log 2a )2-log 2a +b =b ,∴log 2a =1,∴a =2.又∵log 2f (a )=2,∴f (a )=4.∴a 2-a +b =4,∴b =2.∴f (x )=x 2-x +2.∴f (log 2x )=(log 2x )2-log 2x +2=(log 2x -12)2+74.∴当log 2x =12,即x =2时,f (log 2x )有最小值74.(2)由题意知⎩⎪⎨⎪⎧ (log 2x )2-log 2x +2>2,log 2(x 2-x +2)<2.∴⎩⎪⎨⎪⎧log 2x <0或log 2x >1,0<x 2-x +2<4. ∴⎩⎪⎨⎪⎧0<x <1或x >2,-1<x <2.∴0<x <1. B 组1.(2009年高考北京卷改编)为了得到函数y =lg x +310的图象,只需把函数y =lg x 的图象上所有的点________.解析:∵y =lg x +310=lg(x +3)-1,∴将y =lg x 的图象上的点向左平移3个单位长度得到y =lg(x +3)的图象,再将y =lg(x +3)的图象上的点向下平移1个单位长度得到y =lg(x +3)-1的图象.答案:向左平移3个单位长度,再向下平移1个单位长度2.(2010年安徽黄山质检)对于函数f (x )=lg x 定义域中任意x 1,x 2(x 1≠x 2)有如下结论:①f (x 1+x 2)=f (x 1)+f (x 2);②f (x 1·x 2)=f (x 1)+f (x 2);③f (x 1)-f (x 2)x 1-x 2>0;④f (x 1+x 22)<f (x 1)+f (x 2)2.上述结论中正确结论的序号是________.解析:由运算律f (x 1)+f (x 2)=lg x 1+lg x 2=lg x 1x 2=f (x 1x 2),所以②对;因为f (x )是定义域内的增函数,所以③正确;f (x 1+x 22)=lg x 1+x 22,f (x 1)+f (x 2)2=lg x 1+lg x 22=lg x 1x 2,∵x 1+x 22≥x 1x 2,且x 1≠x 2,∴lg x 1+x 22>lg x 1x 2,所以④错误.答案:②③3.(2010年枣庄第一次质检)对任意实数a 、b ,定义运算“*”如下:a *b =⎩⎪⎨⎪⎧a (a ≤b )b (a >b ),则函数f (x )=log 12(3x -2)*log 2x 的值域为________.解析:在同一直角坐标系中画出y =log 12(3x -2)和y =log 2x 两个函数的图象,由图象可得f (x )=⎩⎪⎨⎪⎧log 2x (0<x ≤1)log 12(3x -2) (x >1),值域为(-∞,0].答案:(-∞,0]4.已知函数y =f (x )与y =e x 互为反函数,函数y =g (x )的图象与y =f (x )的图象关于x 轴对称,若g (a )=1,则实数a 的值为________.解析:由y =f (x )与y =e x 互为反函数,得f (x )=ln x ,因为y =g (x )的图象与y =f (x )的图象关于x 轴对称,故有g (x )=-ln x ,g (a )=1⇒ln a =-1,所以a =1e.答案:1e5.已知函数f (x )满足f (2x +|x |)=log 2x |x |,则f (x )的解析式是________.解析:由log 2x |x |有意义可得x >0,所以,f (2x +|x |)=f (1x ),log 2x |x |=log 2x ,即有f (1x )=log 2x ,故f (x )=log 21x=-log 2x .答案:f (x )=-log 2x ,(x >0)6.(2009年高考辽宁卷改编)若x 1满足2x +2x =5,x 2满足2x +2log 2(x -1)=5,则x 1+x 2=________.解析:由题意2x 1+2x 1=5,①2x 2+2log 2(x 2-1)=5,②所以2x 1=5-2x 1,x 1=log 2(5-2x 1),即2x 1=2log 2(5-2x 1).令2x 1=7-2t ,代入上式得7-2t =2log 2(2t -2)=2+2log 2(t -1),∴5-2t =2log 2(t -1)与②式比较得t =x 2,于是2x 1=7-2x 2.∴x 1+x 2=T 2.答案:727.当x ∈[n ,n +1),(n ∈N )时,f (x )=n -2,则方程f (x )=log 2x 根的个数是________.解析:当n =0时,x ∈[0,1),f (x )=-2; 当n =1时,x ∈[1,2),f (x )=-1; 当n =2时,x ∈[2,3),f (x )=0; 当n =3时,x ∈[3,4),f (x )=1; 当n =4时,x ∈[4,5),f (x )=2;当n =5时,x ∈[5,6),f (x )=3.答案:2 8.(2010年福建厦门模拟)已知lg a +lg b =0,则函数f (x )=a x与函数g (x )=-log b x 的图象可能是________.解析:由题知,a =1b ,则f (x )=(1b)x =b -x ,g (x )=-log b x ,当0<b <1时,f (x )单调递增,g (x )单调递增,②正确;当b >1时,f (x )单调递减,g (x )单调递减.答案:② 9.已知曲线C :x 2+y 2=9(x ≥0,y ≥0)与函数y =log 3x 及函数y =3x 的图象分别交于点A (x 1,y 1),B (x 2,y 2),则x 12+x 22的值为________.解析:∵y =log 3x 与y =3x 互为反函数,所以A 与B 两点关于y =x 对称,所以x 1=y 2,y 1=x 2,∴x 12+x 22=x 12+y 12=9.答案:910.已知函数f (x )=lg kx -1x -1(k ∈R 且k >0).(1)求函数f (x )的定义域;(2)若函数f (x )在[10,+∞)上是单调增函数,求k 的取值范围.解:(1)由kx -1x -1>0及k >0得x -1k x -1>0,即(x -1k )(x -1)>0.①当0<k <1时,x <1或x >1k ;②当k =1时,x ∈R 且x ≠1;③当k >1时,x <1k或x >1.综上可得当0<k <1时,函数的定义域为(-∞,1)∪(1k,+∞);当k ≥1时,函数的定义域为(-∞,1k)∪(1,+∞).(2)∵f (x )在[10,+∞)上是增函数,∴10k -110-1>0,∴k >110.又f (x )=lg kx -1x -1=lg(k +k -1x -1),故对任意的x 1,x 2,当10≤x 1<x 2时,恒有f (x 1)<f (x 2),即lg(k +k -1x 1-1)<lg(k +k -1x 2-1),∴k -1x 1-1<k -1x 2-1,∴(k -1)·(1x 1-1-1x 2-1)<0,又∵1x 1-1>1x 2-1,∴k -1<0,∴k <1.综上可知k ∈(110,1).11.(2010年天津和平质检)已知f (x )=log a 1+x1-x(a >0,a ≠1).(1)求f (x )的定义域;(2)判断f (x )的奇偶性并给予证明;(3)求使f (x )>0的x 的取值范围.解:(1)由1+x1-x>0 ,解得x ∈(-1,1).(2)f (-x )=log a 1-x1+x=-f (x ),且x ∈(-1,1),∴函数y =f (x )是奇函数.(3)若a >1,f (x )>0,则1+x 1-x >1,解得0<x <1;若0<a <1,f (x )>0,则0<1+x1-x<1,解得-1<x <0.12.已知函数f (x )满足f (log a x )=a a 2-1(x -x -1),其中a >0且a ≠1.(1)对于函数f (x ),当x ∈(-1,1)时,f (1-m )+f (1-m 2)<0,求实数m 的集合; (2)x ∈(-∞,2)时,f (x )-4的值恒为负数,求a 的取值范围.解:令log a x =t (t ∈R ),则x =a t ,∴f (t )=a a 2-1(a t -a -t ),∴f (x )=a a 2-1(a x -a -x ).∵f (-x )=a a 2-1(a -x -a x )=-f (x ),∴f (x )是R 上的奇函数.当a >1时,a a 2-1>0,a x 是增函数,-a -x 是增函数,∴f (x )是R 上的增函数;当0<a <1,a a 2-1<0,a x 是减函数,-a -x 是减函数,∴f (x )是R 上的增函数.综上所述,a >0且a ≠1时,f (x )是R 上的增函数.(1)由f (1-m )+f (1-m 2)<0有f (1-m )<-f (1-m 2)=f (m 2-1),∴⎩⎪⎨⎪⎧1-m <m 2-1,-1<1-m <1,-1<m 2-1<1.解得m ∈(1,2).(2)∵f (x )是R 上的增函数,∴f (x )-4也是R 上的增函数,由x <2,得f (x )<f (2), ∴f (x )-4<f (2)-4,要使f (x )-4的值恒为负数,只需f (2)-4≤0,即a a 2-1(a 2-a -2)-4≤0,解得2-3≤a ≤2+3, ∴a 的取值范围是2-3≤a ≤2+3且a ≠1.第三节 幂函数与二次函数的性质A 组1.若a >1且0<b <1,则不等式a log b (x -3)>1的解集为________.解析:∵a >1,0<b <1,∴a log b (x -3)>1⇔log b (x -3)>0⇔log b (x -3)>log b 1⇔0<x -3<1⇔3<x <4.答案:{x |3<x <4}2.(2010年广东广州质检)下列图象中,表示y =x 32的是________.解析:y =x 32=3x 2是偶函数,∴排除②、③,当x >1时,32xx =x 31>1,∴x >x 32,∴排除①.答案:④3.(2010年江苏海门质检)若x ∈(0,1),则下列结论正确的是__________.①2x >x 21>lg x ②2x >lg x >x 21 ③x 21>2x >lg x ④lg x >x 21>2x 解析:∵x ∈(0,1),∴2>2x>1,0<x 21<1,lg x <0.答案:① 4.(2010年东北三省模拟)函数f (x )=|4x -x 2|-a 恰有三个零点,则a =__________.解析:先画出f (x )=4x -x 2的图象,再将x 轴下方的图象翻转到x 轴的上方,如图,y =a 过抛物线顶点时恰有三个交点,故得a 的值为4.答案:45.(原创题)方程x 12=log sin1x 的实根个数是__________.解析:在同一坐标系中分别作出函数y 1=x 21 和y 2=log sin1x 的图象,可知只有惟一一个交点.答案:16.(2009年高考江苏卷)设a 为实数,函数f (x )=2x 2+(x -a )·|x -a |.(1)若f (0)≥1,求a 的取值范围;(2)求f (x )的最小值;(3)设函数h (x )=f (x ),x ∈(a ,+∞),直接写出(不需给出演算步骤)不等式h (x )≥1的解集.解:(1)因为f (0)=-a |-a |≥1,所以-a >0,即a <0.由a 2≥1知a ≤-1.因此,a 的取值范围为(-∞,-1].(2)记f (x )的最小值为g (a ).则有f (x )=2x 2+(x -a )|x -a |=⎩⎪⎨⎪⎧3(x -a 3)2+2a 23,x >a , ①(x +a )2-2a 2,x ≤a , ②(ⅰ)当a ≥0时,f (-a )=-2a 2,由①②知f (x )≥-2a 2,此时g (a )=-2a 2.(ⅱ)当a <0时,f (a 3)=23a 2.若x >a ,则由①知f (x )≥23a 2;若x ≤a ,则x +a ≤2a <0,由②知f (x )≥2a 2>23a 2.此时g (a )=23a 2.综上,得g (a )=⎩⎪⎨⎪⎧-2a 2, a ≥0,2a 23, a <0.(3)(ⅰ)当a ∈(-∞,-62]∪[22,+∞)时,解集为(a ,+∞); (ⅱ)当a ∈[-22,22)时,解集为[a +3-2a 23,+∞);(ⅲ)当a ∈(-62,-22)时,解集为(a ,a -3-2a 23]∪[a +3-2a 23,+∞).B 组1.(2010年江苏无锡模拟)幂函数y =f (x )的图象经过点(-2,-18),则满足f (x )=27的x 的值是__________.解析:设幂函数为y =x α,图象经过点(-2,-18),则-18=(-2)α,∴α=-3,∵x -3=27,∴x =13.答案:132.(2010年安徽蚌埠质检)α则不等式f (|x |)≤2的解集是解析:由表知22=(12)α,∴α=12,∴f (x )=x 12.∴(|x |)12≤2,即|x |≤4,故-4≤x ≤4.答案:{x |-4≤x ≤4}3.(2010年广东江门质检)设k ∈R ,函数f (x )=⎩⎪⎨⎪⎧1x (x >0),e x (x ≤0),F (x )=f (x )+kx ,x ∈R .当k =1时,F (x )的值域为__________.解析:当x >0时,F (x )=1x+x ≥2;当x ≤0时,F (x )=e x +x ,根据指数函数与幂函数的单调性,F (x )是单调递增函数,F (x )≤F (0)=1,所以k =1时,F (x )的值域为(-∞,1]∪[2,+∞).答案:(-∞,1]∪[2,+∞)4.设函数f (x )=⎩⎪⎨⎪⎧-2 (x >0),x 2+bx +c (x ≤0),若f (-4)=f (0),f (-2)=0,则关于x 的不等式f (x )≤1的解集为__________.解析:由f (-4)=f (0),得b =4.又f (-2)=0,可得c =4,∴⎩⎪⎨⎪⎧ x ≤0,x 2+4x +4≤1或⎩⎪⎨⎪⎧x >0,-2≤1,可得-3≤x ≤-1或x >0.答案:{x |-3≤x ≤-1或x >0}5.(2009年高考天津卷改编)已知函数f (x )=⎩⎪⎨⎪⎧x 2+4x , x ≥0,4x -x 2, x <0.若f (2-a 2)>f (a ),则实数a 的取值范围是__________.解析:函数f (x )=⎩⎪⎨⎪⎧x 2+4x ,x ≥0,4x -x 2,x <0,的图象如图. 知f (x )在R 上为增函数. ∵f (2-a 2)>f (a ),即2-a 2>a . 解得-2<a <1.答案:-2<a <16.(2009年高考江西卷改编)设函数f (x )=ax 2+bx +c(a <0)的定义域为D ,若所有点(s ,f (t ))(s ,t ∈D )构成一个正方形区域,则a 的值为__________.解析:由题意定义域D 为不等式ax 2+bx +c ≥0的解集.∵ax 2+bx +c =a (x +b 2a )2+4ac -b24a ,∵a <0,∴0≤y ≤ 4ac -b 24a,∴所有点(s ,f (t )),(s ,t ∈D )构成一个正方形区域,意味着方程ax 2+bx +c =0的两根x 1,x 2应满足|x 1-x 2|= 4ac -b 24a,由根与系数的关系知4ac -b 24a =b 2a 2-4c a =b 2-4aca 2,∴4a =-a 2.∵a <0,∴a =-4.答案:-47.(2010年辽宁沈阳模拟)已知函数f (x )=⎩⎪⎨⎪⎧-2+x ,x >0,-x 2+bx +c ,x ≤0.若f (0)=-2f (-1)=1,则函数g (x )=f (x )+x 的零点的个数为__________.解析:∵f (0)=1,∴c =1.又f (-1)=-12,∴-1-b +1=-12,∴b =12.当x >0时,g (x )=-2+2x =0,∴x =1;当x ≤0时,g (x )=-x 2+12x +1+x =0,∴x 2-32x -1=0,∴x =2(舍)或x =-12,所以有两个零点.答案:28.设函数f (x )=x |x |+bx +c ,给出下列四个命题:①c =0时,f (x )是奇函数;②b =0,c >0时,方程f (x )=0只有一个实根;③f (x )的图象关于(0,c )对称;④方程f (x )=0至多有两个实根.其中正确的命题是__________.解析:c =0时,f (-x )=-x |-x |+b (-x )=-x |x |-bx =-f (x ),故f (x )是奇函数;b =0,c >0时,f (x )=x |x |+c =0,∴x ≥0时,x 2+c =0无解,x <0时,f (x )=-x 2+c =0,∴x =-c ,有一个实数根.答案:①②③9.(2010年湖南长沙质检)对于区间[a ,b ]上有意义的两个函数f (x )与g (x ),如果对于区间[a ,b ]中的任意数x 均有|f (x )-g (x )|≤1,则称函数f (x )与g (x )在区间[a ,b ]上是密切函数,[a ,b ]称为密切区间.若m (x )=x 2-3x +4与n (x )=2x -3在某个区间上是“密切函数”,则它的一个密切区间可能是________.①[3,4] ②[2,4] ③[2,3] ④[1,4]解析:|m (x )-n (x )|≤1⇒|x 2-5x +7|≤1,解此绝对值不等式得2≤x ≤3,故在区间[2,3]上|m (x )-n (x )|的值域为[0,1],∴|m (x )-n (x )|≤1在[2,3]上恒成立.答案:③10.设函数f (x )=x 2+2bx +c (c <b <1),f (1)=0,方程f (x )+1=0有实根.(1)证明:-3<c ≤-1且b ≥0;(2)若m 是方程f (x )+1=0的一个实根,判断f (m -4)的正负并加以证明.解:(1)证明:f (1)=0⇒1+2b +c =0⇒b =-c +12.又c <b <1,故c <-c +12<1⇒-3<c <-13.方程f (x )+1=0有实根,即x 2+2bx +c +1=0有实根,故Δ=4b 2-4(c +1)≥0,即(c +1)2-4(c +1)≥0⇒c ≥3或c ≤-1.又c <b <1,得-3<c ≤-1,由b =-c +12知b ≥0.(2)f (x )=x 2+2bx +c =x 2-(c +1)x +c =(x -c )(x -1),f (m )=-1<0, ∴c <m <1,∴c -4<m -4<-3<c ,∴f (m -4)=(m -4-c )(m -4-1)>0, ∴f (m -4)的符号为正.11.(2010年安徽合肥模拟)设函数f (x )=ax 2+bx +c ,且f (1)=-a2,3a >2c >2b ,求证:(1)a >0且-3<b a <-34;(2)函数f (x )在区间(0,2)内至少有一个零点;(3)设x 1、x 2是函数f (x )的两个零点,则2≤|x 1-x 2|<574.证明:(1)∵f (1)=a +b +c =-a2,∴3a +2b +2c =0.又3a >2c >2b ,∴3a >0,2b <0,∴a >0,b <0.又2c =-3a -2b ,由3a >2c >2b ,∴3a >-3a -2b >2b .∵a >0,∴-3<b a <-34.(2)∵f (0)=c ,f (2)=4a +2b +c =a -c ,①当c >0时,∵a >0,∴f (0)=c >0且f (1)=-a2<0,∴函数f (x )在区间(0,1)内至少有一个零点.②当c ≤0时,∵a >0,∴f (1)=-a2<0且f (2)=a -c >0,∴函数f (x )在区间(1,2)内至少有一个零点.综合①②得f (x )在(0,2)内至少有一个零点.(3)∵x 1、x 2是函数f (x )的两个零点,则x 1、x 2是方程ax 2+bx +c =0的两个根,∴x 1+x 2=-b a ,x 1x 2=c a =-32-b a ,∴|x 1-x 2|=(x 1+x 2)2-4x 1x 2= (-b a )2-4(-32-b a )=(b a +2)2+2.∵-3<b a <-34,∴2≤|x 1-x 2|<574. 12.已知函数f (x )=ax 2+4x +b (a <0,a 、b ∈R ),设关于x 的方程f (x )=0的两实根为x 1、x 2,方程f (x )=x 的两实根为α、β.(1)若|α-β|=1,求a 、b 的关系式;(2)若a 、b 均为负整数,且|α-β|=1,求f (x )的解析式;(3)若α<1<β<2,求证:(x 1+1)(x 2+1)<7.解:(1)由f (x )=x 得ax 2+3x +b =0(a <0,a 、b ∈R )有两个不等实根为α、β,∴Δ=9-4ab >0,α+β=-3a ,α·β=ba.由|α-β|=1得(α-β)2=1,即(α+β)2-4αβ=9a 2-4ba=1,∴9-4ab =a 2,即a 2+4ab =9(a <0,a 、b ∈R ).(2)由(1)得a (a +4b )=9,∵a 、b 均为负整数, ∴⎩⎪⎨⎪⎧a =-1a +4b =-9或⎩⎪⎨⎪⎧ a =-9a +4b =-1或⎩⎪⎨⎪⎧a =-3,a +4b =-3,显然后两种情况不合题意,应舍去,从而有⎩⎪⎨⎪⎧a =-1,a +4b =-9,∴⎩⎪⎨⎪⎧a =-1,b =-2.故所求函数解析式为f (x )=-x 2+4x -2.(3)证明:由已知得x 1+x 2=-4a ,x 1·x 2=b a ,又由α<1<β<2得α+β=-3a <3,α·β=ba<2,∴-1a <1,∴(x 1+1)(x 2+1)=x 1·x 2+(x 1+x 2)+1=b a -4a +1<2+4+1=7,即(x 1+1)(x 2+1)<7.第四节 函数的图像特征A 组1.命题甲:已知函数f (x )满足f (1+x )=f (1-x ),则f (x )的图象关于直线x =1对称.命题乙:函数f (1+x )与函数f (1-x )的图象关于直线x =1对称.则甲、乙命题正确的是__________.解析:可举实例说明如f (x )=2x ,依次作出函数f (1+x )与函数f (1-x )的图象判断.答案:甲2.(2010年济南市高三模拟考试)函数y =x |x |·a x(a >1)的图象的基本形状是_____.解析:先去绝对值将已知函数写成分段函数形式,再作图象即可,函数解析式:y =⎩⎪⎨⎪⎧ax (x >0)-ax (x <0),由指数函数图象易知①正确.答案:①3.已知函数f (x )=(15)x -log 3x ,若x 0是方程f (x )=0的解,且0<x 1<x 0,则f (x 1)的值为__________(正负情况).解析:分别作y =(15)x 与y =log 3x 的图象,如图可知,当0<x 1<x 0时,(15)x1>log 3x 1,∴f (x 1)>0.答案:正值4.(2009年高考安徽卷改编)设a <b ,函数y =(x -a )2(x -b )的图象可能是_____.解析:∵x >b 时,y >0.由数轴穿根法,从右上向左下穿,奇次穿偶次不穿可知,只有③正确.答案:③5.(原创题)已知当x ≥0时,函数y =x 2与函数y =2x 的图象如图所示,则当x ≤0时,不等式2x ·x 2≥1的解集是__________.解析:在2x ·x 2≥1中,令x =-t ,由x ≤0得t ≥0, ∴2-t ·(-t )2≥1,即t 2≥2t ,由所给图象得2≤t ≤4, ∴2≤-x ≤4,解得-4≤x ≤-2. 答案:-4≤x ≤-26.已知函数f (x )=⎩⎨⎧.(2,5]∈,3-,1,2]-[∈,-32x x x x(1)画出f (x )的图象;(2)写出f (x )的单调递增区间.解:(1)函数f (x )的图象如图所示.,(2)由图象可知,函数f (x )的单调递增区间为[-1,0],[2,5].B 组 1.(2010年合肥市高三质检)函数f (x )=ln 1-x1+x的图象只可能是__________.解析:本题中f (x )的定义域为{x |-1<x <1},从而排除②③选项.又由于u (x )=-1+21+x在定义域{x |-1<x <1}内是减函数,而g (x )=ln x 在定义域(0,+∞)内是增函数,从而f (x )=ln 1-x 1+x =ln(-1+21+x )在定义域{x |-1<x <1}是减函数. 答案:①2.家电下乡政策是应对金融危机、积极扩大内需的重要举措.我市某家电制造集团为尽快实现家电下乡提出四种运输方案,据预测,这四种方案均能在规定时间T 内完成预期的运输任务Q 0,各种方案的运输总量Q 与时间t 的函数关系如下图所示.在这四种方案中,运输效率(单位时间的运输量)逐步提高的是解析:运输效率是运输总量Q 与时间t 的函数的导数,几何意义为图象的切线,切线斜率的增长表明运输效率的提高,从图形看,②正确.答案:②3.如图,过原点O 的直线与函数y =2x 的图象交于A ,B 两点,过B作y 轴的垂线交函数y =4x的图象于点C ,若AC 平行于y 轴,则点A 的坐标是__________.解析:设C (a,4a ),所以A (a,2a ),B (2a,4a ),又O ,A ,B 三点共线,所以2a a =4a 2a,故4a =2×2a ,所以2a =0(舍去)或2a =2,即a =1,所以点A 的坐标是(1,2).答案:(1,2)4.已知函数f (x )=4-x 2,g (x )是定义在(-∞,0)∪(0,+∞)上的奇函数,当x >0时,g (x )=log 2x ,则函数y =f (x )·g (x )的大致图象为__________.解析:f (x )为偶函数,g (x )是奇函数,所以f (x )·g (x )为奇函数,图象关于原点对称,当x →+∞时,f (x )→-∞,g (x )→+∞,所以f (x )·g (x )→-∞答案:②5.某加油机接到指令,给附近空中一运输机加油.运输机的余油量为Q 1(吨),加油机加油箱内余油Q 2(吨),加油时间为t 分钟,Q 1、Q 2与时间t 的函数关系式的图象如右图.若运输机加完油后以原来的速度飞行需11小时到达目的地,问运输机的油料是否够用?________.解析:加油时间10分钟,Q 1由30减小为0.Q 2由40增加到69,因而10分钟时间内运输机用油1吨.以后的11小时需用油66吨.因69>66,故运输机的油料够用.答案:够用 6.已知函数y =f (x )(x ∈R )满足f (x +2)=f (x ),且x ∈(-1,1]时,f (x )=|x |,则y =f (x )与y =log 7x 的交点的个数为__________.解析:由f (x +2)=f (x )知函数y =f (x )为周期为2的周期函数,作图. 答案:67.函数y =x mn (m ,n ∈Z ,m ≠0,|m |,|n |互质)图象如图所示,则下列结论正确的是__________.①mn >0,m ,n 均为奇数②mn <0,m ,n 一奇一偶 ③mn <0,m ,n 均为奇数 ④mn >0,m ,n 一奇一偶解析:由于幂函数在第一象限的图象趋势表明函数在(0,+∞)上单调递减,此时只需保证mn<0,即mn <0,有y =x m n =x -|m ||n |;同时函数只在第一象限有图象,则函数的定义域为(0,+∞),此时|n |定为偶数,n 即为偶数,由于两个数互质,则m 定为奇数.答案:②8.(2009年高考福建卷改编)定义在R 上的偶函数f (x )的部分图象如图所示,则在(-2,0)上,下列函数中与f (x )的单调性不同的是①y =x 2+1②y =|x |+1③y =⎩⎪⎨⎪⎧2x +1,x ≥0x 3+1,x <0④y =⎩⎪⎨⎪⎧e x ,x ≥0e -x ,x <0解析:∵f (x )为偶函数,由图象知,f (x )在(-2,0)上为减函数,而y =x 3+1在(-∞,0)上为增函数.答案:③9.(2010年安徽合肥模拟)已知函数图象C ′与C :y (x +a +1)=ax +a 2+1关于直线y =x 对称,且图象C ′关于点(2,-3)对称,则a 的值为__________.解析:∵C ′与C :y (x +a +1)=ax +a 2+1关于直线y =x 对称,∴C ′为x (y +a +1)=ay +a 2+1.整理得,y +1+a =1-ax -a.∵C ′关于点(2,-3)对称,∴a =2.答案:2 10.作下列函数的图象:(1)y =1|x |-1;(2)y =|x -2|(x +1);(3)y =1-|x ||1-x |;(4)y =|log 2x -1|;(5)y =2|x -1|.解:(1)定义域{x |x ∈R 且x ≠±1},且函数是偶函数.又当x ≥0且x ≠1时,y =1x -1.先作函数y =1x 的图象,并将图象向右平移1个单位,得到函数y =1x -1(x ≥0且x ≠1)的图象(如图(a)所示).又函数是偶函数,作关于y 轴对称图象,得y =1|x |-1的图象(如图(b)所示).(2)函数式可化为y =⎩⎨⎧(x -12)2-94 (x ≥2),-(x -12)2+94(x <2).其图象如图①所示.(3)函数式化为y =⎩⎪⎨⎪⎧1+x 1-x (x <0),1 (0≤x <1),-1 (x >1).其图象如图②所示.(4)先作出y =log2x 的图象,再将其图象向下平移1个单位长度,保留x 轴上方的部分,将x 轴下方的图象翻折到x 轴上方,即得y =|log2x -1|的图象,如图③所示.(5)先作出y =2x的图象,再将其图象在y 轴左边的部分去掉,并作出y 轴右边的图象关于y 轴对称的图象,即得y =2|x |的图象,再将y =2|x |的图象向右平移1个单位长度,即得y=2|x -1|的图象,如图④所示.11.已知函数f (x )=-a a x +a(a >0且a ≠1).(1)证明:函数y =f (x )的图象关于点(12,-12)对称;(2)求f (-2)+f (-1)+f (0)+f (1)+f (2)+f (3)的值.解:(1)证明:函数f (x )的定义域为R ,任取一点(x ,y ),它关于点(12,-12)对称的点的坐标为(1-x ,-1-y ).由已知,y =-a a x +a ,则-1-y =-1+a a x +a =-a xa x +a.,f (1-x )=-a a 1-x +a =-a a a x+a =-a ·a x a +a ·a x =-a xa x +a .∴-1-y =f (1-x ).即函数y =f (x )的图象关于点(12,-12)对称.(2)由(1)有-1-f (x )=f (1-x ).即f (x )+f (1-x )=-1. ∴f (-2)+f (3)=-1,f (-1)+f (2)=-1,f (0)+f (1)=-1. 则f (-2)+f (-1)+f (0)+f (1)+f (2)+f (3)=-3.12.设函数f (x )=x +b ax -1(x ∈R ,且a ≠0,x ≠1a ).(1)若a =12,b =-32,指出f (x )与g (x )=1x 的图象变换关系以及函数f (x )的图象的对称中心;(2)证明:若ab +1≠0,则f (x )的图象必关于直线y =x 对称.解:(1)a =12,b =-32,f (x )=x -3212x -1=2x -3x -2=2+1x -2,∴f (x )的图象可由g (x )的图象沿x 轴右移2个单位,再沿y 轴上移2个单位得到,f (x )的图象的对称中心为点(2,2).(2)证明:设P (x 0,y 0)为f (x )图象上任一点,则y 0=x 0+bax 0-1,P (x 0,y 0)关于y =x 的对称点为P ′(y 0,x 0).由y 0=x 0+b ax 0-1得x 0=y 0+bay 0-1.∴P ′(y 0,x 0)也在f (x )的图象上.故f (x )的图象关于直线y =x 对称.。
新高考数学复习考点知识与题型专题练习14 指数函数一、选择题:本题共8小题,在每小题给出的四个选项中,只有一项是符合题目要求的 1.已知函数y =2a x -1+1(a >0且a ≠1)恒过定点A (m ,n ),则m +n =( ) A .1B .3 C .4D .2 【答案】C【解析】由题意知,当x =1时,y =3,故A (1,3),m +n =4, 故选:C.2.已知函数()2xy a =-,且当0x <时,1y >,则实数a 的取值范围是( ) A .3a >B .23a <<C .4a >D .34a << 【答案】B【解析】当0x <时,1021y a >∴<-<,, 解得23a <<, 故选:B.3.已知a =0.82b =,0.24c =,则,,a b c 的大小关系为( ) A .c b a <<B .c a b <<C .b a c <<D .b c a << 【答案】B【解析】0.52a ,0.20.442c ==, ∵2x y =递增,且0.40.50.8<<, ∴0.40.50.8222<<,即c a b <<. 故选:B.4.已知11 3xy⎛⎫= ⎪⎝⎭,23xy=,310xy-=,410xy=,则在同一平面直角坐标系内,它们的图象大致为()A.B.C.D.【答案】A【解析】23xy=与410xy=是增函数,11 3xy⎛⎫= ⎪⎝⎭与311010xxy-⎛⎫== ⎪⎝⎭是减函数,在第一象限内作直线1x=,该直线与四条曲线交点的纵坐标的大小对应各底数的大小,易知:选A.故选:A5.若函数f(x)的定义域是[1,+∞),则a的取值范围是()A.[0,1)∪(1,+∞)B.(1,+∞)C.(0,1)D.(2,+∞)【答案】B【解析】∵a x -a ≥0,∴a x ≥a ,∴当a >1时,x ≥1.故函数定义域为[1,+∞)时,a >1. 故选:B .6.已知()xf x a -=(0a >,且1a ≠),且()()23f f ->-,则a 的取值范围是( )A .(0,+∞)B .(1,+∞)C .(-∞,1)D .(0,1) 【答案】D【解析】由0a >,且1a ≠,排除AC ; ∵()1xxa f x a-⎛⎫= ⎪⎝⎭=, 当1a >时,()101,f x a<<为单调递减函数,∴()()23f f ->-,与已知矛盾矛盾,故B 错误; 当01a <<时,()11,f x a>为单调递增函数,∴()()23f f ->-,符合题意. 故选:D.7.函数()()(),0()23,0x a x f x a x a x ⎧<⎪=⎨-+≥⎪⎩,满足对任意12x x ≠,都有()()12120f x f x x x -<-成立,则a 的取值范围是( )A .()0,1a ∈B .1,13a ⎡⎫∈⎪⎢⎣⎭C .10,3a ⎛⎤∈ ⎥⎝⎦D .1,23a ⎡⎫∈⎪⎢⎣⎭【答案】C 【解析】解:()f x 满足对任意12x x ≠,都有1212()()0f x f x x x -<-成立,()f x ∴在R 上是减函数,因为()()(),0()23,0x a x f x a x a x ⎧<⎪=⎨-+≥⎪⎩∴00120(2)03a a a a a <<⎧⎪-<⎨⎪-⨯+⎩,解得103a <,a ∴的取值范围是10,3⎛⎤ ⎥⎝⎦.故选:C .8.设函数f (x )=a -|x |(a >0且a ≠1),f (2)=4,则( ) A .f (-1)>f (-2)B .f (1)>f (2) C .f (2)<f (-2)D .f (-3)>f (-2) 【答案】D【解析】由f (2)=4得a -2=4,又∵a >0,∴a =12,f (x )=2|x |,∴函数f (x )为偶函数,在(-∞,0)上单调递减,在(0,+∞)上单调递增,则A,B 错误,D 正确. 而f (-2)=f (2),故C 错误. 故选:D.二、选择题:本题共4小题,在每小题给出的选项中,有多项符合题目要求. 9.若指数函数x y a =在区间[1,1]-上的最大值和最小值的和为103,则a 的值可能是( ) A .12B .13C .3D .2【答案】BC【解析】当1a >时,函数x y a =在区间[1,1]-上为单调递增函数,当1x =时,max y a =,当1x =-时,1min y a -=,所以1103a a -+=,即231030a a -+=,解得3a =或13a =, 因为1a >,所以3a =;当01a <<时,函数x y a =在区间[1,1]-上为单调递减函数,当1x =时,min y a =,当1x =-时,1max y a -=,所以1103a a -+=,即231030a a -+=,解得3a =或13a =,因为01a <<,所以13a =.综上可得,实数a 的值为3或13.故选:BC10.已知函数()1xxf x a a ⎛⎫=- ⎪⎝⎭其中0a >且1a ≠,则下列结论正确的是( )A .函数()f x 是奇函数B .函数()f x 0=在其定义域上有解C .函数()f x 的图象过定点()0,1D .当1a >时,函数()f x 在其定义域上为单调递增函数 【答案】ABD【解析】()1xxx x f x a a a a -⎛⎫=-=- ⎪⎝⎭,定义域为R ,()()x x f x a a f x --=-=-,所以()f x 为奇函数,且()00f =,故选项A ,B 正确,选项C 错误;1a >,101a <<,xy a =,1xy a ⎛⎫=- ⎪⎝⎭在R 上均为增函数,()f x 在其定义域上为单调递增函数,所以选项D 正确. 故选:ABD .11.已知{}2,0,1,2,3a ∈-,则函数()()22e xf x a b =-+为减函数的实数a 的值可以是( )A .0B .1C .2D .3 【答案】AB【解析】由函数()()22e xf x a b =-+为减函数,得220a -<,即a <<.又{}2,0,1,2,3a ∈-,所以只有0a =,1a =满足题意. 故选:AB.12.对于函数()f x 的定义域中任意的()1212,x x x x ≠,有如下结论:当()2xf x =时,上述结论正确的是( )A .()()()1212f x x f x f x +=⋅B .()()()1212f x x f x f x ⋅=+C .()()12120f x f x x x ->-D .()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭【答案】ACD【解析】对于A ,()12122x x f x x ++=,()()121212222x x x xf x f x +⋅=⋅=,()()()1212f x x f x f x +=⋅,正确;对于B ,()12122x x f x x ⋅⋅=,()()121222x xf x f x +=+,()()()1212f x x f x f x ⋅≠+,错误;对于C ,()2x f x =在定义域中单调递增,()()12120f x f x x x -∴->,正确;对于D ,()1212122122222x x x x x x f ++⎛⎫==≤+= ⎪⎝⎭()()122f x f x +,又12x x ≠,则()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭,正确;故选:ACD三、填空题:本题共4小题.13.已知函数2x y a =⋅和2x b y +=都是指数函数,则a b +=______. 【答案】1【解析】因为函数2x y a =⋅是指数函数,所以1a =, 由2x b y +=是指数函数,所以0b =, 所以1a b +=, 故答案为:1.14.若函数()233xy a a a =-+是指数函数,则a =________.【答案】2【解析】由()233xy a a a =-+是指数函数,可得2331,0,1,a a a a ⎧-+=⎪>⎨⎪≠⎩解得2a =.故答案为:2.15.在某个时期,某湖泊中的蓝藻每天以6.25%的增长率呈指数增长,已知经过30天以后,该湖泊的蓝藻数大约为原来的6倍,那么经过60天后该湖泊的蓝藻数大约为原来的_____ 【答案】36倍【解析】某湖泊中的蓝藻每天以6.25%的增长率呈指数增长,经过30天以后,该湖泊的蓝藻数大约为原来的6倍,设湖泊中原来蓝藻数量为a ,则30(1 6.25%)6a a +=,∴经过60天后该湖泊的蓝藻数量为:26030(1 6.25%)(1 6.25%)36.y a a a ⎡⎤=+=+=⎣⎦∴经过60天后该湖泊的蓝藻数大约为原来的36倍.故答案为:36倍16.函数f (x )=33233x xx x ---++,若有f (a )+f (a -2)>4,则a 的取值范围是________.【答案】(1,+∞)【解析】设F (x )=f (x )-2,则F (x )=3333x x x x ---+,易知F (x )是奇函数,F (x )=3333x x x x ---+=223131x x-+=1-2231x +在R 上是增函数, 由f (a )+f (a -2)>4得F (a )+F (a -2)>0, 于是可得F (a )>F (2-a ),即a >2-a ,解得a >1. 答案:(1,+∞)四、解答题:本题共4小题.解答应写出文字说明、证明过程或演算步骤. 17.已知函数f (x )=11x x a a -+(a >0,且a ≠1).(1)若f (2)=35,求f (x )解析式;(2)讨论f (x )奇偶性.【答案】(1)()2121x x f x -=+;(2)奇函数.【解析】解:(1)()11x x a f x a -=+,()325f =.即221315a a -=+,2a ∴=. 即()2121x x f x -=+.(2)因为f (x )的定义域为R , 且()()1111x xxxa a f x f x a a -----===-++, 所以f (x )是奇函数. 18.求下列各式的值.(1)指数函数()x f x a =(0a >且1a ≠)的图象经过点()3π,,求π(3)f -的值; (2)211511336622263a b a b a b ⎛⎫⎛⎫⎛⎫-÷- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭;【答案】(1)1;(2)4a .【解析】(1)因为()xf x a =的图象经过点()3π,, 所以()33πf a ==,所以13πa =于是()xf x =,所以()3π3π1f --=⋅=(2)211511336622263a b a b a b ⎛⎫⎛⎫⎛⎫-÷- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭()()211115326236263ab+-+-=⨯-÷-⎡⎤⎣⎦1044a b a ==19.截止到2018年底,我国某市人口约为130万.若今后能将人口年平均递增率控制在3‰,经过x 年后,此市人口数为y (万).(1)求y 与x 的函数关系y =f (x ),并写出定义域; (2)若按此增长率,2029年年底的人口数是多少? (3)哪一年年底的人口数将达到135万?【答案】(1)y =f (x )=130(1+3‰)x (x ∈N *);(2)134;(3)2031年. 【解析】解:(1)2018年年底的人口数为130万;经过1年,2019年年底的人口数为130+130×3‰=130(1+3‰)(万);经过2年,2020年年底的人口数为130(1+3‰)+130(1+3‰)×3‰=130(1+3‰)2(万); 经过3年,2021年年底的人口数为130(1+3‰)2+130(1+3‰)2×3‰=130(1+3‰)3(万). ……所以经过的年数与(1+3‰)的指数相同,所以经过x 年后的人口数为130(1+3‰)x (万).即y =f (x )=130(1+3‰)x (x ∈N *). (2)2029年年底,经过了11年,过2029年底的人口数为130(1+3‰)11≈134(万). (3)由(2)可知,2029年年底的人口数为130(1+3‰)11≈134<135. 2030年年底的人口数为130(1+3‰)12≈134.8(万), 2031年年底的人口数为130(1+3‰)13≈135.2(万). 所以2031年年底的人口数将达到135万.20.已知定义在R 上的奇函数()f x 和偶函数()g x 满足()()2(0x x f x g x a a a -+=-+>且1a ≠), (1)若(2)g a =,求(2)f .(2)记()()()2F x f x g x =+,求()()()2G x F x mF x =-的最小值()G m .【答案】(1)154;(2)()242.4,44m m G m m m -≤⎧⎪=⎨->⎪⎩. 【解析】(1)()f x 是奇函数,()g x 是偶函数,∴由()()2x x f x g x a a -+=-+,①得()()()()2x xf xg x f x g x a a --+-=-+=-+,②①+②得()2g x =,①-②得()x xf x a a -=-.又()2g a =,2a ∴=,()22x xf x -∴=-,()22152224f -∴=-=. (2)由(1)可得()()222x x f x g x a a -+=+,故()22x xF x a a -=+,由基本不等式可得()2≥F x ,令()t F x =,则2t ≥且()2G x t mt =-,设()2,2h t t mt t =-≥,当4m ≤即22m≤时,()()min 42G m h t m ==-; 当4m >即22m >时,()()2min 4m G m h t ==-,故()242.4,44m m G m m m -≤⎧⎪=⎨->⎪⎩.。
专题9 指数函数的图象及应用指数函数的图象及应用★★★○○○○1.指数函数的图象函数y =a x (a >0,且a ≠1)0<a <1a >1图象图象特征在x 轴上方,过定点(0,1)当x 逐渐增大时,图象逐渐下降当x 逐渐增大时,图象逐渐上升2.指数函数图象画法的三个关键点画指数函数y =a x(a >0,且a ≠1)的图象,应抓住三个关键点:(1,a ),(0,1),⎝ ⎛⎭⎪⎫-1,1a .3.指数函数的图象与底数大小的比较如图是指数函数(1)y =a x,(2)y =b x,(3)y =c x,(4)y =d x的图象,底数a ,b ,c ,d 与1之间的大小关系为c >d >1>a >b .由此我们可得到以下规律:在y轴右(左)侧图象越高(低),其底数越大. 指数函数的性质函数y=a x(a>0,且a≠1)0<a<1a>1性质定义域R值域(0,+∞)单调性在R上是减函数在R上是增函数函数值变化规律当x=0时,y=1当x<0时,y>1;当x>0时,0<y<1当x<0时,0<y<1;当x>0时,y>1指数幂的运算规律(1)有括号的先算括号里的,无括号的先算指数运算.(2)先乘除后加减,负指数幂化成正指数幂的倒数.(3)底数是负数,先确定符号,底数是小数,先化成分数,底数是带分数的,先化成假分数.(4)若是根式,应化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答.函数y=a x-1a(a>0,a≠1)的图象可能是()[解析]当a>1时函数单调递增,且函数图象过点⎝⎛⎭⎪⎫0,1-1a,因为0<1-1a<1,故A,B均不正确;当0<a<1时,函数单调递减,且函数恒过点⎝⎛⎭⎪⎫0,1-1a,因为1-1a<0,所以选D.[答案] D1.(1)已知实数a ,b 满足等式⎝ ⎛⎭⎪⎫12a =⎝ ⎛⎭⎪⎫13b,下列五个关系式:①0<b <a ;②a <b <0;③0<a <b ;④b <a <0;⑤a =b . 其中不可能成立的关系式有( ) A .1个 B .2个 C .3个D .4个(2)若曲线y =|2x-1|与直线y =b 有两个公共点,则b 的取值范围为________.[解析] (1)函数y 1=⎝ ⎛⎭⎪⎫12x 与y 2=⎝ ⎛⎭⎪⎫13x的图象如图所示.由⎝ ⎛⎭⎪⎫12a =⎝ ⎛⎭⎪⎫13b得,a <b <0或0<b <a 或a =b =0. 故①②⑤可能成立,③④不可能成立.(2)曲线y =|2x-1|与直线y =b 的图象如图所示,由图象可得,如果曲线y =|2x-1|与直线y =b 有两个公共点,则b 的取值范围是(0,1). [答案] (1)B (2)(0,1)2.(·全国丙卷)已知a =243,b =425,c =2513,则( ) A .b <a <c B .a <b <c C .b <c <aD .c <a <b[解析] 因为a =243,b =425=245,由函数y =2x在R 上为增函数知,b <a ; 又因为a =243=423,c =2513=523,由函数y =x 23在(0,+∞)上为增函数知,a <c . 综上得b <a <c .故选A. [答案] A3. (1)(·福州模拟)已知实数a ≠1,函数f (x )=⎩⎨⎧4x,x ≥0,2a -x,x <0,若f (1-a )=f (a -1),则a 的值为________.(2)若偶函数f (x )满足f (x )=2x-4(x ≥0),则不等式f (x -2)>0的解集为________.1.函数f (x )=21-x的大致图象为( )解析:选A ∵f (x )=21-x=2·2-x .∴f (x )在R 上为减函数,排除C 、D ;又f (0)=21=2>1,排除B ,故选A.2.函数f(x)=1-e|x|的图象大致是()解析:选A将函数解析式与图象对比分析,因为函数f(x)=1-e|x|是偶函数,且值域是(-∞,0],只有A满足上述两个性质.3. 函数f(x)=a x-b的图象如图,其中a,b为常数,则下列结论正确的是()A.a>1,b<0B.a>1,b>0C.0<a<1,b>0D.0<a<1,b<0解析:选D由f(x)=a x-b的图象可以观察出,函数f(x)=a x-b在定义域上单调递减,所以0<a<1,函数f(x)=a x-b的图象是在y=a x的基础上向左平移得到的,所以b<0.4.已知函数f(x)=4+a x-1的图象恒过定点P,则点P的坐标是________.解析:令x-1=0,则x=1,f(1)=5,即P点坐标是(1,5).答案:(1,5)5.若关于x的方程|a x-1|=2a(a>0,且a≠1)有两个不相等的实数根,则a的取值范围是________.答案:⎝ ⎛⎭⎪⎫0,12 6.已知a =⎝ ⎛⎭⎪⎫1223,b =243-,c =⎝ ⎛⎭⎪⎫1213,则下列关系式中正确的是( ) A .c <a <b B .b <a <c C .a <c <bD .a <b <c解析:选B 把b 化简为b =⎝ ⎛⎭⎪⎫1243,而函数y =⎝ ⎛⎭⎪⎫12x 在R 上为减函数,43>23>13,所以⎝ ⎛⎭⎪⎫1243-<⎝ ⎛⎭⎪⎫1223<⎝ ⎛⎭⎪⎫1213,即b <a <c .7. (·青岛模拟)函数y =4x+2x +1+1的值域为( )A .(0,+∞)B .(1,+∞)C .[1,+∞)D .(-∞,+∞)解析:选B 令2x=t ,则函数y =4x+2x +1+1可化为y =t 2+2t +1=(t +1)2(t >0).∵函数y =(t +1)2在(0,+∞)上递增,∴y >1.∴所求值域为(1,+∞).故选B. 8.已知函数y =221-++x ax 在区间(-∞,3)内单调递增,则a 的取值范围为________.9.不等式2x 2-x <4的解集为________.解析:∵2x 2-x <4,∴2x 2-x <22,∵函数y =2x 在R 上为增函数,∴x 2-x <2,即x 2-x -2<0,∴-1<x <2,即不等式的解集为{x |-1<x <2}. 答案:{x |-1<x <2}10. (·江苏南通调研)函数f (x )=⎝ ⎛⎭⎪⎫1422-x x 的值域为________.解析:令t =x 2-2x ,则有y =⎝ ⎛⎭⎪⎫14t ,根据二次函数的图象可求得t ≥-1,结合指数函数y =⎝ ⎛⎭⎪⎫14x 的图象可得0<y ≤⎝ ⎛⎭⎪⎫14-1,即0<y ≤4.答案:(0,4]____________________________________________________________________________________________ ____________________________________________________________________________________________ ____________________________________________________________________________________________ ____________________________________________________________________________________________ ____________________________________________________________________________________________ ____________________________________________________________________________________________。
. . .页脚 指数函数 A组 1.(2010年模拟)若a>1,b<0,且ab+a-b=22,则ab-a-b的值等于________. 解析:∵a>1,b<0,∴01.又∵(ab+a-b)2=a2b+a-2b+2=8,∴a2b+a-2b=6,∴(ab-a-b)2=a2b+a-2b-2=4,∴ab-a-b=-2.答案:-2 2.已知f(x)=ax+b的图象如图所示,则f(3)=________. 解析:由图象知f(0)=1+b=-2,∴b=-3.又f(2)=a2-3=0,∴a=3,则f(3)=(3)3-3=33-3. 答案:33-3
3.函数y=(12)2x-x2的值域是________. 解析:∵2x-x2=-(x-1)2+1≤1, ∴(12)2x-x2≥12.答案:[12,+∞) 4.(2009年高考卷)若函数f(x)=ax-x-a(a>0,且a≠1)有两个零点,则实数a的取值围是________.
解析:函数f(x)的零点的个数就是函数y=ax与函数y=x+a交点的个数,由函数的图象可知a>1时两函数图象有两个交点,0点,故a>1. 答案:(1,+∞)
5.(原创题)若函数f(x)=ax-1(a>0,a≠1)的定义域和值域都是[0,2],则实数a等于________.
解析:由题意知 0
a>1
a0-1=0
a2-1=2
⇒a=3.答案:3
6.已知定义域为R的函数f(x)=-2x+b2x+1+a是奇函数.(1)求a,b的值; . . .页脚 (2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值围. 解:(1)因为f(x)是R上的奇函数,所以f(0)=0,即-1+b2+a=0,解得b=1.
从而有f(x)=-2x+12x+1+a.又由f(1)=-f(-1)知-2+14+a=--12+11+a,解得a=2. (2)法一:由(1)知f(x)=-2x+12x+1+2=-12+12x+1, 由上式易知f(x)在R上为减函数,又因f(x)是奇函数,从而不等式f(t2-2t)+f(2t2-k)<0⇔f(t2-2t)<-f(2t2-k)=f(-2t2+k). 因f(x)是R上的减函数,由上式推得t2-2t>-2t2+k.
即对一切t∈R有3t2-2t-k>0,从而Δ=4+12k<0,解得k<-13.
法二:由(1)知f(x)=-2x+12x+1+2,又由题设条件得-2t2-2t+12t2-2t+1+2+-22t2-k+122t2-k+1+2<0 即(22t2-k+1+2)(-2t2-2t+1)+(2t2-2t+1+2)(-22t2-k+1)<0 整理得23t2-2t-k>1,因底数2>1,故3t2-2t-k>0
上式对一切t∈R均成立,从而判别式Δ=4+12k<0,解得k<-13. B组 1.如果函数f(x)=ax+b-1(a>0且a≠1)的图象经过第一、二、四象限,不经过第三象限,那么一定有________. ①00 ②01且b<0 ④a>1且b>0 解析:当0b-1<0,即02.(2010年模拟)若f(x)=-x2+2ax与g(x)=(a+1)1-x在区间[1,2]上都是减函数,则a的取值围是________. 解析:f(x)=-x2+2ax=-(x-a)2+a2,所以f(x)在[a,+∞)上为减函数, . . .页脚 又f(x),g(x)都在[1,2]上为减函数,所以需
a≤1
a+1>1
⇒0
3.已知f(x),g(x)都是定义在R上的函数,且满足以下条件①f (x)=ax·g(x)(a>0,a≠1);②g(x)≠0;若f(1)g(1)+f(-1)g(-1)=52,则a等于________.
解析:由f(x)=ax·g(x)得f(x)g(x)=ax,所以f(1)g(1)+f(-1)g(-1)=52⇒a+a-1=52,解得a=2或12.答案:2或12 4.(2010年模拟)已知函数f(x)=ax(a>0且a≠1),其反函数为f-1(x).若f(2)=9,则f-1(13)+f(1)的值是________.
解析:因为f(2)=a2=9,且a>0,∴a=3,则f(x)=3x=13,∴x=-1, 故f-1(13)=-1.又f(1)=3,所以f-1(13)+f(1)=2.答案:2 5.(2010年质检)已知f(x)=(13)x,若f(x)的图象关于直线x=1对称的图象对应的函数为g(x),则g(x)的表达式为________. 解析:设y=g(x)上任意一点P(x,y),P(x,y)关于x=1的对称点P′(2
-x,y)在f(x)=(13)x上,∴y=(13)2-x=3x-2.答案:y=3x-2(x∈R)
6.(2009年高考卷改编)函数y=ex+e-xex-e-x的图象大致为________.
解析:∵f(-x)=e-x+exe-x-ex=-ex+e-xex-e-x=-f(x),∴f(x)为奇函数,排除④.
又∵y=ex+e-xex-e-x=e2x+1e2x-1=e2x-1+2e2x-1=1+2e2x-1在(-∞,0)、(0,+∞)上都是减函数,排除②、③.答案:① . . .页脚 7.(2009年高考卷改编)已知函数f(x)满足:当x≥4时,f(x)=(12)x;当x<4时,f(x)=f(x+1),则f(2+log23)=________. 解析:∵2<3<4=22,∴1
=f(3+log23)=f(log224)=(12)log224=2-log224=2log2124=124.答案:124 8.(2009年高考卷改编)设函数y=f(x)在(-∞,+∞)有定义,对于给定的正数K,定义函数fK(x)= f(x),f(x)≤K,K, f(x)>K.取函数f(x)=2-|x|,当K=12时,函数fK(x)的单调递增区间为________. 解析:由f(x)=2-|x|≤12得x≥1或x≤-1,∴fK(x)=
2-|x|,x≥1或x≤-1,12,-1
则单调增区间为(-∞,-1].答案:(-∞,-1] 9.函数y=2|x|的定义域为[a,b],值域为[1,16],当a变动时,函数b=g(a)的图象可以是________.
解析:函数y=2|x|的图象如图. 当a=-4时,0≤b≤4, 当b=4时,-4≤a≤0,答案:② 10.(2010年模拟)已知函数f(x)=a2x+2ax-1(a>0,且a≠1)在区间[-1,1]上的最大值为14,数a的值. 解:f(x)=a2x+2ax-1=(ax+1)2-2,∵x∈[-1,1],
(1)当0. . .页脚 ∴(1a+1)2-2=14,∴1a=3,∴a=13. (2)当a>1时,1a≤ax≤a,∴当ax=a时,f(x)取得最大值. ∴(a+1)2-2=14,∴a=3.综上可知,实数a的值为13或3. 11.已知函数f(x)=-22x-a+1.(1)求证:f(x)的图象关于点M(a,-1)对称; (2)若f(x)≥-2x在x≥a上恒成立,数a的取值围. 解:(1)证明:设f(x)的图象C上任一点为P(x,y),则y=-22x-a+1, P(x,y)关于点M(a,-1)的对称点为P′(2a-x,-2-y).
∴-2-y=-2+22x-a+1=-2·2x-a2x-a+1=-21+2-(x-a)=-22(2a-x)-a+1,
说明点P′(2a-x,-2-y)也在函数y=-22x-a+1的图象上,由点P的任意性知,f(x)的图象关于点M(a,-1)对称. (2)由f(x)≥-2x得-22x-a+1≥-2x,则22x-a+1≤2x,化为2x-a·2x+2x-2≥0,则有(2x)2+2a·2x-2·2a≥0在x≥a上恒成立.令g(t)=t2+2a·t-2·2a,则有g(t)≥0在t≥2a上恒成立.∵g(t)的对称轴在t=0的左侧,∴g(t)在t≥2a上为增函数. ∴g(2a)≥0.∴(2a)2+(2a)2-2·2a≥0,∴2a(2a-1)≥0,则a≥0.即实数a的取值围为a≥0. 12.(2008年高考)若f1(x)=3|x-p1|,f2(x)=2·3|x-p2|,x∈R,p1、p2为常数,且
f(x)= f1(x),f1(x)≤f2(x),f2(x),f1(x)>f2(x).(1)求f(x)=f1(x)对所有实数x成立的充
要条件(用p1、p2表示);(2)设a,b是两个实数,满足af(a)=f(b),求证:函数f(x)在区间[a,b]上的单调增区间的长度之和为b-a2(闭
区间[m,n]的长度定义为n-m). 解:(1)f(x)=f1(x)恒成立⇔f1(x)≤f2(x)⇔3|x-p1|≤2·3|x-p2|⇔3|x-p1|-|x-