贝叶斯网络基础知识

比较简单的贝叶斯网络总结贝叶斯网络贝叶斯网络是一系列变量的联合概率分布的图形表示。

一般包含两个部分，一个就是贝叶斯网络结构图，这是一个有向无环图（DAG），其中图中的每个节点代表相应的变量，节点之间的连接关系代表了贝叶斯网络的条件独立语义。

另一部分，就是节点和节点之间的条件概率表（CPT），也就是一系列的概率值。

如果一个贝叶斯网络提供了足够的条件概率值，足以计算任何给定的联合概率，我们就称，它是可计算的，即可推理的。

3.5.1 贝叶斯网络基础首先从一个具体的实例（医疗诊断的例子）来说明贝叶斯网络的构造。

假设：命题S(moker)：该患者是一个吸烟者命题C(oal Miner)：该患者是一个煤矿矿井工人命题L(ung Cancer)：他患了肺癌命题E(mphysema)：他患了肺气肿这两个条件缺一不可。

贝叶斯网由一个有向无环图（DAG）及描述顶点之间的概率表组成。

其中每个顶点对应一个随机变量。

这个图表达了分布的一系列有条件独立属性：在给定了父亲节点的状态后，每个变量与它在图中的非继承节点在概率上是独立的。

该图抓住了概率分布的定性结构，并被开发来做高效推理和决策。

贝叶斯网络能表示任意概率分布的同时，它们为这些能用简单结构表示的分布提供了可计算优势。

假设对于顶点xi，其双亲节点集为Pai，每个变量xi的条件概率P(xi|Pai)。

则顶点集合X={x1,x2,…,xn}的联合概率分布可如下计算：。

双亲结点。

该结点得上一代结点。

该等式暗示了早先给定的图结构有条件独立语义。

它说明贝叶斯网络所表示的联合分布作为一些单独的局部交互作用模型的结果具有因式分解的表示形式。

从贝叶斯网的实例图中，我们不仅看到一个表示因果关系的结点图，还看到了贝叶斯网中的每个变量的条件概率表（CPT）。

因此一个完整的随机变量集合的概率的完整说明不仅包含这些变量的贝叶斯网，还包含网中变量的条件概率表。

图例中的联合概率密度：P(S,C,L,E)=P(E|S,C)*P(L|S)*P(C)*P (S)推导过程：P(S,C,L,E)=P(E|S,C,L)*P(L|S,C)*P(C |S)*P(S)（贝叶斯定理）＝P(E|S,C)*P(L|S)*P(C)*P(S)即：P(E|S,C,L) ＝P(E|S,C), E与L 无关P(L|S,C)= P(L|S)L与C 无关P(C|S)=P(C) C与S 无关以上三条等式的正确性，可以从贝叶斯网的条件独立属性推出：每个变量与它在图中的非继承节点在概率上是独立的。

贝叶斯网络的基本原理贝叶斯网络是一种概率图模型，它能够描述变量之间的依赖关系，并通过概率推断来进行推理和决策。

贝叶斯网络的基本原理包括概率论、图论和贝叶斯定理。

概率论是贝叶斯网络的基础，它描述了不同变量之间的概率关系。

在贝叶斯网络中，每个节点代表一个随机变量，节点之间的连接表示了它们之间的依赖关系。

每个节点都有一个条件概率表，描述了在给定父节点条件下，子节点的条件概率分布。

这种条件概率表的建立是基于领域知识和数据统计的结果，它能够有效地捕捉到变量之间的依赖关系。

另一个重要的原理是图论，贝叶斯网络是一种有向无环图。

有向边表示了变量之间的因果关系，而无环则保证了网络的一致性和可推断性。

通过图论的方法，可以对贝叶斯网络进行结构学习和参数学习，从而能够从数据中学习到变量之间的依赖关系和概率分布。

最重要的原理是贝叶斯定理，它是贝叶斯网络的核心。

贝叶斯定理描述了在给定观测数据的条件下，变量之间的概率分布是如何更新的。

贝叶斯网络通过贝叶斯定理进行推理，可以根据已知的观测数据，推断出其他变量的概率分布。

这种基于贝叶斯定理的推理方法，使得贝叶斯网络能够在不确定性和不完整信息的情况下进行有效的推断和决策。

除了这些基本原理之外，贝叶斯网络还有一些特点和应用。

首先，它能够有效地处理不确定性和噪声，因为它能够通过概率推断来量化不确定性，并能够灵活地处理缺失和不完整数据。

其次，贝叶斯网络可以通过结构学习和参数学习来从数据中学习到变量之间的依赖关系和概率分布，因此能够适应不同领域的应用。

最后，贝叶斯网络在医疗诊断、风险评估、工程决策等领域有着广泛的应用，它能够帮助人们从复杂的数据中推断出有用的信息，帮助人们做出更好的决策。

总之，贝叶斯网络是一种强大的概率图模型，它基于概率论、图论和贝叶斯定理，能够描述变量之间的依赖关系，并通过概率推断进行推理和决策。

它具有处理不确定性的优势，能够从数据中学习到知识，并且在各个领域有着广泛的应用。

贝叶斯网络 贝叶斯网络是一系列变量的联合概率分布的图形表示。

一般包含两个部分，一个就是贝叶斯网络结构图，这是一个有向无环图（DAG），其中图中的每个节点代表相应的变量，节点之间的连接关系代表了贝叶斯网络的条件独立语义。

另一部分，就是节点和节点之间的条件概率表（CPT），也就是一系列的概率值。

如果一个贝叶斯网络提供了足够的条件概率值，足以计算任何给定的联合概率，我们就称，它是可计算的，即可推理的。

3.5.1 贝叶斯网络基础 首先从一个具体的实例（医疗诊断的例子）来说明贝叶斯网络的构造。

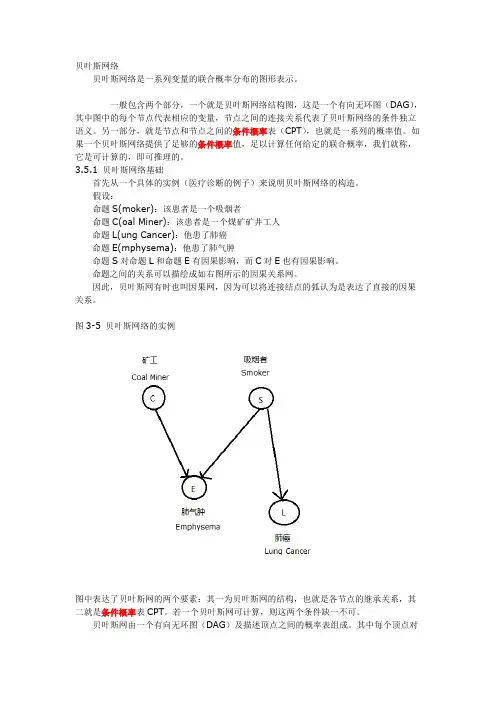
假设： 命题S(moker)：该患者是一个吸烟者 命题C(oal Miner)：该患者是一个煤矿矿井工人 命题L(ung Cancer)：他患了肺癌 命题E(mphysema)：他患了肺气肿 命题S对命题L和命题E有因果影响，而C对E也有因果影响。

命题之间的关系可以描绘成如右图所示的因果关系网。

因此，贝叶斯网有时也叫因果网，因为可以将连接结点的弧认为是表达了直接的因果关系。

图3-5 贝叶斯网络的实例图中表达了贝叶斯网的两个要素：其一为贝叶斯网的结构，也就是各节点的继承关系，其二就是条件概率表CPT。

若一个贝叶斯网可计算，则这两个条件缺一不可。

贝叶斯网由一个有向无环图（DAG）及描述顶点之间的概率表组成。

其中每个顶点对应一个随机变量。

这个图表达了分布的一系列有条件独立属性：在给定了父亲节点的状态后，每个变量与它在图中的非继承节点在概率上是独立的。

该图抓住了概率分布的定性结构，并被开发来做高效推理和决策。

贝叶斯网络能表示任意概率分布的同时，它们为这些能用简单结构表示的分布提供了可计算优势。

假设对于顶点xi，其双亲节点集为Pai，每个变量xi的条件概率P(xi|Pai)。

则顶点集合X={x1,x2,…,xn}的联合概率分布可如下计算：。

双亲结点。

该结点得上一代结点。

该等式暗示了早先给定的图结构有条件独立语义。

贝叶斯网络的模型解释方法贝叶斯网络是一种概率图模型，它能够很好地描述变量之间的概率依赖关系。

在实际应用中，人们往往需要对贝叶斯网络进行解释，以便更好地理解模型的结构和推理过程。

本文将介绍贝叶斯网络的模型解释方法，并讨论其在实际应用中的意义。

一、贝叶斯网络的基本概念首先，我们需要了解贝叶斯网络的基本概念。

贝叶斯网络由节点和有向边组成，节点表示随机变量，有向边表示变量之间的依赖关系。

每个节点都有一个条件概率表，描述了该节点在给定父节点条件下的条件概率分布。

贝叶斯网络可以用来进行推理、预测和因果推断。

二、贝叶斯网络的模型解释方法在实际应用中，人们往往需要对贝叶斯网络进行解释，以便更好地理解模型的结构和推理过程。

贝叶斯网络的模型解释方法包括两个方面：结构解释和参数解释。

结构解释：结构解释是指理解贝叶斯网络的拓扑结构和节点之间的依赖关系。

通常可以通过观察节点之间的有向边来进行结构解释，了解变量之间的因果关系。

此外，还可以通过分析节点的条件概率表来推断节点之间的依赖关系。

结构解释可以帮助人们理解变量之间的关联性，以及模型中的因果关系。

参数解释：参数解释是指理解贝叶斯网络中每个节点的条件概率表。

通过分析条件概率表，可以了解每个节点在给定父节点条件下的条件概率分布。

参数解释可以帮助人们理解每个节点的影响因素，以及不同因素对节点的影响程度。

参数解释还可以帮助人们理解贝叶斯网络的推理过程，以及在给定观测数据下的预测结果。

三、贝叶斯网络的模型解释在实际应用中的意义贝叶斯网络的模型解释在实际应用中具有重要的意义。

首先，模型解释可以帮助人们更好地理解贝叶斯网络的结构和参数，从而提高对模型的信任度。

其次，模型解释可以帮助人们发现模型中的潜在问题，以及改进模型的方法。

此外，模型解释还可以帮助人们进行模型的有效传播和应用，使得模型能够更好地为决策提供支持。

总之，贝叶斯网络的模型解释方法包括结构解释和参数解释两个方面，它们在实际应用中具有重要的意义。

贝叶斯网络的基本理论及其应用贝叶斯网络是一种流行的概率图模型，被广泛应用于人工智能、机器学习、数据挖掘、自然语言处理等领域。

贝叶斯网络的基本理论是贝叶斯定理，指望条件概率A给定条件B的情况下，事件B发生的概率P(B|A)与A发生的概率P(A|B)成正比。

贝叶斯网络通过图形化的方式表达了这种概率关系，可以用来实现推理、分类、预测、诊断等任务。

贝叶斯网络的结构由有向无环图(Directed Acyclic Graph, DAG)表示，每个节点代表一个随机变量，边表示变量之间的条件依赖关系。

例如，两个节点之间的边表示后一个节点的取值受先前节点的取值的影响。

贝叶斯网络将整个系统的关系拆分成多个小的依赖关系，简化了复杂系统的处理和管理。

这种模型不但易于解释和理解，而且可以从少量的数据中学得模型，并利用它进行有效的推理。

贝叶斯网络中一个重要的概念是条件概率表(Conditional Probability Table, CPT)，它表示某一变量取值在给定父节点取值的条件下的概率。

节点的概率就是其CPT中对应的概率之积。

CPT是贝叶斯网络推理的核心。

如果已知某些变量的取值，贝叶斯网络可以通过贝叶斯推理计算出其他节点的后验概率分布。

贝叶斯网络的实质就是根据观测数据和先验知识，推断出事实之间的因果关系，从而得到具体的结论。

贝叶斯网络应用广泛，可以应用于医学、金融、工业、环保等许多领域。

以医学为例，一个贝叶斯网络可以用于肺癌诊断。

网络中包括搜索病因以及和早期诊断因素相关的节点，如吸烟、气道炎症、咳嗽和发热等。

这些因素的CPT可以从患者的临床数据中学习而来。

当患者来诊断室时，医生可以输入患者的个人信息和症状来观测并得出可能的诊断结果。

贝叶斯网络还可以用于分析有限状态机的行为和缺陷分析，这是它在工业界中被广泛使用的领域。

例如，一个贝叶斯网络可以用于分析交通系统中的故障问题。

在这种情况下，节点代表不同的组件状态和故障原因，边代表各组件之间的依赖关系。

贝叶斯网络和神经网络的比较分析一、概述在机器学习和人工智能领域，贝叶斯网络和神经网络是两种最常用的模型。

它们基于不同的数学方法和理论，但在某些情况下也可以用于解决相同的问题。

接下来，本篇文章将从不同的方面对它们进行比较分析。

二、基础知识介绍1. 贝叶斯网络贝叶斯网络是一种用于表示和推理不确定性的图形模型。

它使用有向无环图（DAG）来表示变量之间的依赖关系，并使用概率分布来表示变量的联合分布。

一个贝叶斯网络的节点代表一个变量，边表示变量之间的条件依赖关系。

贝叶斯网络是有向的，这意味着边连接的节点有明确的方向。

这个方向表示相关变量之间的因果关系，即一个节点的值可以影响另一个节点的值，但反过来不行。

2. 神经网络神经网络是一种仿生学模型，它的设计灵感来源于人类神经系统。

它由许多连接的神经元（节点）组成，每个神经元可以接收其他神经元的输入，并生成输出。

在神经网络中，权重是变量之间的连接强度，而偏置则是变量的基础值。

神经网络的核心是通过反向传播算法来更新权重和偏置，从而优化模型的性能。

三、应用领域比较1. 贝叶斯网络应用领域贝叶斯网络广泛应用于医学、生物、金融和工程领域等。

例如，在医学领域，它可以用于诊断某些疾病，预测病人的病情和肿瘤生长等。

在工程领域，它可以用于优化智能制造系统、控制质量和改进生产效率。

2. 神经网络应用领域神经网络被广泛应用于语音识别、图像识别和自然语言处理等领域。

例如，在语音识别中，它可以用于将语音转换为文本；在图像识别中，它可以用于识别对象和场景；在自然语言处理中，它可以用于翻译、分类和生成文本等。

四、性能比较1. 训练速度在模型训练方面，神经网络通常比贝叶斯网络更快。

这是因为神经网络可以并行计算，而贝叶斯网络的参数更新需要处理概率分布，需要更多的计算资源。

2. 学习效果然而，贝叶斯网络通常会产生更好的学习效果。

这是因为贝叶斯网络使用了概率分布，可以处理不精确和不完整的数据，而神经网络通常需要更多的数据和特征工程才能取得好的效果。

贝叶斯网络的原理与应用贝叶斯网络，又称为信念网络，是一种基于概率模型的图形化推理工具，它通过节点与节点之间概率关系的联系，对一个系统中的所有因果关系进行建模和分析，这种建模方法被广泛应用在人工智能、数据挖掘、风险评估等领域。

下面我们来详细了解一下贝叶斯网络的原理与应用。

一、基本原理1、概率概率是贝叶斯网络中最基本的概念，它表示一个随机事件发生的可能性大小。

以掷骰子为例，假设一个骰子的可能结果是1、2、3、4、5和6，那么每个结果的概率就是1/6。

2、条件概率条件概率是指在已知某一事件发生的情况下，另一个事件发生的可能性大小。

例如，假设我们知道某个人患有肺癌的概率是0.01，而患肺癌的人吸烟的概率是0.8，那么在吸烟的前提下该人患肺癌的概率为0.01*0.8=0.008。

3、贝叶斯定理贝叶斯定理是贝叶斯网络中最重要的数学公式，描述的是在已知一个事件发生后，另一个事件发生的概率。

其公式为：P(A|B)= P(B|A) * P(A) / P(B)其中，P(A)是事件A的先验概率；P(B|A)是在已知事件A发生的情况下，事件B发生的概率，也叫做条件概率；P(B)是事件B 的先验概率；P(A|B)表示在已知事件B发生的情况下，事件A发生的概率，也叫做后验概率。

4、有向无环图有向无环图是贝叶斯网络的建模工具，它由节点和边组成，节点代表随机变量，边代表变量之间的依赖关系。

贝叶斯网络中的边都是有向的，且无环。

这样做的好处在于可以清晰地表示出变量之间的因果关系。

二、应用方向1、人工智能贝叶斯网络在人工智能领域有广泛应用，可以用于机器学习、自然语言处理、机器视觉等方面。

例如，利用贝叶斯网络建立一个中文文本分类器，可以根据文本的关键词，快速准确地分类文本内容。

2、数据挖掘贝叶斯网络也可以应用于数据挖掘领域，用于发现数据之间的关系和规律。

例如，在健康领域，可以利用贝叶斯网络分析患者的症状和疾病之间的关系，辅助医生诊断疾病。

机器学习技术中的贝叶斯网络介绍与应用引言：在现代科技的推动下，机器学习（Machine Learning）成为了近年来十分热门的领域。

作为机器学习的一种重要技术，贝叶斯网络（Bayesian Network）因其能够处理不确定性的优势而备受瞩目。

本文将介绍贝叶斯网络的基本概念、原理和应用案例，以帮助读者更好地了解该领域。

一、贝叶斯网络的基本概念贝叶斯网络是一种用图模型表示随机变量之间依赖关系的方法，它由一个有向无环图（DAG）表示，节点表示随机变量，边表示变量之间的依赖关系。

贝叶斯网络使用概率论和图论的方法来描述和推断随机事件之间的关系。

贝叶斯网络的节点可以分为两类：隐变量和观察变量。

隐变量是无法直接观测到的，而观察变量是已知的或者可以通过实际观测得到的。

贝叶斯网络通过联合概率分布来表示各个节点之间的关系，它利用贝叶斯定理根据先验概率和观测数据来计算后验概率，从而进行推理和预测。

二、贝叶斯网络的原理贝叶斯网络是基于贝叶斯定理的推理模型。

贝叶斯定理表达了在给定观测数据的条件下，计算一个假设的后验概率的公式。

贝叶斯网络利用这一公式来推导节点之间的联合概率分布。

贝叶斯网络的推理过程可以分为两个步骤：学习和推断。

学习阶段通过观测数据来构建网络结构和参数。

推断阶段根据网络结构和已知观测数据来计算未观测节点的后验概率分布。

贝叶斯网络的推理算法主要有变量消除法、采样法和近似推理法等。

三、贝叶斯网络的应用1. 医学诊断贝叶斯网络在医学诊断中有着广泛的应用。

通过构建一个贝叶斯网络模型，可以将患者的症状和病因联系起来，从而帮助医生进行准确的诊断。

例如，可以利用患者的症状和实验室检查结果来推断患者是否患有某种疾病，或者预测某种疾病的发展趋势。

2. 智能推荐系统贝叶斯网络也被广泛运用于智能推荐系统中。

通过分析用户的行为数据和偏好，建立一个贝叶斯网络模型来推荐用户感兴趣的内容或产品。

例如，根据用户过去的购买记录和浏览行为，可以预测用户下一次购买的商品。

贝叶斯网络的基本原理贝叶斯网络是一种概率图模型，利用概率和图结构来描述变量之间的依赖关系。

它是基于贝叶斯定理而建立的一种数学模型，能够用来表示不同变量之间的概率关系，从而在不确定性条件下进行推理和决策。

贝叶斯网络在人工智能、机器学习、医学诊断、风险评估等领域都有着广泛的应用。

一、贝叶斯网络的基本概念首先，我们来了解一下贝叶斯网络的一些基本概念。

贝叶斯网络由两部分组成：一部分是一组表示变量的节点，另一部分是一组描述这些节点之间依赖关系的有向边。

其中，节点表示某一变量，有向边表示变量之间的依赖关系。

节点之间的边可以形成一个有向无环图，这样的图称为贝叶斯网络。

每个节点都对应一个概率分布，描述了该节点的概率和条件概率。

二、贝叶斯网络的条件概率在贝叶斯网络中，每个节点都对应一个条件概率表，描述了该节点在不同条件下的概率分布。

这些条件概率表可以用来表示变量之间的依赖关系，从而实现对不同变量之间的概率推理。

通过条件概率表，我们可以计算给定某些变量条件下，其他变量的概率分布，这就是贝叶斯网络的核心功能之一。

三、贝叶斯网络的推理贝叶斯网络可以用来进行不确定性条件下的推理。

通过给定一些证据变量，贝叶斯网络可以计算其他变量的概率分布，从而对未知变量进行推理。

这种推理方式可以帮助我们在不完全信息的情况下做出合理的决策，有着广泛的应用价值。

四、贝叶斯网络的学习除了推理，贝叶斯网络还可以进行学习，即从数据中学习变量之间的依赖关系和概率分布。

通过观察数据，我们可以使用贝叶斯网络的学习算法来学习每个节点的条件概率表，从而构建一个贝叶斯网络模型。

这种学习方式可以帮助我们从数据中挖掘出有用的信息，为后续的推理和决策提供支持。

五、贝叶斯网络的应用贝叶斯网络在很多领域都有着广泛的应用。

比如，在医学诊断中，我们可以利用贝叶斯网络来分析病人的症状和疾病之间的关系，从而进行准确的诊断和治疗。

在风险评估中，我们可以使用贝叶斯网络来分析各种风险因素之间的复杂关系，从而进行合理的风险评估和管理。

贝叶斯网络的概率推断技巧贝叶斯网络是一种概率图模型，用于描述变量之间的依赖关系，并在给定一些变量的情况下推断其他变量的概率分布。

贝叶斯网络在人工智能、生物信息学、医学诊断等领域有着广泛的应用。

在本文中，我们将探讨贝叶斯网络的概率推断技巧，以及其在实际问题中的应用。

一、贝叶斯网络的基本概念贝叶斯网络由一组节点和一组有向边组成，每个节点代表一个随机变量，有向边表示节点之间的依赖关系。

节点之间的依赖关系可以用条件概率表来表示，即给定父节点的取值，子节点的取值的概率分布。

这种表示方式使得我们可以通过已知的观测数据，推断未知变量的概率分布。

二、贝叶斯网络的概率推断技巧1. 条件概率分布的计算贝叶斯网络的推断问题通常可以转化为计算给定一些观测变量的情况下，其他变量的后验概率分布。

这个计算过程可以通过贝叶斯定理和条件概率分布来完成。

具体来说，我们可以通过联合概率分布和边缘概率分布来计算后验概率分布。

2. 采样方法除了精确计算后验概率分布外，我们还可以使用采样方法来进行概率推断。

蒙特卡洛方法是常用的一种采样方法，通过从联合概率分布中抽取样本，并根据观测数据进行修正，得到未知变量的概率分布。

3. 近似推断方法对于大规模的贝叶斯网络，精确计算后验概率分布是非常困难甚至不可行的。

此时，我们可以使用一些近似推断方法，如变分推断、马尔科夫链蒙特卡洛法等。

这些方法可以在一定程度上近似计算后验概率分布，并在时间和空间上有所优化。

三、贝叶斯网络在实际问题中的应用1. 医学诊断贝叶斯网络在医学诊断中有着广泛的应用。

通过建立疾病、症状、检测结果等变量之间的依赖关系，可以帮助医生进行疾病诊断和风险评估。

同时，贝叶斯网络还可以用于预测患者的治疗效果，辅助医生进行治疗决策。

2. 金融风险管理在金融领域，贝叶斯网络可以用于评估投资组合的风险和收益，并帮助投资者进行资产配置。

同时，贝叶斯网络还可以用于欺诈检测、信用评分等领域，帮助金融机构降低风险，提高盈利能力。

贝叶斯网络（基础知识）1基本概率公理1）命题我们已经学过用命题逻辑和一阶谓词逻辑表达命题。

在概率论中我们采用另外一种新的表达能力强于命题逻辑的命题表达方式，其基本元素是随机变量。

如：Weather=snow; Temperature=high, etc。

在概率论中，每个命题赋予一个信度，即概率2）在随机现象中，表示事件发生可能性大小的一个实数称为事件的概率用P(A)表示。

如P(硬币＝正面)＝0.5。

3）在抛硬币这个随机现象中，落地后硬币的所有可能结果的集合构成样本空间。

4）P(A)具有以下性质:0 ≤P(A) ≤1, P(A)+P(-A)=1P(true) = 1 and P(false) = 0P(A∨B) = P(A) + P(B) - P(A∧B)(or, P(A∨B)=P(A)+P(B), if A∩B=Φ，即A,B互斥)2随机变量随机变量是构成语言的基本元素：如本书提到的天气、骰子、花粉量、产品、Mary，公共汽车，火车等等。

1）典型情况下，随机变量根据定义域的类型分成3类：布尔随机变量：如：牙洞Cavity的定义域是<true, false>离散随机变量：如：天气Weather的定义域是<sunny, rainy, cloudy, snow>连续随机变量：如：温度Temperature的定义域是[0, 100]。

这里我们主要侧重于离散随机变量。

2）随机变量的性质✓每个随机变量都有有限个状态，（即状态有限的定义域），且定义域中的值必须互斥。

如天气变量的状态有：<晴朗、多云、雨、雪>，✓并且每个状态都同一个实数相联系，该实数表明变量处于该状态时的概率。

如今天的天气情况：P(天气＝晴)＝0.8P(天气＝多云)＝0.1P(天气＝雨)＝0.1P(天气＝雪)＝0。

或简单的写作：P(Weather)=<0.8,0.1,0.1,0>✓变量的所有状态的概率取值构成这些状态的概率分布：))(),(),(()(21n v v v V P φφφ =每个变量状态的概率值为0～1的实数，所有状态的概率和为1。