立体几何中档题组

2020年高考备考资料——《临考一个月训练计划》第七天——《中档解答题计划》——立体几何（一）一.面面垂直证明，求线面角（逆向二面角）1．如图，在四棱锥P ABCD -中，//AD BC ，AD AB ⊥，侧面PAB ⊥底面ABCD ． （1）求证：平面PAB ⊥平面PBC ；（2）若2PA AB BC AD ===，且二面角P BC A --等于45︒，求直线BD 与平面PBC 所成角的正弦值．二.线面垂直证明，求线线角（翻折问题）2．如图1，在直角梯形ABCD 中，//AB CD ，90A ∠=︒，2AB =，6CD =，3AD =，E 为CD 上一点，且4DE =，过E 作//EF AD 交BC 于F 现将CEF ∆沿EF 折起到PEF ∆，使60PED ∠=︒，如图2．（Ⅰ）求证：PE ⊥平面ADP ；（Ⅱ）求异面直线BD 与PF 所成角的余弦值；（Ⅲ）在线段PF 上是否存在一点M ，使DM 与平在ADP 所成的角为30︒？若存在，确定点M 的位置；若不存在，请说明理由．三. 面面垂直、线面平行证明，求二面角（棱锥载体）3．如图，在三棱锥P ABC -中，AB ⊥平面PAC ，90APC ∠=︒，1AB =，2AC E 是AB 的中点，M 是CE 的中点，N 点在PB 上，且4PN PB =．（1）证明：平面PCE ⊥平面PAB ； （2）证明：//MN 平面PAC ；（3）若60PAC ∠=︒，求二面角P CE A --的大小．四. 线面垂直证明，求二面角（棱柱载体）4．如图，直三棱柱111ABC A B C -中，底面是等腰直角三角形， 2AB BC ==，13BB =，D 为11A C 的中点，F 在线段1AA 上．（1）AF 为何值时，CF ⊥平面1B DF ？（2）设1AF =，求平面1B CF 与平面ABC 所成的锐二面角的余弦值．第七天——《中档解答题计划》——立体几何（一）参考答案1．如图，在四棱锥P ABCD -中，//AD BC ，AD AB ⊥，侧面PAB ⊥底面ABCD ． （1）求证：平面PAB ⊥平面PBC ；（2）若2PA AB BC AD ===，且二面角P BC A --等于45︒，求直线BD 与平面PBC 所成角的正弦值．【解答】解：（1）证明：由//AD BC ，AD AB ⊥，可得BC AB ⊥， Q 侧面PAB ⊥底面ABCD ，交线为AB ，BC ⊂底面ABCD ，且BC AB ⊥，则BC ⊥侧面PAB ，BC ⊥平面PBC ，∴平面PAB ⊥平面PBC ．（2）解：由BC ⊥侧面PAB ，可得BC PB ⊥，BC AB ⊥， 则PBA ∠是二面角P BC A --的平面角，45PBA ∴∠=︒， 由PA AB =，可得PAB ∆为等腰直角三角形， 取PB 的中点E ，连接AE ，可得AE PB ⊥，Q 平面PAB ⊥平面PBC ，交线为PB ，AE ⊂平面PAB ，且AE PB ⊥，AE ∴⊥平面PBC ，点A 到平面PBC 的距离为AE ，//AD BC Q ，AD ⊂/平面PBC ，BC ⊂平面PBC ，则//AD 平面PBC ，∴点D 到平面PBC 的距离d 等于点A 到平面PBC 的距离，d AE =．设1AD =，则2PA AB BC ===，在PAB ∆中，2AE =；在ABD ∆中，5BD ， 设直线BD 与平面PBC 所成角为θ， 则210sin 5d AE BD BD θ==== ∴直线BD 与平面PBC 10．2．如图1，在直角梯形ABCD 中，//AB CD ，90A ∠=︒，2AB =，6CD =，3AD =，E 为CD 上一点，且4DE =，过E 作//EF AD 交BC 于F 现将CEF ∆沿EF 折起到PEF ∆，使60PED ∠=︒，如图2．（Ⅰ）求证：PE ⊥平面ADP ；（Ⅱ）求异面直线BD 与PF 所成角的余弦值；（Ⅲ）在线段PF 上是否存在一点M ，使DM 与平在ADP 所成的角为30︒？若存在，确定点M 的位置；若不存在，请说明理由．【解答】解：（Ⅰ）解法一：4DE =Q ，2PE =，60PED ∠=︒，由弦定理得23PD =， 22216PD PE DE +==Q ，PE PD ∴⊥．EF PE ⊥Q ，EF DE ⊥∴，EF ⊥平面PDE ，又//EF AD Q ，AD ∴⊥平面PDE ，AD PE ∴⊥，又Q 直线AD ，PD 在平面APD 内，且相交于D ，PE ∴⊥平面APD ．解法二：EF PE ⊥，EF DE ⊥∴，EF ⊥平面PDE ∴平面DEF ⊥平面PDE以DA 所在的直线为x 轴，以DE 所在的直线为y 轴，在平面DPE 内过D 作DE 的垂线，以垂线所在直线为z 轴，建立空间直角坐标系，如图则(0D ，0，0)，(3A ，0，0)，(0P ，33)，(0E ，4，0)∴(3DA =u u u r ，0，0)，(0DP =u u u r ，33)，(0EP =u u u r ，1-3)．Q 0DA EP =u u u r u u u rg ，0DP EP =u u u r u u u r g ，∴DA EP ⊥u u u r u u u r ，DP EP DA EP ⊥∴⊥u u u r u u u r，DP EP ⊥，DA Q ，DP 是平面ADP 内的相交直线，PE ∴⊥平面APD ．（Ⅱ）由（Ⅰ）知AD ⊥平面PDE ，∴平面ADE ⊥平面PDE以DA 所在的直线为x 轴，以DE 所在的直线为y 轴，在平面DPE 内过D 作DE 的垂线，以垂线所在直线为z 轴，建立空间直角坐标系，如图则(0D ，0，0)，(3A ，0，0)，(0P ，3，(0E ，4，0)，3(2F ，4，0)，(3B ，2，0)，∴(3DB =u u u r ，2，0)，3(2PF =u u u r ，1，∴cos ,||||DB PF DB PF DB PF <>==⨯u u u r u u u ru u u r u u u r g u u u r u u u r设BD 与PF 所成的角为θ，则,DB PF θ=<>u u u r u u u r ，∴cos θ=（Ⅲ）由（Ⅱ）知(0EP =u u u r ，1-3(2PF =u u u r ，1，PE ⊥Q 平面ADP ，∴平面ADP 的法向量为(0n EP ==u u ur r ，1-． 设M 是线段PF 上一点，则存在01λ剟，使PM PF λ=u u u u r u u u r ∴(0DM DP PM =+==u u u u r u u u r u u u u r ，33(2λ+，1，3(2λ=，3λ+，3)+.cos ,||||n DM n DM n DM <>==⨯u u u u r r u u u ur g r u u u u r r ，如果直线DM 与平面ADC 所成的角为30︒， 那么|cos ,|sin 30n DM <>=︒u u u ur r12=±解得21613λ= Q 此方程在[0，1]内无解，∴在线段PF 上不存在一点M ，使DM 与平在ADP 所成的角为30︒．3．如图，在三棱锥P ABC -中，AB ⊥平面PAC ，90APC ∠=︒，1AB =，2AC =，E 是AB 的中点，M 是CE 的中点，N 点在PB 上，且4PN PB =．（1）证明：平面PCE ⊥平面PAB ； （2）证明：//MN 平面PAC ；（3）若60PAC ∠=︒，求二面角P CE A --的大小．【解答】证明：（1）90APC ∠=︒Q ，PC AP ∴⊥，AB ⊥Q 平面PAC ，PC ⊂平面PAC ，AB PC ∴⊥， AP AB A =Q I ，PC ∴⊥平面PAB ， PC ⊂Q 平面PCE ，∴平面PCE ⊥平面PAB ；（2）取AE 的中点F ，连接FN ，FM ，M Q 是CE 的中点，MF ∴是AEC ∆的中位线，则//MF AC ，24AB AE AF ==4PN PB =Q ，::PB PN AB AF ∴=，则//FN AP ， AP PC C =Q I ，∴平面//MNF 平面PAC ；MN ⊂Q 面MNF ； //MN ∴平面PAC ，（3）过P 作PO AC ⊥于O ，则PO ⊥平面ABC ，过O 作AB 的平行线交BC 于H ， 以O 坐标原点建立空间坐标系如图： 若60PAC ∠=︒，90APC ∠=︒Q ，1AB =，AC E 是AB 的中点，M 是CE 的中点，12AP AC ∴==，12OA AP ==OC AC OA =-sin 60OP AP =︒==12AE =，则A 0，0)，E 12，0)，(C ，0，0)，(0P ，0， 则平面AEC 的一个法向量为(0m =r，0，1)，设平面PEC 的一个法向量为(n x =r，y ，)z ，则CE =u u u r 12，0)，(PC =u u u r 0，，则00n CE n PC ⎧=⎪⎨=⎪⎩u u u r r gu u u rr g，即1020y +=⎨⎪=⎪⎩，即y z ⎧=-⎪⎨=⎪⎩，令1x =，则z =y = 即(1n =r，，则||n =r则cos m <r，1||||2m n n m n >====-r r g r r r ， 即m <r ，120n >=︒r，Q 二面角P CE A --是锐二面角，∴二面角P CE A --的大小为60︒．4．如图，直三棱柱111ABC A B C -中，底面是等腰直角三角形， 2AB BC ==，13BB =，D 为11A C 的中点，F 在线段1AA 上．（1）AF 为何值时，CF ⊥平面1B DF ？（2）设1AF =，求平面1B CF 与平面ABC 所成的锐二面角的余弦值．【解答】解：（1）因为直三棱柱111ABC A B C -中， 1BB ⊥面ABC ，2ABC π∠=．以B 点为原点，BA 、BC 、1BB 分别为x 、y 、z 轴建立如图所示空间直角坐标系．因为2AC =，90ABC ∠=︒，所以AB BC = 从而(0B ，0，0)，0,0)A，(0,0)C ，1(0B ，0，3)，10,3)A，1(0,3)C，3)D ，所以13)CA =-u u u r， 设AF x =，则F ，0，)x，111),0,3),0).(00CF x B F x B D CF B D x ==-==u u u r u u u u r u u u u r u u u r u u u u r g g ，所以1CF B D ⊥u u u r u u u u r．要使CF ⊥平面1B DF ，只需1CF B F ⊥． 由12(3)0CF B F x x =+-=u u u r u u u u rg ，得1x =或2x =，故当1AF =或2时，CF ⊥平面1B DF ．（5分） （2）由（1）知平面ABC 的法向量为1(0n =，0，1)．设平面1B CF 的法向量为(n x =，y ，)z ，则由100n CF n B F ⎧=⎪⎨=⎪⎩u u u rg u u u u rg得020z z +=-= 令1z =得1)n =， 所以平面1B CF 与平面ABC所成的锐二面角的余弦值1cos ,n n 〈>==．。

中档题目强化练——立体几何A组 专项基础训练(时间：35分钟，满分：57分)一、选择题(每小题5分，共20分)1．以下关于几何体的三视图的论述中，正确的是() A．球的三视图总是三个全等的圆B．正方体的三视图总是三个全等的正方形C．水平放置的正四面体的三视图都是正三角形D．水平放置的圆台的俯视图是一个圆答案 A解析 画几何体的三视图要考虑视角，但对于球无论选择怎样的视角，其三视图总是三个全等的圆．2．设α、β、γ是三个互不重合的平面，m、n是两条不重合的直线，下列命题中正确的是() A．若α⊥β，β⊥γ，则α⊥γB．若m∥α，n∥β，α⊥β，则m⊥nC．若α⊥β，m⊥α，则m∥βD．若α∥β，m⊄β，m∥α，则m∥β答案 D解析 对于A，若α⊥β，β⊥γ，α，γ可以平行，也可以相交，A错；对于B，若m∥α，n∥β，α⊥β，则m，n可以平行，可以相交，也可以异面，B错；对于C，若α⊥β，m⊥α，则m可以在平面β内，C错；易知D正确．3．设α、β、γ为平面，l、m、n为直线，则m⊥β的一个充分条件为() A．α⊥β，α∩β＝l，m⊥l B．n⊥α，n⊥β，m⊥αC．α∩γ＝m，α⊥γ，β⊥γD．α⊥γ，β⊥γ，m⊥α答案 B解析 如图①知A错；如图②知C错；如图③在正方体中，两侧面α与β相交于l，都与底面γ垂直，γ内的直线m⊥α，但m与β不垂直，故D错；由n⊥α，n⊥β，得α∥β.又m⊥α，则m⊥β，故B正确．4． 如图，在正四棱柱ABCD －A1B 1C 1D 1中，E 、F 分别是AB 1、BC 1的中点，则下列结论不成立的是 ( )A ．EF 与BB 1垂直 B ．EF 与BD 垂直C ．EF 与CD 异面 D ．EF 与A 1C 1异面 答案 D解析 连接B1C ，AC ，则B 1C 交BC 1于F ，且F 为B 1C 的中点，又E 为AB 1的中点，所以EF 綊12AC ， 而B 1B ⊥平面ABCD ，所以B 1B ⊥AC ，所以B 1B ⊥EF ，A 正确；又AC ⊥BD ，所以EF ⊥BD ，B 正确；显然EF 与CD 异面，C 正确；由EF 綊12，AC ∥A 1C 1， 得EF ∥A 1C 1.故不成立的选项为D. 二、填空题(每小题5分，共15分)5． (2011·福建)三棱锥P －ABC 中，P A ⊥底面ABC ，P A ＝3，底面ABC 是边长为2的正三角形，则三棱锥P －ABC 的体积等于________． 答案3解析 ∵P A ⊥底面ABC ，∴P A 为三棱锥P －ABC 的高，且P A ＝3.∵底面ABC 为正三角形且边长为2，∴底面面积为12×22×sin 60°＝3，∴V P －ABC ＝13×3×3＝ 3.6． 已知四棱锥P —ABCD 的底面ABCD 是矩形，P A ⊥底面ABCD ，点E 、F 分别是棱PC 、PD 的中点，则①棱AB 与PD 所在直线垂直； ②平面PBC 与平面ABCD 垂直； ③△PCD 的面积大于△P AB 的面积； ④直线AE 与直线BF 是异面直线．以上结论正确的是________．(写出所有正确结论的编号) 答案 ①③解析 由条件可得AB ⊥平面P AD ，∴AB ⊥PD ，故①正确；若平面PBC ⊥平面ABCD ，由PB ⊥BC ，得PB ⊥平面ABCD ，从而P A ∥PB ，这是不可能的，故②错； S △PCD ＝12CD ·PD ，S △P AB ＝12AB ·P A ， 由AB ＝CD ，PD >P A 知③正确； 由E 、F 分别是棱PC 、PD 的中点， 可得EF ∥CD ，又AB ∥CD ，∴EF ∥AB ，故AE 与BF 共面，④错．7． 三棱锥S －ABC 中，∠SBA ＝∠SCA ＝90°，△ABC 是斜边AB ＝a 的等腰直角三角形，则以下结论中：①异面直线SB 与AC 所成的角为90°； ②直线SB ⊥平面ABC ； ③平面SBC ⊥平面SAC ； ④点C 到平面SAB 的距离是12. 其中正确结论的序号是________． 答案 ①②③④解析 由题意知AC ⊥平面SBC ，故AC ⊥SB ，SB ⊥平面ABC ，平面SBC ⊥平面SAC ，①②③正确；取AB 的中点E ，连接CE ，(如图)可证得CE ⊥平面SAB ，故CE 的长度即为C 到平面SAB 的距离12a ，④正确．三、解答题(共22分)8． (10分)如图所示，直三棱柱ABC －A1B 1C 1中，∠ACB ＝90°，M ，N 分别为A 1B ，B 1C 1的中点．求证： (1)BC ∥平面MNB 1； (2)平面A 1CB ⊥平面ACC 1A . 证明 (1)因为BC ∥B 1C 1，且B 1C 1⊂平面MNB 1，BC ⊄平面MNB 1，故BC ∥平面MNB 1.(2)因为BC ⊥AC ，且ABC －A 1B 1C 1为直三棱柱， 故BC ⊥平面ACC 1A 1. 因为BC ⊂平面A 1CB ，故平面A1CB⊥平面ACC1A1.9． (12分)如图，四棱锥P—ABCD中，P A⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB.(1)求证：CE⊥平面P AD；(2)若P A＝AB＝1，AD＝3，CD＝2，∠CDA＝45°，求四棱锥P—ABCD的体积．(1)证明 因为P A⊥平面ABCD，CE⊂平面ABCD，所以P A⊥CE.因为AB⊥AD，CE∥AB，所以CE⊥AD.又P A∩AD＝A，所以CE⊥平面P AD.(2)解 由(1)可知CE⊥AD.在Rt△ECD中，DE＝CD·cos 45°＝1，CE＝CD·sin 45°＝1.所以AE＝AD－ED＝2.又因为AB＝CE＝1，AB∥CE，所以四边形ABCE为矩形．所以S四边形ABCD＝S矩形ABCE＋S△ECD＝AB·AE＋12CE·DE＝1×2＋12×1×1＝5 2.又P A⊥平面ABCD，P A＝1，所以V四棱锥P—ABCD＝13S四边形ABCD·P A＝13×52×1＝56.B组 专项能力提升(时间：25分钟，满分：43分)一、选择题(每小题5分，共15分)1．已知直线l1，l2与平面α，则下列结论中正确的是() A．若l1⊂α，l2∩α＝A，则l1，l2为异面直线B．若l1∥l2，l1∥α，则l2∥αC．若l1⊥l2，l1⊥α，则l2∥αD．若l1⊥α，l2⊥α，则l1∥l2答案 D解析 对于选项A，当A∈l1时，结论不成立；对于选项B、C，当l2⊂α时，结论不成立．2．已知直线l⊥平面α，直线m⊂平面β，有下面四个命题：①α∥β⇒l⊥m； ②α⊥β⇒l∥m；③l∥m⇒α⊥β； ④l⊥m⇒α∥β.其中正确的命题有()A ．①②B ．①③C ．②④D ．③④答案 B解析 ①中， ⎭⎪⎬⎪⎫α∥βl ⊥α⇒⎭⎪⎬⎪⎫l ⊥βm ⊂β⇒l ⊥m ，故①正确； ②中，l 与m 相交、平行、异面均有可能，故②错； ③中， ⎭⎪⎬⎪⎫l ∥m l ⊥α⇒⎭⎪⎬⎪⎫m ⊥αm ⊂β⇒α⊥β，故③正确； ④中，α与β也有可能相交，故④错误．3． 如图所示，是一几何体的平面展开图，其中ABCD 为正方形，E 、F 分别为P A 、PD 的中点．在此几何体中，给出下面四个结论： ①直线BE 与直线CF 异面； ②直线BE 与直线AF 异面； ③直线EF ∥平面PBC ； ④平面BCE ⊥平面P AD . 其中正确的有( ) A ．①②B ．②③C ．①④D ．②④答案 B解析 对于①，因为E 、F 分别是P A 、PD 的中点， 所以EF ∥AD .又因为AD ∥BC ，所以EF ∥BC .所以BE 与CF 共面．故①不正确．对于②，因为BE 是平面APD 的斜线，AF 是平面APD 内与BE 不相交的直线，所以BE 与AF 不共面．故②正确．对于③，由①，知EF ∥BC ，所以EF ∥平面PBC .故③正确． 对于④，条件不足，无法判断两平面垂直． 二、填空题(每小题5分，共15分)4． 有一个内接于球的四棱锥P －ABCD ，若P A ⊥底面ABCD ，∠BCD ＝π2，∠ABC ≠π2，BC＝3，CD ＝4，P A ＝5，则该球的表面积为________． 答案 50π解析 由∠BCD ＝90°知BD 为底面ABCD 外接圆的直径，则2r ＝32＋42＝5. 又∠DAB ＝90°⇒P A ⊥AB ，P A ⊥AD ，BA ⊥AD .从而把P A ，AB ，AD 看作长方体的三条棱，设外接球半径为R ，则(2R )2＝52＋(2r )2＝52＋52，∴4R 2＝50，∴S 球＝4πR 2＝50π.5. 矩形ABCD 中，AB ＝1，BC ＝a (a >0)，P A ⊥平面AC ，BC 边上存在点Q ，使得PQ ⊥QD ，则实数a 的取值范围是________． 答案 [2，＋∞) 解析 如图，连接AQ ， ∵P A ⊥平面AC ，∴P A ⊥QD ，又PQ ⊥QD ，PQ ∩P A ＝P ， ∴QD ⊥平面PQA ，于是QD ⊥AQ ，∴在线段BC 上存在一点Q ，使得QD ⊥AQ ， 等价于以AD 为直径的圆与线段BC 有交点， ∴a2≥1，a ≥2.6. 如图所示的几何体中，四边形ABCD 是矩形，平面ABCD ⊥平面ABE ，已知AB ＝2，AE ＝BE ＝3，且当规定正视方向垂直平面ABCD 时，该 几何体的侧视图的面积为2.若M 、N 分别是线段DE 、CE 上的动点， 则AM ＋MN ＋NB 的最小值为________． 答案 3解析 依题意得，点E 到直线AB 的距离等于(3)2－⎝⎛⎠⎞222＝2，因为该几何体的侧视图的面积为12·BC ×2＝2，所以BC ＝1，DE ＝EC ＝DC ＝2，△DEC 是正三角形，∠DEC ＝60°，tan ∠DEA ＝AD AE ＝33，∠DEA ＝∠CEB ＝30°.把△DAE 、△DEC 与△CEB 展在同一平面上，此时连接AB ，AE ＝BE ＝3，∠AEB ＝∠DEA ＋∠DEC ＋∠CEB ＝120°，AB 2＝AE 2＋BE 2－2AE ·BE ·cos 120°＝9，AB ＝3，即AM ＋MN ＋NB 的最小值为3. 三、解答题7． (13分)(2012·浙江改编)如图，在侧棱垂直底面的四棱柱ABCD －A 1B 1C 1D 1中，AD ∥BC ，AD ⊥AB ，AB ＝2，AA 1＝2，E 是DD 1的 中点，F 是平面B 1C 1E 与直线AA 1的交点． 证明：(1)EF ∥A 1D 1； (2)BA 1⊥平面B 1C 1EF .证明 (1)因为C 1B 1∥A 1D 1，C 1B 1⊄平面A 1D 1DA ， 所以C 1B 1∥平面A 1D 1DA .又因为平面B 1C 1EF ∩平面A 1D 1DA ＝EF ，所以C 1B 1∥EF ，所以EF ∥A 1D 1.(2)因为BB1⊥平面A1B1C1D1，所以BB1⊥B1C1. 又因为B1C1⊥B1A1，所以B1C1⊥平面ABB1A1，所以B1C1⊥BA1.在矩形ABB1A1中，F是AA1的中点，tan∠A1B1F＝tan∠AA1B＝2 2，即∠A1B1F＝∠AA1B，故BA1⊥B1F. 所以BA1⊥平面B1C1EF.。

中档大题规范练——立体几何1．如图所示，已知三棱锥A－BPC中，AP⊥PC，AC⊥BC，M为AB的中点，D为PB的中点，且△PMB为正三角形．(1)求证：DM∥平面APC；(2)求证：平面ABC⊥平面APC；(3)若BC＝4，AB＝20，求三棱锥D－BCM的体积．(1)证明由已知，得MD是△ABP的中位线，所以MD∥AP.又MD⊄平面APC，AP⊂平面APC，故MD∥平面APC.(2)证明因为△PMB为正三角形，D为PB的中点，所以MD⊥PB.所以AP⊥PB.又AP⊥PC，PB∩PC＝P，所以AP⊥平面PBC.因为BC⊂平面PBC，所以AP⊥BC.又BC⊥AC，AC∩AP＝A，所以BC⊥平面APC.因为BC⊂平面ABC，所以平面ABC⊥平面APC.(3)解由(2)知，可知MD⊥平面PBC，所以MD是三棱锥D－BCM的一条高，又AB＝20，BC＝4，△PMB为正三角形，M，D分别为AB，PB的中点，经计算可得MD＝53，DC＝5，S△BCD＝12×BC×BD×sin∠CBD＝12×5×4×215＝221.所以V D－BCM＝V M－DBC＝13×S△BCD×MD＝13×221×53＝107. 2．如图，在Rt △ABC 中，AB ＝BC ＝4，点E 在线段AB 上．过点E 作EF ∥BC 交AC 于点F ，将△AEF 沿EF 折起到△PEF 的位置(点A 与P 重合)，使得∠PEB ＝30°.(1)求证：EF ⊥PB ；(2)试问：当点E 在何处时，四棱锥P —EFCB 的侧面PEB 的面积最大？并求此时四棱锥P —EFCB 的体积．(1)证明 ∵EF ∥BC 且BC ⊥AB ，∴EF ⊥AB ，即EF ⊥BE ，EF ⊥PE .又BE ∩PE ＝E ，∴EF ⊥平面PBE ，又PB ⊂平面PBE ，∴EF ⊥PB .(2)解 设BE ＝x ，PE ＝y ，则x ＋y ＝4.∴S △PEB ＝12BE ·PE ·sin ∠PEB＝14xy ≤14⎝ ⎛⎭⎪⎫x ＋y 22＝1.当且仅当x ＝y ＝2时，S △PEB 的面积最大．此时，BE ＝PE ＝2.由(1)知EF ⊥平面PBE ，∴平面PBE ⊥平面EFCB ，在平面PBE 中，作PO ⊥BE 于O ，则PO ⊥平面EFCB .即PO 为四棱锥P —EFCB 的高．又PO ＝PE ·sin 30°＝2×12＝1.S 梯形EFCB ＝12×(2＋4)×2＝6.∴V P —BCFE ＝13×6×1＝2.3.如图，在矩形ABCD 中，AB ＝2BC ，P 、Q 分别是线段AB 、CD 的中点，EP ⊥平面ABCD .(1)求证：DP ⊥平面EPC ；(2)问在EP 上是否存在点F ，使平面AFD ⊥平面BFC ？若存在，求出FP AP的值；若不存在，说明理由．(1)证明 ∵EP ⊥平面ABCD ，∴EP ⊥DP .又ABCD 为矩形，AB ＝2BC ，P 、Q 分别为AB 、CD 的中点，连接PQ ，则PQ ⊥DC 且PQ ＝12DC .∴DP ⊥PC .∵EP ∩PC ＝P ，∴DP ⊥平面EPC .(2)解 假设存在F 使平面AFD ⊥平面BFC ，∵AD ∥BC ，BC ⊂平面BFC ，AD ⊄平面BFC ，∴AD ∥平面BFC .∴AD 平行于平面AFD 与平面BFC 的交线l .∵EP ⊥平面ABCD ，∴EP ⊥AD ，而AD ⊥AB ，AB ∩EP ＝P ，∴AD ⊥平面EAB ，∴l ⊥平面F AB .∴∠AFB 为平面AFD 与平面BFC 所成二面角的平面角．∵P 是AB 的中点，且FP ⊥AB ，∴当∠AFB ＝90°时，FP ＝AP .∴当FP ＝AP ，即FP AP ＝1时，平面AFD ⊥平面BFC .4．(2013·课标全国Ⅱ)如图，直三棱柱ABC －A 1B 1C 1中，D ，E 分别是AB ，BB 1的中点．(1)证明：BC 1∥平面A 1CD ；(2)设AA 1＝AC ＝CB ＝2，AB ＝22，求三棱锥C －A 1DE 的体积．(1)证明 连接AC 1交A 1C 于点F ，则F 为AC 1中点．又D 是AB 中点，连接DF ，则BC 1∥DF .因为DF ⊂平面A 1CD ，BC 1⊄平面A 1CD ，所以BC 1∥平面A 1CD .(2)解 因为ABC －A 1B 1C 1是直三棱柱，所以AA 1⊥CD .又因为AC ＝CB ，D 为AB 的中点，所以CD ⊥AB .又AA 1∩AB ＝A ，于是CD ⊥平面ABB 1A 1.由AA 1＝AC ＝CB ＝2，AB ＝22，得∠ACB ＝90°，CD ＝2，A 1D ＝6，DE ＝3，A 1E ＝3，故A 1D 2＋DE 2＝A 1E 2，即DE ⊥A 1D .所以1C A DE V －＝13×S △A 1ED ×CD ＝13×12×6×3×2＝1.5．(2013·辽宁)如图，AB 是圆O 的直径，P A 垂直圆O 所在的平面，C 是圆O 上的点．(1)求证：BC ⊥平面P AC ；(2)设Q 为P A 的中点，G 为△AOC 的重心，求证：QG ∥平面PBC . 证明 (1)由AB 是圆O 的直径，得AC ⊥BC ，由P A ⊥平面ABC ，BC ⊂平面ABC ，得P A ⊥BC .又P A ∩AC ＝A ，P A ⊂平面P AC ，AC ⊂平面P AC ，所以BC ⊥平面P AC .(2)连接OG 并延长交AC 于M ，连接QM ，QO ，由G 为△AOC 的重心，得M 为AC 中点．由Q 为P A 中点，得QM ∥PC ，又O 为AB 中点，得OM ∥BC .因为QM ∩MO ＝M ，QM ⊂平面QMO ，MO ⊂平面QMO ，BC ∩PC ＝C ，BC ⊂平面PBC ，PC ⊂平面PBC .所以平面QMO ∥平面PBC .因为QG ⊂平面QMO ，所以QG ∥平面PBC .6．(2014·四川)在如图所示的多面体中，四边形ABB 1A 1和ACC 1A 1都为矩形．(1)若AC ⊥BC ，证明：直线BC ⊥平面ACC 1A 1；(2)设D ，E 分别是线段BC ，CC 1的中点，在线段AB 上是否存在一点M ，使直线DE ∥平面A 1MC ？请证明你的结论．(1)证明 因为四边形ABB 1A 1和ACC 1A 1都是矩形，所以AA 1⊥AB ，AA 1⊥AC .因为AB ∩AC ＝A ，AB ⊂平面ABC ，AC ⊂平面ABC ， 所以AA 1⊥平面ABC .因为直线BC ⊂平面ABC ，所以AA 1⊥BC .又由已知，AC ⊥BC ，AA 1∩AC ＝A ，AA 1⊂平面ACC 1A 1，AC ⊂平面ACC 1A 1， 所以BC ⊥平面ACC 1A 1.(2)解 取线段AB 的中点M ，连接A 1M ，MC ，A 1C ，AC 1，设O 为A 1C ，AC 1的交点． 由题意知，O 为AC 1的中点．连接MD ，OE ，OM ，则MD ，OE 分别为△ABC ，△ACC 1的中位线，所以MD 綊12AC ，OE 綊12AC ， 因此MD 綊OE .从而四边形MDEO 为平行四边形，则DE ∥MO .因为直线DE ⊄平面A 1MC ，MO ⊂平面A 1MC ，所以直线DE ∥平面A 1MC .即线段AB 上存在一点M (线段AB 的中点)，使直线DE ∥平面A 1MC .。

中档大题分类练(四) 立体几何(建议用时：60分钟) (对应学生用书第139页)1．(2018·沈阳质检三)如图48，在三棱柱ABC -A 1B 1C 1中，侧面AA 1B 1B ⊥底面ABC ，△ABC 和△ABB 1都是边长为2的正三角形．图48(1)过B 1作出三棱柱的截面，使截面垂直于AB ，并证明； (2)求AC 1与平面BCC 1B 1所成角的正弦值．[解] (1)设AB 中点为O ，连接OC ，OB 1，B 1C ，则截面OB 1C 为所求， OC ，OB 1分别为△ABC ，△ABB 1的中线，所以AB ⊥OC ，AB ⊥OB 1，又OC ，OB 1为平面OB 1C 内的两条相交直线，所以AB ⊥平面OB 1C ， (2)以O 为原点，OB 方向为x 轴正方向建立如图所示的空间直角坐标系，易求得B (1,0,0)，A (－1,0,0)，C (0，3，0)，B 1(0,0，3)，C 1(－1，3，3)，CB →＝(1，－3，0)，B 1B →＝(1,0，－3)，AC 1→＝(0，3，3)，设平面BCC 1B 1的一个法向量为n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧ n ⊥CB →n ⊥B 1B →⇔⎩⎪⎨⎪⎧x －3y ＝0，x －3z ＝0，解得平面BCC 1B 1的一个法向量为n ＝(3，1,1)，又|cos 〈AC 1→，n 〉|＝|AC 1→·n ||AC 1→|·|n |＝3＋36·5＝105，所以AC 1与平面BCC 1B 1所成角的正弦值为105. 【教师备选】如图，在三棱锥A -BCD 中，平面ABD ⊥平面BCD ，AB ＝AD ，∠CBD ＝60°，BD ＝2BC ＝4，点E 在CD 上，DE ＝2EC .(1)求证：AC ⊥BE ；(2)若二面角E -BA -D 的余弦值为155，求三棱锥A -BCD 的体积．[解] (1)证明：取BD 的中点O ，连接AO ，CO ，EO . 因为AB ＝AD ，BO ＝OD ， 所以AO ⊥BD ，又平面ABD ⊥平面BCD ，平面ABD ∩平面BCD ＝BD ，AO ⊂平面ABD ， 所以AO ⊥平面BCD .又BE ⊂平面BCD ，所以AO ⊥BE . 在△BCD 中，BD ＝2BC ，DE ＝2EC ， 所以BD BC ＝DEEC ＝2，由角平分线定理，得∠CBE ＝∠DBE .又BC ＝BO ＝2，所以BE ⊥CO ，又因为AO ∩CO ＝O ，AO ⊂平面ACO ，CO ⊂平面ACO ， 所以BE ⊥平面ACO ，又AC ⊂平面ACO ，所以AC ⊥BE .(2)在△BCD 中，BD ＝2BC ＝4，∠CBD ＝60°， 由余弦定理，得CD ＝23，所以BC 2＋CD 2＝BD 2， 即∠BCD ＝90°，所以∠EBD ＝∠EDB ＝30°，BE ＝DE ，所以EO ⊥BD ，结合(1)知，OE ，OD ，OA 两两垂直，以O 为原点，分别以OE ，OD ，OA 的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系O -xyz (如图)，设AO ＝t (t >0)，则A (0,0，t )，B (0，－2,0)，E ⎝ ⎛⎭⎪⎫233，0，0， 所以BA ＝(0,2，t )，BE ＝⎝ ⎛⎭⎪⎫233，2，0， 设n ＝(x ，y ，z )是平面ABE 的一个法向量， 则⎩⎪⎨⎪⎧n ·BA ＝0，n ·BE ＝0，即⎩⎨⎧2y ＋tz ＝0，233x ＋2y ＝0，整理，得⎩⎨⎧x ＝－3y ，z ＝－2t y ，令y ＝－1，得n ＝⎝ ⎛⎭⎪⎫3，－1，2t .因为OE ⊥平面ABD ，所以m ＝(1,0,0)是平面ABD 的一个法向量． 又因为二面角E -BA -D 的余弦值为155， 所以|cos 〈m ，n 〉|＝33＋1＋4t 2＝155， 解得t ＝2或t ＝－2(舍去)．又AO ⊥平面BCD ，所以AO 是三棱锥A -BCD 的高， 故V A -BCD ＝13·AO ·S △BCD ＝13×2×12×2×23＝433.2.在如图49所示的六面体中，平面ABCD 是边长为2的正方形，平面ABEF 是直角梯形，∠F AB ＝90°，AF ∥BE ，BE ＝2AF ＝4.图49(1)求证：AC ∥平面DEF ；(2)若二面角E -AB -D 为60°，求直线CE 和平面DEF 所成角的正弦值． [解] (1)证明：连接BD 交AC 于点O ，取DE 的中点为G ，连接FG ，OG . ∵平面ABCD 是正方形，∴O 是BD 的中点，∴OG ∥BE ，OG ＝12BE ，又∵AF ∥BE ，AF ＝12BE ，∴OG ∥AF 且OG ＝AF ， ∴四边形AOGF 是平行四边形， ∴AC ∥FG .又∵FG ⊂平面DEF ，AC ⊄平面DEF ， ∴AC ∥平面DEF .(2)∵四边形ABCD 是正方形，四边形ABEF 是直角梯形，∠F AB ＝90°， ∴DA ⊥AB ，F A ⊥AB .∵AD ∩AF ＝A ，∴AB ⊥平面AFD ， 同理可得AB ⊥平面EBC .又∵AB ⊂平面ABCD ，∴平面AFD ⊥平面ABCD ， 又∵二面角E -AB -D 为60°，∴∠F AD ＝∠EBC ＝60°，BE ＝2AF ＝4，BC ＝2， 由余弦定理得EC ＝23，∴EC ⊥BC . 又∵AB ⊥平面EBC ，∴EC ⊥AB ， ∵AB ∩BC ＝B ，∴EC ⊥平面ABCD .以C 为坐标原点，CB 为x 轴，CD 为y 轴，CE 为z 轴建立如图所示空间直角坐标系．则C (0,0,0)，D (0,2,0)，E (0,0,23)， F (1,2，3)，∴CE→＝(0,0,23)，DF →＝(1,0，3)，EF →＝(1,2，－3)， 设平面DEF 的一个法向量为n ＝(x ，y ，z )， 则⎩⎨⎧n ·DF →＝0，n ·EF →＝0，即⎩⎪⎨⎪⎧x ＋3z ＝0，x ＋2y －3z ＝0. 令z ＝3，则⎩⎪⎨⎪⎧x ＝－3，y ＝3.∴n ＝(－3,3，3)．设直线CE 和平面DEF 所成角为θ， 则sin θ＝|cos 〈CE→，n 〉|＝623×21＝77.3．(2018·安庆市高三二模)如图50，四边形ABCD 是矩形，沿对角线AC 将△ACD 折起，使得点D 在平面ABC 上的射影恰好落在边AB 上．图50(1)求证：平面ACD ⊥平面BCD ；(2)当ABAD ＝2时，求二面角D -AC -B 的余弦值．[解] (1)设点D 在平面ABC 上的射影为点E ，连接DE ，则DE ⊥平面ABC ，所以DE ⊥BC .因为四边形ABCD 是矩形，所以AB ⊥BC ，所以BC ⊥平面ABD ，所以BC ⊥AD . 又AD ⊥CD ，所以AD ⊥平面BCD ，而AD ⊂平面ACD ，所以平面ACD ⊥平面BCD .(2)以点B 为原点，线段BC 所在的直线为x 轴，线段AB 所在的直线为y 轴，建立空间直角坐标系，如图所示．设|AD |＝a ，则|AB |＝2a ，所以A (0，－2a ，0)，C (－a,0,0)．由(1)知AD ⊥BD ，又ABAD ＝2，所以∠DBA ＝30°，∠DAB ＝60°，那么|AE |＝|AD |cos ∠DAB ＝12a ，|BE |＝|AB |－|AE |＝32a ， |DE |＝|AD |sin ∠DAB ＝32a ， 所以D ⎝⎛⎭⎪⎫0，－32a ，32a ，所以AD →＝⎝⎛⎭⎪⎫0，12a ，32a ，AC →＝(－a,2a,0)．设平面ACD 的一个法向量为m ＝(x ，y ，z )，则⎩⎨⎧m ·AD →＝0，m ·AC →＝0，即⎩⎨⎧12ay ＋32az ＝0，－ax ＋2ay ＝0.取y ＝1，则x ＝2，z ＝－33，所以m ＝⎝ ⎛⎭⎪⎫2，1，－33.因为平面ABC 的一个法向量为n ＝(0,0,1)，所以cos 〈m ，n 〉＝m·n|m ||n |＝－3312＋22＋⎝ ⎛⎭⎪⎫－332＝－14.故所求二面角D -AC -B 的余弦值为14. 【教师备选】(2018·东莞市二调)如图，平面CDEF ⊥平面ABCD ，四边形ABCD 是平行四边形，四边形CDEF 为直角梯形，∠ADC ＝120°，CF ⊥CD ，且CF ∥DE ，AD ＝2DC ＝DE ＝2CF .(1)求证：BF ∥平面ADE ；(2)设P 点是线段DE 上一点，若平面BCD 与平面BFP 所成的锐二面角为30°，求点P 的位置．[解] (1)证明：取DE 的中点H ，连接AH ，HF .∵四边形CDEF 为直角梯形，DE ＝2CF ，H 是DE 的中点，∴HF ＝DC ，且HF ∥DC .∵四边形ABCD 是平行四边形，∴AB ＝DC ，且AB ∥DC ，∴AB ＝HF ，且AB ∥HF ，∴四边形ABFH 是平行四边形， ∴BF ∥AH .∵AH ⊂平面ADE ，BF ⊄平面ADE ，∴BF ∥平面ADE . (2)∵在△BCD 中，BC ＝2DC ， ∴∠BDC ＝90°，建立如图所示的空间直角坐标系D -xyz ，设AD ＝2，则DC ＝1，CF ＝1，设DP ＝h ，则B (3，0,0)，C (0,1,0)，F (0,1,1)，P (0,0，h )，BP→＝(－3，0，h )，BF →＝(－3，1,1)， 设平面BFP 的法向量为n ＝(x ，y ，z )， ∵n ⊥BP →，n ⊥BF →，∴⎩⎪⎨⎪⎧－3x ＋hz ＝0，－3x ＋y ＋z ＝0，不妨令x ＝3，则n ＝⎝ ⎛⎭⎪⎫3，3－3h ，3h ， 平面BCD 的一个法向量为m ＝(0,0,1)， ∵平面BCD 与平面BFP 所成锐二面角为30°， ∴|n·m ||n ||m |＝3h(3)2＋⎝ ⎛⎭⎪⎫3－3h 2＋⎝ ⎛⎭⎪⎫3h 2＝32，解得h ＝12，或h ＝1. ∴点P 在线段DE 的中点或线段DE 的靠近点D 的四等分点处．4.如图51，在四棱锥P -ABCD 中，底面ABCD 是平行四边形，AB ＝AC ＝2，AD ＝22，PB ＝32，PB ⊥AC .图51(1)求证：平面P AB ⊥平面P AC ；(2)若∠PBA ＝45°，试判断棱P A 上是否存在与点P ，A 不重合的点E ，使得直线CE 与平面PBC 所成角的正弦值为33，若存在，求出AEAP 的值；若不存在，请说明理由．[解] (1)因为四边形ABCD 是平行四边形，AD ＝22，所以BC ＝AD ＝22， 又AB ＝AC ＝2，所以AB 2＋AC 2＝BC 2，所以AC ⊥AB ， 又PB ⊥AC ，且AB ∩PB ＝B ，所以AC ⊥平面P AB ， 因为AC ⊂平面P AC ，所以平面P AB ⊥平面P AC . (2)由(1)知AC ⊥AB ，AC ⊥平面P AB ，如图，分别以AB ，AC 所在直线为x 轴、y 轴，平面P AB 内过点A 且与直线AB 垂直的直线为z 轴，建立空间直角坐标系A -xyz ，则A (0,0,0)，B (2,0,0)，C (0,2,0)，AC →＝(0,2,0)，BC →＝(－2,2,0)，由∠PBA ＝45°，PB ＝32，可得P (－1,0,3)，所以AP→＝(－1,0,3)，BP →＝(－3,0,3)， 假设棱P A 上存在点E ，使得直线CE 与平面PBC 所成角的正弦值为33， 设AE AP ＝λ(0＜λ＜1)，则AE→＝λAP →＝(－λ，0,3λ)，11/11 CE →＝AE →－AC →＝(－λ，－2,3λ)，设平面PBC 的法向量为n ＝(x ，y ，z )，则⎩⎨⎧ n ·BC →＝0，n ·BP →＝0，即⎩⎪⎨⎪⎧ －2x ＋2y ＝0，－3x ＋3z ＝0，令z ＝1，得x ＝y ＝1， 所以平面PBC 的一个法向量为n ＝(1,1,1)，设直线CE 与平面PBC 所成的角为θ，则sin θ＝|cos 〈n ，CE→〉|＝|－λ－2＋3λ|3·(－λ)2＋(－2)2＋(3λ)2＝|2λ－2|3·10λ2＋4＝33，整理得3λ2＋4λ＝0，因为0＜λ＜1，所以3λ2＋4λ＞0，故3λ2＋4λ＝0无解，所以棱P A 上不存在与点P ，A 不重合的点E ，使得直线CE 与平面PBC 所成角的正弦值为33.。

专题分层训练(三十一) 中档大题规范练(4)——立体几何1.如图，四边形ABCD为正方形，PD⊥平面ABCD，∠DPC＝30°，AF⊥PC于点F，FE∥CD，交PD于点E.(1)证明：CF⊥平面ADF；(2)求二面角D－AF－E的余弦值．解(1)证明：由题意可知DA⊥DC，DA⊥DP，DC⊥DP，故可以D为原点，DP所在直线为x轴，DC所在直线为y轴，DA所在直线为z轴建立空间直角坐标系．设正方形ABCD 的边长为a ， 则C (0，a,0)，A (0,0，a )，由平面几何知识可求得F ⎝⎛⎭⎪⎪⎫34a ，34a ，0， 所以CF →＝⎝⎛⎭⎪⎪⎫34a ，－14a ，0， DF →＝⎝⎛⎭⎪⎪⎫34a ，34a ，0， DA →＝(0,0，a )，CF →·DF →＝34a ×34a ＋⎝ ⎛⎭⎪⎫－14a ×34a ＋0＝0，CF →·DA →＝⎝⎛⎭⎪⎪⎫34a ，－14a ，0·(0,0，a )＝0， 故CF ⊥DF ，CF ⊥DA .又DF ∩DA ＝D ，所以CF ⊥平面ADF .(2)可求得E ⎝ ⎛⎭⎪⎪⎫34a ，0，0，则AE →＝⎝⎛⎭⎪⎪⎫34a ，0，－a ， 又AF →＝⎝⎛⎭⎪⎪⎫34a ，34a ，－a ， 设平面AEF 的法向量为n ＝(x ，y ，z )，则n ·AE →＝(x ，y ，z )·⎝ ⎛⎭⎪⎪⎫34a ，0，－a ＝34ax －az ＝0，n ·AF →＝(x ，y ，z )·⎝ ⎛⎭⎪⎪⎫34a ，34a ，－a ＝34ax ＋34ay －az ＝0，取x ＝1，得平面AEF 的一个法向量n ＝⎝⎛⎭⎪⎪⎫1，0，34.又由(1)知平面ADF 的一个法向量为CF →＝⎝⎛⎭⎪⎪⎫34a ，－14a ，0， 故cos 〈n ，CF →〉＝⎝ ⎛⎭⎪⎪⎫1，0，34·⎝ ⎛⎭⎪⎪⎫34a ，－14a ，0194×12a ＝25719，由图可知二面角D －AF －E 为锐二面角，所以其余弦值为25719.2.如图，四棱锥P －ABCD 中，底面是以O 为中心的菱形，PO ⊥底面ABCD ，AB ＝2，∠BAD ＝π3，M 为BC 上一点，且BM ＝12，MP ⊥AP .(1)求PO 的长；(2)求二面角A －PM －C 的正弦值． 解 (1)如图，连接AC ，BD ，OM ，因ABCD 为菱形，则AC ∩BD ＝O ，且AC ⊥BD .以O 为坐标原点，OA →，OB →，OP →的方向分别为x 轴、y 轴、z 轴的正方向，建立空间直角坐标系O －xyz .因∠BAD ＝π3，故OA ＝AB ·cos π6＝3，OB ＝AB ·sin π6＝1，所以O (0,0,0)，A (3，0,0)，B (0,1,0)，C (－3，0,0)， OB →＝(0,1,0)，BC →＝(－3，－1,0)． 由BM ＝12，BC ＝2知，BM →＝14BC →＝⎝⎛⎭⎪⎪⎫－34，－14，0， 从而OM →＝OB →＋BM →＝⎝⎛⎭⎪⎪⎫－34，34，0， 即M ⎝⎛⎭⎪⎪⎫－34，34，0. 设P (0,0，a )，a >0，则AP →＝(－3，0，a )，MP →＝⎝⎛⎭⎪⎪⎫34，－34，a . 因为MP ⊥AP ，故MP →·AP →＝0，即－34＋a 2＝0，所以a ＝32，a ＝－32(舍去)，即PO ＝32.(2)由(1)知，AP →＝⎝⎛⎭⎪⎪⎫－3，0，32， MP →＝⎝ ⎛⎭⎪⎪⎫34，－34，32，CP →＝⎝⎛⎭⎪⎪⎫3，0，32. 设平面APM 的法向量为n 1＝(x 1，y 1，z 1)，平面PMC 的法向量为n 2＝(x 2，y 2，z 2)．由n 1·AP →＝0，n 1·MP →＝0，得⎩⎪⎨⎪⎧ －3x 1＋32z 1＝0，34x 1－34y 1＋32z 1＝0，故可取n 1＝⎝ ⎛⎭⎪⎪⎫1，533，2. 由n 2·MP →＝0，n 2·CP →＝0，得⎩⎪⎨⎪⎧34x 2－34y 2＋32z 2＝0，3x 2＋32z 2＝0，故可取n 2＝(1，－3，－2)． 从而法向量n 1，n 2的夹角的余弦值为cos 〈n 1，n 2〉＝n 1·n 2|n 1||n 2|＝－155，故所求二面角A －PM －C 的正弦值为105. 3.如图，在三棱柱ABC －A 1B 1C 1中，AA 1C 1C 是边长为4的正方形．平面ABC ⊥平面AA 1C 1C ，AB ＝3，BC ＝5.(1)求证：AA 1⊥平面ABC ；(2)求二面角A 1－BC 1－B 1的余弦值；(3)证明：在线段BC 1上存在点D ，使得AD ⊥A 1B ，并求BDBC 1的值．解(1)证明：在正方形AA 1C 1C 中，A 1A ⊥AC .又平面ABC ⊥平面AA 1C 1C ，且平面ABC ∩平面AA 1C 1C ＝AC ，∴AA 1⊥平面ABC .(2)在△ABC 中，AC ＝4，AB ＝3，BC ＝5， ∴BC 2＝AC 2＋AB 2，AB ⊥AC ，∴以A 为坐标原点，建立如图所示空间直角坐标系A －xyz .A 1(0,0,4)，B (0,3,0)，C 1(4,0,4)，B 1(0,3,4)，A 1C 1→＝(4,0,0)，A 1B →＝(0,3，－4)，B 1C 1→＝(4，－3,0)，BB 1→＝(0,0,4)．设平面A 1BC 1的法向量n 1＝(x 1，y 1，z 1)， 平面B 1BC 1的法向量n 2＝(x 2，y 2，z 2)．∴⎩⎨⎧A 1C 1→·n 1＝0，A 1B →·n 1＝0⇒⎩⎪⎨⎪⎧4x 1＝0，3y 1－4z 1＝0.∴取向量n 1＝(0,4,3)．由⎩⎨⎧B 1C 1→·n 2＝0，BB 1→·n 2＝0⇒⎩⎪⎨⎪⎧4x 2－3y 2＝0，4z 2＝0.取向量n 2＝(3,4,0)．∴cos 〈n 1·n 2〉＝n 1·n 2|n 1|·|n 2|＝165×5＝1625.∴所求二面角A 1－BC －B 1的余弦值为1625.(3)证明：设D (x ，y ，z )是直线BC 1上一点，且BD →＝λBC 1→.∴(x ，y －3，z )＝λ(4，－3,4)，解得x ＝4λ，y ＝3－3λ，z ＝4λ， ∴AD →＝(4λ，3－3λ，4λ)．又AD ⊥A 1B ，∴0＋3(3－3λ)－16λ＝0， 则λ＝925，因此BD BC 1＝925.4.如图，在四棱锥P －ABCD 中，平面PAC ⊥平面ABCD ，且PA ⊥AC ，PA ＝AD ＝2.四边形ABCD 满足BC ∥AD ，AB ⊥AD ，AB ＝BC ＝1.点E ，F 分别为侧棱PB ，PC 上的点，且PE PB ＝PFPC＝λ.(1)求证：EF ∥平面PAD ；(2)当λ＝12时，求异面直线BF 与CD 所成角的余弦值；(3)是否存在实数λ，使得平面AFD ⊥平面PCD ？若存在，试求出λ的值；若不存在，请说明理由．解 (1)证明：由已知PE PB ＝PFPC＝λ，∴EF ∥BC ， 又BC ∥AD ，∴EF ∥AD ， 而EF ⊄平面PAD ，AD ⊂平面PAD ， ∴EF ∥平面PAD .(2)∵平面ABCD ⊥平面PAC ，平面ABCD ∩平面PAC ＝AC ，且PA ⊥AC ， ∴PA ⊥平面ABCD . ∴PA ⊥AB ，PA ⊥AD . 又∵AB ⊥AD ，∴PA ，AB ，AD 两两垂直．如图所示，建立空间直角坐标系． ∵AB ＝BC ＝1，PA ＝AD ＝2，∴A (0,0,0)，B (1,0,0，)，C (1,1,0)，D (0,2,0)，P (0,0,2)， 当λ＝12时，F 为PC 中点，∴F ⎝ ⎛⎭⎪⎫12，12，1， ∴BF →＝⎝ ⎛⎭⎪⎫－12，12，1，CD →＝(－1,1,0)，设异面直线BF 与CD 所成的角为θ， ∴cos θ＝|cos 〈BF →，CD →〉|＝12＋1262×2＝33. 故异面直线BF 与CD 所成角的余弦值为33.(3)设F (x 0，y 0，z 0)，则PF →＝(x 0，y 0，z 0－2)，PC →＝(1,1，－2)，又PF →＝λPC →，∴⎩⎪⎨⎪⎧x 0＝λ，y 0＝λ，z 0＝2－2λ，∴AF →＝(λ，λ，2－2λ)，设平面AFD 的一个法向量为m ＝(x 1，y 1，z 1)，则⎩⎨⎧m ·AF →＝0，m ·AD →＝0，即⎩⎪⎨⎪⎧λx 1＋λy 1＋(2－2λ)z 1＝0，2y 1＝0，令z 1＝λ，得m ＝(2λ－2,0，λ)．设平面PCD 的一个法向量为n ＝(x 2，y 2，z 2)．则⎩⎨⎧n ·PD →＝0，n ·CD →＝0，即⎩⎪⎨⎪⎧2y 2－2z 2＝0，－x 2＋y 2＝0，取y 2＝1，则x 2＝1，z 2＝1， ∴n ＝(1,1,1)，由m ⊥n ，得m ·n ＝(2λ－2,0，λ)·(1,1,1)＝2λ－2＋λ＝0， 解得λ＝23.∴当λ＝23时，使得平面AFD ⊥平面PCD .5.如图，在四棱锥S －ABCD 中，底面ABCD 是直角梯形，侧棱SA ⊥底面ABCD ，AB 垂直于AD 和BC ，SA ＝AB ＝BC ＝2，AD ＝1.M 是棱SB 的中点．(1)求证：AM ∥平面SCD ；(2)求平面SCD 与平面SAB 所成二面角的余弦值；(3)设点N 是直线CD 上的动点，MN 与平面SAB 所成的角为θ，求sinθ的最大值．解(1)证明：以点A 为原点建立如图所示的空间直角坐标系，则A (0,0,0)，B (0,2,0)，C (2,2,0)，D (1,0,0)，S (0,0,2)，M (0,1,1)．则AM →＝(0,1,1)，SD →＝(1,0，－2)，CD →＝(－1，－2,0)．设平面SCD 的法向量为n ＝(x ，y ，z )，则⎩⎨⎧ SD →·n ＝0，CD →·n ＝0，即⎩⎪⎨⎪⎧ x －2z ＝0，－x －2y ＝0. 令z ＝1，得n ＝(2，－1,1)．∵AM →·n ＝0，∴AM →⊥n . ∴AM ∥平面SCD .(2)易知平面SAB 的一个法向量为n 1＝(1,0,0)．设平面SCD 与平面SAB 所成的二面角为φ，易知0<φ<π2， 则|cos φ|＝⎪⎪⎪⎪⎪⎪n 1·n |n 1|·|n |＝21·6＝63，即cos φ＝63.∴平面SCD 与平面SAB 所成二面角的余弦值为63. (3)设N (x,2x －2,0)，则MN →＝(x,2x －3，－1)．∵平面SAB 的一个法向量为n 1＝(1,0,0)，∴sin θ＝⎪⎪⎪⎪⎪⎪⎪⎪x 5x 2－12x ＋10 ＝110×⎝ ⎛⎭⎪⎫1x 2－12×1x ＋5＝110×⎝ ⎛⎭⎪⎫1x －352＋75，当1x ＝35，即x ＝53时，(sin θ)max ＝357.。

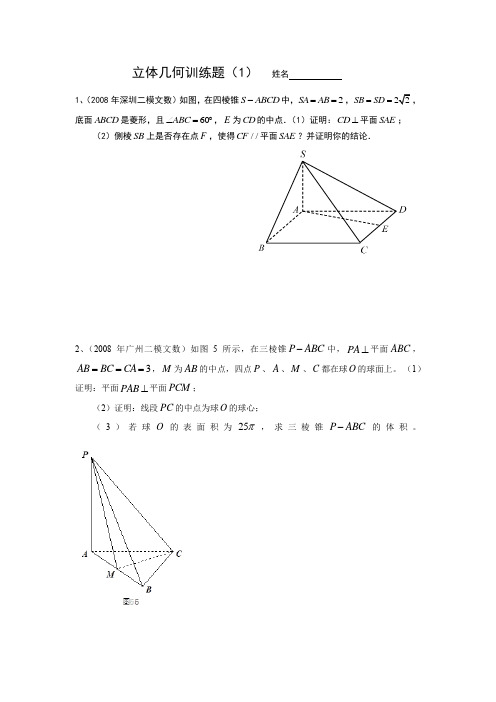
SAB CDE立体几何训练题（1） 姓名1、（2008年深圳二模文数）如图，在四棱锥S ABCD -中，2SAAB ==，SB SD ==底面ABCD 是菱形，且60ABC ∠=︒，E 为CD 的中点．（1）证明：CD ⊥平面SAE ；（2）侧棱SB 上是否存在点F ，使得//CF 平面SAE ？并证明你的结论．2、（2008年广州二模文数）如图5所示，在三棱锥P ABC -中，PA ⊥平面ABC ，3AB BC CA ===，M 为AB 的中点，四点P 、A 、M 、C 都在球O 的球面上。

（1）证明：平面PAB ⊥平面PCM ； （2）证明：线段PC 的中点为球O 的球心；（3）若球O 的表面积为25π，求三棱锥P ABC -的体积。

C3、（2009年广州一模文数）如图4，A A 1是圆柱的母线，AB 是圆柱底面圆的直径，C 是底面圆周上异于,A B 的任意一点，12AA AB ==．（1）求证：BC ⊥平面AC A 1；（2）求三棱锥1A ABC -的体积的最大值．4、（2009年深圳一模文数）如图，AB 为圆O 的直径，点E 、F 在圆O 上，EF AB //，矩形ABCD 所在的平面和圆O 所在的平面互相垂直，且2=AB ，1==EF AD . （Ⅰ）求证：⊥AF 平面CBF ；（Ⅱ）设FC 的中点为M ，求证：//OM 平面DAF ；（Ⅲ）设平面CBF 将几何体EFABCD 分成的两个锥体的体积分别为ABCD F V -，CBE F V -，求ABCD F V -CBE F V -:．5、（2009年深圳二模文数）在直三棱柱111C B A ABC -中，⊥AD 平面1A BC ，其垂足D 落在直线1A B 上．（Ⅰ）求证：B A BC 1⊥；（Ⅱ）若=AD 2==BC AB ，P 为AC 的中点，求三棱锥BC A P 1-的体积．6、（2009年广州二模文数）在长方体1111ABCD A BC D -中，2AB BC ==，过1A 、1C 、B 三点的平面截去长方体的一个角后，得到如图4所示的几何体111ABCD AC D -，且这个几何体的体积为403．（1）证明：直线1A B 平面11CDD C ；（2）求棱1A A 的长；（3）求经过11A C B D 、、、四点的球的表面积．BACDP1B 1A 1C7、（2010年广州二模文数）在长方体1111ABCD A BC D -中，1AB BC ==，12AA =，点M 是BC 的中点．点N 和1AA 的中点． (1) 求证：//MN 平面1ACD ； (2) 过N ，C ，D 三点的平面把长方体1111ABCD A BC D -截成两部分几何体，求所截成的两部分几何体的体积的比值．8、（2010年广州一模文数）如图6，正方形ABCD 所在平面与三角形CDE 所在平面相交于CD ，AE ⊥平面CDE ，且3AE =，6AB =．（1）求证：AB ⊥平面ADE ；（2）求凸多面体ABCDE 的体积．ABCD E图5立体几何训练题（2） 姓名1、（2010年深圳一模文数）如图，在长方体1111ABCD A B C D -中，点E 在棱1CC 的延长线上，且11112CC C E BC AB ====．（Ⅰ）求证：1D E ∥平面1ACB ； （Ⅱ）求证：平面11D B E ⊥平面1DCB ；（Ⅲ）求四面体11D B AC 的体积．2、（2010年深圳二模文数）一个三棱柱111ABC A B C -直观图和三视图如图所示（主视图、俯视图都是矩形，左视图是直角三角形），设E 、F 分别为1AA 和11B C 的中点．（Ⅰ）求几何体11E B C CB -的体积； （Ⅱ）证明：1//A F 平面1EBC ； （Ⅲ）证明：平面EBC ⊥平面11EB C .3、（2011年深圳一模文数）如图，在四棱锥S ABCD -中，AB AD ⊥，//AB CD ，3CD AB =，平面SAD ⊥平面ABCD ，M 是线段AD 上一点，AM AB =，DM DC =，SM AD ⊥．（1）证明：BM ⊥平面SMC ；（2）设三棱锥C SBM -与四棱锥S ABCD -的体积分别为1V 与V ，求1V V的值．4、（2011年深圳二模文数）如图1，在直角梯形ABCD 中，CD AB //，AD AB ⊥，且121===CD AD AB ． 现以AD 为一边向形外作正方形ADEF ，然后沿边AD 将正方形ADEF 翻折，使平面ADEF 与平面ABCD 垂直，M 为ED 的中点，如图2．（1）求证：AM ∥平面BEC ； （2）求证：⊥BC 平面BDE ； （3）求点D 到平面BEC 的距离.MSDCBA FE D CBA 图1ABCDFE 图2M5、（2011年广州一模文数）如图5，在三棱柱ABC —A 1B 1C 1中，侧棱1AA ⊥底面ABC ，AB BC ⊥，D 为AC 的中点，12, 3.A A AB BC ===（1）求证：AB 1//平面BC 1D ；（2）求四棱锥B —AA 1C 1D 的体积。

精品基础教育教学资料，仅供参考，需要可下载使用！中档大题分类练(四) 立体几何（建议用时：60分钟）1．如图57，已知多面体PE ­ABCD 的底面ABCD 是边长为2的菱形，且PA ⊥平面ABCD ，ED ∥PA ，且PA ＝2ED ＝2.图57(1)证明：平面PAC ⊥平面PCE ；(2)若∠ABC ＝60°，求点P 到平面ACE 的距离．[解] (1)证明：连接BD ，交AC 于点O ，设PC 中点为F ， 连接OF ，EF .因为O ，F 分别为AC ，PC 的中点，所以OF ∥PA ，且OF ＝12PA ，因为DE ∥PA ，且DE ＝12PA ，所以OF ∥DE ，且OF ＝DE .所以四边形OFED 为平行四边形，所以OD ∥EF ，即BD ∥EF . 因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以PA ⊥BD . 因为ABCD 是菱形，所以BD ⊥AC .因为PA ∩AC ＝A ，所以BD ⊥平面PAC, 因为BD ∥EF ，所以EF ⊥平面PAC ，因为EF ⊂平面PCE ，所以平面PAC ⊥平面PCE .(2)因为∠ABC ＝60°，所以△ABC 是等边三角形，所以AC ＝2. 又因为PA ⊥平面ABCD ，AC ⊂平面ABCD ， ∴PA ⊥AC ，∴S △PAC ＝12×PA ×AC ＝2，因为EF ⊥面PAC ，所以EF 是三棱锥E ­PAC 的高，EF ＝DO ＝BO ＝3，∴V P ­ACE ＝V E ­PAC ＝13S △PAC ×EF ＝13×2×3＝233，∵DE ∥PA ，PA ⊥平面ABCD ，∴DE ⊥平面ABCD ，∴DE ⊥AD ，DE ⊥CD ， ∵DE ＝1，∴AE ＝CE ＝5，∴S △ACE ＝2×2×12＝2，所以点P 到平面ACE 的距离h ＝V P ­ACE13S △ACE＝23323＝3.2．如图58，在四棱锥P ­ABCD 中，四边形ABCD 是菱形，△PAD ≌△BAD ，平面PAD ⊥平面ABCD ，AB ＝4，PA ＝PD ，M 在棱PD 上运动．图58(1)当M 在何处时，PB ∥平面MAC ；(2)已知O 为AD 的中点，AC 与OB 交于点E ，当PB ∥平面MAC 时，求三棱锥E ­BCM的体积．[解] (1)如图，设AC 与BD 相交于点N ，当M 为PD 的中点时，PB ∥平面MAC ，证明：∵四边形ABCD 是菱形，可得：DN ＝NB ，又∵M 为PD 的中点，可得：DM ＝MP ，∴NM 为△BDP 的中位线，可得NM ∥PB ，又∵NM ⊂平面MAC ，PB ⊄平面MAC ，∴PB ∥平面MAC .(2)∵O 为AD 的中点，PA ＝PD ，则OP ⊥AD ，又△PAD ≌△BAD ， ∴OB ⊥AD ，且OB ＝23，又∵△AEO ∽△CEB ，∴OE BE＝OA BC＝12. ∴BE ＝23OB ＝433.∴S △EBC ＝12×4×433＝833.又∵OP ＝4×32＝23，点M 为PD 的中点，∴M 到平面EBC 的距离为3. ∴V E ­BCM ＝V M ­EBC ＝13×833×3＝83.3．在三棱柱ABC ­A 1B 1C 1中，AB ＝BC ＝CA ＝AA 1＝2，侧棱AA 1⊥平面ABC ，且D ，E 分别是棱A 1B 1，AA 1的中点，点F 在棱AB 上，且AF ＝14AB .图59(1)求证：EF ∥平面BDC 1； (2)求三棱锥D ­BEC 1的体积． [解] (1)取AB 的中点O ，连接A 1O ，∵AF ＝14AB ，∴F 为AO 的中点，又E 为AA 1的中点，∴EF ∥A 1O ，∵A 1D ＝12A 1B 1，BO ＝12AB ，AB 綊A 1B 1，∴A 1D 綊BO ，∴四边形A 1DBO 为平行四边形，∴A 1O ∥BD ， ∴EF ∥BD ，又EF ⊄平面BDC 1，BD ⊂平面BDC 1， ∴EF ∥平面BDC 1.(2)∵AA 1⊥平面A 1B 1C 1，C 1D ⊂平面A 1B 1C 1， ∴AA 1⊥C 1D ，∵A 1C 1＝B 1C 1＝A 1B 1＝2，D 为A 1B 1的中点， ∴C 1D ⊥A 1B 1，C 1D ＝3，又AA 1⊂平面AA 1B 1B ，A 1B 1⊂平面AA 1B 1B ，AA 1∩A 1B 1＝A 1， ∴C 1D ⊥平面AA 1B 1B ，∵AB ＝AA 1＝2，D ，E 分别为A 1B 1，AA 1的中点， ∴S △BDE ＝22－12×1×2－12×1×2－12×1×1＝32.∴VD ­BEC 1＝VC 1­BDE ＝13S △BDE ·C 1D ＝13×32×3＝32. 4．如图60所示，在四棱锥P ­ABCD 中，△BCD ，△PAD 都是等边三角形，平面PAD ⊥平面ABCD ，且AD ＝2AB ＝4，CD ＝23.图60(1)求证：平面PCD ⊥平面PAD ；(2)E 是AP 上一点，当BE ∥平面PCD 时，求三棱锥C ­PDE 的体积． [解] (1)因为AD ＝4，AB ＝2，BD ＝23，所以AD 2＝AB 2＋BD 2，所以AB ⊥BD ，∠ADB ＝30°，又因为△BCD 是等边三角形，所以∠ADC ＝90°，所以DC ⊥AD ，因为平面PAD ⊥平面ABCD ， 平面PAD ∩平面ABCD ＝AD ，所以CD ⊥平面PAD ，因为CD ⊂平面PCD ，所以平面PCD ⊥平面PAD . (2)过点B 作BG ∥CD 交AD 于G ，过点G 作EG ∥PD 交于AP 于点E ， 因为BG ∥CD ，BG ⊄平面PCD ，CD ⊂平面PCD ，所以BG ∥平面PCD ， 同理可得EG ∥平面PCD ，所以平面BEG ∥平面PCD ， 因为BE ⊂平面BEG ，所以BE ∥平面PCD . 因为EG ∥PD ，所以PE PA ＝DGDA，在直角三角形BGD 中，BD ＝23，∠BDG ＝30°，所以DG＝23cos 30°＝3，所以PEPA＝DGDA＝34，在平面PAD内过E作EH⊥PD于H，因为CD⊥平面PAD，EH⊂平面PAD，所以CD⊥EH，因为PD∩CD＝D，所以EH⊥平面PCD，所以EH是点E到平面PCD的距离，过点A作AM⊥PD于M，则AM＝32×4＝23，由AM∥EH，得EHAM＝PEPA＝34，所以EH＝323.因为S△PCD＝12×4×23＝43，所以V C­PDE＝13×43×323＝6.(教师备选)1．如图，已知三棱柱ABC­A1B1C1的侧棱长和底面边长均为2，A1在底面ABC内的射影O为底面△ABC的中心，如图所示．(1)求异面直线AA1与BC1所成角的大小；(2)求三棱锥C1­BCA1的体积．[解] (1)连接AO ，并延长与BC 交于点D ， 则D 是BC 边上的中点．因为点O 是正△ABC 的中心，且A 1O ⊥平面ABC ， 所以BC ⊥AD ，BC ⊥A 1O . 因为AD ∩A 1O ＝O ， 所以BC ⊥平面ADA 1. 所以BC ⊥AA 1.又AA 1∥CC 1，所以BC ⊥CC 1，所以异面直线AA 1与BC 1所成的角为∠BC 1C . 因为BC ＝CC 1＝2，所以异面直线AA 1与BC 1所成角的大小为π4.(2)因为三棱柱的所有棱长都为2， 所以可求得AD ＝3，AO ＝23AD ＝233 ，A 1O ＝AA 21－AO 2＝263.因为S △ABC ＝12×2×3＝3，所以VABC ­A 1B 1C 1＝S △ABC ·A 1O ＝22，VA 1­BCC 1B 1＝VABC ­A 1B 1C 1－VA 1­ABC ＝423.所以VC 1­BCA 1＝VA 1­BCC 1＝12VA 1­BCC 1B 1＝223.2．如图①，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝90°，AB ＝BC ＝12AD ＝a ，E 是AD 的中点，O 是AC 与BE 的交点．将△ABE 沿BE 折起到图②中△A 1BE 的位置，得到四棱锥A 1­BCDE .图① 图②(1)证明：CD ⊥平面A 1OC ；(2)当平面A 1BE ⊥平面BCDE 时，四棱锥A 1­BCDE 的体积为362，求a 的值．[解] (1)证明：在图题①中，连接EC (图略)， 因为AB ＝BC ＝12AD ＝a ，∠BAD ＝90°，AD ∥BC ，E 是AD 的中点，所以四边形ABCE 为正方形，所以BE ⊥AC ，即在图题②中，BE ⊥A 1O ，BE ⊥OC . 又A 1O ∩OC ＝O ，从而BE ⊥平面A 1OC ， 又CD ∥BE ，所以CD ⊥平面A 1OC . (2)由已知，平面A 1BE ⊥平面BCDE ， 且平面A 1BE ∩平面BCDE ＝BE ，又由(1)可知A 1O ⊥BE ，所以A 1O ⊥平面BCDE ， 即A 1O 是四棱锥A 1­BCDE 的高， 由图1知，A 1O ＝22AB ＝22a ，平行四边形BCDE 的面积S ＝BC ·AB ＝a 2， 从而四棱锥A 1­BCDE 的体积V ＝13×S ×A 1O ＝13×a 2×22a ＝26a 3，由26a 3＝362，解得a ＝6.。

立体几何中档题汇编一．解答题（共24小题）1．如图，设长方体ABCD﹣A1B1C1D1中，AB=BC=3，AA1=4．（1）求四棱锥A1﹣ABCD的体积；（2）求异面直线A1B与B1C所成角的大小．（结果用反三角函数值表示）2．如图，△ABC是以∠ABC为直角的三角形，SA⊥平面ABC，SA=BC=2，AB=4，M，N分别是SC，AB的中点．（1）求证：MN⊥AB；（2）D为线段BC上的点，当二面角S﹣ND﹣A的余弦值为时，求三棱锥D ﹣SNC的体积．3．在长方体ABCD﹣A1B1C1D1中，AB=AA1=4，BC=3，E，F分别是所在棱AB，BC 的中点，点P是棱A1B1上的动点，联结EF，AC1．如图所示．（1）求异面直线EF，AC1所成角的大小（用反三角函数值表示）；（2）求以E，F，A，P为顶点的三棱锥的体积．4．如图，长方体ABCD﹣A1B1C1D1中，AB=BC=2，A1C与底面ABCD所成的角为60°，（1）求四棱锥A1﹣ABCD的体积；（2）求异面直线A1B与B1D1所成角的大小．5．如图所示的圆锥的体积为，底面直径AB=2，点C是弧的中点，点D 是母线PA的中点．（1）求该圆锥的侧面积；（2）求异面直线PB与CD所成角的大小．6．如图，四棱锥P﹣ABCD底面为等腰梯形，AD∥BC且BC=2AD=4，点E为PC 中点．（1）证明：DE∥平面PAB；（2）若PA⊥平面ABCD，∠ABC=60°，直线PB与平面ABCD所成角的正切值为，求四棱锥P﹣ABCD的体积V．7．如图，四棱锥P﹣ABC中，PA⊥平面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．（I）证明直线MN∥平面PAB；（II）求四面体N﹣BCM的体积．8．在四棱锥P﹣ABCD中，AD∥BC，平面PAC⊥平面ABCD，AB=AD=DC=1，∠ABC=∠DCB=60°，E是PC上一点．（Ⅰ）证明：平面EAB⊥平面PAC；（Ⅱ）若△PAC是正三角形，且E是PC中点，求三棱锥A﹣EBC的体积．9．如图，四边形ABCD是矩形AB=3，PE⊥平面ABCD，PE=．（1）证明：平面PAC⊥平面PBE；（2）设AC与BE相交于点F，点G在棱PB上，且CG⊥PB，求三棱锥F﹣BCG的体积．10．如图四棱锥P﹣ABCD，底面梯形ABCD中，AB∥DC，平面PAD⊥平面ABCD，已知BD=2AD=4，AB=2DC=2BC=2．（1）求证：BD⊥PA；（2）线段PC上是否存在点M，使三棱锥P﹣ABD体积为三棱锥P﹣MBD体积的6倍．若存在，找出点M的位置；若不存在，说明理由．11．长方形ABCD中，AB=2AD，M是DC中点（图1）．将△ADM沿AM折起，使得AD⊥BM（图2）．在图2中：（1）求证：平面ADM⊥平面ABCM；（2）若BE=2DE，AM=2，求三棱锥E﹣ABC的体积．12．如图，在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD是边长为2的正方形，E，F分别为线段DD1，BD的中点．（1）求证：EF∥平面ABC1D1；（2）四棱柱ABCD﹣A1B1C1D1的外接球的表面积为16π，求异面直线EF与BC所成的角的大小．13．如图，在直角梯形ABCD中，AD∥BC，AD=AB，∠A=90°，BD⊥DC，将△ABD 沿BD折起到△EBD的位置，使平面EBD⊥平面BDC．（1）求证：平面EBD⊥平面EDC；（2）求ED与BC所成的角．14．如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，PA=PB，且侧面PAB⊥平面ABCD，点E是AB的中点．（1）求证：PE⊥AD；（2）若CA=CB，求证：平面PEC⊥平面PAB．15．如图1，已知知矩形ABCD中，点E是边BC上的点，AE与BD相交于点H，且，现将△ABD沿BD折起，如图2，点A的位置记为A'，此时．（1）求证：BD⊥面A'HE；（2）求三棱锥D﹣A'EH的体积．16．如图，在四面体PABC中，已知PA⊥平面ABC，PA=AC，∠ACB=90°，D为PC 的中点．（1）求证：AD⊥BD；（2）若M为PB的中点，点N在直线AB上，且AN：NB=1：2，求证：直线AD∥平面CMN．17．如图，在三棱锥V﹣ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC=BC=，O，M分别为AB，VA的中点．（Ⅰ）求证：VB∥平面M OC；（Ⅱ）求证：平面MOC⊥平面VAB；（Ⅲ）求三棱锥A﹣MOC的体积．18．如图，在四棱柱ABCD﹣A1B1C1D1中，AA1⊥平面ABCD，AB∥CD，AB⊥AD，AD=CD=1，AA1=AB=2，E为AA1的中点．（Ⅰ）求四棱锥C﹣AEB1B的体积；（Ⅱ）求证：BC⊥C1E；（Ⅲ）判断线段B1C上是否存在一点M（与点C不重合），使得C，D，E，M四点共面？（结论不要求证明）19．如图，在正方体ABCD﹣A1B1C1D1中，E、F分别是BB1、CD的中点，（1）证明：AD⊥D1F；（2）求异面直线AE与D1F所成的角；（3）证明：平面AED⊥平面A1FD1．20．如图，四棱锥P﹣ABCD中，底面ABCD为矩形，侧面PAD为正三角形，且平面PAD⊥平面ABCD，E为PD中点，AD=2．（Ⅰ）求证：平面AEC⊥平面PCD．（Ⅱ）若二面角A﹣PC﹣E的平面角大小θ满足cosθ=，求四棱锥P﹣ABCD的体积．21．如图，直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．（1）求三棱柱ABC﹣A1B1C1的体积；（2）设M是BC中点，求直线A1M与平面ABC所成角的大小．22．如图，四棱锥P﹣ABCD中，底面ABCD边长为4的正方形，PA=PD=2，平面PAD⊥平面ABCD．（Ⅰ）求证：平面PAD⊥平面PCD；（Ⅱ）点E为线段PD上一点，且三棱锥E﹣BCD的体积为，求平面EBC与平面PAB所成锐二面角的余弦值的大小．23．如图，四棱锥P﹣ABCD的底面ABCD是平行四边形，∠DAB=60°，AB=2AD=2，PD⊥平面ABCD（1）求证：AD⊥PB；（2）若BD与平面PBC的所成角为30°，求三棱锥P﹣BCD的体积．24．如图，在四棱锥E﹣ABCD中，平面ABE⊥底面ABCD，侧面AEB为等腰直角三角形，∠AEB=，底面ABCD为直角梯形，AB∥CD，AB⊥BC，AB=2CD=2BC （1）求直线EC与平面ABE所成角的正弦值；（2）线段EA上是否存在点F，使EC∥平面FBD？若存在，求出；若不存在，说明理由．立体几何中档题汇编参考答案与试题解析一．解答题（共24小题）1．如图，设长方体ABCD﹣A1B1C1D1中，AB=BC=3，AA1=4．（1）求四棱锥A1﹣ABCD的体积；（2）求异面直线A1B与B1C所成角的大小．（结果用反三角函数值表示）【分析】（1）A1到平面ABCD的距离d=AA1=4，S正方体ABCD=AB×BC=9，由此能求出四棱锥A1﹣ABCD的体积．（2）由A1B∥D1C，知∠D1CB1是异面直线A1B与B1C所成角（或所成角的补角），由此能求出异面直线A1B与B1C所成角．【解答】解：（1）∵A1到平面ABCD的距离d=AA1=4，长方体ABCD﹣A1B1C1D1中，AB=BC=3，∴S=AB×BC=3×3=9，正方体ABCD∴四棱锥A1﹣ABCD的体积V==．（2）∵A1B∥D1C，∴∠D1CB1是异面直线A1B与B1C所成角（或所成角的补角），∵B1D1==3，B1C=D1C==5，∴cos∠D1CB1===，∴∠D1CB1=arccos．∴异面直线A1B与B1C所成角为．【点评】本题考查四棱锥的体积的求法，考查异面直线所成角的求法，考查空间中线线、线面、面面的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．2．如图，△ABC是以∠ABC为直角的三角形，SA⊥平面ABC，SA=BC=2，AB=4，M，N分别是SC，AB的中点．（1）求证：MN⊥AB；（2）D为线段BC上的点，当二面角S﹣ND﹣A的余弦值为时，求三棱锥D ﹣SNC的体积．【分析】（1）以B为坐标原点，BC，BA为x，y轴的正方向垂直于平面ABC的直线为z轴，建立空间直角坐标系，利用向量法能证明MN⊥AB．（2）求出平面SND的一个法向量和平面AND的法向量，利用向量法能求出D 为BC中点，从而能求出三棱锥D﹣SNC的体积．【解答】证明：（1）以B为坐标原点，BC，BA为x，y轴的正方向，垂直于平面ABC的直线为z轴，建立空间直角坐标系，如图，由题意得A（0，4，0），B（0，0，0），M（1，2，1），N（0，2，0），S（0，4，2），D（1，0，0），∴=（﹣1，0，﹣1），=（0，﹣4，0），∵=0，∴MN⊥AB．解：（2）设平面SND的一个法向量为=（x，y，z），设D（m，0，0），（0≤m≤2），=（0，﹣2，﹣2），=（﹣m，2，0），∴，令y=m，得=（2，m，﹣m），又平面AND的法向量为=（0，0，1），cos＜＞==，解得m=1，即D为BC中点．∴三棱锥D﹣SNC的体积：V D﹣SNC=V S﹣DNC===．【点评】本题考查线线垂直的证明，考查三棱锥的体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．3．在长方体ABCD﹣A1B1C1D1中，AB=AA1=4，BC=3，E，F分别是所在棱AB，BC 的中点，点P是棱A1B1上的动点，联结EF，AC1．如图所示．（1）求异面直线EF，AC1所成角的大小（用反三角函数值表示）；（2）求以E，F，A，P为顶点的三棱锥的体积．【分析】（1）联结AC，则AC∥EF，∠CAC1就是异面直线EF，AC1所成的角，由此能求出异面直线EF，AC1所成角．（2）由题意可知，点P到底面ABCD的距离与棱AA1的长相等．由此能出以E，F，A，P为顶点的三棱锥的体积．【解答】（本题满分12分）本题共有2个小题，第1小题满分（6分），第2小题满分（6分）．解：（1）联结AC，在长方体ABCD﹣A1B1C1D1中，有AC∥EF．又∠CAC1是直角三角形ACC1的一个锐角，∴∠CAC1就是异面直线EF，AC1所成的角．由AB=AA1=4，BC=3，得AC==5．∴tan∠CAC1==，即异面直线EF，AC1所成角为arctan．（2）由题意可知，点P到底面ABCD的距离与棱AA1的长相等．∵，∴=．【点评】本题考查异面直线所成角的求法，考查三棱锥体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想、函数与方程思想，是中档题．4．如图，长方体ABCD﹣A1B1C1D1中，AB=BC=2，A1C与底面ABCD所成的角为60°，（1）求四棱锥A1﹣ABCD的体积；（2）求异面直线A1B与B1D1所成角的大小．【分析】（1）推导出AA1⊥平面ABCD，从而∠A1CA是A1C与底面ABCD所成的角，进而∠A1CA=60°，AA1=AC•tan60°=2，由此能求出四棱锥A1﹣ABCD的体积．（2）由BD∥B1D1，得∠A1BD是异面直线A1B与B1D1所成角（或所成角的补角），由此能求出异面直线A1B与B1D1所成角．【解答】解：（1）∵长方体ABCD﹣A1B1C1D1中，AB=BC=2，∴AA1⊥平面ABCD，AC==2，∴∠A1CA是A1C与底面ABCD所成的角，∵A1C与底面ABCD所成的角为60°，∴∠A1CA=60°，∴AA1=AC•tan60°=2•=2，=AB×BC=2×2=4，∵S正方形ABCD∴四棱锥A1﹣ABCD的体积：V===．（2）∵BD∥B1D1，∴∠A1BD是异面直线A1B与B1D1所成角（或所成角的补角）．∵BD=，A1D=A1B==2，∴cos∠A1BD===．∴∠A1BD=arccos．∴异面直线A1B与B1D1所成角是arccos．【点评】本题考查四棱锥的体积的求法，考查异面直线所成角的求法，考查空间中线线、线面、面面的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．5．如图所示的圆锥的体积为，底面直径AB=2，点C是弧的中点，点D 是母线PA的中点．（1）求该圆锥的侧面积；（2）求异面直线PB与CD所成角的大小．【分析】（1）由圆锥的体积为，底面直径AB=2，求出PO=，从而PA=2，由此能求出该圆锥的侧面积．（2）以O为原点，OC为x轴，OB为y轴，OP为z轴，建立空间直角坐标系，利用向量法能求出异面直线PB与CD所成角．【解答】解：（1）∵圆锥的体积为，底面直径AB=2，∴，解得PO=，∴PA==2，∴该圆锥的侧面积S=πrl=π×1×2=2π．（2）∵圆锥的体积为，底面直径AB=2，点C是弧的中点，点D是母线PA的中点．∴PO⊥平面ABC，OC⊥AB，∴以O为原点，OC为x轴，OB为y轴，OP为z轴，建立空间直角坐标系，则A（0，﹣1，0），P（0，0，），D（0，﹣，），B（0，1，0），C（1，0，0），=（0，1，﹣），=（﹣1，﹣，），设异面直线PB与CD所成角为θ，则cosθ===，∴θ=．∴异面直线PB与CD所成角为．【点评】本题考查圆锥的侧面积的求法，考查异面直线所成角的求法，考查空间中线线、线面、面面的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．6．如图，四棱锥P﹣ABCD底面为等腰梯形，AD∥BC且BC=2AD=4，点E为PC 中点．（1）证明：DE∥平面PAB；（2）若PA⊥平面ABCD，∠ABC=60°，直线PB与平面ABCD所成角的正切值为，求四棱锥P﹣ABCD的体积V．【分析】（1）取BC中点F，连接DF、EF．证明EF∥PB，推出EF∥平面PAB．证明DF∥平面PAB．然后证明平面DEF∥平面PAB．即可证明DE∥平面PAB．（2）作AG⊥BC于点G，则BG=1．直线PB与平面ABCD所成角为∠PBA，求解PA=3．然后求解四棱锥P﹣ABCD的体积．【解答】证明：（1）取BC中点F，连接DF、EF．由于EF为△PBC中位线，所以EF∥PB，又EF⊄平面PAB，PB⊂平面PAB，所以EF∥平面PAB．由于AD∥BC且BC=2AD，则AD BF，所以四边形ABFD为平行四边形，所以DF∥AB，因为DF⊄平面PAB，AB⊂面PAB，所以DF∥平面PAB．因为EF∥平面PAB，DF∥平面PAB，EF∩DF=F，EF，DF⊂平面DEF，所以平面DEF∥平面PAB．又DE⊂平面DEF，所以DE∥平面PAB．解：（2）作AG⊥BC于点G，则BG=1．在△ABG中，∠ABG=60°，BG=1，则，AB=2．由PA⊥平面ABCD知，直线PB与平面ABCD所成角为∠PBA，故，即在△PAB中，有，则PA=3．所以，四棱锥P﹣ABCD的体积=．【点评】本题考查直线与平面平行的判定定理以及性质定理的应用，几何体的体积的求法，考查空间想象能力以及计算能力．7．如图，四棱锥P﹣ABC中，PA⊥平面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．（I）证明直线MN∥平面PAB；（II）求四面体N﹣BCM的体积．【分析】（Ⅰ）取BP的中点T，连结AT，TN，推导出四边形AMNT是平行四边形，从而MN∥AT，由此能证明MNⅡ平面PAB．（Ⅱ）N到平面ABCD的距离为=2，取BC的中点E，连结AE，由AB=AC=3，得AE⊥BC，由AM∥BC，得M到BC的距离为，由此能求出四面体N﹣BCM 的体积．【解答】证明：（Ⅰ）∵四棱锥P﹣ABC中，PA⊥平面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．∴AM=，取BP的中点T，连结AT，TN，∴由N为PC的中点知TN∥BC，TN=BC=2，又AD∥BC，∴TN AM，∴四边形AMNT是平行四边形，∴MN∥AT，又AT⊂平面PAB，MN⊄平面PAB，∴MNⅡ平面PAB．解：（Ⅱ）∵PA⊥平面ABCD，N为PC的中点，∴N到平面ABCD的距离为=2，取BC的中点E，连结AE，由AB=AC=3，得AE⊥BC，AE==，==2，由AM∥BC，得M到BC的距离为，∴S△BCM∴四面体N﹣BCM的体积：==．【点评】本题考查线面平衡地的证明，考查四面体的体积的求法，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．8．在四棱锥P﹣ABCD中，AD∥BC，平面PAC⊥平面ABCD，AB=AD=DC=1，∠ABC=∠DCB=60°，E是PC上一点．（Ⅰ）证明：平面EAB⊥平面PAC；（Ⅱ）若△PAC是正三角形，且E是PC中点，求三棱锥A﹣EBC的体积．【分析】（Ⅰ）推导出AB⊥AC，从而AB⊥平面PAC，由此能证明平面EAB⊥平面PAC．=V B﹣EAC，由（Ⅱ）法一：推导出AB⊥平面PAC，三棱锥A﹣EBC的体积为V A﹣EBC此能求出结果．法二：过P作PO⊥AC于点O，推导出PO⊥平面ABC，过E作EF⊥AC于点F，=V E﹣ABC，由此能求出结果．推导出EF⊥平面ABC，三棱锥A﹣EBC的体积为V A﹣EBC【解答】证明：（Ⅰ）依题意得四边形ABCD是底角为60°的等腰梯形，…（1分）∴∠BAD=∠ADC=120°..…（2分）∵AD=DC，∴∠DAC=∠DCA=30°．…（3分）∴∠BAC=∠BAD﹣∠DAC=120°﹣30°=90°，即AB⊥AC．…（4分）∵平面PAC⊥平面ABCD，平面PAC∩平面ABCD=AC，∴AB⊥平面PAC，…（5分）又平面AB⊂平面EAB，∴平面EAB⊥平面PAC．…（6分）解：（Ⅱ）解法一：由（Ⅰ）及已知得，在Rt△ABC中，∠ABC=60°，AB=1，∴AC=AB∙tan60°=，BC=2AB=2，且AB⊥平面PAC，…（7分）∴AB是三棱锥B﹣EAC的高，正△PAC的边长为…（8分）∵E是PC的中点，∴S=S△PAC=．…△EAC（10分）∴三棱锥A﹣EBC的体积为…（12分）（Ⅱ）解法二：过P作PO⊥AC于点O，∵平面PAC⊥平面ABCD，平面PAC∩平面ABCD=AC，∴PO⊥平面ABC，过E作EF⊥AC于点F，同理得EF⊥平面ABC，∴EF是三棱锥E﹣ABC的高，且PO∥EF，…（7分）又E是PC中点，∴EF是△POC的中位线，故．由（Ⅰ）及已知得，在Rt△ABC中，∠ABC=60°，AB=1，∴BC=2AB=2，AC=AB∙tan60°=，即正△PAC的边长为，…（8分）∴PO=，故EF=…（9分）=．…（10分）在Rt△ABC中，S△ABC∴三棱锥A﹣EBC的体积为…（12分）【点评】本题考查面面垂直的证明，考查三棱锥的体积的求法，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．9．如图，四边形ABCD是矩形AB=3，PE⊥平面ABCD，PE=．（1）证明：平面PAC⊥平面PBE；（2）设AC与BE相交于点F，点G在棱PB上，且CG⊥PB，求三棱锥F﹣BCG 的体积．【分析】（1）由四边形ABCD是矩形，，推导出△ABC～△BCE，∠BCE=∠ACB，从而AC⊥BE，由PE⊥平面ABCD，得AC⊥PE，由此能证明AC⊥平面PBE．=V G﹣BCF，能求（2）推导出CG⊥PB，G到平面ABC的距离等于，由V F﹣BCE出三棱锥F﹣BCG的体积．【解答】证明：（1）因为四边形ABCD是矩形，，所以，又，所以△ABC～△BCE，∠BCE=∠ACB，因为，所以AC⊥BE，又PE⊥平面ABCD，所以AC⊥PE，又面PE∩BE=E，所以AC⊥平面PBE．（2）因为，所以，又BC=3，CG⊥PB，所以G为棱PB的中点，G到平面ABC的距离等于，由（1）知△ABF～△CEF，所以，所以，所以．【点评】本题考查线面垂直的证明，考查三棱锥体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想、函数与方程思想，是中档题．10．如图四棱锥P﹣ABCD，底面梯形ABCD中，AB∥DC，平面PAD⊥平面ABCD，已知BD=2AD=4，AB=2DC=2BC=2．（1）求证：BD⊥PA；（2）线段PC上是否存在点M，使三棱锥P﹣ABD体积为三棱锥P﹣MBD体积的6倍．若存在，找出点M的位置；若不存在，说明理由．【分析】（1）证明BD⊥AD，BD⊥面PAD，然后证明BD⊥PA．（2）假设存在点M满足条件，设CM=mCP（m∈[0，1]），点P到面ABCD的距离为h1，点M到面ABCD的距离为h2，由相似三角形可知，利用几何体的体积的比转化求解即可．【解答】（1）证明：，∴AB2=AD2+BD2，∴BD⊥AD，又∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，∴BD⊥面PAD，又AP⊂面PAD，∴BD⊥PA．（2）解：假设存在点M满足条件，设CM=mCP（m∈[0，1]），点P到面ABCD 的距离为h1，点M到面ABCD的距离为h2，由相似三角形可知，，∴，∴点M是PC上的一个靠近点P的三等分点．【点评】本题考查几何体的体积的求法，考查空间想象能力以及计算能力．11．长方形ABCD中，AB=2AD，M是DC中点（图1）．将△ADM沿AM折起，使得AD⊥BM（图2）．在图2中：（1）求证：平面ADM⊥平面ABCM；（2）若BE=2DE，AM=2，求三棱锥E﹣ABC的体积．【分析】（1）连结BM，通过AM2+BM2=AB2，说明AM⊥BM．结合AD⊥BM，证明BM⊥平面ADM．然后证明平面ADM⊥平面ABCM．（2）设F是AM中点，连结DF，DF⊥AM，DF=1．平面ADM⊥平面ABCM，交线是AM，说明DF⊥平面ABCM．推出E到平面ABCM距离等于．求出底面面积，即可求解几何体的体积．【解答】解：（1）长方形ABCD中，连结BM，因为AB=2AD，M是DC中点，所以，从而AM2+BM2=AB2，所以AM⊥BM．因为AD⊥BM，AD∩AM=A，所以BM⊥平面ADM．因为BM⊂平面ABCM，所以平面ADM⊥平面ABCM．…（6分）（2）设F是AM中点，连结DF，则DF⊥AM，DF=1．因为平面ADM⊥平面ABCM，交线是AM，所以DF⊥平面ABCM．因为BE=2DE，所以E到平面ABCM距离等于．因为AM=2，所以，，△ABC面积为2．所以三棱锥E﹣ABC的体积为．…（12分）【点评】本题考查平面与平面垂直的判定定理的应用，几何体的体积的求法，考查空间想象能力以及计算能力．12．如图，在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD是边长为2的正方形，E，F分别为线段DD1，BD的中点．（1）求证：EF∥平面ABC1D1；（2）四棱柱ABCD﹣A1B1C1D1的外接球的表面积为16π，求异面直线EF与BC所成的角的大小．【分析】（1）连接BD1，由中位线定理证明EF∥D1B，由线面平行的判定定理证明EF∥平面ABC1D1；（2）由（1）和异面直线所成角的定义，得异面直线EF与BC所成的角是∠D1BC，由题意和球的表面积公式求出外接球的半径，由勾股定理求出侧棱AA1的长，由直四棱柱的结构特征和线面垂直的定义，判断出BC⊥CD1，在RT△CC1D1中求出tan∠D1BC，求出∠D1BC可得答案．【解答】解：（1）连接BD1，在△DD1B中，E、F分别为线段DD1、BD的中点，∴EF为中位线，∴EF∥D1B，∵D1B⊂面ABC1D1，EF⊄面ABC1D1，∴EF∥平面ABC1D1；（2）由（1）知EF∥D1B，故∠D1BC即为异面直线EF与BC所成的角，∵四棱柱ABCD﹣A1B1C1D1的外接球的表面积为16π，∴四棱柱ABCD﹣A1B1C1D1的外接球的半径R=2，设AA1=a，则，解得a=，在直四棱柱ABCD﹣A1B1C1D1中，∵BC⊥平面CDD1C1，CD1⊄平面CD﹣D1C1，∴BC⊥CD1，在RT△CC1D1中，BC=2，CD1=，D1C⊥BC，∴tan∠D1BC=，则∠D1BC=60°，∴异面直线EF与BC所成的角为60°．【点评】本题考查了异面直线所成角的定义以及求法，线面平行的判定定理，球的表面积公式，以及直四棱柱的结构特征，属于中档题．13．如图，在直角梯形ABCD中，AD∥BC，AD=AB，∠A=90°，BD⊥DC，将△ABD 沿BD折起到△EBD的位置，使平面EBD⊥平面BDC．（1）求证：平面EBD⊥平面EDC；（2）求ED与BC所成的角．【分析】（1）通过证明CD⊥平面EBD，利用平面与平面垂直的潘多拉证明平面EBD⊥平面EDC．（2）说明∠EDA即为ED与BC所成的角．通过解三角形即可求出∠EDA，得到ED与BC所成的角．【解答】（1）证明：∵平面EBD⊥平面BDC，且平面EBD∩平面BDC=BD，CD⊥BD，∴CD⊥平面EBD，∵CD⊂平面EDC，∴平面EBD⊥平面EDC．（2）解：如答图，连接EA，取BD的中点M，连接AM，EM，∵AD∥BC，∴∠EDA即为ED与BC所成的角．又∵AD=AB，∴ED=EB．∴EM⊥BD，∴EM⊥平面ABCD．设AB=a，则ED=AD=a，EM=MA=a，∴AE=a，∴∠EDA=60°．即ED与BC所成的角为60°．【点评】本题考查平面与平面垂直的判定定理的应用，异面直线所成角的求法，考查计算能力．14．如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，PA=PB，且侧面PAB⊥平面ABCD，点E是AB的中点．（1）求证：PE⊥AD；（2）若CA=CB，求证：平面PEC⊥平面PAB．【分析】（1）证明PE⊥AB，推出PE⊥平面ABCD，然后证明PE⊥AD．（2）证明CE⊥AB．PE⊥AB，然后证明AB⊥平面PEC，即可证明平面PAB⊥平面PEC．【解答】（12分）证明：（1）因为PA=PB，点E是棱AB的中点，所以PE⊥AB，因为平面PAB⊥平面ABCD，PE⊂平面PAB，所以PE⊥平面ABCD，因为AD⊂平面ABCD，所以PE⊥AD．…（6分）（2）因为CA=CB，点E是AB的中点，所以CE⊥AB．由（1）可得PE⊥AB，又因为CE∩PE=E，所以AB⊥平面PEC，又因为AB⊂平面PAB，所以平面PAB⊥平面PEC．…（12分）【点评】本题考查直线与平面垂直，平面与平面垂直的判定定理的应用，考查空间想象能力以及计算能力．15．如图1，已知知矩形ABCD中，点E是边BC上的点，AE与BD相交于点H，且，现将△ABD沿BD折起，如图2，点A的位置记为A'，此时．（1）求证：BD⊥面A'HE；（2）求三棱锥D﹣A'EH的体积．【分析】（1）推导出AE⊥BD，BD⊥A'H，BD⊥EH，由此能证明BD⊥面A'HE．（2）推导出AH=A′H=4，EH=1，DH=8，A′H⊥EH，由此能求出三棱锥D﹣A'EH的体积．【解答】证明：（1）∵ABCD为矩形，，∴AE⊥BD，∴图2中，BD⊥A'H，BD⊥EH，∵A'H∩HE=H，∴BD⊥面A'HE．（2）∵矩形ABCD中，点E是边BC上的点，AE与BD相交于点H，且，∴AE==5，BD==10，△BEH∽△DAH，∴==，∴AH=A′H=4，EH=1，DH=8，∵，∴A′H⊥EH，∴==2，∴三棱锥D﹣A'EH的体积：===．【点评】本题考查线面垂直的证明，考查三棱锥的体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、空间想象能力、运算求解能力，考查化归与转化思想、数形结合思想、函数与方程思想，是中档题．16．如图，在四面体PABC中，已知PA⊥平面ABC，PA=AC，∠ACB=90°，D为PC 的中点．（1）求证：AD⊥BD；（2）若M为PB的中点，点N在直线AB上，且AN：NB=1：2，求证：直线AD∥平面CMN．【分析】（1）推导出AD⊥PC，PA⊥BC，BC⊥AC，从而BC⊥平面PAC，进而BC ⊥AD，再由AD⊥PC，由此能证明AD⊥平面PBC，从而AD⊥BD．（2）连接DM，设BD与CM交于点G，连接NG，则DM∥BC且，从而DG：GB=DM：BC=1：2．进而AN：NB=DG：GB，AD∥NG，由此能证明直线AD ∥平面CMN．【解答】证明：（1）∵PA=AC，D为PC的中点，∴AD⊥PC．…（1分）∵PA⊥平面ABC，BC⊂平面ABC，∴PA⊥BC．∵∠ACB=90°，BC⊥AC，且PA∩AC=A，PA，AC⊂平面PAC∴BC⊥平面PAC．…（3分）∵AD⊂平面PAC，∴BC⊥AD．…（4分）且AD⊥PC，AD∩PC=D，PC，BC⊂平面PBC，∴AD⊥平面PBC．…（6分）∵BD⊂平面PBC，∴AD⊥BD．…（7分）（2）连接DM，设BD与CM交于点G，连接NG，∵D、M为中点，∴DM∥BC且，…（9分）∴DG：GB=DM：BC=1：2．∵AN：NB=1：2，∴AN：NB=DG：GB．…（11分）∴△BNG∽△BAD，∴AD∥NG，∵AD⊄平面CMN，NG⊂平面CMN，∴直线AD∥平面CMN．…（14分）【点评】本题考查线线垂直、线面平行的证明，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．17．如图，在三棱锥V﹣ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC=BC=，O，M分别为AB，VA的中点．（Ⅰ）求证：VB∥平面M OC；（Ⅱ）求证：平面MOC⊥平面VAB；（Ⅲ）求三棱锥A﹣MOC的体积．【分析】（Ⅰ）利用三角形的中位线得出OM∥VB，利用线面平行的判定定理证明VB∥平面MOC；（Ⅱ）证明OC⊥平面VAB，即可证明平面MOC⊥平面VAB；（Ⅲ）利用等体积法求三棱锥A﹣MOC的体积即可．【解答】（Ⅰ）证明：∵O，M分别为AB，VA的中点，∴OM∥VB，∵VB⊄平面MOC，OM⊂平面MOC，∴VB∥平面MOC；（Ⅱ）证明：∵AC=BC，O为AB的中点，∴OC⊥AB，又∵平面VAB⊥平面ABC，平面ABC∩平面VAB=AB，且OC⊂平面ABC，∴OC⊥平面VAB，∵OC⊂平面MOC，∴平面MOC⊥平面VAB；（Ⅲ）解：在等腰直角三角形ACB中，AC=BC=，∴AB=2，OC=1，∴等边三角形VAB的边长为2，S=，△VAB∵O，M分别为AB，VA的中点．∴．又∵OC⊥平面VAB，∴三棱锥．【点评】本题考查线面平行的判定，考查平面与平面垂直的判定，考查体积的计算，正确运用线面平行、平面与平面垂直的判定定理是关键，是中档题．18．如图，在四棱柱ABCD﹣A1B1C1D1中，AA1⊥平面ABCD，AB∥CD，AB⊥AD，AD=CD=1，AA1=AB=2，E为AA1的中点．（Ⅰ）求四棱锥C﹣AEB1B的体积；（Ⅱ）求证：BC⊥C1E；（Ⅲ）判断线段B1C上是否存在一点M（与点C不重合），使得C，D，E，M四点共面？（结论不要求证明）【分析】（Ⅰ）由已知可得AA1⊥AD．结合AB⊥AD，利用线面垂直的判定可得AD⊥平面ABB1A1．得到AD为四棱锥C﹣AEB1B的高，然后直接利用棱锥体积公式求解；（Ⅱ）在底面ABCD中，求解三角形可得BC⊥AC．再由已知得CC1⊥BC，利用线面垂直的判定可得BC⊥平面CAEC1，从而得到BC⊥C1E；（Ⅲ）由CD为平面CEB1的一条斜线可知，线段B1C上不存在点M（与点C不重合），使得C，D，E，M四点共面．【解答】（Ⅰ）解：∵AA1⊥平面ABCD，AD⊂平面ABCD，∴AA1⊥AD．又∵AB⊥AD，AA1∩AB=A，∴AD⊥平面ABB1A1．∵AB∥CD，∴四棱锥C﹣AEB1B的体积=；（Ⅱ）证明：在底面ABCD中，∵AB∥CD，AB⊥AD，AD=CD=1，AB=2，∴，，∴AB2=AC2+BC2，即BC⊥AC．在四棱柱ABCD﹣A1B1C1D1中，∵AA1⊥平面ABCD，∴CC1⊥BC，又∵CC1∩AC=C，∴BC⊥平面CAEC1，又∵C1E⊂平面CAEC1，∴BC⊥C1E；（Ⅲ）解：对于线段B1C上任意一点M（与点C不重合），C，D，E，M四点都不共面．【点评】本题考查线面垂直的判定与性质，考查空间想象能力与思维能力，训练了多面体体积的求法，是中档题．19．如图，在正方体ABCD﹣A1B1C1D1中，E、F分别是BB1、CD的中点，（1）证明：AD⊥D1F；（2）求异面直线AE与D1F所成的角；（3）证明：平面AED⊥平面A1FD1．【分析】（1）证明线线垂直可先证线面垂直，欲证AD⊥D1F，可先证AD⊥面DC1，即可证得；（2）先通过平移将两条异面直线平移到同一个起点，取AB的中点G，将D1F平移到A1G，AB与A1G构成的锐角或直角就是异面直线所成的角，利用三角形全等求出此角即可．（3）取AB的中点G，连接FG，A1G，运用三角函数的知识，证得AE⊥A1G，再由线面垂直的判定和面面垂直的判定定理，即可得证；【解答】解：（1）∵AC1是正方体，∴AD⊥面DC1．又D1F⊂面DC1，∴AD⊥D1F．（2）取AB中点G，连接A1G，FG．因为F是CD的中点，所以GF、AD平行且相等，又A1D1、AD平行且相等，所以GF、A1D1平行且相等，故GFD1A1是平行四边形，A1G∥D1F．设A1G与AE相交于点H，则∠AHA1是AE与D1F所成的角，因为E是BB1的中点，所以Rt△A1AG≌Rt△ABE，∠GA1A=∠GAH，从而∠AHA1=90°，即直线AE与D1F 所成角为直角．（3）由（2）得D1F∥A1G，在正方形ABB1A1中，tan∠A1GA==2，tan∠EAB=，即有∠A1GA+∠EAB=90°，即有AE⊥A1G，即有AE⊥D1F，又AD⊥D1F，则D1F⊥平面AED，D1F⊂平面A1D1F，则面AED⊥面A1FD1；【点评】题考查空间直线与平面垂直的判定和性质，以及面面垂直的判定定理和运用，考查空间的直线和平面所成的角的求法：运用法向量求解，考查运算能力，属于中档题．20．如图，四棱锥P﹣ABCD中，底面ABCD为矩形，侧面PAD为正三角形，且平面PAD⊥平面ABCD，E为PD中点，AD=2．（Ⅰ）求证：平面AEC⊥平面PCD．（Ⅱ）若二面角A﹣PC﹣E的平面角大小θ满足cosθ=，求四棱锥P﹣ABCD的体积．【分析】（Ⅰ）取AD中点为O，BC中点为F，由已知得PO⊥平面ABCD，则FO ⊥PO，再由FO⊥AD，得FO⊥平面PAD，得到FO⊥AE，可得CD⊥AE，由E是PD中点，可得AE⊥PD，利用线面垂直的判定定理知AE⊥平面PCD，进一步得到平面AEC⊥平面PCD；（Ⅱ）如图所示，建立空间直角坐标系O﹣xyz，令AB=a，求出P，A，C的坐标，由（Ⅰ）知=（）为平面PCE的法向量，进一步求出平面PAC的一个法向量，由二面角A﹣PC﹣E的平面角大小θ满足cosθ=求出a值，再由棱锥体积公式求四棱锥P﹣ABCD的体积．【解答】（Ⅰ）证明：取AD中点为O，BC中点为F，由侧面PAD为正三角形，且平面PAD⊥平面ABCD，得PO⊥平面ABCD，故FO⊥PO，又FO⊥AD，则FO⊥平面PAD，∴FO⊥AE，又CD∥FO，则CD⊥AE，又E是PD中点，则AE⊥PD，由线面垂直的判定定理知AE⊥平面PCD，又AE⊂平面AEC，故平面AEC⊥平面PCD；（Ⅱ）解：如图所示，建立空间直角坐标系O﹣xyz，令AB=a，则P（0，0，），A（1，0，0），C（﹣1，a，0）．由（Ⅰ）知=（）为平面PCE的法向量，令=（1，y，z）为平面PAC的法向量，由于=（1，0，﹣），=（2，﹣a，0）均与垂直，∴，解得，则，由cos θ=||=，解得a=．故四棱锥P﹣ABCD的体积V=S ABCD•PO=•2••=2．【点评】本题考查平面与平面垂直的判定，考查空间想象能力与思维能力，训练了利用空间向量求解二面角的平面角，是中档题．21．如图，直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．（1）求三棱柱ABC﹣A1B1C1的体积；（2）设M是BC中点，求直线A1M与平面ABC所成角的大小．【分析】（1）三棱柱ABC﹣A1B1C1的体积V=S△ABC×AA1=，由此能求出结果．（2）连结AM，∠A1MA是直线A1M与平面ABC所成角，由此能求出直线A1M 与平面ABC所成角的大小．【解答】解：（1）∵直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．∴三棱柱ABC﹣A1B1C1的体积：V=S△ABC×AA1===20．（2）连结AM，∵直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5，M是BC中点，∴AA1⊥底面ABC，AM==，∴∠A1MA是直线A1M与平面ABC所成角，tan∠A1MA===，∴直线A1M与平面ABC所成角的大小为arctan．【点评】本题考查三棱柱的体积的求法，考查线面角的大小的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、函数与方程思想、数形结合思想，是中档题．22．如图，四棱锥P﹣ABCD中，底面ABCD边长为4的正方形，PA=PD=2，平面PAD⊥平面ABCD．（Ⅰ）求证：平面PAD⊥平面PCD；（Ⅱ）点E为线段PD上一点，且三棱锥E﹣BCD的体积为，求平面EBC与平面PAB所成锐二面角的余弦值的大小．【分析】（I）利用面面垂直的性质得出CD⊥平面PAD，故而平面PAD⊥平面PCD；（II）利用体积公式计算E到平面ABCD的距离得出E点位置，建立坐标系求出。

专题：立体几何(适合北京高三数学理，中档题)一、选择题1 ．一四面体的三视图如图所示,则该四面体四个面中最大的面积是（ ）A ．2B ．22C ．3D ．322 ．已知一个几何体的三视图如图所示(单位:cm), 那么这个几何体的侧．面积是 （ ）A．2B．2C．2(4 D．2（第2题图） （第3题图）3 ．某四面体三视图如图所示,则该四面体的四个面中,直角三角形的面积和是（ ）A ．2B ．4C．2D．4+4 ．如图所示,为一几何体的三视图,则该几何体的体积是（ ）A ．1B ．21 C ．13 D ．65（第4题图） （第6题图）5 ．已知平面βα,,直线n m ,,下列命题中不．正确的是 （ ）（第1题图）左视图A ．若α⊥m ,β⊥m ,则α∥βB ．若m ∥n ,α⊥m ,则α⊥nC ．若m ∥α,n =βα ,则m ∥nD ．若α⊥m ,β⊂m ,则βα⊥.6 ．某正三棱柱的三视图如图所示,其中正(主)视图是边长为2的正方形,该正三棱柱的表面积是 （ ）A ．6B ．12C ．12+D ．24+7 ．如图,正方体1111ABCD A B C D -中,E 是棱11B C 的中点,动点P 在底面ABCD 内,且11PA A E =,则点P 运动形成的图形是（ ）A ．线段B ．圆弧C ．椭圆的一部分D ．抛物线的一部分（第7题图）8 ．某三棱椎的三视图如图所示,该三棱锥的四个面的面积中,最大的是 （ ）A ．B ．8C ．D ．9 ．若一个直六棱柱的三视图如图所示,则这个直六棱柱的体积为（ ）A ．4B ．29C ．5D ．21110．设,m n 是不同的直线，,αβ是不同的平面，下列命题中正确的是（ ）A ．若//,,m n m n αβ⊥⊥，则αβ⊥B ．若//,,m n m n αβ⊥⊥，则//αβC ．若//,,//m n m n αβ⊥，则α⊥βD ．若//,,//m n m n αβ⊥，则//αβ11．某三棱锥的三视图如图所示，该三棱锥的体积是（ ）A ．38B ．4 C ．2 D ．3412．已知一个空间几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的体积为（ ）A ．4B ．8C ．12D ．2413．已知三棱锥的底面是边长为1的正三角形，其正视图与俯视图如图所示，则其侧视图的面积为（ ）AB．C ．34D ．114．在棱长为1的正方体1111ABCD A BC D 中，1P，2P 分别为线段AB ，1BD （不包括端俯视图点）上的动点，且线段12P P 平行于平面11A ADD ，则四面体121PP AB 的体积的最大值是 （ ）A ．124B ．112 C ．16D ．1215．如图，某三棱锥的三视图都是直角边为2的等腰直角三角形，则该三棱锥的体积是（ ）A ．43B ．83C ．4D ．816．如图，在棱长为1的正方体1111ABCD A B C D -中，点, E F 分别是棱1,BC CC 的中点，P 是侧面11BCC B 内一点，若1//A P 平面,AEF 则线段1A P 长度的取值范围是 （ ）A． B． C． D．B 1C 1D 1A 1FE BCD A17．一个几何体的三视图如图所示，该几何体的体积是 （ ）（第18题图）A．16+B．12+C ．8D ．418．某四棱锥的三视图如图所示，该四棱锥的体积是（ ） （ ）A．B．CD19．若正三棱柱的三视图如图所示，该三棱柱的表面积是（ ）ABC．6+ D．6+二、填空题20．某几何体的三视图如图所示,则它的体积为______.（第20题） （第21题） （第22题）21．一个几何体的三视图如图所示，则该几何体的体积为 ．22．三棱锥D ABC -及其三视图中的主视图和左视图如图所示，则棱BD 的长为______. 三、解答题23．如图,四棱锥ABCD P -的底面ABCD 为菱形, 60=∠ABC ,PA ⊥底面ABCD ,2==AB PA ,E 为PA 的中点.(Ⅰ)求证://PC 平面EBD ;(Ⅱ)求三棱锥PAD C -的体积PAD C V -;(Ⅲ)在侧棱PC 上是否存在一点M ,满足⊥PC 平面MBD ,若存在,求PM 的长;若不存在,说明理由.D A BC左视图侧视图D专题：立体几何参考答案一、选择题 1. D 2. C 3. C 4. D 5. C 6. C; 7. B. 8. C 9. A 10. 【答案】C解：C 中，当//,//m m n α，所以，//,n α或,n α⊂当n β⊥，所以α⊥β，所以正确。