积分中值定理应用PPT课件
- 格式:ppt
- 大小:700.00 KB
- 文档页数:11




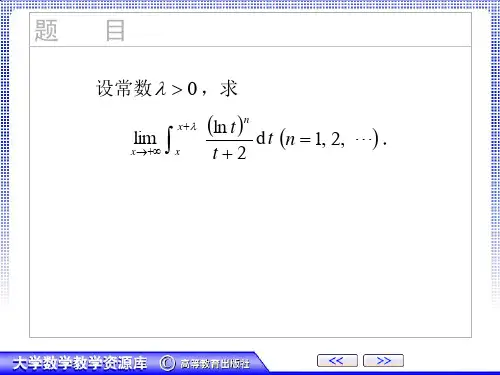





积分中值定理的应用
积分中值定理,也称为贝尔定理,是指在连续函数 f(x) 在闭区间 [a,b] 上的值取得最大值或最小值时,存在 c∈[a,b],使得f'(c)=0。
积分中值定理的应用非常广泛,在数学、物理、工程等领域都有重要的作用。
一些典型的应用如下:
在数学中,积分中值定理可以用来证明连续函数的单调性和单峰性。
在物理学中,积分中值定理可以用来求解力学问题,例如求解弹性力学问题中的应变能定理。
在工程学中,积分中值定理可以用来设计最优化结构,例如在桥梁工程中求解桥墩的最优截面。
在经济学中,积分中值定理也有应用,例如在求解最优生产率问题时,可以使用积分中值定理来求解。