第五课：计算机中数的表示

《计算机中数的表示》教学设计教材分析本课内容选自四川人民出版社岀版的《信息技术》七年级上册第5课机中数的表示》，重点介绍了计算机中数的表示方式，本节内容对学生的数学认知能力要求较高。

二进制是计算机工作的基本形式，也是汁算机理论知识中的最基本的原理，对于信息技术的学习及了解计算机的工作原理具有不可忽视的奠基作用。

但二进制转十进制算是初一教材中较难部分，所以用比划手势的方式，让学生在破解魔术中不知不觉学会如何转换为十进制。

二进制如何在计算机中的表示这一节内容，也相对抽象不易理解,所以通过用灯光闪烁传递信息、为数字填涂颜色的活动帮助学生理解。

二、教学对象分析本课教学对象为初一的学生。

初一的学生活泼好动，但其逻辑思维能力和抽象思维能力相对较弱，对于二进制的概念，二进制如何转换十进制，以及二进制的工作原理不一左能够直观地理解，所以，在教学设计中，以情景为主线，环环相扣，让学生在情景中不断体悟二进制的妙用。

三、教学目标（-）知识与技能：能够说出二进制的概念：能够进行二进制数与十进制数之间的转化：能够说岀计算机中表示字符的原理。

（二）过程与方法：通过手势比划，掌握二进制与十进制转换的方法：通过模拟灯光闪烁传递信息的活动体会计算机对字符的表示方法：通过填涂颜色体会计算机表示图案的方法。

（三）情感态度价值观：通过不同学习活动环节，养成相互之间合作和沟通的能力，了解二进制与十进制转换的方法，二进制的原理在计算机中和生活中的应用，养成创新思考的能力。

四、$点难点分析教学重点：二进制的概念，二进制与十进制的转换教学难点：二进制与十进制的转换，二进制在计算机中如何表示五、教学手段讲授法、游戏法，情景导入法六、教学过程教学环节（一）导入师：你能用一只手表示的最大数为多少？目前我们能表示的最大数是9.当我们学习完本课一一计算机中数的表示、二进制后，我们可以用一只手表示更多的数。

师：现在请同学们伸出左手，在小手指上写1、无名指写2 ......... 伸出手，在手上分别写数字1,2,4,8,16i l l 让学生动起来，能够在短时间内吸引学生的注意力,使学生对本节课产生兴趣, 而且每个手指的点数隐含着二进制位数的权，为本节课的内容做好铺垫。

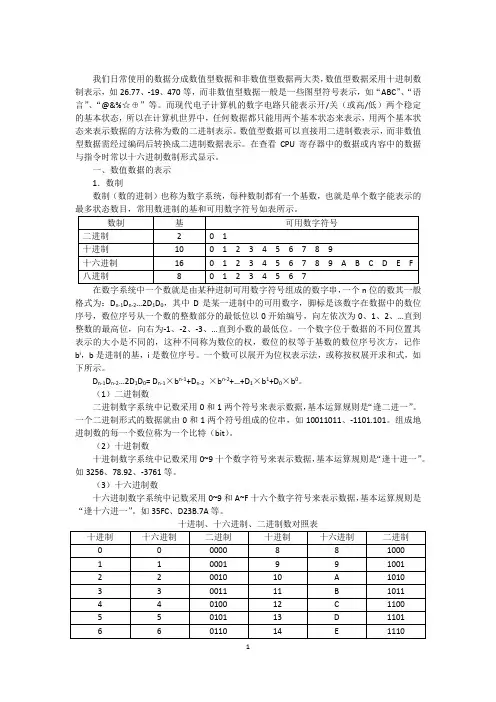
我们日常使用的数据分成数值型数据和非数值型数据两大类，数值型数据采用十进制数制表示，如26.77、-19、470等，而非数值型数据一般是一些图型符号表示，如“ABC”、“语言”、“@&%☆⊕”等。

而现代电子计算机的数字电路只能表示开/关（或高/低）两个稳定的基本状态，所以在计算机世界中，任何数据都只能用两个基本状态来表示，用两个基本状态来表示数据的方法称为数的二进制表示。

数值型数据可以直接用二进制数表示，而非数值型数据需经过编码后转换成二进制数据表示。

在查看CPU寄存器中的数据或内容中的数据与指令时常以十六进制数制形式显示。

一、数值数据的表示1．数制数制（数的进制）也称为数字系统，每种数制都有一个基数，也就是单个数字能表示的在数字系统中一个数就是由某种进制可用数字符号组成的数字串，一个n位的数其一般格式为：D n-1D n-2…2D1D0，其中D是某一进制中的可用数字，脚标是该数字在数据中的数位序号，数位序号从一个数的整数部分的最低位以0开始编号，向左依次为0、1、2、…直到整数的最高位，向右为-1、-2、-3、…直到小数的最低位。

一个数字位于数据的不同位置其表示的大小是不同的，这种不同称为数位的权，数位的权等于基数的数位序号次方，记作b i，b是进制的基，i是数位序号。

一个数可以展开为位权表示法，或称按权展开求和式，如下所示。

D n-1D n-2…2D1D0= D n-1×b n-1+D n-2×b n-2+…+D1×b1+D0×b0。

（1）二进制数二进制数字系统中记数采用0和1两个符号来表示数据，基本运算规则是“逢二进一”。

一个二进制形式的数据就由0和1两个符号组成的位串，如10011011、-1101.101。

组成地进制数的每一个数位称为一个比特（bit）。

（2）十进制数十进制数字系统中记数采用0~9十个数字符号来表示数据，基本运算规则是“逢十进一”。

第五课计算机中数的表示1、从结构上分析，此教学设计方案十分完整，具备教学内容分析、学生情况分析、教学目标设置、教学策略设定、教学重难点、教学环境及资源准备、教学过程设计等，教学过程的各个环节又有清晰的教师活动、学生学习活动设计和设计意图，教学教程与教学课件各页对应，便于使用者快速把握本教案的特色和设计者的意图，有利于再设计。

2、从备课的基本环节看，本教案对本课的基本内容分析简洁明快，并根据七年级学生的基本特征确定了以理论联系实际、不断激发学生兴趣，由浅入深的小任务实验探究策略。

三维目标表述精确，知识技能定位适度，过程与方法有利于培训学生的自主能力和激发学生创造力，并在情感上让学生领悟实践与知识建构之间的关系。

3、多数学生并未接触二进制的概念，因此如何引导学生理解二进制计数的基本方法尤为重要，本课引入部分的那张“视觉差”图片，对吸引学生注意力、激发兴趣有一定帮助，但与二进制概念本身联系不大，使用者若有更好的引入方案可另行选择。

4、引入二进制概念时，老师向学生提出：根据二进制的计数法则，1+1=？当学生回答“2”时，教师可告诉学生，二进制里没有数字“2”，只有“0”和“1”两个数字，又该怎么表示与十进制数“2”同样大的数呢？5、学习新知部分首先通过几种进制的对比使学生重点理解二进制的运算法则，然后联系电脑硬件（存储器）的特征说明了为什么要使用二进制，通过电路演示让学生理解二进制在电脑中的工作方式，通过电筒实验总结出二进制与十进制的对应关系。

这样可化抽象为具体，便于学生理解掌握。

6、进制转换是本节的难点，教师采用与十进制类比的方法进行教学，让学生找出两种进制展开式的共同点和不同点，理解各数位所表示的意义，生形象地了解二进制转换为十进制的过程，通过练习增强转换能力。

当然，也可先让学生理解二进制的1,10,100,1000,10000中的1在不同数位上所代表的值（1，2，4，8，16），即（20，21，22，23，24），再讲展开式的用法可能会更有利于理解为什么要这样转换。

第二章计算机中数据的表示方法第一节计算机中数据的分类和表示方法计算机内部传送的信息分为两大类：控制信息和数据信息。

数据信息又分为两种，数值型数据和非数值型数据。

注意：任何数据在计算机中都是用二进制表示的。

一、数据的单位1．位（bit）：是计算机中最小的数据单位，常用小写字母b来表示。

2．字节（Byte）：用大字母B来表示，1B=8b表示文件的长度，衡量存储器的容量，存储器编址用字节做单位。

磁盘的存储单位是：簇磁盘存放信息的最小编址单位是：扇区信息编码的的最小单位是：码元3．字（word）：由若干字节组成，是字节的整数倍。

在计算机内部进行数据传送，或CPU进行数据处理时，用它作基本单位。

字的长度即字长，并不是所有的计算机字长都一样，常见的字长有16位，32位，64位。

字长是CPU一次能够处理二进制的位数。

字长越长，计算机速度越快，精度越高。

4．常用的存储单位之间的换算1TB=1024GB 1GB=1024MB 1MB=1024KB 1KB=1024B 210 1B=8b二、数据的分类1．按数据处理方式分类数值型和非数值型非数值型又分为：字符数据和逻辑数据2．按数据传输形式分类数字数据和模拟数据数字数据：离散型的；模拟数据：连续的值模拟数据被数字化后存入计算机，采用模数转化将模拟数据数字化后存入计算机。

三、数据的表示方法1．数值型数据的表示（1）按小数点的处理可分为定点数和浮点数。

（2）按符号位有原码、补码，反码三种形式的机器数2．非数值型数据的表示第二节各种数制及其转换方法一、数制的组成数制是指计数的方法，任何一种数制都有两个要素：基数和权。

例如二进制数1001.01，它的基数是2，最左边1的权是23，最右边的1的权是2-2。

234二、常用字的数制二进制（B），八进制（Q），十进制（D），十六进制（H）三、不同进制之间的转换1．十进制转换成非十进制分成整数部分和小数部分：整数部分：除基数倒取余小数部分：乘基数取整注意：十进制数转换在二进制数的方法是除2倒取余。

数字在计算机中的表⽰ 现实⽣活中，我们通常使⽤10进制来表⽰我们的数字，⽽在计算机中使⽤的是“0”和“1”表⽰数字的⼆进制。

如果我们⽤⼀个字节来存储⼀个数字，那么这个数字在计算机中的存储形式可能是这样的：00010011。

最左边的0位在带符号数字中⽤来表⽰正负号，0代表正号，1代表负号，所以它也就叫做符号位；其他位数⽤来表⽰具体数字，因此叫做数值位。

00010011如果⽤来表⽰带符号整数，那么它代表的数字是+19。

+19叫做真值，00010011⽤于在计算机中表⽰，所以叫做机器数。

机器数在计算机中的表⽰形式有三种，原码，反码和补码。

原码的表⽰： 左边是符号位，正数为0，负数为1。

其他位表⽰数值 【+10】原码 = 00001010 【-10】原码 = 10001010 【+0】原码 = 00000000 【-0】原码 = 10000000 反码的表⽰： 正数的反码和原码相同，负数的反码由原码除了符号位的其余位取反（即0表1,1表0） 【+10】反码 = 00001010 【-10】反码 = 11110101 【+0】反码 = 00000000 【-0】反码 = 11111111 补码的表⽰： 正数的补码与原码相同，负数的补码由原码的反码加1得到 【+10】补码 = 00001010 【-10】补码 = 【-10】反码 + 1 = 11110101 + 1 = 11110110　 【+0】补码 = 00000000 【-0】补码 = 【-0】反码 + 1 = 11111111 + 1 = 【1】00000000（mod（256）） 补码的意义：补码实际上是⼀种模运算，以时钟为例，时钟⼀圈是12个⼩时，即时钟的模为12。

如果当前时刻是3点钟，在12个⼩时之后时刻变为15点，15在模12之后，依然是3点。

再如，将3点的时针调慢⼀个⼩时，即调成2点，和将时针向前调整11个⼩时的效果是⼀样的。

因此⽤3-1和（3+11）mod（12）的结果⼀样。

第五节计算机中的数制在数学上和日常生活中，通常使用十进制数，计算时，逢十进一。

但在现实生活中也绝非一切全用十进制，比如，1年等于12个月，这是十二进制；1小时等于60分钟，1分钟等于60秒，这都是六十进制。

可见，用什么进制完全取决于人们的需要。

在计算机内部，根据电路的特点，只有低电平和高电平，即一切信息都是用“0”和“1”这两种状态表示的，所以在计算机内部都使用二进制计数。

一、计算机中的二进制数在计算机中使用的是二进制数，其特点是只有“0”和“l”两个基本符号。

计算机中使用二进制，主要有以下3个原因。

1．可行性二进制码在物理上最容易实现。

因为可以用电平的高或低两个状态表示“1”和“0”，也可以用脉冲的有或无两个状态表示“1”和“0”。

2．简易性二进制码用来表示的二进制数其编码、计数、加减运算规则简单。

二进制码的两个符号“1”和“0”正好与逻辑命题的两个值“真”和“假”相对应，为计算机实现逻辑运算和程序中的逻辑判断提供了便利的条件。

3．可靠性使用二进制数，用电信号表示只需两个状态，数码越少，电信号就越少、越简单、越清楚，数字的传输和处理越不容易出错，计算机工作的可靠性就越高。

二、常用的进位计数制1．十进制计数十进制数制有0，1，2，…，9十个基本数字符号，计数特点是“逢十进一”。

2．二进制计数二进制数制有0和1两个基本数字符号，其特点是“逢二进一”。

表1.1为各进位制数对应关系：表1.1 各进位制数对应关系三、字符编码计算机只能识别二进制数据，对于数值型的数据，可以很方便地用上述方法将其转换成二进制数据。

除此之外，还要把大量的非数值型数据，如英文字母、各种符号等转换成二进制。

目前使用最多、最普遍的是ASCII码（American Standard Code for Information Interchange，美国标准信息交换代码）。

ASCII码的每个字符用7位二进制数表示，因此，ASCII码是由27＝128个字符组成的字符集。