第4章 管柱的摩阻扭矩计算
- 格式:doc
- 大小:79.50 KB
- 文档页数:4

顶管施工中管壁摩阻力理论公式应用摘要:顶管施工中管道四周受土体摩擦产生摩擦阻力,阻止管道前进。
阻力的大小受多种因素的影响是比较复杂的,其中的因素是施工误差引起的管道轴线弯曲。
管道轴线弯曲严重时可使摩阻力成倍增长。
正是由于这一原因,引出了许多计算摩阻力的经验公式。
但本文仅限于讨论理论公式,而且仅限于管轴线严格为直线状态下的摩阻力理论公式,即在排除由于管轴线弯曲所引起的附加摩阻力的前题下讨论管道摩阻力的理论公式,这时管道摩阻力的理论公式可以简化为平面问题,可以以管道的横断面为模型例出计算图式。
关键词:理论公式摩阻力一、规范公式存在的问题管道摩阻力的理论公式在许多文章和手册中都曾经出现过,后来集中反映在GB 50268-97《给水排水管道工程施工及验收规范》中。
规范的6.4.8条规定,顶管的顶力可按下式计算:式中P-计算的总顶力(kN);γ-管道所处土层的重力密度(kN/m3);D1-管道的外径(m);H-管道顶部以上覆盖土层的厚度(m);φ-管道所处土层的内摩擦角(°);ω-管道单位长度的自重(kN/m),(笔者:应改为由自重产生的力);L-管道的计算顶进长度(m);f-顶进时,管道表面与其周围土层之间的摩擦系数;PF-顶进时,工具管的迎面阻力(kN)。
仅就管道摩擦力而言,上述公式可以简化。
设p为单位长度管道的摩阻力,则:这一公式引用了摩擦力的基本理论:摩擦阻力等于正压力乘摩擦系数。
摩擦系数f采用已有的成果,所以问题的讨论重点转移到正压力的计算上来,式中的tg2(45°-φ/2)是主动土压力系数,用K1来表示:K1=tg2(45°-φ/2),代入上式得:稍作变化,将上式改写如下:此式的物理意义是:管道摩助力等于管顶土压力强度与水平管轴线处主动土压力强度之和的2倍,乘以管道直径,再乘以摩擦系数,另外再加上管道自重所产生的摩阻力。
上式中第1项是管顶土压力和管底地基应力引起的摩阻力,第2项是管道两侧主动土压力引起的摩阻力,计算时采用了每个方向上的单位土压力乘以管道外径D1作为正压力,这种计算方法即违背了摩擦力的基本理论,因为除管顶、管底和水平管轴线两侧共4处土压力以外,所有的土压力与管道表面不垂直,并非是正压力。


压裂施工中摩阻计算压裂施工是油气田开发中常用的一种技术,通过将一定压力下的流体注入岩石裂缝中,从而扩大岩石裂缝的面积,提高油气井的产能。
在压裂施工中,摩阻的计算是十分重要的,下面将详细介绍压裂施工中摩阻的计算方法。
首先,我们需要了解摩阻的概念。
摩阻是指流体在管道中流动时受到的阻力,也叫做流体的动力阻力。
在压裂施工中,摩阻的计算主要用于确定压裂施工所需的泵功率和压裂液体分配等。
摩阻的计算可以分为两个部分:管道摩阻和喷嘴摩阻。
下面分别介绍这两个部分的计算方法。
1.管道摩阻的计算管道摩阻是指液体在管道中流动时受到的阻力。
管道摩阻主要考虑泵入口处的压力损失和油管全长的摩阻损失。
管道摩阻的计算可以按照一定的公式进行。
常用的管道摩阻公式有达西公式和弗洛伊德公式。
其中,达西公式适用于属于均匀流动的情况,而弗洛伊德公式适用于属于非均匀流动的情况。
达西公式:ΔP1=f*(L1/D1)*(ρ*V^2)/2其中,ΔP1为管道摩阻损失压力,f为摩阻系数,L1为管道长度,D1为管道直径,ρ为液体密度,V为液体流速。
弗洛伊德公式:ΔP2=f*[(L2/D2)+1.51*(ρ*V^2/(2*g))]*(ρ*V^2)/2其中,ΔP2为管道摩阻损失压力,f为摩阻系数,L2为管道长度,D2为管道直径,ρ为液体密度,V为液体流速,g为重力加速度。
2.喷嘴摩阻的计算喷嘴摩阻是指岩石缝隙中液体流动时受到的阻力。
喷嘴摩阻主要与液体流速、缝隙形状和缝隙宽度等因素有关。
喷嘴摩阻的计算可以通过试验和经验公式进行。
常用的喷嘴摩阻计算方法有威海斯公式和霍桑公式。
其中,威海斯公式适用于缝隙宽度较小,液体流速较大的情况,而霍桑公式适用于缝隙宽度较大,液体流速较小的情况。
威海斯公式:ΔP3=K*(ρ*V^2)/2其中,ΔP3为喷嘴摩阻损失压力,K为摩阻系数,ρ为液体密度,V为液体流速。
霍桑公式:ΔP4=(ρ*V^2)/(2*g*c^2)*[1+1.54*(1-c)^2*L/(D*c^3)]其中,ΔP4为喷嘴摩阻损失压力,ρ为液体密度,V为液体流速,g为重力加速度,c为缝隙宽度比例(缝隙宽度与管道直径的比值),L为岩石缝隙长度,D为岩石缝隙直径。

大斜度井作业管柱摩阻力学的模型摩阻分析对水平井施工具有重要的影响,尤其对于大斜度井而言,因其具有长水平段、大井斜角等特点,摩阻的预测和控制是成功地完成大斜度井修井的关键和难点所在。
准确计算套管柱的轴向载荷,以便进行套管柱强度设计与校核。
事实上,在整个钻进、完井及修井过程中,管柱的摩阻研究都很重要,它对井眼设计,包括钻井设备选择、轨道形式与参数、钻柱设计、管柱下入,施工过程中轨道控制和井下作业等阶段都具有指导意义。
在水平井及大斜度井中,由于管柱自重及井眼弯曲等多种因素的作用,导致了较大的摩阻力。
管柱的摩阻计算虽是整个磨铣打捞管柱力学分析的一小部分,但提高其摩阻计算精度仍是完成井下作业修井工作的一个重点,这主要是因为:①精确计算出摩阻,可以预侧套管柱下入的难度,以便选择合理套管柱组合和正确的下入方法,或考虑是否需采用特殊工具;②能够准确计算套管柱的轴向载荷,以便进行套管柱强度设计与校核。
1.大斜度井三维摩阻扭矩模型国内外学者对摩阻扭矩进行了大量的研究工作,分别建立了软绳模型和刚杆模型。
两种模型各有自己的优点和适用范围,软绳模型忽略了钻柱刚度及稳定器的影响,在曲率不大的光滑井眼条件下,用来计算由刚度较小的常规钻杆组成的钻柱段的摩阻扭矩能够给出足够的精度。
因此,现在有的商业软件仍在采用,但应用在井眼曲率变化较大或钻柱刚性较大的单元,会产生明显的误差;刚杆模型在曲率较大的井眼或由刚度较大的加重钻杆组成的钻柱段条件下,其计算结果具有更高的精度,但用于曲率较小刚度较小的平滑井眼中,计算结果收敛困难,对测点数据敏感,解的稳定性较差。
1.1大斜度井三维摩阻扭矩分析刚杆模型建立如图1所示的坐标系。
N轴、E轴、H轴分别指向地理北向、地理东向、重力方向,它们相互垂直,组成固定坐标系。
、、分别是井眼轴线的切线方向、主法线方向、副法线方向的单位矢量,它们相互垂直,组成自然坐标系。
图1 三维摩阻分析的坐标系图在钻柱上取一单元段ds,通过力学分析,可得下面方程组:力学模型力学模型大斜度井摩阻其中: 大斜度井大斜度井作业管柱摩阻力学模型摩阻式中:T为轴向拉力;为弯矩;为扭矩;EI为抗弯刚度;q为钻柱单位长度有效重量;力学模型分别为管柱在井眼内的轴向和周向摩阻系数;为管柱外径;N为钻柱单位长度所受的横向支承力;分别为钻柱变形线的曲率和挠率。

第四章 桩基础的设计计算横向荷载作用下桩身内力与位移的计算方法国内外已有不少,我国普遍采用的是将桩作为弹性地基上的梁,按文克尔假定(梁身任一点的土抗力和该点的位移成正比)进行求解,简称弹性地基梁法。
根据求解的方法不同,通常有半解析法(幂级救解、积分方程解、微分算子解等)、有限差分法和有限元解等。
以文克尔假定为基础的弹性地基梁解法从土力学的观点认为不够严密。
但其基本概念明确,方法较简单,所得结果一般较安全,故国内外使用较为普遍。
我国铁路、水利、公路及房屋建筑等领域在桩的设计中常用的“m ”法以及“K ”法、“常数”法(或称张有龄法)、“C ”法等均属于此种方法。
第一节 单排桩基桩内力和位移计算一、基本概念(一)土的弹性抗力及其分布规律1.土的弹性抗力桩基础在荷载(包括轴向荷载、横轴向荷载和力矩)作用下产生位移(包括竖向位移、水平位移和转角),桩的竖向位移引起桩侧土的摩阻力和桩底土的抵抗力。
桩身的水平位移及转角使桩挤压桩侧土体,桩侧土必然对桩产生一横向土抗力σzx (见图4-1及图4-2),它起抵抗外力和稳定桩基础的作用,土的这种作用力称为土的弹性抗力。
σzx 即指深度为Z 处的横向(X 轴向)土抗力,其大小取决于土体性质、桩身刚度、桩的入土深度、桩的截面形状、桩距及荷载等因素。
假定土的横向土抗力符合文克尔假定,即z zx Cx =σ (4-1) 式中:σzx ——横向土抗力(kN/m 2);C ——地基系数(kN/m 3);x z ——深度Z 处桩的横向位移(m )。
2.地基系数地基系数C 表示单位面积土在弹性限度内产生单位变形时所需要的力。
它的大小与地基土的类别、物理力学性质有关。
如能测得x z 并知道C 值,σzx 值即可解得。
地基系数C 值是通过对试桩在不同类别土质及不同深度进行实测x z 及σzx 后反算得到。
大量试验表明,地基系数C 值不仅与土的类别及其性质有关,而且也随深度而变化。
由于实测的客观条件和分析方法不尽相同等原因,所采用的C 值随深度的分布规律也各有不同。

*川西地区压裂施工过程中管柱摩阻计算摘要:以降阻比法为基础,分别对有机硼交联(HPG)压裂液的前置液、携砂液的沿程管柱摩阻计算方法进行分析,结合川西地区部分井压裂施工现场的施工数据,对管柱摩阻计算公式进行修正改进后,提高了压裂施工设计和数值模拟中摩阻参数计算的准确性;同时用计算机程序实现了施工过程管柱沿程摩阻的计算,可用于模拟压裂施工全过程的摩阻计算。
对四川川西地区以油管方式注入井的水力压裂施工设计及现场施工过程中井底压力的分析具有重要意义。
关键词:压裂施工;降阻比;管柱摩阻;公式;计算前言压裂施工管柱沿程摩阻值的准确性直接影响到压裂工艺的设计过程,是确定井底压力的必要数据,也是压裂施工成功与否的主要因素。
在实际压裂设计中,大多数采用经验估计法对管柱的摩阻损失进行计算,往往不能准确地预测实际摩阻,尤其不能模拟压裂施工整个过程的实际摩阻值。
管柱的摩阻计算单纯的从流变学和水力学的角度去计算,目前还不能被实际应用。
文章以降阻比法为基础,分别就HPG压裂液、相应的携砂液沿程管柱摩阻计算方法进行分析对比,并结合川西地区大部分压裂井的现场施工数据,对压裂液的沿程摩阻有关计算公式进行改进,实现压裂施工全过程摩阻计算的计算机程序化。
实例计算表明,改进后的摩阻计算公式以及压裂施工过程摩阻计算结果与现场实际数据有较高的符合率,可以用于川西地区压裂施工过程摩阻的模拟计算。
1 压裂液摩阻的计算Lord和MC Gowen等人[1,2]利用其他人的实验资料提出了计算溶胶及混砂液摩阻的方法。
采用延迟交联技术,使交联HPG与HPG溶胶在井筒中的摩阻相差不大,因此,Lord等人仍用溶胶的数据提出了一个降阻比(δ)的概念:(1)式中:(△Pf)0为清水的摩阻损失,MPa;(△Pf)P为压裂液的摩阻损失,MPa。
清水的摩阻损失可以用经典水力学雷诺数与摩阻系数关系进行计算,或者同样采用Lord等人提出的回归公式:(2)式中:D为压裂油管柱的内径,mm;Q为施工过程泵注排量,m3/min;H为油管长度,m。

(完整版)管道阻力的基本计算方法管道阻力计算空气在风管内的流动阻力有两种形式:一是由于空气本身的黏滞性以及空气与管壁间的摩擦所产生的阻力称为摩擦阻力;另一是空气流经管道中的管件时(如三通、弯头等),流速的大小和方向发生变化,由此产生的局部涡流所引起的阻力,称为局部阻力。
一、摩擦阻力根据流体力学原理,空气在管道内流动时,单位长度管道的摩擦阻力按下式计算:242v R R s m(5—3) 式中Rm ——单位长度摩擦阻力,Pa /m ;υ——风管内空气的平均流速,m /s ;ρ——空气的密度,kg /m 3;λ——摩擦阻力系数;Rs ——风管的水力半径,m 。
对圆形风管:4D R s(5—4)式中D ——风管直径,m 。
对矩形风管)(2b a ab R s(5—5)式中a ,b ——矩形风管的边长,m 。
因此,圆形风管的单位长度摩擦阻力22v D R m (5—6)摩擦阻力系数λ与空气在风管内的流动状态和风管内壁的粗糙度有关。
计算摩擦阻力系数的公式很多,美国、日本、德国的一些暖通手册和我国通用通风管道计算表中所采用的公式如下:)Re 51.27.3lg(21D K (5—7)式中K ——风管内壁粗糙度,mm ;Re ——雷诺数。
vd Re(5—8) 式中υ——风管内空气流速,m /s ;d ——风管内径,m ;ν——运动黏度,m 2/s 。
在实际应用中,为了避免烦琐的计算,可制成各种形式的计算表或线解图。
图5—2是计算圆形钢板风管的线解图。
它是在气体压力B =101.3kPa 、温度t=20℃、管壁粗糙度K =0.15mm 等条件下得出的。
经核算,按此图查得的Rm 值与《全国通用通风管道计算表》查得的λ/d 值算出的Rm 值基本一致,其误差已可满足工程设计的需要。
只要已知风量、管径、流速、单位摩擦阻力4个参数中的任意两个,即可利用该图求得其余两个参数,计算很方便。


流体摩阻计算公式一、层流时的流体摩阻(粘性摩擦阻力)1. 圆管中层流。
- 对于牛顿流体在圆管中作层流流动时,沿程阻力(摩阻)损失的计算公式为:- h_f=(64)/(Re)(l)/(d)frac{v^2}{2g}- 其中h_f为沿程水头损失(表示摩阻损失的一种形式,单位为长度单位,如米),Re=(vd)/(ν)为雷诺数(无量纲),v为管内流体的平均流速,d为圆管内径,ν为流体的运动粘度,l为管长,g为重力加速度(g = 9.81m/s^2)。
- 从另一个角度看,圆管层流时的切应力τ与半径r的关系为:- τ=(Δ p)/(l)(r)/(2)(Δ p为管段两端的压力差),在管壁处(r =R=(d)/(2)),壁面切应力τ_0=(Δ p)/(l)(d)/(4),而沿程阻力损失h_f=(Δ p)/(ρ g),所以也可以通过压力差来反映摩阻的情况。
2. 平板层流边界层。
- 对于平板层流边界层的摩擦阻力,当平板长度为L,宽度为b,来流速度为U时,平板一侧的摩擦阻力D_f为:- D_f = C_f(1)/(2)ρ U^2S- 其中S = L× b为平板的一侧面积,摩擦系数C_f=(1.328)/(√(Re_L)),Re_L=(UL)/(ν)。
二、湍流时的流体摩阻。
1. 圆管湍流。
- 对于光滑圆管湍流,沿程阻力损失系数λ可由布拉修斯公式计算(当Re<10^5时):- λ=(0.3164)/(Re^0.25)- 则沿程水头损失h_f=λ(l)/(d)frac{v^2}{2g}。
- 对于粗糙圆管湍流,沿程阻力损失系数λ与相对粗糙度(varepsilon)/(d)(varepsilon为管壁的绝对粗糙度)和雷诺数Re有关,可由莫迪图查得,然后同样用h_f=λ(l)/(d)frac{v^2}{2g}计算沿程水头损失(摩阻损失)。
2. 平板湍流边界层。
- 当平板湍流边界层时,摩擦系数C_f的计算公式有多种形式。

大位移钻井技术与分解摘要大位移钻井技术是目前世界上最先进的钻井技术之一,它已成为海上和摊海油田勘探开发最有效的手段。
它能够大范围的控制含油面积和提高油气采收率,降低油田开发成本,具有显著的经济效益和社会效益。
文章介绍了国内外大位移钻井技术的现状,大位移井的关键技术和发展趋势,分析对比了国内大位移钻井技术存在的差距和应努力的方向,对其未来发展前景做了详细的预测与分析,并就其存在的问题也提出了一些解决的办法和意见。
关键词:大位移井钻井技术;井眼剖面;扭矩;摩阻;旋转导向目录第1章大位移井的概况分析 (1)1.1 大位移井的基本概念 (1)1.2 大位移井的特点,难点及用途 (1)1.2.1 大位移井的特点 (1)1.2.2 大位移近水平井的钻井难点 (1)1.2.3 大位移井的用途 (2)第2章大位移井的发展状况 (4)2.1 世界上钻大位移井成熟的配套技术主要表现在 (4)2.2 国内大位移井的发展现状 (4)第3章大位移井的关键技术 (6)3.1 管柱的摩阻和扭矩 (6)3.1.1钻柱扭矩和摩阻力的计算 (6)3.1.2 减小管柱扭矩和摩阻的措施 (8)3.2 钻柱设计 (9)3.3 轨道设计 (11)3.4 井壁稳定 (11)3.4.1 影响大位移井井壁不稳定的因素 (11)3.4.2 井壁稳定性机理 (12)3.5 井眼清洗 (13)3.6 固井完井 (14)3.7 轨迹控制 (15)3.8 装备配套要求 (16)第4章大位移井钻井工具与仪器 (17)4.1 变径稳定器 (17)4.2 旋转导向系统 (17)4.3 加长/串联马达 (18)4.4 地质导向钻井系统 (18)4.5 随钻测量(井)与录井工具(MWD/LWD) (19)4.6 减摩接头 (19)4.7 钻压推加器 (20)4.8 顶部驱动装置 (20)第5章结论 (21)参考文献 (23)致谢 (24)第1章大位移井的概况分析1.1 大位移井的基本概念大位移井是在定向井、水平井技术之后又出现的一种特殊工艺井,英文名称ERW(ExtendedReachwell),大位移钻井技术称ERD (ExtendedReachDrilling),顺名思义,大位移井具有很大的水平位移和很长的高井斜稳斜井段。
3钻柱摩阻计算与分析 (1)3.1 摩阻研究的意义、现状及存在问题 (1)3.1.1 研究目的和意义 (1)3.1.2 研究现状和发展趋势 (2)3.1.3 摩阻分析存在的主要问题 (3)3.2 钻柱动力学基本方程 (5)3.3 钻柱摩阻预测与分析 (11)3.3.1 摩阻分析方法与对象 (11)3.3.2 三维刚杆摩阻模型 (13)3.3.3 三维软杆摩阻模型 (22)3.3.4 摩阻分析结果的表述 (29)3.3.5 摩阻预测与分析 (31)3.3.6 摩擦系数反演 (35)3.3.7 摩阻影响因素分析 (35)3.3.8 计算结果验证与分析 (37)3.4 钻柱的屈曲 (39)3.4.1 斜直井中杆管柱屈曲的微分方程 (39)3.4.2 水平井段钻柱几何线性屈曲的数学模型 (44)3.4.3 水平井段钻柱几何非线性屈曲的数学模型 (45)3.4.4 斜直井段钻柱正弦屈曲和螺旋屈曲的临界载荷 (46)3.4.5 无重钻柱的几何线性螺旋屈曲 (50)3.4.6 无重钻柱的几何非线性螺旋屈曲 (52)3.5 实钻井眼轨道参数的插值计算 (55)3.5.1 概述 (55)3.5.2 典型轨迹模型插值 (55)3.5.3 典型曲线的曲率和挠率 (58)4 钻柱强度分析与校核 (64)4.1 钻柱应力状况分析 (64)4.1.1 轴向拉力产生的拉应力 (64)4.1.2 扭矩产生的剪应力 (64)4.1.3 钻柱弯曲产生的弯曲应力 (65)4.1.4 屈曲产生的应力和接触压力 (65)4.1.5 内压力产生的拉应力 (66)4.2 钻柱强度分析模型 (67)4.2.1 钻柱抗拉强度 (67)4.2.2 钻柱抗弯强度 (68)4.2.3 钻柱抗扭强度 (69)4.2.4 钻柱三轴应力强度 (71)4.3 钻柱强度校核 (72)3钻柱摩阻计算与分析3.1 摩阻研究的意义、现状及存在问题3.1.1 研究目的和意义随着油气田勘探开发的进行,钻井重点向深部、西部和海上发展。
管柱转动惯量公式管柱转动惯量是描述一个物体绕其中一轴线旋转时所具有的惯性量的物理量。
在刚体力学中,转动惯量被定义为质点在相对于旋转轴的距离平方与质点质量的乘积的积分。
对于一个管柱,转动惯量的计算方法取决于管柱的几何形状。
首先考虑一根无质量的直杆,长度为L,质量为m。
直杆绕通过一端的垂直轴线旋转,轴线与杆的质心距离为d。
可以使用平行轴定理计算这个直杆的转动惯量。
平行轴定理告诉我们,如果已经知道了物体关于通过质心的转动惯量Icm,那么我们可以通过使用平行轴定理将其转换为关于其他轴线的转动惯量I。
平行轴定理的公式为:I = Icm + md^2对于一根无质量的直杆来说,其转动惯量相对于通过质心的轴线可由以下公式计算得到:Icm = (1/12)mL^2现在,我们考虑一个实际的管柱,由多个不同形状的部分组成。
我们可以将管柱分割为多个小元件(例如薄片或薄环),然后计算每个小元件的转动惯量并将它们相加,得到整个管柱的转动惯量。
对于一个小薄片或薄环来说,其质量可以用密度乘以其面积来表示,即m=ρA,其中ρ是薄片或薄环的密度,A是薄片或薄环的面积。
令小薄片或薄环的距离轴线的垂直距离为r,那么其转动惯量为:dI = r^2 dm根据薄片或薄环的几何形状,可以得到它们的质心距离轴线的垂直距离r。
通过积分计算,可以将所有的小薄片或薄环的转动惯量相加,得到整个管柱的转动惯量。
以下是针对特定管柱形状的转动惯量公式示例:1.管柱为细长的圆柱体:管柱质量为m,半径为R,长度为L,绕通过其轴线的横截面质心旋转。
转动惯量公式为:I=(1/12)mL^2+(1/4)mR^22.管柱为细长的长方体:管柱质量为m,长方体的边长为a、b和c,绕通过其质心的轴线旋转。
转动惯量公式为:I=(1/12)m(a^2+b^2)+(1/3)m(a^2+c^2)3.管柱为细长的螺旋体(例如螺旋钢筋):管柱质量为m,螺旋体的高度为h,螺旋体半径为R,绕通过其轴线的旋转。
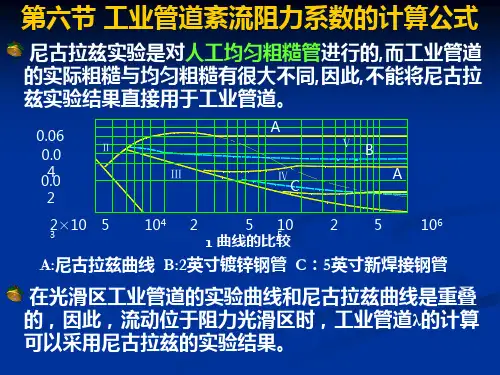
第4章管柱的摩阻扭矩计算
●摩阻扭矩计算概述
●摩阻扭矩计算的软模型
●摩阻扭矩计算的一般步骤
一、摩阻扭矩计算概述
●随着水平井、大位移井等大斜度定向井的出现,摩阻扭矩问题逐渐被人们认识和重视;
●大斜度井的突出特点是水平位移较大,且大部分井段井斜超过60°,这使得在钻进、起下钻和下套管等作业过程中摩阻扭矩问题非常突出;
●摩阻扭矩过大,轻则会增加施工难度,延长钻井作业时间,重则使钻井作业无法进行,导致井眼提前完钻或报废。
1. 摩阻扭矩的主要危害
●钻柱起钻负荷很大,下钻阻力很大;
●滑动钻进时加不上钻压,钻速很低;
●旋转钻进时扭矩很大,导致钻柱强度破坏;
●钻柱与套管摩擦,套管磨损严重,甚至被磨穿;
●套管下入困难,甚至下不到底。
2. 摩阻扭矩计算的主要模型
●现有的摩阻扭矩计算模型主要有三种,软模型、硬模型和有限元模型;
●不管哪种计算模型其核心都是通过合理地假设以便求出管柱与井壁的接触正压力,从而求出摩阻扭矩;
●软模型和硬模型都假设管柱与井眼轴线形状一致,且与井壁连续接触,虽然硬模型考虑了管柱的刚性对摩阻扭矩的影响,但其计算精度有时还不如软模型,因为管柱刚性与“管柱与井眼轴线形状一致”是不符合实际情况的;
●有限元模型假设与实际很接近,精度高,但计算困难。
二、摩阻扭矩计算的软模型
1. 软模型的基本假设
●管柱类似于软绳,其刚性很小,可以忽略;
●管柱与井眼轴线形状完全一致,且与井壁连续接触;
●井壁为近似刚性的;
● 忽略管柱和井眼局部形状如钻杆接头、扶正器、井径扩大等对摩阻扭矩的影响; ● 忽略钻柱动态因素的影响。
2. 软模型的计算思路
● 根据井眼轨迹测斜数据或分点计算数据将管柱分为相应的计算单元(微元);
● 对于每个微元来说,它的单位长度的浮重是已知的,只要知道微元的下端轴向力就可以计算出该微元的接触正压力、摩阻摩扭和上端轴向力;
● 最下面一个微元的下端轴向力就是钻压或为零,这样自下而上逐个微元进行计算就可以计算出整个管柱的摩阻扭矩和大钩载荷。
3. 管柱微元受力分析
● 右图所示,1平面为管柱微元所在的斜平面,2平面为过微元中点切线方向的铅垂面 ● 以微元中点为原点,分别以中点的切线、主法线和副法线方向为三个坐标轴的方向建立微元随动坐标系(e t ,e n ,e b )。
● 将重力向随动坐标系三个坐标轴方向上分解,则有:
()()γϕ
ααγααγααsin sin sin sin 2/sin 2cos cos 2/cos 2cos cos 211
21
2∆=-=+=W
W W W W
W b n t (4-1)
● 根据管柱微元的合力在三个坐标方向上均为零列平衡方程,则有:
()()()()⎪⎩⎪
⎨⎧=++=++=b b
n n t W
N W T T N W F T T 2/sin 2/sin 2/cos 2/cos 2121γγγγ (4-2)
4. 管柱微元正压力计算
()2
2
22
22sin 2b n t b
n W W W T N N N +⎥⎦
⎤⎢⎣⎡++=+=γ (4-3)
5. 摩阻扭矩计算递推公式
对于一段单元管柱来说,已知的力有T2和Wb ,当根据式(4-3)求出管柱与井壁的正压力之后,就可以计算出T1、F 和摩扭矩M 。
由于求得的本段T1正是其上一段单元管柱的T2,这样,就可以从最下面的单元管柱开始,逐段进行求解,将各段的摩阻力F 和摩扭矩M 进行累加,就可计算出全井的摩阻扭矩。
显然,整个计算过程的开始需要知道最下面单元管柱的T2,其大小由不同工况下的边界条件决定。
针对不同的工况,可以从单元管柱的受力分析出发,推导出单元管柱的摩阻扭矩计算公式。
由于利用它可以递推出全井的摩阻扭矩,故也可将其视为管柱摩阻扭矩的递推公式。
(1)起下钻工况
起下钻工况下,管柱在井眼中主要作轴向运动,因此管柱所受的扭矩和摩扭矩均为零,而摩阻的计算公式如下:
⎩⎨
⎧±+=⋅=F
W T T f
N F t 21 (4-4) 式中,f 为综合摩阻系数;F 为单元管柱所受的摩阻力,N ;其他参数同前。
式(4-4)中的±,起钻取“+”,下钻取“-”。
在起下钻工况下,最下面的单元管柱下端轴向力T2=0。
(2)划眼工况
划眼时,管柱有轴向运动和转动,应先将综合摩擦系数作如下分解:
⎪⎪
⎪⎩
⎪
⎪⎪
⎨⎧⋅=⋅=⋅⋅⋅=-θθ
πθsin cos 601f f f f V D n tg c a a
o
(4-5) 式中,θ为过渡参数;Va 为单元管柱轴向运动速度,m/s ;n 为单元管柱转速,r/min ;Do 为管柱外径,m ;fa 为综合摩擦系数在轴向分量;fc 为综合摩擦系数在圆周方向分量。
可以得到划眼工况下的摩阻扭矩计算公式:
⎪
⎪⎩
⎪
⎪⎨⎧
⋅⋅⋅=±+=⋅=o c t a D f N M F W T T f N F 2121 (4-6)
式中:倒划眼取“+”,正划眼取“-”,其它参数同前。
在划眼工况下,最下面的单元管柱下端轴向力T2=0。
(3)旋转钻进工况
在旋转钻进工况下,管柱既有轴向运动,又有转动,因此可以按正划眼工况处理,但由于钻压WOB 的存在,最下面的单元管柱下端轴向力T2=-WOB。
(4)滑动钻进工况
在滑动钻进工况下,管柱只有轴向向下运动,因此可以按下钻工况处理,但由于钻压WOB的存在,同样,最下面的单元管柱下端轴向力T2=-WOB。
三、摩阻扭矩计算的一般步骤
●收集数据,包括:井眼轨迹测斜数据(对于设计轨道来说是其分点计算数据)、管柱组合数据(包括各段长度、外径、内径、接头外径、扶正器外径、每米重量等)、泥浆密度、钻压、转速、套管下深、摩阻系数、井眼直径等;
●将管柱组合划分为若干个微元或单元,对于软模型或硬模型,可以将一个测段划成一个微元,若一个测段内管柱参数不一样,则需要将不同的管柱分成不同的微元;对于有限元模型,需要划分成若干个单元,单元长度不能相差太大。
●采用摩阻扭矩递推计算公式求解或采用有限元法求解。